Identifying Anomalies in SBVR-based Business Rules using Directed
Graphs and SMT-LIBv2
Sayandeep Mitra, Kritika Anand and Pavan Kumar Chittimalli
Tata Research Development and Design Centre, TCS Innovation Labs, Pune, India
Keywords:
Business Rules, Verification, Directed Graph, SMT, Clustering, SBVR, Anomalies.
Abstract:
In modern times, business rules have grown exponentially with enterprises becoming more complex in diverse
fields. Due to this growth, different forms of anomalies creep into the business rules, causing business en-
terprise to take wrong decisions, which can impact it’s performance and reputation. It is time and resource
consuming to examine the rules manually due to the large number of rules intermingled with each other. The
process of manual verification is also not free of human induced errors. Thus, automatic verification of busi-
ness rules is the need of the hour. We present a tool to detect different anomalies in business rules represented
in SBVR format. The tool uses a combination of Directed Graphs and SMT solvers to perform the verification
task. We show the implementation of our tool along with it’s evaluation on industry level benchmarks.
1 INTRODUCTION
Business Rules are operational regulations, decision
rules that are followed by a business organization to
perform their day to day activities. The business rules
are usually embodied in the system artifacts such as
governing policies, guidelines, operating procedures,
legacy source code, etc.
Humans and information systems together are in-
volved in various business operations, with the corre-
sponding business rules distributed across the enter-
prise in different forms (policy documents, operatio-
nal procedures and in the source code of the informa-
tion systems). Varying market conditions and exter-
nal regulatory reasons cause constant changes to the
business structure, policies and strategies. Business
transformation is a process of adjusting business acti-
vities to accommodate the above changes. The aging
business information systems may also require chan-
ges in order to respond to changing business environ-
ment, i.e., competition and growth for superior busi-
ness products and services. Due to the large number
of rules of a business enterprise co-existing together
in such a state of constant flux, various form of ano-
malies such as conflicts, redundancies, duplicates and
circularity may creep in. Thus both IT transformation
and business transformation force the enterprises to
revisit their business rules, pushing forward the need
for automatic verification of business rules.
In recent time, various epresentation of business
rules have been used (IBM, 2017; JBoss, 2017;
OMG, 2013). We have selected SBVR (OMG, 2013)
in our tool due to its base in First Order Logic (FOL)
and similarity to natural language. The SBVR model
has been presented as result of the request for propo-
sal on Business Semantics of Business Rules (BSBR)
made by OMG, which is a part of the business mo-
del layer in the Model Driven Architecture (MDA).
The purpose of SBVR is to describe formally and wit-
hout ambiguities the semantics of a business model
which in turn benefits business analysts and modelers,
as well as business vocabulary & rules administra-
tors and software tool developers. SBVR works as a
bridge between business enterprises and Information
Technology (IT), aiming to provide a way to express
business knowledge to the IT group unambiguously
using natural language. SBVR meta-model is used to
represent business knowledge as:
1. Specifying business vocabularies.
2. Specifying business rules.
Organizations or communities specify the conduct
of business using a cohesive set of interconnected
concepts known as Business vocabulary. These con-
cepts are entities represented through name, term, and
verb while fact is expressed as relation between these
concepts. SBVR Structured English (SSE) is a po-
pular textual representation of SBVR, providing the
option to write business rules in plain English. De-
tailed explanation about SBVR can be found at (OMG,
2013).
Mitra, S., Anand, K. and Chittimalli, P.
Identifying Anomalies in SBVR-based Business Rules using Directed Graphs and SMT-LIBv2.
DOI: 10.5220/0006669802150222
In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 215-222
ISBN: 978-989-758-298-1
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
215

Previously, works like (He et al., 2003; Chavarria-
Baez and Li, 2006; Nazareth and Kennedy, 1991; Ra-
maswamy et al., 1997) focused on verification of kno-
wledge base or rule base verification. The approaches
presented in these works suffered from the problems
of large computational complexity, which if applied
on huge and complex rule systems existing at present
will be extremely inefficient. Presently, some work
has been done aiming at verification of business ru-
les and specifications. Some of these works are (dos
Santos Guimar
˜
aes et al., 2014; Karpovi
ˇ
c et al., 2016;
Reynares et al., 2014; Solomakhin et al., 2013). Ho-
wever most of them fail to present results on complex
and real life business rules, along with their efficiency
on the proposed approaches.
In our background study, we observe that most of
the work has been done aiming to detect all forms of
anomalies (errors) using one particular method. In
our opinion, this causes a spike in the computational
complexity of the approaches and reduces efficiency.
We present our tool using a compliance of two diffe-
rent methods, utilizing them to detect targeted class
of anomalies, aiming at high efficiency and low com-
plexity. Initially, a directed graph based technique is
used to identify various structural anomalies in the
business rule set, followed by modeling the rules in
SMT-LIBv2 (Barrett et al., 2010) and then using a sol-
ver to detect a different set of anomalies. In our tool,
the targeted elimination of errors from the rule set in
each step leads to less complexity and high efficiency
in the complete verification task.
The rest of the paper is arranged as follows. In
Section 2 we present the classification of anomalies
that exist in business rule systems, followed by the de-
tailed explanation of our method in Section 3. Section
4 shows the performance of our tool on industry level
benchmarks and snapshots of our tool. We present va-
rious related works in Section 5, followed by Future
Work and Conclusion in Section 6.
2 CLASSIFICATION OF
ANOMALIES
Various works have been made presenting the taxo-
nomy of the different anomalies that exist in rule-
based systems (Preece and Shinghal, 1994; Nazareth,
1989). Based on these works, we define the anoma-
lies that exist in Business Rules along with examples.
Figure 1 presents a collection of some rules in SBVR
format.
• Conflicting Rules: Business rules conflict with
others, when same premise leads to mutually ex-
r
1
:
It is necessary that if car is luxury car then car has driver.
r
2
:
It is necessary that if car has driver then driver owns license.
r
3
:
It is necessary that if car has driver and car does not has driver then
car is rented car.
r
4
:
It is necessary that if driver owns license then car has driver .
r
5
:
It is necessary that if car has driver then driver does not owns license
and driver follows traffic rules.
r
6
:
It is necessary that if car has driver then driver does not owns li-
cense.
Figure 1: Example of Anomalies in Business Rules.
clusive conclusions. A simple example of con-
flicting rules occur when the conditions in antece-
dents are the same, but the consequents are con-
tradictions of each other. e.g., in Figure 1, Rules
r
2
and r
6
have the same conditions in their ante-
cedent, however the consequents are the opposite
of each other.
• Redundancy: Different form of redundancies ex-
ist in Business Rules, namely Non-executable Ru-
les, Subsuming rules and Logical Equivalence.
Non-executable Rules are the group of rules which
never fire (execute) in a business rule set, gi-
ven any possible conditions. In broad terms, we
can say that non-executable rules are those which
have conflicting conditions in their antecedents,
thus never allowing the consequents to materia-
lize. These conflicting conditions can exist in a
single rule or in form of a chain of rules, the latter
being much more harder to detect. In Figure 1,
Rule r
3
is an example of non-executable rule.
Subsuming Rules exist in two different ways, pai-
rwise and in a chain of rules. The former occurs
when the antecedents of one rule is a proper sub-
set of another while the consequents are exactly
the same and vice versa. The latter occurs due to
different inference paths, involving multiple rules,
from a given antecedent to a final conclusion. We
say that rules R subsumes R
0
, if for some substi-
tution σ, R
0
→ Rσ, where Rσ denotes the instance
of R obtained by carrying out substitution σ in R
(Preece and Shinghal, 1994). For example, in Fi-
gure 1, rules r
5
and r
6
are examples of subsump-
tion, where the consequents of Rule r
6
is a subset
of the consequents of Rule r
5
, thus causing Rule
r
5
to subsume Rule r
6
.
Logical Equivalence is present when two rules ef-
fectively convey the same logical meaning, i.e.,
they logically imply one another. These type of
rules are also called duplicate rules. We say that
rules R and R
0
are duplicates iff (R → R
0
σ) ∧
(R
0
→ Rσ) for some substitution σ.
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
216

3 DETAILED METHODOLOGY
We present a detailed explanation of the approach
used in our tool to perform automatic verification of
business rules. The tool applies two different met-
hods, layered in a systematic way to achieve efficient
verification. Initially, the rules are clustered on the
SBVR facts level, aided by the definitions provided in
the corresponding SBVR vocabulary. Clustering is fol-
lowed by simultaneous transformation of the business
rules provided in natural language to a simplified re-
presentation (stripping off any restrictive quantificati-
ons that are present in the rules) and SMT-LIBv2 re-
presentation. The transformed rules are used for the
verification techniques.
3.1 Clustering
The major concern for business rule verification has
been the huge spike in computation time and cost,
due to the large size of real life business rule sets.
Thus to reduce the number of business rules as in-
put to our tool, we present a method of clustering the
business rules beforehand, based on their relationship
with each other and the SBVR vocabulary definitions.
We intend to put ‘related’ business rules in one clus-
ter, and rules belonging to a particular cluster are ta-
ken as input to the verification approaches. Let there
be n number of business rules, m clusters are formed
and c
i
denote the number of rules in cluster i, i.e.,
∑
m
i=1
c
i
= n. Since c
i
< n, the input size to the tool
is reduced. In real life scenarios, rules of a business
enterprise are function specific, e.g., a bank will have
different rules regarding legal charges and database
change for payment failure. Clustering will ensure
that we verify the two set of rules separately, rather
than together.
As mentioned earlier, SBVR representation con-
sists of a vocabulary, where the noun concepts and
facts are specified. Rules are generated by creating
conditions and relations among the facts. Thus SBVR
provides us with a definition file which simplifies our
goal of clustering. We put rules sharing a common
fact in one cluster. Figure 2 provides us with an ex-
ample of our clustering method. Cluster 1 has two
rules, which are related by the common fact customer
rents car. The third rule is formed using two facts
which are not used in any of the rules of Cluster 1,
resulting in it being in a separate cluster.
3.2 Transformation
SBVR provides the option to apply quantification on
rules, enabling the domain experts to represent busi-
Cluster 1:
It is necessary that if customer rents car then customer has at least
2 credit card.
It is necessary that if customer rents car then customer age is greater
than 18.
Cluster 2:
It is necessary that if customer owns luxury credit card then custo-
mer gets surprise gift.
Figure 2: Example of Clustering SBVR rules.
ness rules as close to the real world as possible. Rule
r
1
in Figure 3 shows an example of SBVR business ru-
les with quantification, where we quantify the number
of credit card that a customer has to own in order to
rent a car. We undertake two different transformati-
ons on the business rules, preserving quantification
and discarding quantification. The latter generates
a set of simplified rules, unifying the quantification
throughout the entire set of rules. We use these newly
generated rules as input to our digraph based verifica-
tion technique. An example of this transformation is
shown in Rule r
1
in Figure 3.
Each simplified rule is represented as a relation bet-
ween its underlying base facts. The simplified rules
are made free from disjunctions by transforming ru-
les with disjunction into a set of rules and made to
involve implications, without loss of generality. e.g.,
a simplified business rule of the form f
1
∨ f
2
→ f
3
is
represented as f
1
→ f
3
and f
2
→ f
3
, where f
1
, f
2
and
f
3
are SBVR facts.
To ensure that our tool captures the anomalies invol-
ving the quantifications present in modern business
rules, we perform another form of transformation.
The SBVR rules are mapped to SMT-LIBv2. The map-
pings are generated based on the SBVR XMI and the
generated SMT-LIBv2 representation incorporates the
quantifications that were present in the original rule.
3.3 Directed Graph Based Verification
The use of graphical techniques for verification of
rules is attractive, since graphs provide an easy to
use framework to represent conceptual dependencies.
Complex relationships between rules can be represen-
ted as paths in the graph, and the verification pro-
blem is reformulated as one of reachability of spe-
cific nodes in the graph. From our study, we observe
that most of the approaches involve building the entire
r
1
:
SBVR Rule: It is necessary that if customer rents car then customer
owns at least 2 credit card.
Simplified Rule: rents(customer , car) → owns(customer , cre-
dit card)
Figure 3: Transformation of SBVR to Simplified Rules.
Identifying Anomalies in SBVR-based Business Rules using Directed Graphs and SMT-LIBv2
217

f
1
f
3
f
7
f
6
f
4
f
5
f
9
r
1
sibling, r
5
r
4
r
5
r
3
r
3
r
2
,r
5
r
1
f
1
: car is luxury car f
6
: ¬ driver owns license
f
3
: car has driver f
7
: car is rented car
f
4
: ¬ car has driver f
9
: driver follows traffic rules
f
5
: driver owns license
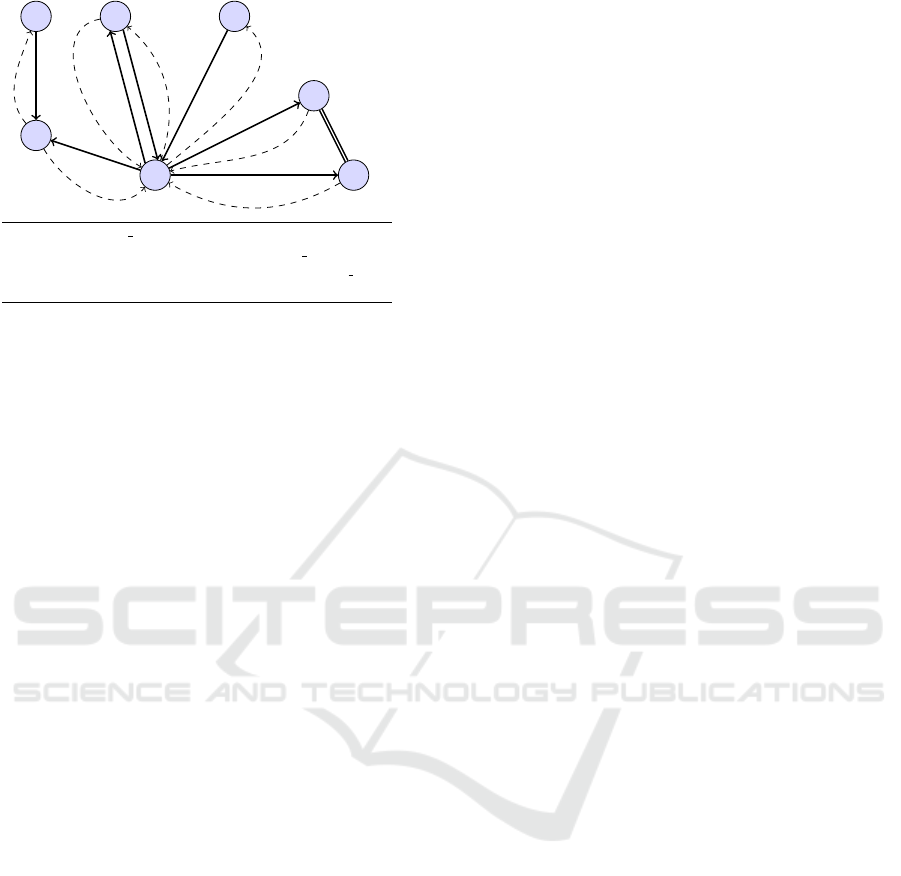
Figure 4: Representation of rules (Figure 2) according to
our proposed graph structure.
graph initially, followed by performing various com-
putations on the corresponding graph representations
(mostly adjacency matrices) to identify errors, which
due to the large size of the graphs becomes extremely
inefficient. We present a different approach, where
we identify errors among the rules while the graph
is built in an incremental manner, i.e., rule by rule,
without undergoing any complex computations on the
complete graph representation at the end.
We represent our set of business rules as a col-
lection of nodes and directed edges, i.e., a directed
graph. Each fact used in the representation of a rule
and it’s negation, is represented as a node in the graph.
We draw directed edges from the facts present in the
antecedent to the facts forming the consequent of the
rule. These edges are called the successor links. Si-
milarly, directed edges are drawn from the facts be-
longing to the consequent to the facts forming the an-
tecedent. We call these edges ancestor links. Both an-
cestor and successor relationships are transitive in our
graph representation. For example, we draw a succes-
sor link from x to y for rule x → y. If y has as succes-
sor two nodes p and q, then a successor link is drawn
from x to both p and q. Thus we ensure that from a
node, any of it’s ancestor or successor can be visited.
We introduce a new form of relationships among the
facts belonging to the consequent of a rule termed as
sibling relationship, to show that they are asserted to-
gether. e.g., in Rule r
5
in Figure 1, if car has driver
then driver does not own license as well as driver fol-
lows traffic rules. Both of the facts in the consequent
are termed siblings. Along with sibling relationship
we further introduce two new relationships ancestor-
sibling and successor-sibling. We say that facts which
share a sibling relationship with any of ancestors of a
fact δ, are ancestor-sibling of δ, while siblings of any
successor of δ are termed as successor-sibling of δ.
To give an example of our graph representation,
let us consider the rules in Figure 1. The set of ru-
les represented according to our proposed graph struc-
ture is shown in Figure 4. Successor relationships are
shown by the solid edges, ancestor relationships by
the dashed edges and the sibling relationship by dou-
ble lines. The rule numbers corresponding to the rela-
tionships are mentioned between the dashed and solid
edges.
Each node in the graph has the following infor-
mation stored: list of ancestors, list of siblings, list
of successors, list of successor-siblings and list of
ancestor-siblings along with the corresponding rule
sequences through which these relations have been
formed. A fact can have the same relationship with
another fact in multiple rules, thus leading to multi-
ple rule sequences being stored corresponding to each
fact in each of the relation list. For a new rule, ed-
ges are established and the new nodes (if any) ex-
change information from their immediate ancestor or
immediate successor node. For example, if there are
two nodes n
1
and n
2
and we encounter a new rule
r
1
:
n
1
→ n
2
, an ancestor edge from n
2
to n
1
is created
and the ancestor list from n
1
is added to n
2
. A succes-
sor edge will be created from n
1
to n
2
with the succes-
sor list of n
2
being added to that of n
1
. This updated
successor list will be propagated to all the ancestors
of n
1
. Thus for each node x ∈ ancestor(n
1
), now
x ∈ ancestor(n
2
) through the union of rule number r
1
and the chain of rules via which x ∈ ancestor(n
1
). Si-
milarly, each x will have n
2
in its successor list. Next
the updated ancestor information from n
2
is passed
onto each of it’s successors. Each x ∈ ancestor(n
2
), is
now an ancestor of every y ∈ successor(n
2
) with rule
r
1
added to the corresponding rule sequence, while y
is added to successor(x). e.g., n
2
has a successor n
0
via rule numbers r
λ
, r
β
. Then the ancestor n
1
of n
2
,
will store n
0
in it’s successor list with corresponding
rule sequence as r
1
, r
λ
, r
β
, while n
0
∈ successor(n
1
)
through rule sequence r
1
, r
λ
, r
β
.
We use this graphical representation to identify
non-executable conditions and circularity among bu-
siness rules. While the graph is being generated in
an incremental fashion, we check for anomaly con-
ditions among the different lists stored in each node.
As explained earlier, non-executable rules are those
where conflicting facts are present in the antecedent
of a business rule, or a sequence of rules, resulting
in the consequent of some rule to be never asserted.
After the addition of a new rule, non-executable con-
ditions can exist in the following combinations.
1. Node n previously has node n
α
as it’s ancestor and
¬n
α
is added to the ancestor list.
2. We add ¬n to the ancestor/ successor list of n or
vice versa.
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
218

3. Node n has n
α
in it’s ancestor list and ¬n
α
is
added as a sibling to some ancestor (ancestor-
sibling) of n, or vice versa.
Circularity condition exists when a node n has the
same node n
γ
in it’s ancestor and successor list,
ancestor-sibling and successor list or ancestor and
successor-sibling list.
If a SBVR fact n
δ
∈ ancestor(n), due to the pre-
sence of multiple rule sequences, i.e.,


RID
a
n
(n
δ
)


> 1,
and n
δ
is a direct ancestor (rule sequence of size 1)
of n at least once, we say that chained subsumption
exists.
When any of the above conditions are detected, it
flags the presence of a possible anomaly. The set
of rules causing the possible anomaly are found out
by combining the rule sequences via which the rela-
tions were established to the conflicting nodes. e.g.,
n
0
∈ ancestor(n) via rule sequences R
φ
, R
ψ
and ¬n
0
∈
ancestor(n) via rule sequence R
ξ
. The possible rule
combinations generating the non-executable conditi-
ons are
D
R
φ
, R
ξ
E
and
D
R
ψ
, R
ξ
E
.
Implementation: The digraph proposed in this work
involves each node storing copious amount of infor-
mation. It is evident that traditional methods of graph
representation, i.e., adjacency matrix and lists will not
suffice. We use a modified version of adjacency lists
for our implementation, with the aim of fast access
to enable rapid information exchange between multi-
ple nodes for a rule. To ensure direct and fast access
to the different lists of each node and quick checks
for anomaly conditions between the lists after each
update, we represent each SBVR fact by an odd num-
ber. The next even number denotes the negation of
the fact. Equation 1 presents a formal representation
of the mapping, where S is a set of SBVR facts and
their negation.
S = { f
1
, ¬ f
1
, f
2
, ¬ f
2
, . . . , f
n
, ¬ f
n
}
O = {1, 2, 3, 4, . . . , 2n − 1, 2n}
We define a function z, such that
z
:
S 7→ O
(1)
Due to this representation the checks for anomaly
condition become very straightforward, e.g., for non-
executable condition while inserting an even number
to a list l we need to check for the presence of the
previous odd number in list l
0
(based on the error con-
dition check) and vice versa. Also, the use of numbers
as node representation makes access to the lists of a
particular node in the graph similar to how an array
position is accessed given the index, i.e., in a direct
manner.
3.4 SMT-LIBv2 based Verification
Modern day business rules along with structural ano-
malies contains anomalies due to quantifications.
Graphical techniques are not sufficient to detect these
form of anomalies, leading to a different verification
approach.
3.4.1 Mapping SBVR XMI to SMTLibv2
From the SBVR vocabulary shown in Figure 1, it can
be seen that the rule r : ‘It is obligatory that if rented
car has driver then driver has license’ is based on SBVR
fact f : ‘car has driver’. The binary fact bf → n
1
v
1
n
2
,
where n
1
(subject) and n
2
(object) are noun concepts
related through verb concept v
1
is mapped as,
(declare-fun v
1
( Thing Thing) Bool)
The concepts n
1
and n
2
are declared as constants
of sort ‘Thing’. SBVR also permits a noun con-
cept n
2
to be derived from another noun concept n
1
.
For instance, noun concept ‘rented car’ is derived
from another noun concept ‘car’. The corresponding
SMT-LIBv2 representation is generated as:
(declare-const rented car Thing)
(declare-fun rented car fun ( Thing ) Bool)
(assert (rented car fun rented car ) )
(assert (forall((x Thing))
(implies(rented car fun x)(car fun x))))
In Figure 1, the execution of rules r
2
and r
6
can
create an ambiguity in business system resulting in
inconsistent state of knowledge base.
An instance of SBVR rule mapping to SMT-LIBv2
for rules r
2
and r
6
is given below:
smt(r
2
:)
(assert (forall((x Thing)(y Thing)(z Thing))
(implies
(and (car fun x)(driver fun y)
(license fun z) ( has x y))
(owns y z))))
smt(r
6
:)
(assert (forall((x Thing)(y Thing)(z Thing))
(implies
(and (car fun x)(driver fun y)
(license fun z) ( has x y))
(not(owns y z)))))
The aim of mapping SBVR rules to SMT-LIBv2 is to be
able to use SMT solvers for verification. This appro-
ach has the following advantages.
1. SMT generalizes Boolean Satisfiabilty (SAT) by
adding equality reasoning, arithmetic, fixed size
bit vectors, arrays, quantifiers and other logics
and useful first order theories (Barrett et al., 2009;
De Moura and Bjørner, 2011). SMT solvers are
efficiently able to handle such theories, thus provi-
ding the support for verification considering quan-
tifications.
Identifying Anomalies in SBVR-based Business Rules using Directed Graphs and SMT-LIBv2
219

2. SMT provides a provision to check satisfiability,
validity and un-satisfiabilty of the formulas repre-
sented in SMT-LIBv2 format which is captured in
our approach to detect conflicting rules.
Mappings have been completed for 50 SBVR con-
structs to the corresponding SMT-LIBv2 which is an
extension of the work performed by (Chittimalli and
Anand, 2016) which includes SBVR vocabulary, rules,
definitions and various other concepts (e.g. synonym,
synonymous form, inverse verb concept, atleast-n ,
atmost-n, exactly-n, universal and existential quanti-
fications).
3.4.2 Conflicting Rules Detection
The presence of conflicting conditions in a set of ru-
les shall cause the latter to be inconsistent. There-
fore it is important to check for conflicting conditi-
ons within individual rules and between different ru-
les. Conflicting rules can exist in one of the following
two scenarios:
1. When a rule is enumerated using AND operator,
i.e., r
1
: ‘It is obligatory that f
1
and f
2
and..... f
3
’
( f
i
’s are fact types) and conjunction of some fact
types contradicts with another fact type in the
rule. Formally, the conflicting condition can be
represented as fol( f
i
) ∧ fol( f
j
).......∧ fol( f
k
) ⇒ ¬
fol( f
m
), where fol( f
i
) is the FOL formula corre-
sponding to f
i
.
2. A rule base R consists of rules = {r
1
, r
2
,....
r
n
} and the conjunction of some rules in R is
contradictory with some other rule/ rules in R,
i.e.,
fol(r
i
) ∧ fol(r
j
).......∧ fol(r
k
) ⇒ ¬ fol(r
m
) where
fol(r
i
) is the FOL formula corresponding to r
i
.
Our tool aims to find the minimal set of rules that
are inconsistent with respect to each other, i.e., the
minimal unsatisfiable cores, aided by the Satisfiable
Modulo Theories (SMT) solvers. We use the defini-
tion of validity and satisfiability that exists in
First Order Logic in our verification approach.
DPLL(T )-BASED SMT SOLVERS checks for
the satisfiability of the SMT formulas (generated from
SBVR rules). The underlying logic is that if formulas
given as input to the solvers are consistent, i.e., the bu-
siness rules have no conflict present among them then
sat will be returned by the solvers else unsat. The
working of the DPLL(T )-BASED SMT SOLVERS
can be visualized as that of a transition system. The
initial state of the transition system is given as {
/
0, F
0
,
/
0}, where F
0
is a given set of clauses to be checked
for satisfiability (i.e., the input formula). When F
0
is unsatisfiable in T the expected final states is fail
or
/
0. Here T is the background theory considered
while mapping from SBVR to SMT-LIBv2, i.e., effecti-
vely the transformations (Katz et al., 2016).
A conflicting set of rules can be found by putting
assert statements in SMT-LIBv2, which compels the
solvers to check the satisfiability until the point of in-
vocation. We add labels to the assertions to identify
the exact rules which caused the unsatisfiability (con-
flict) to occur. The command ‘get-unsat-core’ use
these labels to generate UNSAT core output in a re-
presentation which is easily understandable by logic
experts.
3.4.3 Redundancy : Subsuming and Duplicate
Rules Detetction
We use the generated SMT-LIbv2 formulas to detect
the pair of subsuming rules involving quantifications
in business rule set. A formula F subsumes another
formula F
0
(FF
0
) if for each interpretation I, I |= F
0
implies I |= F (Lukichev, 2010). We use this defi-
nition to devise our verification approach of detecting
subsumption. Let smt(r
i
) be the SMT-LIBv2 represen-
tation of rule r
i
∈ R. As per the definition of subsump-
tion provided in Section 2, in order to check whether a
rule r
0
∈ R is subsumed by another rule r ∈ R, we pro-
pose to assert the negation of the formula obtained
by smt(r) →smt(r
0
).
¬(smt(r) → smt(r
0
))
≡ ¬(¬smt(r) ∨ smt(r
0
)).........[MaterialImplication]
≡ (smt(r) ∧ ¬smt(r
0
)).........[DeMorgan
0
sLaw]
Our assumption is if r subsumes r
0
, then the solver
should find a solution to the formula smt(r) →smt(r
0
).
Since we check for the satisfiability of the negation
of the formula, if the solver returns UNSAT, i.e., no
solution exists where smt(r) is satisfied but smt(r
0
)is
not, it is deduced that r subsumes r
0
. Figure 5 shows
rules which are subsumed due to quantifications.
r
3
: It is permitted that if car rental is insured by at least 2 credit cards
then car rental is luxury car rental.
r
4
: It is permitted that if car rental is insured by exactly 3 credit cards
then car rental is luxury car rental.
Figure 5: SBVR Rules created from EURent vocabulary
that are subsuming.
While checking for the satisfiability of smt(r
3
)
∧ ¬smt(r
4
), the SMT solvers fail to find a value
x ∈ Thing that satisfies smt(r
3
) but does not satisfy
smt(r
4
), resulting in unsat. This happens because
if a constant satisfies the antecedent of rule r
4
then
by default it is going to satisfy the antecedent of r
3
as the formula EqualsTo(credit card.quantity (x), 3)
is subsumed by GreaterThan(credit card.quantity (x),
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
220

Table 1: Performance of our Tool on Business Rules.
Business Rule Set Number of Rules
Anomalies Detected
Conflicting Rules Redundant Rules Circularity
EU-Rent Car Rental 84 14 5 1
Industrial Insurance Application 125 12 6 0
Photo Equipment 35 2 3 0
Loan Contracts 11 2 2 0
2). Satisfiability check on smt(r
4
) ∧ ¬smt(r
3
) gives
SAT while that on smt(r
3
) ∧ ¬smt(r
4
) gives an UNSAT,
depicting that r
3
subsumes r
4
, but the reverse is not
true.
As explained earlier in Section 2, logical equiva-
lence or duplicates are special cases of subsumption.
From the corollary of the approach employed to de-
tect subsumption in rules, we propose that two rules
are duplicates or logical equivalent of one another if
¬ (smt(r) → smt(r
0
)) and ¬ (smt(r
0
) → smt(r)) yields
UNSAT.
4 IMPLEMENTATION AND
EXPERIMENTAL RESULTS
We have developed an intelligent editor to specify bu-
siness rules in SBVR. The editor removes spelling mis-
takes and SBVR syntactical errors like duplicate fact
detection, absence of term from SBVR vocabulary but
used in rules or facts. The business rules specified in
the editor undergo the pre-processing step, where they
are clustered and then transformed to simplified
rules and SMT-LIBv2. We check the satisfiability
of the generated SMT-LIBv2 formulas using z3 sol-
ver (De Moura and Bjørner, 2008), while the graph
based verification algorithm has been implemented in
Java. For both the approaches, we highlight the set
of rules which are the cause of the possible anomaly.
While performing experiments of our tool, we felt
that there was a dearth of universally accepted ben-
chmarks for this verification problem. The work done
by (Mitra and Chittimalli, 2017) also stated about the
same drawback in this research field.
Table 1 shows the distribution of anomalies iden-
tified by our tool. EU-Rent Car Rental, Photo Equip-
ment and Loan Contracts consists of seeded anoma-
lies, where the anomalies were injected in by a bu-
siness expert ignorant of our approaches. The tool
performed exceptionally well identifying all the ano-
Figure 6: Snapshot of our Tool.
malies injected. We executed the Industrial Insurance
Application Case Study twice. Initially the original
version was given as input, i.e., no anomalies were in-
jected from our side. Our tool identified 6 redundan-
cies in the rule set. The business expert could iden-
tify only these 6 anomalies on manual inspection of
the case study. This experiment enabled us to show
that our tool performs efficiently well on real life bu-
siness rules. Later we executed the Case Study with
conflicting conditions injected by our business expert.
Our tool could identify 12 conflicting rules while 15
were injected by the expert. 3 rules were not identi-
fied by our tool because they involved quantifications
via numerical computations (addition, multiplication,
etc.), for which we have not yet generated SMT-LIBv2
mappings. Figure 6 shows a snapshot of our tool in
work.
5 RELATED WORK
Various solutions had been proposed for automatic
rule base knowledge verification, where the rules
were mostly represented in sentential logic form. The
approaches included verification with the aid of petri
nets (He et al., 2003; Chavarria-Baez and Li, 2006),
directed graphs (Nazareth and Kennedy, 1991), di-
rected hypergraph (Ramaswamy et al., 1997), infe-
rence graphs (Nguyen et al., 1987) and hypergraphs
(Valiente, 1993). These approaches presents extreme
computational complexity on present day business ru-
les, along with not detecting anomalies involving data
and quantifications. (Yeh and Chu, 2008) proposed a
DNA-based computing algorithm to detect structural
errors in rule based systems, which had low compu-
tational complexity but failed to deal with anomalies
involving quantifications. Recently the problem of
automatic verification of large and complex business
rules has gained popularity. (Mitra and Chittimalli,
2017) presents a survey showing the present state of
research for this problem. Conversion of SBVR ba-
sed business rules to ontologies and then using rea-
soners to identify anomalies is an approach that has
been presented by (Ceravolo et al., 2007; Karpovi
ˇ
c
et al., 2016; Reynares et al., 2014; Solomakhin et al.,
2013). Most of these works fail to show the efficiency
and completeness of their approach, and results on
Identifying Anomalies in SBVR-based Business Rules using Directed Graphs and SMT-LIBv2
221

real life complex business rules. A different approach
was presented by (dos Santos Guimar
˜
aes et al., 2014),
where the business rules were modeled into Alloy no-
tation and the Alloy tool was used to detect anoma-
lies. This approach suffered from high execution time
and completely failed to detect anomalies existing in
a sequence of rules. (Chittimalli and Anand, 2016)
detected only inconsistencies modeling the rules into
SMT-LIBv2.
6 CONCLUSION AND FUTURE
WORK
In this paper, we present a tool to automatically detect
anomalies present in business rules using a assortment
of different techniques. We successfully detect ano-
malies with quantifications along with the ones not
involving quantification. We better previous graph
based rule verification techniques bypassing the adja-
cency matrix computations of high complexity, while
we present mappings to SMT-LIBv2 enabling use of
solvers. As per our knowledge, our tool is the first
to use a combined approach to tackle the problem of
detecting anomalies in business rules. We show expe-
rimental results on standard benchmarks along with
some industrial data sets. In the future, the aim is
to extend the graph based verification to be able to
detect anomalies involving quantifications along with
optimizing the performance of the logic solvers. We
also intend to test our approaches on more complex
real life business systems.
REFERENCES
Barrett, C. et al. (2010). The smt-lib standard: Version 2.0.
Barrett, C. W., Sebastiani, R., Seshia, S. A., and Tinelli, C.
(2009). Satisfiability modulo theories. Handbook of
satisfiability.
Ceravolo, P. et al. (2007). Modeling semantics of business
rules. In 2007 Inaugural IEEE-IES Digital EcoSys-
tems and Technologies Conference, pages 171–176.
IEEE.
Chavarria-Baez, L. and Li, X. (2006). Structural error veri-
fication in active rule-based systems using petri nets.
In Artificial Intelligence, 2006. MICAI’06. IEEE.
Chittimalli, P. K. and Anand, K. (2016). Domain-
independent method of detecting inconsistencies in
sbvr-based business rules. In Proceedings of the Inter-
national Workshop on Formal Methods for Analysis of
Business Systems.
De Moura, L. and Bjørner, N. (2008). Z3: An efficient
smt solver. In 14th International Conference on Tools
and Algorithms for the Construction and Analysis of
Systems. Springer-Verlag.
De Moura, L. and Bjørner, N. (2011). Satisfiability modulo
theories: introduction and applications. Communica-
tions of the ACM.
dos Santos Guimar
˜
aes, D. et al. (2014). A method for veri-
fying the consistency of business rules using alloy. In
Proceedings of the Twenty-Sixth International Confe-
rence on Software Engineering & Knowledge Engi-
neering.
Group, B. R. (2016). EU-Rent Car Rental case study.
http://www.kdmanalytics.com/sbvr/EU-Rent.html.
He, X. et al. (2003). A new approach to verify rule-based
systems using petri nets. Information and Software
Technology.
IBM (2017). Business action language. https://goo.gl/
Ybqj1m.
JBoss (2017). Drools. https://goo.gl/KivdD2.
Karpovi
ˇ
c, J. et al. (2016). Experimental investigation
of transformations from sbvr business vocabularies
and business rules to owl 2 ontologies. Information
Technology And Control.
Katz, G., Barrett, C., Tinelli, C., Reynolds, A., and Had-
arean, L. (2016). Lazy proofs for dpll (t)-based smt
solvers. In Formal Methods in Computer-Aided De-
sign (FMCAD), 2016. IEEE.
Lukichev, S. (2010). Improving the quality of rule-based
applications using the declarative verification appro-
ach. International Journal of Knowledge Engineering
and Data Mining.
MIT (2015). Alloy: A language and tool for relational mo-
dels. http://alloy.mit.edu/alloy/index.html.
Mitra, S. and Chittimalli, P. K. (2017). A systematic review
of methods for consistency checking in sbvr-based bu-
siness rules.
Nazareth, D. (1989). Issues in the verification of knowledge
in rule-based systems. Int. J. Man-Mach. Stud.
Nazareth, D. L. and Kennedy, M. H. (1991). Verification of
rule-based knowledge using directed graphs. Know-
ledge Acquisition.
Nguyen, T. A. et al. (1987). Verifying consistency of pro-
duction systems. In Proceedings of the Third Con-
ference on Artificial Intelligence Applications, pages
4–8.
OMG (2013). Semantics of business vocabulary and rules
1.2. http://www.omg.org/spec/SBVR/1.2/.
Preece, A. D. and Shinghal, R. (1994). Foundation and ap-
plication of knowledge base verification. Internatio-
nal Journal of Intelligent Systems.
Ramaswamy, M. et al. (1997). Using directed hypergraphs
to verify rule-based expert systems. IEEE Trans. on
Knowl. and Data Eng.
Reynares, E. et al. (2014). Sbvr to owl 2 mappings: an au-
tomatable and structural-rooted approach. CLEI Elec-
tronic Journal.
Sirin, E. et al. (2007). Pellet: A practical owl-dl reasoner.
Web Semantics: science, services and agents on the
World Wide Web.
Solomakhin, D. et al. (2013). Logic-based reasoning sup-
port for sbvr. Fundamenta Informaticae.
Valiente, G. (1993). Verification of knowledge base redun-
dancy and subsumption using graph transformations.
International Journal of Expert Systems, 6:341–355.
Yeh, C.-W. and Chu, C.-P. (2008). Molecular verification of
rule-based systems based on dna computation. IEEE
Transactions on Knowledge and Data Engineering.
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
222