
Experience Filtering for Robot Navigation using Deep Reinforcement
Learning
Phong Nguyen
1
, Takayuki Akiyama
1
and Hiroki Ohashi
2
1
R&D Group, Hitachi Ltd., 1-280, Higashi-Koigakubo, Kokubunji-shi, Tokyo, Japan
2
European R&D Group, Hitachi Europe GmbH, Kaiserslautern, Germany
Keywords:
Reinforcement Learning, Experience Replay, Similarity, Distance, Experience Filtering.
Abstract:
We propose a stochastic method of storing a new experience into replay memory to increase the performance
of the Deep Q-learning (DQL) algorithm, especially under the condition of a small memory. The conventional
standard DQL method with the Prioritized Experience Replay method attempts to use experiences in the replay
memory for improving learning efficiency; however, it does not guarantee the diversity of experience in the
replay memory. Our method calculates the similarity of a new experience with other existing experiences in
the memory based on a distance function and determines whether to store this new experience stochastically.
This method leads to the improvement in experience diversity in the replay memory and better utilization of
rare experiences during the training process. In an experiment to train a moving robot, our proposed method
improved the performance of the standard DQL algorithm with a memory buffer of less than 10,000 stored
experiences.
1 INTRODUCTION
A reinforcement learning algorithm is considered a
prominent solution for robot navigation. A state-of-
the-art reinforcement learning algorithm is the stan-
dard Deep Q-learning (DQL) algorithm recently pro-
posed by Mnih (Mnih et al., 2015). It uses an artifi-
cial neural network to map state spaces to Q-values
of actions, which will be used by an agent to select
the best action in a given state. This algorithm sto-
res all the experiences of the agent in a replay me-
mory and the artificial neural network learns by sam-
pling the stored experiences. For the agent to per-
form well after training, positive experiences (exam-
ples of success) and negative experiences (examples
of failures) are theoretically essential to acquire and
store in the replay memory. The balance of the re-
play memory determines the efficiency of the training
process. When positive or negative experiences are
difficult to acquire, the replay memory becomes im-
balanced. An artificial neural network may not learn
well under such conditions because the experiences
are sampled randomly for learning. Shaul presented
the Prioritized Experience Replay (PER) method to
prioritize the sampling process to obtain experiences
with high temporal difference error (TD-error) and
improve the training process (Schaul et al., 2015).
However, this method does not improve the balance
of the replay memory. In a scenario in which some ex-
periences are extremely difficult to acquire and the re-
play memory is relatively small, such experiences are
quickly removed due to the first-in-first-out (FIFO)
mechanism. Such rare experiences should be retained
in the replay memory long enough for the artificial
neural network to reduce the TD-error and learn well.
Therefore, the diversity of the replay memory plays
an important role in the efficiency of the training pro-
cess.
In the Internet-of-Things (IoT) era, the DQL algo-
rithm is expected to be applied to embedded devices,
which usually have small memories. In our research,
we aimed at applying the DQL algorithm under such
a limited condition. Therefore, in this paper, we pro-
pose a stochastic method of storing a new experience
into the replay memory to improve the performance
of the DQL algorithm. Our method calculates the si-
milarity of a new experience with other existing ex-
periences in the memory based on a distance function
and determines whether to store this new experience
stochastically.
We achieved higher learning efficiency by obser-
ving the average reward of the agent after the training
process is completed. In an experiment to teach a ro-
bot to move (by avoiding obstacles and approach hu-
Nguyen, P., Akiyama, T. and Ohashi, H.
Experience Filtering for Robot Navigation using Deep Reinforcement Learning.
DOI: 10.5220/0006671802430249
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 2, pages 243-249
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
243

mans for interaction) using the DQL algorithm, our
proposed method improved the performance of the
DQL algorithm with a memory buffer of less than
10,000 stored experiences by almost 20% in the ro-
bot’s average reward.
2 RELATED WORK
To make a robot move without it hitting obstacles and
approach a certain goal, a path-planning algorithm
and rule based algorithm have been investigated (Fa-
himi, 2008) (LaValle, 2006). While the path-planning
algorithm is negatively affected by a dynamic and
constantly changing environment because it always
requires re-planning when the environment changes,
a rule-based algorithm usually cannot cover all situa-
tions. Moreover, these algorithms are not adaptable to
different types of environments. With rein-forcement
learning, however, a robot can learn how to execute
better actions through trial-and-error processes wit-
hout any prior history or knowledge (Kaelbling et al.,
1996) (Sutton and Barto, 1998). Thus, rule definiti-
ons and map information are not needed in advance
to train a moving model.
Reinforcement learning has recently received a lot
of attention in many research fields (Mirowski et al.,
2016) (Sadeghi and Levine, 2016) (Jaderberg et al.,
2016) (Wang et al., 2016). Mnih et al. (Mnih et al.,
2015) (Mnih et al., 2013) reported a method of com-
bining an artificial neural network with a Q-learning
algorithm to estimate the action value. The method
was tested on teaching a machine to play Atari games
from the input of raw image data. In games like Mon-
tezumas Revenge, the machine failed to learn from
the replay memory because the small number of po-
sitive experiences was subservient. In another paper,
Shaul et. al attempted to utilize useful experiences
by using a prioritized sampling method (Schaul et al.,
2015). Using TD-error as the metric to prioritize the
experience sampling process, this method can learn
more efficiently from the rare experiences in the re-
play memory. However, this method cannot lead to a
diversity of experiences in the memory, and rare and
useful experiences can be pushed out of the memory
quickly when the memory is small.
To ensure the replay memory is well diversified
and rare and useful experiences in the memory can be
kept longer, our proposed method uses a filtering me-
chanism in the experience storing process. The filte-
ring mechanism works to filter out the new experien-
ces that are similar to many existing experiences in the
memory and only store the new experiences that are
different from other existing experiences. Even with
the limited size of replay memory, the neural network
can learn more effectively from a diversified and ba-
lanced replay memory. Our proposed method is com-
patible with the conventional PER method, and we
can combine them to achieve a superior performance
in term of achieving higher reward after the training
process is completed.
Other research on robotic systems that traverse
indoor environments using deep reinforcement lear-
ning for collision avoidance focuses on transfering
knowledge from simulation world to real world like in
(Sadeghi and Levine, 2016) , or using recurrent neu-
ral network to encode the history of experience like
in (Jaderberg et al., 2016). None of the above mentio-
ned research has tackled the problem of limited replay
memory size.
3 STANDARD DQL METHOD
AND PER METHOD
Deep reinforcement learning represents the Q-
function with a neural network, which takes a state
as input and outputs the corresponding Q-values of
actions in that state. Q-values can be any real values,
which makes it a regression task that can be optimized
with a simple squared error loss (Mnih et al., 2015):
L =
1
2
[r + γ · max
a
0
Q(s
0
, a
0
)
| {z }
target
− Q(s, a)
| {z }
prediction
]
2
(1)
An experience of a DQL agent is a tuple of ¡state,
action, reward, next state¿, hereby known as <
s, a, r, s
0
>. The DQL agent at state s, takes the action
a, and move on to the next state s’, in which it receives
a reward r. In each iteration, a transition experience
< s, a, r, s
0
> is stored in a replay memory. To train
the artificial neural network, uniformed random sam-
ples from the replay memory are used instead of the
most recent transition. This breaks the similarity of
subsequent training samples, which otherwise might
drive the network into a local minimum. PER met-
hod modifies the standard DQL method from random
sampling to prioritized sampling (Schaul et al., 2015).
Experiences with high TD-error (the artificial neural
network does not estimate the Q-values accurately),
are most likely get sampled. There are two variations
with PER method: proportional PER and rank-based
PER. In proportional PER method, an experience has
the probability of getting sampled proportional with
its TD-error. On the other hand, in rank-based PER
method, an experience has the probability of getting
sampled negatively proportional with its TD-errors
rank in the replay memory.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
244

4 PROPOSED METHOD
In our method, instead of storing all the experiences in
the replay memory, each new experience is evaluated
on whether it should be stored or dropped out. We
present three filtering mechanisms for our method to
filter new experiences.
4.1 Greedy Experience Filtering (EF)
When a new experience is observed, we compute
the distances of the new experience with other ex-
periences in the memory. The distance between
two experiences E1 < s1, a1, r1, s1
0
> and E2 <
s2, a2, r2, s2
0
> is defined as follows:
• Distance between s
1
and s
2
(Bernstein et al.,
2001):
d(s
1
, s
2
) = Euclidean Distance (s
1
, s
2
)
normalized in range [0, 1] (2)
• Distance between a
1
and a
2
:
d(a
1
, a
2
) =
0 if a
1
= a
2
1 if a
1
6= a
2
(3)
• Distance between r
1
and r
2
:
d(r
1
, r
2
) =
0 if r
1
= r
2
1 if r
1
6= r
2
(4)
• Distance between s
0
1
and s
0
2
(Bernstein et al.,
2001):
d(s
0
1
, s
0
2
) = Euclidean Distance (s
0
1
, s
0
2
)
normalized in range [0, 1] (5)
• Distance d of E1 < s1, a1, r1, s1
0
> and E2 <
s2, a2, r2, s2
0
>:
d(E
1
, E
2
) = min
1,
1
2
d(s
1
, s
2
)
+
1
2
d(s
0
1
, s
0
2
)
+ d(a
1
, a
2
)
+ d(r
1
, r
2
)
(6)
After computing all the distances of the new expe-
rience with other experiences in the replay memory,
we make a stochastic decision to store the new expe-
rience in the replay memory with the following pro-
bability:
P(E
new
) = D(E
new
, E
memory
) =
1
N
N
∑
i=1
d(E
new
, E
i
)
(7)
Figure 1: Probability of storing new experience.
where N is the number of experiences in the replay
memory at the point before storing a new experience.
In formula (6), the distance between two experiences
are capped maximum at 1 because later in formula (7)
we will use the average distances to assign the proba-
bilities of storing the new experience. Capping the the
distance at 1 leads a more stable performance. The
way we design the distance d between 2 experiences
also ensures that when the agent is at a same state,
but takes different action or gains different rewards,
the algorithm would consider these 2 experiences very
different from each other.
Distance D shows how different a new experience
is to the existing memory. If D is high, the replay
memory is more likely to store the new experience.
However, if D is low, it is not likely to store it. Fig. 1
illustrates the process of computing the probability to
store a new experience. In this figure, similar expe-
riences (experiences with small D) are represented in
a similar color (e.g. blue), while rare experiences (ex-
periences with large D) are represented in different
colors (e.g. red, green, orange). When the replay me-
mory buffer is filled and it is decided that the new ex-
perience is stored, we need to drop an old experience
in the replay memory to make space for the new ex-
perience. To do so, we compute the sum of the dis-
tances between an experience and other experiences
in the replay memory and choose the experience with
the lowest distance sum:
ExperienceIDto drop = argmax
i
N
∑
j=1
d(E
i
, E
j
)
!
(8)
By dropping the experience with the lowest dis-
tance sum, we maximize D among experiences. The-
refore, the experiences in the memory are well diver-
sified, and the rare and useful experiences will be kept
inside the memory.
Experience Filtering for Robot Navigation using Deep Reinforcement Learning
245

4.2 FIFO EF
The difference of FIFO EF and Greedy EF is when
we have to drop an old experience to add a new expe-
rience. Instead of choosing the lowest distance sum
of an experience with other experiences, we simply
drop the oldest experience in the replay memory. The
reason to do this is to avoid over-fitting in training the
neural network to a certain set of experiences without
having more updated experience. When only drop-
ping the experience with the lowest distance sum in
the memory, some experiences in the memory are ne-
ver dropped. The neural network can only learn well
with these old experiences; hence, it cannot genera-
lize to other situations. By implementing FIFO EF,
we still achieve our purpose of trying to achieve a bet-
ter balance of experiences in the replay memory by a
filtering process, while providing the neural network
with new data along the training process and having
the neural network generalize better.
4.3 Combination of FIFO EF and PER
Our proposed method can work compatibly with the
conventional PER method. In each training iteration,
we use FIFO EF method to decide whether to store a
new experience into the memory or not, and then pro-
ceed with sampling method presented in Shaul et. al.’s
paper. Our method ensures the diversity of replay me-
mory, which would be impossible to achieve if storing
whatever experiences the agent observes. Prioritized
experience sampling method in a diversed replay me-
mory makes more sense than in a monotonous replay
memory.
In addition, our method can retain the rare expe-
rience inside the replay memory, in comparsion to the
conventional way of storing experience because each
new experience is stored based on a probability, which
makes the rate of storing expriences is slower than
Figure 2: Simulated environment.
storing all experiences. For that reason, prioritizing
experience with high TD-error can resample rare ex-
periences more frequently and improve the learning
efficiency.
5 EXPERIMENTAL SETUP
The simulation environment we used contains a la-
yout of walls (called a map). Moving objects inclu-
ding a robot and human (in the role of a customer)
who can only move within the boundary of the map.
The robot has distance sensors that sense the distance
to objects in front of it. There are five distance sen-
sors, which sense five angles equally divided in front
of the robot. The maximum distance a distance sensor
can sense is 4 m. With a human detection sensor (e.g.
like a camera), the robot can detect the targeted cus-
tomer, the distance between it and the customer, and
the angle of the customer in relation to it.
We designed a reward system so that the robot can
receive a positive reward +1 when it is successfully
approaches and faces the customer and the distance
between it and the customer is less than 1 m. Howe-
ver, it receives a negative reward of -1 when it hits the
walls. It will then be reset to a random position on the
map.
The deep neural networks we used for action se-
lection and training are fully connected networks,
which contain an input layer, two hidden layers, and
an output layer. The input layer contains:
• five distance values from the distance sensor of
the robot,
• current information about the robot: current
speed, and current angular speed,
• the estimated distance to the customer,
• the angle α to the customer, which is represented
by two values: sinα and cos α, and
• the relative speed of the robot toward the custo-
mer.
And all these input values are normalized to a suit-
able range: the distance values, the current speed of
robot, the distance to the customer have a range from
0 to 1, and the current angular speed of the robot, the
relative speed of the robot toward the customer have
the range from -1 to 1. Each hidden layer contains
256 nodes. The output layer contains 9 nodes corre-
sponding to Q-values of 9 actions for the robot. Each
action is a combination of the robot making two deci-
sions about whether to change its speed and angular
velocity (decrease the speed, maintain speed, incre-
ase the speed, increase the angular velocity to the left,
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
246
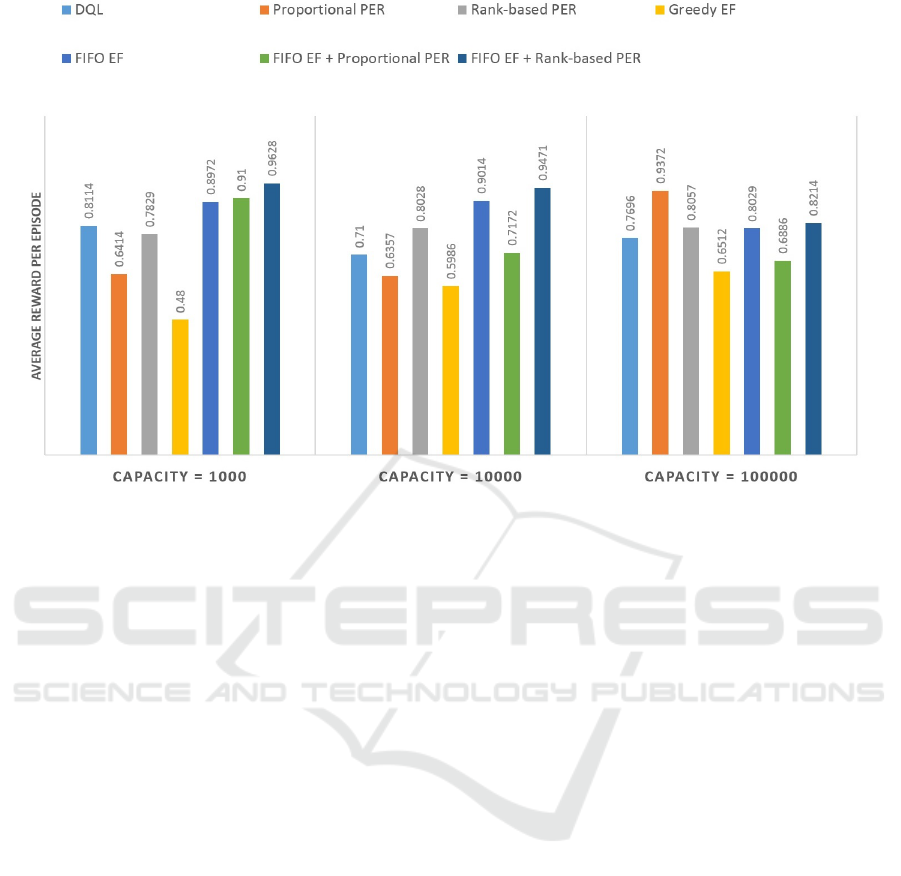
Figure 3: Average reward per episode after training.
keep the same angular velocity, and increase the angu-
lar velocity to the right). In other words, nine actions
of the robot are a product of three actions in changing
speed and three actions in changing angular velocity.
We trained the robot for 10
6
iterations with a re-
play memory capacity of 10
3
, 10
4
, and 10
5
. We used
a tunnel-like map with a customer moving inside (the
customer moved randomly). Fig. 2 illustrates the si-
mulated training environment. The red circle repre-
sents the robot. Five short green lines and small cir-
cles on them represent the distance sensors and their
sensing values. The picture of a face represents a hu-
man customer. The long green line represents the dis-
tance between the robot and the customer. In the eva-
luation process (after the training process is comple-
ted), we let the robot start at a random position on
the map, at a fixed given time, and observed whether
it could avoid obstacles and approach the customer
successfully. An episode of evaluation starts when the
robot starts and ends when either the robot meets the
customers, hits the walls, runs out of time (we defined
as in 200 iterations). We compared the performance
of the robot by using a conventional standard DQL
method (Mnih et al., 2015), PER method (both pro-
portional and rank-based) alone (Schaul et al., 2015),
our proposed method with FIFO EF, that with greedy
EF, that with FIFO EF and proportional PER, and that
with FIFO EF and rank-based PER.
6 RESULTS
The performance of the robot was evaluated based on
the rate it could approach the customer successfully
without hitting obstacles. The rate the robot hit the
obstacles is also a reference of its performance. We
observed the robot in 1000 episodes and calculated
the average reward for each episode. Fig. 3 shows the
results of a testing phase with the different methods in
different memory size settings. Our proposed method
with FIFO EF and that with FIFO EF and rank-based
and proportional PER outperformed the DQL method
and the PER methods alone when the memory size
was 10
3
, 10
4
. When the replay memory capacity re-
ached 10
5
, our proposed methods with FIFO EF and
that with FIFO EF and rank-based and proportional
PER still performed better than the DQL method and
about the same with the PER methods alone. Ho-
wever, our proposed method with greedy EF did not
achieve the expected performance and had the lowest
performance.
When the capacity size was 10
3
, the average re-
ward per episode the robot could receive with our pro-
posed method, except with greedy EF, were higher
than those with the DQL method. Fig. 4 shows the
improvement (or deterioration) of our proposed met-
hod compared with that of the DQL method. With
our method with FIFO EF and rankbased PER , we
could increase performance by 18.66% after training.
Experience Filtering for Robot Navigation using Deep Reinforcement Learning
247
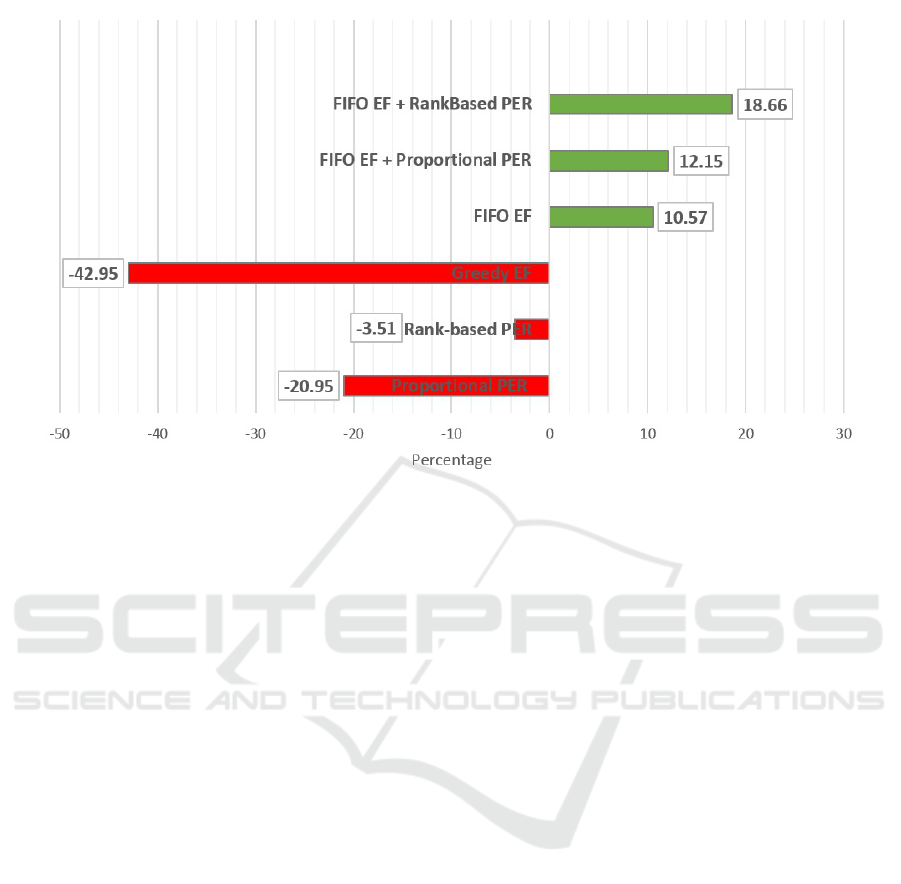
Figure 4: Robot’s performance compared with standard DQL method (capacity = 10
3
).
In other words, the robot could receive 18.66% more
rewards per episode. This implies it successfully ap-
proached the customer more often and hit less obsta-
cles after training by using our proposed method.
We break down the robot’s performance of recei-
ving rewards into successfully approaching the custo-
mer and hitting obstacles. The rate of finding and ap-
proaching a customer after training was 97.57% while
that of only hitting obstacles was 1.1%, as shown in
Fig. 5. The top left of the chart is the desired region
for ideal performance after training: approached cus-
tomer 100% and hit walls 0%.
Our results have demonstrated that with a smaller
memory size (10
3
experience instances compared to
10
6
experience instances), our proposed method can
give the DQL algorithm a good performance on two
learning tasks: avoiding obstacles and approaching
a goal (in this case, a customer), while conventional
methods cannot perform well.
7 DISCUSSION
In this chapter, we discuss the strength and weakness
of our method based on the results. The strength of
our method is providing more diversity in experien-
ces; hence, breaking the dominance of similar expe-
riences in the memory, which causes neural networks
to be unable to learn efficiently. With our method
with FIFO EF alone, the performance of the robot
after training was better than with the DQL method
and with the PER methods. In addition, our met-
hod did not affect the uniformed random sampling
process of the experience replay mechanism, and the
implementation was simpler compared that with the
PER methods, with which we have to create a spe-
cial heap structure to store experiences in the replay
memory. Our method performed better than the DQL
method especially when the replay memory was re-
latively small. With a smaller memory, it is difficult
for the replay memory to maintain important expe-
riences, and they also are forgotten quicker than with
a larger replay memory. With our experience filtering
mechanism, not only important experiences are kept
longer, but also diversity of replay memory is also im-
proved. These factors make the deep neural network
learn more efficiently.The weakness of our method is
with greedy EF. Instead of letting the agent forget the
oldest memory, we let the agent forget the memory
with highest similarity in the existing replay memory.
This creates a bias when a neural network learns and
causes overfitting on a set of fixed experiences. The
FIFO EF does not have this problem; thus, it outper-
forms greedy EF.
8 CONCLUSION
We proposed a method of filtering and deciding whet-
her to store a new experience in the replay memory to
make the DQL algorithm work more effectively. Our
method calculates the similarity (or distance) between
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
248
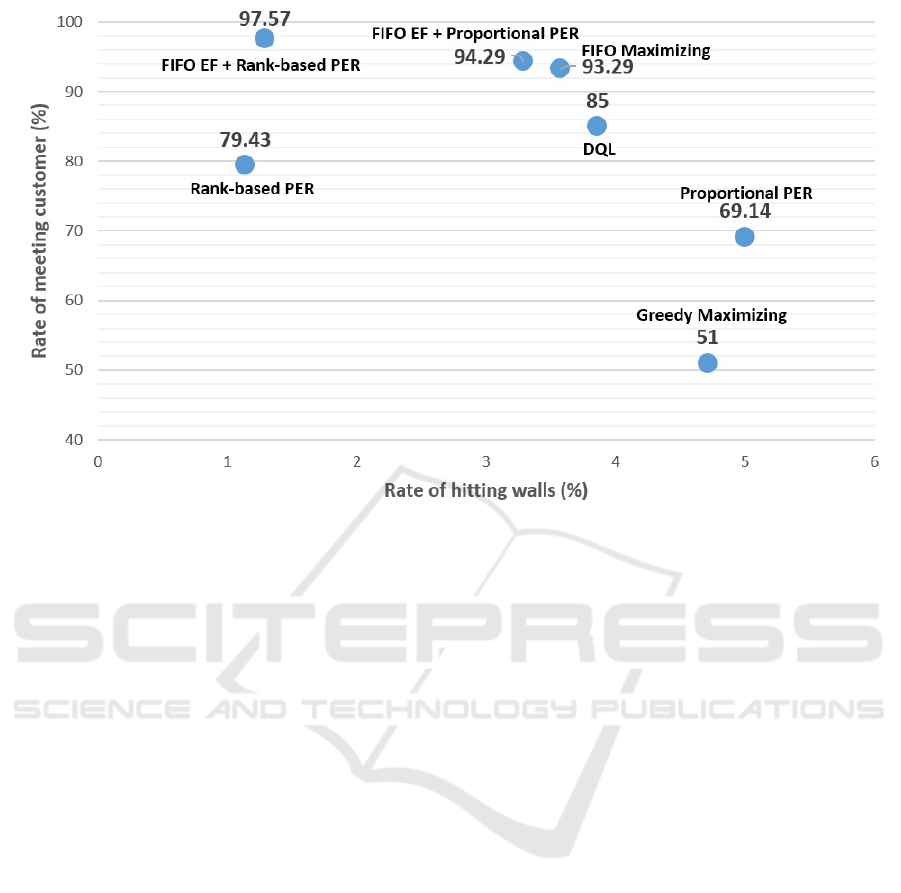
Figure 5: Robot’s performance (capacity = 10
3
).
a new experience and the rest of the existing experien-
ces in the memory and converts the similarity (or dis-
tance) to a probability of storing this new experience.
The higher the similarity (or the lower the distance),
the lower the probability to store this new experience.
This method demonstrated superior performance
to conventional methods when the replay memory has
a limited size. Our method is compatible with the
DQL and PER methods and further improves the per-
formance of the DQL algorithm. In our experiment
of training a robot to move in a virtual environment,
the average reward it could receive was 18.66% hig-
her than with the DQL method. We intend to apply
our method to embedded devices and robots that have
low-memory resources.
REFERENCES
Bernstein, S., Poznanski, R. R., Solomon, P., Wilson, S.,
Swift, R. J., and Salimi, B. (2001). Issn 0312-3685
subscription rates subscription rates (post free) for
the 2001 volume of the mathematical scientist are:£
11.00, us 18.15or a28. 60 all enquiries about the mat-
hematical scientist, as well as other subscriptions,
should be sent to the. The Mathematical Scientist,
26(2):136.
Fahimi, F. (2008). Autonomous robots: modeling, path
planning, and control, volume 107. Springer Science
& Business Media.
Jaderberg, M., Mnih, V., Czarnecki, W. M., Schaul, T.,
Leibo, J. Z., Silver, D., and Kavukcuoglu, K. (2016).
Reinforcement learning with unsupervised auxiliary
tasks. arXiv preprint arXiv:1611.05397.
Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996).
Reinforcement learning: A survey. Journal of artifi-
cial intelligence research, 4:237–285.
LaValle, S. M. (2006). Planning algorithms. Cambridge
university press.
Mirowski, P., Pascanu, R., Viola, F., Soyer, H., Ballard, A.,
Banino, A., Denil, M., Goroshin, R., Sifre, L., Kavuk-
cuoglu, K., et al. (2016). Learning to navigate in com-
plex environments. arXiv preprint arXiv:1611.03673.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Anto-
noglou, I., Wierstra, D., and Riedmiller, M. (2013).
Playing atari with deep reinforcement learning. arXiv
preprint arXiv:1312.5602.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Ve-
ness, J., Bellemare, M. G., Graves, A., Riedmiller,
M., Fidjeland, A. K., Ostrovski, G., et al. (2015).
Human-level control through deep reinforcement le-
arning. Nature, 518(7540):529–533.
Sadeghi, F. and Levine, S. (2016). (cad2rl: Real single-
image flight without a single real image. arXiv pre-
print arXiv:1611.04201.
Schaul, T., Quan, J., Antonoglou, I., and Silver, D.
(2015). Prioritized experience replay. arXiv preprint
arXiv:1511.05952.
Sutton, R. S. and Barto, A. G. (1998). Reinforcement le-
arning: An introduction, volume 1. MIT press Cam-
bridge.
Wang, Z., Bapst, V., Heess, N., Mnih, V., Munos, R., Ka-
vukcuoglu, K., and de Freitas, N. (2016). Sample ef-
ficient actor-critic with experience replay. arXiv pre-
print arXiv:1611.01224.
Experience Filtering for Robot Navigation using Deep Reinforcement Learning
249
