SLA Non-compliance Detection and Prevention in Batch Jobs

Alok Patel, Abhinay Puvvala and Veerendra K. Rai

Tata Research Development and Design Centre, Tata Consultancy Services,

54B, Hadapsar Industrial Estate, Pune- 411013, India

Keywords: Batch Job Systems, Levers, SLA Compliance, Optimization, Constraints.

Abstract: This paper reports the study done on SLA non-compliance detection and prevention in batch job systems. It

sets out the task of determining optimal and the smallest set of levers to minimize SLA non-compliance at

minimum impact business requirements. The methodology to address the problem consists of a four-step

process that includes inputs, pre-processing, modelling & solving and post processing. This paper uses Integer

Linear Programming (ILP) to achieve global optima given a set of varied constraints such as sacrosanct con-

straints, auxiliary constraints, reach time constraints and SLA non-compliant identifier constraints. Method-

ology has been tested on two sets of data- synthetic data of small size to corroborate the correctness of ap-

proach and a real batch job system data of a financial institution to test the rigor of the approach.

1 INTRODUCTION

Batch jobs have become ubiquitous in enterprise IT

of today’s organizations. Batch jobs are so called due

to a particular mode of processing- execution of jobs

in a sequence i.e. batch. The IT infrastructure under-

lying business processes of modern day organizations

are tuned to perform high volume, repetitive

tasks/jobs that require little or no human intervention.

Most of these tasks/jobs need not be handled in real

time. Data integration, compliance checks, analytics,

reporting, billing and image processing jobs are some

examples of Batch applications.

Typically, a batch system is characterized by jobs

and interdependence among jobs. Business processes

(streams) are broken down into series of steps re-

ferred to as jobs. Each job can only start after its pre-

decessors have completed their execution. Business

requirements define these precedence relations

among jobs. In addition, business requirements entail

various other constraints such as ‘start time’, critical-

ity, batch completion time etc. These constraints are

described in greater detail in subsequent sections.

A vital aspect of batch systems is the Service

Level Agreements (SLAs). SLAs are defined by

measuring the ‘start time’ and ‘end time’ of business

critical jobs and processes. In a typical investment

bank setting, for instance, bulk of batch applications

are scheduled to run after trading hours and are ex-

pected to finish before the start of next day’s trading.

To fulfil this business requirement, SLAs are defined

for each batch process separately. However, spikes in

workload, inadequately provisioned computational

resources along with many other reasons often lead to

SLA violations. The onus is on the system adminis-

trators to handle such scenarios and ensure that SLA

violations are minimized. To do so, it is essential to

not only predict potential SLA violations, but also to

identify the right set of levers that can be used to min-

imize SLA non-compliance.

SLAs are critical to businesses. Firms view SLAs

as instruments to establish measurable targets of per-

formance with the objective of achieving required

levels of service. SLAs for enterprise IT translate the

expectations from the business perspective to quanti-

fiable performance targets for various IT systems.

Thus enabling them to monitor and steer the engage-

ments from a distance. An important aspect of SLAs

is the associated financial penalties with adverse out-

comes. A customer having signed such an agreement

with a service provider may claim compensation in

case of non-compliance. Non-compliance, in the con-

text of batch systems may include reduced through-

put, longer wait times, poor Quality of Service (QoS),

deadline misses, etc.

In a complex system there could be multiple ob-

jectives such as efficiency, cost, compliance etc. In a

systemic setting these objectives are often intertwined

and there is a trade-off in meeting them. Set of levers

available to meet these objectives also overlap and

Patel, A., Puvvala, A. and Rai, V.

SLA Non-compliance Detection and Prevention in Batch Jobs.

DOI: 10.5220/0006673903970406

In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 397-406

ISBN: 978-989-758-298-1

397

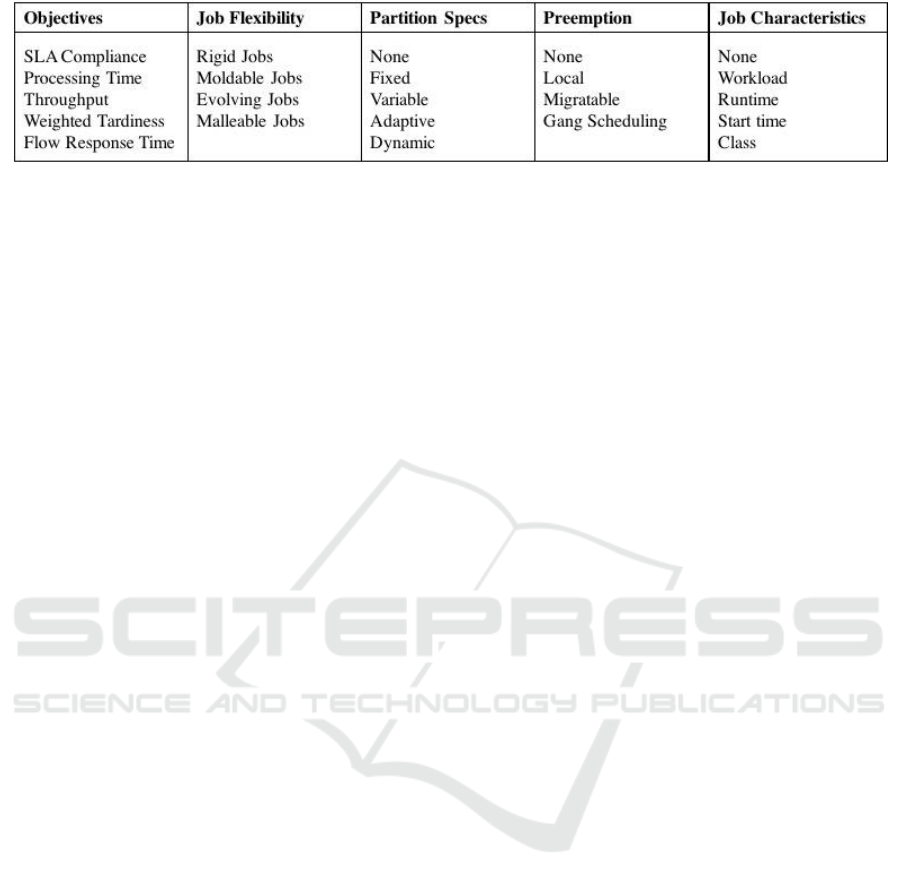
Figure 1: Literature Classification: Dimensions of Scheduling Models.

there is many to many relationships between objec-

tives and levers.

Levers are assessed on their potential impact on

the objectives and business logic to arrive at an opti-

mal selection. Postponing the run of a particular job

to another day, deleting dependencies between jobs,

reducing the ‘run time’ of a job by provisioning addi-

tional capacity or limiting workload and preponing a

job’s run within the batch are examples of levers. By

business logic mean the interrelationships among jobs

which are defined by business imperatives at business

level and not at the IT level and cannot be arbitrarily

changed to meet the objectives.

1.1 Purpose of This Paper

The purpose of this paper is to propose an optimiza-

tion based approach to determine the smallest set of

levers to minimize SLA violations. Considerations

such as reducing the overall batch execution time and

other issues are not part of the scope of this paper

even though these issues are interrelated.

1.2 Organization of This Paper

This paper briefly discusses batch job system and its

ubiquitous nature in modern business organizations in

its introduction in section 1. Section 1 also discusses

the background literature and context of this study.

Section 2 discusses the methodology and section 3

consists of ILP (Integer Linear Programming) formu-

lation of the problem and the mathematical model.

Section 2 & 3 constitute the main body of the paper.

Section 4 reports and discusses the results produced

by the model on 2 sets of data-synthetic and real. Sec-

tion 5 concludes the paper with a pointer to the future

work as an extension of this study.

1.3 Literature

A part of this study corresponds to the field of parallel

job scheduling. The parallel job scheduling literature

broadly addresses both the temporal and spatial (pro-

cessor space) dimensions of job scheduling. We,

however, restrict this study to the temporal aspect of

job scheduling. Large number of batch jobs, complex

dependency structure and large solution space due to

multiple lever combinations make this problem chal-

lenging despite confining the scope of this study to

temporal dimension alone.

The primary purpose of this study is to realign a

given batch job system to maximize SLA compliance.

Job scheduling is one of the ways to realize the afore-

mentioned objectives. The study of computer archi-

tectures with parallel processors has prompted the de-

sign and analysis of algorithms for scheduling paral-

lel jobs. The studies in this area differentiate them-

selves based on the level of indigeneity in their mod-

els. Feitelson et al, (1997) have characterized studies

based on various aspects of batch job systems that are

incorporated in scheduling models. These aspects in-

clude partition specifications, job flexibility, pre-

emption support, amount of job and workload data

available, memory allocation and the optimization

objectives.

Models proposed in these studies try to optimize

one or more of the following objectives – throughput,

deadline misses (SLA non-compliance), completion

time (batch processing time), flowtime and tardiness.

These objectives are broadly interconnected to each

other. Some of these objectives closely follow each

other. Optimizing one of them can potentially opti-

mize others in similar conditions. Kellerer et al

(1996) and Leonardi and Raz (2007) have shown in

their work that a batch job system configuration with

optimal completion time would also have optimal

flow time under the same model constraints. Feitelson

et al (1997) argue that a good management policy for

a batch job system requires optimization of different

objectives over different time frames. For example,

during working hours, when users wait for comple-

tion of jobs, response time might be the most critical

objective. However, during non-working hours, sys-

tem throughput might be the most vital objective.

Also, there are a host of studies that consider multi

criteria optimization. Zhu and Heady (2000) have ad-

dressed the scheduling problem by considering both

throughput and completion time as objectives. The

model proposed in this paper considers the objective

of minimizing the aggregate deadline misses.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

398

The next aspect of batch job systems that has been

extensively studied in the literature is partition speci-

fications. Batch jobs are executed on processors

which are architected in multiple ways. These archi-

tectures have a major bearing on the scheduling. Feit-

elson et al (1997) roughly classifies partition specifi-

cations into four types – fixed, variable, adaptive and

dynamic. While fixed partitions (Feldmann et al,

1994) can only be altered by a system reboot, variable

partition sizes can be determined at the time of job

submission. Adaptive partitions (Turek et al, 1992)

consider the job’s request for partition along with the

overall system load and allot the best possible parti-

tion based on a preset distribution policy. Dynamic

partition (Deng et al, 2000) sizes can change even

during the execution of jobs. Some batch job systems

have memory along with processing power as a re-

source constraint. Parsons and Sevcik (1996) and Se-

tia (1995) have taken memory into account in sched-

uling algorithms. As discussed earlier, our model

does not consider the spatial dimension (processor

space). The ever dropping costs combined with the

ease of leasing processing power and memory over

the cloud have made this constraint redundant over

the years (Bahl et al, 2007, Singh et al, 2013, Agarwal

et al, 2011 and Suter 2014).

Like processors, jobs too are categorized into four

kinds (Feitelson et al, 1997) depending on how they

are programmed. A rigid job has a processor(s) as-

signed and it runs on the same processor in every

batch. Also the processor requirement is not expected

to change during its execution. Moldable job’s pro-

cessor allotment is dynamic and is decided by the sys-

tem scheduler right before its execution. However,

the processor requirement remains constant through-

out the execution, similar to a rigid job. An evolving

job, as the name suggests, goes through multiple

phases where the processor requirement varies based

on the incoming workload. A malleable job is low on

criticality (Ex: maintenance jobs). It can be starved of

processors, if more critical jobs are in need of proces-

sors. Turek et al (1994) have studied the aggregate

impact of having more rigid jobs on the scheduling

efficiency. Mason et al (2002) have studied the posi-

tive impact of presence of moldable jobs and the de-

lay in the onset of a bottleneck like scenario. For this

study, we consider the first two kinds of jobs – Rigid

and Moldable jobs. Rigid jobs are referred to as criti-

cal jobs in this paper. Another aspect of batch job

scheduling is level of pre-emption supported by the

scheduler. No pre-emption indicates that once a job

starts its execution, it finishes without interruptions

while holding its assigned processors. With local pre-

emption, threads of a job may stop and resume their

execution albeit on the same processor unlike migrat-

able pre-emption (Deng et al, 2000), where threads

may be suspended on one processor and resumed on

another. Gang scheduling (Schwiegelshohn, 2004)

refers to suspension and resumption of all the threads

of a job simultaneously.

Most of the scheduling studies have not consid-

ered pre-emption in their models. Motwani et al

(1994) and Schwiegelshohn (2004) have studied the

overheads associated with pre-emption due to which

pre-emption is not often seen in actual batch job sys-

tems. In our study, we too have assumed that jobs

would finish their execution without any pre-emption.

Feitelson et al (1997)’s last characteristic to clas-

sify studies on batch job scheduling is the amount of

job related data used in models. While some of the

above mentioned aspects such as level of rigidity and

pre-emption support are job characteristics that are vi-

tal, any additional details about job can improve the

overall scheduling efficiency. Literature has seen the

use of job characteristics such as workload, parallel-

ism level and ‘run time’ in various studies (Agnetis et

al, 2004, Janiak et al, 2005). Our model incorporates

job characteristics such as ‘run time’, SLA definitions

and ‘start time’ constraints.

2 THE MODEL

The schema in figure 2 shows the four components of

the model - inputs, pre-processing, post processing,

modelling & solving and post-processing.

2.1 Inputs

Inputs to the model include job dependencies, run his-

tory, SLA definitions, and batch schedule. Job de-

pendencies describe a graph that captures the depend-

ency relationship among jobs. These relationships are

defined by underlying business logic and cannot be

changed arbitrarily. Run history data comprises of job

‘start time’, ‘end time’, ‘from time’ and ‘run time’.

‘Start time’ is the time when job execution starts

while ‘end time’ is the time when job execution ends.

‘From time’ is a constraint that restricts the ‘start

time’ of a job and ‘run time’ is the amount of time

taken to complete the job execution. These data are

very important for efficient and feasible scheduling of

jobs. Batch schedule tells us what jobs of a batch are

scheduled to be executed on a particular day. Busi-

ness critical jobs in a given batch have SLA definition

and these jobs should be completed within the speci-

fied definition. Failure to do so results in non-compli-

ance.

SLA Non-compliance Detection and Prevention in Batch Jobs

399

2.2 Pre-processing

In the pre-processing module, we pool input data

from multiple sources such as job and dependency

data tables, transaction history, batch schedule and

SLA definitions. We clean these data sets to ensure

data consistency, completeness and uniformity. This

module comprises of the following sub-modules.

2.2.1 Job Profiles

Job profiles are the collection of individual job char-

acteristics that are useful in scheduling. Each job pro-

file includes ‘job name’, ‘run time’, ‘from time’, crit-

icality and SLAs (if defined).

2.2.2 Predecessor List

The predecessor list represents the dependencies

among the jobs. A job can only start executing if all

of its predecessor jobs are executed. It captures the

relationship between jobs.

2.2.3 Dependency Graph

By using job profiles and dependency list, we form a

directed graph called dependency graph, where each

node represents a job and an edge represents the prec-

edence relationship. This helps in visualising the

batch job system as a graph and thereby letting us use

graph theoretic approaches to achieve the objectives.

2.2.4 ‘Reach Time’

We define a metric called ‘reach time’ for each job. It

is defined as the earliest time epoch a job can start

execution. This metric helps us identifying the poten-

tial SLA non-compliant jobs by comparing ‘reach

time’ and SLAs. For a job (j), the ‘reach time’ (j) can

be calculated from the following equation.







































(1)

2.2.5 Potential SLA Non-compliance

We identify the jobs that are likely to violate SLAs

defined on them using ‘reach time’ and SLAs. Our

objective is to keep the non-compliance as minimum

as possible. Once we identify these potential SLA

non-compliant jobs, we find the optimal set of levers

to minimize SLA non-compliance.

2.3 Modelling and Solving

In this module, we discuss about business objectives,

business constraints and solution space. Thereafter

we discuss the mathematical model formulation and

solving.

2.3.1 Business Objectives

The business objective that we are trying to achieve

here is minimization of SLA non compliant jobs with

minimum impact on business logic. The SLAs are

defined on ‘‘from time’’ and ‘‘end time’’ of jobs. For

a batch job system, it is very important to meet these

SLAs as a batch may be dependent on the outcomes

of another batch. The subsequent batch cannot be

executed if its predecessor batch is not yet completed.

Delay in a batch leads to delays in its subsequent

batches.

Figure 2: The Methodology Schema.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

400

2.3.2 Business Constraints

Business constraints are generally derived from the

jobs relationships and requirements. A typical busi-

ness constrains could be something like, “a job can

start only after its defined ‘from time’”; “a job can

start only after all its predecessors are completed” etc.

If a job or dependency is defined as critical then it

cannot be perturbed.

2.3.3 Solution Space and Optimal Solution

The following levers can be used to meet the stated

business objective.

 The amount of time by which a job can be

preponed.

 The fraction by which a job’s ‘run time’ can be

reduced.

 Whether a job needs to be deleted from the cur-

rent batch.

 Whether a dependency can be removed.

The solution space is comprised of all possible com-

binations of these levers. For example, if the ‘from

time’ of a job is 1000 seconds the first lever can take

any values between 0 and 1000. Similarly, for a given

job, the second lever can assume any value between

0 and 100. For the fourth lever, the combinations can

go as high as 2

with ‘n’ being the number of depend-

encies in the system. Putting all these together, the

size of solution space of 1000 jobs of a batch job sys-

tem can run into billions. The challenge is to find an

optimal solution within reasonable time limits.

3 ILP FORMULATION

The general structure of the proposed optimization

model is to minimize SLA non-compliance with least

impact on business logic, subject to ‘from time’ and

dependecy constraints. The proposed optimization

model is an Integer Linear Program (ILP). An ILP

guarantees the global optimal solution if it is feasible

(Wolsey et al, 2014; Brucker, 2007). Integer Linear

Program (ILP) is a tool for solving optimization

problems. The first step towards modeling an

optimization problem is identifying inputs and

decision variables. The nature of the decision

variables determines the problem type (continuous,

integer or mixed integer). The problem is then

formulated by identifying objectives and its

constraints. When both objectives and constraints are

linear, and decision variables are integer the problem

is called ILP. Operations research practitioners have

been formulating and solving ILPs since the 1940s

(Klotz and Newman, 2013a) However, in recent

years, the availability of large computing power and

development of powerful optimization solvers has

empowered practitioners to be able to solve complex

real-world problems(Klotz and Newman, 2013b).

This work uses ILP to find the smallest set of levers

that minimizes SLA violations. The input parameters

of the proposed model are as follows.



cJ = set of critical jobs

 











cE = set of critical edges

























The decision variables of the proposed model are

shown in table 1. The objective of the proposed

mathematical model is to minimize SLA non-

compliance with minimal impact on business logic.

So, the objective function has two parts. First part

() takes care of the SLA non-

compliance and the second part

() ensures minimum

possible changes to the existing system configuration.

The objective function is given below.



















(2a)

 





 



   





















 



 









(2b)

We have two types of SLA non-compliance, ‘end

time’ SLA non-compliance 



) and ‘start time’

SLA non-compliance (



). A very large number ‘M’

is multiplied to , that ensures

that the model will minimize the non-compliance

whenever feasible. We have four levers (delete a job

(



), delete a dependency (



), reduce ‘run

time’/workload (



) and reduce ‘from time’ (



)) to

achieve the objective. We want to use theses levers as

minimimum as possible and minimize the SLA non-

compliance. The second term

() ensures this objective.

3.1 Constraints

The model needs to consider following set of con-

straints to obtain optimal set of levers that minimizes

SLA non-compliance.

SLA Non-compliance Detection and Prevention in Batch Jobs

401

Table 1: Decision Variables.





















.

(3)











(4)







(5)







(6)











 















(7)



















(8)

















(9)





























(10)

















(11)





























(12)





























(13)

3.1.1 Sacrosanct Constraints

There are a few business critical jobs or dependen-

cies, which cannot be altered. Constraints below en-

sure that we do not delete a business critical job from

the current batch or reduce its workload or ‘run time’.

Constraint (15) puts bound on ‘runtime’ reduction of

a job. Constraint (16) ensures that no business critical

dependencies are deleted.

















(14)









 (puts bound on ‘run time’

reduction of a job)

(15)



















(16)

3.1.2 Reach Time Constraints

We define ‘reach time’ (



) of a job j as the

earliest time epoch, when the job j can start executing.

Constraint (17) ensures that the job j can start execut-

ing after it’s ‘‘from time’’ only. Constraint (18)

makes sure that the job j can start executing only after

all its predecessor jobs are executed.





     







 





(17)





     

























(18)

3.1.3 SLA Non-compliant Identifier

Constraints

Constraints (19) and (20) ensure that when a job j

violates ‘end time’ SLA (



), it is registered through

the decision variable 



. Simillarly, constraints (21)

and (22) ensure ‘start time’ SLA (



) violation is

recorded in variable 







 









 



 



     





(19)





 







   









 



    





(20)





 







     





(21)





     









 



    





(22)

3.1.4 Auxiliary Constraints

These constraints help in estabilishing the

relationships between different variables. Constraint

(23) records if ‘run time’ reduction is required for job

j. Constraints (24) – (26) are the equivalent of the

non-linear constraint, 











. The varia-

ble, 



, captures the ‘run time’ reduction for job j

if dependency between job j and k are not deleted.

This value is required for ‘reach time’ calculation.





  





(23)









   











(24)

  



  









(25)

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

402





 





(26)

Constraints (27)-(29) are the equivalent of the

non-linear constraint, 











The variable, 



, updates the ‘reach time’ for job j

depending upon the dependency between job k & j.









   













(27)

  



  











(28)





 











(29)

Constraints (30)-(32) are the equivalent of the

non-linear constraint, 











. The variable





captures whether job j is SLA complaint or not.









 



 

(30)











(31)











(32)

We discuss the model solving approach in the

following sub-subsection.

3.2 Optimal Solution

The formulated mathematical model is an Integer

Liner Program (ILP). We have coded the proposed

model using Python-PuLP to create an optimizer

consumable input format (.lp file). This LP file is

passed to the optimization solver for optimal solution.

We have used CBC solver (open source) for our

study. More efficient, proprietary solvers (Cplex,

Gurobi etc.) can also be used to obtain the optimal

solutions.

3.3 Post Processing

The post-processing module is further divided into

two sub-modules. Actionable levers and reconfigured

batch job systems.

3.3.1 Actionable Levers

We translate the obtained optimal solutions, which is

expressed in mathematical terms into implementable

actions such as identifying the jobs that can be

postponed to another batch, executing batch jobs

partially by reducing the workload or running the job

on multiple cores simultaneously, identifying the

dependencies that can be relaxed or identifying those

jobs whose ‘from time’ constraint can be relaxed.

3.3.2 Reconfigured Batch Job Systems

Once we identify all the actionable levers we re-

configure the batch job system’s run to achieve the

stated objective by updating the job and dependency

tables.

4 RESULTS AND DISCUSSION

4.1 Illustration with Synthetic Data

To illustrate the method presented in the previous sec-

tion, we use two different sets of data. The first illus-

tration is on synthetic data for demonstrating solu-

tion’s correctness. The second illustration is on a real

batch job system of a large financial institution. The

batch job system shown in figure 3 comprises of 14

jobs. These jobs vary in terms of attributes such as

‘run time’, ‘from time’, SLA definitions and critical-

ity. ‘Run time’ of all the jobs and the interdependen-

cies among them are shown in figure 3. For example,

job N1 cannot be scheduled for a run unless jobs J3

and J4 are executed. Job criticality is indicated by en-

circling nodes in red. Jobs J1, J2 and J5 are critical

(Figure 3) and cannot be used as levers to perturb the

system. Jobs J11 and J12 in red. These jobs have pre-

defined ‘end time’ SLAs and are not expected to be

used as levers. The dependencies between jobs in this

case are also considered critical. Next to each node in

the dependency graph is the ‘end time’.

In the as-is configuration of this system, jobs J11

and J12 are violating their SLA definitions by 7 and

14 time units respectively. Job J5 has ‘from time’ de-

fined at 180

time unit, which means even if job J5’s

predecessors finish execution before 180

time unit,

it cannot start execution. As seen in this case, job N1

completes execution at 80

time unit but, due to the

‘from time’ constraint, job J5 had to wait for 100

more time units. Although, such constraints are de-

rived from business logic and often unalterable, it is

vital to identify and minimize such slacks to reduce

spikes in CPU utilization.

With the objective being minimization of SLA non-

compliance, there are multiple feasible solutions.

However, the ‘Impact on Business Logic’ component

of the objective function given in section 3 ensures

that lever usage is confined. The solution obtained

from the model is to reduce the ‘run time’ of job J5

by 70% (from 20 mins to 6 mins). In cases where

there is a cap on the amount of ‘run time’ reduction,

the feasible solution set shrinks. When we set a cap

on ‘run time’ reduction at 50%, the optimal solution

would then be to reduce the ‘run time’ of jobs J5 and

SLA Non-compliance Detection and Prevention in Batch Jobs

403

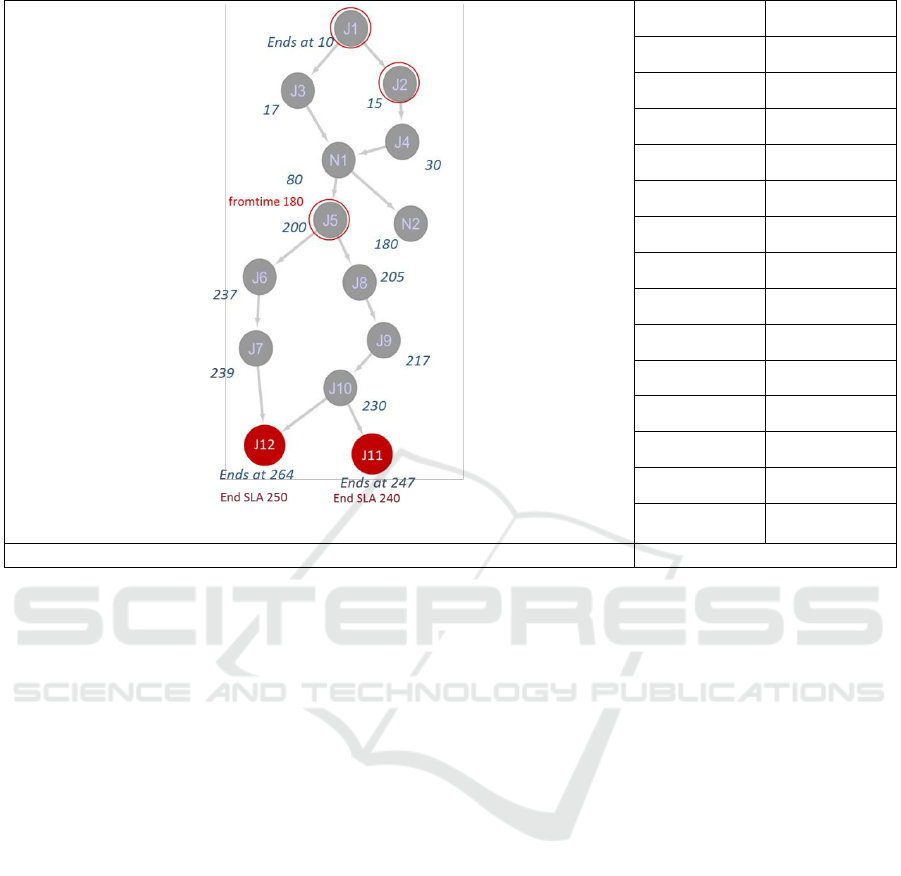
Figure 3: Dependency graph and job ‘run time’ with synthetic data.

J6 by 50% and 10% respectively. Both these solutions

are as expected.

4.2 Illustration with Real Data

We tested the model on a real batch job system with

518 jobs and 738 interdependencies. Due to a pre-

scheduled maintenance activity over the weekend

batch runs, there might be an adverse impact on SLA

compliance. Around 14 jobs are expected to have a

50% increase in their ‘run time’. The model has iden-

tified 18 SLA violations as a result. Some other im-

portant characteristics of this system include- 62 jobs

with ‘from time’ constraints, 21 critical jobs, 137 crit-

ical dependencies and 35 jobs with ‘end time’ SLA

definitions.

Figure 4 shows the partial dependency graph of

the batch system used in this illustration. The node

size depicts the ‘run time’ of a job. The nodes marked

in blue are the jobs affected by the scheduled mainte-

nance activity and are expected to see an increase in

their ‘run time’. The nodes marked in yellow are the

ones expected to violate SLAs. The optimal solution

suggested by our model includes deletion of 3 jobs,

reduction of ‘run time’ of 2 jobs while preponing the

‘from time’ of 2 jobs. However, despite these inter-

ventions, the total SLA violations could only be

brought down from 18 to 4. This configuration of

batch system makes 100% SLA compliance an unat-

tainable target.

5 CONCLUSION

In this study, we proposed an optimizer for batch job

systems that maximizes SLA compliance with mini-

mum possible impact on the business logic. Although,

there exists an extensive body of literature on solu-

tions to achieve this objective, the levers used to do

so are mostly focussed on job scheduling. Our study

considers a more practical approach wherein a wider

range of levers such as Job and Dependency deletion

and ‘run time’ reduction are also considered while de-

signing the optimizer. By taking these additional lev-

ers into consideration, the solution space increases

many fold. Despite this, our approach finds the opti-

mal set of levers within reasonable time limits as we

have modeled the complex optimization problem as

an integer linear program (ILP). Linear formulation

guarantees the global optimal solution and has better

computational efficiency than the non-linear models.

In its current state, the model can handle batch job

systems of size around 1000 jobs and 1800 depend

Job

‘run time’

100

J10

J11

J12

Dependency Graph

Job run times

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

404

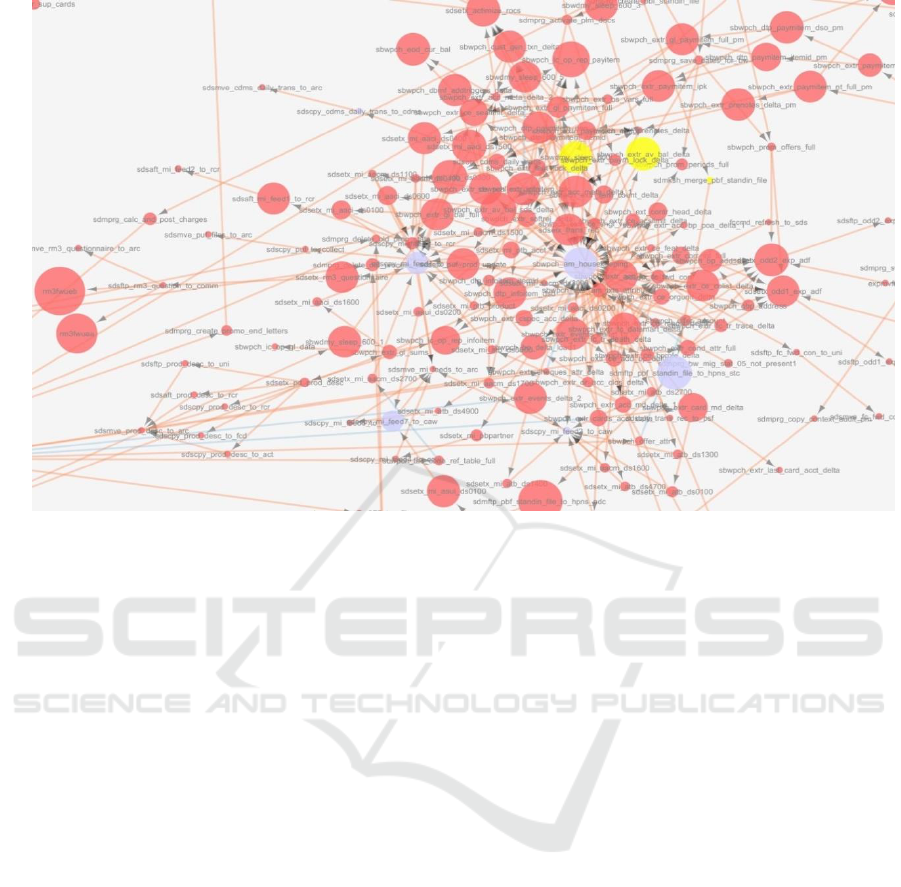
Figure 4: A real batch job system.

encies. Beyond this, the ‘run time’ shoots up substan-

tially. An interesting direction for future research

would be to build heuristics that intelligently prune

the solution space without compromising the optimal-

ity of the solution.

A major consideration of batch system optimizers

is their ‘run time’. As described in the previous sec-

tion, we have programmed this solution on Python-

PuLP with CBC solver. When implemented on a

2.6GHz, i5 processor with 4GB RAM, the solution

takes less than 2 minutes to handle 1000 jobs and

1800 dependencies batch system to find the optimal

solution.

REFERENCES

Agnetis, A., Alfieri, A., Nicosia, G., 2004. A heuristic ap-

proach to batching and scheduling a single machine to

minimize setup costs. Computers & Industrial Engi-

neering 46, 793-802.

Agrawal, R. and Sadaphal, V., 2011. “Batch systems: Opti-

mal scheduling and processor optimization”, In Pro-

ceedings of 18th International Conference on High Per-

formance Computing (HiPC), Bangalore, India.

Bahl, P., Chandra, R., Greenberg, A., Kandula, S., Maltz,

D., and Zhang, M. 2007. "Towards highly reliable en-

terprise network services via inference of multi-level

dependencies", ACM SIGCOMM Computer Communi-

cation Review (37:4), p. 13(doi: 10.1145/1282427.

1282383).

Brucker, P. 2007. Scheduling algorithms, Berlin [u.a.]:

Springer.

Chakrabarty, K. 2000. "Test scheduling for core-based sys-

tems using mixed-integer linear programming", IEEE

Transactions on Computer-Aided Design of Integrated

Circuits and Systems(19:10), pp. 1163-1174(doi:

10.1109/43.875306).

Deng, X., Gu, N., Brecht, T., and Lu, K. 2000. "Preemptive

Scheduling of Parallel Jobs on Multiprocessors", SIAM

Journal on Computing (30:1), pp. 145-160(doi:

10.1137/s0097539797315598).

Ed Klotz, Alexandra M. Newman. 2013a, Practical guide-

lines for solving difficult mixed integer linear pro-

grams, In Surveys in Operations Research and Manage-

ment Science, Volume 18, Issues 1–2, Pages 18-32,

ISSN 1876-7354

Ed Klotz, Alexandra M. Newman. 2013b, Practical guide-

lines for solving difficult linear programs, In Surveys in

Operations Research and Management Science, Vol-

ume 18, Issues 1–2, , Pages 1-17, ISSN 1876-7354

Feitelson, D., Rudolph, L., Schwiegelshohn, U., Sevcik, K.,

and Wong, P. 1997. "Theory and practice in parallel job

scheduling", Job Scheduling Strategies for Parallel

Processing, pp. 1-34(doi: 10.1007/3-540-63574-2_14).

Feldmann, A., Sgall, J., and Teng, S. 1994. "Dynamic

scheduling on parallel machines", Theoretical Com-

puter Science (130:1), pp. 49-72(doi: 10.1016/0304-

3975(94)90152-x).

Janiak, A., Kovalyov, M.Y., Portmann, M.C., 2005. Single

machine group scheduling with resource dependent

setup and processing times. European Journal of Oper-

ational Research 162, 112-121.

SLA Non-compliance Detection and Prevention in Batch Jobs

405

Kellerer, H., Tautenhahn, T., and Woeginger, G. 1999.

"Approximability and Nonapproximability Results for

Minimizing Total Flow Time on a Single Machine",

SIAM Journal on Computing (28:4), pp. 1155-

1166(doi: 10.1137/s0097539796305778).

Leonardi, S., and Raz, D. 2007. "Approximating total flow

time on parallel machines", Journal of Computer and

System Sciences (73:6), pp. 875-891(doi:

10.1016/j.jcss.2006.10.018).

Mason, S.J., Fowler, J.W., Carlyle, W.M., 2002. A modi-

fied shifting bottleneck heuristic for minimizing total

weighted tardiness in complex job shops. Journal of

Scheduling 5, 247-262.

Parsons, E., and Sevcik, K. 1996. "Benefits of speedup

knowledge in memory-constrained multiprocessor

scheduling", Performance Evaluation (27-28), pp. 253-

272(doi: 10.1016/s0166-5316(96)90030-9).

Schwiegelshohn, U. 2004. "Preemptive Weighted Comple-

tion Time Scheduling of Parallel Jobs", SIAM Journal

on Computing (33:6), pp. 1280-1308(doi:

10.1137/s009753979731501x).

Setia, S.K., 1995, April. “The interaction between memory

allocation and adaptive partitioning in message-passing

multicomputers”, In Workshop on Job Scheduling

Strategies for Parallel Processing (pp. 146-164).

Springer, Berlin, Heidelberg.

Singh, R., Shenoy, P., Natu, M., Sadaphal, V., and Vin, H.

2013. "Analytical modeling for what-if analysis in com-

plex cloud computing applications", ACM SIGMET-

RICS Performance Evaluation Review (40:4), p.

53(doi: 10.1145/2479942.2479949).

Suter, F., 2014. Bridging a Gap Between Research and Pro-

duction: Contributions to Scheduling and Simulation

(Doctoral dissertation, Ecole normale supérieure de

Lyon).

Turek, J., Wolf, J., Pattipati, K., and Yu, P. 1992. "Sched-

uling parallelizable tasks", ACM SIGMETRICS Perfor-

mance Evaluation Review (20:1), pp. 225-236(doi:

10.1145/149439.133111).

Wolsey, L., and Nemhauser, G. 2014. Integer and Combi-

natorial Optimization, Hoboken: Wiley.

Zhu, Z., Heady, R.B., 2000. Minimizing the sum of earli-

ness/tardiness in multi-machine scheduling: a mixed in-

teger programming approach. Computers & Industrial

Engineering 38, 297-305

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

406