
Incremental Bidirectional Transformations:
Applying QVT Relations to the Families to Persons Benchmark
Bernhard Westfechtel
Applied Computer Science I, University of Bayreuth, D-95440 Bayreuth, Germany
Keywords:
Model Transformation, Bidirectional Transformation, Benchmark, QVT Relations.
Abstract:
Model transformations constitute a key technology for model-driven software engineering. In round-trip engi-
neering processes, model transformations are performed not only in forward, but also in backward direction.
Since defining forward and backward transformations separately is both awkward and error-prone, bidirectio-
nal transformation languages provide a single definition for both directions. This paper evaluates the transfor-
mation language QVT Relations (QVT-R) which allows to specify incremental bidirectional transformations
— as required for round-trip engineering for propagating changes in both directions — declaratively at a high
level of abstraction. We apply QVT-R to a well-known benchmark example, the Families to Persons case.
This case study demonstrates a number of limitations of the QVT-R language which result from the strictly
state-based design of the language as well as from the way in which the semantics of QVT-R transformations
are defined.
1 INTRODUCTION
Model transformations (Czarnecki and Helsen, 2006)
constitute a key technology for model-driven software
engineering. A model transformation takes a set of
source models as input and creates or updates a set
of target models. A transformation operates in ba-
tch mode if it generates the target models from scra-
tch; in contrast, an incremental transformation propa-
gates changes from sources to targets. Furthermore,
we may distinguish between unidirectional transfor-
mations which are executed only from source to tar-
get, and bidirectional transformations which are exe-
cuted also in the opposite direction. Bidirectional
transformations occur in a wide variety of application
domains (Czarnecki et al., 2009), including, but not
restricted to model-driven software engineering. In
this paper, we focus specifically on incremental bidi-
rectional transformations, as they are required e.g. in
round-trip engineering processes.
A bidirectional transformation language is a lan-
guage which allows to define bidirectional transfor-
mations with the help of a single transformation de-
finition being executable in both directions; see (Hi-
daka et al., 2016) for a survey. A bidirectional trans-
formation language promises to save specification ef-
fort since the transformation developer does not need
to code each direction separately. Furthermore, a bidi-
rectional transformation language may assist in defi-
ning mutually consistent forward and backward trans-
formations. For example, the forward and backward
transformations may satisfy certain round-trip laws
such as that the execution of a backward transfor-
mation, immediately following a forward transforma-
tion, leaves the original source model untouched (Fos-
ter et al., 2007).
QVT Relations (QVT-R) is a model transformation
language which was defined by the Object Manage-
ment Group (OMG) as part of the QVT standard (Ob-
ject Management Group, 2016a). QVT-R is based
on the Meta Object Facility (MOF (Object Manage-
ment Group, 2016b)) for defining models as instan-
ces of metamodels, and the Object Constraint Lan-
guage (OCL (Object Management Group, 2014)) for
expressing queries and constraints on MOF models.
QVT-R is a declarative language which allows to spe-
cify consistency relationships between patterns. In
QVT-R, a transformation developer may define a bi-
directional transformation which may be executed in
different ways: in forward or backward direction, in
batch or incremental mode, as well as in checkonly or
enforcing mode. In checkonly mode, the consistency
between a source and a target model is checked; in
enforcing mode, the target model is updated (or cre-
ated anew) to make it consistent with the source mo-
del. Thus, a single declarative transformation defini-
Westfechtel, B.
Incremental Bidirectional Transformations: Applying QVT Relations to the Families to Persons Benchmark.
DOI: 10.5220/0006679700390053
In Proceedings of the 13th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2018), pages 39-53
ISBN: 978-989-758-300-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
39
Families
Model
Persons
Model
Updates
Updates
Change
Propagation
Change
Propagation
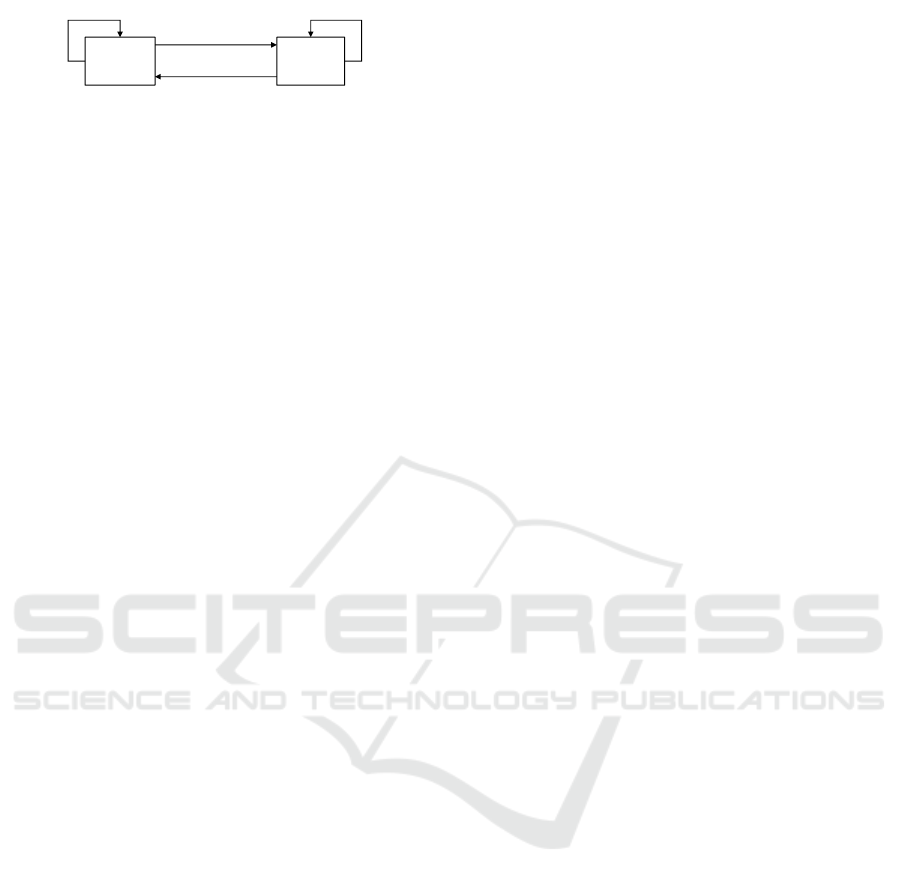
Figure 1: The Families to Persons case.
tion may be executed in up to six different ways. This
approach promises to make the development of bidi-
rectional transformations considerably easier.
In the light of the diversity of bidirectional trans-
formation languages, the need for benchmarks has
been identified early (Czarnecki et al., 2009). Later, a
proposal for structuring benchmarks for bidirectional
transformations was published (Anjorin et al., 2014).
Only recently, this proposal was materialized into an
implementation called Benchmarx, which constitu-
tes a practical benchmark framework for bidirectional
transformations (Anjorin et al., 2017b). Based on this
framework, a popular case from the literature — the
Families to Persons case — was implemented (Anjo-
rin et al., 2017a). In this paper, we evaluate incre-
mental bidirectional transformations in QVT-R with
the help of the Families to Persons benchmark case as
described in (Anjorin et al., 2017a).
The Families to Persons benchmark case is illus-
trated in Figure 1. In this informal diagram, boxes
represent models, while arrows stand for model up-
dates. Two related, but differently structured models
have to be kept consistent: A families model with pa-
rents and children, and a persons model containing a
flat set of males and females. Updates may be per-
formed on both models, and have to be propagated in
both directions. While the Families to Persons case is
rather small and thus implementable with acceptable
effort, it poses a number of challenges such as hetero-
geneous metamodels, loss of information, the absence
of keys (uniquely identifying properties of model ele-
ments), non-determinism, configurability (of the bac-
kward transformation), renamings and moves, order
dependent update behavior, and application-specific
requirements to change operations.
Our contribution consists in the solution of the Fa-
milies to Persons case in QVT-R and its evaluation.
Surprisingly, our evaluation reveals a number of limi-
tations, resulting in a large number of failed test ca-
ses. A detailed examination shows that these failures
are due the semantic rules determining the execution
behavior of QVT-R transformation definitions. The
problems are not primarily caused by ambiguities or
contradictions in the semantics definition. Rather, the
Persons to Families case demands for behavior that
deviates from the semantics which QVT-R incorpora-
tes. Thus, our main intent is to clearly elaborate the
reasons for failures in the benchmark and discuss the
lessons learned from this case study.
In particular, we identified the following problems
when applying QVT-R to the Families to Persons
case:
Imprecise Change Propagation. Due to the strictly
state-based design and the absence of persistent
traces, changes may be propagated only impreci-
sely. For example, if the name of a family member
is changed, the corresponding person is deleted
and recreated, implying that the birthday is lost.
Unidirectional Transformations. Although QVT-R
supports the specification of bidirectionally exe-
cutable transformations, our best-effort solution
requires to write two unidirectional transformati-
ons because the rules for forward and backward
transformations differ significantly.
Non-injective Mappings. Due to the check-before-
enforce semantics of QVT-R, multiple family
members sharing the same name would be map-
ped onto the same person (and vice versa) unless
the transformation definition is written in such a
way that an injective mapping is enforced. Unfor-
tunately, enforcing injective mappings turns out to
be awkward, and it requires pairs of unidirectional
transformations (see above).
Duplicate Transformations. QVT-R applies all ru-
les to all matches, without checking for conflicts.
This may result in undesirable behavior. For ex-
ample, in the backward transformation from the
persons model to the families model there are two
rules for mapping females to mothers and daugh-
ters, respectively. The transformation developer
must ensure that the preconditions for applying
these rules are mutually exclusive.
The rest of this paper is structured as follows:
Section 2 introduces QVT-R. Section 3 describes the
Families to Persons case, which is solved in Section 4.
Section 5 evaluates the solution. Section 6 discusses
related work, and Section 7 concludes the paper.
2 QVT RELATIONS
This section summarizes some global properties of
QVT Relations (QVT-R); the language constructs will
be explained on demand in parallel to the solutions
presented in Section 4. For a detailed description of
QVT-R, the reader is referred to the standard (Object
Management Group, 2016a).
QVT-R is a declarative language for specifying
transformations between models which are typed by
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
40

Table 1: Properties of QVT-R.
Property Explanation
State-based Transformation depends only
on model states, not on deltas
Trace-less Transformation does not rely
on a persistent trace
n : 1
mappings
Multiple source pattern
instances may be mapped to the
same target pattern instance
Non-
conflicting
relations
Relations are applied
independently of each other
MOF-based metamodels. In general, any number n
of models may be involved in a transformation; in
the following explanations, we will assume n = 2.
A transformation is defined in terms of relations bet-
ween patterns in the participating models.
A transformation is executed in the direction of a
specific model. A transformation is unidirectional if
it can be executed only in a specific direction; it is
bidirectional if it can be executed in both directions.
In the latter case, the transformation definition must
satisfy a number of restrictions (dataflow constraints)
ensuring that the transformation is actually executable
in both directions. QVT-R does not distinguish expli-
citly between uni- and bidirectional transformations.
QVT-R distinguishes between two modes of trans-
formation executions. In checkonly mode, it is chec-
ked whether the target model is consistent with the
source model. In enforcing mode, the target model is
updated in order to make it consistent with the source
model. With respect to enforcing transformations, ba-
tch transformations are considered as a special case of
incremental transformations (initially, the target mo-
del is empty).
QVT-R transformations are based on a for-all-
exists semantics: In checkonly mode, it is checked
for each relation and each match of a source pattern
whether a match of the corresponding target pattern
exists in the target model. In enforcing mode, a ma-
tch of the target pattern is created when it does not
exist yet. The for-all-exists semantics results in n : 1
mappings, i.e., it is allowed that multiple matches in
the source model are mapped to the same match in
the target model. This statement holds both within a
specific relation and across different relations.
Due to the for-all-exists semantics, a directed
check reports consistency of the target model with the
source model even if the target model contains “too
many” elements. Therefore, checking mutual consis-
tency requires two directed checks. In contrast, in en-
forcing mode all unmatched target elements are dele-
ted to ensure mutual consistency.
In QVT-R, all relations are non-conflicting. Thus,
if two relations are applicable to the same match, both
of them are applied. If it is intended that at most
one of them is executed, the transformation developer
must specify the application conditions accordingly.
Similarly, matches may have arbitrary overlaps —
both within a single relation and across multiple re-
lations.
QVT-R follows a purely state-based approach to
incremental transformations: The only information
which is assumed to be present are the states of the
source and the target model. In this way, the prerequi-
sites for the execution of incremental transformations
are minimized. Thus, for any pair of models s and t,
an incremental transformation for updating t may be
executed, regardless of the history of changes.
In particular, QVT-R does not assume the pre-
sence of deltas, which record sequences of change
operations on the source model and could be exploited
to improve change propagation. Nor does QVT-R rely
on (persistent) traces, which record the relationships
between source and target model elements of previous
transformation executions. Thus, in QVT-R an incre-
mental transformation from s to t may be performed
even if s and t have been created independently and
no knowledge regarding the changes on s is available.
Finally, incremental QVT-R transformations rely
on a check-before-enforce semantics: If a match of a
source pattern of some relation is located, it is chec-
ked first whether a match of the corresponding target
pattern already exists. In this case, the match of the
source pattern is related to the already existing match
of the target pattern. The check-before-enforce se-
mantics differs from a trace-based semantics, where
a new target pattern instance is created when the re-
spective source pattern instance has not been transfor-
med yet.
Table 1 summarizes essential properties of QVT-R
being relevant to the case studied in this paper.
3 FAMILIES TO PERSONS
Different variants of the Families to Persons case have
been proposed. To make this paper self-contained, we
describe the variant on which our work is based, follo-
wing (Anjorin et al., 2017a). The case is rather small
such that it is implementable with acceptable effort.
On the other hand, it includes several challenges to be
summarized at the end of this section.
Below, the Families to Persons case is described in
an informal way (apart from the definition of metamo-
dels, see below). While informal descriptions suffer
from a lack of precision, we refrain from a formaliza-
Incremental Bidirectional Transformations: Applying QVT Relations to the Families to Persons Benchmark
41

FamilyRegister
Family
+name :String
FamilyMember
+name :String
father
0..1
father
Inverse
0..1
mother
0..1
mother
Inverse
0..1
sons
0..*
sons
Inverse
0..1
daughters
0..*
daughters
Inverse
0..1
families
0..*
families
Inverse
0..1
PersonRegister
Person
+name :String
+birthday :Date
persons
0..*
persons
Inverse
0..1
Male
Female
Figure 2: Metamodels.
tion, e.g., with the help of finite model theory (Libkin,
2004), which constitutes a challenge on its own and
considerably goes beyond the scope of this paper.
3.1 Metamodels and Consistency
The Families to Persons case deals with the synchro-
nization of a families model with a persons model.
The underlying metamodels are displayed in Figure 2
as class diagrams. For metamodeling, we employ
Ecore - an implementation of Essential MOF, a sub-
set of MOF, provided by the Eclipse Modeling Fra-
mework (Steinberg et al., 2009). Please note that we
adopt the following terminology: A model represents
a collection of instance data. A metamodel is a “mo-
del for models” and defines the types of objects, attri-
butes, and links, as well as the rules for their compo-
sition.
We assume a unique root in each model. A fa-
mily register stores a collection of families. Each fa-
mily has members who are distinguished by their ro-
les. The metamodel allows for at most one father and
at most one mother as well as an arbitrary number of
daughters and sons. A person register maintains a flat
collections of persons who are either male or female.
Note that key properties may be assumed in neither
model: There may be multiple families with the same
name, name clashes are even allowed within a single
family, and there may be multiple persons with the
same name and birthday.
A families model is consistent with a persons mo-
del if a bijective mapping between family members
and persons can be established such that (i) mothers
and daughters (fathers and sons) are paired with fe-
males (males), and (ii) the name of every person p is
“ f .name, m.name”, where m is the member (in family
f ) paired with p.
3.2 Batch Transformations
After running a transformation in any direction, it is
required that the participating models are mutually
consistent according the definition given above. Ho-
wever, this requirement does not suffice to define the
functionality of transformations in a unique way. Be-
low, we first consider batch transformations, where
the target model is created from scratch.
The functionality of a forward transformation is
straightforward: Map each family member to a person
of the same gender and compose the person’s name
from the family name and the first name; the birthday
remains unset. The backward transformation is more
involved: A person may be mapped either to a parent
or a child, and persons may be grouped into families
in different ways.
To reduce non-determinism, two Boolean para-
meters control the backward transformation, resulting
in a configurable backward transformation: prefer-
ParentToChild defines whether a person is mapped
to a parent or a child. preferExistingToNewFamily
determines whether a person is added to an existing
family (if available), or a new family is created along
with a single family member. If both parameters are
set to true, the second parameter takes precedence: If
a family is available with a matching family name,
but there is no matching family with an unoccupied
parent role, the member is inserted into an existing
family as a child.
3.3 Incremental Transformations
For incremental transformations, updates such as in-
sertions, deletions, changes of attribute values, and
move operations have to be considered. In forward
direction, insertion of a family has no effect on the
target model. Insertion of a member results in inser-
tion of a corresponding person; likewise for deletions.
If a family is deleted, all persons corresponding to its
members are deleted. If a member is renamed, the
corresponding person is renamed accordingly. If a fa-
mily is renamed, all persons corresponding to family
members are renamed. If a member is moved, diffe-
rent cases have to be distinguished. If the gender is re-
tained, the corresponding person object is preserved;
otherwise, it is deleted, and a new person object with
a different gender is created whose attributes are co-
pied from the old person object. A local move within
a family does not affect the corresponding person’s
name; a move to another family results in a potential
update of the person’s name.
In backward direction, the effect of an update
depends on the values of the configuration parame-
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
42

ters which may vary between different transformation
executions. Please note that the parameter settings
must not affect already established correspondences;
rather, they apply only to future updates. Deletion of a
person propagates to the corresponding family mem-
ber. If a person is inserted, it depends on the confi-
guration parameters how insertion propagates to the
families model (see above). Persons cannot be moved
because the persons model consists of a single, flat,
and unordered collection. Changes of birthdays do
not propagate to the opposite model. If the first name
of a person is changed, the first name of the corre-
sponding family member is updated accordingly. Fi-
nally, if the family name of a person is changed, this
change does not affect the current family and its mem-
bers: The family preserves its name even if it does
not contain other members; thus, the update has no
side effects on the existing family. Rather, the corre-
sponding family member is moved to another family,
which may have to be created before the move; the
precise update behavior depends on the parameter set-
tings.
3.4 Transformation Laws
The transformations developed for the Families 2 Per-
sons benchmark should satisfy a set of general laws
(Stevens, 2010). First, the result of a transformation
from s to t should be correct, i.e., s and t should
be mutually consistent (see Section 3.1). Further-
more, transformations should be hippocratic: The tar-
get model should not be changed if consistency has al-
ready been established. Thus, an immediate re-run of
a transformation establishing correctness should have
no effect (even if configuration paramaters are swit-
ched in the backward transformation). Finally, round-
trip laws (Foster et al., 2007) should be satisfied: A
backward transformation following a forward trans-
formation should leave the original source model un-
touched; likewise for a forward transformation follo-
wing a backward transformation.
3.5 Challenges
The Families to Persons case includes a number of
challenges which are summarized below:
Heterogeneous Metamodels. The transformation
has to perform a mapping between heterogeneous
metamodels, where the same information is
represented in different ways (concerning e.g.
names and genders).
Loss of Information. The family structure is lost in
the forward transformation; birthdays are lost in
the backward transformation.
No Keys. There are no uniquely identifying proper-
ties for family members or persons, which makes
propagation of changes difficult.
Non-determinism. The families model does not
contain information for defining birthdays in the
persons model. Conversely, the persons model
does not contain information about the family
structure. The forward and backward transforma-
tions have to resolve non-determinism.
Configurability. Non-determinism in the backward
transformation is handled by configuration para-
meters which affect the family structure. The pa-
rameters may be changed from execution to exe-
cution and should affect only new elements of the
person model in each run.
Renamings and Moves. Change operations to be
propagated include not only creations and deleti-
ons, but also renamings and moves which must
not be reduced to deletions and creations (ot-
herwise, the principle of least change (Macedo
and Cunha, 2016), which demands that the chan-
ges are propagated in a minimally invasive way,
would be violated).
Order-dependent Update Behavior. The bac-
kward transformation depends on the order in
which changes to the persons model are pro-
cessed. For example, if two persons are to be
inserted into the same family as parents, the first
one will be inserted as parent, and the second one
will follow as a child.
Specific Requirements to Change Operations.
The case description includes specific require-
ments to change operations. For example, if the
family name of a person is changed, the person
should be moved to another family (rather than
having the family name updated, with side effects
on other members).
4 SOLUTION
In the following, we will first present an initial solu-
tion which is easy to understand (Section 4.1). Since
this proposal suffers from several deficits, we will
refine it into an improved, more sophisticated solu-
tion. In passing, we will mention a number of issues
which we faced in developing the solutions; these
will be summarized and discussed systematically in
Section 5.
Incremental Bidirectional Transformations: Applying QVT Relations to the Families to Persons Benchmark
43

Listing 1: QVT-R transformation, initial version.
1 tran s form a tion f a mili e s 2 p e r so n s _ b x ( f am D B : Famili e s , p e rDB : P er s o n s ) {
2
3 top r e l a t io n F a mi l y R e g i s t e r 2 P e r s o n R e g i s t e r {
4 en f or ce d o ma in fa m DB f a m i ly R e g i s t e r : F am il i e s :: F am i l y R e g i s t e r {};
5 en f or ce d o ma in pe r DB p e r s on R e g i s t e r : P er s on s :: P e rs o n R e g is t e r {};
6 whe r e {
7 Fa th er 2 M a l e ( fa mi l yR eg i st er , p e r s o n Re g i s t e r );
8 So n 2 M al e ( f a m il y R e gi s t e r , p e r s o nR e g i s t e r );
9 Mo t h e r 2 Fe m a l e ( f am il y Re gi s te r , p e r s o nR e g i s t er );
10 Da u g h te r 2 F em a l e ( f a mi l y R eg i s t er , p e r s on R e g i s te r );
11 }
12 }
13
14 r e l a ti on Fa t h e r 2M al e {
15 fam i lyN a me , firs t N ame , f u ll Na m e : S t ri n g ;
16 en f or ce d oma in fa m DB f a m i ly R e g i s t e r : F am il i e s :: F am i l y R e g i s t e r {
17 fa m i l ie s = fa m il y : Fa m i l i e s :: F am i ly {
18 name = fa m il y N am e ,
19 fa t he r = fa t he r : F a m il ie s :: F a m i l y M e mb er {
20 name = f ir st N a m e
21 }
22 }
23 };
24 en f or ce d oma in pe r DB p e r s on R e g i s t e r : P er s on s :: P e rs o n R e g is t e r {
25 pe r so n s = mal e : P er s o n s :: Ma l e {
26 name = f u l l N a me
27 }
28 };
29 whe r e {
30 fu l l N am e = f a m i l y N a m e + ’, ’ + f i r s t N am e ;
31 fi r s t N a m e = fi rs tN a m e ( f u l lN am e );
32 fa mi ly Na me = f a m i l y N a m e ( f u l l Na me );
33 }
34 }
35 ...
36 }
4.1 Initial Version
Listing 1 shows a straightforward bidirectional trans-
formation. The candidate models — models involved
in the transformation — are declared in line 1. Ple-
ase notice that there is no distinction between inputs
and outputs; e.g., the families model serves as input
for the forward transformation and as output for the
backward transformation.
The transformation definition consists of five re-
lations, two of which are shown in Listing 1. The re-
lation starting in line 3 is a top-level relation, i.e., it is
not called in any relation and is applied automatically
to each match located in the source model. This rela-
tion serves to relate the root elements of the families
and persons models. The source and target patterns
of a relation are defined by domains. Each domain
belongs to one of the candidate models (e.g., the fa-
milies model famDB in line 4). Furthermore, it has a
unique root node which is typed (familyRegister).
The modifier enforce allows to use the domain for
enforcement (instantiation of the domain in the tar-
get model). Since both domains in lines 4–5 are mar-
ked by this modifier, the relation may be enforced in
both transformation directions. Finally, further relati-
ons are called in the where clause (lines 7–10). Only
one of these relations (Father2Male) is shown; the
other relations are defined analogously.
The relation starting in line 14 is a called rela-
tion, which is applied only when it is called expli-
citly. Then, it is applied to all matches of its source
pattern for the root element fixed in the call. Thus,
Father2Male is applied to all fathers in the families
register (implicit iteration). Each father is mapped to
a male person whose name is composed from the fa-
mily name and the first name. If executed in backward
direction, the person is mapped to a father; the name
is decomposed accordingly. The variables declared in
line 15 are used for storing the values of the name at-
tributes involved in the transformation. The equations
in the where clause (lines 30–32) compose or decom-
pose name attributes, depending on the transforma-
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
44

tion direction. In forward direction, the equation in
line 30 binds the variable fullName; the following
equations perform redundant checks. In backward di-
rection, firstName and lastName are bound in li-
nes 31–32, followed by a redundant check in line 30.
Please notice that the order of execution of equations
is determined by dataflow constraints, not by the tex-
tual order (which is immaterial). All equations are
executed in each direction, but perform different tasks
(binding of a variable vs. checking of a constraint).
The transformation definition presented in Lis-
ting 1 is executable in both directions and easy to
understand (compared to the transformation definiti-
ons to be presented below). However, it suffers from
two fundamental flaws which will be addressed by
the improved version presented below. First, due to
QVT-R’s check-before-enforce semantics, mappings
are n : 1 rather than 1 : 1: For example, different mem-
bers in the families model sharing the same family
name and first name will be mapped to the same per-
son in the persons model. Second, in backward di-
rection each person will be transformed twice, both
as a parent and as a child.
4.2 Improved Version
When implementing a bidirectional transformation in
QVT-R, the transformation developer may either pro-
vide a single transformation definition which is exe-
cutable in both directions (see above), or may create
two unidirectional transformation definitions. For full
consideration of the requirements in the Families to
Persons case, we have to resort to the latter option
because the rules for forward and backward transfor-
mations differ significantly. These differences result
from the fact that the backward transformation needs
to be configurable with respect to the mapping of per-
sons to parents or children and to existing or new fa-
milies, respectively. Furthermore, the enforcement of
1 : 1 mappings is realized with the help of rules which
can be executed only in one direction.
4.2.1 Forward Transformation
Listing 2 shows a unidirectional forward transfor-
mation which enforces 1 : 1 mappings. In contrast
to the bidirectional transformation definition in Lis-
ting 2, domains in the families model are marked
as checkonly, indicating that they may not be used
for enforcement. In the transformation definition, we
make use of a language construct which has not been
mentioned so far: Primitive domains (e.g., line 19) are
parameters which are passed to called relations; here,
we employ them for passing collections.
Enforcing injective mappings requires a procedu-
ral style of specification: The collection of elements
which have been matched or created so far is supp-
lied as parameter to called relations; a postcondition
ensures that the where clause fails if an element is
reused according to the check-before-enforce seman-
tics. The failing postcondition enforces the creation
or matching of a new element.
From the top-level relation, the relation Member2-
Person is called. Please notice that members are pro-
cessed sequentially; this is achieved by calling the
relation on a specific member (lines 9, 49). Furt-
hermore, the relation is supplied with two collecti-
ons: the collection of other members which still need
to be processed (line 19), and the collection of per-
sons which have already been created or matched
(line 21). These parameters are passed on to the re-
lations handling the specific cases. Thus, the relation
Member2Person acts as a switch; please notice that
exactly one of the called relations will be applicable,
such that sequential processing of matches is retained.
From the specific relations, only Daughter2Female
is shown. In its where clause, line 46 prevents reuse
of a person object in spite of the check before en-
force semantics: The person to be created or matched
must not be contained in the collection of elements
having been gathered so far. In the recursive call of
Member2Person, the new element is added to the col-
lection of persons which was passed as parameter. Si-
milarly, the collection of members which still need to
be processed is reduced by the current member.
While this approach works, it is a laborious way
to guarantee injective mappings. Furthermore, in the
opposite direction the roles of the collections passed
as parameters need to be switched. As a consequence,
different transformation definitions are needed for dif-
ferent directions.
4.2.2 Backward Transformation
To enforce injective mappings, we may apply the
same method in the backward transformation as in
the forward transformation. To simplify matters and
to avoid redundancies in the presentation, we will
provide a simplified backward transformation which
does not enforce injective mappings, but avoids du-
plicate transformations of persons into parents and
children (see remark at the end of Section 4.1). Furt-
hermore, the backward transformation is configurable
with respect to the mappings to parents or children
and existing or new families, respectively. Excerpts
from the transformation definition are displayed in
Listings 3 and 4.
Since only models may be passed as parameters to
transformations, we introduce a configuration model
Incremental Bidirectional Transformations: Applying QVT Relations to the Families to Persons Benchmark
45

Listing 2: Forward transformation.
1 tr a n s f o rm a t i o n fa m i l ie s 2 p er s o n s ( fam D B : Fami l i es , p erD B : P e r so n s ) {
2 top r e l a t io n F a mi l y R e g i s t e r 2 P e r s o n R e g i s t e r {
3 me m be rs : S eq u e n c e ( F am i l i e s :: F am il y M e m b e r );
4 ch ec ko n l y do m ai n f amD B fa m i l y R e g i s t er : F a m i l ie s :: F a mi l y R e g is t e r {};
5 en f or ce d o ma in pe r DB p e r s on R e g i s t e r : P er s on s :: P e rs o n R e g is t e r {};
6 whe r e {
7 me m be r s = a ll Me mb er s ( f a m i l yR e g i s t e r );
8 if m e m b ers -> s ize () > 0 then
9 M em be r 2 P e r so n ( m embers -> fi r st () ,
10 members -> e xc lu di n g ( member s - > f i rst ()) ,
11 p e rs o n R eg i s t er , S e q u en ce { })
12 e lse
13 true
14 endi f ;
15 }
16 }
17 r e l a ti on Me mb e r 2 P e r s on {
18 ch ec ko n l y do m ai n f amD B mem b er : F am il i e s :: F am i l y M e m b e r {};
19 pr im it i v e do m ai n m e m be r s : S eq u e n ce ( F am i l i es :: F a m il yM e m b e r ) ;
20 en f or ce d oma in pe r DB p e r s on R e g i s t e r : P er s on s :: P e rs o n R e g is t e r {};
21 pr im it i v e do m ai n p e r so n s : S eq u e n ce ( P e r s on s :: P e rs o n );
22 whe r e {
23 Fa th er 2 M a l e ( m e m b e r , members , per s o n Re g i s te r , p er so n s );
24 So n 2 M al e ( member , m e m bers , p er so n Re gi s te r , pe r so ns );
25 Mo t h e r 2 Fe m a l e ( member , m e m b ers , p er so n Re g i s te r , p e r so n s );
26 Da u g h te r 2 F em a l e ( member , me m b e rs , p er s o n Re g i s te r , p er so n s );
27 }
28 }
29 ...
30 r e l a ti on Da ug h t e r2 F e m a l e {
31 firs t N ame , fam i ly N a me , f u ll Na m e : S t ri n g ;
32 ch ec ko n l y do m ai n f amD B mem b er : F am il i e s :: F am i l y M e m b e r {
33 n ame = fi r s tNa m e ,
34 d a u g h t e r s I n v e r s e = f a mi l y : F a mi li e s :: Fam i ly {
35 name = f am il yN am e
36 }
37 };
38 pr im it i v e do m ai n m e m be r s : S eq u e n ce ( F am i l i es :: F a m il yM e m b e r ) ;
39 en f or ce d o ma in pe r DB p e r s on R e g i s t e r : P er s on s :: P e rs o n R e g is t e r {
40 pe r so n s = f e ma l e : Pe rs o ns :: Fe m al e {
41 name = f u l l N a me
42 }
43 };
44 pr im it i v e do m ai n p e r so n s : S eq u e n ce ( P e r s on s :: P e rs o n );
45 whe r e {
46 p ersons -> e x c l u d es ( f e ma l e );
47 fu l l N am e = f a m i l y N a m e + ’, ’ + f i r s t N am e ;
48 if m e m b ers -> s ize () > 0 then
49 M em be r 2 P e r so n ( m e mbers -> fi r st () ,
50 members -> e xc lu di n g ( member s - > f i rst ()) ,
51 p e rs o n R eg i s t er , person s - > a ppe nd ( fe m al e ))
52 e lse
53 true
54 endi f ;
55
56 }
57 }
58 }
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
46

Listing 3: Backward transformation (part 1).
1 tr a n s f o rm a t i o n pe r s o ns 2 f a mi l i e s
2 ( p erD B : P e r s ons , c o n f : C o n f i g , fam D B : Fa mi l i e s ) {
3 top r e l a t io n F a mi l y R e g i s t e r 2 P e r s o n R e g i s t e r {
4 pre fe r Pa r en t , p r e f er E x i s t in g : B oo l ea n ;
5 ch ec ko n l y do m ai n p erD B pe r s o n R e g i s t er : P e r so n s :: Pe r s o n R eg i s t e r {};
6 ch ec ko n l y do m ai n c o nf c o n fi g u r a t io n : C o nf i g :: C o nf i g u r a t i on {
7 p r e fe r P a r e n tT o C h i l d = p re f er P ar e nt ,
8 p r e f e r E x i s t i n g T o N e w F a m i l y = p r e f er E x i s t in g
9 };
10 en f or ce d oma in fa m DB f a m i ly R e g i s t e r : F am il i e s :: F am i l y R e g i s t e r {};
11 whe r e {
12 Ma le 2M e m b e r
13 ( pe r so nR e gi st e r , pr e fe r Pa r en t , p re f e r Ex i st in g , f a m i l y R eg i s t e r );
14 Fe m a l e 2 Me m b e r
15 ( pe r so nR e gi st e r , pr e fe r Pa r en t , p re f e r Ex i st in g , f a m i l y R eg i s t e r );
16 }
17 }
18 r e l a ti on Fe ma l e 2 M e m b er {
19 f ullN a m e , f i rst N ame , fa mi ly Na me : S tr i ng ;
20 m a p T o M o t h e r : B oo l e a n ;
21 ch ec ko n l y do m ai n p erD B pe r s o n R e g i s t er : P e r so n s :: Pe r s o n R eg i s t e r {
22 pe r so n s = f e ma l e : Pe rs o ns :: Fe m al e {
23 name = f u l l N a me
24 }
25 };
26 pr im it i v e do m ai n pr ef e r P a r e n t : B o ol e a n ;
27 pr im it i v e do m ai n pr e f e r E xi s t i n g : B oo le a n ;
28 en f or ce d oma in fa m DB f a m i ly R e g i s t e r : F am il i e s :: F am i l y R e g i s t e r {};
29 whe r e {
30 fi r s t N a m e = fi rs tN a m e ( f u l lN am e );
31 fa mi ly Na me = f a m i l y N a m e ( f u l l Na me );
32 ma pT oM o t h e r = m a p T o M o t h e r ( f am il y Re g i s te r ,
33 pr e fe r Pa r en t , p re f er Ex i st in g ,
34 firs t Nam e , f a m i l y N a m e );
35 if ma pT oM o t h e r th e n
36 F em al e 2 M o t he r ( f e m a l e ,
37 p r ef e r E xi s t i ng , fi r s tNa m e ,
38 fa m ily N ame , f am i l y R e gi s t e r )
39 e lse
40 F em a l e 2 D a u g h t e r ( female ,
41 pr e fe rE x is ti n g , firs t Nam e ,
42 fam i l yN a me , f a m i l yR e g i s t er )
43 endi f ;
44 }
45 }
46 ...
(parameter conf in line 2 in Listing 3) which contains
a single configuration object storing the values of the
configuration parameters. Accordingly, the top-level
relation for mapping family to person registers is ex-
tended with a third domain from which the parameter
values are read (lines 6–9). These values are passed
on to called relations. Please recall that QVT-R al-
lows to define transformations among more than two
models; here, two models serve as input, and one mo-
del is created or updated as output.
From the top-level relation, two relations are cal-
led which are used to map males and females, re-
spectively. These relations serve as switches for de-
ciding whether a person should be mapped either to
a parent or to a child. This decision is performed
in the where clause. For example, in the relation
Female2Member the predicate mapToMother is eva-
luated which depends on the current state of the fa-
mily register, the configuration parameters, and the
first name and the family name of the female to be
transformed (lines 32–34). Depending on the result
of the evaluation, the female is mapped to a mother
or to a daughter by calling corresponding relations
Female2Mother or Female2Daughter, respectively.
Incremental Bidirectional Transformations: Applying QVT Relations to the Families to Persons Benchmark
47

Listing 4: Backward transformation (part 2).
1 ...
2 qu e ry m a p T o M o t h e r ( fa mi l y R e g is t e r : F am il i e s :: F a mi ly R eg i s t er ,
3 pr ef e r P a r e n t : Boolean , p r e f e rE x i s t i ng : B o o lean ,
4 fi r s t N a m e : St r i n g , fa mi ly Na me : S tr i ng ) : B oo l ea n {
5 if m a t c h i n g M o t h e r Ex i s t s ( f a mi l y R eg i st er , fi r s tNa m e , f a m i l y N a m e ) th e n
6 pr ef e r P a r e n t or
7 n o t m a t c h i n g D a u g h t er E x i s t s ( f am i ly Re g is te r , f i rst N a me , fa mi ly Na me )
8 e lse
9 n o t m a t c h i n g D a u g h t er E x i s t s
10 ( fa m il yR e gi st e r , firs t Nam e , f a m i l y N a m e ) a n d
11 pr e f e r P a r e n t and
12 n o t ( p r e f e r E x i s t in g and
13 ma t c h i n g F a m il y E x i s t s ( fa mi l yR e g i st e r , f a m i l y N a m e ) and
14 not m a t c h i n g F a m i l y W i t h o u t M o t h e r E x i s t s
15 ( f a m il y R e gi s t e r , f a mi ly N a me ))
16 end i f
17 }
18 r e l a ti on Fe ma l e 2 M o t h er {
19 ch ec ko n l y do m ai n p erD B fem a le : P er s o n s :: F em a le {};
20 pr im it i v e do m ai n pr e f e r E xi s t i n g : B oo le a n ;
21 pr im it i v e do m ai n fi r s t N a m e : S tr i ng ;
22 pr im it i v e do m ai n fa m i l y N a m e : S tr i ng ;
23 en f or ce d oma in fa m DB f a m i ly R e g i s t e r : F am il i e s :: F am i l y R e g i s t e r {
24 fa m i l ie s = fa m il y : Fa m i l i e s :: F am i ly {
25 name = fa m il y N am e ,
26 mo t he r = mo t he r : F a m il ie s :: F a m i l y M e mb er {
27 name = f ir st N a m e
28 }
29 }
30 };
31 w hen {
32 mot h er =
33 if m at c h i n g M o t h er E x i s t s
34 ( f a m il y R e gi s t e r , firs t Nam e , f a m i l y N a m e ) t h en
35 m at c h i n g Mo t h e r ( f am il y Re gi s te r , first N ame , f a m i l y N a m e )
36 else
37 mo t he r
38 end i f ;
39 fam i ly =
40 if n o t m o th e r . o c l Is U n d e f in e d () th e n
41 mo t he r . m o th e r I n v e r se
42 else
43 if p r e fe r E x i s ti n g a n d
44 m a t c h i n g F a m i l y W i t h o u t M o t h e r E x i s t s
45 ( f a m il y R e gi s t e r , f a mi ly N a me )
46 then
47 m a t c h i n g F a m i l y W i t h o u t M o t h e r ( f am i ly Re g is t e r , f a m i l y N a m e )
48 else
49 fam i ly
50 end i f
51 end i f ;
52 }
53 }
54 ...
55 }
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
48

The predicate mapToMother is defined by an OCL
query (lines 2–17 in Listing 4) which realizes the
mapping rules explained in Section 3.2. As menti-
oned in Section 3.3, these rules should become ef-
fective only for new persons; the previous mappings
should remain untouched. Thus, it is checked first
whether a matching member already exists in the fa-
milies model. For example, if the transformation is
configured such that children are preferred and a ma-
tching mother is available (but not a matching daugh-
ter), the current female is mapped to a mother rather
than to a daughter.
Finally, four relations are responsible for actu-
ally performing the required mapping. For exam-
ple, Female2Mother (lines 18–53) maps a female to a
mother. This relation is equipped with a when clause
which is executed before the target domain is instan-
tiated (lines 31–52). If the when clause were omit-
ted, either the check-before-enforce semantics would
apply, resulting in a reuse of both the family and
the mother, or both elements would be instantiated
anew. In this way, it would not be possible to insert
a new mother into an existing family. Therefore, the
when clause contains two equations which conditio-
nally bind the variables mother and family before
the target domain is processed. If the respective bin-
ding conditions do not hold, the variables retain their
previous bindings, i.e., they remain unbound. If the
mother may be reused, both variables are bound. If
only the family may be reused, the first variable re-
mains unbound, while the second variable is bound.
5 EVALUATION
In the following, we will first examine the behavior of
the transformations presented above. Subsequently,
we will discuss a number of issues which emerged
in the development of the solution to the benchmark
case.
5.1 Behavior
The following statements refer to the improved ver-
sion of the solution presented in Section 4.2. More
specifically, we will refer to the forward transfor-
mation ensuring injective mappings (Section 4.2.1)
and the configurable backward transformation avoi-
ding duplicate mappings (Section 4.2.2). Although
the backward transformation does not ensure injecti-
vity, it may be easily rewritten into an injective trans-
formation by applying the method demonstrated for
the forward transformation. Altogether, the injective
forward transformation and the injective and configu-
rable backward transformation constitute a best effort
solution in the sense that its functional behavior can-
not be improved further if QVT-R is used as the trans-
formation language (assuming the semantics defined
in the standard).
5.1.1 Batch Transformations
The solution satisfies all requirements concerning ba-
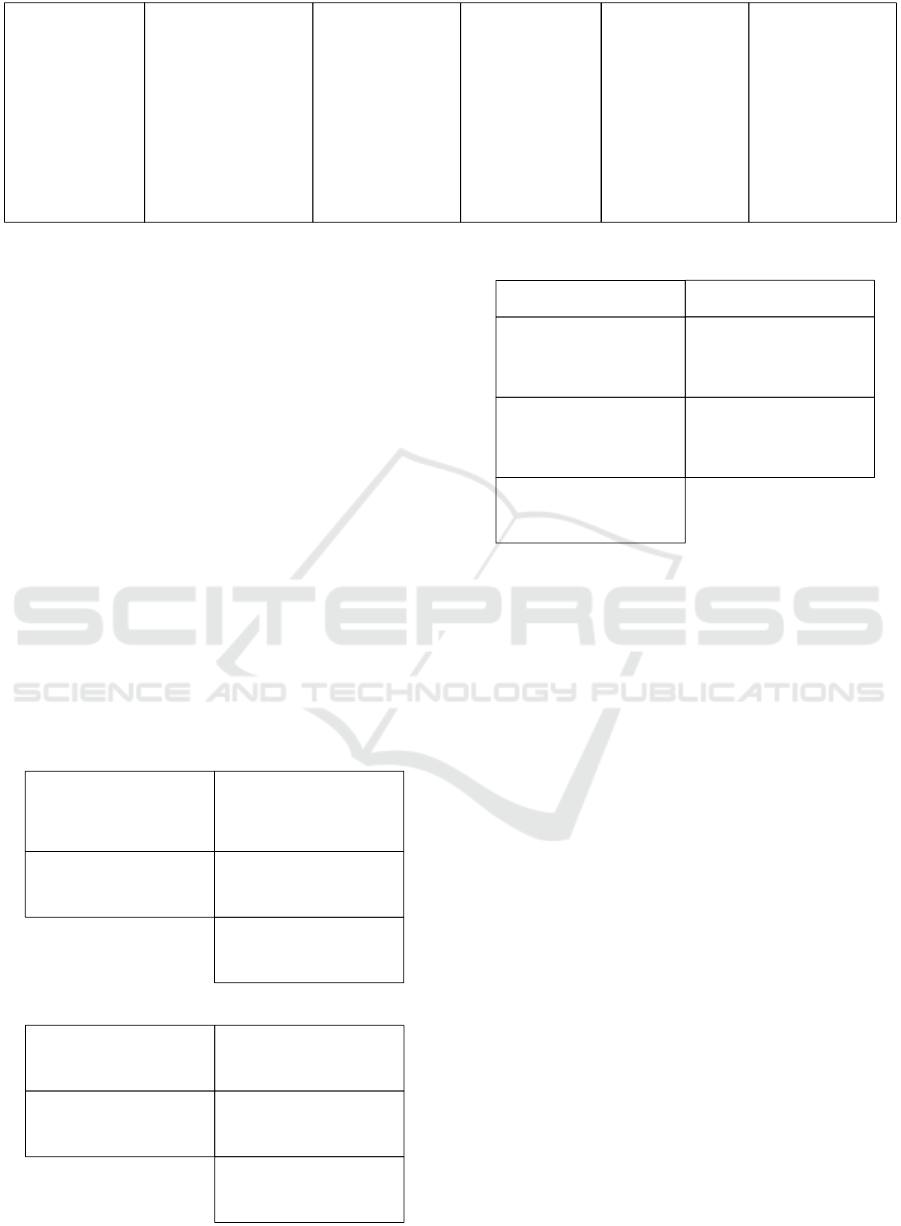
tch transformations (Section 3.2). This is illustrated in
Figure 3, in which models are represented by a sim-
ple and intuitive textual notation. The family regis-
ter shown in Figure 3a is transformed into the per-
son register (b), even though the family register con-
tains two family members with the same name (John
Smith). Furthermore, a batch backward transforma-
tion of (b) results in (c) if parents and existing fami-
lies are preferred, in (d) if parents and new families
are preferred, in (e) for preferred children and exis-
ting families, and in (f) for preferred children and new
families. Notably, (c) depends on the order in which
family members are processed. Since there is no way
to resolve this non-determinism for batch transforma-
tions (please recall that all collections are assumed to
be unordered), this behavior does conform to the pro-
blem specification.
5.1.2 Incremental Transformations
The requirements to incremental transformations
(Section 3.3) are satisfied only partially. Insertions
and deletions are propagated correctly in both directi-
ons as long as there are no duplicate names (see be-
low). In particular, in backward direction the transfor-
mation definition ensures that the configuration para-
meters take effect only for new persons (e.g., it is en-
sured that a person who has already been mapped to a
parent is not re-mapped to a child).
The problems which are caused by duplicate na-
mes are illustrated by Figure 4. Let us assume that
the person register (a) has been transformed into the
family register (b), with both parents and existing fa-
milies being preferred. During this transformation,
a temporary trace is constructed which records the
mappings between family members and persons. This
trace is thrown away after the transformation; thus,
the correspondences are lost. Next, one of the per-
sons is deleted (c). When propagating this change,
we would like to ensure that the
corresponding family
member is deleted. However, it can only be guaran-
teed that a
corresponding family member is deleted,
resulting either in (d) or (e). Thus, propagation is
non-deterministic. A deterministic behavior could be
achieved only with the help of a persistent trace.
Incremental Bidirectional Transformations: Applying QVT Relations to the Families to Persons Benchmark
49
a)
FamilyRegister
FamilySmith
FatherJohn
MotherMary
SonKevin
DaughterKatie
FamilySmith
FatherJohn
MotherClaire
FamilyMiller
b)
PersonRegister
MaleSmith,John
FemaleSmith,Mary
MaleSmith,Kevin
FemaleSmith,Katie
MaleSmith,John
FemaleSmith,Claire
c)
FamilyRegister
FamilySmith
FatherJohn
MotherMary
SonKevin
SonJohn
DaughterKatie
DaughterClaire
d)
FamilyRegister
FamilySmith
FatherJohn
FamilySmith
MotherMary
FamilySmith
FatherKevin
FamilySmith
MotherKatie
FamilySmith
Father John
FamilySmith
MotherClaire
e)
FamilyRegister
FamilySmith
SonJohn
SonKevin
SonJohn
DaughterMary
DaughterKatie
DaughterClaire
f)
FamilyRegister
FamilySmith
SonJohn
FamilySmith
DaughterMary
FamilySmith
SonKevin
FamilySmith
DaughterKatie
FamilySmith
Son John
FamilySmith
DaughterClaire
Figure 3: Test cases for batch transformations.
Furthermore, there is no way to recognize name
changes or moves. This is illustrated in Figure 5 for
name changes. Initially, the family register (a) has
been transformed into the person register (b). Con-
currently, the first name is changed in the family re-
gister (c), and the birthday is set in the person regis-
ter (d). Transforming incrementally in forward di-
rection results in the person register (e), where Mary
has been deleted and Mary-Anne has been re-inserted
(with an unset birthday). Thus, name changes result
in deletions and insertions. This behavior is caused
by the check-before-enforce semantics: Since there is
no matching target pattern any more, the old person
is deleted. Furthermore, a new person is inserted with
the matching full name. There is no way to “fix” an
existing target pattern instance such it matches again
a modified source pattern instance.
Finally, it is not possible to propagate changes in
the order in which they occurred. This is illustrated
in Figure 6. Let us assume that an empty person re-
gister (a) has been transformed into an empty family
b)
FamilyRegister
FamilySmith
FatherJohn
SonJohn
d)
FamilyRegister
FamilySmith
FatherJohn
a)
PersonRegister
MaleSmith,John
MaleSmith,John
c)
PersonRegister
MaleSmith,John
e)
FamilyRegister
FamilySmith
SonJohn
Figure 4: Test case for duplicates.
a)
FamilyRegister
FamilySmith
MotherMary
b)
PersonRegister
FemaleSmith,Mary
Birthday=undefined
d)
PersonRegister
FemaleSmith,Mary
Birthday=1980‐05‐07
c)
FamilyRegister
FamilySmith
MotherMary‐Anne
e)
PersonRegister
FemaleSmith,Mary‐Anne
Birthday=undefined
Figure 5: Test case for name changes.
b)
FamilyRegister
a)
PersonRegister
c)
1:InsertMale
("Smith,John")
2:InsertMale
("Smith,Jack")
d)
FamilyRegister
FamilySmith
FatherJohn
SonJack
e)
1:InsertMale
("Smith,Jack")
2:InsertMale
("Smith,John")
f)
FamilyRegister
FamilySmith
FatherJack
SonJohn
g)
PersonRegister
MaleSmith,John
MaleSmith,Jack
Figure 6: Test case for order-dependent changes.
register (b). For further propagations, both parents
and families are preferred. In the delta (sequence of
change operations) shown in (c), John is inserted be-
fore Jack. An order-preserving propagation of these
changes results in (d). If changes are applied in the
opposite order (e), order-preserving propagation re-
sults in (f), which differs from (d). Since both deltas
result in the same person register (g), the QVT-R en-
gine cannot reconstruct the delta and returns either (d)
or (f), depending on the non-deterministic selection of
the order in which source pattern instances are proces-
sed.
5.1.3 Transformation Laws
In Section 3.4, we introduced the notions of correct-
ness and hippocraticness, as well as round-trip laws.
Correctness has already been discussed above. Both
forward and backward transformations are hippocra-
tic: If the transformation is re-executed in the same
direction, the target model is not modified any more.
Please notice that this property holds even if configu-
ration parameters are changed for the backward trans-
formation: The parameters affect only the transfor-
mation of new persons. Since no changes are applied
after the first run, there are no new persons; rather, all
persons already have matching family members being
reused in the transformation.
Likewise, round-trip laws hold for both trans-
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
50

formation orders (forward-backward and vice versa).
For example, after having transformed the family re-
gister in Figure 3a into the person register (b), an im-
mediate incremental transformation in the opposite
direction does not modify the original family regis-
ter any more — even though this state of the families
model could not have been created by any batch trans-
formation.
However, it should be noted that in general neither
hippocraticness nor round-trip laws are guaranteed
per se: In QVT-R, transformations may be defined
which violate these laws. Thus, transformation laws
need to be checked for each transformation definition.
5.2 Issues
In the case study presented in this paper, we identified
the following issues summarized below.
Issue 1 (Imprecise change propagation). Due to the
strictly state-based design, changes may be propaga-
ted only imprecisely.
As already mentioned in Section 2, QVT-R fol-
lows a purely state-based approach to incremental
transformations: The only information which is as-
sumed to be present are the states of the source and
the target model. In this way, the prerequisites for the
execution of incremental transformations are minimi-
zed. In particular, QVT-R assumes neither deltas nor
persistent traces. As shown in Section 5.1.2, this de-
cision limits the preciseness of change propagations:
In the presence of duplicates, precise change propaga-
tion requires persistent traces. For example, if one of
two family members with the same name is deleted, it
is impossible to guarantee deletion of “the correspon-
ding person” because the correspondences are not sto-
red. Furthermore, order-dependent changes can be
supported only with the help of deltas. Finally, chan-
ges in source pattern instances cannot be propagated
to target pattern instances, due to the check-before-
enforce semantics. Thus, name changes and moves
cannot be propagated.
Issue 2 (Unidirectional transformations). Bidirectio-
nal transformation problems may have to be solved by
pairs of unidirectional transformation definitions.
The Familes to Persons case demands for bidi-
rectional transformations. QVT-R supports the de-
finition of both uni- and bidirectional transformati-
ons. While we proposed a bidirectional transforma-
tion definition as an initial solution (Section 4.1),
the improved solution required two unidirectional
transformation definitions because the rules for for-
ward and backward transformations differ signifi-
cantly (Section 4.2). First, the approach for ensuring
injective mappings requires a unidirectional transfor-
mation definition, due to the bookkeeping of mat-
ches in the source and the target model. Second,
the backward transformation needs to resolve non-
determinism in a configurable way; the respective ru-
les have no counterpart in the definition of the forward
transformation.
Issue 3 (Non-injective mappings). Due to the check-
before-enforce semantics, multiple source pattern in-
stances may be mapped to the same target pattern in-
stance.
The Families to Persons case is designed judici-
ously such that keys may be assumed neither in the
families nor in the persons model. Thus, the check-
before-enforce semantics results in a reuse of a per-
son if a person with the same name is already pre-
sent (likewise in the opposite direction). Neverthe-
less, we managed to present a solution which enfor-
ces injective mappings (Section 4.2.1). However, this
solution requires to keep track of matches in both the
source and the target model and has a strongly pro-
cedural flavor. Furthermore, it excludes the develop-
ment of a single bidirectional transformation defini-
tion.
Issue 4 (Duplicate transformation). Since relations
are applied independently of each other, model ele-
ments may be transformed multiple times.
In QVT-R, relations are applied to source pattern
instances when they satisfy the constraints defined in
the relation. Thus, the same source pattern instan-
ces may be transformed multiple times. This problem
occurred in the initial version of the transformation
definition in backward direction (a person is mapped
both to a parent and a child, see Section 4.1). We sol-
ved this problem by rewriting the relations such that
each person is considered only once for being trans-
formed. This problem is not uncommon in rule-based
languages, but there are other approaches where con-
flicts are recognized and resolved during execution
(Becker et al., 2007).
6 RELATED WORK
Research on QVT-R has primarily focused on theore-
tical work concerning the semantics definition (Ste-
vens, 2010). For example, (Bradfield and Stevens,
2012) and (Bradfield and Stevens, 2013) address the
formalization of check-only and enforcing transfor-
mations, respectively. Deviating from the standard,
(Macedo and Cunha, 2016) proposes a semantics de-
finition following the principle of least change. Ho-
wever, this proposal retains the restrictions resulting
Incremental Bidirectional Transformations: Applying QVT Relations to the Families to Persons Benchmark
51

from the state-based approach to change propagation.
A small number of application-oriented papers
aim at evaluating different aspects of QVT-R such
as expressiveness and conciseness. So far, all of
these studies have dealt with bidirectional batch (rat-
her than incremental) transformations (Westfechtel,
2016a; Westfechtel, 2015; Westfechtel, 2016b).
A precursor of the solution to the Families to Per-
sons benchmark presented in this paper was deve-
loped for the Transformation Tool Contest (Anjorin
et al., 2017a), based on the Benchmarx framework
proposed in (Anjorin et al., 2017b). This preliminary
solution was provided as an illustrative reference to
case developers, but it was not published and did not
take part in the contest. Furthermore, the preliminary
solution suffered from several limitations (e.g., non-
injective mappings) which were addressed in the im-
proved solution presented in this paper.
All solutions were developed and tested with me-
dini QVT — to the best of our knowledge the only
tool for QVT-R which is currently available (ikv++
technologies, 2017). While medini QVT conforms to
the syntax of the QVT-R standard, it deviates conside-
rably from the semantics defined in the standard. To
avoid the discussion of tool-specific behavior, the cur-
rent paper exclusively uses the semantics definition in
the standard as reference point; medini QVT was em-
ployed primarily for syntax checking.
7 CONCLUSION
We presented a solution to the Families to Persons
case in QVT-R, a declarative bidirectional model
transformation language defined as a standard by the
Object Management Group. The solution constitutes
a best effort approach in the sense that all require-
ments from the Families to Persons case were addres-
sed which can be addressed in QVT-R. An evaluation
of the solution identified several issues such as im-
precise change propagation, the need of providing a
pair of unidirectional transformation definitions, n : 1
mappings, and duplicate transformations. These ob-
servations motivate further studies concerning the ex-
pressiveness of QVT-R with respect to the definition
of bidirectional incremental transformations.
Furthermore, future work will address a detailed
analysis of the solutions to the Families to Persons
case, as described briefly in (Anjorin et al., 2017b)
and the papers accepted for the Tool Transformation
Contest (Garcia-Dominguez et al., 2017). All of this
work is based on the Benchmarx framework, which
we consider the first operational framework for eva-
luating bidirectional transformations. In addition, we
are implementing additional cases in the Benchmarx
framework, based on the cases proposed in (West-
fechtel, 2016a). In this way, we hope to trigger more
work on the evaluation of bidirectional transformati-
ons — which, as we believe, is urgently needed.
ACKNOWLEDGEMENTS
The author gratefully acknowledges the support pro-
vided by Anthony Anjorin and Erhan Leblebici for the
integration of the medini QVT implementation of the
Families to Persons benchmark into the Benchmarx
framework.
REFERENCES
Anjorin, A., Buchmann, T., and Westfechtel, B. (2017a).
The families to persons case. In (Garcia-Dominguez
et al., 2017).
Anjorin, A., Cunha, A., Giese, H., Hermann, F., Rensink,
A., and Sch
¨
urr, A. (2014). BenchmarX. In Candan,
K. S., Amer-Yahia, S., Schweikardt, N., Christophi-
des, V., and Leroy, V., editors, Workshop Proceedings
of the EDBT/ICDT 2014 Joint Conference, volume
1133 of CEUR Workshop Proceedings, pages 82–86,
Athens, Greece.
Anjorin, A., Diskin, Z., Jouault, F., Ko, H.-S., Leblebici, E.,
and Westfechtel, B. (2017b). Benchmarx reloaded: A
practical framework for bidirectional transformations.
In Eramo, R. and Johnson, M., editors, Sixth Internati-
onal Workshop on Bidirectional Transformations (BX
2017), volume 1827 of CEUR Workshop Proceedings,
pages 15–30, Uppsala, Sweden.
Becker, S. M., Herold, S., Lohmann, S., and Westfechtel,
B. (2007). A graph-based algorithm for consistency
maintenance in incremental and interactive integration
tools. Software and Systems Modeling, 6(3):287–316.
Bradfield, J. and Stevens, P. (2012). Recursive checkonly
QVT-R transformations with general when and where
clauses via the modal mu calculus. In de Lara, J. and
Zisman, A., editors, Proceedings of the 15th Inter-
national Conference on Fundamental Approaches to
Software Engineering (FASE 2012), volume 7212 of
Lecture Notes of Computer Science, pages 194–208,
Tallinn, Estonia. Springer-Verlag.
Bradfield, J. and Stevens, P. (2013). Enforcing QVT-
R with mu-calculus and games. In Cortellessa, V.
and Varr
´
o, D., editors, Proceedings of the 16th Inter-
national Conference on Fundamental Approaches to
Software Engineering (FASE 2013), volume 7793 of
Lecture Notes of Computer Science, pages 282–296,
Rome, Italy. Springer-Verlag.
Czarnecki, K., Foster, J. N., Hu, Z., L
¨
ammel, R., Sch
¨
urr, A.,
and Terwilliger, J. F. (2009). Bidirectional transforma-
tions: A cross-discipline perspective. In Paige, R. F.,
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
52

editor, Proceedings of the Second International Con-
ference on Theory and Practice of Model Transforma-
tions (ICMT 2009), volume 5563 of Lecture Notes of
Computer Science, pages 260–283, Zurich, Switzer-
land. Springer-Verlag.
Czarnecki, K. and Helsen, S. (2006). Feature-based sur-
vey of model transformation approaches. IBM Sys-
tems Journal, 45(3):621–645.
Foster, J. N., Greenwald, M. B., Moore, J. T., Pierce, B. C.,
and Schmitt, A. (2007). Combinators for bidirecti-
onal tree transformations: A linguistic approach to
the view-update problem. ACM Transactions on Pro-
gramming Languages and Systems, 29(3):17:1–17:65.
Garcia-Dominguez, A., Hinkel, G., and Krikava, F., editors
(2017). Proceedings of the 10th Transformation Tool
Contest (TTC 2017), volume 2026 of CEUR Workshop
Proceedings, Marburg, Germany.
Hidaka, S., Tisi, M., Cabot, J., and Hu, Z. (2016).
Feature-based classification of bidirectional transfor-
mation approaches. Software and Systems Modeling,
15(3):907–928.
ikv++ technologies (2017). medini QVT.
http://projects.ikv.de/qvt.
Libkin, L. (2004). Elements of Finite Model Theory.
Springer-Verlag, Berlin.
Macedo, N. and Cunha, A. (2016). Least-change bidirectio-
nal model transformation with QVT-R and ATL. Soft-
ware and Systems Modeling, 15(3):783–810.
Object Management Group (2014). Object Constraint Lan-
guage Version 2.4. Needham, MA, formal/2014-02-03
edition.
Object Management Group (2016a). Meta Object Facility
(MOF) 2.0 Query/View/Transformation Specification
Version 1.3. Needham, MA, formal/2016-06-03 edi-
tion.
Object Management Group (2016b). OMG Meta Object Fa-
cility (MOF) Core Specification Version 2.5.1. Need-
ham, MA, formal/2016-11-01 edition.
Steinberg, D., Budinsky, F., Paternostro, M., and Merks,
E. (2009). EMF Eclipse Modeling Framework. The
Eclipse Series. Addison-Wesley, Upper Saddle River,
NJ, 2nd edition.
Stevens, P. (2010). Bidirectional model transformations in
QVT: Semantic issues and open questions. Software
and Systems Modeling, 9(1):7–20.
Westfechtel, B. (2015). A case study for evaluating bidi-
rectional transformations in QVT Relations. In Filipe,
J. and Maciaszek, L., editors, Proceedings of the 10th
International Conference on the Evaluation of Novel
Approaches to Software Engineering (ENASE 2015),
pages 141–155, Barcelona, Spain. INSTICC, SCITE-
PRESS.
Westfechtel, B. (2016a). Case-based exploration of bidi-
rectional transformations in QVT relations. Software
and Systems Modeling. Online First.
Westfechtel, B. (2016b). A case study for a bidirectional
transformation between heterogeneous metamodels in
QVT Relations. In Filipe, J. and Maciaszek, L., edi-
tors, Proceedings of the 10th International Conference
on the Evaluation of Novel Approaches to Software
Engineering (ENASE 2015) — Revised Selected Pa-
pers, volume 599 of Communications in Computer
and Information Science, pages 141–161, Berlin, Hei-
delberg, New York. Springer-Verlag.
Incremental Bidirectional Transformations: Applying QVT Relations to the Families to Persons Benchmark
53
