
Forecasting Short-term Solar Radiation for
Photovoltaic Energy Predictions
Alessandro Aliberti
1
, Lorenzo Bottaccioli
1
, Giansalvo Cirrincione
2
,
Enrico Macii
1
, Andrea Acquaviva
1
and Edoardo Patti
1
1
Dept. of Control and Computer Engineering, Politecnico di Torino, Torino, Italy
2
Universite de Picardie Jules Verne, Amiens, France
{giansalvo.cirrincione}@u-picardie.fr
Keywords:
Solar Radiation Forecast, Artificial Neural Networks, Photovoltaic System, Energy Forecast, Renewable
Energy.
Abstract:
In the world, energy demand continues to grow incessantly. At the same time, there is a growing need to
reduce CO
2
emissions, greenhouse effects and pollution in our cities. A viable solution consists in producing
energy by exploiting renewable sources, such as solar energy. However, for the efficient use of this energy,
accurate estimation methods are needed. Indeed, applications like Demand/Response require prediction tools
to estimate the generation profiles of renewable energy sources.
This paper presents an innovative methodology for short-term (e.g. 15 minutes) forecasting of Global Ho-
rizontal Solar Irradiance (GHI). The proposed methodology is based on a Non-linear Autoregressive neural
network. This neural network has been trained and validated with a dataset consisting of solar radiation sam-
ples collected for four years by a real weather station. Then GHI forecast, the output of the neural network, is
given as input to our Photovoltaic simulator to predict energy production in short-term time periods. Finally,
experimental results for both GHI forecast and Photovoltaic energy prediction are presented and discussed.
1 INTRODUCTION
The widespread development of Renewable Energy
Sources (RES) in our cities, such as Photovoltaic (PV)
systems, is changing the electrical energy production,
consumption and distribution. Our society is facing
the transition from centralized and hierarchical po-
wer distribution systems to distributed and coopera-
tive ones, generally called Smart Grids. Smart Grid
technologies are opening the electrical marketplace
to new actors (e.g. prosumers and energy aggrega-
tors). Currently, power grid stability is achieved by
classic generation plants using primary and secon-
dary reserve at large-scale. Whilst, in a Smart Grid
scenario, such a new actors can actively contribute to
load balancing by fostering novel services for network
management and stability. Demand/Response (Siano,
2014) is an example of application for Smart Grid
management. It permits achieving a temporary vir-
tual power plant (Vardakas et al., 2015) by changing
the energy consumption pattern of consumers to ma-
tch RES energy production or to fulfil grid operation
requirements. This process is generally done every
15 minutes. To achieve these goals, prediction tools
for both RES energy generation and consumption are
needed.
In this work, we present a methodology for Pho-
tovoltaic energy prediction starting from forecasting
short-term solar radiation. The forecast of solar radi-
ation is obtained exploiting a Nonlinear Autoregres-
sive neural network. We trained and validated this
neural network with a dataset consisting of four ye-
ars of Global Horizontal Solar Irradiance (GHI) sam-
ples collected by a real weather station. The neural
network is a Multilayer Perceptron exploiting a high
number of regressors to predict GHI in 15 minutes up
to 2 hours range. Then, GHI forecast is given as input
to our PV simulator that exploits GIS tools for simu-
lating energy production. The rest of the paper is or-
ganized as follows. Section 2 reviews literature solu-
tion on solar radiation forecast. Section 3 introduces
the followed methodology to define a neural network
for short-term solar radiation forecasting. Section 4
details all the steps performed to initialize, train and
validate our neural network. Section 5 discusses the
results on solar radiation forecast. Section 6 descri-
44
Aliberti, A., Bottaccioli, L., Cirrincione, G., Macii, E., Acquaviva, A. and Patti, E.
Forecasting Short-term Solar Radiation for Photovoltaic Energy Predictions.
DOI: 10.5220/0006683600440053
In Proceedings of the 7th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2018), pages 44-53
ISBN: 978-989-758-292-9
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

bes the adopted Photovoltaic simulator. Section 6 pre-
sents also results and accuracy on PV energy genera-
tion that exploits foretasted solar radiation given by
the proposed neural network. Finally, Section 7 dis-
cusses concluding remarks.
2 RELATED WORK
Nowadays, solar energy represents a very attractive
solution to produce green and clean energy. However,
for an efficient conversion and utilization of solar po-
wer, solar radiation should be estimated and forecas-
ted through accurate methods and tools. For exam-
ple in Demand/Response applications (Siano, 2014),
the amount of available energy must be known in ad-
vance to optimize the production of power plants (Ag-
haei and Alizadeh, 2013) and to match energy pro-
duction with consumption. Hence, several studies
were proposed in the literature to find mathematical
and physical models to estimate and forecast the so-
lar radiation, such as stochastic models based on time
series (Kaplanis and Kaplani, 2016), (Voyant et al.,
2014) and (Badescu, 2014). Moreover, classical li-
near time series models, like autoregressive moving
average, have been widely used (Brockwell and Da-
vis, 2016). However, it has been proven that these
methodologies often are not sufficient in the analy-
sis and prediction of solar radiation. This is due to
the non-stationary and non-linearity of the solar radi-
ation time series data (Madanchi et al., 2017), (Naza-
ripouya et al., 2016). Furthermore, stochastic models
are based on the probability estimation. This leads to
a difficult forecast of the solar radiation time series.
To overcome these limits, non-linear approaches,
such as artificial neural networks (ANNs), were con-
sidered by many researchers as powerful methodo-
logies to predict phenomenons, such as solar radia-
tion (Voyant et al., 2017). Generally, ANNs do not re-
quire knowledge of internal system parameters. Furt-
hermore, these models offer a compact solution for
multiple variable problem (Qazi et al., 2015). Howe-
ver, also the use of an ANN to forecast a phenomenon
introduces an error, the so-called prediction error (Ya-
dav and Chandel, 2014). As a result, these models
need optimizations to reduce this error.
With respect to literature solutions, the scienti-
fic novelty of the proposed methodology consists in
using a neural network based on the Multilayer Per-
ceptron to forecast solar radiation. Generally, most
literature methodologies rely on the single past value
to perform the forecast (Box et al., 2015). Whilst, the
proposed solution allows to reduce significantly the
prediction error by using a high number of regressors
to perform predictions. In addition, we perform the
forecast of solar radiation in short- and medium-term,
i.e. from future 15 minutes up to next 2 hours.
3 METHODOLOGY
A time series identifies an ordered sequence of values
of a variable at equally spaced time intervals (Hamil-
ton, 1994). The usage of time series models brings
two great benefits: i) understanding the underlying
forces and structure that produced the observed data
and ii) fitting a model and proceeding to forecast
and monitor or even feedback and feed-forward cont-
rol (Oancea and Ciucu, 2014).
3.1 The Multilayer Perceptron
Generally, one of the most effective methods for pre-
diction based on time series consists in neural net-
work (Montgomery et al., 2015), such as the Multi-
layer Perceptron (MLP), which is the artificial neu-
ral network most used in applications (Demuth et al.,
2014). It is composed of units, called nodes or neu-
rons, and organized in a layer of inputs, one or more
hidden layers and an output layer. It is a feed-forward
network with full connection between layers. The
connections are characterized by adjustable parame-
ters called weights. Hence, a weight refers to the
strength of a connection between two nodes (Kubat,
2017). Each neuron computes a function of the sum
of the weighted inputs. This function is called activa-
tion function.
In this work, we use an MLP-network architec-
ture characterized by i) one hidden layer of neurons
with hyperbolic tangent activation function f and ii)
an output layer with a linear activation function F.
The functional model is given by:
ˆy
i
(w,W) = F
i
(
q
∑
j=1
W
i j
h
j
+W
i0
) =
= F
i
(
q
∑
j=0
W
i j
f
j
(
m
∑
l=1
w
jl
u
l
+ w
j0
) +W
i0
)
(1)
The weights are specified by the matrix W = [W
i j
] and
by the matrix w = [w
jl
], where W
i j
scales the con-
nection between the hidden unit j and the output unit
i and w
jl
scales the connection between the hidden
unit j and the input unit l. W
i0
and w
j0
are the cor-
responding biases. All this weights can be vectorized
in a vector θ. The input units are represented by the
vector u(t) and the hidden neuron outputs are repre-
sented by the vector h. The outputs of the network,
Forecasting Short-term Solar Radiation for Photovoltaic Energy Predictions
45
ˆy
i
, are estimated by Eq. 1. The parameters are deter-
mined during the training process, which requires a
training set Z
N
, composed of a set of inputs, u(t), and
corresponding desired outputs, y(t), specified by:
Z
N
= [u(t), y(t)], t = 1, ..., N (2)
The training phase allows to determine a mapping
from the set of training data to the set of possible
weights:
Z
N
→
ˆ
θ (3)
so that the network can produce prediction ˆy(t), to be
compared to the true output y(t).
The prediction error approach is instead based on
the introduction of a measure of closeness in terms of
a mean square error criterion, as specified by:
V
N
(θ, Z
N
) =
1
2N
N
∑
t=1
[y(t)− ˆy(t|θ)]
T
[y(t)− ˆy(t|θ)] (4)
The weights are then found as:
ˆ
θ = arg
θ
minV
N
(θ, Z
N
) (5)
by some kind of iterative minimization scheme:
θ
i+1
= θ
i
+ µ
i
+ f
i
(6)
where θ
i
specifies the current iteration, f
i
the search
direction and µ
i
the step size.
3.2 System Identification
The following section details the adopted methodo-
logy to use an artificial neural network for short-term
solar radiation predictions. Based on the process pre-
sented in (Norgaard et al., 2000), the procedure to
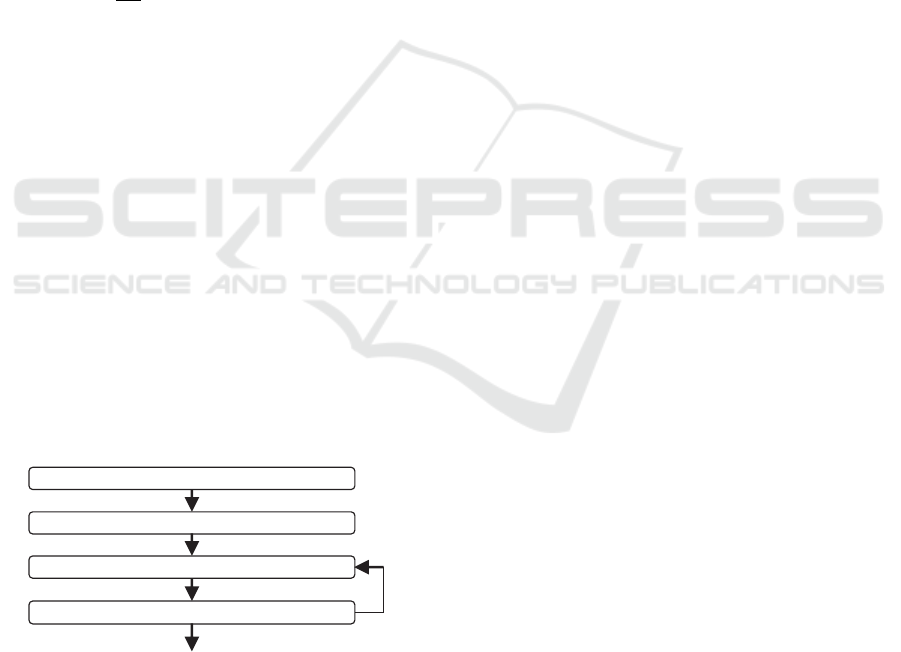
identify a dynamical system consists of four steps: i)
Experiment, ii) Model Structure Selection, iii) Model
Estimation and iv) Model Validation (see Fig. 1).
OPTIMIZATION
EXPERIMENT
SELECT MODEL STRUCTURE
ESTIMATE MODEL
VALIDATE MODEL
VALIDATION
Figure 1: System identification procedure.
Experiment. This step corresponds to the problem
analysis and the sampling and data collection. In
neural network applications, once the scope has been
identified, an adequate amount of data is needed. Ge-
nerally, an higher number of data allows better fore-
casting performances (Srivastava et al., 2014). Then
the available data must be divided into two different
datasets: the training set and the validation set, re-
spectively. These datasets are used in the training and
validation phases of the neural network, which are
the Estimate Model and the Validate Model steps in
Fig. 1, respectively.
Model Structure Selection. This step allows iden-
tifying the correct architecture model to use (Nor-
gaard et al., 2000). Generally, this selection is
more difficult in the nonlinear case than in the li-
near (Chandrashekar and Sahin, 2014). At this aim,
the system regressor must be studied. In mathema-
tical modeling, these regressors identify independent
variables able to influence the dependent variables. In
time series, then, these regressors represent previous
samplings with respect to the predicted ones (Mont-
gomery et al., 2015). Consequently, the best neural
structure can be chosen.
Model Estimation. In this step, once the network
model and the number of regressors are identified, the
network is first implemented and then trained. In time
series scenario, training a neural network is needed to
provide: i) the vector containing desired output data;
ii) the number of regressors to define the prediction;
iii) the vector containing the weights of both input-
to-hidden and hidden-to-output layers and lastly iv)
the data structure containing the parameters associa-
ted with the selected training algorithm. Finally, the
training phase produces a training error, which re-
presents the network performance index (Srivastava
et al., 2014).
Model Validation. This step validates the trained
network. Generally, validating a network allows eva-
luating its capabilities (Miller et al., 1989). In time
series predictions, the most common validation met-
hod consists of analysing the residuals (i.e. prediction
errors) by cross-validating the test set. This method
allows to perform a set of tests including also the au-
tocorrelation function of the residuals and the cross-
correlation function between controls and residuals.
This analysis provides the test error (Srivastava et al.,
2014), that is an index considered as a generalization
of the error estimation. This index should not be too
high compared to training error. If this happens, the
network could over-fit the training set.
Network Optimization and Final Validation. Ge-
nerally, if the network is over-fitting the training set,
the selected model structure contains too many weig-
hts. It is required to return in the Estimate Model step
in order to change and redefine some structural para-
meters by optimizing the whole architecture. For this
purpose, the superfluous weight must be pruned ac-
cording to the Optimal Brain Surgeon (OBS) strategy,
SMARTGREENS 2018 - 7th International Conference on Smart Cities and Green ICT Systems
46

that represents one of the most important optimization
strategies (Han et al., 2015). Consequently, once the
new weights are given, the network architecture must
be re-validated.
4 NAR NEURAL NETWORK FOR
SHORT-TERM GHI FORECAST
In this work, we aim at forecasting the short-term
Global Horizontal Solar Irradiance (GHI) for photo-
voltaic energy predictions. For this purpose, we used
a dataset of about four years (from 2010 to 2013).
It provides GHI values sampled every 15 minutes by
the weather station in our University Campus. In de-
tail, we considered all values in the time period from
8 a.m. to 6 p.m. Thus, we excluded evening and
night time. Then, we split the dataset into training
set (2010-2011) and validation set (2012-2013). This
dataset appears to be statistically relevant. Nonet-
heless, we believe that if we could have used a lar-
ger accurate training set we could have achieved even
more accurate prediction results. In order to deal with
time series data, we adopted the Nonlinear Autore-
gressive neural network (NAR) belonging to the Non-
linear Autoregressive Exogenous Model (NARX) fa-
mily (Siegelmann et al., 1997). Other choices, like
NARMA (Norgaard et al., 2000) are possible. Howe-
ver, NARX is considered as the best tool in time series
analysis (used as NAR) and does not suffer from sta-
bility problems. It is a nonlinear autoregressive model
which has exogenous inputs. It is basically a choice
of the inputs of a nonlinear model (an MLP neural
network, as in (Norgaard et al., 2000)), which repla-
ces the traditional linear model ARX (as in (Ljung,
1998)). It bases its predictions on i) past values of the
series and ii) current and past values of the driving
exogenous series, producing an error that represents
the error of prediction. This error means that the kno-
wledge of the past terms does not enable the future
value of the time series to be predicted exactly. These
network models are characterized by:
y
t
= F(y
t−1
, y
t−2
, y
t−3
, ..., u
t
, u
t−1
, u
t−2
, u
t−3
, ...) + ε
t
(7)
where y
t
represents the variable of interest and u
t
is
the externally determined variable at time t respecti-
vely. In detail, information about u
t
and previous va-
lues of u and y, helps predicting y
t
, with a prediction
error ε
t
.
Once the model has been chosen, we analysed the
number of past signals used as regressors for the pre-
diction. We used Lipschiz method for determining the
lag-space (Rajamani, 1998). This methodology al-
lows identifying the orders of Input-Output Models
for Nonlinear Dynamic Systems. However, as de-
tailed in (He and Asada, 1993), this methodology is
not always effective but it represents a good starting
point to define the number of regressors. Fig. 2 details
the result of the applied Lipschiz method, in which
the number of past inputs is increased simultaneously
from 1 to 20.
Figure 2: Evaluation of Order Index criterion for different
lag-space.
In this way, we deduced that the architecture can yield
a good performance with only 9 regressors (i.e. 9 pre-
vious values for y and u, respectively, in Eq. 7). Ho-
wever, considering that the value of 10 is very close to
the knee of the curve, 10 regressors have been chosen
in order to have more conservative results, in the sense
of the use of more information from the time series.
Then, we chose an initial fully connected network ar-
chitecture with one hidden layer of 30 hyperbolic tan-
gent units. This large number of units is redundant,
but justified by the pruning technique. The weights
of the network are then initialized randomly before a
training. This choice allows to initialize i) the weig-
hts, ii) their decay threshold and iii) the maximum
number of iterations. However, these data structure
parameters are overestimated during the first training.
After this phase, we proceed training the neural net-
work. Training is a minimization technique in order
to compute the best weights for the network. Here we
used the Levenberg-Marquardt algorithm, which in-
terpolates between the Gauss-Newton algorithm and
the method of gradient descent, using a trust region
approach (Norgaard et al., 2000).
According to the purpose of this study, we chose
to use the methodology illustrated in (Norgaard et al.,
2002) for the network validation. This methodo-
logy allows the models systems validation of the out-
puts, performing a set of tests including autocorre-
lation function of the residuals and cross-correlation
function between controls and residuals. This pro-
Forecasting Short-term Solar Radiation for Photovoltaic Energy Predictions
47

cess produces the test error index as a result. The
test error represents an estimation of the generaliza-
tion error. This should not be too large compared to
training error. If the test error (NSSE) is greater than
the training error, it means that the predicted results
are over-fitting the training set. In our case, the va-
lidation process yield this index equal to 3.27 × 10
3
,
which is a good value. Then, we proceeded to the op-
timization phase of the network. Our purpose was to
remove excess weights and obtain a smaller training
error than the one given during the first validation. In
order to do so, we adopted the Optimal Brain Surgeon
(OBS) strategy (Hansen et al., 1994), which prunes
superfluous weights. OBS computes the Hessian ma-
trix weights iteratively, which leads to a more exact
approximation of the error function. The inverse Hes-
sian is calculated by means of recursion. This method
allows finding the smallest saliency S
i
:
S
i
=
w
2
i
2[H
−1]
]
i,i
(8)
where [H
−1
]
i,i
is the (i, i)th element of the inverse
Hessian matrix and w
i
is the ith element of the vector
θ containing network weights. The saliency identi-
fies the quality of the connection between the various
network units. This methodology allows to verify the
state of the saliency iteratively. If the saliency S
i
is
much smaller than the mean-square error, then some
synaptic weights are deleted and the remaining ones
are updated. The computation stops when no more
weights can be removed from the network without a
large increase of the mean-square error. Once the new
weights are given, we re-validated the network archi-
tecture.
Through the same methodology used in the first
validation phase, we proceeded to the final network
validation using the new weights. The resulting test
error index NSSE was 3.11 × 10
3
, that is lower than
the previous one. Thus, the prediction error has been
further lowered, giving more precise GHI forecast.
Fig. 3 shows the final structure of the neural network
after the optimization process.
Figure 3: NAR optimized structure.
5 RESULTS ON GHI FORECAST
The phases of the neural network characterization
described in Section 4 allow defining an architecture
that bases its prediction on 10 previous regressors.
This represents a big advantage, as in literature these
kinds of networks generally use just the single pre-
vious value to predict the next one. This implies a
higher prediction error. In our case, by using a more
large number of previous instances the prediction is
good.
Our goal is to predict GHI in very short time win-
dows (i.e. 15 minutes). We moved further predicting
also GHI up to next two hours with 15 min. time inter-
val. Using the dataset described in Section 4, we per-
form predictions by employing the methodology pre-
sented in (Norgaard et al., 2002). This methodology
allows to determine the prediction value (that corre-
sponds to the ahead k-step prediction of the system)
and compare it to the measured output. The predicti-
ons are determined i) by feeding past predictions in
the neural network where observations are not avai-
lable and ii) by setting unavailable residuals to zero.
Before starting the simulations, we set the prediction
function to 10 regressors. In this section, we present
the obtained results.
To evaluate the performance of our predicti-
ons, we used the indicators reported by Gueymard
in (Gueymard, 2014). These indices of dispersion are:
i) the Root Mean Square Difference (RMSD) that re-
presents the standard deviation of differences between
predicted and observed values; ii) the Mean Absolute
Difference (MAD) that represents a measure of sta-
tistical dispersion obtained by the average absolute
difference of two independent values drawn from a
probability distribution; iii) the Mean Bias Difference
(MBD) that measures the average squares of errors be-
tween predicted and measured values; iv) the Coeffi-
cient of determination (r
2
) that represent the propor-
tion between the variance and the predicted variable.
RMSD, MAD and MBD are expressed in percentage
rather than absolute units. Furthermore, we also con-
sidered two indicators for the overall network perfor-
mance: i) the Willmotts Index of Agreement (WIA) that
represent the standardized measure of the degree of
model prediction error (Willmott et al., 2012) and ii)
the Legatess Coefficient of Efficiency (LCE) that is the
ratio between the mean square error and the variance
in the observed data (Legates and McCabe, 2013).
Fig. 4 shows the comparison among GHI results
given by our neural network (dashed lines) and me-
asured values sampled by the weather station (con-
tinues line) for different steps, from k = 1 (i.e next
15 min.) to k = 8 (i.e next 120 min.). These GHI
SMARTGREENS 2018 - 7th International Conference on Smart Cities and Green ICT Systems
48

Figure 4: GHI prediction for 1 ≤ k ≤ 8 (June 2013).
Forecasting Short-term Solar Radiation for Photovoltaic Energy Predictions
49
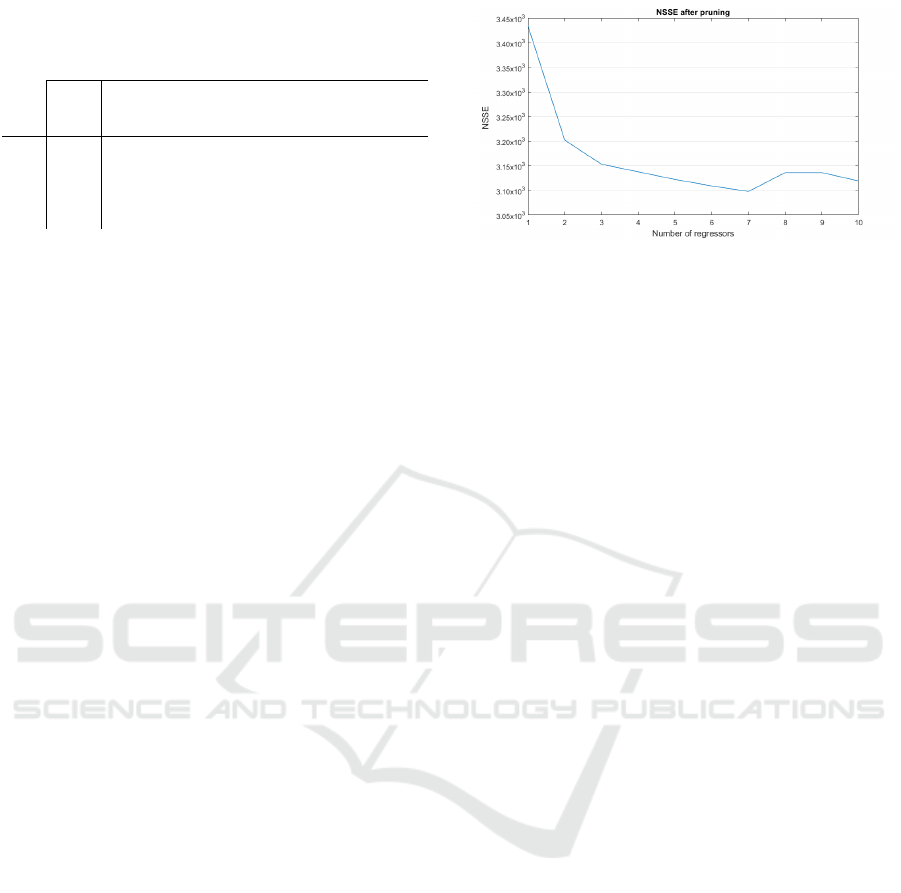
Table 1: Performance Indicators for GHI prediction.
Time
[min]
MAD
[%]
MDB
[%]
r
2
RMSD
[%]
LCE WIA
k=1 15 13.56 0.26 0.91 25.37 0.81 0.98
k=2 30 19.82 0.70 0.84 32.92 0.72 0.96
k=3 45 24.28 1.08 0.80 37.61 0.66 0.94
k=4 60 28.02 1.27 0.75 41.55 0.60 0.93
k=5 75 31.30 1.52 0.71 45.10 0.56 0.91
k=6 105 34.43 1.42 0.66 48.48 0.51 0.90
k=7 115 37.88 0.97 0.61 52.15 0.46 0.88
k=8 120 41.32 0.14 0.55 55.97 0.41 0.86
predictions refer to the first week of June 2013. As
shown in Fig. 4-(a), Fig. 4-(b) and Fig. 4-(c), the
trends of our results for 1 ≤ k ≤ 3 follow the real GHI
behaviour with a good accuracy. Instead for k > 3,
the prediction accuracy decreases (from Fig. 4-(d) to
Fig. 4-(g)). This is also highlighted by Table 1 that
reports the results of GHI predictions in terms of per-
formance indicators considering the whole validation
set (i.e. 2012-2013).
Performance indices clearly show that the architec-
ture performance worsens by increasing the predictive
steps. As a result, GHI prediction for high values of k
has a greater error than real data. The analysis of indi-
ces highlights that the best GHI predictions are given
at smaller intervals. For example, the MAD indicates
that GHI prediction error grows as the prediction step
k increases. Indeed, for prediction step k = 1 the er-
ror is about 13.6% while for k = 8 the error is around
41%. Also, RMSD has a similar trend. Furthermore,
the coefficient of determination r
2
is much better than
it is closer to 1. This index for prediction step k = 1
is equal to 0.91. Whilst, the error increases with an
r
2
= 0.55 for k = 8.
This is also confirmed by LCE and WIA that high-
light a decreasing of the overall performance on high
prediction steps. Increasing the forecasting steps in-
crease the errors and, consequently, the performances
of prediction gets worst. Also for LCE and WIA, va-
lues closer to 1 represent the best case. For k = 8,
LCE and WIA are equal to 0.41 and 0.86, respectively.
However, the performance indexes for 1 ≤ k ≤ 3 are
acceptable to perform Photovoltaic energy estimati-
ons (see Section 6). In this scenario, the maximum
error for GHI prediction is less than 25% for k = 3.
The correctness of the choice of the number of re-
gressors by the Lipschitz method seen previously is
confirmed by the following additional analysis whose
results are shown in Fig. 5. The technique proposed
here has been repeated for different numbers of in-
puts and the corresponding NSSE has been recorded.
It can be seen that too few regressors are not enough
and seven or ten inputs give the best results. It con-
firms the choice in the proposed experiment.
Figure 5: Evaluation of NSSE after pruning with regard to
the number of regressors.
6 PV ENERGY ESTIMATION
As discussed in Section 5, the results on GHI fore-
cast are satisfactory especially on short-term time pe-
riods. This forecast of GHI allows estimating in ad-
vance the energy production of renewable, such as PV
systems. In our case, we used GHI predictions as
input to our PV energy simulator (Bottaccioli et al.,
2017b). Estimating the PV production for the next
short-term time windows enables the development of
more accurate control policies for Smart Grid ma-
nagement, such as Demand/Response (Siano, 2014).
Furthermore, this estimation allows to analyse the pe-
netration level and the impact of renewable energy in
existing districts and smart grids and. Also, to test and
validate complex systems as presented in (Bottaccioli
et al., 2017a).
6.1 PV Simulator
This work exploits the software infrastructure presen-
ted in our previous work (Bottaccioli et al., 2017b) to
estimate the energy generation profiles of PV systems
in real-sky conditions. The inputs of this simulator are
i) a Digital Surface Model (DSM) and ii) GHI trends.
The DSM is a high-resolution raster image represen-
ting terrain elevation of buildings of interest. It al-
lows recognizing encumbrances on rooftops, such as
chimneys and dormers, that prevent the deployment
of PV panels. From the DSM, the PV simulator es-
timates the evolution of shadows in the rooftops over
one year, with 15 minutes intervals. The result is the
identification of the suitable area that is the available
area on the rooftop where PV panels can be deployed.
The evolution of irradiance in real-sky conditions
is given by combining GHI trends retrieved from per-
sonal or third-party weather stations (Weather Under-
ground, ) with the shadow model. In case of short-
term prediction of PV energy production, the forecast
of GHI trends is given by the proposed neural network
SMARTGREENS 2018 - 7th International Conference on Smart Cities and Green ICT Systems
50

Table 2: Performance Indicator for PV simulation.
Time
[min]
MAD
[%]
MDB
[%]
r
2
RMSD
[%]
LCE WIA
k=1 15 11.33 -0.70 0.91 21.34 0.82 0.98
k=2 30 16.87 -0.81 0.84 28.81 0.73 0.96
k=3 45 20.97 -0.86 0.77 34.28 0.67 0.94
(see Section 4). Then, the PV simulator decomposes
GHI to estimate both Direct Normal Incident radia-
tion (DNI) and Diffuse Horizontal Incident radiation
(DHI) (Hofierka and Ka
ˇ
nuk, 2009). This decompo-
sition is done by exploiting state-of-the-art decom-
position models, such as (Engerer, 2015) and (Ruiz-
Arias et al., 2010), and considering the attenuation
caused by air pollution applying the Linke turbidity
coefficient (Linke, 1922). Finally, the PV energy pro-
duction is given by applying the methodology presen-
ted in (Brihmat and Mekhtoub, 2014).
6.2 Results on PV Generation Forecast
In this section, we present the results of PV genera-
tion forecast in short-term time periods. In this scena-
rio, the PV simulator exploits GHI trends given by the
proposed neural network (see Section 4) with diffe-
rent time steps: i) k = 1 (i.e next 15 min.), ii) k = 2 (i.e
next 30 min.) and iii) k = 3 (i.e next 45 min.). To eva-
luate the errors of this approach, we repeated the PV
simulations with real GHI trends sampled by the we-
ather station in our campus. Fig. 6reports the plots of
the instant power for three generic days in June 2013:
i) sunny, ii) cloudy and iii) rainy. Generally, the trends
of our results with GHI forecast (dashed line) follow
with a good accuracy the behaviour of measured GHI
(continues line). As expected, simulations with k = 1
performs better than simulations with k = 2 and k = 3.
As shown in the three plots in Fig. 6, PV energy simu-
lations are more affected by errors during rainy days
especially during the early hours in the morning. This
is because the algorithm expects higher GHI values.
However, the algorithm is also able to recognize the
wrong GHI estimation and correct the error after few
time-steps.
Table 2 reports the performance indicators for si-
mulations with 1 ≤ k ≤ 3 with respect to simulati-
ons with sampled GHI trends. The performance in-
dicators show that increasing the predictive steps (k)
the accuracy on the results decreases. MAD increa-
ses from 11.33% for k = 1 to 20.97% for k = 3. Also
RMSD has a similar trend. r
2
for prediction step k = 1
is equal to 0.91. Whilst, the error increases with an
r
2
= 0.77 for k = 3. Finally, LCE varies from 0.82 to
0.67 and WIA decreases from 0.98 to 0.94.
These results confirm that PV simulations with
GHI trends for 1 ≤ k ≤ 3 given by the proposed neu-
Figure 6: Simulations of PV energy production with k = 1
and k = 2 (June 2013).
ral network are acceptable to estimate the energy pro-
duction in the short-term time periods.
7 CONCLUSIONS
In this paper, we presented a methodology to forecast
the short-term solar radiation, suitable for photovol-
taic energy predictions. We discussed the results of
the neural network forecast, introducing the NAR ar-
chitecture able to base its prediction on a high number
of regressors. Furthermore, we compared our results
with real GHI values sampled by a real weather sta-
tion in our University campus. The analysis of per-
formance indicators highlighted an overall good per-
Forecasting Short-term Solar Radiation for Photovoltaic Energy Predictions
51

formance in predicting the solar radiation, especially
for the next 15, 30 and 45 minutes. As discussed, this
short-term forecast of solar radiation allows estima-
ting in advance the energy production of PV systems
with a good accuracy. This enables the design of more
accurate control policies for smart grids management,
such as Demand/Response.
ACKNOWLEDGEMENTS
This work was partially supported by the EU project
FLEXMETER and by the Italian project ”Edifici a
Zero Consumo Energetico in Distretti Urbani Intel-
ligenti”.
REFERENCES
Aghaei, J. and Alizadeh, M.-I. (2013). Demand response
in smart electricity grids equipped with renewable
energy sources: A review. Renewable and Sustainable
Energy Reviews, 18:64–72.
Badescu, V. (2014). Modeling solar radiation at the earth’s
surface. Springer.
Bottaccioli, L., Estebsari, A., Patti, E., Pons, E., and Acqua-
viva, A. (2017a). A novel integrated real-time simu-
lation platform for assessing photovoltaic penetration
impacts in smart grids. Energy Procedia, 111:780–
789.
Bottaccioli, L., Patti, E., Macii, E., and Acquaviva, A.
(2017b). Gis-based software infrastructure to model
pv generation in fine-grained spatio-temporal domain.
IEEE Systems Journal.
Box, G. E., Jenkins, G. M., Reinsel, G. C., and Ljung, G. M.
(2015). Time series analysis: forecasting and control.
John Wiley & Sons.
Brihmat, F. and Mekhtoub, S. (2014). Pv cell tempera-
ture/pv power output relationships homer methodo-
logy calculation. In International Journal of Scien-
tific Research & Engineering Technology, volume 1.
International Publisher &C. O.
Brockwell, P. J. and Davis, R. A. (2016). Introduction to
time series and forecasting. springer.
Chandrashekar, G. and Sahin, F. (2014). A survey on feature
selection methods. Computers & Electrical Engineer-
ing, 40(1):16–28.
Demuth, H. B., Beale, M. H., De Jess, O., and Hagan, M. T.
(2014). Neural network design. Martin Hagan.
Engerer, N. (2015). Minute resolution estimates of the dif-
fuse fraction of global irradiance for southeastern au-
stralia. Solar Energy, 116:215–237.
Gueymard, C. A. (2014). A review of validation methodo-
logies and statistical performance indicators for mo-
deled solar radiation data: Towards a better banka-
bility of solar projects. Renewable and Sustainable
Energy Reviews, 39:1024–1034.
Hamilton, J. D. (1994). Time series analysis, volume 2.
Princeton university press Princeton.
Han, S., Pool, J., Tran, J., and Dally, W. (2015). Learning
both weights and connections for efficient neural net-
work. In Advances in Neural Information Processing
Systems, pages 1135–1143.
Hansen, L. K. et al. (1994). Controlled growth of cascade
correlation nets. In ICANN94, pages 797–800. Sprin-
ger.
He, X. and Asada, H. (1993). A new method for identifying
orders of input-output models for nonlinear dynamic
systems. In American Control Conference, 1993, pa-
ges 2520–2523. IEEE.
Hofierka, J. and Ka
ˇ
nuk, J. (2009). Assessment of photo-
voltaic potential in urban areas using open-source so-
lar radiation tools. Renewable Energy, 34(10):2206–
2214.
Kaplanis, S. and Kaplani, E. (2016). Stochastic prediction
of hourly global solar radiation profiles.
Kubat, M. (2017). Artificial neural networks. In An Intro-
duction to Machine Learning, pages 91–111. Sprin-
ger.
Legates, D. R. and McCabe, G. J. (2013). A refined in-
dex of model performance: a rejoinder. International
Journal of Climatology, 33(4):1053–1056.
Linke, F. (1922). Transmissions-koeffizient und
tr
¨
ubungsfaktor. Beitr. Phys. Fr. Atmos, 10:91–103.
Ljung, L. (1998). System identification. In Signal analysis
and prediction, pages 163–173. Springer.
Madanchi, A., Absalan, M., Lohmann, G., Anvari, M.,
and Tabar, M. R. R. (2017). Strong short-term non-
linearity of solar irradiance fluctuations. Solar Energy,
144:1–9.
Miller, G. F., Todd, P. M., and Hegde, S. U. (1989). De-
signing neural networks using genetic algorithms. In
ICGA, volume 89, pages 379–384.
Montgomery, D. C., Jennings, C. L., and Kulahci, M.
(2015). Introduction to time series analysis and fo-
recasting. John Wiley & Sons.
Nazaripouya, H., Wang, B., Wang, Y., Chu, P., Pota, H.,
and Gadh, R. (2016). Univariate time series prediction
of solar power using a hybrid wavelet-arma-narx pre-
diction method. In Transmission and Distribution
Conference and Exposition (T&D), 2016 IEEE/PES,
pages 1–5. IEEE.
Norgaard, M., Ravn, O., and Poulsen, N. K. l. (2002).
Nnsysid-toolbox for system identification with neural
networks. Mathematical and computer modelling of
dynamical systems, 8(1):1–20.
Norgaard, P. M., Ravn, O., Poulsen, N. K., and Hansen,
L. K. (2000). Neural networks for modelling and con-
trol of dynamic systems-a practitioner’s handbook.
Oancea, B. and Ciucu, S¸. C. (2014). Time series fo-
recasting using neural networks. arXiv preprint
arXiv:1401.1333.
Qazi, A., Fayaz, H., Wadi, A., Raj, R. G., Rahim, N., and
Khan, W. A. (2015). The artificial neural network for
solar radiation prediction and designing solar systems:
a systematic literature review. Journal of Cleaner Pro-
duction, 104:1–12.
SMARTGREENS 2018 - 7th International Conference on Smart Cities and Green ICT Systems
52

Rajamani, R. (1998). Observers for lipschitz nonlinear
systems. IEEE transactions on Automatic Control,
43(3):397–401.
Ruiz-Arias, J., Alsamamra, H., Tovar-Pescador, J., and
Pozo-Vzquez, D. (2010). Proposal of a regressive
model for the hourly diffuse solar radiation under all
sky conditions. Energy Conversion and Management,
51(5):881 – 893.
Siano, P. (2014). Demand response and smart gridsa survey.
Renewable and Sustainable Energy Reviews, 30:461–
478.
Siegelmann, H. T., Horne, B. G., and Giles, C. L. (1997).
Computational capabilities of recurrent narx neural
networks. IEEE Transactions on Systems, Man, and
Cybernetics, Part B (Cybernetics), 27(2):208–215.
Srivastava, N., Hinton, G. E., Krizhevsky, A., Sutskever, I.,
and Salakhutdinov, R. (2014). Dropout: a simple way
to prevent neural networks from overfitting. Journal
of machine learning research, 15(1):1929–1958.
Vardakas, J. S., Zorba, N., and Verikoukis, C. V. (2015). A
survey on demand response programs in smart grids:
Pricing methods and optimization algorithms. IEEE
Communications Surveys & Tutorials, 17(1):152–178.
Voyant, C., Darras, C., Muselli, M., Paoli, C., Nivet, M.-L.,
and Poggi, P. (2014). Bayesian rules and stochastic
models for high accuracy prediction of solar radiation.
Applied Energy, 114:218–226.
Voyant, C., Notton, G., Kalogirou, S., Nivet, M.-L., Paoli,
C., Motte, F., and Fouilloy, A. (2017). Machine le-
arning methods for solar radiation forecasting: A re-
view. Renewable Energy, 105:569–582.
Weather Underground. http://www.wunderground.com.
Willmott, C. J., Robeson, S. M., and Matsuura, K. (2012).
A refined index of model performance. International
Journal of Climatology, 32(13):2088–2094.
Yadav, A. K. and Chandel, S. (2014). Solar radiation pre-
diction using artificial neural network techniques: A
review. Renewable and Sustainable Energy Reviews,
33:772–781.
Forecasting Short-term Solar Radiation for Photovoltaic Energy Predictions
53
