Hybrid Model of Emotions Inference

An Approach based on Fusion of Physical and Cognitive Informations

Ernani Gottardo

and Andrey Ricardo Pimentel

Instituto Federal de Educac¸

ao, Ci

encia e Tecnologia do RS - IFRS, Erechim, RS, Brazil

Universidade Federal do Paran

a - UFPR, Curitiba, PR, Brazil

Keywords:

Affective Computing, Emotion Inference, Emotion and Learning, Adaptive Systems.

Abstract:

Adapting to users’ affective state is a key feature for building a new generation of more user-friendly, engaging

and interactive software. In the educational context this feature is especially important considering the intrinsic

relationship between emotions and learning. So, this paper presents as its main contribution the proposal of

a hybrid model of learning related emotion inference. The model combines physical and cognitive elements

involved in the process of generation and control of emotions. In this model, the facial expressions are used

to identify students’ physical emotional reactions, while events occurring in the software interface provide

information for the cognitive component. Initial results obtained with the model execution demonstrate the

feasibility of this proposal and also indicate some promising results. In a ﬁrst experiment with eight students

an overall emotion inference accuracy rate of 60% was achieved while students used a game based educational

software. Furthermore, using the model’s inferences it was possible to build a pattern of students’ learning

related affective states. This pattern should be used to guide automatic tutorial intervention or application of

speciﬁc pedagogical techniques to soften negative learning states like frustration or boredom, trying to keep

the student engaged on the activity.

1 INTRODUCTION

The use of computational environments as supporting

tool in educational process is common nowadays.

However, questions about the effectiveness and

possible contributions of these environments to

improve the learning process are frequent (Khan

et al., 2010). One of the main criticism related to

educational software refers to the lack of features

to customize or adapt the software according to

individual needs of the learner (Alexander, 2008).

Environments such as Intelligent Tutoring Systems

(ITS) are examples of software that implement

adaptive features based on learners’ individual needs.

Nevertheless, one of the main gap presented by most

of ITS available today is the absence of features to

adapt to the emotional states of the students or users

(Baker et al., 2010; Khan et al., 2010).

These limitations are important considering that

emotions play an important role in learning.

According to (Picard, 1997), research on

neuroscience shows that cognitive and affective

functions are intrinsically integrated into the

human brain. Furthermore, (Calvo and D’Mello,

2010) observe that automatically recognizing

and responding to users’ affective states during

interaction with a computer can improve the quality

of the interaction, making the interface more

user-friendly or empathic.

Previous works have shown also that usability

improvements obtained by computing environments

that are able to infer and adapt to affective students’

reactions (Becker-Asano and Wachsmuth, 2010). As

an example, some environments try to detect when a

student is frustrated and encourage him to continue

studying (Baker et al., 2006). Another example is

the use of so-called ‘virtual animated pedagogical

agents’ (Jaques et al., 2003) capable of interact

and demonstrate affectivity based on the learners’

emotions.

In order to provide any kind of adaptation to

users’ emotions it’s ﬁrst necessary that emotions

are properly recognized by the computational

environment. However, automatically inferring users’

emotions by computers is a hard task and still

presents several barriers and challenges to overcome

(Grafsgaard et al., 2013; Baker et al., 2012).

The challenges range from conceptual deﬁnitions

Gottardo, E. and Ricardo Pimentel, A.

Hybrid Model of Emotions Inference.

DOI: 10.5220/0006684004410450

In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 441-450

ISBN: 978-989-758-298-1

441

related to emotions, to mapping of signals and

computationally treatable patterns into emotions

(Picard, 1997). In order to overcome these challenges,

researchers have used a wide range of techniques and

methods from a relatively new research area, known

as Affective Computing.

In this context, this paper presents a proposal of a

Hybrid Model for Emotions Inference - ModHEmo

(in its Portuguese acronym) in a computational

learning environment. The model presents as its main

characteristic the fusion of physical and cognitive

informations.

In this way, we intend to improve the emotion

inference process in a learning environment by

investigating how different kind of data can be

combined or complemented each other. Also, we

try to ﬁll the gap of correlated studies that use a

set of sensors, but only include devices designed to

capture physiological signals. Thus, even using a

set of sensors, only aspects of physical reactions are

considered, completely ignoring the context in which

the emotional reactions has occurred.

2 CONCEPTUAL BASES AND

CORRELATED WORKS

In this work we used concepts from the research

area named ‘Affective Computing’ by (Picard, 1997).

Affective Computing is a multidisciplinary ﬁeld that

uses deﬁnitions related to emotions coming from the

areas like psychology and neuroscience, as well as

computer techniques such as artiﬁcial intelligence and

machine learning (Picard, 1997).

This work relates with one of the areas of

affective computing that deals with the challenge

of recognizing humans’ emotions by computers.

In this sense, (Scherer, 2005) observes that there

is no single or deﬁnitive method for measuring a

person’s subjective experience during an emotional

episode. However, people voluntarily or involuntarily

reveal some patterns of expressions or behaviors.

Based on these patterns, people or systems can

apply techniques to infer or estimate the emotional

state, always considering a certain level of error and

uncertainty.

The construction of the ModHEmo was tightly

based on some assumptions presented in (Picard,

1997). This author advocates that an effective process

of emotions inference should take into account three

steps or procedures that are common when a person

tries to recognize someone else’s emotions. These

three steps are: i) identify low-level signals that

carry information (facial expressions, voice, gestures,

etc.), ii) detect signal patterns that can be combined

to provide more reliable recognition (e.g., speech

pattern, movements) and iii) search for environmental

information that underlies high level or cognitive

reasoning, relating what kind of behavior is common

in similar situations.

Considering the three steps or procedures

described above and the correlated works consulted

we observed that several studies have been based only

on the steps i or i and ii. Much of this research makes

the inference of emotions based on physiological

response patterns that could be correlated with

emotions. Physiological reactions are captured

using sensors or devices that measure speciﬁc

physical signals, such as the facial expressions (used

in this work). Among these devices, it may be

mentioned: sensors that measure body movements,

(Grafsgaard et al., 2013), heartbeat (Grafsgaard

et al., 2013; Picard, 1997), gesture and facial

expressions (Alexander, 2008; Sarrafzadeh et al.,

2008; Grafsgaard et al., 2013; D’Mello and Graesser,

2012), skin conductivity and temperature (Picard,

1997).

On the other hand, some research like (Conati,

2011; Jaques et al., 2003; Paquette et al., 2016)

use a cognitive approach, heavily relying on step iii,

described above. These researches emphasize the

importance of considering the cognitive or contextual

aspects involved in the process of generation and

control of humans’ emotions. In this line, it is

assumed that the emotions are activated based on

individual perceptions of positive or negative aspects

of an event or object

As can be seen below in section 4, the

hybrid model proposed in this work stands out by

simultaneously integrating physical and cognitive

elements, which are naturally integrated by humans

when inferring someone else’s emotions

3 LEARNING RELATED

EMOTION

Application of affective computing techniques in

computational learning environments requires the

observation of educational domain speciﬁc aspects.

So, the set of emotions to be taken into account must

be carefully evaluated and deﬁned considering the

singularities of educational activities (Baker et al.,

2010).

However, does not exist yet a complete

understanding of which emotions are the most

important in the educational context and how they

inﬂuence learning (Picard et al., 2004; Pour et al.,

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

442

2010). Even so, affective states such as confusion,

annoyance, frustration, curiosity, interest, surprise,

and joy have emerged in the scientiﬁc community as

highly relevant because their direct impact in learning

experiences (Pour et al., 2010).

In this context, choosing the set of emotions to

be included in this work was carried out seeking

to reﬂect relevant situations for learning. Thus, the

‘circumplex model’ of (Russel, 1980) and the ‘spiral

learning model’ of (Kort et al., 2001) were used as

reference. These theories have been consolidated and

frequently referenced in related works such as (Posner

et al., 2005; Baker et al., 2010; Pour et al., 2010;

Conati, 2011).

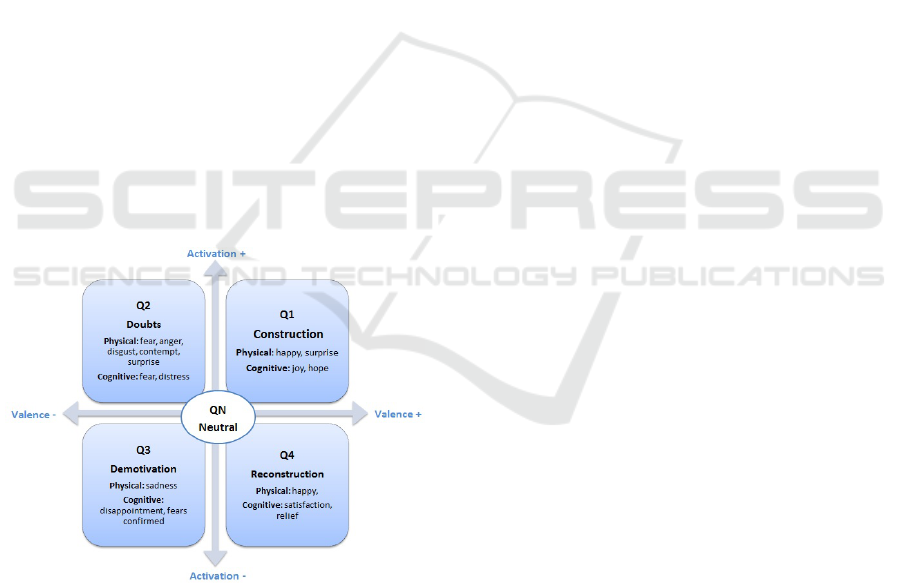
Figure 1 shows the approach used in this work

to arrange the emotions related to learning. In

this proposal the dimensions ‘Valence’ (positive or

negative) and ‘Activation’ or intensity (agitated or

calm) are used for representing emotions in quadrants

named as: Q1, Q2, Q3 and Q4. It was also

assigned a representative name (see Figure 1) for

each of the quadrants considering learning related

states. To represent the neutral state its was create

a category named QN, denoting situations in which

both valence and activation dimensions are zeroed.

These quadrants plus the neutral stated played the role

of classes in the classiﬁcation processes performed

by the ModHEmo that will be described in the next

section.

Figure 1: Quadrants and Learning Related Emotions.

Figure 1 also included the main emotions

contained in each quadrant, divided into two groups:

i) physical and ii) cognitive. These groups represent

the two distinct type of data sources considered in

ModHEmo. Each emotion was allocated in the

quadrants considering its values of the valence and

activation dimensions. The values for these two

dimensions for each emotion were obtained in the

work of (Gebhard, 2005) for the cognitive emotions

and in (Posner et al., 2005) for the physical emotions.

The emotions in the physical group are the eight

basic or primary emotions described in the classic

model of (Ekman, 1992) which are: anger, disgust,

fear, happy, sadness, surprise, contempt and neutral.

This set of emotions are inferred through the students’

facial expressions observed during the use of an

educational software.

The cognitive emotions are based on the cognitive

model of Ortony, Clore e Collins - OCC (Ortony

et al., 1990). The OCC model is based on the

cognitivist theory, explaining the origins of emotions

and grouping them according to the cognitive process

that generates them. The OCC model consists of 22

emotions. However, based on the scope of this work,

eight emotions were considered relevant: joy, distress,

disappointment, relief, hope, fear, satisfaction and

fears conﬁrmed. These set of emotions were chosen

because, according to the OCC model, its include all

the emotions that are triggered as a reaction to events.

In the context of this work, the events occurring in

the computational environment (e.g., error or hits in

question answer) was considered for inference of the

eight cognitive emotions.

It is important to note in Figure 1 that the physical

emotions ‘happy’ and ‘surprise’ appear repeated in

two quadrants. In the case of ‘happy’, due to

the high variance in the activation dimension (see

(Posner et al., 2005)), it appears in the Q1 and

Q4 quadrants. To deal with this ambiguity, in

the implementation of the hybrid model described

below, its observed the intensity of the happy emotion

inferred: if happy has a score greater than 0.5 it was

classiﬁed in the Q1 quadrant and, otherwise, in the

Q4 quadrant. For ‘surprise’ emotion, which may have

positive or negative valence, the solution used in the

implementation of the model was to check the type

of event occurring in the computational environment:

if the valence of the event is positive (e.g. correct

answer) ‘surprise’ was classiﬁed in the quadrant Q1

and, otherwise, in the Q2 quadrant.

In addition, the OCC model does not include the

neutral state. This affective state was included in

the cognitive component of ModHEmo, taking into

account the situations in which the scores of all the

eight emotions of the cognitive component are equal

to zero.

4 THE HYBRID MODEL OF

EMOTION INFERENCE

To implement the inference of the emotions delimited

in the previous section, a hybrid inference model

Hybrid Model of Emotions Inference

443

Figure 2: Hybrid Model of Learning Related Emotions Inference.

of emotions -ModHEmo was deﬁned. Figure 2

schematically shows the proposed model. The main

feature of ModHEmo is the initial division of the

inference process into two fundamentals components:

physical and cognitive. Figure 2 also shows the

modules of each component and the fusion of the

components to obtain the ﬁnal result.

The physical component of the model is

responsible to deal with learners’ facial expression,

that is the physical observable effect monitored.

Facial expression was chosen because there is a strong

relationship between facial features and affective

states (Ekman, 1992) and does not require expensive

or highly intrusive devices for their implementation.

The initial classiﬁcation of the physical component in

ModHEmo was performed using the EmotionAPI

https://azure.microsoft.com/pt-br/services/cognitive-

services/emotion/ developed by the University of Oxford

The main function of the cognitive component

is the handling of behavioral data (e.g. correct or

wrong answers) that may indicate the context and

the potential generation causes of affective states.

The implementation of the cognitive component

was accomplished through the customization of

the ALMA (A Layered Model of Affect) model

(Gebhard, 2005), which is based on the OCC theory.

Initially, both the cognitive and the physical

components perform the inference process and the

results are normalized in [0,1] interval for each of

the eight emotions of both components (see Section

3). Based on these initial inferences, a classiﬁcation

process is performed to relates the emotions to the

quadrants and the neutral state depicted in Figure 1.

At the end of this step, a normalized score in the

interval [0,1] is obtained for each quadrants and also

and Microsoft

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

444

for the neutral stated in the two components.

The Softmax function (Kuncheva, 2004) showed

in Equation 1 was the method used to normalize in

interval [0,1] the ModHEmo’s cognitive and physical

score results. In this equation, g

(x), ..., g

(x) are

the values returned for the eight emotion for each

ModHEmo’s components. Then, in Equation 1 new

scores values are calculated by g

(x), ..., g

(x), g

(x)

∈ [0, 1],

∑

j=1

(x) = 1.

(x) =

exp{g

(x)}

∑

K=1

exp{g

(x)}

(1)

For the fusion of the classiﬁers it is assumed

that some combination technique is applied. Thus,

if we denote the scores assigned to class i by the

classiﬁer j as s

, then a typical combining rule is a

f function whose combined ﬁnal result for class i is

= f ({s

} j = 1, ....M).

The ﬁnal result is expressed as argmax

, ..., S

}

(Tulyakov et al., 2008). In the context of this

work, j plays the role of the physical and cognitive

components while i is represented by the ﬁve classes

depicted in Figure 1.

In a ﬁrst ModHEmo’s implementation the

function f chosen was sum. This function was used

because it is a less noise-sensitive technique and,

despite its simplicity, its results are similar to more

complex methods (Kuncheva, 2004; Tulyakov et al.,

2008).

In the next section, a ModHEmo’s running

example depict the process described above.

5 EXPERIMENT AND RESULTS

In order to show the feasibility and check the results

of the model, an experiment was performed with a

ﬁrst ModHEmo’s version. In this experiment we used

‘Tux, of Math Command’ or TuxMath

, an open

source arcade game educational software. Tuxmath

lets kids to practice their arithmetic skills while they

defend penguins from incoming comets. The players

must answer a comet’s math equation to destroy it

before it hits one of the igloos or penguins.

In a ﬁrst experiment with the ModHEmo

integrated in a customized version of TuxMath, eight

students with age ranging from ten to fourteen years

old played the game. The experiment was approved

and follows the procedures recommended by the

ethics committee in research of the public federal

educational institution in which the ﬁrst author is

professor.

http://tux4kids.alioth.debian.org/tuxmath/index.php

The level of the game was chosen considering the

age and math skill of the students. It’s important

to note that the experiment was conducted trying

to make the research interfere as little as possible

in the students’ habitual or natural behavior when

using educational software. So, the learners were

informed about the research, but no restriction about

natural position and movements of the students were

imposed.

While students played the game, a list of

events were monitored by the customized version

of TuxMath. As examples of these events we can

mention: correct and wrong answers, comets that

damaged penguins’ igloos or killed the penguins,

game over, win the game, success or failure in

capturing power up comets

. Additionally, in order to

artiﬁcially create some situations that could generate

emotions, a random bug generator procedures was

developed in Tuxmath. Whenever a bug was

artiﬁcially inserted, it would also become a monitored

event. These bugs include, among others, situations

such as: i)non-detonation of a comet even with the

correct response, ii) display of comets in the middle

of the screen, decreasing the time for the student to

enter the correct answer until the comet hits the igloo

or penguin at the bottom of the screen. The students

were only informed about these random bugs after the

end of the game.

These events was used as input to the cognitive

component of the ModHEmo. Following the

occurrence of a monitored event in TuxMath,

student’s face image was captured with a basic

webcam and this image is used as input to the physical

component of ModHEmo. With these inputs the

model is then executed, resulting in the inference

of the probable affective state of the student in that

moment.

In order to facilitate understanding about

ModHEmo’s operation, will be detailed below the

results of a speciﬁc student. The student id 6 (see

table 1) was chosen for this detailing because he was

the participant with the highest number of events in

the game session. Figure 3 shows the results of the

inferences made by ModHEmo with student id 6. It

is important to emphasize that in the initial part of

the game depicted in Figure 3 the student showed

good performance, correctly answering the arithmetic

operations and destroying the comets. However, in

the middle part of the game, several comets destroyed

the igloos and killed some penguins. But, at the

end, the student recovered after capturing a power up

comet and won the game.

Special type of comet that, if its math question are

correctly answered, the player gain a special weapon

Hybrid Model of Emotions Inference

445

The lines in Figure 3 represent the inferences of

the physical and cognitive component and also the

fusion of both. The horizontal axis of the graph

represents the time and the vertical axis the quadrants

plus the neutral state (see Figure 1). The order of

the quadrants in the graph was organized so that the

most positive quadrant/class Q1 ( positive valence and

activation) is placed on the top and the most negative

Q3 (negative valence and activation) on the bottom

with neutral state in the center.

Aiming to provide additional details of

ModHEmo’s inference process, two tables with

the scores of each quadrant (plus neutral state) in the

physical and cognitive components were added to the

Figure 3 chart. These table show the values at the

instant 10/05/2017 13:49:13 when a comet destroyed

an igloo. It can be observed in the tables that in the

cognitive component the quadrant with the highest

score (0.74) was Q3 (demotivation) reﬂecting the bad

event that has occurred (comet destroyed an igloo).

In the physical component the highest score (0.98)

was obtained by QN state (neutral) indicating that

student remained neutral, regardless of the bad event.

Considering the scores of these tables, the fusion

process is then performed. For this, initially the

scores of the physical and cognitive components for

each quadrant and neutral state are summed and the

class that obtained greater sum of scores is chosen.

As can be seen in the graph, the fusion process at

these instant results in neutral state (QN), which

obtained the largest sum of scores (0.98).

In the game session shown in Figure 3 it can be

seen that the physical component of the model has

relatively low variation remaining most of the time

in the neutral state. On the other hand, the line of

the cognitive component shows a greater amplitude

including points in all the quadrants of the model. In

turn, the fusion line of the components remained for

a long time in the neutral state, indicating a tendency

of this student in not to react negatively to the bad

events of the game. However, in a few moments the

fusion line presented some variations accompanying

the cognitive component. Important to emphasize that

this behavior was not generalized for all the students

in the experiment.

After ﬁnishing the session in the game, students

were presented with a tool developed to label the data

collected during the experiment. This tool allows

students to review the game session through a video

that synchronously shows the student’s face along

with the game screen. The video is automatically

paused by the labeling tool at the speciﬁc time that

a monitored event has happened. At this moment

an image with ﬁve representative emoticons (one for

each quadrant and one for neutral state) is shown and

asked the student to choose the emoticon that best

represents their feeling at that moment. After the

student’s response, the process continues.

The Figure 4 shows a screen of the tool developed

to the labeling process described above. It is

highlighted in this ﬁgure four main parts: I) the upper

part shows the student’s face at timestamp 2017-10-

02 12:36:42.450. II) at the bottom it is observed

the screen of the game synchronized with the upper

part, III) emoticons and main emotions representative

of each of the quadrants plus the neutral state and

IV) description of the event occurred in that speciﬁc

timestamp (Bug - comet displayed in the middle of

screen).

Using the data collected with the labeling process

describe above, it was possible to check the accuracy

of the inferences made by ModHEmo. For the student

id 6 used in Figure 3, the accuracy of ModHEmo

inferences achieved 69%, ie, inferences were correct

in 18 of 26 events for this students’ playing session.

The Figure 5 shows two lines depicting the ﬁtness

between values of labels and ModHEmo inferences

using the data of student id 6.

Table 1 shows the results of the eight students

participating in the experiment. This table shows

the number of monitored events, the number of

correct inferences of the ModHEmo (Hits) and the

percentage of accuracy. The number of monitored

events in Table 1 is variable due to the fact that it

depends, among others, on the game difﬁculty and

student performance in the game. For conﬁdentiality

reasons, Table 1 shows only a number as students’

identiﬁcation. Student 6 data was used in the

examples of Figures 3 and 5 above.

Table 1: ModHEmo Prediction Accuracy.

Student #Events #Hits % Accuracy

1 15 7 47

2 18 10 56

3 9 5 56

4 9 8 89

5 14 7 50

6 26 18 69

7 11 6 55

8 8 5 63

Total 110 66 60

Comparing the results shown in Table 1 with

related work is a very difﬁcult and sensitive task.This

is due to the fact that a lot of aspects need to be

considered for a correct comparison. Among such

aspects may be mentioned: i) the types of sensors

used in the experiments, ii) the experiment applied

in a real environment or laboratory, iii) number of

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

446

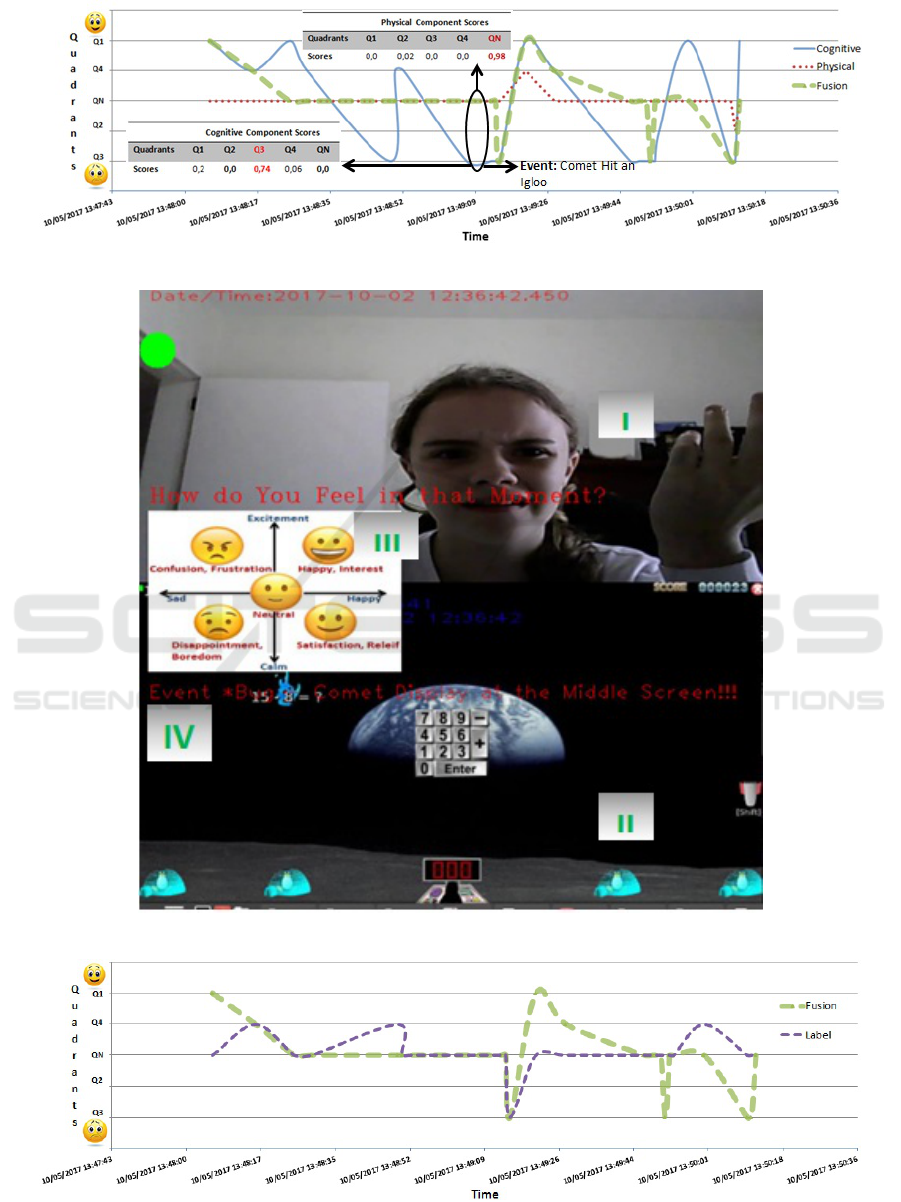
Figure 3: ModHEmo Results in One Game Session.

Figure 4: Labeling Tool Screen.

Figure 5: Comparasion Between ModHEmo Inferences em Labels.

Hybrid Model of Emotions Inference

447

classes, iv) kinds of emotions (primary or secondary)

v)type of interaction with the computing environment

(text, voice, reading, etc.), vi) who does the labeling

of the data (students, classmates, external observers).

As an example, (Picard, 1997) notes that using voice

it’s possible to reach up to 91 % of accuracy for

inference of sadness. However, this approach imposes

severe limitations because it can only be used when

interaction with educational software includes voice.

The works of (Woolf et al., 2009) and (D’Mello

et al., 2007) has some similarities with the present

proposal because they use an identical set of

emotions and experiments are made in a real learning

environment. In (Woolf et al., 2009), accuracy

rates reported range between 80 % and 89 %.

However, this higher accuracy is achieved by fusing

a set of expensive or intrusive physical sensors,

including: highly specialized camera (Kinect), chair

with posture sensor, mouse with pressure sensor and

skin conductivity sensor. (D’Mello et al., 2007)

reports accuracy rates between 55% and 65% using

text mining to predict emotion of students using an

Intelligent Tutoring System.

Thus, taking into account the speciﬁc aspects of

the ModHEmo’s construction, type of data used and

the design of the experiment carried out, it is difﬁcult

to ﬁnd related works whose comparison can be direct.

Even so, it is believed that the initial results presented

above are promising taking into account two main

aspects: i) the approach proposed in this work has

the potential to incorporate a reasonable number of

improvements by incorporating new sensors or tuning

some parameters of the model ii) the initial accuracy

rates obtained can be considered good, taking into

account the complexity of the area and the use of

minimal intrusive and widely available sensors.

With the results of ModHEmo’s inference shown

above its possible to build a proﬁle of individual

student’s learning affective states. Based on

these inferences, adaptation strategies could be

implemented in an educational software. The

affective states represented by the quadrants could

be used to identify the so-called ‘vicious-cycle’

(D’Mello et al., 2007) which occurs when affective

states related to poor learning succeed each other

repeatedly. In the context of this work this

‘vicious-cycle’ could be detected in case of constant

permanence or alternation in the quadrants Q2 and

Q3. In these cases, pedagogical strategies to motivate

the student should be applied.

In addition, the affective states inferred by

ModHEmo could be used to choose the most

appropriate cognitive-affective tutorial intervention

strategy. As described in (Woolf et al., 2009)

interventions are not appropriate if the student

does not continuously show signs of frustration or

annoyance (quadrants Q2 and Q3, in the case of

this work). So, looking for the speciﬁc student

id 6 described above, it can be pointed out that

interventions would not be necessary and that, if

applied, would possibly disturb the student.

6 CONCLUSIONS AND FUTURE

WORKS

Even with the continuously developments in research

and technology, today it is a consensus in the

scientiﬁc community that more advances are needed

until it is possible to provide access to really affect-

aware software. In this context, this work presents as

it main contribution the proposal of a hybrid model

of emotion inference applicable in an educational

software. The model is based on physical and

cognitive information, seeking improvements in the

emotion inference process through the integration

of these two important components involved in the

generation and control of human emotions.

Aware of information about individual students’

affective reactions, computational learning

environments could increase their effectiveness

by including adaptive features to the learners’

emotions. These features are relevant considering

that emotions and learning have an intrinsic relation.

Another relevant contribution of this work refers

to the deﬁnition of the ﬁve classes of affective

learning situations using an approach based on

the quadrants. These quadrants represent relevant

affective situations that impact in learning. So, they

could be used as reference in the implementation

of adaptive features in an affect-aware educational

software.

The experiment presented in this paper indicate

ﬁrstly the computational feasibility of this proposal.

This fact is relevant, considering that the proposal

is based on the fusion of quite distinct components

(cognitive and physical) and that this approach is

currently little explored by the scientiﬁc community.

Even considering some limitations in the initial

experiment described here, it can be pointed that the

model presents promising results combining minimal

or no intrusive data source sensors. The results

obtained during the experiment could be used to

identify the so-called ‘vicious-cycle’ which occurs

when continuous or repeated relapses into negative

affective states (Q2 and Q3 quadrants). In this

case the educational software could, for example,

change its feedback strategy or try to correct detected

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

448

misconceptions.

Analyzing the results of the student id 6 presented

in the previous section it can be veriﬁed that

no ‘vicious-cycle’ could be detected nor repeated

occurrences or permanence in the Q2 or Q3

quadrants. Therefore, speciﬁc actions of the

educational software would not be necessary or

advisable for the students used as example.

Tutorial intervention strategies also could be

based on the results of ModHEmo. These intervention

strategies should not be applied to students who are

interested or focused on the activity, even if some

mistakes occurs. Furthermore, for students with

constant signs of frustration or annoyance (quadrants

Q2 and Q3) educational software could try strategies

such as a challenged or a game trying to alleviate the

effects of these negative states .

It is important to note that the construction of

this proposal was focused on the educational ﬁeld,

but it is supposed that this approach, with some

adaptations, could be applied in other areas like

games, for example.

As a continuation of this work we intend to

improve the accuracy rate by tuning ModHEmo

parameters and implement and test others fusion

techniques. It is also intended to evaluate the results

obtained when teachers or specialists (psychologists)

perform the data labeling task.

Future works could be developed with the aim

of expanding the information contained in the

physical and cognitive components. Information like

head movements or ﬁxation of the eyes in certain

components of the screen could be included in the

physical component. In the cognitive component

information such as interaction patterns with the

interface or previous knowledge of the student could

be considered.

ACKNOWLEDGMENT

The authors thank the Instituto Federal de Educac¸

ao,

encia e Tecnologia do RS - IFRS and the

Universidade Federal do Paran

a - UFPR for ﬁnancial

support for this work.

REFERENCES

Alexander, S. T. V. (2008). An affect-sensitive intelligent

tutoring system with an animated pedagogical agent

that adapts to student emotion like a human tutor. PhD

thesis, Massey University, Albany, New Zealand.

Baker, R. S., Corbett, A. T., Koedinger, K. R., Evenson,

S., Roll, I., Wagner, A. Z., Naim, M., Raspat, J.,

Baker, D. J., and Beck, J. E. (2006). Adapting to

when students game an intelligent tutoring system.

In International Conference on Intelligent Tutoring

Systems, pages 392–401. Springer.

Baker, R. S., DMello, S., Rodrigo, M., and Graesser,

A. (2010). Better to be frustrated than bored:

The incidence and persistence of affect during

interactions with three different computer-based

learning environments. International Journal of

human-computer studies, 68(4):223–241.

Baker, R. S., Gowda, S., Wixon, M., Kalka, J., Wagner, A.,

Salvi, A., Aleven, V., Kusbit, G., Ocumpaugh, J., and

Rossi, L. (2012). Sensor-free automated detection of

affect in a cognitive tutor for algebra. In Educational

Data Mining 2012.

Becker-Asano, C. and Wachsmuth, I. (2010). Affective

computing with primary and secondary emotions in

a virtual human. Autonomous Agents and Multi-Agent

Systems, 20(1):32.

Calvo, R. A. and D’Mello, S. (2010). Affect detection:

An interdisciplinary review of models, methods, and

their applications. IEEE Transactions on affective

computing, 1(1):18–37.

Conati, C. (2011). Combining cognitive appraisal and

sensors for affect detection in a framework for

modeling user affect. In New perspectives on affect

and learning technologies, pages 71–84. Springer.

D’Mello, S. and Graesser, A. (2012). Dynamics of

affective states during complex learning. Learning

and Instruction, 22(2):145–157.

D’Mello, S., Picard, R. W., and Graesser, A. (2007). Toward

an affect-sensitive autotutor. IEEE Intelligent Systems,

22(4).

Ekman, P. (1992). An argument for basic emotions.

Cognition & emotion, 6(3-4):169–200.

Gebhard, P. (2005). Alma: a layered model of affect.

In Proceedings of the fourth international joint

conference on Autonomous agents and multiagent

systems, pages 29–36. ACM.

Grafsgaard, J. F., Wiggins, J. B., Boyer, K. E., Wiebe,

E. N., and Lester, J. C. (2013). Embodied affect

in tutorial dialogue: student gesture and posture. In

International Conference on Artiﬁcial Intelligence in

Education, pages 1–10. Springer.

Jaques, P. A., Pesty, S., and Vicari, R. (2003). An animated

pedagogical agent that interacts affectively with the

student. AIED 2003, shaping the future of learning

through intelligent technologies, pages 428–430.

Khan, F. A., Graf, S., Weippl, E. R., and Tjoa, A. M. (2010).

Identifying and incorporating affective states and

learning styles in web-based learning management

systems. IxD&A, 9:85–103.

Kort, B., Reilly, R., and Picard, R. W. (2001). An

affective model of interplay between emotions

and learning: Reengineering educational pedagogy-

building a learning companion. In Advanced Learning

Technologies, 2001. Proceedings. IEEE International

Conference on, pages 43–46. IEEE.

Hybrid Model of Emotions Inference

449

Kuncheva, L. I. (2004). Combining pattern classiﬁers:

methods and algorithms. John Wiley & Sons.

Ortony, A., Clore, G. L., and Collins, A. (1990). The

cognitive structure of emotions. Cambridge university

press.

Paquette, L., Rowe, J., Baker, R., Mott, B., Lester,

J., DeFalco, J., Brawner, K., Sottilare, R., and

Georgoulas, V. (2016). Sensor-free or sensor-full: A

comparison of data modalities in multi-channel affect

detection. International Educational Data Mining

Society.

Picard, R. W. (1997). Affective computing, volume 252.

MIT press Cambridge.

Picard, R. W., Papert, S., Bender, W., Blumberg,

B., Breazeal, C., Cavallo, D., Machover, T.,

Resnick, M., Roy, D., and Strohecker, C. (2004).

Affective learninga manifesto. BT technology journal,

22(4):253–269.

Posner, J., Russell, J. A., and Peterson, B. S. (2005). The

circumplex model of affect: An integrative approach

to affective neuroscience, cognitive development, and

psychopathology. Development and psychopathology,

17(03):715–734.

Pour, P. A., Hussain, M. S., AlZoubi, O., DMello, S.,

and Calvo, R. A. (2010). The impact of system

feedback on learners affective and physiological

states. In International Conference on Intelligent

Tutoring Systems, pages 264–273. Springer.

Russel, J. A. (1980). A circumplex model of affect. Journal

of Personality and Social Psychology, 39:1161–1178.

Sarrafzadeh, A., Alexander, S., Dadgostar, F., Fan, C., and

Bigdeli, A. (2008). how do you know that i dont

understand? a look at the future of intelligent tutoring

systems. Computers in Human Behavior, 24(4):1342–

1363.

Scherer, K. R. (2005). What are emotions? and how

can they be measured? Social science information,

44(4):695–729.

Tulyakov, S., Jaeger, S., Govindaraju, V., and Doermann,

D. (2008). Review of classiﬁer combination methods.

In Machine Learning in Document Analysis and

Recognition, pages 361–386. Springer.

Woolf, B., Burleson, W., Arroyo, I., Dragon, T.,

Cooper, D., and Picard, R. (2009). Affect-aware

tutors: recognising and responding to student affect.

International Journal of Learning Technology, 4(3-

4):129–164.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

450