Adaptive Decision Making based on Temporal Information Dynamics

Tobias Meuser, Martin Wende, Patrick Lieser, Bj

orn Richerzhagen and Ralf Steinmetz

Multimedia Communications Lab, Technische Universitaet Darmstadt, Germany

Keywords:

Decision-making, Distributed, Quality of Information, Information Lifetime, Information Accuracy.

Abstract:

To increase road safety and efﬁciency, connected vehicles rely on the exchange of information. On each

vehicle, a decision-making algorithm processes the received information and determines the actions that are to

be taken. State-of-the-art decision approaches focus on static information and ignore the temporal dynamics

of the environment, which is characterized by high change rates in a vehicular scenario. Hence, they keep

outdated information longer than necessary and miss optimization potential. To address this problem, we

propose a quality of information (QoI) weight based on a Hidden Markov Model for each information type,

e.g., a road congestion state. Using this weight in the decision process allows us to combine detection accuracy

of the sensor and the information lifetime in the decision-making, and, consequently, adapt to environmental

changes signiﬁcantly faster. We evaluate our approach for the scenario of trafﬁc jam detection and avoidance,

showing that it reduces the costs of false decisions by up to 25% compared to existing approaches.

1 INTRODUCTION

In recent years, vehicles have become increasingly

connected. Consequently, an increasing number of

assistance functions relies on information that is

provided by other vehicles, e.g., intelligent route

planning. With ongoing research towards autono-

mous vehicles, the amount of shared information and

functions relying on this information is expected to

grow.

However, as the information is sensed by other

vehicles with their onboard sensors, its quality can

vary signiﬁcantly. Furthermore, information received

from multiple vehicles can be contradicting or even

wrong. In a conventional vehicle with a human dri-

ver, the driver validates and rates information intuiti-

vely and makes a decision based on prior knowledge.

In comparison to that, autonomous and partly autono-

mous vehicles lack human intuition for information

rating and decision-making. Hence, analytical met-

hods need to be developed to make decisions in light

of ambiguous or even contradictory information.

Assuming that the majority of information is cor-

rect, vehicles can use approaches that rely on ma-

jority voting with simple static thresholds (Kakkas-

ageri and Manvi, 2014). Depending on the selected

threshold, these approaches adapt either slowly ma-

king them unsuitable for dynamic conditions or fast,

making them vulnerable to false information. Howe-

ver, as information about road and trafﬁc conditions

changes frequently—and measurements are not 100%

reliable—this threshold needs to be adapted for an op-

timal solution under dynamic conditions.

In this work, we propose a decision-making pro-

cess based on an information quality rating method

that can cope with ambiguous or contradictory infor-

mation. We focus on two information quality factors:

the false detection rate describing the percentage of

erroneous measurements and the expected event life-

time of the information type. We combine both fac-

tors using an exponential function to decide on the

quality of information. To this end, the event life-

time and the false detection rate are modeled using a

Hidden Markov Model (HMM). Based on the HMM,

we derive a weighting function that is then used in

a weighted majority voting. Consequently, informa-

tion of high quality has a higher impact on the deci-

sion than low-quality information. As a result, we can

drastically decrease the adaption time for information

with high detection rate by lowering the impact of old

information in the voting procedure.

We evaluate our approach for the scenario dis-

played in Figure 1. The vehicles in the Area of In-

exit

POA

car

AOI

Figure 1: Blocked Road.

Meuser, T., Wende, M., Lieser, P., Richerzhagen, B. and Steinmetz, R.

Adaptive Decision Making based on Temporal Information Dynamics.

DOI: 10.5220/0006687900910102

In Proceedings of the 4th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2018), pages 91-102

ISBN: 978-989-758-293-6

terest (AOI) drive on the road and may still take the

exit, leading to a longer overall route. Consequently,

if there is a trafﬁc jam at the Place of Action (POA),

the vehicles should take the exit to achieve optimal

routing. However, the information about the state of

the road (jammed or not jammed) needs to be distribu-

ted from vehicles in the POA to those in the AOI. We

evaluate the impact of false information and the time

it takes to adapt to changed road state relying on an

accurate model of vehicular mobility. Our evaluation

shows that our decision-making process outperforms

state-of-the-art approaches signiﬁcantly, reducing the

amount of false decisions by up to 25%.

The remainder of the paper is structured as fol-

lows: We provide relevant background on HMMs in

Section 2, followed by a discussion of existing ca-

ching systems and their handling of contradicting in-

formation in Section 3. We present our contribu-

tion, the freshness-based majority voting approach for

decision-making under ambiguous or contradictory

information in Sections 4 and 5. Section 6 contains

an in-depth evaluation of our approach, comparing its

performance against state-of-the-art decision-making

processes and the optimal solution derived numeri-

cally. The paper is concluded in Section 7.

2 HIDDEN MARKOV MODEL

A Hidden Markov Model (HMM) is a statistical mo-

del in which the system states cannot be observed di-

rectly. The hidden states depend on the observable

ones. Thus, the value of the hidden states cannot be

assured.

We model the road conditions and the associated

detection as a HMM. Figure 2 displays a general sy-

stem model. There are two reasons for modeling the

detection of road conditions as a HMM:

2.1 Measurement Error

The connections between the Observable and the Hid-

den Layer symbolize the measurement process. The

real state (Hidden State (HS)) of the road (HS

...HS

)

is hidden from the vehicles. The vehicles cannot di-

rectly measure the hidden states due to the restrictions

of their onboard sensors. They can only measure the

Observable State (OS) (OS

...OS

) on the observable

layer, which maps to the associated hidden state with

a certain probability. The solid lines symbolize a high

probability for the mapping. If a vehicle measures a

state OS

, there is a high probability that the real state

of the road is HS

. However, this cannot be assured. If

the measurement of the vehicle is erroneous, the real

Observable LayerHidden Layer

OS1 OS2

HS1 HS2

OSn

HSn

...

Figure 2: Hidden Markov Model for a general system.

state of the road differs from HS

. This error is sym-

bolized by the dotted line. The number of observable

states n and the number of hidden states m can differ.

We assume the measurement error to be equal for all

vehicles. Thus, the number of observable states and

hidden states are equal.

2.2 State Change

The hidden state of the road changes over time. Each

state has a probability to stay the same state and a

probability of a state change. The arrows between the

hidden states symbolize the transitions between the

hidden states. If the probability of a state change is

high, the event is highly dynamic. If this probability

is low, the event is considered static.

We will use this speciﬁc behavior for the optimi-

zation of our decision algorithm.

3 RELATED WORK

In this section, we summarize the previous works in

the context of this paper. As our approach is based on

the quality of the information for decision making, we

ﬁrst provide an overview of the respective literature.

After that, we provide an overview of previous works

towards decision making in distributed systems.

3.1 Quality of Information (QoI) in

Distributed Networks

In the literature, Quality of Information (QoI) asses-

sment is a repetitive topic. QoI consists of different

dimensions, each dimension describing a speciﬁc pro-

perty of the information. The importance of each di-

mension depends on the application. Not every di-

mensions is applicable useful for all applications.

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

Wang and Strong (Wang and Strong, 1996) sur-

veyed data consumers on essential quality dimensi-

ons for information management systems. Based on

this work, other researchers adapted the QoI dimen-

sions for their applications. Chae et al. (Chae et al.,

2002) adapted the concept of QoI for mobile inter-

net applications. They took four dimensions into ac-

count, which describe the connection, content, inte-

raction and contextual quality. They survey people to

determine how the different quality dimensions com-

bine to an overall QoI metric.

In vehicular networks, QoI is pivotal for correct

decision making in vehicular applications (Kakkas-

ageri and Manvi, 2014). Each vehicle performs the

information validation by itself. The idea of Fawaz

et al. (Fawaz and Artail, 2013) is to choose the Time

to Live (TTL) dynamically dependent on the history

of changes. With their work, it is possible to esti-

mate the TTL of an information type. For vehicular

networks, three dimensions are most important: the

content quality, the trust between the vehicles and the

spatiotemporal relevance of information. The neces-

sary meta-information are available for every vehicle.

Delot et al. (Delot et al., 2008) estimated the geo-

graphical relevance of information in vehicular net-

works. They calculated the geographical relevance

using the encounter probability of the vehicle and the

information. For the temporal quality, Kuppusamy

et al. (Kuppusamy and Kalaavathi, 2012) publis-

hed an approach called Cluster Based Data Consis-

tency (CBDC). They concentrated on increasing the

data consistency and accessibility in clustered Mo-

bile Ad-hoc Networks (MANETs). They assured the

freshness of information using a TTL value. After the

expiration of the TTL, the information is considered

invalid and removed from the cache. These metrics

are made for their respective use cases. Though, to

the best of our knowledge, there is no metric for deci-

sion making available, which can handle uncertainty.

For this, the temporal relevance, the content quality

and the trust between vehicles are pivotal. We extend

the work of Meuser et al. (Meuser et al., 2017) with

an approach to explicitly model the decrease of infor-

mation value based on the TTL of the information.

3.2 Decision Making under Uncertainty

In most vehicular applications, vehicles rely on a

threshold for the number of messages required to up-

date their decision (Kakkasageri and Manvi, 2014).

Molina et al. (Molina-Gil et al., 2010) researched

on the security consideration in vehicular networks.

They proposed a probabilistic signature validation

scheme to reduce computational overhead while pre-

venting incorrect messages. Hsiao et al. (Hsiao et al.,

2011) modeled the validation of message based on

their quality implicitly. Although their approach focu-

ses on trust, it can be used for inaccurate information

likewise. They validated messages of other vehicles

using the already received messages. The vehicles

only perform an adaptation if the message amount is

sufﬁciently high.

In previous work, Meuser et al. (Meuser et al.,

2017) used a HMM to model information with dis-

crete event space. Using the spatiotemporal relation

between information, they were able to aggregate in-

formation of different time and location. In their

work, the impact of old information decreases expo-

nentially. Moreover, they took the content quality into

account and decreased the impact of inaccurate infor-

mation. In their work, they did not mention how to

derive the spatiotemporal dependency between infor-

mation.

To our best knowledge, there is still a gap in ra-

ting QoI for dynamic information in vehicular net-

works. Previous work focused either on static infor-

mation or provided non-optimal solutions for dyna-

mic information. Thus, we will focus on a freshness-

and accuracy-aware validation scheme for informa-

tion in vehicular networks.

4 PRELIMINARIES

Vehicles can exchange information using multiple

communication technologies. Available communi-

cation technologies are the cellular network and the

wiﬁ-based 802.11p standard. In general, 802.11p

is used for emergency communication, while non-

safety-related services need to be performed via mo-

bile communication, as 802.11p is not suitable for

high distances due to its multihop behavior. An ex-

ample for non-safety-related services is the distribu-

tion of jam information.

Non-safety-related information contains meta-

information to enhance the information. This meta-

information are the detection time, the detection place

and the expected lifetime. That information is essen-

tial for other vehicles to rate the information.

This information is distributed among the affected

vehicles using a Publish/Subscribe system. For this

system, we assume that every vehicle is equipped with

a cellular network connection. A Publish/Subscribe

server manages subscriptions and publications.

Adaptive Decision Making based on Temporal Information Dynamics

4.1 Publish/Subscribe System

The Publish/Subscribe system used is an attribute-

based Publish/Subscribe system. The attributes are

the ids of the road segments on which the informa-

tion is located. These ids can, e. g., be extracted from

OpenStreetMap

While driving on the streets, each vehicle percei-

ves its environment and shares the information with

interested vehicles. For that, the vehicle publishes the

information with the id of the affected road segment.

Interested vehicles subscribe to road segments to

receive this information. Those road segments are

parts of the planned route of the vehicle. Once a vehi-

cle receives information, this information is stored in

the cache until the information lifetime expires.

4.2 Scenario Description

In this work, we focus on an example scenario, which

is visualized in Figure 3. It can be divided into 4 dif-

ferent phases.

exit

Figure 3: Visualization of the different road Phases.

In the ﬁrst phase, there is no trafﬁc jam, and the

trafﬁc ﬂows as usual.

In the second phase, an obstacle blocks the road,

e. g., a broken car. Due to the road blockage, the traf-

ﬁc jams. Several hundred meters distant from this

point, there is an exit to bypass the accident. Howe-

ver, the drivers near this exit do not know about this

incident. Hence, they do not leave the road and drive

into the trafﬁc jam. As the vehicles in the jam know

about the blockage, they publish this information. A

vehicle near the exit receives this information. After

it believes the other vehicles that there is a jam, the

system changes to the third phase.

In the third phase, the vehicles take the exit. We

assume that under normal trafﬁc conditions the exit of

the road is a diversion. However, during the blockage

of the road, the detour is the fastest route.

In the fourth phase, once the road blockade is over,

the drivers still take the detour because they have no

http://www.openstreetmap.org

Observable Layer

Hidden Layer

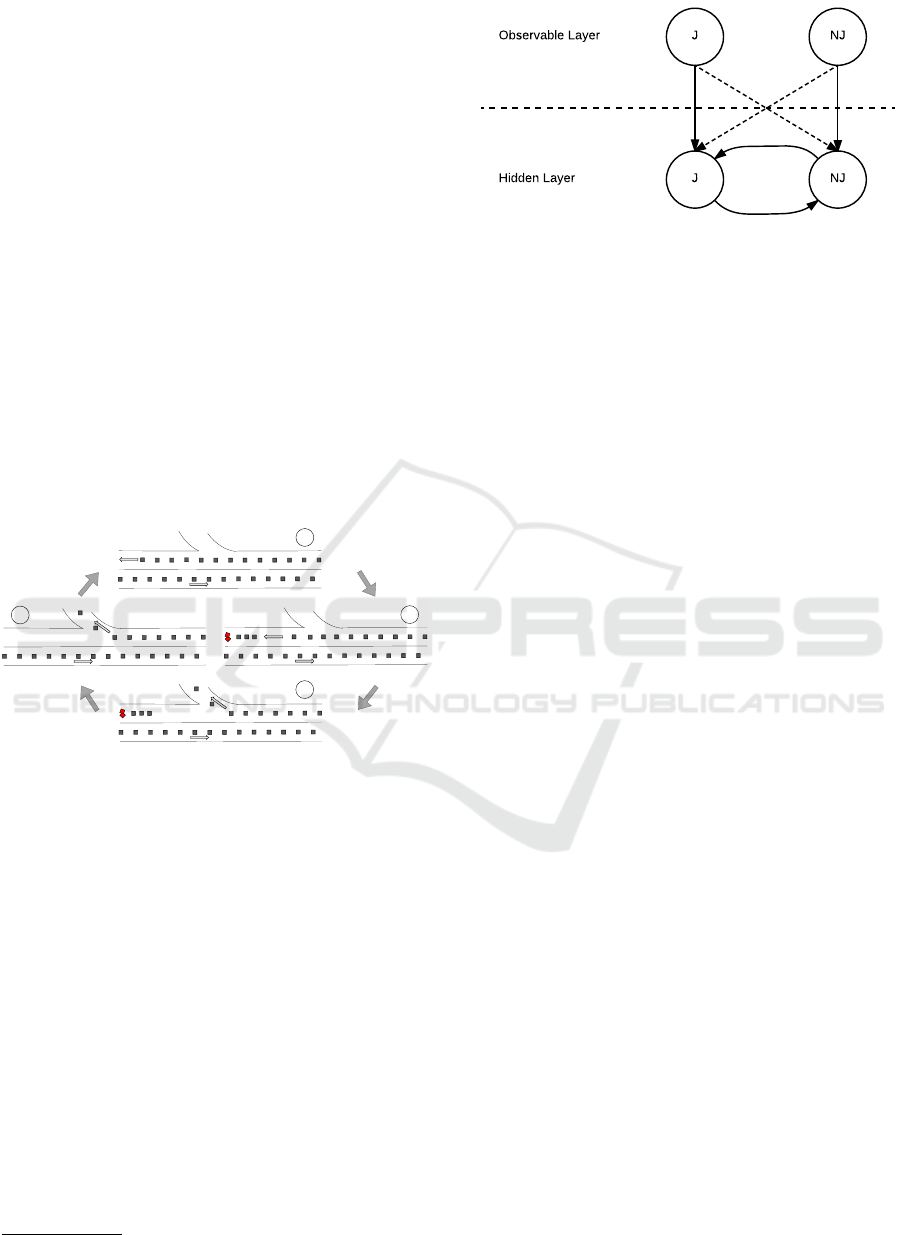
J NJ

Figure 4: Hidden Markov Model for a trafﬁc jam.

information about the jam dissolution. Thus, the vehi-

cles at the former trafﬁc jam publish the information

that the jam has resolved. After the vehicles near the

exit are conﬁdent in the received information, they

stay on the road and do not take the detour anymore.

4.3 Trafﬁc Jam Modeling

The example scenario uses a trafﬁc jam as an exam-

ple for road blockage. To make decisions based on

the information type, we need to model the informa-

tion. We use the model of a HMM as already used in

(Meuser et al., 2017). With the HMM, the transition

between states can be predicted easily. This model is

trained with historic data.

The HMM for a trafﬁc jam is shown in Figure 4.

We assume there are two states for this information

type: either a road segment is jammed or not jammed.

Once a vehicle tries to measure the state of a road

segment, it has a certain probability to measure the

correct state, i. e., measuring the road is jammed, and

the road is jammed. With a low probability, the mea-

surement is wrong, i. e. the vehicles measure the road

is jammed, but the road is not jammed. The solid line

between the observable layer and the hidden layer is

of high probability, while the dotted line is of low pro-

bability.

The change of a road naturally changes over time.

If a vehicle has measured the state of the road in the

past, this measurement cannot predict the future state

with certainty. We model this behavior with the state

transition in the hidden layer.

4.4 Decision Making

Every time a vehicle has the chance of a detour, it

checks the information in its cache. If there is a road-

related information for the road segments after the

current and the next exit, the vehicle evaluates the

available information. If the vehicle expects the in-

formation to be correct and valid, it takes the exit.

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

A trafﬁc jam is a dynamic information in the vehi-

cular context. As vehicles can only observe their close

environment, the quality of a jam detection is varying.

5 QUALITY OF INFORMATION

BASED DECISION-MAKING

Decision-making algorithms can beneﬁt many vehi-

cular applications. In this paper, we investigate the

example of jam detection. Like most other informa-

tion required by vehicular applications, the jam state

of the road changes regularly.

Existing approaches from literature do not use the

full potential of the information, as they do not con-

sider these information-speciﬁc properties and thus,

adapt either too slow or too fast.

Slow adaptation leads to decisions based on false

knowledge. If the environment changes, the vehicle

still considers the old information as correct. This

misinformation produces costs for the vehicles, which

is, e. g., the unnecessary rerouting in case of a trafﬁc

jam.

On the opposite, fast adaptation is very sensitive

to false information and creates costs through incor-

rect information. The costs of slow and fast adapta-

tion are obviously contrary. The costs through false

information rise if an approach adapts very fast to in-

coming information. On the other hand, the costs rise

with increasing change rate of the environment if an

approach adapts slowly.

In the following, we derive a formula for the costs

of both fast and slow adaptation. We solve the re-

sulting optimization problem to achieve the lowest

possible cost.

5.1 Problem Formulation

For convenience, Table 1 provides an overview of the

used variables.

We minimize the total costs c

total

(n) for wrong de-

cisions as shown in Equation 1. The variable n is the

number of messages after which the vehicle adapts to

incoming information and updates its decision. Chan-

ging the value of n inﬂuences the adaptation speed of

the algorithm.

minc

total

(n) (1)

The total costs c

total

(n) for a wrong decision con-

sist of two costs, the costs of slow and fast adaptation.

They are shown in Equation 2.

Table 1: Overview of used Variables.

Variable Description

total

Total costs of wrong decisions

slow

Costs of slow adaptation

f ast

Costs of fast adaptation

n Number of messages for adaptation

opt

Optimal number of messages for

adaptation

Rate of incorrectly sensed information

Change probability of the sensed en-

vironment per time interval

T Time to Live (TTL) for the informa-

tion type

f ast

Costs of an incorrect change of deci-

sion per time interval

slow

Costs of an incorrect keep of decision

per time interval

Age of information i

State of information i

f (t

) Impact function of information i

I(s) Impact of all information of state s

total

(n) = c

f ast

(n) + c

slow

(n) (2)

The ﬁrst summand is the costs c

f ast

(n) for a too

fast adaptation. Too fast adaptation leads to a high

impact for erroneous measurements. Thus, for low

accuracy measurements, the adaptation is required to

be slow. The second summand is the costs c

slow

(n) for

a too slow adaptation. If the real variable value chan-

ges, but the vehicle does not adapt to this change, the

vehicle makes the wrong decision. For high accuracy

information, the adaptation time can be low to decre-

ase this costs.

The costs c

f ast

(n) are calculated in Equation 3.

They consist of the probability for a vehicle receiving

a sufﬁciently high number of wrong information to

adapt to the false information. The vehicle calculates

this probability using the false detection rate p

de-

rived from the HMM. For this, the average false de-

tection rate is used. The variable C

f ast

represents the

costs that describe the negative impact of the deci-

sion. These costs depend on the additional costs that

emerge for the vehicle in case of a false adaptation.

They are the difference between the costs of the adap-

tation and the costs of the correct decision.

f ast

(n) = p

∗C

f ast

(3)

The costs c

slow

(n) are shown in Equation 5. These

costs consist of the number of messages required for

the change n, the probability for a change p

and the

costs of the wrong decision C

slow

. n states the number

of messages that a vehicle requires to update its deci-

sion. As long as the vehicle has not received the requi-

Adaptive Decision Making based on Temporal Information Dynamics

red amount of messages, it will make the wrong deci-

sion. We derive the probability for a change p

from

the rate r of incoming messages per second. Vehicles

individually measure this rate, but consider this rate

to be constant. We calculate p

under the assump-

tion that the message is invalid after the TTL T . A

message is invalid once the probability for any state

is equal to the probability for the current state. Equa-

tion 4 shows the value for p

with

being the num-

ber of possible states.

= 1 −

(4)

The costs C

slow

are calculated similarly to the

costs C

f ast

, using the difference in cost of the best de-

cision and the decision that has been made.

slow

(n) = n ∗ p

∗C

slow

(5)

5.2 Optimization Problem

As we want to minimize the costs of wrong decisions,

we minimize the costs c

total

. We search for this mi-

nimum by deriving the costs c

total

(n) for n and set it

equal to 0 as shown in Equation 6. We transform this

equation to Equation 7.

δn

total

(n) = 0 (6)

∗ln(p

) ∗C

f ast

+ p

∗C

slow

= 0 (7)

Solving Equation 7 results in the optimal number

of messages n

opt

. If a vehicles adapts to incoming in-

formation after n

opt

messages, the total costs for this

value is minimal, which can be derived from the be-

havior of the cost function. Equation 8 shows the op-

timal value n

opt

. We require the number n

opt

to be

integral, thus round it.

opt



−

ln(p

)

∗

slow

f ast



ln(p

)

(8)

We need to develop an algorithm that adapts to

new information after n

opt

messages. An intuitive ap-

proach uses the approach from the literature, which

adapts after a certain amount of information. This ap-

proach is robust to false information. However, its

adaptation is still slower than possible.

This slow adaptation is justiﬁed by the algorithm

behavior, which requires n

opt

messages in a row to

perform the adaptation. Assuming a vehicle receives

opt

−1 messages with the new information and after-

ward one message with the old information, it cancels

the adaptation and needs to restart it. Thus, we deve-

lop an algorithm that solves this problem.

5.3 Quality of Information-based

Majority Voting

We propose a freshness-based majority voting algo-

rithm which optimizes the costs. In the existing lite-

rature, two main approaches are proposed for decision

making:

A conventional approach is to decide after a cer-

tain amount of information. This approach considers

information to be correct if the vehicle has received a

certain amount of messages with that information in a

row. The issue with this approach is the determination

of the exact message amount. For low amounts, this

approach is very prone to false information.

The other standard approach decides using the

amount of available information. This approach con-

siders the information as correct, of which it has sto-

red the most messages in the cache. This approach is

resilient to incorrect information but adapts to chan-

ges slowly.

Our approach is based on majority voting and

combines the advantages of both these approaches.

In conventional majority voting, every vote has equal

weight. Majority voting by itself is very resilient to

incorrect information but adapts to changes slowly.

We solve this problem by changing the weights for

the information in the voting process. The weight the

information is chosen in a way that a vehicle adapts

after an optimal amount n

opt

of information.

Our approach considers the freshness and accu-

racy of the information and works as follows: Given

a set of messages M for a particular edge, the vehi-

cle can calculate the voting score using the age t

and

the state s

of the messages i = 1..|M| as shown in

Equation 9. M

is the subset of messages containing

messages of the state s. The function f (t) is an im-

pact function, which adapts to the information type.

The parameter t is the age of the information in the

cache.

I(s) =

∑

i|s=s

f (t

)

∑

|M|

i=1

f (t

)

(9)

The vehicle chooses the state with the highest im-

pact score I(s). The advantage of our approach is that

it adapts faster to environmental changes than conven-

tional majority-voting, as old information are assig-

ned smaller weights. Compared to always adapting

to the newest available information, our approach is

less prone to false information and can, thus, ensure a

higher percentage of correct decisions.

The impact function f (t) weights information in

the cache. This function describes the tradeoff bet-

ween fast adaptability and resilience to false informa-

tion. In the next part, we will derive the function f (t).

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

5.4 The Impact Function f (t)

The impact function f (t) depends on the expected rate

of false information p

and the change rate of the in-

formation p

. As described in section 4, we model the

road information using a Markov chain. Thus, f (t)

is a general exponential function as shown in Equa-

tion 10.

f (t) = a ∗e

+ d (10)

Based on f (t), any exponential function can be

created using the appropriate values for a, b and d. In

the following, we will derive the values for the para-

meters a, b and d using the three requirements of this

function.

5.4.1 Impact of New Information

The initial weight of detected information needs to be

equal to the expected accuracy of this information. As

t is the age of the information, Equation 11 must be

true.

f (0) = a + d = 1 − p

(11)

5.4.2 Invalidation of Information After the TTL

A vehicle removes information from the cache after

the TTL has expired. The weighting function gradu-

ally decreases the impact of the information. Thus,

the impact of the information at the expiration of the

TTL equals 0 and Equation 12 must hold true.

f (T ) = a ∗e

+ d = 0 (12)

Using these two requirements, we can derive the

family of parametric functions with the parameter b in

Equation 13. For this, Equation 11 and Equation 12

are inserted to replace the values of a and d. Thus,

this family of parametric functions ensures that the

two requirements of Equation 11 and Equation 12 are

satisﬁed regardless of the value of b.

(t) =

(1 − p

) ∗



−e



1 −e

(13)

Figure 5 displays the impact of the parameter b on

the behavior of the respective functions. For variables

with a low detection accuracy, the impact function

needs to stay at its start value for a long time to com-

pensate for the high amount of measurement errors.

For variables with high detection accuracy, the impact

function reduces the impact drastically after a short

time to utilize the high reliability of the detected in-

formation.

To determine the exact value for the parameter b,

the third and ﬁnal requirement to this function is used.

For this, we developed a trial-and-error based heuris-

tic to approximate b.

0 1 2 3 4 5

Age of the information [min]

0.00

0.25

0.50

0.75

1.00

Value for f

(t)

b = ∞

b = 0.1

b ≈ 0

b = −0.01

b = −∞

Figure 5: Visualization of the family of functions for diffe-

rent parameters b.

5.5 Approximation of b

We use the message amount n

opt

with the minimal

cost value to choose the appropriate value for b. We

choose b such that the vehicle updates its decision af-

ter n

opt

messages. However, the vehicle cache con-

tains only a certain amount of messages with certain

timestamps. To map the amount n

opt

to the local kno-

wledge of the vehicle, we derive the rate of messages

r per second from the information already stored in

the cache. Using the rate r, we assume a uniform dis-

tribution of information in the cache.

For the approximation of b, we look at a consistent

cache with uniformly distributed messages. This con-

sistent cache is a simpliﬁcation, but in the evaluation,

we can show that it performs well in simulations. We

cannot use the actual distribution of the information

in the cache as we cannot evaluate the correctness of

the information in the cache and have no insights on

future messages.

Equation 14 shows the impact I(s

) for the former

state s

. This state has been active before a change.

The impact of the state sums the results of the impact

function for all information in the cache starting from

message n

opt

to the last message T /r. We use n

opt

the ﬁrst message because the messages from 0 to n

opt

are the messages with the new state.

I(s

) =

bT /rc

∑

n=n

opt

(n ∗r) (14)

In addition to the impact of the old state, Equa-

tion 15 shows the impact I(s

) of the current state s

The change happened at the time t = n

opt

∗r. As the

information with the new state comes in with same

rate r as before the change, we sum the impact of all

messages between 0 and n

opt

I(s

) =

opt

∑

n=0

(n ∗r) (15)

We want to have a decision update after n

opt

mes-

sages. For all n smaller than n

opt

, the vehicle does not

Adaptive Decision Making based on Temporal Information Dynamics

change its decision. After the vehicle has changed its

decision, the impact of the new decision raises con-

stantly and thus it sticks to that decision. To ﬁnd the

optimal value of b, at which the adaptation is perfor-

med after n

opt

, the impact of the old and the new state

need to be similar. Equation 16 shows this equality.

bT /rc

∑

n=n

opt

[ f

(n ∗r)] =

opt

∑

n=0

[ f

(n ∗r)] (16)

We solve this equation by trying out different va-

lues for b until we ﬁnd a b for which this equality

holds. Once we ﬁnd b, we have completed our im-

pact function, which a vehicle uses for its decision

making. We deﬁne the two extreme cases separately.

For n

opt

= 0, b is equal to ∞ and for n

opt

+1 > T /r, b

is equal to −∞. Using b, we can exactly calculate the

impact of old information and thus make good decisi-

ons based on that information.

5.6 Uniform Distribution of Messages

For the described approach, the messages in the ca-

che need to be uniformly distributed. This distribu-

tion is automatically achieved for information which

the vehicles detect bypassing, as vehicles are natu-

rally driving over the road segment one after the ot-

her. However, if the vehicles get stuck at the informa-

tion location, each vehicle transmits the information

on detection and retransmits it after the expiration of

the TTL. This approach leads to many messages at

roughly the same time.

We solve this problem by adding a random factor

to the ﬁrst retransmission interval. Instead of retrans-

mitting after the expiration of the TTL, the vehicle

performs the ﬁrst retransmission after a random time,

which is between 0 and the TTL T . This way, the

messages are distributed more uniformly.

6 EVALUATION

For the evaluation of our developed decision appro-

ach, we simulate a trafﬁc jam on a highway. In front

of the trafﬁc jam, each vehicle has the possibility to

leave the road. Figure 6 displays the road scenario.

Initially, there is no information about trafﬁc jams

in the network. At a certain point in time, the traf-

ﬁc congests and the vehicles distribute the informa-

tion about the trafﬁc jam using a Publish-Subscribe

system. As there were no messages in the network

before, the adaptation for the initial jamming of the

road is fast. After a certain amount of time, the trafﬁc

Figure 6: Schematic overview of the road scenario.

jam resolves and thus, the vehicles at the jam loca-

tion publish the information that the trafﬁc jam has

resolved. However, there are already information in

the vehicle’s cache indicating that there is a trafﬁc

jam. Hence, the adaptation to the new requirements

is far more challenging as each vehicle needs to de-

cide on the correctness of the cached information. We

consider this scenario as an appropriate scenario for

decision-making, as each vehicle decides to leave or

stay on the road.

We implement this scenario in the event-based Si-

monstrator framework (Richerzhagen et al., 2015).

The Simonstrator is a network simulator, which sup-

ports different communication technologies (mobile

and ad-hoc communication) and, beyond others, the

Publish/Subscribe paradigm. As the movement mo-

dels in the Simontrator are not suitable for our vehi-

cular usecase, we extend the Simonstrator with Simu-

lation of Urban Mobility (SUMO) (Behrisch et al.,

2011). The connection to SUMO is accomplished

using the TraCI interface of SUMO.

In the evaluation, we used two metrics to compare

our approach to the state-of-the-art approaches: the

costs of wrong decisions and the ratio of correct deci-

sions. We put special focus on the reduction of costs

induced by wrong decisions. We assume that costs

occur every time a vehicle would have made a wrong

decision. Thus, we observe the cache and make a de-

cision every second. If this decision is wrong, we add

the appropriate costs to the total costs.

For comparison, we implemented both an optimal

strategy and a random strategy. The optimal strategy

chooses the correct information out of the cache using

global knowledge, but can still make the wrong deci-

sion if there is no correct information in the cache.

The random strategy chooses information out of the

cache randomly and considers this information as cor-

rect. We expect none of the described approaches

to perform better than the optimal or worse than a

random approach. Thus, these are suitable bounds.

We combine those two strategies to determine the

used optimization potential of every approach. We

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

0% 1% 5% 20%

False detection rate

0.0

0.2

0.4

0.6

0.8

1.0

Used optimization potential

QoI-based

Newest-information

Majority-voting

(a) Used optimization po-

tential

0% 1% 5% 20%

False detection rate

100

150

200

250

Total Costs

Optimal

QoI-based

Newest-information

Majority-voting

(b) Total costs

Figure 7: Total costs for different false detection rates.

calculate the used optimization potential as shown in

Equation 17.

opt =

approach

−c

random

optimal

−c

random

(17)

Table 2 gives an overview of the considered para-

meters and their values. We varied the false detection

rate, the jam duration and the costs of a wrong detour.

The bold values in the table are the default ones. The

costs are calculated based on the cost ratio. To ensure

a comparability of costs, we set C

f ast

slow

= 2. The

evaluation source code is freely available

Table 2: Overview of used variables.

Evaluation parameter Value

False Detection Rate [0%, 1%, 5%, 20%]

Jam Duration [200s, 300s, 400s]

Cost Ratio between the

costs of a wrong stay

and a wrong exit

[0.1, 1, 10]

We ﬁrst have a look at the metrics for the diffe-

rent false detection rates, as the false detection rate

has the highest impact on the results. For the other

parameters, we only investigate on the costs of wrong

decisions.

6.1 Impact of the False Detection Rate

for the different Approaches

At ﬁrst, we investigate on the costs and after that on

the percentage of correct decisions for different false

detection rates.

6.1.1 Costs of False Decisions

Figure 7(a) shows the used optimization potential of

our approach compared to the approaches in the li-

terature dependent on the false detection rate. For

https://dev.kom.e-technik.tu-darmstadt.de/simonstrator/

0% 1% 5% 20%

False detection rate

100

125

Costs for slow adaptation

Optimal

QoI-based

Newest-information

Majority-voting

(a) Costs of slow adapta-

tion

0% 1% 5% 20%

False detection rate

100

150

200

250

Costs for fast adaptation

Optimal

QoI-based

Newest-information

Majority-voting

(b) Costs of fast adapta-

tion

Figure 8: Costs by cause for different false detection rates.

a false detection rate of 0%, our approach and the

newest-information approach perform as well as the

optimal approach, while the majority-voting based

approach performs much worse due to its slow adap-

tation to environmental changes. The used opti-

mization potential of our approach and the newest-

information approach drops with increasing false de-

tection rate. In contrast, the optimization potential of

the majority-voting based approach increases. Our

approach converges towards the majority-voting ba-

sed approach for high false detection rates. The re-

ason for the increased performance of the majority-

voting based approach is the decrease of time for

adaptation to environmental changes, as the number

of correct messages in the cache is lower.

Figure 7(b) displays the total costs. Regarding to-

tal costs, our QoI-based approach has almost equal to-

tal costs regardless of the false detection rate. Compa-

red to the approach selecting the newest information,

our approach has up to 56% reduced overall costs de-

pendent on the false detection rate and up to 43% re-

duced costs compared to the conventional majority-

voting based approach. The total costs of the opti-

mal approach decrease with increasing false detection

rate, as false messages lower the adaptation time af-

ter the trafﬁc jam. We explain this behavior in more

detail in the next paragraph.

In Figure 8(a) the costs of slow adaptation are

shown. We can observe that the costs of our QoI-

based approach are almost equal to the costs of the

fastest approach, which immediately adapts to new

information. This is a great result, as our approach

is far more robust to false information. The majority-

voting approach has high costs of slow adaptation,

as expected, since many message are required for a

decision change. Interestingly, some of the appro-

aches have lower costs of slow adaptation with hig-

her false detection rate. Normally, it is expected that

those costs increase with increasing false detection

rate. However, this behavior happens if a vehicle

performs a false measurement during the trafﬁc jam,

i. e., a message stating that the trafﬁc jam has resol-

Adaptive Decision Making based on Temporal Information Dynamics

0% 1% 5% 20%

False detection rate

0.0

0.2

0.4

0.6

0.8

1.0

Correct decision ratio

Optimal

QoI-based

Newest-information

Majority-voting

(a) Percentage of correct

decisions during the jam

0% 1% 5% 20%

False detection rate

0.0

0.2

0.4

0.6

0.8

1.0

Correct decision ratio

Optimal

QoI-based

Newest-information

Majority-voting

(b) Percentage of correct

decisions after the jam

Figure 9: Percentage of correct decisions for different false

detection rates.

ved. Although that measurement was incorrect at

this point, it becomes true as the trafﬁc jam resolves

shortly after. As this originally false message is also

used in the decision process, the adaptation time and

thus the costs can be lower with increasing false de-

tection rate.

Figure 8(b) shows the costs of fast adaptation.

Those costs are 0 for all approaches for a false de-

tection rate of 0%, as there are no false measurements

in the system. With increasing false detection rate, the

costs of fast adaptation of the algorithm increase. This

is caused by the increasing number of false informa-

tion in the system, which challenges the robustness of

each approach. The newest-information approach is

not robust to false information, thus the costs of fast

adaptation increase drastically. Compared to that, the

costs of fast adaptation of our QoI-based approach in-

crease only slightly and are much lower than the costs

of the newest-information approach. In contrast, our

approach has higher costs of fast adaptation than the

majority-voting based approach, but this behavior is

intentional, as the higher costs of the fast adaptation

produce lower costs of slow adaptation. Interestingly,

even the optimal approach has costs of fast adapta-

tion. This is not intuitive, as the optimal approach ne-

ver makes a wrong decision. However, even the op-

timal algorithm makes wrong decisions, if there are

only false information in the cache. This happens if

the last correct message is removed from the cache

due to its age.

6.1.2 Percentage of Correct Decisions

This metric investigates the effects that the decision

approach has on the vehicles. Every time, a vehicle

makes a decision, this decision is stored and inﬂuen-

ces the metric. Two phases are investigated. The ﬁrst

phase is for the decision-making during the jam. Me-

aning, this metric is the percentage of vehicles that

have successfully taken an exit. The second phase is

for the decision-making after the jam. This metric is

400 300 200

Event lifetime [s]

0.0

0.2

0.4

0.6

0.8

1.0

Used optimization potential

QoI-based

Newest-information

Majority-voting

(a) Used optimization po-

tential

400 300 200400 300 200

Event lifetime [s]

100

150

200

250

Costs

Optimal

QoI-based

Newest-information

Majority-voting

Costs for slow adaptation

Costs for fast adaptation

(b) Total costs of wrong

decisions with cause

Figure 10: Costs for different jam durations.

for the percentage of vehicles that have stayed on the

road after the trafﬁc jam has resolved.

Figure 9(a) shows the correct decision ratio during

the trafﬁc jam. At the beginning of the jam, there is

no information in the cache, as the vehicles do not

share any information prior to the jam. Thus, the ra-

tio is generally higher compared to the situation after

the jam. However, a high correct decision ratio du-

ring jam means that only a few vehicles are in the jam

and able to measure the road state. Thus, the ratio of

correct decisions drops with increasing false detection

rate, as the impact of false information is higher with

fewer messages in the system. Moreover, we can see

that our QoI-based approach perform better than the

newest-information approach for every false detection

rate and only slightly worse than the majority-voting

based approach.

The ratio of correct decisions after the jam is

shown in Figure 9(b). Our QoI-based approach

is equally good as the newest-information approach

with a false detection rate of 0%, but while the

newest-information approach drops with increasing

false detection rate, our QoI-based approach is robust

to false information and thus stays almost at the same

level. The performance of the majority-voting based

approach also does not drop with increasing false de-

tection rate. However, its correct decision ratio is al-

ways lower than the one of our QoI-based approach.

6.2 Impact of the Jam Duration to the

different Approaches

Figure 10 shows the costs and the cost distribution

for the different jam durations. With decreasing jam

duration, the used optimization potential decreases li-

kewise as shown in Figure 10(a). However, the ratio

between the different approaches is not affected sig-

niﬁcantly.

To explain the decrease of costs with decreasing

jam duration, we use the distribution of costs shown

in Figure 10(b). There are two reasons for this de-

crease. Firstly, the number of messages in the cache

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

100

is lower, as fewer vehicles published the information.

Thus, the number of messages required for adaptation

is also lower. This is true for our QoI-based approach

as well as for the majority-voting based approach. Se-

condly, the possibilities for wrong decisions during

the jam is lower, as the jam duration is shorter. The

newest-information approach is one of the examples,

where the costs of fast adaptation decrease due to the

shorter jam duration. However, the costs of fast adap-

tation does not decrease strongly. This is due to the

lacking robustness of the newest-information appro-

ach. This leads to a very time until the system has

recovered after the jam, which increases the costs of

this approach.

Conclusively, we derive that our QoI-based appro-

ach outperforms the other approaches independently

of the jam length.

6.3 Impact of the Costs Ratio to the

different Approaches

Figure 11 shows the costs for different cost ratios. In

this example, a cost ratio of 10 means that a wrong

stay on the road is 10 times more expensive than a

wrong leave. Similarly, a cost ratio of 0.1 means that

it is 10 times more expensive to leave the road than to

stay. Figure 11(a) shows the used optimization poten-

tial of the different approaches. Our QoI-based appro-

ach performs best for all of the considered cost ratios.

It is also the only approach that reaches the full op-

timization potential in some cases. With increasing

cost ratio, the used optimization potential of all ap-

proaches increases. This behavior is analyzed using

Figure 11(b).

For the optimal approach, the costs of slow adap-

tation are almost 0. As this approach adapts fast to

the jam resolving, the main costs arise through the

road jamming. Thus, the costs of falsely staying on

the road are the most signiﬁcant factor for the opti-

mal approach. As these costs increase with increa-

sing cost ratio, staying on the road is punished addi-

tionally. Thus, the overall costs of the optimized ap-

proach increase with increasing cost ratio. For all the

other approaches, the overall costs decrease as a part

of the costs are caused by leaving the road wrongly.

This is justiﬁed by the evaluation scenario, as the out-

dated information in the cache slows down the adapta-

tion process. Thus, the costs of slow adaptation decre-

ase if the costs of leaving the road wrongly are small.

We can observe that our QoI-based approach outper-

forms the other two approaches for a cost ratio of 0.1

and 1 signiﬁcantly. For a cost ratio of 10, in which

slow adaptation after the jam is not costly, our appro-

ach performs only slightly better than the majority-

0.1 1 10

Cost ratio

0.0

0.2

0.4

0.6

0.8

1.0

Used optimization potential

QoI-based

Newest-information

Majority-voting

(a) Used optimization po-

tential

0.1 1 100.1 1 10

Cost ratio

100

150

200

250

Costs

Optimal

QoI-based

Newest-information

Majority-voting

Costs for slow adaptation

Costs for fast adaptation

(b) Total costs of wrong

decisions with cause

Figure 11: Costs for different cost ratios.

voting based approach, as the slow adaptability of the

majority-voting based approach is balanced by its ro-

bustness.

6.4 Evaluation Results

The evaluation shows that our approach reduces the

total costs compared to both of the existing approa-

ches dependent on the scenario by up to 25%. Additi-

onally, our approach has never a higher total cost va-

lue than the other approaches. It achieves that impro-

vement by balancing its robustness and fast adapta-

bility to environmental conditions to achieve optimal

results. For the extreme cases, our algorithm conver-

ges to the newest-information and the majority-voting

based approach respectively. Moreover, we observed

that the jam duration has no impact on the perfor-

mance improvements of our approach, which makes

it usable for decisions based on arbitrary information.

7 CONCLUSION

In this paper, we proposed a Quality of Information

(QoI)-based decision making process. In this decision

making process, false decisions produces costs for the

deciding vehicle. False decisions have two reasons,

missing robustness to false measurements and slow

adaptation to environmental changes. Our novel de-

cision making process considers information-speciﬁc

properties, to make decisions inducing the lowest pos-

sible costs.

This decision making process is based on a weig-

hted majority-voting. The used weighting deter-

mines the impact of an information and considers

information-speciﬁc properties. Those properties are

modeled using a Hidden Markov Model (HMM) con-

sidering the false detection rate and the information

lifetime. Those two properties most important for the

information impact function, as missing sensor accu-

racy and outdated information are common challen-

ges in distributed networks.

Adaptive Decision Making based on Temporal Information Dynamics

101

To chose the appropriate impact function f (t), we

construct an optimization problem to minimize the

costs of incorrect decisions. The resulting weighting

function is an exponential function and takes the age

of information as an input to calculate the weighting

of that speciﬁc information. The weighting function

itself depends on the information-speciﬁc properties

information lifetime and false detection rate.

In the decision-making process, we perform a

weighted majority-voting with the weights calculated

by our weighting function. In the evaluation, we show

that our approach signiﬁcantly outperforms compara-

ble approaches by up to 25% and dynamically adapts

to the information-speciﬁc properties.

As future work, we aim to investigate the possibi-

lities to ﬁlter out wrong information and consider the

individual false detection rate of each sensor instead

of the average into account to increase the quality of

the decisions further.

ACKNOWLEDGEMENTS

The work presented in this paper was partly funded by

the LOEWE initiative (Hessen, Germany) within the

NICER project and by the German Research Founda-

tion (DFG) as part of project C2 within the Collabo-

rative Research Center (CRC) 1053 - MAKI.

REFERENCES

Behrisch, M., Bieker, L., Erdmann, J., and Krajzewicz, D.

(2011). Sumo–simulation of urban mobility: an over-

view. In Proceedings of SIMUL 2011, The Third In-

ternational Conference on Advances in System Simu-

lation. ThinkMind.

Chae, M., Kim, J., Kim, H., and Ryu, H. (2002). Informa-

tion quality for mobile internet services: A theoretical

model with empirical validation. Electronic Markets,

12(1):38–46.

Delot, T., Cenerario, N., and Ilarri, S. (2008). Estimating

the relevance of information in inter-vehicle ad hoc

networks. In Mobile Data Management Workshops,

2008. MDMW 2008. Ninth International Conference

on, pages 151–158. IEEE.

Fawaz, K. and Artail, H. (2013). DCIM: Distributed ca-

che invalidation method for maintaining cache consis-

tency in wireless mobile networks. IEEE Transactions

on Mobile Computing, 12(4):680–693.

Hsiao, H.-C., Studer, A., Dubey, R., Shi, E., and Perrig, A.

(2011). Efﬁcient and secure threshold-based event va-

lidation for vanets. In Proceedings of the fourth ACM

conference on Wireless network security, pages 163–

174. ACM.

Kakkasageri, M. and Manvi, S. (2014). Information mana-

gement in vehicular ad hoc networks: A review. Jour-

nal of Network and Computer Applications, 39:334–

350.

Kuppusamy, P. and Kalaavathi, B. (2012). Cluster based

data consistency for cooperative caching over partiti-

onable mobile adhoc network. American Journal of

Applied Sciences, 9:1307.

Meuser, T., Lieser, P., Nguyen, T. A. B., B

ohnstedt, D., and

Steinmetz, R. (2017). Adaptive information aggrega-

tion for application-speciﬁc demands. In Proceedings

of the 1st BalkanCom.

Molina-Gil, J. M., Caballero-Gil, P., Hern

andez-Goya, C.,

and Caballero-Gil, C. (2010). Data aggregation for

information authentication in vanets. In Information

Assurance and Security (IAS), 2010 Sixth Internatio-

nal Conference on, pages 282–287. IEEE.

Richerzhagen, B., Stingl, D., R

uckert, J., and Steinmetz,

R. (2015). Simonstrator: Simulation and prototy-

ping platform for distributed mobile applications. In

Proceedings of the 8th International Conference on

Simulation Tools and Techniques, SIMUTools ’15,

pages 99–108. ICST (Institute for Computer Scien-

ces, Social-Informatics and Telecommunications En-

gineering).

Wang, R. Y. and Strong, D. M. (1996). Beyond accuracy:

What data quality means to data consumer. Journal of

management information systems, 12:5–33.

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

102