
Relative Pose Estimation in Binocular Vision for a Planar Scene using
Inter-Image Homographies
Marcus Valtonen
¨
Ornhag and Anders Heyden
Centre for Mathematical Sciences, Lund University, Sweden
Keywords:
Relative Pose Estimation, SLAM, Visual Odometry, Binocular Vision, Planar Motion, Homography.
Abstract:
In this paper we consider a mobile platform with two cameras directed towards the floor mounted the same
distance from the ground, assuming planar motion and constant internal parameters. Earlier work related to
this specific problem geometry has been carried out for monocular systems, and the main contribution of this
paper is the generalization to a binocular system and the recovery of the relative translation and orientation
between the cameras. The method is based on previous work on monocular systems, using sequences of inter-
image homographies. Experiments are conducted using synthetic data, and the results demonstrate a robust
method for determining the relative parameters.
1 INTRODUCTION
In robotics research, it is of interest to accurately track
the position of a mobile robot relative to its surround-
ings. The emergence of artificial intelligence and au-
tonomous vehicles in recent years demand robust al-
gorithms to handle such problems. During the years
of research in the field many kinds of sensors have
been used—LIDAR, rotary encoders, inertial sensors
and GPS, to mention a few—and often in combina-
tion. The type of sensor one chooses to work with re-
stricts what algorithms that can be used, and how the
resulting map of the robot and its surroundings will
look.
One sensor of particular interest for the robotics
and computer vision community is the image sensor
and there are many reasons why it is popular. One
important factor is that the wide range of algorithms
used in computer vision, e.g. visual feature extraction
and pose estimation, can be used in this setting; how-
ever, from an industrial point of view image sensors
are an often considered design choice since they are
relatively cheap compared to other sensors. Further-
more, they are often available on consumer products,
such as smartphones and tablets, where similar tech-
niques can be used, e.g. in Augmented Reality (AR).
With image sensors one is not limited to sparse 3D
clouds of feature points, but can model the map using
dense and textured 3D models.
Visual SLAM systems have been developed for
nearly three decades, with (Harris and Pike, 1988)
being one of the first. Since then, several improve-
ments have been made, and with the aid of modern
computing power, a variety of methods for real-time
SLAM are available. Among the more recent once are
MonoSLAM (Davison et al., 2007), LSD-SLAM (En-
gel et al., 2014) and ORB-SLAM2 (Mur-Artal and
Tard
´
os, 2017), where the latter includes support for
monocular, stereo and RGB-D cameras.
2 RELATED WORK
In epipolar geometry, the fundamental matrix, intro-
duced by (Faugeras, 1992) and (Hartley, 1992), has
been a tool for many algorithms concerning scene
reconstruction; however, planar motion is known to
be ill-conditioned, see e.g. (Hartley and Zisserman,
2004). The problem geometry considered in this pa-
per is forced to planar motion, which is common in
e.g. indoor environments. To overcome this issue
algorithms that take advantage of planar homogra-
phies have been devised, which by construction are
constrained to planar motion and therefore do not
suffer from being ill-conditioned. Some early work
on planar motion using homographies include that
of (Liang and Pears, 2002) and (Hajjdiab and La-
gani
`
ere, 2004). More recent work on ego-motion re-
covery in a monocular system using inter-image ho-
mographies for a planar scene has been covered in
(Wadenb
¨
ack and Heyden, 2013) for a single homogra-
568
Örnhag, M. and Heyden, A.
Relative Pose Estimation in Binocular Vision for a Planar Scene using Inter-Image Homographies.
DOI: 10.5220/0006695305680575
In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 568-575
ISBN: 978-989-758-276-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
phy and by the same authors for several homographies
in (Wadenb
¨
ack and Heyden, 2014). In (Wadenb
¨
ack
et al., 2017) the same methods are used to calibrate
the fixed parameters initially, transforming the subse-
quent problem to a two-dimensional rigid body mo-
tion problem.
The stereo rig problem involving two cameras
with fixed relative orientation is investigated for auto-
calibration in (Hartley and Zisserman, 2004). In (Ny-
man et al., 2010) a method for multi-camera plat-
form calibration using multi-linear constraints is de-
veloped; however, this method does not rely on the
inter-image homographies, but rather using the cam-
era matrices.
3 THEORY
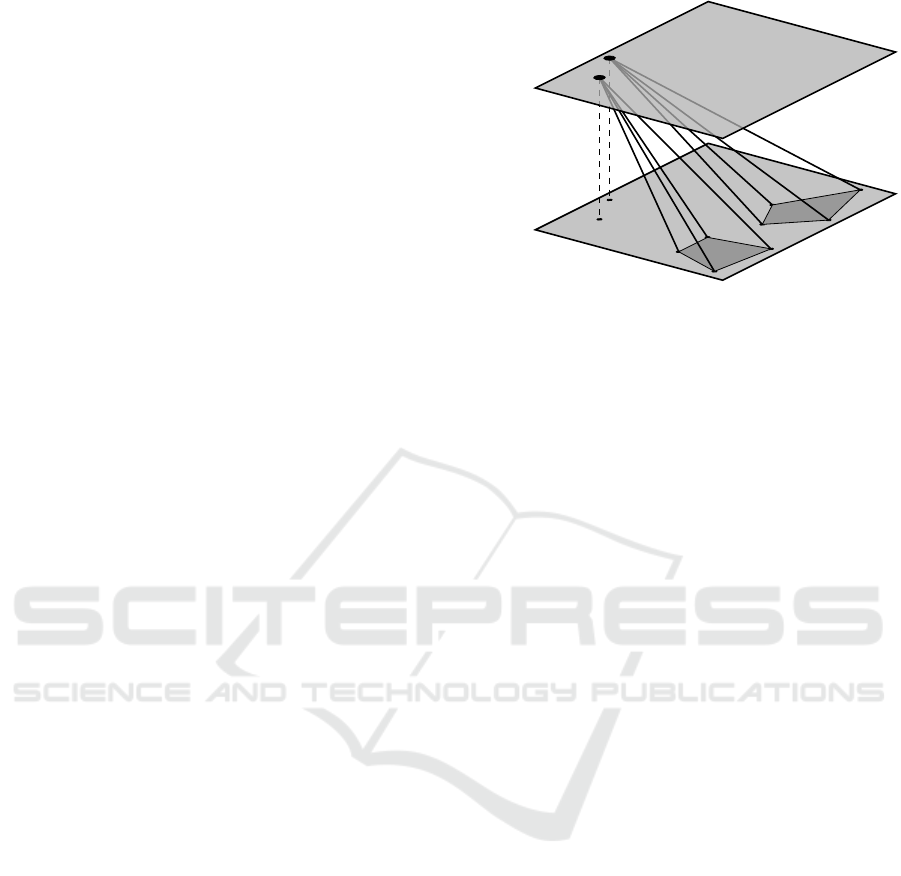
3.1 Problem Geometry
In this paper we consider a mobile platform with two
cameras directed towards the floor mounted the same
distance from the ground. By a suitable choice of
the world coordinate system the cameras move in the
plane z = 0 and relative to the ground plane positioned
at z = 1. Both cameras are assumed to be mounted
rigidly onto the platform and no common scene point
is assumed to be visible in the cameras simultane-
ously. Furthermore, the mobile platform’s center of
rotation is assumed to be located in the first camera
center. In this setting the second camera center is con-
nected to the first by a rigid body motion.
The 3D rotations are parametrized using Tait-
Bryan angles
R
R
R(ψ,θ,ϕ) = R
R
R
x
(ψ)R
R
R
y
(θ)R
R
R
z
(ϕ), (1)
where R
R
R
x
, R
R
R
y
and R
R
R
z
denote the rotation around the
respective coordinate axes with a given angle. The
problem geometry is illustrated in Figure 1.
3.2 Camera Parametrization
As in (Wadenb
¨
ack and Heyden, 2013), consider two
consecutive images, A and B, for the first camera. The
camera matrices are then
P
P
P
A
= R
R
R
ψθ
[I
I
I | 0
0
0],
P
P
P
B
= R
R
R
ψθ
R
R
R
ϕ
[I
I
I | − t
t
t],
(2)
where R
R
R
ψθ
is a rotation θ around the y-axis followed
by a rotation of ψ around the x-axis. The movement
of the mobile platform is modelled by a rotation ϕ
around the z-axis, corresponding to R
R
R
ϕ
and translation
vector t
t
t.
z = 1
plane normals
z = 0
Figure 1: The problem geometry considered in this paper.
The cameras are assumed to move in the plane z = 0 and
the relative orientation between them as well as the tilt to-
wards the floor normal is assumed to be fixed as the mobile
platform moves freely.
The camera matrices for the second camera can be
parametrized as
P
P
P
0
A
= R
R
R
ψ
0
θ
0
R
R
R
η
T
T
T
τ
τ
τ
[I
I
I | 0
0
0],
P
P
P
0
B
= R
R
R
ψ
0
θ
0
R
R
R
η
T
T
T
τ
τ
τ
R
R
R
ϕ
[I
I
I | − t
t
t],
(3)
where R
R
R
ψ
0
θ
0
is the tilt, defined as for the first cam-
era. Furthermore, R
R
R
η
is a fixed rotation by η degrees
around the z-axis relative to the first camera, and τ
τ
τ is
the rigid body translation vector between the first and
the second camera center. The matrix T
T
T
τ
τ
τ
corresponds
to a translation by τ
τ
τ defined as T
T
T
τ
τ
τ
= I
I
I − τ
τ
τn
n
n
T
, where
n
n
n = (0, 0, 1)
T
is a floor normal.
3.3 Homographies
Given point correspondences x
x
x
1
and x
x
x
2
, in homoge-
neous coordinates, the homography H
H
H transforms the
points such that x
x
x
2
= λH
H
Hx
x
x
1
, where λ 6= 0 is due to uni-
versal scale ambiguity. In (Wadenb
¨
ack and Heyden,
2013) the homography for the first camera is derived
and is given by
λH
H
H = R
R
R
ψθ
R
R
R
ϕ
T
T
T
t
t
t
R
R
R
T
ψθ
. (4)
Similarly, the homography H
H
H
0
for the second camera
is given by
λ
0
H
H
H
0
0
0
= R
R
R
ψ
0
θ
0
R
R
R
η
T
T
T
τ
τ
τ
R
R
R
ϕ
T
T
T
t
t
t
T
T
T
−1
τ
τ
τ
R
R
R
T
η
R
R
R
T
ψ
0
θ
0
. (5)
3.4 Parameter Recovery
By separating the fixed angles from ϕ and the transla-
tion t
t
t the following relation holds
R
R
R
ϕ
T
T
T
t
t
t
= λR
R
R
T
ψθ
H
H
HR
R
R
ψθ
= λ
0
T
T
T
−1
τ
τ
τ
R
R
R
T
η
R
R
R
T
ψ
0
θ
0
H
H
H
0
0
0
R
R
R
ψ
0
θ
0
R
R
R
η
T
T
T
τ
τ
τ
,
(6)
It is shown in (Wadenb
¨
ack and Heyden, 2013) how
to recover the parameters for the monocular case, and
Relative Pose Estimation in Binocular Vision for a Planar Scene using Inter-Image Homographies
569

by doing so the parameters ψ, θ, ϕ and t
t
t aswell as ψ
0
and θ
0
can be recovered; the latter two from treating
the second camera as a monocular system. Further-
more, we shall assume that all homographies H
H
H are
normalized such that detH
H
H = 1.
3.4.1 Recovering the Relative Translation τ
τ
τ
The relative translation and rotation can be separated
by putting (3.4) in the form
T
T
T
τ
τ
τ
R
R
R
ϕ
T
T
T
t
t
t
T
T
T
−1
τ
τ
τ
= λ
0
R
R
R
T
η
R
R
R
T
ψ
0
θ
0
H
H
H
0
0
0
R
R
R
ψ
0
θ
0
R
R
R
η
, (7)
and multiplying with the transpose from the left on
both sides yield
T
T
T
T
t
t
t−
−
−τ
τ
τ
R
R
R
T
ϕ
T
T
T
T
τ
τ
τ
T
T
T
τ
τ
τ
R
R
R
ϕ
T
T
T
t
t
t−
−
−τ
τ
τ
= λ
0
R
R
R
T
η
R
R
R
T
ψ
0
θ
0
H
H
H
0
0
0T
H
H
H
0
0
0
R
R
R
ψ
0
θ
0
R
R
R
η
.
(8)
The left hand side of (3.4.1) can be simplified to
L =
1 0 `
1
0 1 `
2
`
1
`
2
`
3
, (9)
where
`
1
= τ
x
−t
x
− τ
y
sinϕ − τ
x
cosϕ,
`
2
= τ
y
−t
y
+ τ
x
sinϕ − τ
y
cosϕ,
`
3
= k
1
τ
x
+ k
2
τ
y
+ cτ
2
x
+ cτ
2
y
+ |t
t
t|
2
+ 1,
(10)
and
k
1
= 2(t
x
cosϕ −t
y
sinϕ −t
x
),
k
2
= 2(t
x
sinϕ +t
y
cosϕ −t
y
),
c = 2(1 − cos ϕ) .
(11)
The eigenvalues of L are given by λ
2
= 1 and λ
1
, λ
3
such that λ
1
λ
3
= `
3
− `
2
1
− `
2
2
= 1. Furthermore, the
right hand side of (3.4.1) has the same eigenvalues
as H
H
H
0
0
0T
H
H
H
0
0
0
, as they are similar. Since the sum of the
eigenvalues is the trace of the corresponding matrix,
the following relation holds
trH
H
H
0
0
0T
H
H
H
0
0
0
= 2 + `
3
, (12)
which is independent of η. By letting h = tr H
H
H
0
0
0T
H
H
H −
3 − |t
t
t|
2
the relation becomes
k
1
τ
x
+ k
2
τ
y
+ cτ
2
x
+ cτ
2
y
− h = 0 . (13)
The other invariants do not give any new relations
for τ
τ
τ since, det L = 1 and
1
2
(trL )
2
− trL
2
= trL .
3.4.2 Solving for the Relative Translation τ
τ
τ
With only one pair of homographies one cannot deter-
mine τ
τ
τ explicitly; however, using multiple pairs one
equation on the form (13) for each pair of homogra-
phy is given, which yields a system of equations
k
(1)
1
τ
x
+ k
(1)
2
τ
y
+ c
(1)
(τ
2
x
+ τ
2
y
) − h
(1)
= 0,
k
(2)
1
τ
x
+ k
(2)
2
τ
y
+ c
(2)
(τ
2
x
+ τ
2
y
) − h
(2)
= 0,
.
.
.
k
(n)
1
τ
x
+ k
(n)
2
τ
y
+ c
(n)
(τ
2
x
+ τ
2
y
) − h
(n)
= 0 .
(14)
The system in (14) is over-determined for n > 2,
hence minimizing
min
τ
τ
τ∈
2
n
∑
i=1
k
(i)
1
τ
x
+ k
(i)
2
τ
y
+ c
(i)
(τ
2
x
+ τ
2
y
) − h
(i)
2
, (15)
gives the desired result. This can be re-formulated as
min
τ
τ
τ∈
2
kK
K
Kτ
τ
τ + c
c
cτ
τ
τ
T
τ
τ
τ − h
h
hk
2
2
, (16)
where
K
K
K =
k
(1)
1
k
(1)
2
k
(2)
1
k
(2)
2
.
.
.
.
.
.
k
(n
1
) k
(n)
2
, c
c
c =
c
(1)
c
(2)
.
.
.
c
(n)
and h
h
h =
h
(1)
h
(2)
.
.
.
h
(n)
(17)
By introducing a new variable r = |τ
τ
τ|
2
, an equivalent
problem is obtained
min
τ
τ
τ∈
2
, r=|τ
τ
τ|
2
kK
K
Kτ
τ
τ + c
c
cr − h
h
hk
2
2
= min
x
x
x∈
3
, r=|τ
τ
τ|
2
kM
M
Mx
x
x − h
h
hk
2
2
,
(18)
where x
x
x = (τ
x
, τ
y
, r)
T
and M
M
M = [K
K
K | c
c
c], where the
objective function can be written as
kM
M
Mx
x
x − h
h
hk
2
2
= x
x
x
T
Q
Q
Qx
x
x + d
d
d
T
x
x
x + h
h
h
T
h
h
h, (19)
where Q
Q
Q = M
M
M
T
M
M
M and d
d
d
T
= −2h
h
h
T
M
M
M. In conclusion,
one may consider minimizing f (x
x
x) = x
x
x
T
Q
Q
Qx
x
x + d
d
d
T
x
x
x,
subject to x
2
1
+ x
2
2
− x
3
= 0. Note that, the constraint
can be written as x
x
x
T
A
A
Ax
x
x + b
b
b
T
x
x
x = 0, where
A
A
A =
1
1
0
and b
b
b =
0
0
−1
. (20)
The Lagrangian is given by
L (x
x
x;λ) = x
x
x
T
Q
Q
Qx
x
x + d
d
d
T
x
x
x + λ(x
x
x
T
A
A
Ax
x
x + b
b
b
T
x
x
x), (21)
and solving ∇
x
x
x
L (x
x
x;λ) = 0
0
0 results in
x
x
x = −
1
2
(Q
Q
Q + λA
A
A)
−1
(d
d
d + λb
b
b) . (22)
The constraint ∇
λ
L (x
x
x;λ) = 0 yields a rational equa-
tion in λ, which can be turned into finding the roots of
a fifth degree polynomial. This in turn can be trans-
lated into an eigenvalue problem, and solved robustly.
Using this approach solving (16) takes ∼100 µs which
is suitable for real-time applications. Furthermore,
due to the precision of modern eigenvalue solvers, the
error is usually negliable.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
570

3.4.3 Solving for the Relative Orientation η
Given τ
τ
τ from the previous step consider (3.4) and
multiply the first homography with the matrix corre-
sponding to the translation τ
τ
τ. This yields
T
T
T
τ
τ
τ
R
R
R
T
ψθ
H
H
HR
R
R
ψθ
T
T
T
−1
τ
τ
τ
∼ R
R
R
T
η
R
R
R
T
ψ
0
θ
0
H
H
H
0
0
0
R
R
R
ψ
0
θ
0
R
R
R
η
, (23)
where η is the only unknown parameter. Define
W
W
W = T
T
T
τ
τ
τ
R
R
R
T
ψθ
H
H
HR
R
R
ψθ
T
T
T
−1
τ
τ
τ
and W
W
W
0
= R
R
R
T
ψ
0
θ
0
H
H
H
0
0
0
R
R
R
ψ
0
θ
0
and
note that W
W
W and W
W
W
0
0
0
share the same eigenvalues since
they are similar and the corresponding eigenvectors
are rotated η degrees.
Let us recall that the null space of a matrix is
spanned by the right-singular vectors corresponding
to zero—or due to noise, vanishing—singular val-
ues. Using the same approach as in (Wadenb
¨
ack and
Heyden, 2014) we conclude that nulldimW
W
W
0
0
0T
W
W
W
0
0
0
= 1.
Consequently, the eigenvectors spanning the null
spaces, x
x
x ∈ N (W
W
W
T
W
W
W ) and x
x
x
0
0
0
∈ N (W
W
W
0
0
0T
W
W
W
0
0
0
), can be
obtained using SVD—this ensures that we work with
real eigenvectors.
We will use the following theorem to recover η
robustly, using all available pairs of homogaphies.
Theorem 1. Let Y
Y
Y ,Y
Y
Y
0
0
0
∈
3×N
and non-zero. Fur-
thermore, let R
R
R
η
= R
R
R
z
(η) be a rotation matrix, cor-
responding to a rotation of angle η around the third
axis. Then
min
η∈(−π,π]
λ6=0
kY
Y
Y
0
0
0
− λR
R
R
η
Y
Y
Y k
F
, (24)
is solved when
η
opt
= α +
(
0, if y
y
y
T
3
y
y
y
0
3
> 0,
π, otherwise,
(25)
where α may be expressed using the programming
friendly atan2 function,
α = atan2
y
y
y
T
1
y
y
y
0
2
− y
y
y
T
2
y
y
y
0
1
, y
y
y
T
1
y
y
y
0
1
+ y
y
y
T
2
y
y
y
0
2
,
. (26)
Here y
y
y
i
denotes the column vector of dimension N
corresponding to the i:th row of Y
Y
Y . The vectors y
y
y
0
i
are
defined analogously. The angles are considered as
equivalence classes, where η ≡ η + 2πk, k ∈ , with
the class representative being in the interval (−π,π].
Proof. Using the relation between the Frobenius
norm and the trace, the square of the objective func-
tion can be simplified
kY
Y
Y
0
0
0
− λR
R
R
η
Y
Y
Y k
2
F
= tr
(Y
Y
Y
0
0
0
− λR
R
R
η
Y
Y
Y )(Y
Y
Y
0
0
0
− λR
R
R
η
Y
Y
Y )
T
= trY
Y
Y
0
0
0
Y
Y
Y
0
0
0T
− λ trY
Y
Y
0
0
0
Y
Y
Y
T
R
R
R
T
η
− λ tr R
R
R
η
Y
Y
YY
Y
Y
0
0
0T
+ λ
2
trR
R
R
η
Y
Y
YY
Y
Y
T
R
R
R
T
η
.
(27)
Since the trace is invariant under cyclic permutations
it follows that the last term is independent of η. Fur-
thermore,
trY
Y
Y
0
0
0
Y
Y
Y
T
R
R
R
T
η
= tr
Y
Y
Y
0
0
0
Y
Y
Y
T
R
R
R
T
η
T
= tr R
R
R
η
Y
Y
YY
Y
Y
0T
. (28)
Combining these observations (24) is equivalent to
solving
min
η∈[−π,π)
λ6=0
λ
2
kY
Y
Y k
2
F
− 2λtrR
R
R
η
Y
Y
YY
Y
Y
0
0
0T
. (29)
The reader can easily verify that the optimum is
reached when η is on the form (24).
In conclusion, the angle η may be obtained using
Theorem 1 where the i:th column of Y
Y
Y corresponds to
the eigenvector spanning the null space of W
W
W
T
i
W
W
W
i
—
the matrix Y
Y
Y
0
0
0
is defined analogously.
4 EXPERIMENTS
4.1 Synthetic Data
In order to validate the theory and evaluate the al-
gorithm synthetic data was generated in form of se-
quences of images mimicking those taken by a mo-
bile platform as described in Section 3.1. A high-
resolution image of a planar scene, in this case a tex-
tured floor, was chosen to yield many key-points. Fur-
thermore, different paths simulating the mobile plat-
form was defined. In order to simulate the tilt the
original image was transformed around a given point
along the pre-defined path and then cropped, such that
the center point in the cropped image coincide with
this point. The parameters used in the transforma-
tion serve as ground truth, and the resolution used in
each image is 400 × 400 pixels. The field of view
of the simulated camera is normalized to 90 degrees,
which affects the impact of the distortion of the im-
ages caused by the cameras being tilted.
4.2 Homography Estimation
The homography estimation was done by extract-
ing SIFT keypoints (Lowe, 2004) from every frame,
keeping the most prominent once as candidates for
key-point matching. The remaining key-points are
then matched between subsequent images only, us-
ing a brute-force matcher based on the K Nearest
Neighbor algorithm. From the matched key-points a
random subset is chosen iteratively in the RANSAC
framework and from these a homography is esti-
mated. The homography with the highest amount of
Relative Pose Estimation in Binocular Vision for a Planar Scene using Inter-Image Homographies
571

Figure 2: Path of the simulated mobile platform for the first camera (left) and the second camera (right). The red dots represent
the absolute position of the camera and the blue squares are the extracted images. The impact of the tilt is illustrated by the
frames not being square, but rather slanted. Note that the second camera path is not elliptic as the translational components
are affected by the rotation of the mobile platform.
inliers is chosen, where the maximum allowed repro-
jection error for a point pair to be considered as an
inlier is five pixels.
4.3 Parameter Recovery
4.3.1 Monocular Case
The parameters were recovered using the method pro-
posed in (Wadenb
¨
ack and Heyden, 2014) for both tra-
jectories, treated as two independent monocular sys-
tems, using five homographies to determine the tilt,
rotation and translation in each step.
4.3.2 Recovering the Relative Translation
The optimal relative translation vector was obtained
by solving (16) using the optimization scheme pro-
posed in Section 3.4.2.
4.3.3 Recovering the Relative Orientation
Using the closed form solution presented in Theo-
rem 1 the relative rotation around the z-axis was es-
timated for the five pairs of homographies used in the
previous step. The computations involves finding the
vectors spanning the null spaces in order to compute
the matrices used in the closed form expression (24)
for η which is computationally inexpensive.
4.4 Test Cases
4.4.1 Elliptic Path
This case simulates the mobile platform moving in an
elliptic path while rotating between the images. The
test case was choosen as it includes general motions
which generates many different combinations of val-
ues for the nonfixed parameters. The sequence of
images for both cameras used in this case is shown
in Figure 2. The parameters used in this experi-
ment are ψ = 3.3
◦
, θ = −1.2
◦
, ψ
0
= 5.1
◦
, θ
0
= −4.6
◦
,
τ
τ
τ = (100, 80) and η = 30
◦
.
The results from analyzing the two paths indepen-
dently are shown in Figure 3 and the estimation of the
relative pose is shown in Figure 4.
4.4.2 Rotation Around the First Camera Center
Estimating the tilt in a monocular system with only
rotations and no translation is generally hard. A pos-
sible benefit of a binocular system is that the rigid
body motion between the cameras results in a trans-
lational component in the second camera. The gen-
erated paths are shown in Figure 5. All fixed angles
are set to 0
◦
and the relative translation τ
τ
τ = (800, 0).
Furthermore, the mobile platform is moving with a
constant rotation.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
572
0 10 20 30 40 50
Homography number
2.3
2.8
3.3
3.8
4.3
ψ (de g rees)
0 10 20 30 40 50
Homography number
−2.2
−1.7
−1.2
−0.7
−0.2
θ (degrees)
0 10 20 30 40 50
Homography number
−30
−20
−10
0
10
20
30
ϕ (degrees)
0 10 20 30 40 50
Homography number
−5.0
−2.5
0.0
2.5
5.0
Error in t
x
and t
y
0 10 20 30 40 50
Homography number
4.1
4.6
5.1
5.6
6.1
ψ
′
(degrees)
0 10 20 30 40 50
Homography number
−5.6
−5.1
−4.6
−4.1
−3.6
θ
′
(degrees)
0 10 20 30 40 50
Homography number
−30
−20
−10
0
10
20
30
ϕ (degrees)
0 10 20 30 40 50
Homography number
−5.0
−2.5
0.0
2.5
5.0
Error in t
x
and t
y
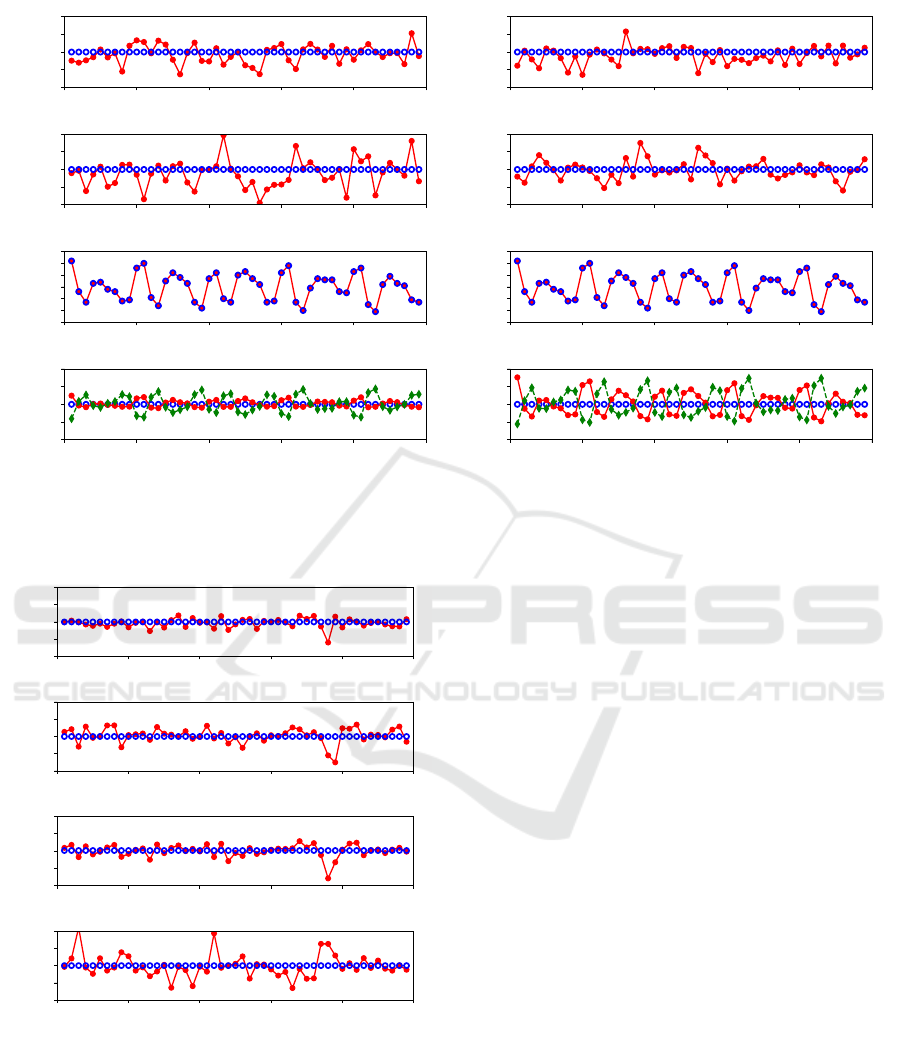
Figure 3: Estimated parameters for the first camera (left) and the second camera (right). In all plots the blue circles represent
the ground truth. The red dots are the estimated parameters for the angles (first three subplots) and in the last subplot the red
dots and the green diamond are the error in t
x
and t
y
respectively. The error in translation is measured in pixels. The estimates
have been calculated using five homographies at each frame.
0 10 20 30 40 50
Homography number
96
98
100
102
104
τ
x
0 10 20 30 40 50
Homography number
76
78
80
82
84
τ
y
0 10 20 30 40 50
Homography number
124
126
128
130
132
|τ |
0 10 20 30 40 50
Homography number
29.0
29.5
30.0
30.5
31.0
η (degrees)
Figure 4: Estimated value of τ
τ
τ = (τ
x
, τ
y
) and η using five
pairs of homographies at each frame. The magnitude of the
translational component |τ
τ
τ| is also shown. The red dots are
the estimated parameter and the blue circles represent the
ground truth.
Since (3.4.1) degenerates, as k
(i)
1
= k
(i)
2
= 0 for all
homographies, one cannot expect to recover the com-
ponents of τ
τ
τ but it is possible to recover |τ
τ
τ|, as shown
in Figure 6.
4.4.3 Mean Error vs. Number of Homographies
The relation between the accuracy and the amount
of homographies used to estimate the relative pose is
shown in Figure 7. The same setup as in Section 4.4.1
was used but the amount of homographies varied.
From the figures one can see that it is not a significant
improvement in the parameter estimation of the rel-
ative pose after approximately twenty homographies.
In practice this means that the calibration could be
done initially, and then be used to track the position
of the mobile platform, without re-computation of the
fixed parameters.
5 CONCLUSION
This paper has extended the work of (Wadenb
¨
ack and
Heyden, 2014) to binocular vision. A method has
been deviced to robustly estimate the relative trans-
lation and orientation of the two cameras using sev-
eral pairs of homographies, by reusing the computa-
tions from the cameras treated as two monocular sys-
tems. The translational component is recovered by
solving a non-convex problem, which can be turned
into an eigenvalue problem. The proposed optimiza-
tion scheme is robust and suitable for real-time appli-
cations. Furthermore, when solving for the relative
Relative Pose Estimation in Binocular Vision for a Planar Scene using Inter-Image Homographies
573

Figure 5: Path of the simulated mobile platform for the first camera (left) in the second test case, and for the second camera
(right). The red dots represent the absolute position of the camera and the blue squares are the extracted images. Due to
the rigid body motion connecting the cameras the second camera rotates around the first camera center causing a non-zero
translational component.
0 10 20 30 40 50
Homography number
795.0
797.5
800.0
802.5
805.0
|τ |
Figure 6: Estimated value of |τ
τ
τ| using five pairs of homo-
graphies at each frame. When considering only rotations
for the first camera, the components of τ
τ
τ cannot be obtained
by the proposed method. The red dots are the estimated pa-
rameter for the magnitude and the blue circles represent the
ground truth.
0.4
0.6
0.8
e
τ
i
= kτ
i
− τ
∗
i
k
2
0 10 20 30 40 50
Number of homographies
0.10
0.15
e
η
i
= |η
i
− η
∗
i
|
Mean error
Figure 7: Mean error for the relative translation and rota-
tion as a function of the number of pairs of homographies
used in the optimization step. The error for the translational
component is measured in the Euclidean norm. The mean
error is computed from 49 pairs of homographies estimated
from the sequence described in Section 4.4.1.
rotation, the closed form solution presented in The-
orem 1 is computationally inexpensive. Experimen-
tal results from synthetic data have demonstrated that
the method has an acceptable accuracy for most prob-
lems, and highlighted problems where the method
fails to recover both of the translational components;
it is also shown that in this case the magnitude can be
recovered accurately.
ACKNOWLEDGEMENTS
This work has been funded by the Swedish Research
Council through grant no. 2015-05639 ‘Visual SLAM
based on Planar Homographies’.
REFERENCES
Davison, A. J., Reid, I. D., Molton, N. D., and Stasse, O.
(2007). Monoslam: Real-time single camera slam.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 29(6):1052–1067.
Engel, J., Sch
¨
ops, T., and Cremers, D. (2014). LSD-
SLAM: Large-Scale Direct Monocular SLAM, pages
834–849. Springer International Publishing, Cham.
Faugeras, O. D. (1992). What can be seen in three di-
mensions with an uncalibrated stereo rig. In Pro-
ceedings of the Second European Conference on Com-
puter Vision, ECCV ’92, pages 563–578, London,
UK. Springer-Verlag.
Hajjdiab, H. and Lagani
`
ere, R. (2004). Vision-based multi-
robot simultaneous localization and mapping. In
Computer and Robot Vision, 2004. Proceedings. First
Canadian Conference on, pages 155–162. IEEE.
Harris, C. and Pike, J. (1988). 3d positional integration
from image sequences. Image and Vision Computing,
6(2):87 – 90.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
574

Hartley, R. and Zisserman, A. (2004). Multiple View Geom-
etry in Computer Vision. Cambridge University Press,
second edition.
Hartley, R. I. (1992). Estimation of relative camera po-
sitions for uncalibrated cameras, pages 579–587.
Springer Berlin Heidelberg, Berlin, Heidelberg.
Liang, B. and Pears, N. (2002). Visual navigation using
planar homographies. In ICRA ’02: Proceedings of
the 2002 IEEE International Conference on Robotics
and Automation, pages 205 – 210.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International Journal of Com-
puter Vision, 60(2):91–110.
Mur-Artal, R. and Tard
´
os, J. D. (2017). Orb-slam2:
An open-source slam system for monocular, stereo,
and rgb-d cameras. IEEE Transactions on Robotics,
33(5):1255–1262.
Nyman, P., Heyden, A., and
˚
Astr
¨
om, K. (2010). Multi-
camera platform calibration using multi-linear con-
straints. 2010 20th International Conference on Pat-
tern Recognition, Pattern Recognition (ICPR), 2010
20th International Conference on, page 53.
Wadenb
¨
ack, M. and Heyden, A. (2013). Planar motion
and hand-eye calibration using inter-image homogra-
phies from a planar scene. In 8th International Joint
Conference on Computer Vision, Imaging and Com-
puter Graphics Theory and Applications (VISIGRAPP
2013), Proceedings of, pages 164–168.
Wadenb
¨
ack, M. and Heyden, A. (2014). Ego-motion recov-
ery and robust tilt estimation for planar motion using
several homographies. In Proceedings of the 9th Inter-
national Conference on Computer Vision Theory and
Applications (VISAPP 2014), pages 635–639.
Wadenb
¨
ack, M., Karlsson, M., Heyden, A., Robertsson, A.,
and Johansson, R. (2017). Visual odometry from two
point correspondences and initial automatic tilt cali-
bration. In 12th International Joint Conference on
Computer Vision, Imaging and Computer Graphics
Theory and Applications (VISIGRAPP 2017), pages
340–346.
Relative Pose Estimation in Binocular Vision for a Planar Scene using Inter-Image Homographies
575
