Predicting the Success of NFL Teams using Complex Network Analysis

Matheus de Oliveira Salim and Wladmir Cardoso Brand

Department of Computer Science, Pontiﬁcal Catholic University of Minas Gerais (PUC Minas), Belo Horizonte, Brazil

Keywords:

Knowledge Discovery, Social Network Analysis, Success Prediction, Sport, Football, NFL.

Abstract:

The NFL (National Football League) is the most popular sports league in the United States and has the hig-

hest average attendance of any professional sports league in the world, moving billions of dollars annually

through licensing agreements, sponsorships, television deals, ticket and product sales. In addition, it moves a

billionaire betting market, which heavily consumes statistical data on games to produce forecasts. Moreover,

game statistics are also used to characterize players performance, dictating their salaries. Thus, the discovery

of implicit knowledge in the NFL statistics becomes a challenging problem. In this article, we model the beha-

vior of NFL players and teams using complex network analysis. In particular, we represent quarterbacks and

teams as nodes in a graph and labor relationships among them as edges to compute metrics from the graph,

using them to discover implicit properties of the NFL social network and predict team success. Experimental

results show that this social network is a scale-free and small-world network. Furthermore, node degree and

clustering coefﬁcient can be effectively used to predict team success, outperforming the usual passer rating

statistic.

1 INTRODUCTION

The NFL (National Football League) was formed in

1920 and today is the most popular sports league in

the United States, having the highest average atten-

dance of any professional sports league in the world.

The NFL is also a successful franchise business, with

its 32 teams ranked among the top 50 most valua-

ble sports teams in the world, moving billions of dol-

lars annually through licensing agreements, sponsors-

hips, television deals, ticket and product sales (Ejio-

chi, 2014). After each NFL game, a large amount of

statistics are generated to describe the performance of

the players. These statistics are used to move a bet-

ting market estimated in $93 billion dollars of legal

and illegal gambling annually (Heitner, 2015). For

instance, Internet sites use NFL game statistics to aid

gamblers, giving them more reliable predictions on

the outcome of upcoming games.

NFL salary structures are notoriously complex,

with base pay, bonuses, and guarantees, and game

statistics are also regularly used to characterize the

performance of each player over time, dictating their

salaries and the duration of their contracts. For in-

stance, Elvis Dumervil, the outside linebacker of the

Baltimore Ravens in the 2014 season, triggered $3

million in base salary escalators and earned $1 mil-

lion in incentives during Week 12’s contest against

the New Orleans Saints by reaching the 12-sack mark.

His 2015, 2016 and 2017 base salaries of $4 million,

$4 million and $5 million each increased by $1 mil-

lion. However, hiring players based exclusively on

their game statistics and paying them the highest sa-

laries is not a guarantee of team success.

In fact, a recent study has provided clues that

large wage distortions is not a good strategy for team

success (Burke, 2012). Analyzing the offensive line

salary and performance, the author shows that the

more teams pay their linemen, the more sacks and

tackles for losses they tend to give up. By the con-

trary, a higher median salary indicates better perfor-

mance. This results suggests that game statistics alone

are not enough to effectively predict team success.

The adoption of models and metrics that capture col-

lective behavior of players appear promising to in-

crease prediction effectiveness. Therefore, the the-

ory of complex networks can be used to investigate

the collective behavior of social agents, including te-

ams and players in a sporting context. Particularly,

a network is a set of nodes and connections between

them, called edges. Complex networks are networks

with a large number of nodes and edges following re-

levant patterns, such as hubs, i.e., clusters with highly

connected nodes. While the analysis of simple net-

works can be done through visual inspection, the dis-

covery of relevant patterns in complex networks de-

Salim, M. and Brandão, W.

Predicting the Success of NFL Teams using Complex Network Analysis.

DOI: 10.5220/0006697101350142

In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 135-142

ISBN: 978-989-758-298-1

135

mands statistical methods.

In this article, we investigate the properties of the

NFL social network, a network with players and te-

ams as nodes and labor relationships among them as

edges. Additionally, we propose to predict the success

of teams by modeling the behavior of players and te-

ams in the NFL social network. Experiments show

that the number of quarterbacks with signiﬁcant im-

pact in the NFL history and in their teams is negligi-

ble if we exclusively rely on game statistics, such as

passer rating. In addition, we show that the NFL so-

cial network is scale-free, i.e., a very small number

of quarterbacks present extraordinary performance,

while a large number of quarterbacks perform poorly.

Moreover, we show that the NFL social network fol-

lows a small-world behavior, where the distance bet-

ween any two nodes are very small. Particularly, the

key contributions of this article are:

• We investigate the properties on the NFL social

network, showing that it can be characterized as a

scale-free and small-world network.

• We propose a method to predict the success of

NFL teams based on the network properties and

metrics.

• We thoroughly evaluate the network metrics used

by our method by contrasting them with usual

passer rating statistic. We show that our metrics

outperform this quarterback performance statistic

to predict the success of NFL teams.

The remainder of this article is organized as fol-

lows: Section 2 reviews the related literature on

complex networks. Section 3 presents related work.

Section 4 show that the usual passer rating statistic

plays a signiﬁcant role in only a small fraction of the

NFL players. Section 5 presents the properties of the

NFL social network, including the method we pro-

pose to predict team success. Section 6 shows ex-

perimental results, attesting the effectiveness of our

method and metrics to predict team success, when

compared with passer rating. Finally, Section 7 pro-

vides a summary of the contributions and the conclu-

sions made throughout the other sections, presenting

directions for future research.

2 BACKGROUND

Complex networks are huge sets of interconnected

items with a structure that do not follow a regular pat-

tern. For instance, the Internet is a complex network

composed by millions of interconnected routers, fol-

lowing a pattern in which a small number of items are

extremely highly-connected, and the great majority

of items have very few connections (Faloutsos et al.,

1999). They usually are represented as graphs, with

items as nodes (or vertices), and the connections bet-

ween the nodes as edges (or links).

Particularly, a complex network models a real-

world problem with nodes and edges storing infor-

mation on the problem (Wasserman and Faust, 1994).

In multi-modal networks, the information are in the

nodes, while in multidimensional or multi-relational

networks, the information are in the edges. We can

also classify complex networks by their application

in real-world problems (Newman, 2010). Biologi-

cal networks represent biological systems, e.g., neu-

ral, protein, vascular and metabolic pathways net-

works. Information networks represent information

and knowledge systems where nodes are informa-

tion items, such as research articles, documents, and

Web pages. Citation networks and the Web are ex-

amples of information networks. Social networks re-

present relationships between people or groups, such

as friendships, family and professional relationships.

Usually, social networks present a small-world beha-

vior, where no one is far from anyone (Watts and Stro-

gatz, 1998). Technological networks represent man-

made systems, usually built for efﬁciently distribution

of resources, e.g., electrical grid, telephony, water dis-

tribution and the Internet (Newman, 2003).

Figures 1, 2, and 3, present three different kind of

complex networks. Particularly, they differ according

to how the connections between nodes are built (Costa

et al., 2007): randomly or non-randomly. Random

networks are built from a graph with n nodes, where e

edges are randomly drawn between the nodes (Erd

and R

enyi, 1959), so that all nodes have the same pro-

bability of receiving new connections. In random net-

works, the more connections one add to the graph, the

greater the chance of a cluster to occur.

Figure 1: Example of a random network.

Scale-free networks are built from a graph with

n nodes, where e edges are not randomly drawn bet-

ween the nodes (Albert and Barab

asi, 2002), so that

the more connections a node has, the greater the

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

136

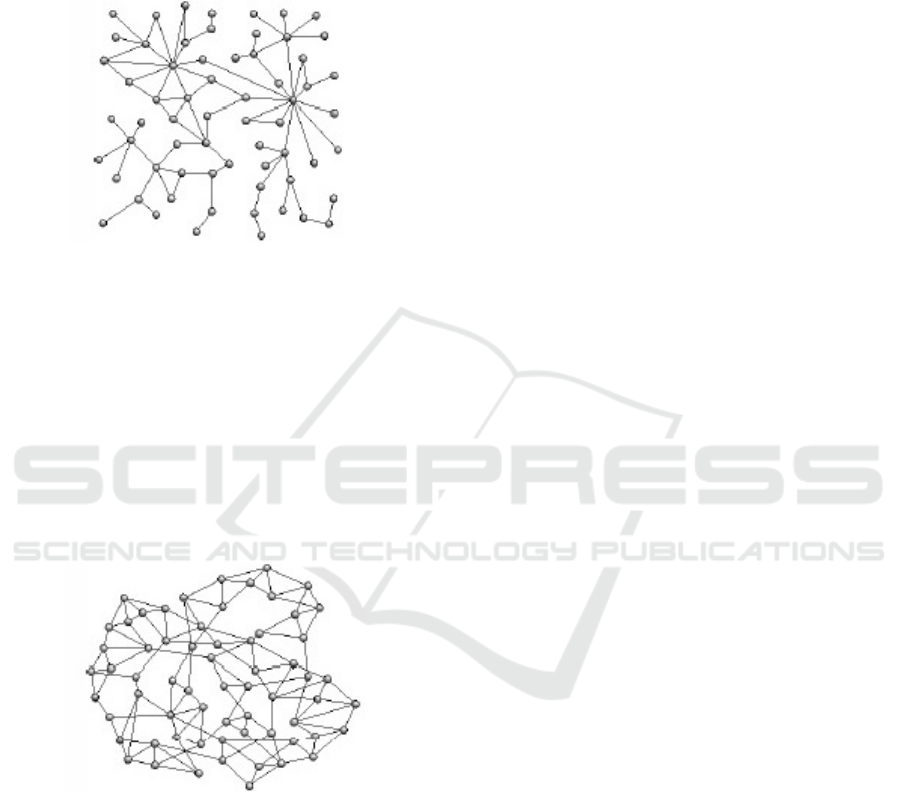
chance of it receives new connections. In scale-free

networks, the more connections one add to the graph,

the greater the chance of a few nodes getting more

connected. As result, scale-free networks have a very

low degree of connectivity and present a behavior

known as the rich get richer.

Figure 2: Example of a scale-free network.

Small-world networks are built from a graph with

n nodes, where e edges are not randomly drawn be-

tween the nodes (Watts and Strogatz, 1998), so that

the closer a node is to another, the greater the chance

of they are connected. In small-world networks, the

average distance between two nodes do not exceed a

small number of nodes, as long as some random ed-

ges between clusters are established. Thus, a few ed-

ges between clusters are necessary to create a small-

world effect, transforming the hole network into a set

of huge clusters.

Figure 3: Example of a small-world network.

3 RELATED WORK

Recently, the theory of complex networks has been

used to address problems in the context of sports.

The interactions between NFL teams and coaches

were modeled as a complex network (Fast and Jen-

sen, 2006). The authors investigate the relationships

between coaches and mentors, characterizing the in-

ﬂuence of champion coaches on their proteg

es. They

also exploit the network to understand how coaches

contribute to team’s success, proposing a model to

predict the success of teams in the NFL playoffs based

on the network topology.

Similarly, the interactions between NBA (Natio-

nal Basketball Association) teams and players were

modeled as a complex network (Vaz de Melo et al.,

2008). The authors model the labor relationships be-

tween NBA players and teams as a complex network

to investigate team’s behavior, proposing different ap-

proaches to predict team success using network me-

trics. The authors also contrast their proposed appro-

aches with box score statistics usually adopted by te-

ams to measure players performance, and show that

network metrics are more effective than box score sta-

tistics for team success prediction.

Additionally, the labor relationships between

NBA players and teams were also modeled as a com-

plex network but, differently from previous work,

no box score statistics are used to predict outcomes

and the network evolves over time (Vaz de Melo

et al., 2012). The knowledge acquired from the evol-

ving network is applied to build a prediction model,

which estimates how well a team will perform in sea-

sons. The use of temporal information to predict team

success was effective and the authors argued that the

proposed model could be applied to other sports.

4 MOTIVATION

Currently, the NFL has 32 teams equally divided be-

tween the AFC (American Football Conference) and

the NFC (National Football Conference). In the ﬁeld,

the players are organized in offensive and defensive

lines, which perform different functions. The quar-

terback is the man in charge, calling signals in the

primary passer, performing passes, and occasionally

running the ball. Quarterbacks are the team’s grea-

test decision-makers with outstanding skills, and their

performance usually determines the success of the

team in a game.

The NFL teams characterize players performance

over time by using several game statistics, which

regularly dictate player’s salaries and the duration

of their contracts. In addition, game statistics are

also used to move a billionaire betting market. For

instance, pass attempts (ATT), passes completed

(COMP), passes intercepted (INT), passing touchdo-

wns (TD), and passing yards (YARDS) are important

game statistics used by teams to evaluate the quarter-

backs, and by gamblers to place bets on games. Par-

ticularly, the NFL ofﬁcially suggests the passer rating

(PR) metric, to estimate the quarterback performance.

The metric is a combination of four factors computed

Predicting the Success of NFL Teams using Complex Network Analysis

137

based on the previous reported game statistics:

a =



COMP

AT T

− 0.3



× 5

b =



YARDS

AT T

− 3



× 0.25

c =



T D

AT T



× 20

d = 2.375 −



INT

AT T

× 25



PR =

mm(a) + mm(b) + mm(c) + mm(d)

× 100 (1)

Equation 1 presents the formula for the passer ra-

ting metric, where mm(x) = max(0, min(x, 2.375)).

According to Equation 1, the minimum value of PR

is 0, when the quarterback complete up to 30% of the

passes, wins less than 3 yards per attempt, fails to tou-

chdowns and is intercepted at least 9.5% of the rolls.

Inversely, the maximum value is 158.3, when a quar-

terback completes at least 77.5% of the passes, wins

at least 12.5 yards per attempt, pass a touchdown on

at least 11.875% of the attempts and is not intercep-

ted. Figure 4 presents the AT T metric of the NFL

quarterbacks.

Figure 4: ATT metric of the quarterbacks.

From Figure 4, we observe that the distribution of

AT T follows a power law, i.e., a very small number

of quarterbacks present extraordinary performance,

while a large number of quarterbacks perform poorly.

This behavior suggests that the NFL can be represen-

ted as a scale-free network. Therefore, we believe that

it is possible to build effective models to predict team

success through the investigation of the network topo-

logy and properties. Additionally, Figure 5 presents

the PR metric of the NFL quarterbacks.

Figure 5: PR metric of the quarterbacks.

From Figure 5, we observe that PR values concen-

trate near the mean, increasing or decreasing signiﬁ-

cantly when PR lies more than a few standard deviati-

ons away from the mean, which characterizes a Gaus-

sian distribution. Therefore, a very small number of

quarterbacks present extraordinary (or mediocre) per-

formance, while a large number of quarterbacks per-

form similarly to each other. We perform the previous

analysis on Figures 4 and 5 by collecting teams, sco-

res, and quarterbacks game statistics from the ofﬁcial

NFL site

. Table 1 summarizes the records we col-

lected.

Table 1: NFL dataset records.

Conferences 2 (AFC-NFC)

Seasons 16 (2000-2015)

Teams 32

Games 512

Quarterbacks 143

From Table 1, we observe that our dataset compri-

ses 2 NFL conferences, 16 seasons, 32 teams equally

divided in the conferences in each season, with each

team playing 16 games per season.

5 THE NFL NETWORK

In this article, we model the labor relationship bet-

ween teams and players as a social network. Particu-

larly, each team and quarterback is represented as a

node, and a labor relation between a team and a quar-

terback is represented as an edge. In addition, two

quarterbacks have an edge connecting them if they

ever played on the same team. We collect labor re-

lationships from the ofﬁcial NFL site from 2000 to

http://www.nﬂ.com

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

138

2015 between 32 teams and 143 quarterbacks. Fi-

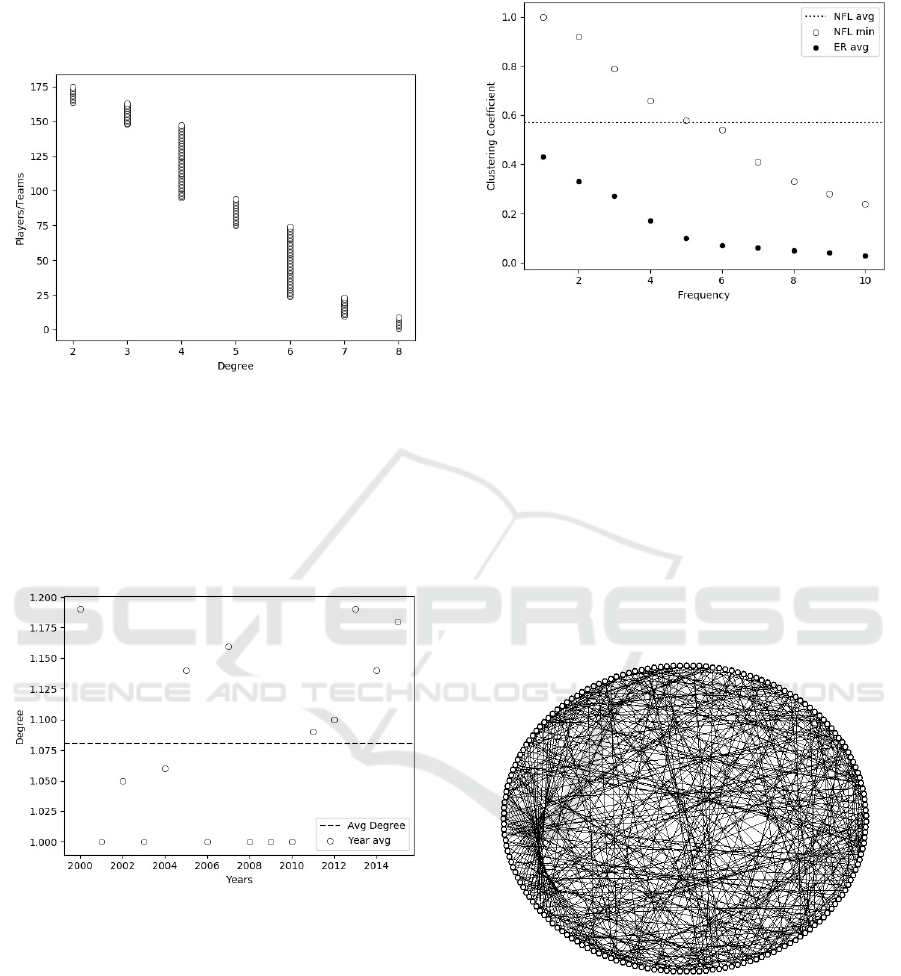
gure 6 show the degrees of the quarterbacks and te-

ams.

Figure 6: Degree of quarterbacks and teams.

From Figure 6 we observe that most players and

teams have the degree between 4 and 6, i.e., the ma-

jority of players and teams are connected with up to 6

other players and teams. In addition, Figure 7 shows

the annually average degree of quarterbacks and te-

ams.

Figure 7: Average degree of quarterbacks and teams by

year.

From Figure 7 we observe that the number of con-

nections between quarterbacks and teams have incre-

ased in the last years, which shows a potential growth

in NFL quarterback turnover, i.e., the rate of quarter-

backs replacement. Moreover, Figure 8 show the dis-

tribution of the clustering coefﬁcients of NFL players

and teams.

Clustering coefﬁcient measures the density of

connections closest to the nodes, and is commonly

used to estimate the connection likelihood between

nodes. From Figure 8 we observe that the values

of the NFL clustering coefﬁcients signiﬁcantly differs

from the Erdos-R

enyi (ER) network, showing that the

Figure 8: Clustering coefﬁcient of quarterbacks and teams.

NFL social network is not a random network. In addi-

tion, we observe that the values of the NFL clustering

coefﬁcients are greater than the clustering coefﬁcients

of the ER network. Small-world networks are charac-

terized by having a clustering coefﬁcient signiﬁcantly

higher than its equivalent ER network (Watts and

Strogatz, 1998). Thus, we observe that the NFL so-

cial network follows a small-world behavior. Conse-

quently, information exchanged between players and

teams, such as game tactics and team attractiveness,

are quickly propagated between players, impacting

the teams’ turnover and performance. Figure 9 pre-

sents the NFL small-world network.

Figure 9: The NFL small-world network.

6 PREDICTION MODELS

In this section we present two models to predict NFL

team success: i) the EM (efﬁciency model), based on

the passer rating statistic; ii) the DM (degree model),

based on the node degree metric. As described in

Section 1, the ﬁrst model is used as baseline to eva-

luate the other model based on network metrics. To

Predicting the Success of NFL Teams using Complex Network Analysis

139

evaluate the models, we use the Pearson coefﬁcient

to measure the correlation r between the performance

metric used by the model and the real team success,

i.e., the team’s ﬁnal rank position in the regular sea-

son.

r =

∑

i=1

− (

∑

i=1

∑

i=1

)

∑

i=1

− (

∑

i=1

)

)(n

∑

i=1

− (

∑

i=1

)

Considering the equation above, The Pearson

coefﬁcient measure the correlation r between the per-

formance metric used by the model (x

) and the real

team success (y

), where r is a real value between −1

and 1, expressing the strength of the correlation be-

tween the two variables, with 1 expressing the most

positive correlation, −1 expressing the most negative

correlation, and 0 expressing no correlation. The sam-

ples were collected only by the top-6 teams in the

AFC and NFC regular seasons, which are the teams

that advanced to the next phase of the NFL champi-

onship.

6.1 Efﬁciency Model

The ﬁrst prediction model is EM (Efﬁciency Mo-

del), which is based on game statistics, as described

in Section 4. Particularly, the quarterback PR me-

tric described in Equation 1 is used to measure team

success. We use the PR metric of one year as predic-

tor for the next year. For instance, we rank quarter-

backs by their performance in 2000 season, and we

predict the rank position of the teams in 2001 season

using their quarterbacks performance in the previous

year. Figure 10 presents the Pearson’s coefﬁcient for

the correlation between PR and team success.

Figure 10: Pearson’s coefﬁcient for the correlation between

PR and team success.

From Figure 10 we observe that there is no clear

pattern of correlation between passer rating and team

success. While in a season we observe a strong cor-

relation, in other seasons we observe a weak or no

correlation at all. For instance, in AFC 2009 sea-

son we observe a strong positive correlation, while

in AFC 2001 and 2014 seasons we observe a strong

negative correlation, and in AFC 2007 season we ob-

serve a negligible value of correlation. We observe

the same for the NFC, a strong positive correlation in

2003, 2008 and 2010 seasons, a negative correlation

in 2005 season and a negligible value of correlation in

2004, 2006 and 2007 seasons.

Although there is no clearly pattern of correlation

between passer rating and team success, in 68.75% of

AFC seasons we observe a positive correlation, with

Pearson’s coefﬁcient varying from 0.31 to 0.94, and

in 56.25% of NFC seasons we also observe a positive

correlation, with Pearson’s coefﬁcient varying from

0.08 to 0.94. Particularly, a strong positive correlation

pattern is more frequent in the AFC, where in 37.5%

of the seasons the Pearson’s coefﬁcient was greater

than 0.71. For NFC, only in 18.75% of the seasons

the Pearson’s coefﬁcient was greater than 0.71.

In addition, in seasons 2001, 2005, 2006, and

2011 we observe a difference in the polarity of the

correlation in the AFC and NFC Conferences, i.e.,

when in one Conference we observe a positive cor-

relation in the other we observe a negative correla-

tion. Moreover, only in season 2010 we observe a

strong and positive correlation in both AFC and NFC

Conferences, with Pearson’s coefﬁcient of 0.77 and

0.82 respectively. In 2002, 2003, 2008, 2009, 2012,

2013, and 2015 we also observe a positive correlation

in both AFC and NFC Conferences, but with a wide

range of values between them.

The AFC 2015 season is a good example on how

unfeasible can be passer rating metric to predict team

success. The Denver Broncos, took the ﬁrst place in

the regular season, being the Superbowl champion.

However, their quarterback Peyton Manning, the best

quarterback in the NFL history, made one of his worst

performance throughout the championship, standing

only one position ahead of the worst quarterback with

a PR = 67.9 in that season.

6.2 Degree Model

The second prediction model is DM (Degree Model),

which is based on the degree distribution of the quar-

terbacks and teams, considering the NFL social net-

work described in Section 5. Particularly, in the mo-

del a team with a high degree is probably a team that

often traded quarterbacks or had quarterbacks who re-

tired. The intuition behind the model is that a team

that recently switches their quarterbacks is a team that

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

140

performs badly in the next seasons.

We use a window of three years to build the social

network and extract the node degrees. For instance,

we rank teams by their degrees extracted from the

NFL social network of 2000, 2001 and 2002 seasons,

and we predict the ranking position of the teams in

2003 season using these degrees. Figure 11 presents

the Pearson’s coefﬁcient for the correlation between

node degree and team success.

Figure 11: Pearson’s coefﬁcient for the correlation between

node degree and team success.

From Figure 11 we observe that there is a clear

pattern of correlation between node degree and team

success in AFC. However, we do not observe the same

for NFC. In 92.85% of AFC seasons we observe a po-

sitive correlation, with Pearson’s coefﬁcient of up to

0.88, and in a half of AFC seasons the Pearson’s coef-

ﬁcient was greater than 0.54. But in 28.57% of AFC

seasons the value of the Pearson’s coefﬁcient is al-

most zero, pointing to a negligible correlation. For

NFC, while in a season we observe a strong correla-

tion, in other seasons we observe a weak or no cor-

relation at all. For instance, in NFC 2008 season we

observe a strong positive correlation, while in NFC

2010 and 2012 seasons we observe a strong negative

correlation, and in NFC 2005 season we observe no

correlation at all.

7 CONCLUSIONS

In this article, we proposed a method that exploits

NFL social network properties and metrics to predict

the success of NFL teams. Particularly, we modeled

the labor relationships between NFL teams and play-

ers (quarterbacks) by representing them as nodes and

their relations as edges in a graph, and we used net-

work metrics extracted from the graph as a predictor

of team success. We thoroughly evaluated the net-

work metrics by contrasting them with usual game

statistics from NFL and the results of this evaluation

showed that node degree is a more effective predictor

than passer rating statistic. In addition, complex net-

work analysis showed that the NFL social network is

a scale-free and small-world network, where a large

number of quarterbacks perform poorly, while a very

small number of quarterbacks perform extraordina-

rily, and the distance between any two quarterbacks

in the network is very small.

For future work, we plan to investigate how the

NFL social network evolves over time to propose and

evaluate new network metrics as team success predic-

tors. We also plan to combine network metrics with

usual game statistics to improve the prediction effecti-

veness.

ACKNOWLEDGEMENTS

The authors are thankful for the support given by

CNPq (Brazilian National Council for Scientiﬁc and

Technological Development), Brazilian Ministry of

Science, Technology, Innovation and Communicati-

ons (MCTIC), FAPEMIG (Foundation for Research

and Scientiﬁc and Technological Development of Mi-

nas Gerais), PUC Minas (Pontiﬁcal Catholic Univer-

sity of Minas Gerais), and the MASWeb Project. Par-

ticularly, this work is supported by PUC Minas under

Grant No.: FIP 2016/11086-S2, FAPEMIG/PRONEX

under Grant APQ-01400-14, and MCTIC/CNPq un-

der Grant No.: 444156/2014-3.

REFERENCES

Albert, R. and Barab

asi, A.-L. (2002). Statistical mechanics

of complex networks. Reviews of Modern Physics,

74(1):47.

Burke, B. (2012). Offensive line salary and performance.

Advanced Football Statistics.

Costa, L. F., Rodrigues, F. A., Travieso, G., and Villas Boas,

P. R. (2007). Characterization of complex networks:

a survey of measurements. Advances in Physics,

56(1):167–242.

Ejiochi, I. (2014). How the NFL makes the most money of

any pro sport. CNBC.

Erd

os, P. and R

enyi, A. (1959). On random graphs, i. Pu-

blicationes Mathematicae (Debrecen), 6:290–297.

Faloutsos, M., Faloutsos, P., and Faloutsos, C. (1999).

On power-law relationships of the Internet topology.

In Proceedings of the Conference on Applications,

Technologies, Architectures, and Protocols for Com-

puter Communication, SIGCOMM ’99, pages 251–

262, New York, NY, USA. ACM.

Predicting the Success of NFL Teams using Complex Network Analysis

141

Fast, A. and Jensen, D. (2006). The NFL coaching net-

work: analysis of the social network among professi-

onal football coaches. Growth, 60:70.

Heitner, D. (2015). $93 billion will be illegally wagered on

NFL and college football. Forbes.

Newman, M. (2003). The structure and function of complex

networks. SIAM Review, 45(2):167–256.

Newman, M. (2010). Networks: an introduction. OUP Ox-

ford.

Vaz de Melo, P. O. S., Almeida, V. A. F., and Loureiro,

A. A. F. (2008). Can complex network metrics pre-

dict the behavior of NBA teams? In Proceedings of

the 14th ACM SIGKDD International Conference on

Knowledge Discovery and Data Mining, pages 695–

703. ACM.

Vaz de Melo, P. O. S., Almeida, V. A. F., Loureiro, A.

A. F., and Faloutsos, C. (2012). Forecasting in

the NBA and other team sports: network effects in

action. ACM Transactions on Knowledge Discovery

from Data (TKDD), 6(3):13.

Wasserman, S. and Faust, K. (1994). Social network analy-

sis: methods and applications, volume 8. Cambridge

University Press.

Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics

of ’small-world’ networks. Nature, 393(6684):440–

442.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

142