Blind Estimation of OFDM Sampling Frequency Offset and

Application to Power Line Communication in Aircrafts

Navish Lallbeeharry

, Rose Mazari

, Virginie Degardin

, Martine Lienard

and Christophe Trebosc

University of Lille, IEMN/Telice, Villeneuve d’Ascq, France

Safran Electrical and Power, R&T EWIS EURASIA, Toulouse, France

christophe.trebosc@safrangroup.com

Keywords: OFDM, Sampling Frequency Offset, Aircraft PLC Channels.

Abstract: Orthogonal Frequency Division Multiplexing (OFDM) is a widely used technique but its practical

implementation sometimes leads to issues related to the synchronization between the transmitter and the

receiver. The sampling frequency offset playing a major role in the degradation of the link performance,

various solutions have been proposed to cope with this effect. The objective of this paper is to present a

simple blind estimation of the offset, calculated on each OFDM symbol and thus only based on the received

data. A correction is then applied on the phase of the received signal. Synchronization of the receiver with a

phased-locked loop is not treated in this paper. After illustrating this approach for an additional white

Gaussian noise channel, a power line communication in an aircraft is envisaged. The architecture of the

network is described and a parametric study is carried out to assess the performance of the proposed offset

estimator and the phase correction technique.

1 INTRODUCTION

The need for reliable communications and electrical

networks monitoring has become a priority in

transportation systems. This is particularly critical in

the aeronautical sector with the emergence of the

“More Electrical Aircraft”, based on the replacement

of hydraulic and pneumatic energy by electrical

sources. To avoid a significant increase of the

number of cables and connections while keeping a

high reliability, a possible solution is to combine

data and power transmission by using a Powerline

Communication (PLC) technique. This approach can

of course be applied to any type of vehicles. Since

the electrical network is not designed as a

communication network, both the presence of

branches and the changes of the cable bundle

architecture along the structure lead to a multipath

propagation and thus to a highly frequency selective

channel. To overcome this problem, the PLC

physical layer is based on an OFDM modulation

technique also allowing a low receiver

implementation cost. This technique has matured

into a well established technology for wireless and

wired broadband delivery. It is used in the digital

video broadcasting (DVB), IEEE 802.11a, xDSL,

LTE and future 5G standards. The main drawback of

OFDM is that it is very sensitive to synchronization

offsets, such as Symbol Timing Offset (STO),

Carrier Frequency offset (CFO) and Sampling

Frequency Offset (SFO), this latter being due to a

sampling frequency mismatch between the

transmitter (Tx) and the receiver (Rx). The impact of

STO has been analyzed in the literature (Schmidl,

1997; Shi, 2004; Moose, 1994; Van de beek, 1997)

using pilot symbols or cyclic prefix, while

algorithms to estimate the CFO and STO are

presented in (Nogami, 1995, Nguyen, 2009, Kim,

2011). In (Cortes, 2006; Larhzaoui, 2014; Crussiere,

2004), sampling frequency errors for OFDM or

DMT systems have been analyzed and error

corrections are based on pilot symbols (Larhzaoui,

2014, Crussiere, 2004) or on complex equalization

schemes (Cortes, 2006).

Since SFO has a strong impact on PLC

performance, the objective of this paper is to present

a simple and efficient blind estimation of the

sampling offset based on phase rotation of each

subcarrier of the data symbols. It must be outlined

that only the phase of the input signals will be

corrected by applying the proposed approach. This

means that the effect of the inter channel

Lallbeeharry, N., Mazari, R., Degardin, V., Lienard, M. and Trebosc, C.

Blind Estimation of OFDM Sampling Frequency Offset and Application to Power Line Communication in Aircrafts.

DOI: 10.5220/0006697803570362

In Proceedings of the 4th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2018), pages 357-362

ISBN: 978-989-758-293-6

357

interference (ICI) is not suppressed. The method has

been applied to various PLC channels, representative

of a dedicated aircraft network, in order to assess its

performance, thus without ICI suppression, as a

function of the signal to noise ratio and the values of

the SFO.

The paper is organized as follows. In Section 2,

the principle of the method for estimating SFO is

first described and, to illustrate this approach, it is

applied to an Additional White Gaussian Noise

(AWGN) channel. Since PLC was identified as a

promising technique to gain weight and reliability in

transportation systems, the architecture of a possible

application in aircraft is recalled in Section 3.

Narrow band and wide band channel characteristics

deduced from numerical modeling based on the

multi conductor transmission line theory are also

given. For an OFDM-PLC link in such frequency

selective channels and assuming noise as an AWGN,

the performance of the SFO estimator is described in

Section 4.

2 PRINCIPLE OF THE

ESTIMATION METHOD

After describing the basic principles of the proposed

method, an illustration is given by considering the

simple case of an AWGN flat-fading channel.

2.1 Presentation of the Method

In presence of SFO, if the sampling frequency of the

Tx signal is F

, the Rx signal will be sampled at

(1+

with

fΔ

(1)

If Ts and Ts' are the sampling periods with and

without SFO, the change

t in the duration of each

symbol is N (Ts - Ts') with N the number of OFDM

subcarriers.

The proposed blind estimation process of

noted ε

est

, is deduced from data symbols and is

summarized in Fig. 1. At Rx, the cyclic prefix is

removed from the received data, the Fast Fourier

Transform (FFT) is performed, and zero forcing

equalization is done to obtain the frequency domain

symbols noted X'. Then, these symbols X' are QPSK

demapped and QPSK remapped to get a new symbol

X".

It is important to recall that to avoid the effects

of windowing on the spectral content of the signal,

the number of active subcarriers is smaller than the

total number of subcarriers, their corresponding

index n varying from Nmin to Nmax. Consequently,

the previous approach is only applied to these active

subcarriers.

Figure 1: Blind estimation process at the receiver.

The sampling error leads to a phase difference

between each successive component X'

and X"

of X' and X" associated to the subcarrier index n.

Therefore, the phase exhibits a linear variation with

the subcarrier frequency f

and can be written as:

estnn

2)( =

(2)

Such an expression allows a direct determination

est

since it is proportional to the slope of the

curve

). Practically, the evaluation of

) is

subject to an error mainly due to the finite value of

the signal to noise (SNR) ratio. A linear least square

algorithm (Crussiere, 2014) is used and leads to:



max

min

max

min

est

(3)

With ∆f the intercarrier space. This simple

algorithm is then applied to each received successive

symbol. The advantage of this approach is that

est

deduced from all the active subcarriers, thus

minimizing the error in the estimation of its value.

The ratio

est

/Ts can be put as the sum of an integer

part and a fractional part. The integer part

corresponds to the offset of the FFT time window

while the fractional part represents the sampling off-

set within the FFT window. Lastly, phase correction

on each subcarrier is made by applying (2).

As an illustration of this method, we consider the

case of a communication in an AWGN channel. The

parameters of the PLC OFDM link have been

chosen in accordance with previous works that we

have done in the aeronautic domain, taking into

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

358

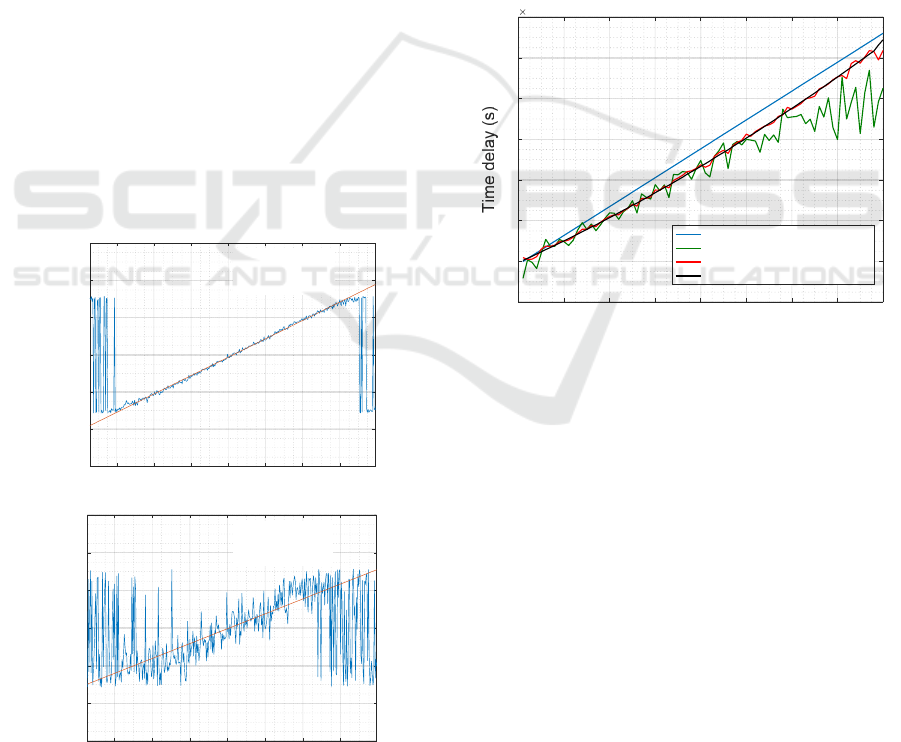
account constraints both on calculation time and on

latency (Larhzaoui, 2014). The number of

subcarriers is set to 512, equal to the FFT size and,

among them, 384 active subcarriers support data

transmission within the 4.6 – 32.7 MHz frequency

band. The sampling frequency is equal to 37.5 MHz

and a QPSK modulation is used.

2.2 Application to the Case of an

AWGN Channel

To illustrate the application of the method we

consider in this paragraph the case of a flat-fading

channel but in presence of AWGN. The sampling

error in the simulation is introduced owing to the

resample function available in Matlab software. In a

first example, we consider an offset of 10 ppm

giving rise to a shift of 1 sample at the 180

OFDM

symbol.

The SNR, expressed in terms of Eb/N

, where E

is the bit energy and N

the noise spectral density,

has been successively chosen equal to 10, 20 and 30

dB. Curves in Fig. 2 (a) and (b) give the variation of

(n) thus as a function of the index of the

subcarrier, calculated for the 80

symbol and for

equal to 30 and 10 dB respectively. The

regression lines associated with these curves have

also been plotted.

Figure 2: Phase variation versus the subcarrier index. (a)

= 10 dB, (b) E

= 30 dB.

From a purely qualitative point of view, we see

from these curves that, for an E

of 10 dB,

important fluctuations of the estimated phase angle

appear. This mainly occurs in the lowest and highest

frequency part of the spectrum, due to the

windowing of the spectral component of the signal.

One can thus expect that this will lead to

uncertainties in the value of the slope of the

regression line and thus on the SFO.

To emphasize this point, curves in Fig. 3 give the

variation of the time delays appearing on 80

successive symbols and deduced from the proposed

approach for E

equal to 10, 20 and 30 dB. These

values can be compared to the exact value calculated

for an SFO of 10 ppm. When time increases the shift

in sampling time also increases and, for an SNR of

10 dB, this leads to significant errors beyond the 60

symbol.

Figure 3: Performance of the estimator with 10 ppm offset.

Lastly, the bit error rate (BER) versus E

presented in Fig. 4 for the following cases: No SFO

(reference case) and in presence of an SFO without

correction or taking it into account by introducing

phase correction as previously explained. We see

that, without correction, BER tends to about 10

-3

for

high SNR. If a correction is introduced, a BER of

-4

is reached for an SNR of 10 dB with correction,

this value being quite comparable of the case of no

SFO (8 dB).

To point out the influence of the value of the

sampling frequency offset, curves in Fig. 5 have

been plotted for SFO = 1, 5 and 10 ppm. For 1 ppm,

BER with correction is nearly identical to the curve

in absence of SFO, errors increasing for 5 and 10

ppm.

100 150 200 250 300 350 400

Active Subcarrier index

-1.5

-1

-0.5

0.5

1.5

Angle (Rad)

100 150 200 250 300 350 400

Active Subcarrier index

-1.5

-1

-0.5

0.5

1.5

Angle (Rad)

0 1020304050607080

Symbol Number

-2

-9

Exact Values

Estimated Values with Eb/No = 10 dB

Estimated Values with Eb/No = 20 dB

Estimated Values with Eb/No = 30 dB

(a)

(b)

Blind Estimation of OFDM Sampling Frequency Offset and Application to Power Line Communication in Aircrafts

359

Figure 4: BER with and without correction and

comparison with the reference case (no SFO).

Figure 5: BER calculated in presence of an SFO equal to

1,5 and 10 ppm and comparison with the case of perfectly

synchronized clocks.

3 DESCRIPTION AND MAIN

CHARACTERISTICS OF A

REPRESENTATIVE NETWORK

OF AN AIRCRAFT

ENVIRONMENT

The chosen application deals with a system

combining lighting and data communication in the

cabin of an aircraft. In this network, the various

lights and display panels distributed inside the cabin

and noted LS, are powered by the electrical power

units (EPU). Since they must be remote controlled, a

PLC link seems to be an elegant solution to decrease

the number of cables and thus their total weight.

The architecture of a sub network is widely

described in (Degardin, 2013) and we briefly

recalled its main geometrical characteristics. As

shown in the schematic diagram in Fig 6, the EPU

feeds a "short" line and a "long" line in parallel. 4

LSs (LS1 to LS4) are connected to the short line and

10 LSs (LS5 to LS14) are connected to the long line.

The length of the PLC line, between the EPU and

each LS is also noted in Fig. 6. The number of wires

in each branch of the network is between 2 and 30.

Figure 6: Geometrical architecture of a sub network of a

cabin lighting system.

A numerical modeling based on a topological

approach of these multi conductor transmission

applied was applied to calculate the channel transfer

functions between each terminal and the channel

impulse responses. The 3 communication channels

chosen to illustrate the application of the SFO

estimation are the following: Channel 1 refers to the

link between EPU and LS2 (11.94 m long), channel

2 between EPU and LS4 (17.97 m) and lastly

channel 3 between EPU and LS8 (40.13 m).

Fig. 7 gives the insertion gain for these 3

channels, deduced from the numerical modeling, in

the [100 kHz-40 MHz] frequency band.

From the cumulative distribution of the path loss,

the attenuation presented by the channel is

calculated for a percentile of 0.5 (median value) or

of 0.9 to get an idea of the maximum attenuation

presented by the channel. This calculation has been

done on the active transmission bandwidth [4.6,

32.7] MHz, i.e. the bandwidth occupied by the

active subcarriers. Results are presented in Table 1.

0 5 10 15 20 25 30 35 40 45 50

Eb/No(dB)

-4

-3

-2

-1

Without Correction

With Correction

Reference

0 2 4 6 8 10 12 14 16 18 20

Eb/No (dB)

-4

-3

-2

-1

With Correction @ 10 ppm

With Correction @ 5 ppm

With Correction @ 1 ppm

Reference

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

360

Figure 7: Insertion gain presented by the network for 3

different channels

Table 1: Path loss presented by different channels. Median

value (percentile of 0.5) and for a percentile of 0.9.

Percentile 0.5 0.9

Channel 1 11,4 dB 15,4 dB

Channel 2 16,1 dB 20,4 dB

Channel 3 24,1 dB 29,7 dB

Figure 8: Channel impulse response for channel 1 (curve

a) and 3 (curve (b), the highest peak being normalized to 0

dB.

Channel impulse responses, deduced from the

transfer function by applying a Fourier Transform,

are given in Fig. 8 for channels 1 and 3.

For a threshold of – 20 dB, these curves show

that the maximum delays are equal to 266 ns and

400 ns, for channels 1 and 3, respectively, while the

root mean square (rms) delay spread (ߪ

ఛ

), are equal

to 52 ns, and 73 ns. One can mention that, for this

application, the length of the cyclic prefix has been

chosen equal to 426 ns, i.e. 16 samples, in

accordance with the usual choice based on about 4

times the delay spread or greater than the maximum

delay of the channel impulse response

4 PERFORMANCE OF THE SFO

ESTIMATOR FOR A PLC LINK

IN AIRCRAFT

To point out the performance of the phase correction

algorithm, simulations have been done on the first

80 symbols where a FFT window shift is not needed.

In the simulation, equalization is assumed to be ideal

to focus only on the synchronization problem.

Equalization based on Zero forcing algorithm is

realized on the theoretical transfer function channel.

Curves in Fig. 9 give the BER as a function of

Eb/N0 at the injection point, i.e. at the transmitter.

We have chosen this approach rather than to plot

BER versus Eb/N0 at the receiver since in this case,

the signal to noise ratio is frequency dependent. In

Fig. 9 and 10 corresponding to channel 1 and

channel 3, respectively, the 3 curves refer to: i) the

ideal case with no SFO (noted “reference”), ii) in

presence of an SFO of 10 ppm without and with

phase correction. Let us recall that the median

attenuation in channel 1 is 11 dB and reaches 24 dB

in channel 3. We see in both cases that if the phase

rotation due to the SFO is not corrected, the

degradation of the BER is quite important, and BER

tends to an asymptotic value of about 10-3 for high

Eb/N0.

For Eb/N0 such as BER becomes smaller than

0.1, the reference curve and the curve in presence of

SFO but with phase correction, are nearly parallel,

the shift being about 2 dB. This small value shows

the good performance of the proposed correction

method and can be due to the ICI, which is not

corrected by our proposed method, but is introduced

in our simulation.

0 0.5 1 1.5 2 2.5 3 3.5 4

Frequenc

(

)

-45

-40

-35

-30

-25

-20

-15

-10

|S21| (dB)

Channel 1

Channel 2

Channel 3

Normalised Pdp (dB)

malised Pdp (dB)

(a)

(b)

Blind Estimation of OFDM Sampling Frequency Offset and Application to Power Line Communication in Aircrafts

361

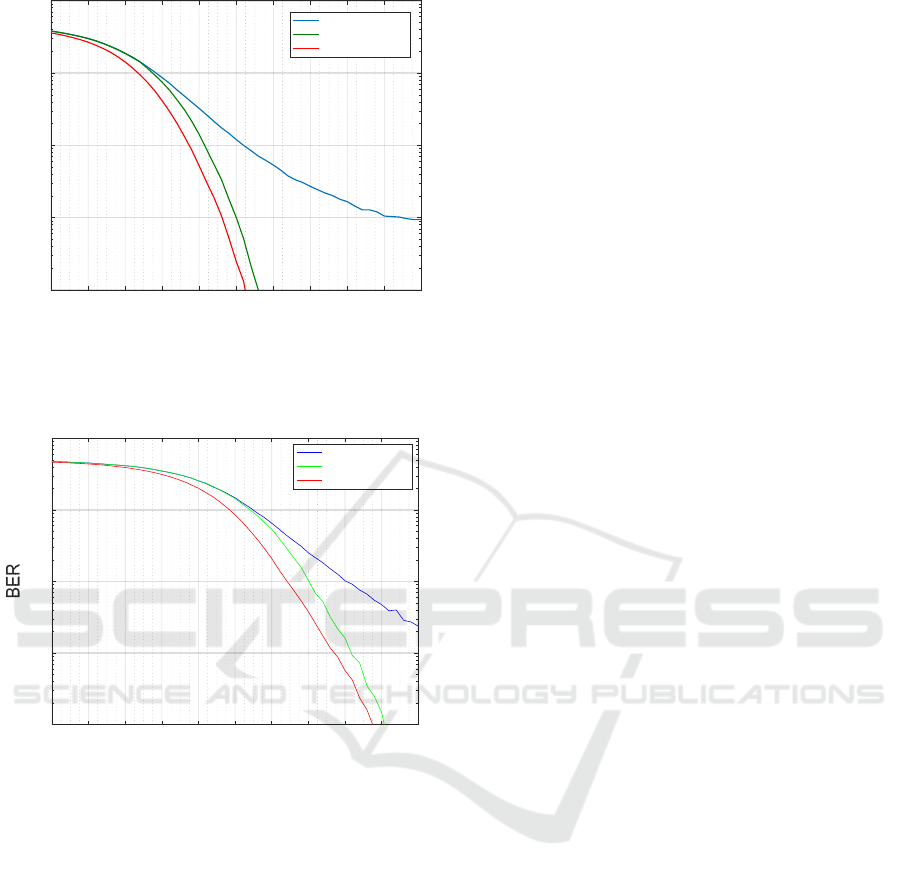
Figure 9: BER with and without correction and

comparison with the reference case (no SFO) in the

aircraft PLC channel 1.

Figure 10: BER with and without correction and

comparison with the reference case (no SFO) in the

aircraft PLC channel 3.

5 CONCLUSIONS

A simple blind estimation technique to determine the

sampling frequency offset which may occur in an

OFDM link has been described. It allows correcting

the phase rotation of each OFDM subcarrier. This

approach has been applied to typical PLC channels,

the examples being based on the architecture of

representative power sub networks in aircraft.

Results have shown that the proposed approach is

quite effective. Indeed, in presence of an SFO of 10

ppm and to get the same BER as in the case of no

SFO the needed additional transmitting power is

only 2 dB.

ACKNOWLEDGEMENTS

This project is co-funded by the European Union

with the European regional development fund

"FEDER" and SAFRAN Electrical & Power.

REFERENCES

Schmidl, T.M., Cox, D.C., 1997, Robust frequency and

timing synchronization for OFDM, in IEEE

communication letters, vol 45, p 1613-1621.

Shi, K., Serpedin, E., Coarse , 2004, Frame and carrier

synchronization of OFDM systems: a new metric and

comparison”, in IEEE transaction on wireless

communications, vol3, p 1271-1284.

Moose, P.H., 1994, A technique for orthogonal frequency

division multiplexing frequency offset correction, in

IEEE transaction on communications, vol 42, p 2908-

2914.

Van De Beek, J.J., Sandell, M., Borjesson, P.O., 1997, ML

estimation of timing and frequency offset in OFDM

systems, in IEEE transaction on signal processing, vol

45, p 1800-1805.

Nogami, H., Nagashima, T., 1995, Frequency and timing

period acquisition technique for OFDM systems, in

Proc. Personal, Indoor and Mobile Radio

Communications (PIMRC), vol. 3, pp 1010-1015.

Nguyen-Le H., Le-Ngoc T., and Ko, C. C., 2009, RLS-

based joint estimation and tracking of channel respon-

se, sampling, and carrier frequency offsets for OFDM,

IEEE Trans. Broadcast., vol.55, no.1, pp.84–94.

Kim Y.-H., Lee J.-H., 2011, Joint maximum likelihood

estimation of carrier and sampling frequency offsets

for OFDM systems, IEEE Trans. Broadcast., vol. 57,

no. 2, pp. 277–283.

Cortes, J.A., Diez, L., Martos, E., Canete, F.J.,

Entrambasaguas, J.T, 2006, Analysis of timing

recovery for DMT systems over Indoor Power Line

Channels", in IEEE Globecom 2006, pp 1-6.

Larhzaoui T., Nouvel F., Baudais J.Y., Degaugue P. and

Dégardin V., 2014, OFDM PLC transmission for

aircraft flight control system", 18th IEEE International

Symposium on Power Line Communications and it's

Applications, pp 220-225.

Crussière, M., Baudais, J.Y., Hélard, J.F., 2004, New

Iterative and Frequency Synchronization Scheme for

MC-CDMA Systems over Power Line Channels", in

ISSSTA2004, Sydney, Australia.

Degardin V., Junqua I., Lienard M., Degauque P., Bertuol

S., 2013, Theoretical approach to the feasibility of

power-line communication in aircrafts, IEEE Trans.

Veh. Technol. , vol 62, pp 1362-1366.

0 5 10 15 20 25 30 35 40 45 50

Eb/No(dB)

-4

-3

-2

-1

BER

Without Correction

With Correction

Reference

0 5 10 15 20 25 30 35 40 45 50

Eb/No(dB)

-4

-3

-2

-1

Without Correction

With Correction

Reference

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

362