
A New Approach for Optimal Implementation of Multi-core
Reconfigurable Real-time Systems
Wafa Lakhdhar
1,5
, Rania Mzid
2,3
, Mohamed Khalgui
1,4
and Georg Frey
5
1
LISI Lab INSAT, University of Carthage, INSAT Centre Urbain Nord BP 676, Tunis, Tunisia
2
ISI, University Tunis-El Manar, 2 Rue Abourraihan Al Bayrouni, Ariana, Tunisia
3
CES Lab ENIS, University of Sfax, B.P:w.3, Sfax, Tunisia
4
SystemsControl Lab, Xidian University, August Bebel Str 70, Halle, China
5
Automation and Energy Systems, Saarland University, Saarbrucken 66123, Germany
Keywords:
Real-time and Reconfiguration, Multi-core, POSIX, Task and Function, MILP and Optimization.
Abstract:
This paper deals with a multi-core reconfigurable real-time system specified with a set of implementations,
each of which is raised under a predefined condition and executes multiple functions which are in turns exe-
cuted by threads. The implementation as threads generates a complex system code. This is due to the huge
number of threads and the redundancy between the different implementations which may lead to an increase
in the energy consumption. Thus we aim in this paper to optimize the system code by avoiding the redundancy
between implementations and reducing the number of threads while meeting all related real-time constraints.
The proposed approach adopts mixed integer linear programming (MILP) techniques in the exploration phase
in order to provide a feasible task model. An optimal reconfigurable POSIX-based code of the system is
manually generated as an output of this technique. An application to a case study and performance evaluation
confirm and validate the expected results.
1 INTRODUCTION
A real-time system has to respond to externally gen-
erated input stimuli within a finite and specified de-
lay (Burns and Wellings, 2009). Such system may
have many implementation scenarios, the transition
from an implementation to another is called reconfig-
uration. Reconfiguration refers to the architectural or
behavioral modifications of a software system during
its execution (Polakovic et al., 2007) to meet user re-
quirements. Currently, some real-time systems such
as automotive electronics, avionics, telecommunica-
tions, and consumer electronics become more com-
plex and need more computational power. Thus, the
necessity for multi-core architecture is a common
answer. The multi-core technology allows increas-
ing the processor clock frequency, which is limited
by available instruction-level parallelism and leads to
challenging power requirements (Geer, 2005). This
paper deals with multi-core reconfigurable real-time
systems.
One challenge during the development of multi-
core reconfigurable real-time systems is to ensure an
appropriate partitioning and scheduling of the ap-
plicative functions across the target platform such
that the timing constraints are met. In that context,
different scheduling policies have been proposed in
the literature (Khan and Hafiz, 2014) (Lakshmanan,
2011). Existing multi-core scheduling policies can be
classified into three different classes: the partitioned,
the global and semi-partitioned approach. The parti-
tioned scheduling allows to choose a core for all tasks
and then runs a local scheduler on each core (i.e., off-
line scheduling). However, the global scheduling al-
lows to choose a task and to assign it to one of the
cores (i.e., on-line scheduling). As opposed to the par-
titioned approach, different instances of the same task
can execute on different cores. The semi-partitioned
approach presents an improvement of the partitioning
scheduling allowing the controlled tasks migration. It
is a hybrid between partitioned and global scheduling
(Lakshmanan, 2011). In this paper, we adopt a parti-
tioned approach because it is easier to implement and
to analyze. Also, it allows no task migration, thus has
low runtime overheads (Funk and Baruah, 2005). For
the three multi-core scheduling approaches, several
scheduling algorithms have been proposed such as
Rate Monotonic RM (Liu and Layland, 1973) which
Lakhdhar, W., Mzid, R., Khalgui, M. and Frey, G.
A New Approach for Optimal Implementation of Multi-core Reconfigurable Real-time Systems.
DOI: 10.5220/0006698100890098
In Proceedings of the 13th International Conference on Evaluation of Novel Approaches to Software Engineer ing (ENASE 2018), pages 89-98
ISBN: 978-989-758-300-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
89

will be adopted for tasks scheduling in this paper.
The multi-core introduces additional challenges
that are still difficult to deal with in real world in-
dustrial domains. Indeed, the huge number of tasks
exhibits a high complexity by increasing the energy
consumption, invoking many redundancies between
the different implementations, and producing a com-
plex system code. Thus, we propose a multi-objective
optimization approach that minimizes both the en-
ergy consumption and the number of tasks in order to
reduce the redundancy between the implementation
sets. Such optimization may reduce the time over-
head and the complexity of the generated code. At the
specification level, the developer defines the function
sets, the condition sets, and the core sets. At the de-
sign level, this approach (i) generates the implemen-
tation sets, (ii) affects the functions to the tasks sets
which are in turns assigned to the core sets, and (iii)
generates a feasible and optimized task model by us-
ing the mixed integer linear programming (MILP) for-
mulation. Finally, at the implementation level, each
task is transformed to a thread to execute the applica-
tive functions.
The originality of the proposed approach follows
from the fact that (i) it deals with the multi-core (i.e.,
partitioning), reconfiguration, and real-time problems
simultaneously, and (ii) it proposes a multi-objective
optimization to minimize both the energy consump-
tion and the number of tasks.
The rest of the paper is organized as follows. Sec-
tion 2 presents the state of the art on multi-core re-
configurable real-time systems. In Section 3, we give
the system formalization. We present the proposed
approach in Section 4. In Section 5 we present the
Global Positioning System (GPS) case study which
is considered to evaluate the proposed approach. Fi-
nally, we summarize our work and discuss future di-
rections in Section 6.
2 RELATED WORKS
In the area of real-time multi-core systems, some ex-
isting works focus on the synthesis problem (Wang
et al., 2016), (Yehia et al., 2011), (Geismann et al.,
2017). In (Wang et al., 2016), the authors propose a
formalization of periodic tasks adapted to engine con-
trol applications in multi-core automotive systems.
The work reported in (Yehia et al., 2011) presents a
system level synthesis approach for multi-core system
architectures from Task Precedence Graphs (TPG)
models. In (Geismann et al., 2017), the authors
present an approach for a semi-automatic synthesis of
models into a deterministic scheduling that respects
real-time requirements for multi-core systems. De-
spite the importance of above related synthesis works,
none of these solutions considers the reconfiguration
property. In contrast, this paper focuses on how the
feasible code may be generated for multi-core recon-
figurable real-time system.
Another related area is the safe deployment to
multi-core real-time systems, where approaches fo-
cus on the mapping of tasks on multi-core platforms
(Monot et al., 2012), (Saidi et al., 2015), (Yi et al.,
2009), (Vulgarakis et al., 2014) (Faragardi et al.,
2013). In (Monot et al., 2012), the authors develop
a heuristic algorithm for the function mapping on a
multi-core architecture. In this work, the functions
are grouped and distributed across cores, then they
are mapped to tasks. Similarly to (Saidi et al., 2015),
which proposes a heuristic algorithm to create a task
set according to the mapping of runnable entities on
the cores. In (Yi et al., 2009) a linear program is de-
veloped for task partitioning, mapping, and schedul-
ing on embedded multi-core systems. Some other re-
lated works propose an end-to-end approach to gen-
erate a full real-time system. In (Vulgarakis et al.,
2014), the authors present a process for the auto-
matic deployment of control applications on multi-
core platforms and generate Java code. The work re-
ported in (Faragardi et al., 2013) addresses the map-
ping problem of hard real-time systems composed of
periodic AUTOSAR runnables in the context of the
multi-core.
The proposed approach differs from the cited
works in several points. First of all, it considers recon-
figurable systems with real-time properties and multi-
core architecture. Secondly, we address the synthe-
sis, the partitioning, the scheduling problem, and the
optimization simultaneously. Finally, the majority of
them do not propose general solutions. They target a
well defined system.
3 SYSTEM FORMALIZATION
In this section, we present a formal description of
a multi-core reconfigurable processor system. We
present in addition real-time prerequisites required to
introduce the paper’s contribution.
3.1 System and Architecture Modeling
It is assumed in this work that a reconfigurable real-
time system Sys is defined as a set of m imple-
mentations: Sys = {imp
1
, imp
2
. . . imp
m
}. We de-
note by Sys(t) the implementation defining the sys-
tem at particular time t (i.e., Sys(t) = imp
i
). An
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
90

Figure 1: Task and function models.
implementation imp
i
is composed of N
i
tasks (i.e.,
imp
i
= {τ
1
, τ
2
, τ
3
. . . τ
N
i
}). Each task τ
j
in the im-
plementation imp
i
is characterized by (top of Fig
1): (r
i j
, s
i j
, T
i j
,C
i j
, D
i j
, P
i j
, E
i j
) where r
i j
is its release
time, we assume that r
i j
= 0, its start time s
i j
which
denotes the effective starting time of a task τ
j
, its ac-
tivation period T
i j
, C
i j
denotes the capacity or worst
case execution time, its deadline D
i j
which is assumed
to be equal to its period in this work D
i j
= T
i j
, the pri-
ority P
i j
that is inversely proportional to the period T
i j
as we use the RM policy, E
i j
presents the energy con-
sumption of task τ
j
which is computed as the sum of
the energy consumed by the functions implemented
by τ
j
.
The task τ
j
may implement a single or several
functions which must have the same period τ
j
=
{F
1
, F
2
, F
3
, . . . F
p
j
}. Each function F
k
is characterized
by static real-time parameters (bottom of Figure 1)
(T
F
k
,C
F
k
, E
F
k
) where T
F
k
is the activation period of
the function F
k
, C
F
k
is an estimation of its worst case
execution time (WCET) and E
F
k
is the energy con-
sumed by the function F
k
during its execution. Note
that these parameters are considered as inputs for the
proposed approach and must be specified by the user.
The system consists of one processor, containing a
set of M identical cores {ζ
1
, ζ
2
. . . ζ
M
} that share com-
mon memory. Each core runs a set of tasks. We as-
sume that the tasks are independent and periodic.
3.2 Energy Model
Each function F
k
is described by two parameters:
(i) the function’s frequency f
F
k
, and (ii) the func-
tion’s voltage V
F
k
. The energy consumption for
the execution of function F
k
that we denote by E
F
k
is computed as E
F
k
= f
F
k
V
2
F
k
C
F
k
. The energy con-
sumption E
i j
of task τ
j
is then equal to the sum
of the energy consumed by the implemented func-
tions E
i j
=
∑
k∈{1...p
j
}
E
F
k
=
∑
k∈{1...p
j
}
f
F
k
V
2
F
k
C
F
k
=
f
i j
V
2
i j
C
i j
where ( f
i j
, V
i j
) are two parameters char-
acterizing task τ
j
in implementation imp
i
. We assume
that f
i j
=
∑
k∈{1...p
j
}
f
F
k
and V
i j
=
∑
k∈{1...p
j
}
V
F
k
. Thus
the total energy consumption (Lei et al., 2016) of im-
plementation imp
i
is given by expression 1
E
i
=
∑
j∈{0,N
i
}
E
i j
=
∑
j∈{0,N
i
}
f
i j
V
2
i j
C
i j
(1)
In expression 2, we denote by f
n
and V
n
the nor-
malized frequency and voltage of the system. We de-
note by η
j
the reduction factor of voltage when τ
j
is executed, V
i j
=
V
n
η
j
and f
i j
=
f
n
η
j
. In addition, we
denote by C
n
the computation time at the normalized
processor frequency i.e., C
i j
= C
n
η
j
. Thus, the total
energy consumption of the implementation imp
i
ac-
cording to (Chniter et al., 2014) is given by
E
i
=
∑
j∈{0,N
i
}
f
n
∗V
2
n
∗C
n
η
2
j
= K
∑
j∈{0,N
i
}
C
n
η
2
j
(2)
where K = V
2
n
f
n
.
3.3 Processor Utilization Factor
Let U
i
be the processor utilization factor of the im-
plementation imp
i
is defined by: U
i
=
∑
N
i
j=1
C
i j
T
i j
(Klein
et al., 1993). As we perform Rate-Monotonic (RM)
assignment and preemptive scheduling, the real-time
system is feasible when the test given by expression 3
is verified.
∀i ∈ {1..m},U
i
≤ N
i
(2
1
N
i
− 1). (3)
3.4 Reconfiguration Time
We define in addition the reconfiguration time T
recon f
(Lakhdhar et al., 2016) as the sum of the time required
to add/remove tasks (i.e., time spent by the system
to jump from one implementation to another) and the
time required for task’s migration. The time for task’s
migration refers to the period of time required for a
task to move from one core to another when the sys-
tem load a new implementation. Thus, we define the
reconfiguration time as follow:
T
recon f
= (A + B) ∗ T
cost
+C ∗ T
migration
(4)
Where A is the number of the deleted tasks, B is
the number of created tasks, T
cost
is the spent time to
delete/add a task, C is the number of migrated tasks
and T
migration
is the time spent to migrate from a core
to another. One objective of the present work is to
reduce the reconfiguration time T
recon f
of the multi-
core reconfigurable real-time system with the aim to
improve its reactivity.
A New Approach for Optimal Implementation of Multi-core Reconfigurable Real-time Systems
91
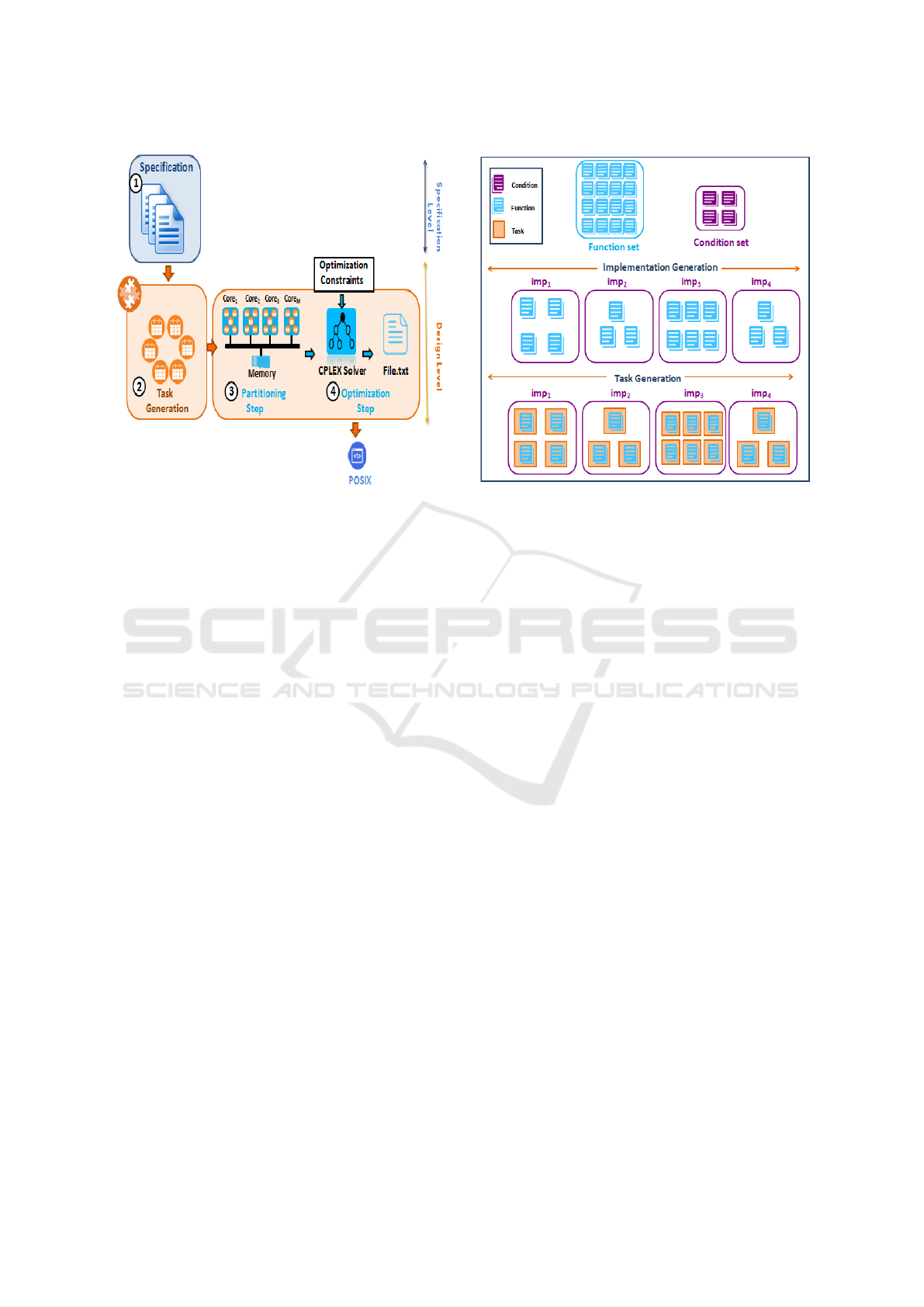
Figure 2: Process overview.
4 PROPOSED APPROACH
In this section, we present the full working process
used in this paper. As shown in Figure 2, the pro-
posed process is composed of four main phases: (i)
Specification, (ii) Task generation, (iii) Partitioning,
and (iv) Optimization.
4.1 System Specification
In the specification level, the designer provides the
specification model which defines (i) the reconfigu-
ration conditions, (ii) the functions that must be ex-
ecuted under a considered condition. Each function
is defined by a set of temporal parameters, and (iii)
the set of cores. This model presents the input of the
generation task step.
4.2 Task Generation
In this step, we aim to generate the initial task model
from the specification model. As shown in Figure 3,
this step is carried out in two sub-steps: (i) the gen-
eration of implementation sets from the condition sets
and the assignment of functions to the appropriate im-
plementation, and (ii) the generation of the task model
from the function sets, such that each function is as-
signed to a task which will take the same parameters
of the corresponding function (i.e., in this step, the
task number is equal to the function number). Let us
note that for the generation of this model, the real-
time feasibility is not considered.
Figure 3: Example Of Initial Task Model.
4.3 Task Partitioning
The partitioning of tasks into multiple cores must con-
sider real-time feasibility. Under the hypotheses con-
sidered in this paper, the partitioning corresponds to
an RM (Wang et al., 2014) scheduling problem re-
lated to periodic tasks. Each generated task must be
affected to a specific core, then in each core, we run
a local scheduler. This partitioning is characterized
by (i) no migration at run time (i.e., in a given im-
plementation a task must always run on a given core),
(ii) the possibility of applying end-to-end worst case
response time analysis, and (iii) off-line core assign-
ment (Tindell and Clark, 1994). The basic principles
of an RM-based partitioning heuristic are:
1. Order tasks according to RM policy,
2. Do task assignment according to their order,
3. For each task, look for an available core, by apply-
ing one of the following policies (Singhoff, 2014),
• Best Fit policy: for each task i, we start with
core j = 0 and assign task i on the core on which
the feasibility test is true and on which the pro-
cessor utilization factor has the highest value
• First Fit policy: for each task i, we start with
core j = 0 and assign task i on the first core on
which the feasibility test (expression 3) is true.
In this paper, we use the First Fit policy.
4. Stop when all tasks are assigned.
Algorithm 1 that illustrates this step considers as in-
puts: the implementations, tasks and the cores set. It
generates as output the partitioning task model.
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
92

Algorithm 1: Partitioning Task Model.
Input:
- Imp: Implementation set
- Task: Task set
- Core: Core set
Output:
- PartTask: Partitioning Task Model
1 Notations:
2 - m: implementation number
3 - N
i
: Number of tasks in the implementation i.
4 - M: Core number
5 for i ← 0 to m do
6 /*** Task Index ***/
7 j ← 0
8 /*** Core Index ***/
9 k ← 0
10 for j ← 0 to N
i
do
11 for k ← 0 to M do
12 if Faisabilty is true then
13 AssignTask[ j]toCore[k]
14 PartTask[ j][k] = Core[k]
15 else
16 k + +
17 return PartTask
4.4 Optimization Step
In order to ensure a reliable implementation of the
multi-core reconfigurable real-time system from the
initial task model and the partitioning task model tak-
ing into consideration the different constraints (Figure
2) (Real-time, no migration, energy), we propose in
this section a MILP model which consists of a linear
objective function to be optimized and a set of linear
inequalities (constraints).
4.4.1 Variable Definition
Let (i) Merge
jq
be a boolean variable used to men-
tion whether two tasks τ
j
and τ
q
are merged such that
Merge
jq
is equal to 1 if task τ
j
and task τ
q
are merged,
the merge corresponds to the situation in which τ
j
ab-
sorbs τ
q
, to be deleted from the model, (ii) x
js
be a
boolean variable used to mention if τ
j
is executed in
core s. Thus if the value of x
js
is equal to 1, then the
corresponding task τ
j
is running in core s, (iii) y
i j
be
a boolean variable used to mention if τ
j
is in the im-
plementation i, (iv) T be the set of period of N task,
(v) C
new
i j
be the new WCET of the task τ
j
in imp
i
,
(vi) T
new
i j
be the new period of the task τ
j
in imp
i
,
(vii) µ
jq
be a binary variable where µ
jq
= 1 when τ
q
is
executed before τ
j
.
4.4.2 Objective Function
maximize
∑
j,q∈{0..N}
Merge
jq
−
∑
i∈{1..m}
∑
j∈{0,N}
E
i j
(5)
The expression 5 defines the objective function. It
aims to maximize the number of merges while mini-
mizing the total energy consumption.
4.4.3 Merging Situation Constraints
The constraints 6 and 7 introduce the merging condi-
tion such as the two tasks τ
j
∈ ζ
s
and τ
q
∈ ζ
s
will be
merged if they have the same period.
∀ j, q ∈ {1..N} s ∈ {1..M}
i f (T
j
∗ x
js
− T
q
∗ x
qs
= 0) then Merge
jq
= 1; (6)
i f (T
j
∗x
js
−T
q
∗x
qs
<> 0) then Merge
jq
= 0; (7)
The constraint in 8 is used to avoid a non-meaningful
situations which corresponds to the merge of a task
already merged i.e., ∀ j, q,r ∈ {1..N},
Merge
jq
≤ 1, , q, r 6= j, Merge
jq
+ Merge
r j
≤ 1 (8)
4.4.4 Real-time Constraints
In each implementation, every pair of tasks ∀ j, q ∈
{1. . . N} τ
j
and τ
q
, we should respect the constraints
9 and 10 to ensure that only one task will be executed
at a single time. ∀i ∈ {1 . . . m}
s
i j
− s
iq
>= C
new
iq
− M ∗ µ
jq
(9)
s
iq
− s
i j
>= C
new
i j
− M ∗ (1 − µ
jq
) (10)
where C
new
i j
and C
new
iq
are the WCET of the tasks τ
j
and τ
q
. Constraints 4.4.4, 12 , and 13 give the com-
putation formula of C
new
i j
.
If a task τ
j
∈ imp
i
does not be merged with any task in
all implementations, the WCET of τ
i
does not change.
∀ j ∈ {1..N} ∀i ∈ {1..m}
i f (
∑
q∈1..N
Merge
q j
+
∑
r∈1..N
Merge
jr
= 0) then C
new
i j
= C
i j
;
(11)
Else if a task τ
j
is merged with another task in
the same implementation or not, the WCET of τ
j
is
calculated in two cases:(i) the task τ
j
and τ
q
are in
the same implementation, so the resulting WCET is
the sum of C
i j
and C
iq
, and (ii) the task τ
j
and τ
q
are
not in the same implementation, so the resulting task
has two different WCETs in the two implementations.
Constraints 12 , and 13 allow to compute the resulting
WCET in the two cases. ∀ j, q ∈ {1..N} i, l ∈ {1..m}
i f (Merge
jq
+ y
i j
+ y
l p
= 3) then C
new
i j
= C
i j
+C
lq
and C
new
lq
= 0; (12)
A New Approach for Optimal Implementation of Multi-core Reconfigurable Real-time Systems
93

i f (Merge
jq
+ y
i j
+ y
l p
= 2) then C
new
i j
= C
i j
and C
new
lq
= C
lq
; (13)
Constraint 14 ensures the feasibility of the system,
∀i ∈ {1..m}:
U
i
≤ N(2
1
N
− 1) (14)
where U
i
is given by
U
i
=
N
∑
j=1
C
new
i j
T
new
i j
(15)
Where T
new
i j
is computed as follow: ∀ j, q ∈
{1..N} i, l ∈ {1..m}
i f (Merge
jq
+ y
i j
+ y
l p
= 3) thenT
new
i j
= T
i j
and T
new
lq
= 0; (16)
i f (Merge
jq
+ y
i j
+ y
l p
= 2) then T
new
i j
= T
i j
and T
new
lq
= T
lq
; (17)
The start time should respect Constraint 18 i.e.,
∀ j ∈ {1..N}, ∀i ∈ {1..m}, s
i j
>= r
i j
(18)
4.4.5 Energy Constraints
E
i j
= K
∑
j∈{1,N}
C
n
η
2
j
(19)
The energy consumption’s equation is fractional,
thus we simplify this program in order to be inter-
pretable by using the CPLEX solver that maximizes
the reduction factor η
j
which is inversely proportional
to the energy consumption as defined in Section 3.
The objective function becomes
Maximise
∑
j,q∈{1,N}
Merge
jq
+
∑
i∈{1,m}
∑
j,q∈{0,N}
x (20)
To ensure the no simultaneous execution of tasks
the constraints 9 and 10 become respectively 21 and
22: ∀ j, q ∈ {1 . . . N} τ
j
and τ
q
∀ i ∈ {1. . . m}
s
i j
− s
iq
>= C
n
∗ η
q
− M ∗ µ
jq
(21)
s
iq
− s
i j
>= C
n
∗ η
j
− M ∗ (1 − µ
jq
) (22)
∀i ∈ {1..m}, j ∈ {1..N}
To ensure that the start time is always greater than
the release time, Constraint 23 is considered:
s
i j
>= r
i j
(23)
We limit the value of x by Constraint 24
x ≤ η
j
(24)
The proposed approach allows to manually gen-
erate the code from the optimized task model. The
optimized task model has properties providing infor-
mation on (i) the core set, (ii) the implementation set,
(iii) the task set, (iv) the function set, (v) the task
assignment, and (vi) the scheduling order. For each
task in the optimized task model, we implement a
POSIX thread by using the POSIX pthread. In the
POSIX code, the assignment of the tasks to the core is
giving by stick this thread system, which allow mov-
ing from implementation to another, following well-
defined conditions (i.e., user requirements).
5 CASE STUDY
In this section, we illustrate the proposed approach
through a classical case study: a Global Positioning
System (GPS) (Lakhdhar et al., 2016).
5.1 Specification Level
The GPS is used to define the position of an object
on a plan or a map using the information provided
via radio signals by the associated satellites. In the
GPS, the satellite sends to the terminal an encrypted
signal containing various information relevant to the
location and timing. The terminal collects and con-
verts radio signals received into information about the
position, speed and time (Lakhdhar et al., 2016). In
order to illustrate the proposed approach, we have en-
riched and extended this case study by introducing
two modes: (i) default mode which consists of a de-
fault use of GPS, and (ii) secure mode which repre-
sents a restricted use of GPS with safety requirements.
The software architecture of the studied applica-
tion is composed of seven functions in default mode
and of eight functions in the secure mode such that
every function is characterized by a period, a WCET
and an energy consumption (Table 1). It is mapped
to a preemptive execution platform composed of one
processor which contains two cores C
1
and C
2
. A tab-
ular description of the specification model is given in
Table 1.
Table 1 depicts two execution modes Default
Mode and Secure Mode. Each mode is characterized
by a set of functions defined by a set of timing param-
eters.
5.2 Initial Task Model
The second step consists in generating the implemen-
tations and their tasks. Proceeding from the specifi-
cation model, for each condition we generate an im-
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
94

Table 1: Specification Model.
Execution
mode
Condition
Function
Name
Period
ms
WCET
ms
Energy
mW
Default Sec=Desabled
F
1
: ControlBase 100 20 1687.5
F
2
: GpsSatellite 200 20 30
F
3
: Position 300 20 270
F
4
: Receiver 300 50 2031.25
F
5
: Decoder 400 40 5760
F
6
: TreatmentUnit 400 50 15000
F
7
: Encoder 500 30 15360
Secure Sec=Enabled
F
1
: ControlBase 100 20 1687.5
F
2
: GpsSatellite 200 20 30
F
0
3
: Position Secure 300 20 270
F
4
: Receiver 300 50 2031.25
F
5
: Decoder 400 40 5760
F
6
: TreatmentUnit 400 50 15000
F
7
: Encoder 400 50 15360
F
8
:AccessController 400 50 10800
plementation so we have two implementations. Then,
we assign each function to a task. The resulting task
model is given in Table 2 that shows two implementa-
tions which are composed of fifteen tasks. Each task
is characterized by the same real-time parameters of
the executed function.
Table 2: Initial Task Model.
Implementation Task
Period
ms
WCET
ms
Energy
mW
Default
τ
1
100 20 1687.5
τ
2
200 20 30
τ
3
300 20 270
τ
4
300 50 2031.25
τ
5
400 40 5760
τ
6
400 50 15000
τ
7
500 30 15360
Secure
τ
8
100 20 1687.5
τ
9
200 20 30
τ
10
300 20 270
τ
11
300 50 2031.25
τ
12
400 40 5760
τ
13
400 50 15000
τ
14
400 50 15360
τ
15
400 50 10800
5.3 Partitioning Task Model
The next step consists in distributing the task model
into a specific multi-core architecture. The targeted
multi-core architecture contains 2 cores and a shared
memory. In order to assign the tasks to the cores, we
apply Algorithm 1. Table 3 presents the partitioning
task model.
Table 3: Partitioning Task Model.
Implementation Core Task
Period/
Deadline
ms
WCET
ms
Default
ζ
1
τ
1
100 20
τ
2
200 20
τ
3
300 20
τ
4
300 50
ζ
2
τ
5
400 40
τ
6
400 50
τ
7
500 30
Secure
ζ
1
τ
8
100 20
τ
9
200 20
τ
10
300 20
τ
11
300 50
ζ
2
τ
12
400 40
τ
13
400 50
τ
14
500 30
τ
15
600 50
For each implementation, we assign the tasks to
the appropriate core based on the feasibility tests. The
resulting partitioning task model represents the input
of the optimization step.
5.4 Optimized Task Model
Once the initial solution is defined, we process the op-
timization step. This step involves the execution using
CPLEX solver of the proposed linear program. We
model the input of this step as two matrices: “tasks to
implementation mapping matrix” (i.e., y) and “tasks
to core assignment matrix” (i.e., x). These two matri-
ces are defined as follows:
A New Approach for Optimal Implementation of Multi-core Reconfigurable Real-time Systems
95

y =
imp
1
imp
2
τ
1
1 0
τ
2
1 0
τ
3
1 0
τ
4
1 0
τ
5
1 0
τ
6
1 0
τ
7
1 0
τ
8
0 1
τ
9
0 1
τ
10
0 1
τ
11
0 1
τ
12
0 1
τ
13
0 1
τ
14
0 1
τ
15
0 1
ζ
1
ζ
2
τ
1
1 0
τ
2
1 0
τ
3
1 0
τ
4
1 0
τ
5
0 1
τ
6
0 1
τ
7
0 1
τ
8
1 0
τ
9
1 0
τ
10
1 0
τ
11
1 0
τ
12
0 1
τ
13
0 1
τ
14
0 1
τ
15
0 1
= x
The linear program generates the following Merge
matrix:
Merge =
0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 1 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 1 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
We note that the MILP program allows to merge the
tasks: (i) τ
1
with τ
8
, (ii) τ
2
with τ
9
, (iii) τ
3
with τ
4
, τ
10
and τ
11
, (vi) the task τ
5
with τ
6
, τ
12
and τ
13
, and (v)
τ
7
with τ
14
. The input matrices become:
y =
imp
1
imp
2
τ
0
1
1 1
τ
0
2
1 1
τ
0
3
1 1
τ
0
5
1 1
τ
0
7
1 1
τ
15
0 1
ζ
1
ζ
2
τ
0
1
1 0
τ
0
2
1 0
τ
0
3
1 0
τ
0
5
0 1
τ
0
7
0 1
τ
15
0 1
= x
The optimized task model is presented in Table 4.
Table 4: Optimized Task Model.
Implementation Core Task
Period
ms
WCET
ms
E
old
mW
E
new
mW
Default
ζ
1
τ
0
1
100 20 1687.5 1181.25
τ
0
2
200 20 30 21
τ
0
3
300 20 2301.25 1610.87
ζ
2
τ
0
5
300 50 20760 14532
τ
0
7
400 40 15360 10752
Secure
ζ
1
τ
0
1
100 20 1687.5 1181.25
τ
0
2
200 20 30 21
τ
0
3
300 20 2301 1610.87
ζ
2
τ
0
5
300 50 20760 14532
τ
0
7
400 40 15360 10752
τ
15
400 50 10800 7560
We note that the task number is reduced as well
as the energy consumption. Finally, we generate a
POSIX code from the optimized task model describ-
ing the GPS. Listing 1 gives an excerpt of the GPS
code. The role of the controller which corresponds to
the main function in Listing 1, is to switch from one
implementation to another under a considered condi-
tion.
1 # i n c l u d e <p t h r e a d . h>
2 v o i d ∗ F1 ( v o i d ∗ a r g ) ;
3 v o i d ∗ F2 ( v o i d ∗ a r g ) ;
4 . . .
5 / ∗ ∗∗∗∗∗ ∗∗∗ C o n t r o l l e r POSIX c o de ∗∗∗∗∗∗∗∗ ∗ /
6 i n t main ( v o i d ) {
7 p t h r e a d t t a u p r i m e 1 ;
8 p t h r e a d t t a u p r i m e 2 ;
9 p t h r e a d t t a u p r i m e 3 ;
10 / / D e f a u l t mode
11 p t h r e a d c r e a t e (& t a u p r i m e 1 , NULL, F1 , ( v o i d ∗ ) 1 0 0 ) ;
/ / C r a a t i o n o f t a u p r i m e 1 t h r e a d
12 p t h r e a d c r e a t e (& t a u p r i m e 2 , NULL, F2 , ( v o i d ∗ ) 2 0 0 ) ;
/ / C r a a t i o n o f t a u p r i m e 2 t h r e a d
13 p t h r e a d c r e a t e (& t a u p r i m e 3 , NULL, F3 , ( v o i d ∗ ) 3 0 0 ) ;
/ / C r a a t i o n o f t a u p r i m e 3 t h r e a d
14 . . .
15 s t i c k t h i s t h r e a d t o c o r e ( 1 ) ; / / a s s i g n t h r e a d 1 t o co r e
1 / /
16 p t h r e a d j o i n ( t a u p r i m e 1 , NULL) ;
17 s t i c k t h i s t h r e a d t o c o r e ( 1 ) ;
18 p t h r e a d j o i n ( t a u p r i m e 2 , NULL) ;
19 . . . . . .
20 s t i c k t h i s t h r e a d t o c o r e ( 2 ) ;
21 p t h r e a d j o i n ( t a u p r i m e 5 , NULL) ;
22 . . .
23 / / S e c u r e Mode
24 i f ( cnd=” Se c u r e ” ) {
25 p t h r e a d c r e a t e (& t a u p r i m e 1 , NULL, F8 , ( v o i d ∗ ) 1 0 0 ) ;
/ / C r a a t i o n o f t a u p r i m e 1 t h r e a d
26 p t h r e a d c r e a t e (& t a u p r i m e 2 , NULL, F9 , ( v o i d ∗ ) 2 0 0 ) ;
/ / C r a a t i o n o f t a u p r i m e 2 t h r e a d
27 . . . }
28 r e t u r n 0 ; }
29 . . .
30 v o i d ∗ F1 ( v o i d ∗ a r g )
31 { / / / }
32 / / c o r e i d = 0 , 1 , . . . n−1 , where n i s t h e s y s t e m ’ s
number o f c o r e s
33 i n t s t i c k t h i s t h r e a d t o c o r e ( i n t c o r e i d ) {
34 i n t nu m c or e s = s y s c o n f ( SC NPROCESSORS ONLN ) ;
35 i f ( c o r e i d < 0 | | c o r e i d >= n u m c o r e s )
36 r e t u r n EINVAL ;
37 c p u s e t t c p u s e t ;
38 CPU ZERO(& cp u s e t ) ;
39 CPU SET ( c o r e i d , &c p u s e t ) ;
40 p t h r e a d t c u r r e n t t h r e a d = p t h r e a d s e l f ( ) ;
41 r e t u r n p t h r e a d s e t a f f i n i t y n p ( c u r r e n t t h r e a d , s i z e o f (
c p u s e t t ) , &c p u s e t ) ; }
Listing 1: GPS POSIX code.
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
96

5
10
20
40
0
20
Number of implementation
Number of tasks
Reconfiguration time
T
Recon f
normal
T
Recon f
optimized
.
Figure 4: Evaluation of the Reconfiguration Time.
5
10
15
20
0
20
40
60
80
Number of tasks
Consumption Energy
E
old
E
new
.
Figure 5: Evaluation of the Energy Consumption.
5.5 Evaluation
In order to generalize the performance evaluation of
our strategy, we generate a random system with ran-
dom task set. The experiments are carried-out on In-
tel Core i5-4200U processor running at 2.8 GHz with
4GB of cache memory. The curve in Figure 4 shows
the variation of the reconfiguration time of the sys-
tem described in section 3 depending on the number
of tasks and the number of implementations.
In Figure 4 we compare the reconfiguration time
using the proposed approach with the normal recon-
figuration time. It can be seen that the proposed ap-
proach allows obtaining a lower reconguration time.
This is due to the task merging technique.
Figure 5 depicts the impact of our approach on the
total energy consumed by the system.
In this figure, we compute the energy consump-
tion and we compare it with the energy consumed by
the system before applying the proposed approach. It
is clear from this figure that we have obtained better
results.
0 20 40
10
20
30
Number of tasks
context switch(ms)
Context switch
normal
. Context switch
optimized
Figure 6: Evaluation of the Context switching.
We also compare in Figure 6 the context switching
of the proposed approach to the context switching be-
fore applying this approach in a randomly generated
system with a number of tasks that varies between 6
and 50. We note that this comparison shows the effi-
ciency of the proposed approach.
The originality of this paper is manifested in the fact
that the proposed approach allows the implementation
of the multi-core reconfigurable real-time systems by
reducing: (i) the task number, (ii) the energy con-
sumption, (iii) the reconfiguration time , (iv) the time
overhead in terms of context switching, and (v) the
redundancies between implementations.
6 CONCLUSIONS
In this paper, we have described a process for the
semi-automatic synthesis of an energy-aware POSIX
code for multi-core reconfigurable real-time systems.
Firstly, we showed how from the input specification
model we generate an initial task model, assign tasks
to the cores using partitioning scheduling while meet-
ing timing properties. Secondly, in order to reduce
the time overhead, energy consumption and the re-
dundancies between the implementations caused by
the huge number of tasks, we proposed a MILP for-
mulation for the problem, which can find the opti-
mal solution for the proposed system model. Thirdly,
we generate the optimized POSIX code from the op-
timized task model. We evaluated the performance
of the proposed approach by comparing the obtained
results against the performance of the system before
applying the approach. As a future work, we want (i)
to introduce other criteria to be optimized, and (ii) to
fully automate the proposed approach by introducing
transformation techniques.
A New Approach for Optimal Implementation of Multi-core Reconfigurable Real-time Systems
97

REFERENCES
Burns, A. and Wellings, A. (2009). Real-Time Systems and
Programming Languages: Ada, Real-Time Java and
C/Real-Time POSIX. Addison-Wesley Educational
Publishers Inc, USA, 4nd edition.
Chniter, H., Jarray, F., and Khalgui, M. (2014). Combinato-
rial approaches for low-power and real-time adaptive
reconfigurable embedded systems. In Proc. Pervasive
and Embedded Computing and Communication Sys-
tems 4th, pages 151–157.
Faragardi, H. R., Lisper, B., and Nolte, T. (2013). To-
wards a communication-efficient mapping of autosar
runnables on multi-cores. In Emerging Technologies
& Factory Automation (ETFA), IEEE 18th Conference
on, pages 1–5. IEEE.
Funk, S. and Baruah, S. (2005). Task assignment on uni-
form heterogeneous multiprocessors. In Real-Time
Systems, Proceedings. 17th Euromicro Conference on,
pages 219–226. IEEE.
Geer, D. (2005). Chip makers turn to multicore processors.
Computer, 38(5):11–13.
Geismann, J., Pohlmann, U., and Schmelter, D. (2017). To-
wards an automated synthesis of a real-time schedul-
ing for cyber-physical multi-core systems. In MOD-
ELSWARD, pages 285–292.
Khan, M. and Hafiz, G. (2014). Simulation of multi-core
scheduling in real-time embedded systems. Master’s
thesis.
Klein, M. H., Ralya, T., Pollak, B., Obenza, R., and Har-
bour, M. G. (1993). Analyzing complex systems.
In A Practitioners Handbook for Real-Time Analysis,
pages 535–578. Springer.
Lakhdhar, W., Mzid, R., Khalgui, M., and Tr
`
eves, N.
(2016). Milp-based approach for optimal implemen-
tation of reconfigurable real-time systems. In Proc.
International Joint Conference on Software Technolo-
gies (ICSOFT) - Volume 1: ICSOFT-EA, Lisbon, Por-
tugal, July 24 - 26, 11th, pages 330–335.
Lakshmanan, K. S. (2011). Scheduling and Synchroniza-
tion for Multi-core Real-time Systems. PhD thesis,
Carnegie Mellon University Pittsburgh, PA.
Lei, H., Wang, R., Zhang, T., Liu, Y., and Zha, Y. (2016). A
multi-objective co-evolutionary algorithm for energy-
efficient scheduling on a green data center. Computers
& Operations Research, 75:103–117.
Liu, C. L. and Layland, J. W. (1973). Scheduling algo-
rithms for multiprogramming in a hard-real-time en-
vironment. Journal of the ACM (JACM), 20(1):46–61.
Monot, A., Navet, N., Bavoux, B., and Simonot-Lion,
F. (2012). Multisource software on multicore auto-
motive ecuscombining runnable sequencing with task
scheduling. IEEE Transactions on Industrial Elec-
tronics, 59(10):3934–3942.
Polakovic, J., Mazare, S., Stefani, J., and David, P. (2007).
Experience with safe dynamic reconfigurations in
component-based embedded systems. In Proceedings
of the 10th International Symposium on Component-
Based Software Engineering (CBSE), USA, pages
242–257. Springer.
Saidi, S. E., Cotard, S., Chaaban, K., and Marteil,
K. (2015). An ilp approach for mapping autosar
runnables on multi-core architectures. In Proceed-
ings of the Workshop on Rapid Simulation and Perfor-
mance Evaluation: Methods and Tools, page 6. ACM.
Singhoff, F. (2014). Real-time scheduling analysis.
Tindell, K. and Clark, J. (1994). Holistic schedulability
analysis for distributed hard real-time systems. Micro-
processing and microprogramming, 40(2-3):117–134.
Vulgarakis, A., Shooja, R., Monot, A., Carlson, J., and
Behnam, M. (2014). Task synthesis for control appli-
cations on multicore platforms. In Information Tech-
nology: New Generations (ITNG), 2014 11th Interna-
tional Conference on, pages 229–234. IEEE.
Wang, H., Shu, L., Yin, W., Xiao, Y., and Cao, J.
(2014). Hyperbolic utilization bounds for rate mono-
tonic scheduling on homogeneous multiprocessors.
IEEE Transactions on Parallel and Distributed Sys-
tems, 25(6):1510–1521.
Wang, W., Camut, F., and Miramond, B. (2016). Generation
of schedule tables on multi-core systems for autosar
applications. In Design and Architectures for Signal
and Image Processing (DASIP), Conference on, pages
191–198. IEEE.
Yehia, K., Safar, M., Youness, H., AbdElSalam, M., and
Salem, A. (2011). A design methodology for sys-
tem level synthesis of multi-core system architectures.
In Electronics, Communications and Photonics Con-
ference (SIECPC), Saudi International, pages 1–6.
IEEE.
Yi, Y., Han, W., Zhao, X., Erdogan, A. T., and Arslan,
T. (2009). An ilp formulation for task mapping and
scheduling on multi-core architectures. In Design, Au-
tomation & Test in Europe Conference & Exhibition,
pages 33–38. IEEE.
ENASE 2018 - 13th International Conference on Evaluation of Novel Approaches to Software Engineering
98
