Positional Accuracy Assessment of the VGI Data from

OpenStreetMap

Case Study: Federal University of Bahia Campus in Brazil

Elias Nasr Naim Elias, Vivian de Oliveira Fernandes and

Mauro José Alixandrini Junior

Cartolab – Cartography Laboratory, Transport Engineering and Geodesy Department,

Federal University of Bahia, Polytechnic School, Rua Aristides Novis nº 02, Salvador - Bahia, Brazil

Keywords: Quality Control, OpenStreetMap, VGI.

Abstract: Geographic information is a crucial part of the daily lives of billions of people and is constantly used in

decision-making processes for geospatial problems. With the increasing dissemination of information

technology in society there has been a great gain in terms of the quantity and quality of spatial information

available to internet users. This paper evaluates the positional quality of data from the Open Street Map

platform (OSM) and uses data from a cartographic accuracy standard from the same region for this

evaluation. The methodology section presents the methodology proposed by the Brazilian PEC-PCD which

divides cartographic products into accuracy classes. For the data evaluated, the vectors from the OSM

obtained better accuracy in the 1:30,000 scale.

1 INTRODUCTION

Rapid computational technological advances have

made it so that users of cartographic products do not

only view these products, but have wanted to

become part of the production of the information

contained in them and of their dissemination and

democratization through the internet. This level of

involvement became possible beginning with the

establishment of the concept of Web 2.0, created by

O'Reilly (2007). According to Cormode and

Krishnamurthy (2008), Web 2.0 is defined as a

cybernetic phenomenon where users become

fundamental players in the generation and

management of certain information, rather than

simply consumers of said information.

In this context, the concept of Volunteered

Geographic Information (VGI), which, according to

Bravo (2014), is a system with the features described

where the maps that were once developed by users

with a certain amount of technical training in

cartography begin instead to be created by

individuals who have access to a computer and

internet. Thus, VGI systems allow the users of this

tool to collect and publish geographic information

and even validate the information posted by other

users (Goodchild, 2007).

Currently, VGI data is stored and accessed on

online platforms that allow users to perform such

operations. Despite the efficiency with which these

products are available and the constant updating of

the information with which individuals make

changes to the geographical setting, VGI data

sources do not constitute model cartography, since

quality parameters for the maps presented are still

provided. With the premise that the data is current

and understanding this to be one of the major

problems with high quality maps, this work consists

in evaluating positional accuracy, one of the quality

parameters of the study area.

2 THEORETICAL REFERENCES

2.1 Systems of Volunteered Geographic

Information

The development of computational technology in the

most diverse areas of the science has brought new

perspectives to cartography regarding the production

and handling of spatial information since these

processes can now occur through any individual who

has access to a computer and the internet (Ganapati

et al, 2011). Thus, according to Goodchild (2007),

Elias, E., Fernandes, V. and Junior, M.

Positional Accuracy Assessment of the VGI Data from OpenStreetMap.

DOI: 10.5220/0006707702310238

In Proceedings of the 4th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2018), pages 231-238

ISBN: 978-989-758-294-3

231

there are systems that enable everyday users, who

are not skilled in spatial data production and

manipulation techniques, to construct and elaborate

products that represent the geographic space

according to their perceptions. The dissemination of

VGI (Volunteered Geographic Information) systems

has modified perceptions of cartography, making it

so that certain information about the environment is

attributed through individuals’ perceptions. In

addition, VGI data has been handled, due to the

constant updating of the products generated in its

platforms, so that it can feasibly be used in

applications for model cartography that feeds

official cartographic basemaps.



Goodchild (2007) also states that activities

involving VGI platforms came from the combination

of the popularization of online maps and the internet

itself, the emergence of Web 2.0, and the growth of

crowdsourcing platforms. Linked to this

combination, the technological advances in

communication tools that allow mobile connection

with internet data has favored the sharing of data in

real time and the consequent localization and

obtaining of information in an automated way

through receivers and GPS devices on tablets and

smartphones.

2.1.1 OpenStreetMap

The goal of the OSM project is to create a free and

editable world map (Ramm et al. 2011). Within the

project volunteers, amateurs and professionals from

different social worlds act as sensors (Flanagin and

Metzger 2008) and collect geographic data. This

bottom up process stands in contrast with the

traditional centralized procedure of collecting

geographic data (Goodchild 2007). The motivation

for contributing to OSM varies heavily: it ranges

from self-expression over manifestation and

representation of people’s online identity to a simple

fun factor. Meaningful extracurricular activities,

interesting technologies and a fascinating general

project development are further motivational reasons

(Budhathoki 2010). In general, data for OSM can be

derived from multiple sources and edited and

imported by means of different freely available

editors. The most popular editors are the Java

OpenStreetMap Editor (JOSM) or the webbased

JavaScript editor iD. The classic approach is the

collection of spatial data with portable and GPS

enabled devices. In addition, several companies such

as Aerowest, Microsoft Bing (Bing 2010) or Yahoo!

released, at least temporarily, their aerial images for

the OSM project. The community is allowed to use

these images as a base layer for tracing geographic

features, such as for example buildings, forests or

lakes. The contributors’ local knowledge is also a

valuable source of geographic Based on Barron et al

(2014) the goal of the OSM project is to create a free

and editable world map Ramm et al.(2011). Within

the project volunteers, amateurs and professionals

from different social worlds act as sensors Flanagin

and Metzger (2008) and collect geographic data.

2.2 Quality Control

According to Barron (2014) quality in general plays

a key role when working with all kinds of geodata,

especially in data production and assessment

(Veregin 1999) or exchange (Goodchild 1995). This

is especially the case with OSM data, as the

contributors are not faced with any restrictions

during the data collection and annotation process. In

the field of geo-information, the principles of the

“International Organization for Standardization”

(ISO) can be taken into account for quality

assessment. The ISO 19113 standard describes

general principles of geodata quality and ISO 19114

contains procedures for quality evaluation of digital

geographic datasets. The ISO 19157 “Geographic

Information: Data Quality” standard currently under

development, aims to harmonize all standards

related to data quality and revises the

aforementioned standards. The quality of spatial data

can be evaluated with the help of following elements

of ISO 19113:

• “Completeness”: describes how complete a dataset

is. A surplus of data is referred to as “Error of

Commission”, a lack of data in contrast as “Error of

Omission”.

• “Logical Consistency”: declares the accuracy of

the relations manifested within a dataset. This

element can be further subdivided into “intra-theme

consistency” and “inter-theme consistency”.

• “Positional Accuracy”: defines the relative and

absolute accuracy of coordinate values.

• “Temporal Accuracy”: the historical evolution of

the dataset.

• “Thematic Accuracy”: describes the accuracy of

the attributes assigned to a geometry. However,

OSM data quality heavily depends on the purpose

for which the data will be deploye.

2.2.1 Positional Accuracy

According to Nero (2017) the control quality process

is quite well-known, having been applied to

positional accuracy of spatial data as in Ariza-López

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

232

et al (2001), Ariza-López (2002a), Atkinson-Gordo,

Ariza-López and García-Balboa (2007) and Cintra

and Nero (2015), generating mappings with different

point percentages with errors in a given coordinate,

above (or below) a limit established by a specific set

of standards (CAS-Circular Accuracy Standard,

LMAS-Linear Accuracy Standard, among others).

Quality control guidelines for cartography are

employed by several countries. The standards set

by CONCAR (2011, 2016 - Brazilian Commission

of Cartography), for example, allow up to 10% of

the points to present an error greater than 0.5mm, in

the scale of B class of cartographic documents.

3 METHODOLOGY

The methodology used in this article is the same as

that applied in the evaluation of cartographic

mapping in Brazil based on the cartographic quality

standard parameters for digital products - PEC-PCD

(2011). In June 2011, the Technical Specifications

for the Acquisition of Geospatial Vector Data

(ETADGV) were created by the National

Commission of Cartography (CONCAR). This

document was based on aspects of England’s

Ordnance Survey. The area included in the study is

Bahia Federal University – UFBA. In 2009 a

topographic planimetric and altimetric survey was

done of the university area, obtaining as its final

product a topographic plan with a scale of 1:500 and

representation in the scale of 1:2000. Thus, from this

cartographic basemap, this same area was obtained

on the OSM online platform. After obtaining this

information, it was then possible to identify

equivalent features between these two cartographic

products, making it possible to perform comparative

analyses to evaluate the positional accuracy of OSM

in the vicinity of the university

3.1 Determining the Number of

Samples

The verification of accuracy with respect to the

characteristics of the features located in a given

cartographic product is done differently in every

country. According to Nogueira Jr. (2003) this

difference is due to the variations and peculiarities

of each locality such as the spatial division, scale,

economic situation, etc.

According to Merchant (1982), the accuracy of a

map must be verified by comparing at least 20 points

of the terrain coordinates to the cartographic product

generated.

The sampling process depends on the type of

information that is to be analyzed. In other words,

when defining the samples to be used, it is necessary

to ensure that they will correctly represent the

attributes of the statistical population, validating

their application.

Although it is extremely important to determine

sample size for the purposes of cartographic

analysis, most methods for geometric quality

assurance do not present recommendations for

sample calculation (Nogueira Jr., 2003).

The minimum size of samples to be used can be

calculated from the expression (01) where it is

determined by means of a finite population with

estimation of the population mean , maximum

admissable error  and confidence level 1  )

in which the parameters are to be defined.

n





















²²

(1)

where:

n = sample size;

Z = confidence interval;

N = population size;

 = sample standard deviation;

 = sample relative error.

3.2 Selecting the Equivalent Features

Using the initial data, the first analyses were based

on the observation of features located in the

topographic plan that could be easily identified in

the OSM vector files. This made it possible to

extract the coordinates of these elements, allowing

the necessary comparisons to be made. Figure 1

shows, respectively, the identification of a certain

point in the topographic plan and its equivalent

feature in the online platform of the OSM. This

point corresponds to the vertex of a building of the

University Restaurant (RU) located in UFBA’s

Ondina campus.

Figure 1: Homologous feature: Topographic plan and

Online Platform - OSM.

Positional Accuracy Assessment of the VGI Data from OpenStreetMap

233

3.3 Determining Positional Accuracy

According to Merchant (1982), the statistical

analysis for determining planimetric positional

accuracy is composed of two phases: trend analysis

and precision analysis.

3.3.1 Trend Analysis

According to Nogueira Jr. (2003), in a given

cartographic product the trend analysis of its

elements consists of statistical analyses between the

real world reference coordinates of certain features

obtained by a given survey method  and the

coordinates of the chart to be evaluated 



). The

main purpose of this analysis is to verify the

existence of trends in errors in some direction in the

chart. First it is necessary to calculate the

discrepancies between the coordinates as follows:

∆Xi  Xi  Xi



2

It is worth emphasizing that the discrepancies

between the coordinates and the statistical analyses

must be performed in relation to the two elements

that make up the pair (latitude and longitude), thus

making it possible to determine the direction of the

error in the chart studied. Knowing the data

concerning the discrepancies between the

coordinates, as well as the sample size used for the

statistical analyses, the average can be calculated

∆



as well as the standard deviation 

∆

)

in order to determine the trend in the chart. In order

to carry out the trend test, the following hypotheses

are used:



Ho:∆X



0(3)



Hi:∆X



0 (4)

Knowing the hypotheses, the next step is the

calculation of the sample statistic "t" in order to

determine if the result is in the range of acceptance

or rejection of the null hypothesis. The sample "t"

value is obtained as follows:

t





∆





∆



√

n (5)

where is the number of samples used.

For the analysis of the value found for "t" it is

necessary to associate it with a tabulated value, thus

determining the initial analysis of whether or not to

reject the null hypothesis. Student's t-test was used

in this way, associated with the number of samples

(n) and the significance level. The confidence

interval for Student’s t-test is found as follows:



t

;







(6)

Where the "t" Student tabulated value has (n - 1)

degrees of freedom at a significance level . Thus,

if the calculated modulus for the sample "t" is less

than the value of "t", the null hypothesis is accepted

(∆



0). In other words the chart can be considered

free of significant trends. However if the inequality

is not satisfied, the null hypothesis is rejected (∆





0) and the chart studied may present significant

errors at a certain confidence level. According to

Galo and Camargo (1994) the fact that there is a

trend indicates possible errors in a certain direction

due to a number of factors. However if the

discrepancies and the direction of the errors are

known, their effect can be minimized by performing

the procedure of subtracting its value in each

analyzed coordinate of the chart.

3.3.2 Accuracy Analysis

According to Nogueira Jr. (2003), the accuracy

analysis consists of the comparison of the standard

deviation found using the discrepancies between the

basemap coordinates and the chart coordinates with

the standard error (SE) evaluated using the

Cartographic Accuracy Standard (PEC) in relation to

the class in which it is desired to evaluate the

accuracy of the chart.

The hypothesis test formulated for the accuracy

analysis is as follows:

Ho:S



∆

σ



x (7)

Hi:S



∆

σ



x (8)

Where ² corresponds to the standard deviation

or standard error expected according to the class of

the chart in which analysis is desired. Assuming the

value of the result generated as being standard error

and considering it to be equivalent in the determined

horizontal components:

σx  EP/

√

2 (9)

With these initial parameters the chi-square test

is applied in order to use statistical methods and

determine the class of the chart. The chi-square

sample is as follows:

X







n1





∆

/σ²x (10)

From this calculation the analysis of the

statement regarding the hypothesis test is performed

where the value of the chi-square table is used

according to the following condition:

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

234

X²



X²

;

(11)

Where the value of the Chi-Square table has (n-

1) degrees of freedom and a confidence interval .

In this way, if the above expression is satisfied,

the null hypothesis that the chart meets the

established class according to its accuracy is

accepted. Otherwise the null hypothesis that the

chart meets the established class is rejected. The

analysis is performed until the expression is met,

characterizing the chart’s class according to its

accuracy.

3.3.3 Application of the PEC-PCD

To classify the cartographic product it is necessary

to determine the quality established by the samples

used, where such classifications are directly related

to the scale in which it is represented. According

to Merchant (1982), the determination of collected

samples (reference points) must occur from methods

in which the error does not exceed 1/3 of the

standard error expected for the class of the chart

under analysis. Table 1 below shows the

classification of the Planimetric Cartographic

Accuracy Standard for Digital Cartographic

Products (PEC-PCD) established in the Technical

Specification for the Acquisition of Vector

Geospatial Data (ET-ADGV, 2011).

Table 1: PEC-PCD.

PEC

(1984)

PEC-

PCD

(2011)

Planimetric

PEC

Planimetric

Standard

Error

- A

0.28 mm X

Scale Factor

0.17 mm X

Scale Factor

A B

0.5 mm X Scale

Factor

0.3 mm X Scale

Factor

B C

0.8 mm X Scale

Factor

0.5 mm X Scale

Factor

C D

1.0 mm X Scale

Factor

0.6 mm X Scale

Factor

4 RESULTS AND DISCUSSION

4.1 Determining the Number of

Samples

The calculations used to determine the number of

samples were developed from equation (1). For the

aforementioned analyses, a confidence interval (Z)

of 99.50% was used, and the statistical sample

population (N) was calculated using the software

Dxf2xyz v.2.0, obtaining a total of approximately

24,000 elements for the Topographic Plan of the

UFBA campuses, this value being applied in said

calculations.

In carrying out the calculations the relative

sampling error () was considered to be 1/5 of the

sample standard deviation (), using the following

equation for the calculation of the number of

samples:

n













/



²

(12)

According to equation 12, the number of

required samples for the UFBA campuses totals a

minimum of 24 samples to be used as control points.

4.2 Obtaining Equivalent Points

The trend and accuracy analyses of this numerical

data should be evaluated together in the cartographic

product, since the trend analysis, carried out by

means of the student t test, allows for the evaluation

of the accuracy of the discrepancies around the zero-

mean. That is, how accurate is the sample of points

collected on the OSM platform in relation to the

model cartographic product? The accuracy analysis,

performed through the chi-square test, makes it

possible to evaluate the accuracy of the samples

considering the dispersion (deviation) of these

around a certain mean value and, by means of the

statistical calculations, assign a scale factor that fits

the results obtained.

Tables 2 and 3 show, respectively, the mean and

standard deviation values found for the

discrepancies in the north and east directions. In the

literature, some authors perform the resulting

calculation to validate the values obtained using the

PEC-PCD. However, in this paper, for a better

analysis of the information contained in the map, it

was decided to arrange the results separately for the

two directions evaluated, thus allowing a better

analysis of the results.

Table 2: Mean of Discrepancies.

Mean Deviation

Delta (E) -0.197

Delta (N) -1.680

Table 3: Standard Deviation of Discrepancies.

Standard Deviation

Delta (E) 2.398

Delta (N) 3.918

Positional Accuracy Assessment of the VGI Data from OpenStreetMap

235

This analysis can be verified by observing the

values of the discrepancies individually for each

point of the sample. For example, in the north

direction the lowest sample value was -4.49 m and

the highest value was 4.59 m, results shown in tables

2 and 3. In the samples from the eastern direction,

discrepancies were also observed, since the lowest

value of discrepancy was -7.61 m and the highest

value was 7.09 m. Some aspects of the platform are

directly related to the heterogeneity obtained in the

discrepancies between these samples, explaining the

results obtained. The numerical data found for these

discrepancies reflects that the scanning of elements

by users in the Bing image that feeds the OSM

platform occurred at different times, since we do not

know in which update the images were inserted or

the positional accuracy parameters that feed them.

Evidence for this analysis was found by checking

the year of digitization of some elements of the

study area, noting that there are large temporal

discrepancies in the vector files of this platform.

Some examples may be cited: Ondina Multi-Sport

Square – Last edited: 2013; Federação Classroom

Pavilion I Parking Lot – Last edited: 2015; Access

road to the Ondina Main Gate – Last edited: 2015;

Geosciences Institute – Last edited: 2016; Ondina

Arts Square – Last edited: 2017. This temporal

variation in the elements contained in the study area

and the lack of knowledge about the images in

which the scans were triggered make it is possible to

indicate certain factors that contribute to this

heterogeneity. In addition, the study area, the UFBA

campuses, which corresponds to an area of 300,000

m², has undergone extensive changes since 2009 in

the elements that make up this setting due to the

university remodeling project, with contributions

increasing in recent years, showing vector files

obtained from different sources and dated to

moments throughout a wide time span.

4.3 Trend Analysis

The discrepancies found for the established samples

allowed the trend analysis for the same and the

identification of the accuracy of these values around

the zero mean. From this analysis it was identified

that for the studied points in the OSM cartographic

product in the area of UFBA, there were error trends

towards the north, since the value found for this

direction was greater in relation to the t student

tabulated value, which indicates that, for this

analysis, the mean obtained cannot be considered

statistically equal to zero. In turn, for the eastern

direction, the result obtained was less than the t

student tabulated value, revealing that there are no

error tendencies for this direction and that it can be

considered statistically equal to zero. Table 4 shows

the results obtained for this analysis.

Table 4: T-Student Analysis.

T-Student

Tabulated (90%) 1.714

Delta (E) -0.402

PASSED

Delta (N) -2.101

DID NOT PASS

4.4 Accuracy Analysis

By means of the chi-square test, an accuracy

analysis was performed for the discrepancies found,

evaluating the dispersion of the data obtained from

the calculation of the standard deviation of the

discrepancies and, consequently, the best scale to fit

the OSM cartographic product in the area of study

was estimated, making it possible to classify it

according to the PEC-PCD. In this analysis the

accuracy was evaluated from the scale of 1:5,000 to

that of 1:30,000, making it possible to identify at

what scale the product is suitable according to the

parameter of positional accuracy. Thus, according to

the tabulated value of 32.007, corresponding to 90%

confidence, this product was evaluated as class C of

the PEC-PCD when evaluated in the scale of

1:10,000, class B in the scale of 1:20,000 and class

A in the 1:30,000 scale. These results confirm that

there was low positional precision in the evaluated

product. In other words, there is a relatively high

dispersion between the obtained discrepancies, since

it was noted that the precision scale was much lower

when compared with the cartographic basemap used

in this research. Tables 5, 6, and 7 show the values

obtained for the scales described respectively.

Table 5: Accuracy Analysis (Scale 1:10,000).

Chi-Square Test (1:10,000)

PEC-PCD Delta (E) Delta (N)

A 91.55 244.31

B 29.40 78.45

C 10.58 28.24

D 7.35 19.61

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

236

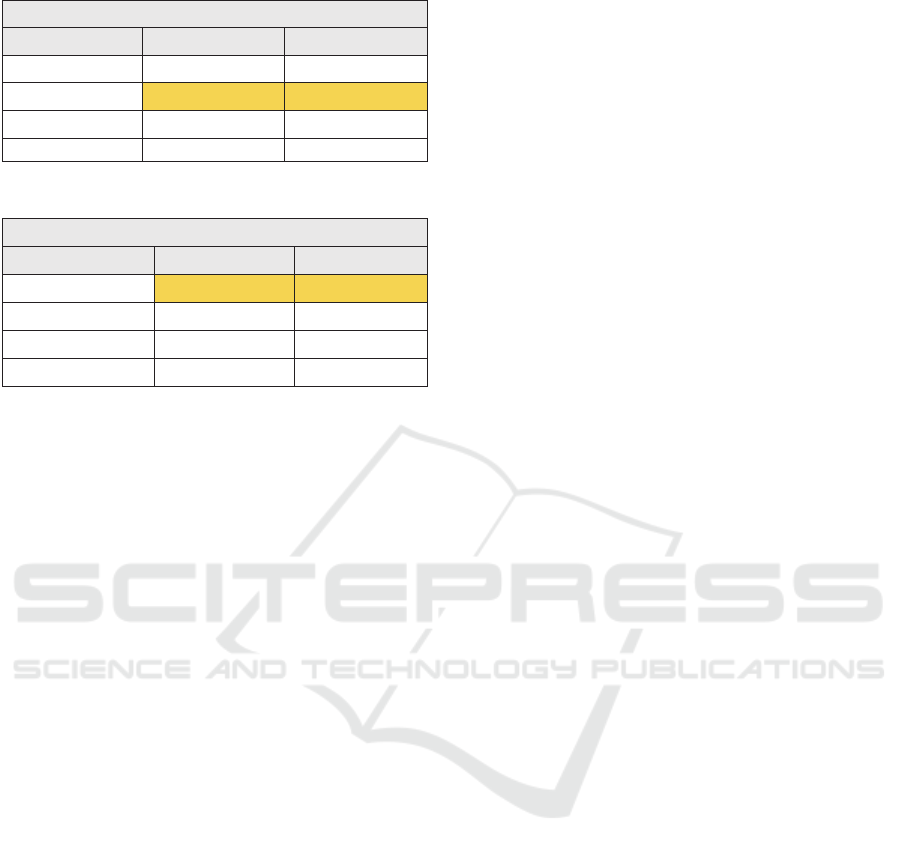
Table 6: Accuracy Analysis (Scale 1:20,000).

Chi-Square Test (1:20,000)

PEC-PCD Delta (E) Delta (N)

22.88 61.08

7.35 19.61

2.64 7.06

1.84 4.90

Table 7: Accuracy Analysis (Scale 1:30,000).

Chi-Square Test (1:30,000)

PEC-PCD Delta (E) Delta (N)

10.17 27.14

3.26 8.71

1.17 3.14

0.82 2.18

5 CONCLUSION AND

RECOMMENDATIONS

This study made it possible to obtain an initial

analysis of the OSM platform in order to quantify

the level of positional accuracy of specific features

in relation to the reference cartographic basemap in

the study area that corresponds to the campuses of

UFBA, making it possible to estimate the levels of

accuracy and precision of samples for this area and

to establish parameters so that information from this

platform can be used to assist in reference data,

given the inherent difficulty in generating and

maintaining cartographic basemaps for different

locations.

Given the results obtained and presented, the

heterogeneity of the data showed that, for this type

of platform, the common sampling techniques

mentioned in the literature and in the mapping

technical specifications do not provide a sufficient

number of samples to determine the pattern of the

observed discrepancies. Instead, they are suitable for

homogeneous data in which a minimum quantity of

samples is sufficient to determine the behavior of the

entire statistical population. Thus, for analysis of

features in products from collaborative mapping it is

necessary to use a larger number of samples in order

to obtain more information about the behavior of the

data, since, as shown, there are temporal variations

in OSM platform elements related to use of Bing

image that are unknown to collaborating users, being

the object of studies of collaborating users.

In addition, from the sampling process of this

data, due to the dispersion obtained, the feasibility of

carrying out certain types of statistical analysis that

better present the information was evaluated, such as

the z test for large samples, the normality test to

evaluate whether it is possible to perform a t student

test, and Wilcoxon's non-parametric test to evaluate

the accuracy of data without the assumption that

certain samples come from a normal distribution.

In spite of the inherent characteristics of the

samples found and the need to perform other

statistical tests and analyses, it is worth noting that a

more in-depth verification of how current the data in

OSM VGI platforms is may present potential to

improve official data, since the fact that data is

updated by online users makes it possible to

generate information faster. However, more studies

must be carried out with the parameter evaluated in

this work because despite having a relatively low

positional precision, when analyzing individual

samples, it was noted that some features presented

errors below 0.27 m, as was the case with points

located in the university restaurant building and in

the Polytechnic School stairway.

Therefore, studies on the efficiency of VGI

platforms for feeding reference bases is of

fundamental importance in order to generate

different references for the cartographic community

and for the contribution of society in the generation

REFERENCES

Atkinson-Gordo, A. D. J., Ariza-López, F. J. y

GarcíaBalboa, J. L. 2007, Estimadores robustos: una

solución en la utilización de valores atípicos para el

control de la calidad posicional, GeoFocus

(Artículos), 7, 171-187, ISSN: 1578-5157.

Ariza-López, F. J., Atkinson-Gordo, A. D. J. and Nero, M.

A. Análisis de Algunas Metodologías de Evaluación

de la Componente Posicional. Topografía y

cartografía: Revista del Ilustre Colegio Oficial de

Ingenieros Técnicos en Topografía, v. 24, p. 32-45,

2007.

Ariza-López, F.J. Calidad en la Producción Cartográfica.

1. ed. Madrid, Espanha: Editora RaMa, 2002a.

BARRON, C., NEIS, P., ZIPF, A.: A comprehensive

framework for intrinsic OpenStreetMap quality

analysis. Transactions in GIS 18 (2014).

BING. Microsoft Bing Maps and MapPoint Web Service

End User Terms of Use and Embedded. Maps Service

BRAVO, J. A confiabilidade semântica das Informações

Geográficas Voluntárias como função da organização

mental do conhecimento espacial. Dissertação de

Mestrado, UFPR, Paraná, 2014.

Positional Accuracy Assessment of the VGI Data from OpenStreetMap

237

BUDHATHOKI, N. R., NEDOVIC-BUDIC, Z. and

Bruce, B. (Chip) (2010). An Interdisciplinary Frame

for Understanding Volunteered Geographic

Information. Geomatica, The Journal of Geospatial

Information Science, Technology, and Practice. 6 (1).

Cintra, J. P. and Nero, M. A. New method for positional

cartographic quality control in digital mapping.

Journal of Surveying Engineering, v. 141, p.

04015001-104015001-10, 2015.

CONCAR. Especificação Técnica para a Aquisição de

Dados Geoespaciais Vetoriais (ET-ADGV) . 2011.

237p.

CORMODE, G.; KRISHNAMURTHY, B. Key

differences between Web 1.0 and Web 2.0. First

Monday, vol.13, n.6, 2008.

FLANAGIN, A. METZGER, M. The Credibility of

Volunteered Geographic Information. GeoJournal.

2008.

GANAPATI, Sukumar. Uses of Public Participation

Geographic Information Systems Applications in

EGovernment. Public Administration Review, v. 71, n.

3, p. 425-434, 2011.

GOODCHILD, M. F. Citizens as sensors: the world of

Volunteered Geography. GeoJournal, vol.69, 2007.

ISO 19113:2005; Geographic information – Quality

principles (ISO 19113:2002).

MERCHANT, D. C. Spatial Accuracy Standards for Large

Scalle Line Maps. In: Techinical Congress on

Surveing and Mapping. Proceedings. v. 1, 1982.

NOGUEIRA JR., J. B. Controle de qualidade de produtos

cartográficos: uma proposta metodológica. Presidente

Prudente. 2003, 147 f. Dissertação (Mestrado em

Engenharia Cartográfica) - UNESP, Campus

Presidente Prudente.

O’REILLY, T. What is Web 2.0: Design patterns and

business models for the next generation of software.

Communications & Strategies, vol.65, n.1, 2007.

Ramm F, Names I, Files SS, Catalogue F, Features P,

Features N, Related T, Infrastructure T, Generation P,

Features L, et al (2011) OpenStreetMap data in

layered GIS format pp 1–21.

ROBERTO, A. J. Extração de Informação Geográfica a

partir de Fotografias Aéreas obtidas com VANTs para

apoio a um SIG Municipal. 93f. Dissertação

(Mestrado. Sistema de Informações Geográfica) –

Departamento de Geociências, Ambiente e

Ordenamento do Território, Universidade do Porto,

Porto, 2013.

MOORE, R., Lopes, J., 1999. Paper templates. In

TEMPLATE’06, 1st International Conference on

Template Production. SCITEPRESS.

SMITH, J., 1998. The book, The publishing company.

London, 2nd edition.

Veregin, H., Data Quality Parameters. In: Longley, P. (ed)

Geographical Information Systems –

Principles and Technical Issues. New York, Wiley &

Sons. 177-190. 1999.

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

238