Visual Support to Filtering Cases for Process Discovery

Luiz Schirmer, Leonardo Quatrin Campagnolo, Sonia Fiol Gonz

alez, Ariane M. B. Rodrigues,

Guilherme G. Schardong, Rafael Franc¸a, Mauricio Lana,

Simone D. J. Barbosa, Marcus Poggi and H

elio Lopes

Pontif

ıcia Universidade Cat

olica do Rio de Janeiro,

Departamento de Inform

atica, Rio de Janeiro, RJ, Brazil

rafael@puc-rio.br, mauriciolana@aluno.puc-rio.br

Keywords:

Visual Filtering, Process Mining, Event Log, Multidimensional Projection.

Abstract:

Working with average-sized event logs is still a major task in process mining, where the main goal is to gain

process-related insights based on event logs created by a wide variety of systems. An event log contains a

sequence of events for every case that was handled by the system. Several discovery algorithms have been

proposed and work well in speciﬁc cases but fail to be generic strategies. Moreover, there is no evidence

that the existing strategies can handle events with a large number of variants. For this reason, a generic

approach is needed to allow experts to explore event log data and decompose information into a series of

smaller problems, to identify outliers and relations between the analyzed cases. In this paper we present a

visual ﬁltering approach for event logs that makes process analysis tasks more feasible and tractable. To

evaluate our approach, we have developed a visual ﬁltering tool and used it with the event log from BPI

Challenge 2017.

1 INTRODUCTION

The business world is complex: various actors are in-

volved in designing, delivering, and offering services

(Mendling et al., 2017), and the knowledge of how

these processes behave is essential in the ﬁeld of Bu-

siness Process Management (BPM). BPM is related

with the management activities around daily business

processes. During the last decade, the need for com-

panies to learn more about how their processes work

in the real world has increased the use of Process

Mining techniques (Tiwari et al., 2008). Grounded

in the data mining ﬁeld, such techniques aim to re-

trieve relevant information from the analyzed work-

ﬂow. Among the topics used in data-driven process

analysis, we highlight Process Discovery, Confor-

mance Checking, and Process Improvement (Van der

Aalst, 2016).

Information retrieval related to BPM aims to ans-

wer several questions to support making decisions

and managing process execution by offering several

features, such as analysis, prediction, monitoring,

control, and optimization.

Following a bottom-up approach, process mining

deals with information gathered as the processes are

executed, recording events of each case as they occur,

and then building a structured process description

from those recorded events (Van der Aalst and Wei-

jters, 2004). In sum, process mining is a research

ﬁeld that acts on the intersection of methods like ma-

chine learning, data mining, and BPM (Van der Aalst,

2016).

In the ﬁeld of Process Discovery, we aim to get an

actual event log and create another controlled struc-

ture, such as a workﬂow, which represents most of the

cases captured by that log. When dealing with sim-

ple examples, the reconstruction of a workﬂow can

be quite easy. However, for large workﬂow models

this can be much more difﬁcult (Van der Aalst et al.,

2004). A recent approach to deal with large datasets

consists of simplifying the large event log into smaller

sublogs, applying the discovery algorithm to these su-

blogs, and then merging the results to generate a solu-

tion to the whole system. By mining smaller logs and

later merging the (sub)solutions, this approach signiﬁ-

cantly speeds the discovery algorithm (Verbeek et al.,

2017). With this in mind, we want to expand the range

of approaches that simplify a model to make it easier

to understand.

In recent years, various techniques were propo-

sed to visualize and generate clusters of BPM data.

Most of these techniques focus on optimizing soluti-

Schirmer, L., Quatrin Campagnolo, L., Fiol González, S., M. B. Rodrigues, A., G. Schardong, G., França, R., Lana, M., D. J. Barbosa, S., Poggi, M. and Lopes, H.

Visual Support to Filtering Cases for Process Discovery.

DOI: 10.5220/0006708200380049

In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 38-49

ISBN: 978-989-758-298-1

ons based on a similarity measure between traces of

data, i.e., the event log is split into homogeneous sub-

sets and for each subset a process model is created

(De Koninck and De Weerdt, 2016). In this paper,

we propose a new visual ﬁltering approach to event

logs, based on multidimensional projection techni-

ques. With this approach, we create a lower dimensi-

onal representation of the cases, preserving their dis-

similarity to one another, and visually select the ones

that stand out or spark interest. Then, we generate

a new, ﬁltered event log using only the selected ca-

ses. Such event log can then be further analyzed using

standard process mining approaches.

The main contribution of our work is a visual ap-

proach for ﬁltering processes based on their low di-

mensionality representation. Our second contribution

is the proposal of a dissimilarity function that uses not

only the attributes of the process cases, but also the

dissimilarity of their paths. Our third and ﬁnal contri-

bution involves the use of entropy to analyze the va-

riability of the processes’ attributes. With those con-

tributions, we expect that our work can be used as a

support tool for process discovery.

The remainder of this paper is organized as fol-

lows: Section 2 presents related work. Next, in

Section 3 we introduce the main components of our

approach and explain the visualization techniques

employed. Section 4 introduces the ﬁltering tool pro-

posed, as well as the interaction mechanisms provi-

ded. Section 5 presents an application of the proposed

approach using real process data in order to demon-

strate its advantages. Finally, Section 6 presents some

concluding remarks and directions for future works.

2 RELATED WORK

In the past, activities related to BPM were conducted

by process analysts with almost no automatic support

for process modeling (Mendling et al., 2017). This

has been changing with the creation of new techni-

ques and algorithms developed to automate or pro-

vide intelligent support for process mining and pro-

cess analysis. The visualization of cases from an

event log, however, still presents challenges.

To overcome problems related to data analysis and

visualization, Van Dongen et al. (2005) have deve-

loped the ProM framework, an extensible environ-

ment for process mining. The system is ﬂexible with

respect to input and output parameters, and easy to

reuse code during the implementation of new process

mining features. It combines different techniques for

data mining and process ﬂow analysis. However, with

Prom it is not possible to look at the log and group ca-

ses by attributes similarities.

Verbeek et al. (2017) proposed a generic appro-

ach to group similar sequences of activities, splitting a

unique event log ﬁle into a number of event logs with

fewer variants each. This was implemented as a plug-

in in ProM6 and allows for easier decomposed disco-

very, using six different discovery algorithms. For the

decomposed discovery, the framework allows the end

user to select the classiﬁer, which maps the event log

at hand onto an activity log; the miner (or discovery

algorithm); and a conﬁguration.

Low et al. (2017) have developed visualization

techniques to provide targeted analysis of resource re-

allocation and activity rescheduling. They have ana-

lyzed differences between event logs and the changes

are conceptualized and realized with a number of vi-

sualizations. Using such visualizations, analysts can

identify resource and time-related changes, which re-

sult in a cost reduction of the process, and investi-

gate them further. They use social network graphs

to illustrate the reallocation of resources and a time-

line visualization approach to depict time-related in-

formation and identify temporal patterns. Moreover,

the system provides a clear view of two event logs

side-by-side, so that differences and similarities can

be visually identiﬁed. However, the proposed system

does have some issues. With a large number of vari-

ants and cases, it is difﬁcult to identify issues in the

data with a visual analysis. In some cases, the use of

the graph and the timeline visualization can confuse

the users (Low et al., 2017).

To solve some of the aforementioned issues, we

developed a visual interactive ﬁltering tool which al-

lows the generation of smaller event logs by selecting

a subset of cases. Contrasting with the approach of

Verbeek et al. (2017), presented in Figure 1, we cre-

ate a visual application to ﬁlter cases and generate su-

blogs. Our strategy can be considered more ﬂexible

and tractable than theirs, as in our approach domain

experts and analysts can freely explore and analyze

the data, and then create sublogs according to their

insights.

3 VISUAL FILTERING

APPROACH

Our visual ﬁltering approach is based on evaluating

the difference between cases using a set of attributes.

There is a multitude of metrics available to accom-

plish this. Paix

ao et al. (2009) propose the use of

weighted additive distances to denoise a vector ﬁeld.

We adapt this metric to our problem, where each at-

tribute f of a case receives a weight α

∈ [0, 1]. We

Visual Support to Filtering Cases for Process Discovery

Figure 1: Conceptual view of a decomposed discovery al-

gorithm given by (Verbeek et al., 2017) and our proposed

approach.

calculate the similarity between each attribute of two

cases i, j|i 6= j and weigh that attribute’s importance

using α

. The product of each attribute similarity for

cases i, j results in a measure of similarity between

the cases. Subtracting this value from 1 gives a mea-

sure of the dissimilarity between i and j, as deﬁned in

Equation 1,

i, j

= 1 −

|F|

∏

f =0

−α

(

− f

)

(1)

where F is the attribute set, (i, j)|i 6= j are the i-th and

j-th case, |F| is the cardinality of the attribute set, α

is a weight factor associated to attribute f ∈ F and

− f

is the difference between attribute f of cases

i and j. When dealing with categorical variables, the

− f

term is replaced by a boolean comparison bet-

ween the categories, which means that we argue whet-

her f

== f

We have also implemented two measures to cal-

culate the distance between the path of two cases: the

Levenshtein distance and the Jaccard index. The Le-

venshtein distance, or edit distance, measures the mi-

nimum number of operations needed to transform a

string into another (Levenshtein, 1966). Here, the in-

sertion, removal or change of characters are conside-

red as valid operations. For example, the edit distance

between case I with an activity sequence of ABCD

and case J with an activity sequence of ABDE is 2,

since activity C of I would be converted to D and acti-

vity D of I would be converted to E. Equation 2 pre-

sents the mathematical deﬁnition of the Levenshtein

distance.

I,J

(a, b) =











max(a, b) min(a, b) = 0











L(a − 1, b) + 1

L(a, b − 1) + 1

L(a − 1, b − 1) + 1

6=J

)

otherwise

(2)

where I and J are two different cases, a and b are

activities belonging to case I and J respectively and

6=J

)

is the indicator function, resulting in 0 if I

and 1 otherwise.

The Jaccard index measures the fraction of com-

mon samples between two ﬁnite sets of samples and

is deﬁned by the number of common samples divided

by the total number of samples in both sets (Jaccard,

1901). We applied this metric by considering that

each case is composed of a set of activities. Thus,

to measure the dissimilarity between cases I and J,

we subtracted their Jaccard index from 1. Equation 3

presents the deﬁnition of the Jaccard dissimilarity.

J(i, j) = 1 −

|I ∩ J|

|I ∪ J|

(3)

In order to visually assess the similarity between

the cases, we employ two multidimensional pro-

jection techniques: Multidimensional Scaling (MDS)

(Kruskal and Wish, 1978) and t-Stochastic Neig-

hbor Embedding (t-SNE) (Maaten and Hinton, 2008).

MDS is a set of algorithms aimed at providing a lo-

wer dimensionality representation of a distance ma-

trix. The main goal is to create a simpler representa-

tion of the cases, but maintaining their relative distan-

ces as close to the original values as possible.

The classical MDS algorithm uses an eigenvalue

decomposition of the distance matrix to calculate a

coordinate matrix in a lower dimensionality space.

This approach requires a full representation of the

distance matrix, which is costly in terms of memory

usage. In addition, the eigenvalue decomposition is

performed by using the power iteration, or power met-

hod (Mises and Pollaczek-Geiringer, 1929), which in

turn is a computationally costly algorithm. Wickel-

maier (2003) provides a good intuition on this parti-

cular algorithm, as well as worked examples.

The primary outcome of an MDS projection is a

spatial conﬁguration, in which the objects are repre-

sented as points and arranged in such a way that their

euclidean distances correspond to the dissimilarities

of the objects in the original space, i.e., similar objects

are represented by points that are close to each other,

whereas dissimilar objects by points that are further

apart. A prominent application of MDS is the visuali-

zation of high-dimensional correlational data, such as

data from process cases.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

The weights assigned to each attribute in Equation

1 have direct inﬂuence on the dissimilarity matrix and

its eigenvalue decomposition. This leads to different

spatial conﬁgurations for different sets of weights. A

careful study of the attributes variability and subse-

quent weight assignments may lead to a conﬁgura-

tion that naturally highlights the different groups in

the data, such as the one presented in Figures 2 and 7.

The second multidimensional projection techni-

que employed is called t-Distributed Stochastic Neig-

hbor Embedding (t-SNE) (Maaten and Hinton, 2008).

The goal of this technique is to embed high dimen-

sional data into a low dimensional space, typically

of 2 or 3 dimensions. Since its inception, it became

widely popular to visualize results of machine lear-

ning techniques (Wattenberg et al., 2016). t-SNE

builds upon the original Stochastic Neighbor Em-

bedding (SNE) algorithm, proposed by Hinton and

Roweis (2003). Both t-SNE and SNE work in two

stages: First, they convert the pairwise dissimilarities

between the data points in the high-dimensional space

into conditional probabilities, such that points with

small dissimilarities will have a high probability of

being neighbors and points with large dissimilarities

will have a lower probability of being neighbors. The

second stage involves the same construction, only for

the low dimensional space. The algorithm then pro-

ceeded by minimizing the sum of Kullback-Leibler

divergences between these two probability distribu-

tions. However, SNE suffers from two problems

that motivated the creation of t-SNE: The Kullback-

Leibler divergence function is difﬁcult to minimize;

and a so-called ”Crowding problem”. Both problems

are heavily detailed by van der Maaten and Hinton

(2008). t-SNE partially solves both problems by pro-

posing a joint probability distribution, called symme-

tric SNE, which solves the Kullback-Leibler minimi-

zation issues; and by proposing the use of a Student

t-distribution to map dissimilarities onto probabilities

in the low dimensional space, alleviating the crow-

ding problem (Maaten and Hinton, 2008).

In practical terms, t-SNE is capable of revealing

both local and global aspects of the data. However, as

stated by Wattenberg et al. (2016), t-SNE is heavily

dependent on the input parameters, and may show

group structures where there are none, besides defor-

ming existing groups, misrepresenting their true size

and inter-group distance.

Figures 2 and 3 show the results of applying the

MDS and t-SNE algorithms, respectively, over the

same 3, 000 cases sampled uniformly at random.

Figure 2: Our proposed case ﬁltering visualization using

MDS projection using 3, 000 cases.

Figure 3: Our proposed case ﬁltering visualization for t-

SNE projection with 3, 000 cases and a perplexity of 50.

4 VISUAL FILTERING TOOL

Our ﬁltering tool comprises a set of 2D charts (MDS

and t-SNE), onto which we project the cases, and a

set of user interface elements to adjust visibility and

weight parameters. Figure 4 shows a prototype of our

tool with some cases plotted. Using the sliders, we

can deﬁne the α

weight for each feature included in

the measure of dissimilarity presented in Equation 1.

Besides the features, it is important to know all

activities of each case. A case can be considered un-

deﬁned if, when analyzing the event log, its end is

not identiﬁed. In our approach, we consider all case

types with a deﬁned endpoint, i.e., either successful

or unsuccessful. We can group cases into different

sets of points, using a speciﬁc marker for each group.

In Figure 4, we project cases which ended in success

(Approved), denial (Denied) or cancellation (Cancel-

led). It is essential to be able to ﬁlter and group the

data, so we can later use them to retrieve information

Visual Support to Filtering Cases for Process Discovery

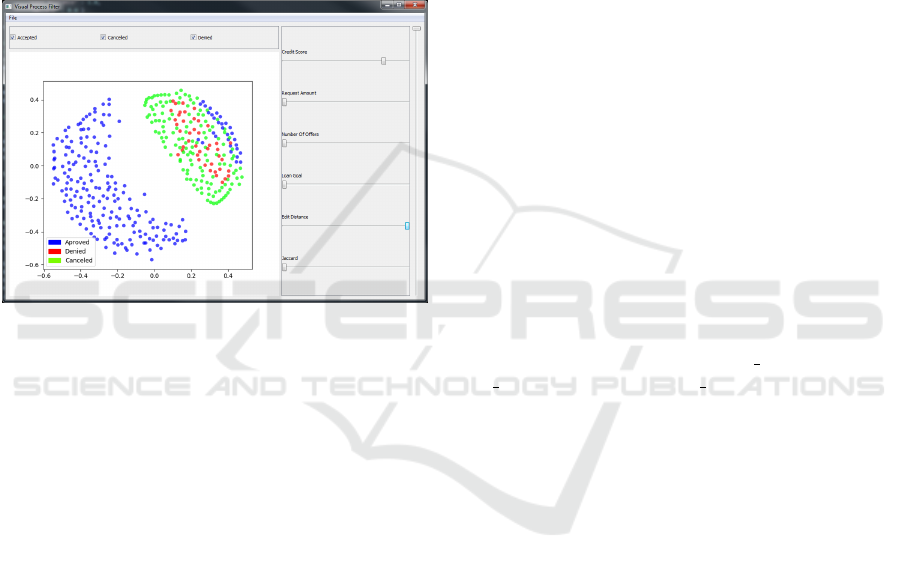
about the identiﬁed groups.

Given the log projected into a 2D chart, we may

select multiple cases, as exempliﬁed in Figure 5. We

can also select multiple cases based on projections ge-

nerated with different weights for each feature. Then,

we can export a CSV ﬁle with the ﬁltered cases to be

used in a process mining software, such as ProM (Ver-

beek et al., 2010) and Fluxicon Disco (Mining, 2014).

These softwares help analyze the activity ﬂow of the

cases.

Our visual ﬁltering tool was implemented in Py-

thon using Sklearn and Matplotlib Packages (Pedre-

gosa et al., 2011; Hunter, 2007).

Figure 4: Our visual ﬁltering prototype with 400 cases.

5 APPLYING VISUAL FILTERING

Process mining results reveal what goes on inside pro-

cesses and can be used to diagnose problems and sug-

gest solutions (Van Der Aalst, 2012). An event log

is composed of a list of events, where all data ex-

tracted from systems is converted to this log. Each

event should have a minimal set of attributes: a case

id (a unique number to represent the case), an activity

name to indicate the performed action, and the date

and time when the action was executed (Rodrigues

et al., 2017).

We have tested our approach using the event log

of BPI Challenge 2017, a real-life log taken from a

ﬁnancial institution. The BPI Challenge provided an

event log that contains all applications ﬁled in 2016,

and at the beginning of 2017. In total, there are

31, 509 loan applications, i.e. cases. Our goal with

the application is to ﬁnd patterns and correlations be-

tween different cases based on the similarity among

attributes that deﬁne a process, because this is an im-

portant task in process discovery.

With this event log, for all applications, the avai-

lable data (attributes) are the following:

• Requested load amount (in Euro),

• The application type,

• The reason for the loan request (Loan Goal), and

• An application ID.

For all offers, the following data are available:

• An offer ID

• The offered amount,

• The initial withdrawal amount,

• The number of payback terms agreed to,

• The monthly costs,

• The customer’s credit score,

• The employee who created the offer,

• Whether the offer was selected, and

• Whether the customer accepted the offer.

For each uniquely identiﬁable event, the employee

who triggered the event is recorded, as well as time

stamp and life-cycle information. In this dataset, there

are more than 1.2 million events, and each event cor-

responds to one of the 26 possible activities of the

process.

Each application is a single case in this dataset

and, for each case, a number of offers can be sent to

a client. A case may have one of three possible en-

dings in the event log: Approved (A Pending), Denied

(A Denied), or Cancelled (A Cancelled). In the event

log, 100 cases were undeﬁned, meaning that none of

the possible endings had been reached. Because of

this, they were discarded in our experiments. In our

preliminary experiments, we performed tests with the

entire data set, i.e., 31, 409 cases.

With this data, we aim to assess our approach use-

fulness in answering questions of common problems

in the domain, by clustering data and analyzing pat-

terns in each of the attributes. This can be considered

an initial step for process discovery, and a meticulous

analysis of the ﬁltered data is needed afterwards.

We transform the event log into a dataset, where

the rows represent the cases and the columns charac-

terize each case, based on the following features: Cre-

dit Score, Requested Amount, Number of Offers, and

Loan Goal. We selected these features to ﬁnd simi-

larities between cases. Also, we added the pairwise

Jaccard index and Levenshtein distance as additional

features.

We use MDS to explore the data. As shown in Fi-

gure 5, we experimented with different projections,

trying to identify visual patterns and relations bet-

ween the cases. We experimented with different weig-

hts for the dissimilarity metric, in order to evaluate the

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

(a) (b) (c)

(d) (e) (f)

Figure 5: Exploring the data and selecting cases using MDS dimensionality reduction. We can select and deselect cases

changing the visualization. For each choice of weights for each feature, we maintain the selection of the cases. In the Figure

(a)(b), we start selecting two groups of points. With a different set of weights, as in Figure (c), we can explore different

visualizations maintaining the same selected points. In the Figures (d)(e), we deselect some other points and then, in Figure

(f), we adjust the weights to visualize the similar projection of (a), but now with a smaller set of selected points.

data and ﬁnd which attributes had a grouping factor in

the dataset.

Using our prototype, it is possible to manually se-

lect a subset of cases using click-and-drag interaction

and export the selection to a CSV ﬁle to load it into a

Process Mining software, such as Disco or ProM. Fi-

gure 6 shows the process ﬂow using Disco with all the

31, 409 valid cases and with a sublog obtained with

our ﬁltering tool.

Unfortunately, MDS is not efﬁcient when dealing

with a large number of cases, both in terms of com-

putational time and memory used. In our study, we

projected 31, 409 cases, with considerable time spent

for each projection, in average 2 hours for each ex-

periment and 60 GB of memory used to store all

data structures used in this technique. We perform

our test in a computer with an Intel core i7-5820K

CPU@3.30GHz, 64GB of memory, 1TB of hard disc

and a graphics card Nvidia Titan Xp DDR5 with 12

GB of memory. However, for smaller dataset, the

MDS does not have such problem. Table 1 shows the

computational time for the same dataset with less ca-

ses.

As a quality measure, we considered the stress of

the projection. This measure depends on the weights

chosen by the user in the dissimilarity equation but,

in the best case, considering only the features of Le-

venshtein distance and loan goal, the stress is 0.15.

Table 2 shows the weights assigned to each at-

Table 1: Run time for each test.

Number of cases time (min)

1 1000 0.366

2 2000 0.576

3 5000 2.010

4 10000 6.880

5 20000 31.400

6 31409 130.02

tribute of the dataset when calculating the pairwise

dissimilarity between the cases. Using these weights,

we projected the full set of cases. The resulting pro-

jection is shown in Figure 7. We then selected 6 clus-

ters using our prototype tool, also shown in Figure 7.

Table 2: Parameters deﬁned to ﬁlter the 31409 cases.

Attribute Value

1 Loan Goal 1.00

2 Credit Score 0.50

3 Number of Offers 0.00

4 Requested Amount 0.50

5 Levenshtein Distance 0.00

6 Jaccard Index 1.00

In order to validate our approach, we used a clus-

tering algorithm on the complete event log to au-

tomatically ﬁnd 6 clusters. We used a version of

K-Medoids (Kaufman and Rousseeuw, 2009) named

Visual Support to Filtering Cases for Process Discovery

(a) (b)

Figure 6: Difference between the process map using all 31, 409 cases (a) and the ﬁltered sublog(b).

Figure 7: Filtered image with 6 clusters selection using the

parameters speciﬁed in Table 2 with MDS.

Partitioning Around Medoids (PAM). The algorithm

searches for k representative objects i.e. medoids of

the clusters, which minimize the sum of pairwise dis-

similarities between each object (case) and the closest

medoid. The k clusters are constructed by assigning

each object of the dataset to the nearest representative

object.

To evaluate how cohesive the clusters are, we cal-

culated their entropy. Shannon’s entropy (Shannon

and Weaver, 1963) quantiﬁes this cohesiveness, i.e.

the uncertainty associated with a discrete random va-

riable X with N possible outcomes (Lopes and Bar-

bosa, 2015). Equation 4 describe this measure.

(S)

[P] = −

∑

j=1

ln(p

) (4)

Where p

is the probability of the outcome j appea-

ring in the variable. Since our dissimilarity measure is

normalized, we decided to use the normalized version

of the Shannon entropy, as shown in Equation 5.

(S)

[P] =

(S)

[P]

(S)

]

= −

∑

j=1

ln(p

)

ln(n)

(5)

Where H

(S)

[P] ∈ [0, 1]. When the entropy is close to

0, the cluster is homogeneous. Conversely, when it is

closer to 1, the cluster is heterogeneous.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

Using K-Medoids with k = 6 and 31, 397, which

is the number of clusters and data points, respectively,

obtained using our ﬁltering tool, we calculated the en-

tropy of each cluster with respect to the variables. Fi-

gure 10 shows this result.

Similarly, we calculated the entropy for each of

the visually selected clusters. Figure 11 shows this

result. It is important to note that we use a gradient

color scale to identify the entropy. Lower entropies

(the most interesting ones for this study) appear in

shades of blue, where the darker blue is entropy close

to 0. The higher (less interesting) entropies appear in

shades of red, where the darker red is entropy near 1.

In general, the separation of data points through

the ﬁltering tool resulted in clusters with low uncer-

tainty value for the Goal and similar to Credit Score

variables, when compared to K-Medoids.

To assist in the descriptive analysis of clusters, we

calculated the frequency of the values in each of the

variables of the MDS approach. The result can be

seen in Figure 12, where each row represents a cluster.

Histogram colors match entropy colors.

From this moment it is possible to describe the

clusters deﬁned by MDS method (see Figures 7, 11

and 12).

Cluster 1 is characterized by a higher percentage

of cases that were Cancelled (10.817%, row 1 in Ta-

ble 3) at the end of the process. Regarding Goal and

Credit Score, the entropy is 0, meaning there is no un-

certainty (Figure 11). In this cluster, all cases have

Goal = Car and Credit Score in the range [0, 500)

(row 1 in Figure 12). Entropy increases for the Num-

ber of Offers (0.42), where most cases received 1 of-

fer, and also to the Requested Amount (0.77), where

the amounts requested are heavily distributed between

cases.

Cluster 2 has similar characteristics to Cluster 1 in

terms of Cancelled cases (7.383%, row 2 in Table 3)

and entropy of the same variables (Figure 11). Howe-

ver, the purpose of the loan for this cluster is Home

Improvement (row 2 in Figure 12). This is evident

when we look at the clusters of Figure 7: they are vi-

sually alike but distant.

Cluster 3 also has mostly Cancelled cases

(15.009%, row 3 in Table 3). The entropy is high

for the variables considered, except for Credit Score,

which is 0 (Figure 11). In this cluster all cases have

Credit Score in the range [0, 500) (row 3 in Figure 12).

Cluster 6, in spite of having practically all Ap-

proved cases (20.350%, row 6 in Table 3), has high

entropy in all considered variables (Figure 11). Only

one case was not approved, getting a Denied endpoint.

This behavior caught our attention and, for this re-

ason, we analyze this particular case. We detected

that the values of the variables are within the limits of

each of these clusters (red dots in Figure 12 represents

this particular case), but it presented a path between

the events totally different from the rest of the cluster.

This, in fact, proves that the MDS can group cases ac-

cording to the similarity of the variables, regardless of

the deﬁned paths.

Clusters 4 and 5, again, have similar characteris-

tics. Both have high entropies, very close to each ot-

her (Figure 11). The types and frequency of values

for the Credit Score, Number of Offers, and Reque-

sted Amount variables are very similar too (rows 4

and 5, respectively in Figure 12). However, Cluster

4 has Goal = Car and Cluster 5, Goal = Home im-

provement. Again we can compare this behavior with

the visual clusters. These clusters are distant but si-

milarly shaped (Figure 7). As we can see in Figure

6, the sublog represents the process obtained with the

ﬁltered log representing cluster 4.

In general, we can verify that the Credit Score se-

parates the clusters in two groups by the diagonal,

where the high entropy are on the left-hand side and

the low entropy are on the right-hand side in Figure 7.

In order to visualize the results of the K-Medoids

clustering, we plotted the projections of 31, 397 ca-

ses selected using our visual approach and colored the

points by their assigned K-Medoids cluster label. Fi-

gure 8 shows this result.

Figure 8: MDS projection of the 31, 397 cases colored by

their K-Medoids assigned cluster.

K-Medoids obtains clusters with silhouette mea-

sure (Rousseeuw, 1987) equivalent to our approach,

as seen in tables 4 and 5, but it visually scrambles

some of the cases (Figure 8). Using the same colors of

the K-Medoids clusters, we painted the concordance

matrix in Figure 9, showing how the data points are

distributed among clusters of each approach. We also

quantiﬁed the amount of information shared between

K-Medoids clustering results and the visual clusters

Visual Support to Filtering Cases for Process Discovery

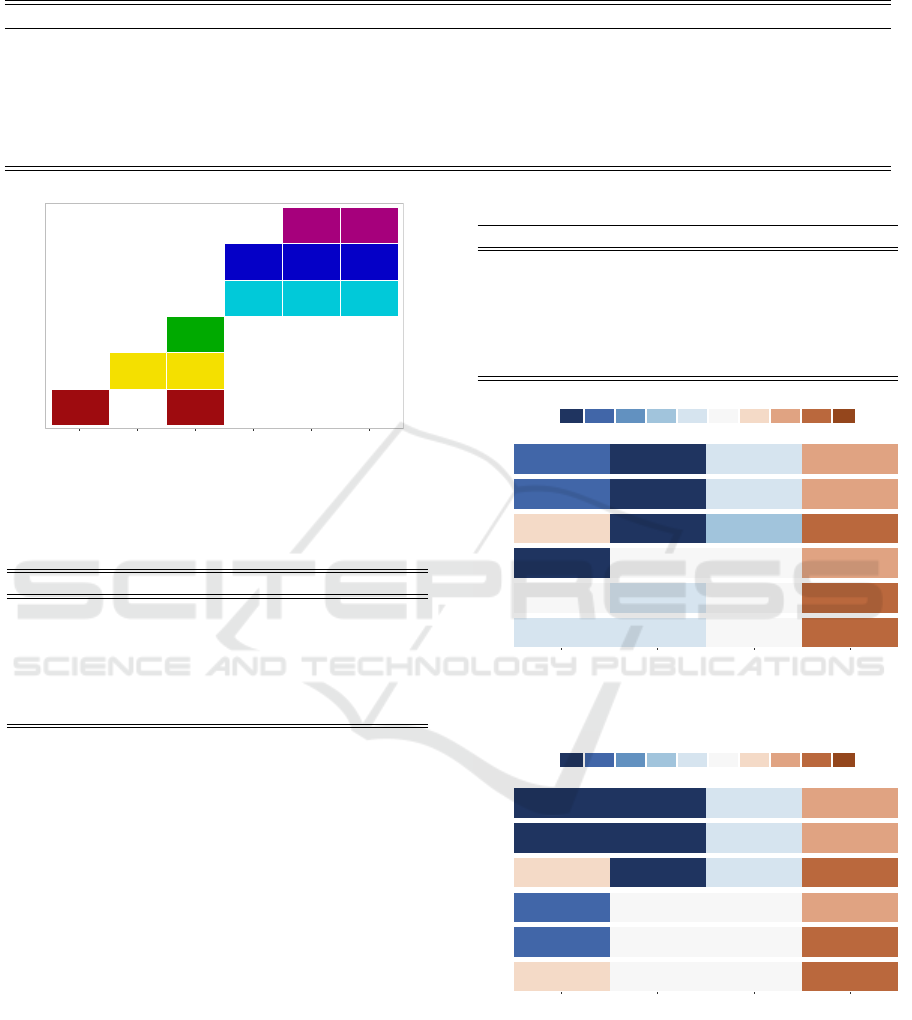
Table 3: Cluster characterization of MDS approach in terms of process (* %with respect to all 31, 397 cases).

Cluster #Cases #Variants Approved %Approved* Denied %Denied Canceled %Canceled

1 5075 656 556 1.771 1123 3.577 3396 10.817

2 3724 570 569 1.812 837 2.666 2318 7.383

3 7349 949 846 2.695 1791 5.705 4712 15.009

4 4524 851 4524 14.410 0 0.000 0 0.000

5 4335 850 4335 13.808 0 0.000 0 0.000

6 6390 1482 6389 20.350 1 0.003 0 0.000

5075 0 311 0 0 0

0 3724 272 0 0 0

0 0 6766 0 0 0

0 0 0 4230 1 12

0 0 0 294 402 4280

0 0 0 0 3932 2098

1 2 3 4 5 6

MDS clusters

K−Medoids clusters

Figure 9: Frequency of datapoints in each cluster. Colors

represent the relation between clusters in K-Medoids and

MDS.

Table 4: K-Medoids silhouette.

Method Cl Mean(sd) Minvalue Maxvalue

1 0.270 (0.090) -0.105 0.550

2 0.271 (0.093) -0.109 0.543

KMed. 3 0.060 (0.049) -0.019 0.241

4 0.258 (0.049) -0.083 0.477

5 0.115 (0.077) -0.011 0.342

6 0.118 (0.085) -0.021 0.352

obtained with our prototype. To do this, we calcula-

ted the Normalized Mutual Information Index (NMII)

(Strehl and Ghosh, 2002). We obtained a NMII value

of 0.84, meaning that 84% of the cases fall into the

same groups in the two approaches. Also, as we can

see in Table 6, there is high variability for some at-

tributes, especially the Requested Amount. This may

explain the high entropy values for this attribute.

The Loan Goal attribute was not included in Table

6 because it is a categorical variable with 14 different

classes.

6 CONCLUSION

In this paper, we proposed a novel approach for un-

derstanding and ﬁltering cases of general event logs.

Our approach is based on evaluating the similarity

between pairs of cases and using multidimensional

projection techniques to plot those cases into a 2D

Table 5: MDS silhouette.

Method Cl Mean(sd) Minvalue Maxvalue

1 0.306 (0.049) 0.236 0.583

2 0.311 (0.044) 0.251 0.582

MDS 3 0.068 (0.040) -0.006 0.219

4 0.220 (0.083) -0.137 0.456

5 0.215 (0.093) -0.150 0.472

6 0.086 (0.054) -0.008 0.243

0.12 0 0.49 0.78

0.14 0 0.45 0.78

0.67 0 0.36 0.85

0.01 0.57 0.54 0.76

0.53 0.46 0.56 0.8

0.48 0.44 0.52 0.84

Goal Credit Score Number of Offers Requested Amount

Variables

Clusters

[0,0.1) [0.1,0.2)[0.2,0.3) [0.3,0.4)[0.4,0.5) [0.5,0.6)[0.6,0.7) [0.7,0.8)[0.8,0.9) [0.9,1]

Figure 10: Entropy value of each cluster by variable in K-

Medoids approach.

0 0 0.42 0.77

0 0 0.42 0.79

0.68 0 0.43 0.85

0.14 0.58 0.52 0.78

0.19 0.52 0.5 0.8

0.62 0.51 0.58 0.82

Goal Credit Score Number of Offers Requested Amount

Variables

Clusters

[0,0.1) [0.1,0.2)[0.2,0.3) [0.3,0.4)[0.4,0.5) [0.5,0.6)[0.6,0.7) [0.7,0.8)[0.8,0.9) [0.9,1]

Figure 11: Entropy value of each cluster by variable in MDS

projection chart.

chart. Using the BPI Challenge 2017 data, our ap-

proach shows that we can not only select some cases,

but also see some correlation of the data, projected

into our reduced space. Also, this ﬁltering approach

allows us to decompose a large event log into small

pieces and analyze them separately, a useful approach

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

Figure 12: Characteristics of each cluster, by variable. Histogram colors match entropy colors. For the Loan Goal variable,

which is a categorical variable, the values are abbreviated as follows: UN = Unknown, TP = Tax payments, RD = Remaining

debt home, OT = Other, see explanation, NA = Not speciﬁed, MO = Motorcycle, HI = Home improvement, EP = Extras

pending limit, EL = Existing loan take over, DR = Debt restructuring, CC = Caravan/Camper, CA = Car, BO = Boat and BG

= Business goal.

Visual Support to Filtering Cases for Process Discovery

Table 6: Summary results for the numeric attributes of the

BPI 2017 dataset.

Statistics Credit Score Nb. Offer R. Amount

Min. 0.000 1.000 0.00

1st Qu. 0.000 1.000 6000.00

Median 0.000 1.000 12500.00

Mean 436.100 1.363 16210.00

3rd Qu. 901.000 2.000 21000.00

Max. 1145.000 10.000 450000.00

in the process discovery ﬁeld (Verbeek et al., 2017).

We are still making improvements to our pro-

totype based on interesting demands that should help

to understand the process and to ﬁlter cases. As fu-

ture work, we want to incorporate our tool as a ProM

plug-in. We also intend to include Local Afﬁne Mul-

tidimensional Projection (LAMP) (Joia et al., 2011;

Pagliosa et al., 2015) in our prototype, which will

enable us to set a group of control points and dyn-

amically project new instances. Another interesting

idea is to incorporate attribute-level linkage, similar

to the analysis we performed in Section 5, to the pro-

totype itself. This way, an analyst may quickly dis-

cover which attributes contribute to the dataset varia-

bility and, thus, ﬁne-tune the attribute weights for the

dissimilarity metric.

ACKNOWLEDGEMENTS

We thank Conselho Nacional de Desenvolvimento

Cient

ıﬁco e Tecnol

ogico (CNPq) and Coordenac¸

ao de

Aperfeic¸oamento de Pessoal de N

ıvel Superior (CA-

PES) for partially ﬁnancing this research.

REFERENCES

De Koninck, P. and De Weerdt, J. (2016). Multi-objective

trace clustering: ﬁnding more balanced solutions. In

International Conference on Business Process Mana-

gement, pages 49–60. Springer.

Hunter, J. D. (2007). Matplotlib: A 2d graphics environ-

ment. Computing In Science & Engineering, 9(3):90–

95.

Jaccard, P. (1901).

Etude comparative de la distribution ﬂo-

rale dans une portion des alpes et des jura. Bull Soc

Vaudoise Sci Nat, 37:547–579.

Joia, P., Coimbra, D., Cuminato, J. A., Paulovich, F. V., and

Nonato, L. G. (2011). Local afﬁne multidimensional

projection. IEEE Transactions on Visualization and

Computer Graphics, 17(12):2563–2571.

Kaufman, L. and Rousseeuw, P. J. (2009). Finding groups

in data: an introduction to cluster analysis, volume

344. John Wiley & Sons.

Kruskal, J. B. and Wish, M. (1978). Multidimensional Sca-

ling, volume 31.

Levenshtein, V. I. (1966). Binary codes capable of cor-

recting deletions, insertions, and reversals. In Soviet

physics doklady, volume 10, pages 707–710.

Lopes, H. and Barbosa, S. (2015). Learning and Inferring:

Festschrift for Alejandro Frery, chapter Uncertainty

Measures and the concentration of probability density

functions. College Publications.

Low, W. Z., Van der Aalst, W. M., ter Hofstede, A. H.,

Wynn, M. T., and De Weerdt, J. (2017). Change vi-

sualisation: Analysing the resource and timing diffe-

rences between two event logs. Information Systems,

65:106–123.

Maaten, L. v. d. and Hinton, G. (2008). Visualizing data

using t-sne. Journal of Machine Learning Research,

9(Nov):2579–2605.

Mendling, J., Baesens, B., Bernstein, A., and Fellmann, M.

(2017). Challenges of smart business process mana-

gement: An introduction to the special issue.

Mining, P. (2014). Automated process discovery soft-

ware for professionals-ﬂuxicon disco. Adres:

http://ﬂuxicon. com/disco/Eris¸im Tarihi, 11.

Mises, R. and Pollaczek-Geiringer, H. (1929). Praktische

verfahren der gleichungsauﬂ

osung. ZAMM-Journal

of Applied Mathematics and Mechanics/Zeitschrift f

Angewandte Mathematik und Mechanik, 9(1):58–77.

Pagliosa, P., Paulovich, F. V., Minghim, R., Levkowitz, H.,

and Nonato, L. G. (2015). Projection inspector: As-

sessment and synthesis of multidimensional projecti-

ons. Neurocomputing, 150:599–610.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P.,

Weiss, R., Dubourg, V., et al. (2011). Scikit-learn:

Machine learning in python. Journal of Machine Le-

arning Research, 12(Oct):2825–2830.

Rodrigues, A. M. B., Almeida, C. F. P., Saraiva, D. D. G.,

Moreira, F. B., Spyrides, G. M., Varela, G., Krieger,

G. M., Peres, I. T., Dantas, L. F., Lana, M., Alves,

O. E., Franca, R., Neira, R. A. Q., Gonzalez, S. F.,

Fernandes, W. P. D., Barbosa, S. D. J., Poggi, M., and

Lopes, H. (2017). Stairway to value: mining a loan

application process. Technical report, Pontif

ıcia Uni-

versidade Cat

olica do Rio de Janeiro.

Rousseeuw, P. J. (1987). Silhouettes: a graphical aid to

the interpretation and validation of cluster analysis.

Journal of computational and applied mathematics,

20:53–65.

Shannon, C. E. and Weaver, W. (1963). A Mathemati-

cal Theory of Communication. University of Illinois

Press, Champaign, IL, USA.

Strehl, A. and Ghosh, J. (2002). Cluster ensembles—

a knowledge reuse framework for combining multi-

ple partitions. Journal of machine learning research,

3(Dec):583–617.

Tiwari, A., Turner, C. J., and Majeed, B. (2008). A re-

view of business process mining: state-of-the-art and

future trends. Business Process Management Journal,

14(1):5–22.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

Van Der Aalst, W. (2012). Process mining. Communicati-

ons of the ACM, 55(8):76–83.

Van der Aalst, W., Weijters, T., and Maruster, L. (2004).

Workﬂow mining: Discovering process models from

event logs. IEEE Transactions on Knowledge and

Data Engineering, 16(9):1128–1142.

Van der Aalst, W. M. (2016). Process mining: data science

in action. Springer.

Van der Aalst, W. M. and Weijters, A. (2004). Process

mining: a research agenda. Computers in industry,

53(3):231–244.

Verbeek, H., Buijs, J., Van Dongen, B., and van der Aalst,

W. M. (2010). Prom 6: The process mining toolkit.

Proc. of BPM Demonstration Track, 615:34–39.

Verbeek, H., Van der Aalst, W., and Munoz-Gama, J.

(2017). Divide and conquer: A tool framework for

supporting decomposed discovery in process mining.

The Computer Journal, pages 1–26.

Wattenberg, M., Vigas, F., and Johnson, I. (2016). How to

use t-sne effectively. Distill.

Visual Support to Filtering Cases for Process Discovery