Managing Graph Modeling Alternatives for Link Prediction

Silas P. Lima Filho, Maria Claudia Cavalcanti and Claudia Marcela Justel

Military Institute of Engineering, Praca General Tiburcio 80, Urca, Rio de Janeiro, Brazil

Keywords:

Modelling Formalism, Link Prediction, Heuristics.

Abstract:

The importance of bringing the relational data to other models and technologies has been widely debated, as

for example their representation as graphs. This model allows to perform topological analysis such as social

analysis, link predictions or recommendations. There are already initiatives to map from a relational database

to graph representation. However, they do not take into account the different ways to generate such graphs

from data stored in relational databases, specially when the goal is to perform topological analysis. This work

discusses how graph modeling alternatives from data stored in relational datasets may lead to useful results.

However, this is not an easy task. The main contribution of this paper is towards managing such alternatives,

taking into account that the graph model choice and the topological analysis to be used, depend on the links the

user intends to predict. Experiments are reported and show interesting results, including modeling heuristics

to guide the user on the graph model choice.

1 INTRODUCTION

One of the reasons to convert data stored in relational

databases into graph representation models is to sup-

port “decision-making”. For decades the graph model

has been widely explored in topological analysis, and

there are plenty of algorithms and applications on the

literature. Usually, these algorithms have been app-

lied in the context of social network, recommendation

systems, link prediction and many others.

In this direction, some alternatives to map relati-

onal data into graphs, more speciﬁcally RDF graphs,

came up, such as D2R (Bizer, 2003). However, such

initiatives focus on syntax mapping, and do not ad-

dress graph modeling issues. On the other hand, there

are works (Virgilio et al., 2014b) (Wardani and Kng,

2014) (Bordoloi and Kalita, 2013) that focus on graph

modeling, but embrace a speciﬁc modeling strategy

and do not take into account modeling strategy alter-

natives, nor the intended topological analysis.

The goal of this paper is to demonstrate that the

use of alternative modelings can provide richer infe-

rences, such as to recommend different pairs of rela-

ted objects, or to predict different types of links. The

key idea consists on assisting the user on the task of

graph modeling, based on the analysis of a conceptual

schema, derived from a relational schema of a data-

base. The main contribution is the identiﬁcation of a

set of heuristics, which take into account the intended

topological analysis and guides the user on choosing

the modelings that may be useful. These heuristics

were identiﬁed based on the results of some experi-

ments using topological analysis (e.g. link prediction)

over different modeling choices.

This work is organized as follows: Section 2 pre-

sents some basic concepts that are used throughout

the paper. Section 3 describes the related works on

graph database modeling and on mapping the relati-

onal data to graph structures. Section 4 presents the

motivation for deriving heuristics and describes how

the experiments were conducted. Section 5 presents

the experiments, as well as their results, and also pre-

sents the heuristics that emerged based on them. Fi-

nally, the last section concludes the work, pointing to

some future directions.

2 BASIC FOUNDATIONS

This section presents basic concepts about social net-

work analysis, graph modeling and relational data-

base modeling.

2.1 Social Networks Analysis

Social networks have received much attention in the

last years because they allow to model relationships

between actors, like people or other objects. For in-

stance, friendship, inﬂuence and collaboration net-

P. Lima Filho, S., Claudia Cavalcanti, M. and Marcela Justel, C.

Managing Graph Modeling Alternatives for Link Prediction.

DOI: 10.5220/0006708700710080

In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 71-80

ISBN: 978-989-758-298-1

works, biological networks, electric distribution net-

works, pages and web links computer networks, were

presented in several applications (Easley and Klein-

berg, 2010). There are different ways to analyze so-

cial networks. We will focus our work in topological

analysis, that is, we model the network as a graph, and

use algorithms to obtain information about degree of

nodes, paths and distances between nodes.

Because of its nature, the social networks are

highly dynamic, that is, they change fast over the

time, by the adding of new nodes or edges. One of the

questions about the dynamic of the network is, how

does the association between nodes change over the

time? We are interested in predict future association

between nodes, knowing that there is no association in

the current state of the graph. This problem is known

as Link Prediction (Aggarwal, 2011).

Nowell and Kleinberg (Liben-Nowell and Klein-

berg, 2007) have adapted some concepts from graph

theory, computer science and social studies as metrics

to determine future connections to be inserted in the

graph. Three formulas have been used in our experi-

ments, taken from Nowell and Kleinberg article, and

can be classiﬁed in two types of metrics: one based

in common neighbors and other based in path assem-

bling. All the considered metrics produce a coefﬁ-

cient for a pair of nodes x, y non connected by an edge

in the graph. Common neighbors metrics analyze in

different ways the number of common neighbors of

x and y. Path assembling metrics measures in some

sense the paths between a pair of nodes in the graphs.

Jaccard and Adamic/Adar coefﬁcients are classi-

ﬁed as common neighbors metrics, meanwhile Katz

coefﬁcient as path assembling metric. Jaccard coef-

ﬁcient is stated by: score(x;y) =

|Γ(x)∩Γ(y)|

|Γ(x)∪Γ(y)|

. The

Adamic/Adar coefﬁcient is deﬁned by: score(x;y) =

∑

z∈Γ(x)∩Γ(y)

log(|Γ(z)|)

. And Katz coefﬁcient is:

score(x, y) =

∑

∞

l=1

|paths

x,y

|, where paths

x,y

is the

set with all the paths with length l between nodes x, y,

and β is an arbitrary value. In our experiments, we

deﬁned β =

, and λ

is the greatest eigenvalue of

the adjacency matrix of the graph.

2.2 Relational and Graph Modeling

Heuser (Heuser, 2009) states that a data model must

be expressive enough to create database schemas. In

other words, it must be sufﬁciently expressive for mo-

deling reality into schemas. Designing a database

schema is a task which usually goes through two steps

with different level of abstraction: conceptual and lo-

gical modeling. These two steps are needed due to

the complexity of the reality that the designer intends

to model. The main idea is to conduct the modeler

from the reality level into some logical data struc-

ture that may represent real objects. The ER model

(Chen, 1976) is commonly used to design conceptual

schemas, where objects and relationships of the real

world are represented as entities (classes of objects)

and their relationship types (see Figure 1). In the

second step, these entities and relationships are then

mapped into a logical schema. The Relational Model

(Codd, 1970) is largely used to create logical sche-

mas, where tables are deﬁned as the structures that

will actually store the data. For instance, if the dom-

ain involves actors and movies, these can be modeled

as entities 1 and 2, and the participation that an actor

can have in a movie can be modeled as a relationship

between those two entities.

Figure 1: Suggested model for an general situation.

Different from database modeling, that aims at

the storage and management of data, graph modeling

aims at data analysis, such as social network analy-

sis or, in particular link prediction. The need to ad-

dress both goals has led to the rise of graph oriented

DBMS (GDBMS). These systems use a graph struc-

ture to store data. Neo4J

is one of the most used

GDBMS.

Rodriguez (Rodriguez and Neubauer, 2010)

points to several different graph structures. For ex-

ample, some graph structures are able to represent

different features for each vertex or edge, such as la-

bels, attributes, weight, etc. In his article, he presents

a hierarchic classiﬁcation, where graph structures are

organized according to their expressivity (number of

features allowed). The structure known as property

graph, is the most commonly used by graph manipu-

lation tools (e.g. Neo4J), due to its expressiveness.

Graphs may be modeled based on data items that

come from databases. In order to map data items from

a relational database to a graph structure, it is neces-

sary to count on both conceptual and logical sche-

mas. The modeler can use them to identify which data

items will be represented as vertices, and which refe-

rences can become edges in the graph database. Ho-

wever, this is not an easy task, specially when there is

a variety of analysis that can be performed.

The following section presents some initiatives in

this direction. However, to the best of our knowledge,

there are no methods or guidelines to assist the graph

modeler in doing such task, taking into account the

analysis to be performed.

http://neo4j.com/developer/example-data/

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

3 RELATED WORK

Some works have already approached the task of

graph modeling based on data from the relational mo-

del databases. One of them (Virgilio et al., 2014b)

focus on graph modeling aiming at the improvement

of query performance on the graph database. Diffe-

rently, another work (Wardani and Kng, 2014) focus

on avoiding semantic losses while modeling, whereas

in (Bordoloi and Kalita, 2013) the focus is on avoi-

ding data redundancy.

The main idea of Wardani and K

ung’s work (War-

dani and Kng, 2014) is to build a graph as close as

possible to the relational database conceptual schema,

avoiding semantic losses. The authors use both rela-

tional and conceptual schemas to create speciﬁc map-

ping rules, such as to use foreign key attributes to map

a(n) relationship/edge between two nodes. Based on

such rules, the graph can be generated.

Similarly, De Virgilio et al.’s work (Virgilio et al.,

2014a) begins with an analysis over the relational

schema. In another work, (Virgilio et al., 2014b), the

same authors highlight that a careful conceptual ana-

lysis, based on the conceptual schema (ER), is needed

to perform the graph modeling. Initially, a ”template”

graph (schema) is conceived. In this schema, the en-

tities and relationships are conveniently grouped in

one single node, respecting the integrity reference ru-

les, which had been deﬁned in the relational schema,

and/or some other rules deﬁned by the authors. Ba-

sed on such schema, mapping rules are created, ena-

bling the graph generation. The idea is to optimize the

query processing by joining instances that will come

out together in some query.

While the previous mentioned works propose the

creation of property graphs, Bordoloi et al. (Bordoloi

and Kalita, 2013) presents a hypergraph construction

method from a relational schema. At ﬁrst, star and de-

pendence graphs are built, evidencing the dependence

relations between table attributes. Secondly, these

graphs are merged in a single hypergraph. Likewise

to what De Virgilio et al. call ”template graph”, the

hypergraph represents the database schema, where the

nodes are relations’ attributes and the edges are attri-

butes’ (functional and referential) dependencies. Ba-

sed on that hypergraph, a new one is generated from

the original data, where each attribute value from the

relation tuples turns into a node, and the dependence

relations are instantiated as well. However, this is

a complex graph with too many nodes. To simplify

this graph and avoid node redundancy, a suggested

method includes an analysis of common domains be-

tween attributes. Therefore, another schema hyper-

graph is built taking that analysis into account, where

attributes from the same domain, which are in diffe-

rent tables, are represented just once. Finally, a data

hypergraph is built based on the schema hypergraph,

where a single node represents a value from a speci-

ﬁc domain. Although, in this approach, all attribute

values are available for analysis, a hypergraph is not

easy to analyze, since most algorithms and tools are

not able to deal with hypergraphs.

Some other authors, although they state that re-

lational data can be represented as a graph, they ar-

gue that it is hard bringing the content stored in re-

lational storages to graph structure. Vertexica (Jin-

dal et al., 2014), for instance, is a relational database

system that provides a vertex-centric interface which

helps the user/programmer to analyze data contained

in a relational database, using graph-based queries.

The authors afﬁrm that Vertexica allows easy-to-use,

efﬁcient and rich analysis on top of a relational en-

gine. They report good performance results, handling

graphs with more than 80 thousand nodes and over

1.5 million edges.

Another work, similar to Vertexica, is the Aster

6 from Teradata (Simmen et al., 2014), which ena-

bles the user/programmer, by a vertex-centric pro-

gramming abstraction, to combine different analy-

sis techniques, such as embedding graph functions

within SQL queries. The solution proposed in this

work is an extended multi-engine processing archi-

tecture, able to handle large-scale graph analytics.

A recent work by Xirogiannopoulos (Xirogianno-

poulos et al., 2015; Xirogiannopoulos et al., 2017)

presents a graph analysis framework called GraphGen

which converts relational data into a graph data mo-

del, and allows the user to make graph analysis tasks

or execute convenient algorithms over the obtained

graph. This framework uses DSL language - which

is based on Datalog - to perform the extractions from

the relational database. Up to our knowledge, this is

the only work that discusses the relevance of obtai-

ning different feasible graph models from the same

dataset. However, it does not guide the user on the

graph modeling choices.

Thus, despite addressing the graph modeling task,

none of these works take into account the topological

analysis while choosing a graph modeling alternative.

4 MANAGING GRAPH

ALTERNATIVES APPROACH

Figure 2 summarizes the proposed approach. First,

we assume that it is possible to get an ER schema

from a relational logical schema (LS) using some re-

verse engineer technique (Heuser, 2009). Sometimes

Managing Graph Modeling Alternatives for Link Prediction

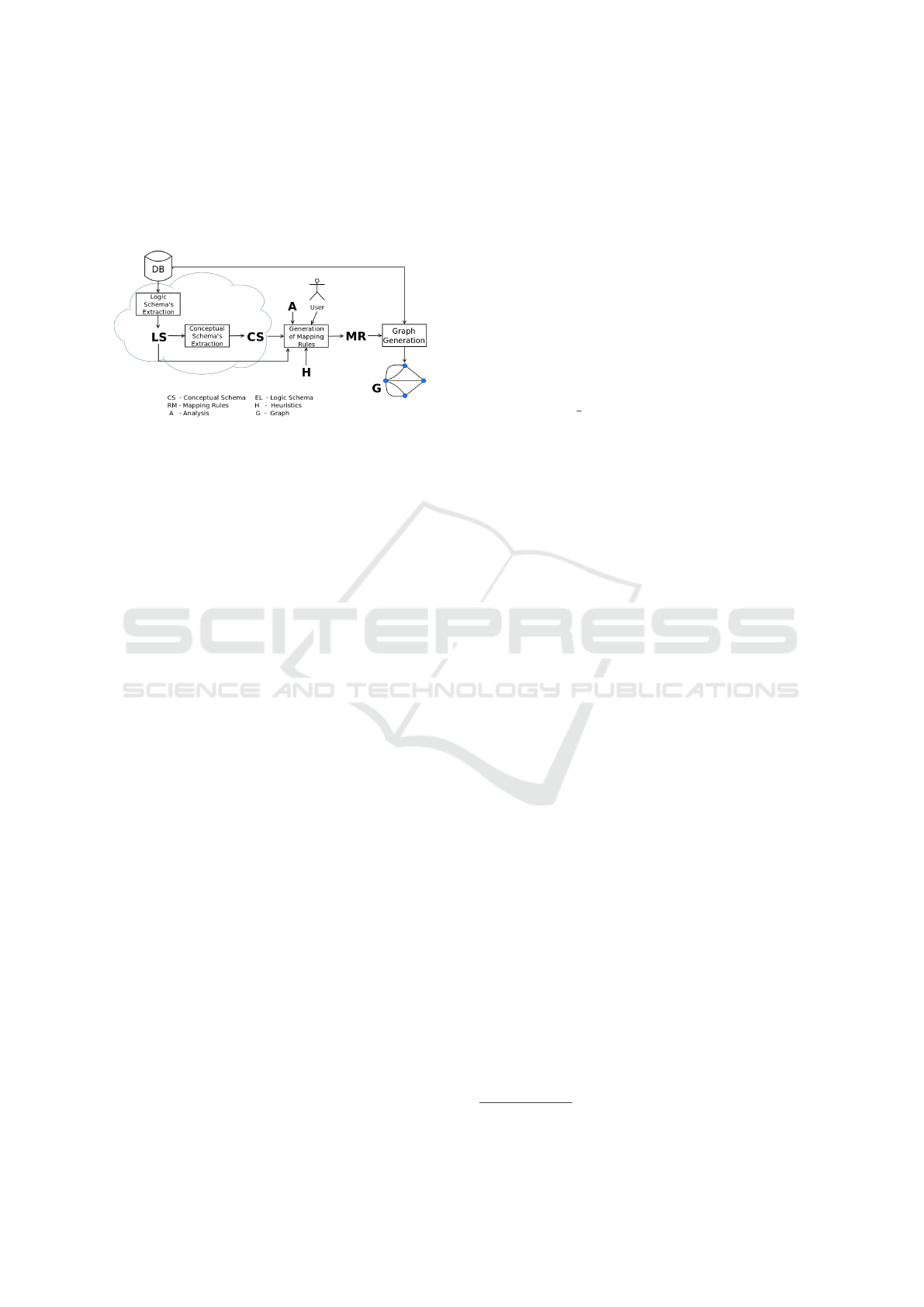
it is difﬁcult to get some automatic support for this

action. However, it is important to produce the ER

schema, due to its semantic richness and expressive-

ness in representing the reality. To do this, it may be

necessary to count on the domain specialists.

Figure 2: Flow chart for the proposed approach.

Then, taking the ER schema (CS), we analyze

each pair of entities (E

, E

) for which there is a re-

lationship (R), as the example in Figure 1. At this

point, the designer may consider different graph mo-

deling alternatives. The idea is to stimulate a deeper

exploration of the schema to obtain different graphs.

However, this is not an easy task, since there are many

different analysis, and besides, there are some (more

than one) graph modeling alternatives that can be ex-

plored. Therefore, the main goal of this work is to

come up with some user support. We assume that gi-

ven a set of analysis algorithms (A) and a set of heu-

ristics (H), it is possible to lead the user on choosing

a useful graph modeling. Finally, based on the user

choice, a set of mapping rules (MR) will transform

data into the desired graph (G).

To identify such heuristics, some experiments

were performed with focus on link prediction algo-

rithms. The next section describes them, as well as

their results and the extracted heuristics.

5 EXPERIMENTS AND RESULTS

5.1 Experiments Settings

For the experiments, an ordinary conceptual modeling

situation was considered, where a pair of entities

, E

) is connected by only one binary relations-

hip with a multivalued attribute (see Figure 1). This

schema situation appears recurrently in database mo-

deling projects. Exploring a speciﬁc ordinary case al-

lows us to apply and compare different analysis and

metrics results. It is worth to mention that it is pos-

sible to explore the whole schema by focusing in its

parts, one at a time.

Figure 3 shows the ﬂow chart for the heu-

ristic construction. Given a dataset (DB) and a

conceptual schema (CS), different graph modelings

, G

, ..., G

) are generated. And for all these op-

tions, a pre-selected analysis set (A

, A

, ..., A

) is ap-

plied. Results have been generated from each pair

graph-analysis R

, A

), such that (1 ≤ k ≤ n × m),

and from such results, heuristics (H) were created.

The experiments were performed over well-

known and open datasets, so it was possible and fe-

asible to check the results.

The ﬁrst dataset, which we name as SMDB (Sam-

ple Movie Database), contains data about persons

(125 instances) and movies (38 instances), with a rela-

tionship “acted in” which contains a multivalued at-

tribute “role” between them. That multivalued attri-

bute means that one person may play more than one

role in the same movie.

The ﬁrst experiment used intentionally a small da-

taset to easily explore the results, their impact on mo-

dels and identify some kind of pattern which can help

in creation of the heuristics. The second experiment

used a larger dataset in order to conﬁrm the behavior

observed in the ﬁrst experiment. This dataset contains

movies and actors data from TMDB

To assure some alignment between the experi-

ments, both datasets have the same domain and ER

schema, which is showed in Figure 4.

Although there are different kinds of graphs, for

this work we used the property graph, presented in

section 2.2. Our choice is laid on its wide use in the

literature.

5.2 SMDB Experiment

We have used in this experiment link prediction me-

trics among persons and movies which they acted for

a time period of twenty years in the dataset. To pre-

dict connections between persons who acted in mo-

vies and to facilitate the prediction of contemporary

actors, it was considered a restricted time window, re-

moving information about old time movies. Just per-

sons and movies between 1992 and 2012 have been

selected from the original database. Data about per-

son name and birthday; movie title, releasing data and

tagline; relationships about acting have been maintai-

ned. In this experiment Neo4j has been used to store

the dataset as a graph. To analyze and visualize the

graphs the igraph R package module was used.

We can divide this experiment in three stages.

Each stage corresponds to a variation in graph mo-

del representation. As it is possible to store informa-

tion about the data in the nodes or in the edges of the

http://www.themoviedb.org/

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

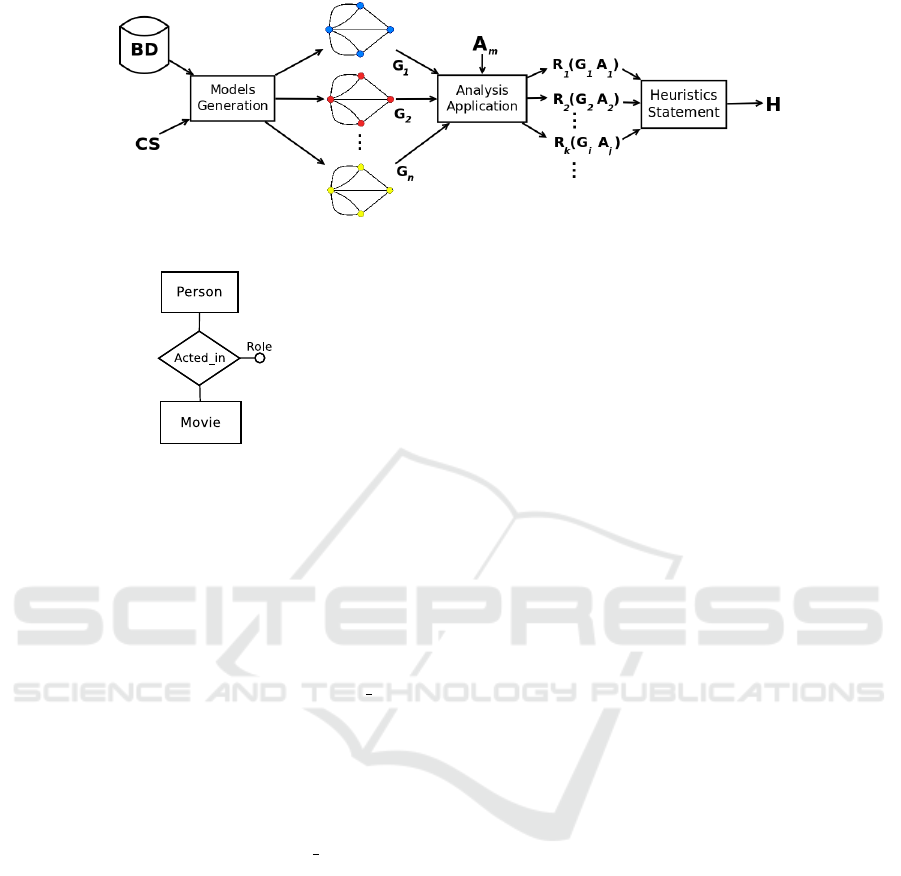
Figure 3: Flow chart for the heuristic construction.

Figure 4: ER schema for the Experiments datasets.

graph, the goal of the ﬁrst two stages is to evaluate the

impact of topological changes in the link prediction

results.

In the ﬁrst stage, the graph model keeps two ty-

pes of nodes and one type of relationship between

them. Nodes can be of Person or Movie type. The

Person nodes have one attribute called Name. Mo-

vie nodes have three attributes: Title, Releasing and

Tagline. The edges have just one type, Acted in, and

only one attribute, Role. Actors can have more than

one role in their attribute. Figure 5(a) shows a graph

cut-off obtained in this stage.

The second stage keeps the same information of

the graph of the ﬁrst stage. However, in the second

stage there are three types of nodes: Person, Movie

and Acting. The edges of type Acted in in the ﬁrst

stage (connecting Person or Movie nodes) are now re-

presented as nodes. Moreover, Acting nodes have an

attribute called Role. In this graph, nodes are con-

nected by edges with no label and no attributes. Fi-

gure 5(b) shows a graph cut-off for this stage.

The graph model of the third stage have a small

difference if compared with the second one. Nodes

and edges are of the same type and have the same at-

tributes. But, in the new graph model, Acting nodes

are split in as many nodes as there are distinct role va-

lues for the Role attribute. For instance, if some actor

has two or more roles in a movie, the acting node of

graph model 2 will be split into two or more different

nodes, each one representing a single role of the actor

in that movie. Figure 5(c) shows a cut-off of the graph

for the third stage.

Using the metrics from the analysis set it was pos-

sible to extract some predictions. Some of them were

easy to understand and easily we comprehended the

settings of each metric to suggest a new edge between

two nodes. Each metric analyzes some graph topolo-

gical information to return the predictions.

For instance, for every pair of existing nodes in

all the three graph models, it is possible to compute

the Katz coefﬁcient (Katz is a path assembling metric

and the graphs are connected). Table 2 shows for four

pairs of nodes the Katz coefﬁcient obtained in each

model. The analyzed pairs are Person x Person and

Movie x Movie, the only kind which are present in

every model. On the other hand, there are some pairs

of nodes that can not be analyzed in all the three mo-

dels. For instance, common neighbor metrics as Jac-

card and Adamic/Adar can not be computed for pairs

of type Person x Person or Movie x Movie in models

2 and 3.

Figure 5 illustrates the different conditions to

compute common neighbor coefﬁcient value for each

type of pairs of nodes in the three models. For a spe-

ciﬁc pair of nodes, Hugo Weaving and Tom Hanks

(highlighted in blue), the Jaccard and Adamic/Adar

coefﬁcients can be computed in ﬁrst model, because

in the corresponding graph they share the same neig-

hbor, Cloud Atlas (Figure 5(a)). In the second model,

it is not possible to compute the last two coefﬁcients

for this speciﬁc pair of nodes, because they do not

share common neighbors (Figure 5(b)). However, in

model 2 it is possible to compute those coefﬁcients for

the corresponding Acting nodes (highlighted in blue).

In model 3, it is not possible to compute the Jaccard

and Adamic/Adar coefﬁcients for the mentioned pair,

for the same reasons mentioned in model 2 (Figure

5(c)).

Another example appears in model 1. It is not

possible to compute Jaccard and Adamic/Adar coefﬁ-

cients for the pairs of nodes Person x Movie, because

these types of nodes are adjacent in the corresponding

graph, so they do not have common neighbors. Ho-

wever, it is possible to compute those coefﬁcients in

models 2 and 3 for that type of pair. The same occurs

for pairs of type Person x Person and Movie x Movie.

Managing Graph Modeling Alternatives for Link Prediction

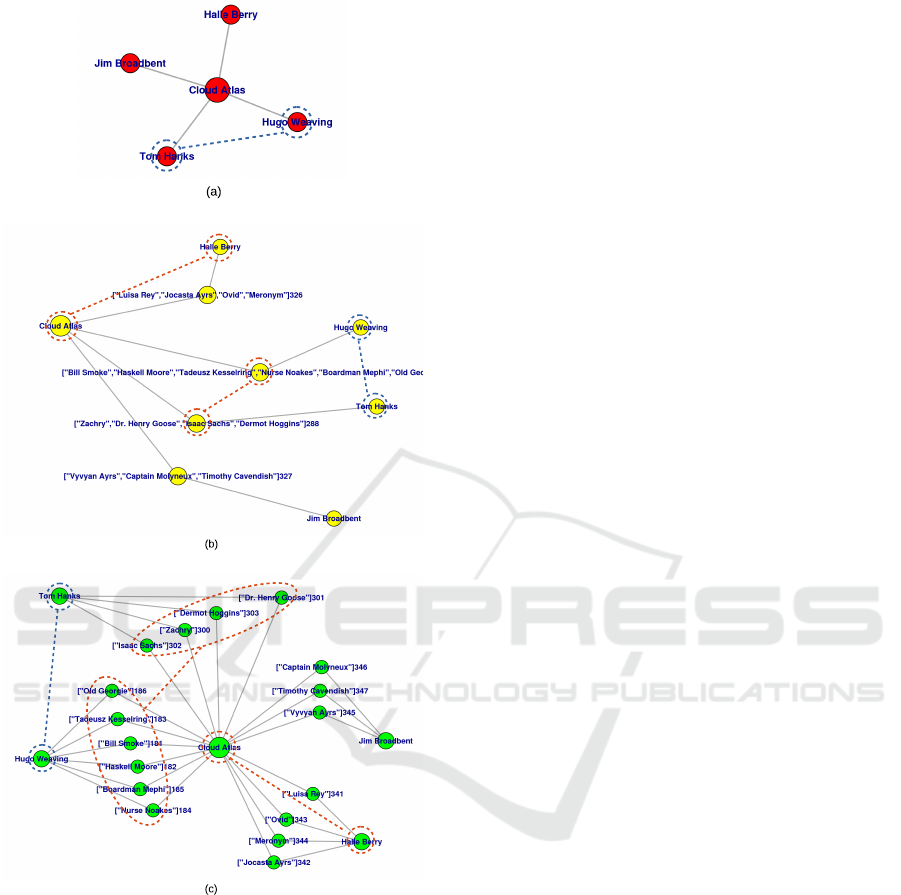
Figure 5: SMDB graph cut-off for models 1, 2 and 3.

As said before, some pairs of nodes can be used to

predict links by common neighbor based coefﬁcients

or not, depending on the chosen model.

5.3 Heuristics

The following heuristics were identiﬁed based on the

previously reported experiment. They were stated ba-

sed on an ordinary conceptual schema situation, fre-

quently found in any domain, where a pair of entities

are connected by one binary relationship, as explained

in Section 4.

With respect to link prediction analysis, different

graph modelings allow different interpretations and

predictions. In other words, the choice of the graph

modeling and the analysis to be used on it, depends

on what it is intended to predict. The following heu-

ristics addresses this issue.

Given the conceptual schema situation represen-

ted by Figure 1, ﬁrst the user needs to decide what

he wants to predict. Possible relations are: E

× E

1 j

× E

2 j

, E

× E

2 j

, R

× R

, A

× A

, E

× R

× A

. Once prediction is deﬁned, then just some

of the following graph modelings possibilities will

attend his need. The alternatives are:

Model 1: Instances of entities E

and E

as nodes,

instances of relationship R as edges with labels;

Model 2: Instances of entities E

and E

, and

instances of relationship R are nodes connected by

edges without labels;

Model 3: Instances of entities E

and E

, and values

of attributes A from R are nodes, which are connected

by edges without labels.

Table 1 shows the correspondence between these

three possible graph modeling, and ﬁve types of re-

lation (pairs) predictions, identifying which metrics

(Jaccard, Adamic/Adar, Katz) may be used on a mo-

del to reach a prediction.

For instance, for the ﬁrst graph modeling possibi-

lity (model 1), if the user intends to predict pairs of

nodes of the same entity, E

1 j

or E

2 j

, then,

all metrics (Jaccard, Adamic/Adar and Katz) are

applicable. On the other hand, if the user intends to

predict relations between different entities, E

2 j

only path assembling predictions, such as Katz,

are applicable. Based on Table 1, more formally,

heuristics can be expressed as follows:

Heuristic 1: For predictions E

× E

1 j

or E

× E

2 j

Model 1 may be used for Jaccard, Katz and Ada-

mic/Adar analysis; Models 2 and 3 may be used only

for Katz analysis.

Heuristic 2: For predictions E

× E

2 j

: Model 1 may

be used only for Katz analysis; Models 2 and 3 may

be used for Katz, Adamic/Adar and Jaccard analysis.

Heuristic 3: For predictions R

× R

: Model 2 may

be used for Katz, Adamic/Adar and Jaccard analysis.

Heuristic 4: For predictions A

× A

: Model 3 may

be used for Katz, Adamic/Adar and Jaccard analysis.

Heuristic 5: For predictions E

× R

: only Model 2

may be used for Katz analysis.

Heuristic 6: For predictions E

× A

: only Model 3

may be used for Katz analysis.

Although these heuristics are limited to three mo-

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

deling alternatives, and three distinct prediction ana-

lysis, they can be extended. Other modeling alternati-

ves and prediction analysis can be addressed.

5.4 TMDB Experiment

Aiming to conﬁrm the previous experiment results,

new experiments have been made using a greater da-

taset with the same previous analysis. A subset from

the original set has been extracted, where movies and

actors refer to “Crime” movies. The TMDB experi-

ment used the same data schema of the last experi-

ment. To assure the link prediction it was considered

the largest connected component from the modeled

graph of each modeling. The obtained graph for the

ﬁrst model has 4486 nodes and 5046 edges. The se-

cond model graph has 9532 nodes and 10092 edges.

And the last and third model graph has 9561 nodes

and 10150 edges.

The goal of this experiment is to assure if the

recognized behaviors from previous experiment are

the same for a largest dataset. Results showed that

the same patterns were found, conﬁrming the heu-

ristics. In addition, it was possible to evaluate the

gains quantitatively (Section 5.4.1) and qualitatively

(Section 5.4.2), as follows. First we show a quantita-

tive analysis highlighting the richness of results that

we can get with the different modelings. Then, we

proceed with a qualitative analysis in order to illus-

trate the usefulness of this approach.

5.4.1 Quantitative Analysis

First we focus the analysis on Katz results, because

this coefﬁcient allowed us to compare the three mo-

deling alternatives.

The types of node pairs suggested by Katz were

the same for each model as in Section 5.2. Note that

in Table 2, the coefﬁcient value for a speciﬁc pair of

nodes, obtained for model 1 is greater than for the ot-

her models. Similarly, this behavior occurred in the

second experiment. This is due to the fact that mo-

dels 2 and 3 are bigger than model 1, in terms of the

number of nodes and edges, which makes the Katz

coefﬁcient values to be diluted in those models.

Table 3 shows the number of suggested pairs

for each model using Katz coefﬁcient. It is worth

to mention that models 2 and 3 provide much more

pairs than model 1. Besides, as mentioned before,

they also provide new types of pairs such as Movie

x Acting and Acting x Acting for model 2, and Role

x Role and Movie x Role for model 3, enriching the

results.

In order to perform a more strict analysis, we

chose to focus on the best ranked results. Therefore,

we established a threshold with the following value 1

x 10

−5

, based on value variation when using model 1.

Using this threshold, Table 4 shows that 14% of the

pairs were selected from those suggested for model 1

in Table 3, and 1.19% and 1.16% were selected for

models 2 and 3, respectively.

Differently from what shows Table 3, the total

number of suggested pairs shown in Table 4, is gre-

ater for model 1 than for models 2 and 3. However,

the variety of node types is greater for models 2 and 3

than model 1, showing richer results.

Now let us analyze the best ranked types of pairs

in the context of the three coefﬁcients. According to

Tables 5, 6 and 7, it is possible to identify different

types of pairs in the top positions for model 1. Note

that for Jaccard (Table 5) the pair Person x Person is

the best ranked, while for Adamic/Adar (Table 6) the

pair Movie x Movie is the best, and ﬁnally for Katz

(Table 7) the best pairs are Movie x Person. The rea-

son of this different behavior is related to the nature of

the coefﬁcients. For instance, since in this model the

graph has edges between Actor and Movie nodes, the

greatest value for Jaccard can happen in two cases:

1. When two actors acted only in the same movies

and no other movie separately, and

2. When two distinct movies have exactly the same

casting.

Case (i) is more probable to happen, because it is

more difﬁcult that two movies have the same casting.

Adamic/Adar also works with common neighbors

as Jaccard. However it penalizes the pair when its

common neighbors are highly connected. For in-

stance, if two actors have many movies in common,

but these movies have a high number of connections

to other actors, this pair is not so signiﬁcant for Ada-

mic/Adar than for Jaccard. Different from Jaccard,

for Adamic/Adar, some pairs of movies will probably

be shown in the top positions of the ranking. Typi-

cally, these are movies with just a few common neig-

hbors (actors), which do not participate in many other

movies. Table 6 shows the ﬁve top movie pairs that

have this characteristic.

Therefore, according to the user needs, i.e. type

of pairs, the right analysis should be chosen, or yet,

results could complement each other.

As said before, the Katz ranking (Table 7) differs

from the other rankings. It prioritizes pairs of nodes

connected by short length paths in the graph. The best

ranked suggestions are pairs Movie × Person, already

linked by an edge in the graph.

Managing Graph Modeling Alternatives for Link Prediction

Table 1: Suggested pairs of nodes for all coefﬁcients.

× E

1 j

× E

2 j

× E

2 j

× R

× A

× R

× A

Model 1

Jaccard, Katz,

Adamic/Adar

Jaccard, Katz,

Adamic/Adar

Katz - - - -

Model 2 Katz Katz

Jaccard, Katz,

Adamic/Adar

Jaccard, Katz,

Adamic/Adar

- Katz -

Model 3 Katz Katz

Jaccard, Katz,

Adamic/Adar

Jaccard, Katz,

Adamic/Adar

- Katz

Table 2: Katz coefﬁcients for suggested pairs for 3 models

in SMDB dataset (enclosed in brackets the ranking of each

pair Person x Person and Movie x Movie).

Model 1 Model 2 Model 3

Tom Hanks x Meg Ryan 0.188 - [363] 0.006 - [4239] 0.023 - [4629]

Tom Hanks x Bill Paxton 0.196 - [360] 0.006 - [4247] 0.022 - [4635]

The Matrix x

The Matrix Reloaded

0.295 - [110] 0.009 - [4030] 0.010 - [6766]

Apollo 13 x

The Polar Express

0.089 - [543] 0.002 - [5246] 0.075 - [2524]

Table 3: Number of suggested pairs for each model with

Katz in TMDB dataset.

Model 1 Model 2 Model 3

Person x Person 6.546.771 6.514.245 6.514.246

Person x Movie 1.353.506 1.332.090 1.332.090

Movie x Movie 69.751 67.896 67.896

Movie x Acting - 1.485.963 -

Movie x Role - - 1.497.033

Acting x Acting - 8.106.351 -

Role x Role - - 8.227.596

Person x Acting - 14.537.471 -

Person x Role - - 14.645.770

Total 7.970.028 32.044.016 32.284.631

Table 4: Number of suggested pairs for each model with

threshold 1 x 10

−5

in TMDB dataset.

Model 1 Model 2 Model 3

Person x Person 1.049.949 32.573 21.677

Person x Movie 328.262 17.340 17.977

Movie x Movie 31.307 1.431 1.431

Movie x Acting - 40.191 -

Movie x Role - - 40.195

Acting x Acting - 168.672 -

Role x Role - - 171.996

Person x Action - 124.114 -

Person x Role - - 124.385

Total 1.409.518 384.321 377.661

Table 5: Jaccard ranking for Model 1 in TMDB dataset.

Model 1

Tony Kendall x Gert Gnther Hoffmann 0,875

Gert Gnther Hoffmann x Brad Harris 0,875

Heinz Weiss x George Nader 0,875

Stringer Davis x Charles ’Bud’ Tingwell 0,8

Charles ’Bud’ Tingwell x Margaret Rutherford 0,8

John Randolph Jones x Udo Kier 0,666

5.4.2 Qualitative Analysis

Because of the richness of TMDB dataset, it was

possible to get new interpretations for the results.

Table 6: Adamic/Adar ranking for Model 1 in TMDB data-

set.

Model 1

Beck - Flickan x Beck - Den japanska 9,566

Dancer in the Dark x Dogville 7,402

The Spider Woman x The Adv. of Sherlock Holmes 5,770

36 x The Last Deadly Mission 5,770

Gert Frobe x Wolfgang Preiss 2,252

Table 7: Katz ranking for Model 1 in TMDB dataset.

Model 1

Armin Mueller Stahl x Angels & Demons 13,33247

Stellan Skarsgrd x Angels & Demons 13,22136

Carmen Argenziano x Angels & Demons 12,31250

Tom Hanks x Angels & Demons 12,25930

Elya Baskin x Angels & Demons 12,24942

Instead of analyzing the rankings for each model, we

selected some speciﬁc suggestions of pairs and have

compared the results that could be obtained with the

different analysis. For instance, to answer the query

which movies are similar, we focused on the Movie

× Movie pair type. Table 8, for Model 1, shows

5 suggested pairs using Katz analysis, which are

different from those suggested using Adamic/Adar,

showed on Table 6. It is worth mention that the bro-

ader nature of Katz analysis enabled to get different

and complementary results.

Table 8: Katz rankings for pairs Movie × Movie of three

models in TMDB dataset.

Model 1 Value

Angels & Demons x Dogville 3,9847

Angels & Demons x Dancer in the Dark 3,3753

Angels & Demons x Identity 2,6619

Angels & Demons x The Green Mile 2,2638

Angels & Demons x The Name of the Rose 2,1899

Model 2 Value

Angels & Demons x Dogville 0,0105

Angels & Demons x Dancer in the Dark 0,0088

Angels & Demons x Identity 0,0087

Angels & Demons x The Name of the Rose 0,0073

Angels & Demons x Eastern Promises 0,0072

Model 3 Value

Angels & Demons x Dogville 0,0105

Angels & Demons x Dancer in the Dark 0,0088

Angels & Demons x Identity 0,0087

Angels & Demons x The Name of the Rose 0,0073

Angels & Demons x Eastern Promises 0,0072

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

Moreover, it was observed (on Table 8) that Katz

analysis results were almost the same for the three

models. At a ﬁrst look, we might think that models

2 and 3 are not useful. However, remember that with

them, it is possible to get different suggested types of

pairs, besides the Movie × Movie pairs. For instance,

we can answer the following question: what roles can

we suggest for a speciﬁc actor/actress?. This ques-

tion can be answered by Katz analysis on models 2

and 3. Let us focus on pairs Person × Role suggested

by Katz on model 3. If we take Joe Pesci as a refe-

rence actor, which roles could be close to him, and

maybe a good suggestion for a future movie part? To

do this, we need to discard Katz analysis top ranked

results, and take just results which include Joe Pesci

own roles (movies in which he acted). The subsequent

top ranked pairs bring roles from Joe Pesci neighbor-

hood. These roles are from actors he co-acted with,

or even more distant ones. For example, we could

take from the ranking, some pairs Person × Role with

Joe Pesci as person and roles from Robert De Niro

(such as Father Bob and Travis Bickle), and from Tom

Hanks (such as Robert Langdon and Paul Edgecomb).

See in Table 9 the corresponding coefﬁcient for these

pairs. We observe that Joe Pesci take part in 4 movies

with Robert De Niro, whereas Joe Pesci never acted in

the same movie with Tom Hanks, considering infor-

mation in our dataset. Observe that actors that acted in

common movies has Katz coefﬁcient greater (for in-

stance, Joe Pesci and Robert De Niro). This fact can

be useful when looking for actors that are able to play

a speciﬁc role, or when looking for a replacement for

an actor.

Table 9: Katz results for pairs Person × Role with Joe Pesci

in TMDB dataset.

Pair Model 3

Joe Pesci x Father Bobby 2,909633e-04

Joe Pesci x Travis Bickle 2,902883e-04

Joe Pesci x Robert Langdon 9,878335e-09

Joe Pesci x Paul Edgecomb 1,757311e-10

Another interesting observation is when we com-

pare again pairs Person × Role and consider the role

Frank Sparks played by actor William Forsythe. The

Katz coefﬁcient for the pair Joe Pesci × Frank Sparks

is 6,64497e-05, lower than the coefﬁcient for the pair

Joe Pesci × Father Bobby. We can observe that there

are shortest paths with the same length between the

nodes Joe Pesci and Father Bobby and between the

nodes Joe Pesci and Frank Sparks in the associated

graph, but Katz coefﬁcient is greater for the pair Joe

Pesci and Father Bobby because exist more than one

shortest path between them.

6 CONCLUSION AND FUTURE

WORKS

This work addressed the task of mapping relational

data into graph representation. It proposes a set of

heuristics, aiming to help the user to model a graph.

We highlight that even with a set of analysis coefﬁ-

cients in hands, before applying them, it is necessary

to acknowledge the conceptual and logical schema

from Relational Databases to better understand the

data and the prediction intention, and thus reach a

well modeled graph.

Initial experiments were reported and enabled to

identify a set of heuristics. These experiments focu-

sed on topological analysis. They applied three link

prediction metrics over two different datasets: SMDB

(a toy example) and TMDB. However, additional ex-

periments are needed, using datasets from different

domains, and a larger set of analytical coefﬁcients, in

order to validate or maybe extend these heuristics.

Finally, in the reported experiments, we focu-

sed only on the binary relationship modeling con-

struct. Although this is an ordinary conceptual mo-

deling construct, that appears recurrently in many da-

tabase modeling projects, we plan to use other mo-

deling constructs, such as n-ary relationships, specia-

lization/generalization, and aggregation.

REFERENCES

Aggarwal, C. C. (2011). Social Network Data Analytics.

Springer Publishing Company, Incorporated, 1st edi-

tion.

Bizer, C. (2003). D2R MAP - A database to RDF mapping

language. In Proc. of the Twelfth Intern. World Wide

Web Conf. - Posters, WWW 2003, Budapest, Hungary,

2003.

Bordoloi, S. and Kalita, B. (2013). Designing graph data-

base models from existing relational databases. Int. J.

of Computer Applications, 74(1):25–31.

Chen, P. P.-S. (1976). The entity-relationship model;toward

a uniﬁed view of data. ACM Trans. Database Syst.,

pages 9–36.

Codd, E. F. (1970). A relational model of data for large

shared data banks. Commun. ACM, pages 377–387.

Easley, D. and Kleinberg, J. (2010). Networks, Crowds,

and Markets: Reasoning About a Highly Connected

World. Cambridge University Press, New York, NY,

USA.

Heuser, C. (2009). Projeto de banco de dados : Volume 4 da

erie Livros did

aticos inform

atica UFRGS. Bookman.

Jindal, A., Rawlani, P., Wu, E., Madden, S., Deshpande, A.,

and Stonebraker, M. (2014). Vertexica: Your relatio-

nal friend for graph analytics! Proc. VLDB Endow.,

7(13):1669–1672.

Managing Graph Modeling Alternatives for Link Prediction

Liben-Nowell, D. and Kleinberg, J. (2007). The link-

prediction problem for social networks. Journal of

the American Soc. for Inf. Sci. and Tech., pages 1019–

1031.

Rodriguez, M. A. and Neubauer, P. (2010). Constructions

from dots and lines. Bulletin of the American Society

for Information Science and Technology, 36(6):35–41.

Simmen, D., Schnaitter, K., Davis, J., He, Y., Lohariwala,

S., Mysore, A., Shenoi, V., Tan, M., and Xiao, Y.

(2014). Large-scale graph analytics in aster 6: Brin-

ging context to big data discovery. Proc. VLDB En-

dow., 7(13):1405–1416.

Virgilio, R. D., Maccioni, A., and Torlone, R. (2014a). Con-

verting relational to graph databases. In First Interna-

tional Workshop on Graph Data Management Expe-

riences and Systems.

Virgilio, R. D., Maccioni, A., and Torlone, R. (2014b).

Model-driven design of graph databases. In Concep-

tual Modeling: 33rd International Conference, ER

2014, Atlanta, GA, USA, October 27-29, 2014. Pro-

ceedings, pages 172–185.

Wardani, D. W. and Kng, J. (2014). Semantic mapping re-

lational to graph model. In Computer, Control, Infor-

matics and Its App., 2014, pages 160–165.

Xirogiannopoulos, K., Khurana, U., and Deshpande, A.

(2015). Graphgen: Exploring interesting graphs in re-

lational data. PVLDB, 8(12):2032–2043.

Xirogiannopoulos, K., Srinivas, V., and Deshpande, A.

(2017). Graphgen: Adaptive graph processing using

relational databases. In Proceedings of the Fifth Inter-

national Workshop on Graph Data-management Ex-

periences & Systems, GRADES’17, pages 9:1–9:7,

New York, NY, USA. ACM.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems