A MapReduce Approach for Mining Multi-Perspective Declarative

Process Models

Christian Sturm, Stefan Sch

onig and Stefan Jablonski

University of Bayreuth, Germany

Keywords:

Process Mining, Process Discovery, Multi-Perspective Process Model, Declare, MapReduce, Business

Process Management.

Abstract:

Automated process discovery aims at generating a process model from an event log. Such models can be

represented as a set of declarative constraints where temporal coherencies can also be intertwined with de-

pendencies upon value ranges of data parameters and resource characteristics. Existing mining tools do not

support multi-perspective constraint discovery or are not efﬁcient enough. In this paper, we propose an efﬁ-

cient mining framework for discovering multi-perspective declarative models that builds upon the distributed

processing method MapReduce. Mining performance and effectiveness have been tested on several real-life

event logs.

1 INTRODUCTION

Process mining is the area of research that embraces

the automated discovery, conformance checking and

enhancement of process models. Automated process

discovery aims at generating a process model from

an event log consisting of traces, such that each trace

corresponds to one execution of the process. Each

event in a trace consists as a minimum of an event

class (i.e., the activity to which the event corresponds)

and a timestamp. In some cases, other information

may be available such as the performer of the acti-

vity as well as data produced by the event in the form

of attribute-value pairs. Discovery is of particular va-

lue for processes that offer various options to execute

them. Those processes are often referred to as ﬂex-

ible, unstructured or knowledge-intense. Frequently,

procedural process models resulting from discovery

are colloquially called Spaghetti models due to their

complex structure (van der Aalst, 2011). Discove-

red process models can alternatively be represented

as a set of declarative constraints, i.e., rules for di-

rectly representing the causality of the behaviour (Pi-

chler et al., 2011). The advantages of declarative

languages such as Declare (Pesic et al., 2007) or

DPIL (Zeising et al., 2014) have been emphasized

in the literature. It is also well known that behavi-

our is typically intertwined with dependencies upon

value ranges of data parameters and resource charac-

teristics (de Leoni et al., 2016). Therefore, Declare

has been extended towards Multi-Perspective Declare

(MP-Declare) (Burattin et al., 2015). However, state-

of-the-art mining tools such as MINERful (Di Cic-

cio and Mecella, 2013; Di Ciccio and Mecella, 2015)

and DeclareMiner (Maggi, 2013) do not support MP-

Declare at this moment. In (Sch

onig et al., 2016) a

ﬁrst approach to enable the discovery of MP-Declare

constraints has been proposed. However, it has not

been investigated how this complex mining task can

be performed in an efﬁcient way.

In this paper, we address this open research pro-

blem by proposing an efﬁcient mining framework for

discovering MP-Declare models that leverages latest

big data analysis technology and builds upon the dis-

tributed processing method MapReduce. We intro-

duce parallelizable algorithms for discovering com-

monly used types of MP-Declare constraints. The

proposed solution, however, can be applied to all ot-

her MP-Declare constraint types as well. In contrast

to related solutions, the proposed framework consi-

ders traces in one direction solely which leads to a

crucial beneﬁt w.r.t. performance. Mining perfor-

mance and effectiveness have been tested on several

real-life event logs.

The paper is structured as follows. Section 2 in-

troduces the language and semantics of MP-Declare.

Section 3 describes the distributed framework we pro-

pose to speed up multi-perspective process discovery.

Section 4 describes the implementation approach that

we developed. Section 4.2 presents the evaluation of

Sturm, C., Schönig, S. and Jablonski, S.

A MapReduce Approach for Mining Multi-Perspective Declarative Process Models.

DOI: 10.5220/0006710305850595

In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 585-595

ISBN: 978-989-758-298-1

585

our technique with real-life cases. Section 5 discus-

ses related work before Section 6 that concludes the

paper.

2 RESEARCH BACKGROUND

In this section, we ﬁrst illustrate the research problem

that we are addressing and summarize concepts of

Declare, MP-Declare and MP-Declare mining.

2.1 Declarative Process Modelling

Declarative constraints are strong in representing the

behaviour of ﬂexible business processes. Modeling

languages like Declare (Pesic et al., 2007) describe

a set of constraints that must be satisﬁed throughout

the process. Constraints, in turn, are based on tem-

plates. Templates are patterns that deﬁne paramete-

rized classes of properties, and constraints are their

concrete instantiations. Semantics of such langua-

ges are formalized using logics such as Linear Tem-

poral Logic over ﬁnite traces (LTL

) (Montali et al.,

2010). Standard Declare only deﬁnes constraints like

response (G(A → FB)) or alternateResponse (G(A →

X(¬AUB))) that exclusively focus on behavioural as-

pects. Here, the F, X, G, and U LTL

future opera-

tors have the following meanings: formula Fψ

me-

ans that ψ

holds sometime in the future, Xψ

means

that ψ

holds in the next position, Gψ

says that ψ

holds forever in the future, and, lastly, ψ

Uψ

means

that sometime in the future ψ

will hold and until that

moment ψ

holds (with ψ

and ψ

LTL

formulas).

The O, Y and S LTL

past operators have the follo-

wing meaning: Oψ

means that ψ

holds sometime in

the past, Yψ

means that ψ

holds in the previous po-

sition, and ψ

Sψ

means that ψ

has held sometime

in the past and since that moment ψ

holds. Consi-

der, for example, the response constraint G(A → FB).

It indicates that if A occurs, B must eventually fol-

low. Therefore, this constraint is fully satisﬁed in

traces such as t

= hA, A,B,Ci, t

= hB,B,C,Di, and

= hA,B,C,Bi, but not for t

= hA,B,A,Ci because,

in this case, the second occurrence of A is not follo-

wed by a B. In t

, it is vacuously satisﬁed (Burat-

tin et al., 2012), i.e., in a trivial way, because A ne-

ver occurs. An activation activity of a constraint in

a trace is an activity whose execution imposes, be-

cause of that constraint, some obligations on the exe-

cution of other activities (target activities) in the same

trace. For example, A is an activation activity for

the response constraint G(A → FB) and B is a tar-

get, because the execution of A forces B to be exe-

cuted, eventually. An activation of a constraint le-

ads to a fulﬁlment or to a violation. Consider, again,

G(A → FB). In trace t

, the constraint is activated and

fulﬁlled twice, whereas, in trace t

, it is activated and

fulﬁlled only once. In trace t

, it is activated twice

and the second activation leads to a violation (B does

not occur subsequently).

A central shortcoming of languages like Declare

is the fact that templates are not capable of expres-

sing the connection between execution order of acti-

vities and other perspectives of the process. Consider

the example of a loan application process. An analyst

would be interested to learn about constraints such as

the following:

1. Activation conditions: When a loan was requested

and account balance > 4,000 EUR, the loan was

subsequently granted in 95% of the cases.

2. Correlation conditions: When a loan was re-

quested, the loan was subsequently granted and

amount requested = amount granted in 95% of

the cases.

3. Target conditions: When a loan was requested, the

loan was subsequently granted in 95% of the cases

by a speciﬁc member of the ﬁnancial board.

4. Temporal conditions: When a loan was requested,

the loan was subsequently granted within the next

30 days in 95% of the cases.

The importance of more complex constraints that

integrate activation, correlation, target and temporal

dependencies has been emphasized by prior research

and has led to the deﬁnition of a multi-perspective

version of Declare (Burattin et al., 2015), multi-

perspective Declare (MP-Declare) formally deﬁned

using LTL

2.2 Mining Metrics

In this subsection, we describe the metrics that we use

to discriminate those constraints that are fulﬁlled in

the majority of cases in the event log, from those that

are rarely satisﬁed, namely support and conﬁdence.

We consider two notions of support already deﬁned

in the literature, namely the event-based support (Di

Ciccio and Mecella, 2015) and the trace-based sup-

port (Maggi et al., 2011).

Support. It is the number of fulﬁlments of a

constraint divided by the number of occurrences

of the condition of a constraint. In the exam-

ple of Section 2.1, the four occurrences of A fulﬁl

response(A,B), out of which 2 occur in t

, 1 in t

and

1 in t

. Thereupon, it scales the number of events ful-

ﬁlling the constraint by the number of events that fulﬁl

the activation only. In the example, the ﬁve occurren-

ces of A satisfy the activation. Therefore, the event-

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

586

based support of response(A,B) is equal to 4/5, na-

mely 0.8.

Conﬁdence. It is the product of support and the

fraction of traces in the log where the condition (im-

plications) or the constrained activity (not implica-

tions) occurs. In the example, the conﬁdence is

4/5 × 3/4 = 0.6, A occurs in 3 traces over 4.

The work conducted in (Sch

onig et al., 2016) ad-

dressed the discovery of MP-Declare models. This

research showed that the discovery of MP-Declare

allows for the acquisition of knowledge that goes

beyond classical declarative mining. However, it has

not been investigated how this complex mining task

can be performed in an efﬁcient way. Until now, no

scalable and high performant mining approach that

can fully support MP-Declare is available.

3 MAP-REDUCE FOR MINING

In this section, we describe an efﬁcient framework

for discovering MP-Declare constraints. After giving

insights into the internal infrastructure, we explain

the parallelisable discovery algorithms for commonly

used MP-Declare constraints that are used to disco-

ver models under consideration of further perspecti-

ves. In contrast to former solutions, this framework

can be used out of the box and the algorithm has to

consider the traces in one direction solely which le-

ads to a crucial beneﬁt with regard to performance.

3.1 Architecture and Infrastructure

The basic idea of the algorithm builds upon the

MapReduce computation model. One key advantage

is the inbuilt opportunity for executing the calculati-

ons in parallel, which gives an enormous performance

boost, also in view of the analysis of an event log. At

ﬁrst, the scaffolding of the MapReduce algorithm is

described brieﬂy w.r.t. the discovery of a process mo-

del described later on. In the next section, we use an

example log containing two traces deﬁned in Equa-

tion 1.

= ha,b, b, ci t

= ha,c, di (1)

MR-I

trace

MR-

memory

Support

Confidence

Figure 1: Infrastructure of the calculation.

To compute the support and conﬁdence metrics, two

MapReduce jobs are required, MR-I and MR-II (cf.

Figure 1).

3.1.1 MR-I

In the map-phase of MR-I, key-value pairs are crea-

ted from the given event data, i.e., a single trace of a

log ﬁle. Each of the key-value pairs is assigned to a

number for further processing. In the case of process

discovery, this number is always 1. The challenge is

to generate these key-value pairs and map them to 1

in order to address the logic for the MP-Declare con-

straints.

Example: Given a trace t

= ha, b,b,ci. In the

scope of the response template, the trace is mapped

to four different key-value pairs in the map phase:

((a,b),1),((a,c),1),((b, c), 1), ((b,c),1). The keys

are exactly those event pairs which fulﬁl the response

template: a is followed by b and c, the ﬁrst b is

followed by c and the second b is followed by c. The

underlying mapping algorithm containing the logic

for all constraint templates is described in Section 3.3.

The reduce-phase ﬁnally obtains the key-value

pairs that have been produced. The reduce-function

must be declared by the user once again. In the

case of constraint checking this phase depicts a

summation of values. To continue the example

above, the result of the reducer with trace t

is:

((a,b),1),((a,c),1),((b, c), 2).

σ-function. The support metric is deﬁned as the

number of fulﬁlments of a constraint divided by the

number of occurrences of the activation. The MR-I

job in the example above calculates exactly the num-

ber of fulﬁlments, thus the numerator of the sup-

port formula. In the following we use a function

: E × E → N, where E are events, for describing

this ﬁgure, e.g. in t

: σ

response

(b,c) = 2. γ is the set of

constraints.

η-function. To calculate the support of a constraint,

the number of occurrences of the activation is neces-

sary. For forward constraints ({∗}response), this is

the ﬁrst event in the constraint template, e.g., b in the

constraint response(b, c). We deﬁne the number of

occurrences of events as η : E → N, for instance in

trace t

: η(b) = 2. In order to obtain the correct va-

lues for the η-function, for each event e in the trace a

key-value pair (e,1) is additionally emitted in the map

phase, e.g., for t

: (a,1),(b,1),(b,1),(c,1) which is

reduced to (a,1),(b,2),(c,1).

A MapReduce Approach for Mining Multi-Perspective Declarative Process Models

587

ε-function. A third value is necessary for determi-

ning the conﬁdence, namely the amount of traces in

which a given event occurs. We introduce the function

ε : E → N, which holds this information. Taking into

account the second trace t

(cf. Equation 1), MR-I

outputs ε(c) = 2 or ε(d) = 1, as c occurs in t

and

, whereas d occurs in t

solely. Transferring this to

MR-I, for each unique event e a key-value pair (e,1)

has to be produced, neglecting multiple occurrences

of events, e.g., for trace t

: (a,1),(b,1),(c,1).

The Tables 1 and 2 shows the complete result of

MR-I for the input log (cf. Equation 1) conside-

ring two constraint templates: response and chainRe-

sponse. The output of all mappers serves as the input

for the reducers.

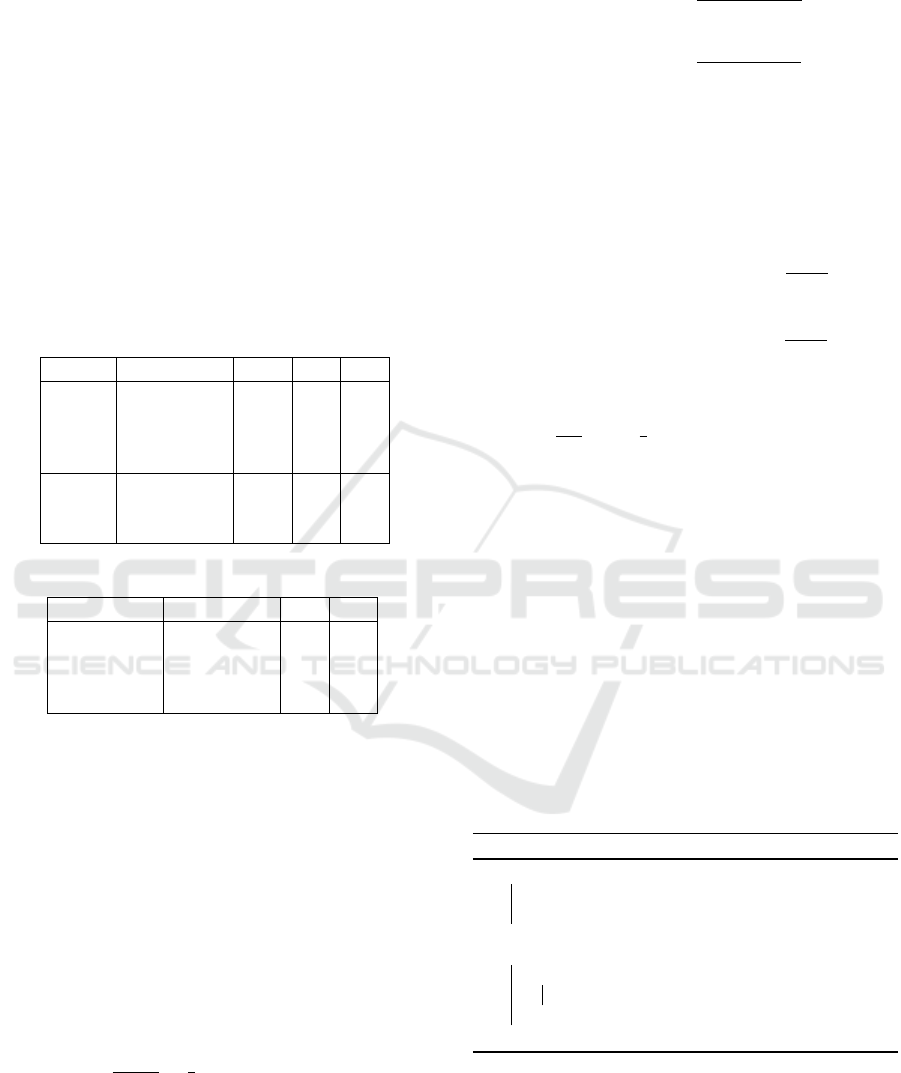
Table 1: Output of the Mapper in MR-I.

Trace σ

η ε

a,b,b,c ab,1 bc,1 ab,1 a,1 a,1

ac,1 bb,1 b,1 b,1

bb,1 bc,1 b,1 c,1

bc,1 c,1

a,c,d ac,1 ac,1 a,1 a,1

ad,1 cd,1 c,1 c,1

cd,1 d,1 d,1

Table 2: Output of the Reducer in MR-I.

η ε

ab,1 bc,2 ab,1 ac,1 a,2 a,2

ac,2 ad,1 bb,1 cd,1 b,2 b,1

bb,1 cd,1 bc,1 c,2 c,2

d,1 d,1

3.1.2 MR-II

Two MapReduce jobs are performed where the event

log only serves as input for the ﬁrst MapReduce job.

The output values of MR-I are used in MR-II to cal-

culate support and conﬁdence. Note that these cal-

culations had to be extracted to a separate job be-

cause every single trace of the provided log needs to

be tackled ﬁrst in MR-I in order to obtain the σ-, η-

and ε-functions. This makes MR-II mandatory; ho-

wever, with a look on the performance, support and

conﬁdence can be computed in parallel again.

Using the functions introduced above, the sup-

port of a constraint response(b,c) can be computed

as S

(b,c) =

(b,c)

η(b)

= 1 (cf. Equation 2), thus as

the fraction between the fulﬁlments of the constraint

and the amount of its activations. Remember that

forward constraints (FW D = {∗}response) are acti-

vated with e

(Equation 2) and backward constraints

(BWD = {∗}precedence) are activated with e

(Equa-

tion 3).

FWD

) =

FWD

)

η(e

)

(2)

BW D

) =

BW D

)

η(e

)

(3)

The conﬁdence of a constraint for an event pair

) is the product of the support of (e

) with

the ratio between the amount of traces in the log in

which event e

occurs (or e

in case of backward con-

straints) and the total number of traces in the log, de-

noted as |l| in Equation 4 and 5.

FWD

) = S

FWD

) ·

ε(e

)

|l|

(4)

BW D

) = S

BW D

) ·

ε(e

)

|l|

(5)

In the running example, the conﬁdence of the con-

straint response(b, c) is calculated as C

(b,c) =

(b,c) · (

ε(b)

|l|

) = 1 ·

= 0.5.

In terms of MapReduce, the MR-II is structured

rather trivial. In the map-phase, the output of MR-I

is conducted directly to the reducer neglecting η and

ε, i.e., all key-value pairs of the σ-function of all con-

straints are emitted and obtained by the reducer. The

reduce-function then consults the DB (cf. Section

3.2) to look up the relevant η- and ε-value for a gi-

ven key and calculates the corresponding support and

conﬁdence values (acc. to Equations 2, 3, 4 and 5).

3.2 Algorithm Overview

This section provides an overview on the algorithm

for declarative process model discovery (Algorithm

1).

Algorithm 1: Overview.

1 for Trace t in l do

2 KVP = mapToKVPairs(t)

3 DB = accumulateKVPairs(DB, KVP)

4 end

5 for Constraint c do

6 for Entry e in DB.σ.c do

7 calcSupportAndConfidence(e, c)

8 end

9 end

Given a log l with traces t, a ﬁrst step is to cre-

ate the key-value pairs KV P (MR-I-Mapper). These

include the KV Ps for each constraint (σ) and for the

functions η and ε. These values are then accumulated

into a database DB (MR-I-Reducer). The DB con-

tains information about the three functions. For the

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

588

σ-function, it holds a list for each constraint separa-

tely and furthermore the entries of the lists compri-

sing tuples (EventTuple, f ul f ilments). This DB is

then used in MR-II. For each constraint c, each tuple

in the σ

-list is considered (MR-II-Mapper). The dis-

covered EventTuple and the corresponding amount

of fulﬁlments is then used to calculate support and

conﬁdence by consulting the corresponding η- and ε-

values relevant to the EventTuple (MR-II-Reducer).

3.3 Mapping MP-Declare Templates

We have to apply the logic of MP-Declare constraints

into the MR-I mapping function to emit the necessary

KV Ps and calculate the correct values for support and

conﬁdence. For this purpose, we developed and deri-

ved algorithms from the support functions introduced

in (Di Ciccio and Mecella, 2015). Therefore, we deﬁ-

ned speciﬁc σ

functions for each of the MP-Declare

relation constraints. Note that all the algorithms are

working at only one trace instead of the whole log

ﬁle, which ensures the capability of parallelization.

For reasons of readability, we use an abbreviated

form for representing the event data in this section.

We let the set of activities be {a,b,c,d}. Further on,

we restrict to one single perspective, e.g., the organi-

zational perspective, thus the deﬁned resources which

can execute the activities are {x,y,z}. For instance,

trace t

in Equation 6 holds the information, that in

the beginning a was executed by x, subsequently c

was executed by z and so forth. In the end, the case is

closed when again a was executed by x.

= hax, cz, by,bx,dz,by,axi (6)

The structure of the algorithm is built upon a nes-

ted for-loop, so that for each event in a given trace,

every successor is considered. Henceforth i denotes

the loop control variable for the outer loop and j is

the counter variable for the inner loop.

In the case of t

(cf. Equation 6), all successors

for ax are addressed in the inner loop (i = 0), whereas

in the next step (i = 1) all successors for cz are con-

sidered and so forth. While iterating over the trace,

different representations of the events are requested to

match the multiperspective constraint templates. We

denote the events for the outer loop as

and for the

inner loop as e

, where Γ takes either A (activation)

or T (target).

For instance, for i = 2 and j = 5 and in search of

activation constraints (i.e. A = (task,resource) and

T = (task)) following representations are detected:

= cz,

= c, e

= dz and e

= d.

In the following, we analyse the example trace

(cf. Equation 6) and mark the pivot situati-

ons which are characteristic for each constraint tem-

plate with 1

,... for response, 1

,... for

alternateResponse and so forth.

3.3.1 Response

The initial assignment of (i, j) is (0,1), thus the events

ax and cz are considered. For activation constraints,

the activating event holds the additional condition so-

lely; hence, response(ax,c) is investigated in this ﬁrst

case. This constraint, activated with

(ax) is fulﬁl-

led with e

(ax,c) is incremented by 1.

Also for (

) the value for σ

(ax,b) is incremen-

ted. In the next step, i.e., (

), the σ-value must

not be modiﬁed, as the constraint response(ax, b),

activated with the event

was already fulﬁlled with

(cf. 1

in Table 3). Similar are the cases 2

to 5

Table 3: MR-I results for response constraints (activation).

c b b d b a

ax 3 3 1

3 2

cz 3 3

3 4

by 3 3 5

bx 3 3 3

dz 3 3

by 3

For target constraints like response(a,cz) the ad-

ditional condition appears on the right-hand side.

That means, the events in the outer loop must ma-

tch the target template:

. Referring to Table 4, in

the cases 6

and 7

, σ

(a,by) and σ

(c,by) respecti-

vely must not be increased, as the constraints are also

already fulﬁlled (with e

= by).

Table 4: MR-I Results for response constraints (target).

cz by bx dz by ax

a 3 3 3 3 6

c 3 3 3 7

b 3 3 3 3

b 3 3 3

d 3 3

b 3

3.3.2 AlternateResponse

The alternateResponse template shares the pivot

constellations for (i, j) for already fulﬁlled con-

straints similar to the response template (cf. 1

to 5

in Table 5). For instance, the constraint

alternateResponse(ax,b) enforces that if the event a

A MapReduce Approach for Mining Multi-Perspective Declarative Process Models

589

occurs and is executed by x than the event b follows,

and there is no recurrence of x executing a in between.

In the case i = 0, this constraint is activated by

(ax) and fulﬁlled with the event e

(b). Therefore, ad-

ditional events b must be ignored (e.g. e

Besides the already-fulﬁlled-errors, another class

of error type is introduced: violations. Con-

sider 6

in Table 5. In this case, the con-

straint alternateResponse(by,a) is checked. Alt-

hough this constellation have not been occurred so

far for this activation, the value σ

(by,a) must

not be modiﬁed, because it is violated by e

(by):

The activating event (by) recurs before a occurs.

This is forbidden within the alternateResponse tem-

plate. Note, that the resource is also decisive, thus

alternateResponse(by, d), activated with

is fulﬁl-

led with e

, although the event b recurs. However,

this is executed by x and so the constraint is not vio-

lated (marked with an asterisk in Table 5.)

Table 5: MR-I res. for alternateResponse constraints (act.).

c(z) b(y) b(x) d(z) b(y) a(x)

ax 3 3 1

3 2

cz 3 3

3 4

by 3 3

∗

bx 3 3 3

dz 3 3

by 3

The analysis of the target constraints (cf. Table.

6) shows the following anomalies: 7

and 8

are

excluded because of the already-fulﬁlled-case and the

cases 9

to 12

are excluded because of violations.

For instance, 9

to 11

are activated with the event

(b) and as the ﬁrst event in the inner loop is also

b (represented with the activation template, i.e. the

activity solely (e

)), all constraints with succeeding

events in the inner loop are violated.

Table 6: MR-I res. for alternateResponse constraints (tar.).

cz bx by dz by ax

a 3 3 3 3 7

c 3 3 3 8

b 3 9

b 3 3 12

d 3 3

b 3

3.3.3 ChainResponse

The logic for the chainResponse template is quite tri-

vial and is located outside the inner loop. For each

event

, the direct successor

i+1

is considered and

(

i+1

) is incremented by one. Examples are

an activation constraint like chainResponse(ax,c) or

a target constraint like chainResponse(a,cz).

Table 7: MR-I res. for chainResponse constraints.

cz by bx dz by ax

ax 3

cz 3

by 3

bx 3

dz 3

by 3

3.3.4 Precedence

Intuitively, one would iterate starting from the latest

event for the backward constraints, e.g. the ﬁrst (i, j)-

tuple would be (5,6) going on with (4,6), i.e. the con-

straints precedence(e

) and precedence(e

)

respectively. The former describes that whene-

ver a occurs and was executed by x, then b has

to precede (in the case of activation constraints

precedence(b,ax)). Referring to the later, an exam-

ple for a target constraint is if a occurs in a trace,

then b has to precede and this has to be executed by y

(precedence(by,a)).

For the sake of a performance boost, we propose

an algorithm, which handle the backward constraints

also by iterating through the events in a forward di-

rection. To do so, the events of the outer loop (i) ﬁlls

the role of the target events and the events of the inner

loop ( j) are now the activating events.

Consider Table 8. The ﬁrst constraint under in-

vestigation will be precedence(a,cz), activated with

(cz) and fulﬁlled with

(a). After than,

precedence(a,by) is inspected. This one now is acti-

vated with e

(by) but also fulﬁlled with the same ou-

ter loop event

(a).

Interesting is the outer loop event

(b) (cf. third

row in Table 8). In the case e

(dz), the value for

(b,dz) must not be modiﬁed (1

). The reason is

that this constraint, activated with dz is fulﬁlled with

the outer loop event

and thus, fulﬁlled in future

(marked with an asterisk in Table 8).

Table 8: MR-I results for the precedence constraint template

(activation).

cz by bx dz by ax

a(x) 3 3 3 3 3 3

c(z) 3 3 3 3 3

b(y) 3 1

b(x) 3

∗

3 4

d(z) 3 3

b(y) 3

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

590

The target constraints show similar behaviour.

Whenever the event

occurs also in the inner

loop in e

, then the rest of the inner loop is neg-

lected because the events are fulﬁlled later on, like

precedence(by,a) (5

) is fulﬁlled in the asterisk-

marked cell in Table 9.

Table 9: MR-I results for the precedence constraint template

(target).

c(z) b(y) b(x) d(z) b(y) a(x)

ax 3 3 3 3 3 3

cz 3 3 3 3 3

by 3 3 3 5

bx 3 3 3

dz 3 3

by 3

∗

3.3.5 AlternatePrecedence

In addition, the alternatePrecedence constraints, as

they are also backward constraints, are activated

with the second given event in the template. The

(activation) constraint alternatePrecedence(a, by) at

the marker 1

in Table 10 is violated because of the

event e

(by). Recurrences of the activating event are

forbidden within the alternatePrecedence template.

Similar is the case at 2

Consider now case 3

with the constraint

alternatePrecedence(b, dz). σ

(b,dz) must

not be incremented there, because this constraint

activated with e

(dz) is fulﬁlled with the event

in the next run of the outer loop (note the asterisk

in Table 10). Similar are the cases 4

to 6

. In

Table 10: MR-I results for the alternatePrecedence con-

straint template (activation).

cz by bx dz by ax

a 3 3 3 3 1

c 3 3 3 2

b 3 3

b 3

∗

3 6

d 3 3

b 3

Table 11, the constraints at the cases 7

to 11

are

violated, because of the reoccurrence of the events e

(b) and e

(b) in the events e

and e

3.3.6 ChainPrecedence

The chainPrecedence constraint template is im-

plemented similar to the chainResponse tem-

plate. However, the events of the constraints

are integrated in reversed order starting with

Table 11: MR-I results for the alternatePrecedence con-

straint template (target).

c b b d b a

ax 3 3 7

3 8

cz 3 9

3 10

by 3 3 11

bx 3 3 3

dz 3 3

by 3

chainPrecedence(c, ax) (activation constraint) and in

general terms σ

(

i+1

) is increased.

3.4 Pivot Characteristics Overview and

Resulting Algorithm

The anomalies detected in the previous section can be

traced to three certain pivot characteristics we have to

take care. They include already fulﬁlled (a), violation

(v) and fulﬁlled later (f), whereby the ﬁrst one corre-

sponds to forward constraints and latter appears only

on backward constraints. In this section, the four ano-

maly classes are identiﬁed, described and the occur-

rence of problems regarding the classes are resolved.

Class I (1

− 7

− 5

− 8

). These si-

tuations occur when a pair of events is considered,

where the activating event was already fulﬁlled in

this case with a previous event. For instance, in a

trace hax,b?, b?i, the constraint R(ax, b) is fulﬁlled

with the ﬁrst event b and must not be considered in

the next step ( j = 2). For this activation constraint,

the additional perspective of the fulﬁlling event is

not crucial (note the ?). A similar case for a tar-

get constraint is ha?,bx,bxi where R(a,bx) is fulﬁlled

when reading the second bx in the inner loop. Also

the alternateResponse template suffers from this ano-

maly: assuming a trace hax,ax,b?,ax, b?i, the value

for σ

(ax,b) referring to the constraint AR(ax, b)

would be incremented with the ﬁrst b and the second

b. Note that in this class it is forbidden for ax to recur

as this would cause a violation (cf. Class II).

Solution. The problem is that the events in the inner

loop ﬁltered by the target template e

are recurring.

To prevent these Class I-failures, all events e

are sto-

red in a list L and σ is only incremented if the current

is not in L.

Class II (6

− 12

). Class II-errors hits the

alternateResponse template solely. The deﬁnition of

this template forbids the activating event to recur be-

fore the second event appears. As an example serves

the trace hax,ax,b?i with the constraint AR(ax, b) for

an activation constraint and ha?,a?,bi with AR(a, bx)

for a target constraint respectively.

A MapReduce Approach for Mining Multi-Perspective Declarative Process Models

591

Algorithm 2: Discovery of relational MP-Declare

constraints.

Input: Trace t

Output: DB

1 for i ← 0 to trace.events.Count do

2 List<Event> eR, eAR, eAP;

3 bool bAR, bP, bAP = false;

4 db.η(

);

5 db.η(

);

6 db.ε(

);

7 db.ε(

);

8 for j ← i + 1 to trace.events.Count do

; /* Response */

9 if !eR.Contains(e

) then

10 db.σ.R(

, e

);

11 eR.Add(e

);

12 end

; /* AlternateResponse */

13 if !bAR ∧ !eAR.Contains(e

) then

14 db.σ.AR(

, e

);

15 eAR.Add(e

);

16 if e

then

17 bAR ← true;

18 end

19 end

; /* Precedence */

20 if !bP then

21 db.σ.P(

, e

);

22 end

23 if

= e

then

24 bP ← true;

25 end

; /* AlternatePrecedence */

26 if !bAP ∧ !eAP.Contains(e

) then

27 db.σ.AP(

, e

);

28 eAP.Add(e

);

29 end

30 if

= e

then

31 bAP ← true;

32 end

33 end

34 if i < |t| − 1 then

35 db.σ.CR(

i+1

);

36 db.σ.CP(

i+1

, i

);

37 end

38 end

Solution. If the activating event

recurs in the inner

loop as event e

, then all succeeding constraints in the

inner loop are violated by this recursion and thus the

inner loop can be cancelled for this template.

Class III (1

− 5

− 6

,12

). These ano-

maly is similar to Class I but for backward constraint

templates. Some constraints must not be considered

because they will be fulﬁlled later on. For instance,

in a trace hb?,b?,axi in the ﬁrst outer loop run it is

checked if the ﬁrst b? fulﬁls a constraint P(b,ax). Ho-

wever, this is not true because this certain constraint

is fulﬁlled in the second outer loop run.

Solution. The problem here is that the event of the

outer loop

recurs in the inner loop event e

. That

means that the succeeding inner loop events are ful-

ﬁlled later on with succeeding outer loop events. In

case of a recurrence, the consideration of succeeding

events in this inner loop run can be cancelled.

Class IV (1

−2

−11

). Similar to Class

II, errors corresponding to Class IV handle violati-

ons of constraints, viz. from the alternatePrecedence

template in this particular case. In a trace ha?,bx, bxi

the activation constraint alternatePrecedence(a,bx),

activated with the second bx event is violated, as bx

recurs, before the fulﬁlling event a preceds.

Solution. As a solution, we store all events e

in a

list. If a next event e

with a greater j occurs, the

consideration of alternatePrecedence templates can

be cancelled for a certain i.

4 IMPLEMENTATION

In this section, we particularly describe the imple-

mentation of MapReduce MP-Declare mining. As the

algorithm is built upon the MapReduce computation

paradigm, we took care to exploit this chance of paral-

lelism by spreading the workload on multiple threads

of a multicore CPU. As a ﬁrst step, the XES log ﬁle

has to be loaded into the applications memory. This is

done by reading the ﬁle with the .NET LIBARY and

parsing the information into POCOs. This step is also

used to collect meta information about the event log

to provide the user for instance a list of available per-

spectives but also some information on the expected

performance of the analysis by means of the ﬁgures

described in Section 4.2. As soon as the user has cho-

sen the perspectives to consider, i.e. he has built the

mining template (e.g. task ∧ resource → task), a ﬁrst

parallel processing step builds the three characteristic

functions σ, η and ε in MR-I. With the parallel exten-

sions of the Language Integrated Query-.NET com-

ponent (PLINQ: Parallel.ForEach();) we dele-

gate the whole parallelization and task generation on

to the framework itself and abstract from low level

programming issues with all the upcoming advanta-

ges. We just had to take care of race hazards when

joining to the global database (cf. lock-keyword).

After then, when each of the traces has been consi-

dered and the characteristic functions are completed,

the MR-II function can be invoked. Again, this step

is executed in parallel with PLINQ.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

592

4.1 Performance Inﬂuence Factors

Distribution of the Events. The most relevant index

number for a performance analysis is the amount of

loop runs the algorithm has to complete as they rise

in a quadratic manner with the amount of events in a

trace. For a trace with n events, the amount of loop

runs L

follows the formula in Equation 7.

= (n − 1) + ... + 1 =

n · (n − 1)

− n

(7)

That means, the higher the amount of traces with a

huge amount of events in a log ﬁle, the higher is

the computation time. For instance, ﬁrst assume a

log ﬁle containing 100 traces with a total amount of

1500 events, evenly distributed with 15 events per

trace. Then the number of loop runs comes up to

−15

= 105 for each trace, or summed up for the

whole log 105 · 100 = 10500. Now consult a log ﬁle

also with 100 traces, but now with 10 traces contai-

ning 90% of the events (945 events per trace) and the

remaining 90 traces with the remaining 12 events per

trace

. Then the total amount of loop runs is calcula-

ted as 10 ·

945

−945

+90 ·

−12

= 4460400 + 5940 =

4466340, which is more than 400 times higher than in

the evenly distributed log. Hence, the crucial factor,

i.e. the total number loop runs, can then be deﬁned

as the sum of the loop runs of each single trace (cf.

Equation 8).

∑

Trace t

|t|

· (|t| − 1)

(8)

0 0.2 0.4

0.6

0.8 1

0.5

% of Traces

% of Events

Figure 2: This caption has one line so it is centered.

Consider Table 12. Four real-life event logs were

analysed while the traces where rearranged in descen-

ding order by the amount of events. It can clearly

be seen that in the Hospital Log (blue line), half of

the traces contains nearly all captured events (94%).

Half of the events are included in the ﬁrst 130 traces

(11.4% of all traces). This raises the necessary loop

round up for simplicity

runs to about 33 · 10

. In contrast, in the Municipa-

lity Log (red line), the ﬁrst half of the traces contains

only about 64% of the events and 50% of the events

are recorded in the ﬁrst 438 traces (36% of all traces),

similar to the Loan Application Log and the Trafﬁc

Log.

Since now, we have not seen a chance in breaking

the quadratic dependency but as stated, compared to

(Di Ciccio and Mecella, 2015) or (Sturm et al., 2017)

we introduced an algorithm which is not in need of

a two-directional investigation of the traces and thus

saves half of the necessary loop runs.

Amount of Traces and Events. Apart from the

dependency of the distribution of the events within

the log discussed above, our implementation could

handle log ﬁles with up to 150000 Traces or 1000000

captured events. Table 12 shows that the absolute

amount of events and traces does not have a strong

impact on the performance. For instance, the Trafﬁc

Log inherits nearly 600000 events and 150000 traces

but is analysed within a mere fraction of time compa-

red to logs either with less traces or less events.

Amount of Discovered Constraints. In order to in-

vestigate a performance restriction caused by a huge

amount discovered constraints, we set the threshold

of support and conﬁdence on a minimal level, for in-

stance 0.05 and 0.02 instead of 0.5 and 0.2. Shown

with the Hospital Log, there is no noticeable change

in performance when discovering about 35000 con-

straints instead of 2000. Therefore, this is not worth

to be further analysed.

4.2 Performance Evaluation

We evaluated the effectiveness of our approach w.r.t.

to several real-life event logs. We ﬁrst evaluated

our approach for the discovery of MP-Declare con-

straints using the Hospital Log

, which records the

treatment of patients diagnosed with cancer from a

large Dutch hospital. In 5 of the traces at least one

event does not include the additional perspective data

(from org:resource) and thus they had to be excluded

from the investigation. Furthermore, we applied our

approach to the publicly available real-life event log

(Trafﬁc Log

) of an Italian local police ofﬁce for ma-

naging ﬁnes for road trafﬁc violations. This log ﬁle

barely contains additional perspective data in a con-

sistent way, so the lifecycle:transition attribute was

considered as additional perspective, but the seman-

tics does not affect the performance anyway. Additi-

https://doi.org/10.4121/uuid:d9769f3d-0ab0-4fb8-

803b-0d1120ffcf54

https://doi.org/10.4121/uuid:270fd440-1057-4fb9-

89a9-b699b47990f5

A MapReduce Approach for Mining Multi-Perspective Declarative Process Models

593

Table 12: Real-Life Event Logs under investigation.

Log Name Events Traces Events/Traces Loop Runs Runtime in s

Trafﬁc Log 561470 150370 3 0,97 133

Municipality Log 52217 1199 43 1,28 153

Loan Application Log 1202267 31509 38 26,73 697

Hospital Log 149489 1138 131 33,17 761

onally, we applied our approach to an event log per-

taining to an administrative process in a Dutch mu-

nicipality (Municipality Log

) as well as a log ﬁle

containing Loan Application

information. All four

event logs have been analysed w.r.t. all six descri-

bed MP-Declare templates. The time measurements

in Table 12 considers activation conditions solely, but

the same tendencies could be recorded for target con-

ditions.

500

1000

0.97 12.8

26.4

33.1

Loop Runs ·10

Seconds

Figure 3: Performance of sequential execution compared to

parallel execution.

The benchmark shows the expected behaviour

with respect to the proposed performance inﬂuencing

ﬁgures. Mapped into the coordinate system shown in

Figure 3 with the total loop runs on the abscissa and

the elapsed time on the ordinate one can clearly see

the dependency. Furthermore, the impact of paralleli-

zation is revealed. When working on the Trafﬁc Log

(0.97), there is almost no difference between the se-

quential (dashed line) and the parallel execution (solid

line). The performance gain through the distributed

computing is cancelled out by the additional workload

for task generation and joining the MR-I mapping re-

sults. Nevertheless, with more challenging log ﬁles in

terms of loop runs (e.g. the Hospital Log (33.1)), the

parallelization is exploited more and more efﬁciently.

5 RELATED WORK

Several approaches have been proposed for the disco-

very of declarative process models. In (Maggi et al.,

https://doi.org/10.4121/uuid:31a308ef-c844-48da-

948c-305d167a0ec1

https://doi.org/10.4121/uuid:5f3067df-f10b-45da-

b98b-86ae4c7a310b

2011), the authors present an approach that allows the

user to select from a set of predeﬁned Declare templa-

tes the ones to be used for the discovery. Other appro-

aches to improve the performances of the discovery

task are presented in (Di Ciccio et al., 2015b; Wes-

tergaard et al., 2013). Additionally, there are post-

processing approaches that aim at simplifying the re-

sulting Declare models in terms of redundancy elimi-

nation (Maggi et al., 2013a; Di Ciccio et al., 2015a)

and disambiguation (Bose et al., 2013). An approach

similar to the SQL-based one used in this paper is pre-

sented in (R

aim et al., 2014) and is based on tempo-

ral logic query checking. In (Westergaard and Maggi,

2012), the authors deﬁne Timed Declare, an extension

of Declare that relies on timed automata. In (Maggi,

2014), an approach for analysing event logs with Ti-

med Declare is proposed. The DPILMiner (Sch

onig

et al., 2016) exploits a discovery approach to incorpo-

rate the resource perspective and to mine for a set of

predeﬁned resource assignment constraints. In (Mon-

tali et al., 2013), the authors introduce for the ﬁrst

time a data-aware semantics for Declare and (Maggi

et al., 2013b) ﬁrst covered the data perspective in de-

clarative process discovery, although this approach

only allows for the discovery of discriminative acti-

vation conditions. (Sch

onig et al., 2016) proposes an

approach to enable the discovery of MP-Declare con-

straints by querying event logs given in relational da-

tabases with SQL. Here, a performance evaluation has

not been described.

6 CONCLUSIONS

In this paper, we proposed an efﬁcient framework for

the discovery of MP-Declare models based on the dis-

tributed processing method MapReduce. We introdu-

ced parallelizable algorithms for discovering six com-

monly used types of MP-Declare constraints. The

mining performance and effectiveness have been tes-

ted with real-life event logs. The experiments show

that our technique solves this complex mining task in

reasonable time. The approach at hand represents a

step into the direction of integrating process and data

science and depicts a customisable and high perfor-

mant declarative process mining technique. For fu-

ture work, we plan to consider also correlation and

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

594

time conditions as well as an additional integration

of all MP-Declare constraints. Furthermore, we will

examine how to improve performance even more,

for instance with alternative MapReduce frameworks

which can be set up and tested with the proposed al-

gorithms.

REFERENCES

Bose, J. C., Maggi, F. M., and van der Aalst, W. (2013). En-

hancing Declare Maps Based on Event Correlations.

In Business Process Management, pages 97–112.

Burattin, A., Maggi, F. M., and Sperduti, A. (2015). Con-

formance checking based on multi-perspective decla-

rative process models. CoRR, abs/1503.04957.

Burattin, A., Maggi, F. M., van der Aalst, W. M., and Sper-

duti, A. (2012). Techniques for a Posteriori Analy-

sis of Declarative Processes. In EDOC, pages 41–50,

Beijing. IEEE.

de Leoni, M., van der Aalst, W. M. P., and Dees, M. (2016).

A general process mining framework for correlating,

predicting and clustering dynamic behavior based on

event logs. Inf. Syst., 56:235–257.

Di Ciccio, C., Maggi, F. M., Montali, M., and Mendling,

J. (2015a). Ensuring model consistency in declarative

process discovery. In BPM, volume 9253 of Lecture

Notes in Computer Science, pages 144–159. Springer.

Di Ciccio, C. and Mecella, M. (2013). A two-step fast algo-

rithm for the automated discovery of declarative work-

ﬂows. In CIDM, pages 135–142. IEEE.

Di Ciccio, C. and Mecella, M. (2015). On the discovery

of declarative control ﬂows for artful processes. ACM

TMIS, 5(4):1–37.

Di Ciccio, C., Schouten, M. H. M., de Leoni, M., and Mend-

ling, J. (2015b). Declarative process discovery with

MINERful in ProM. In BPM Demos, pages 60–64.

Maggi, F., Bose, R., and van der Aalst, W. (2013a). A

knowledge-based integrated approach for discovering

and repairing declare maps. In CAiSE.

Maggi, F. M. (2013). Declarative process mining with the

declare component of prom. In BPM Demo sessions

2013, 26-30, 2013.

Maggi, F. M. (2014). Discovering metric temporal busi-

ness constraints from event logs. In BIR, volume 194

of Lecture Notes in Business Information Processing,

pages 261–275. Springer.

Maggi, F. M., Dumas, M., Garc

ıa-Ba

nuelos, L., and Mon-

tali, M. (2013b). Discovering data-aware declarative

process models from event logs. In BPM, pages 81–

96.

Maggi, F. M., Mooij, A., and van der Aalst, W. (2011).

User-Guided Discovery of Declarative Process Mo-

dels. In CIDM, pages 192–199.

Montali, M., Chesani, F., Mello, P., and Maggi, F. M.

(2013). Towards data-aware constraints in declare. In

SAC, pages 1391–1396. ACM.

Montali, M., Pesic, M., van der Aalst, W. M. P., Chesani,

F., Mello, P., and Storari, S. (2010). Declarative Spe-

ciﬁcation and Veriﬁcation of Service Choreographies.

ACM Transactions on the Web, 4(1).

Pesic, M., Schonenberg, H., and van der Aalst, W. M. P.

(2007). Declare: Full support for loosely-structured

processes. In IEEE International EDOC Conference

2007, pages 287–300.

Pichler, P., Weber, B., Zugal, S., Pinggera, J., Mendling,

J., and Reijers, H. A. (2011). Imperative versus de-

clarative process modeling languages: An empirical

investigation. In BPM Workshops, pages 383–394.

aim, M., Di Ciccio, C., Maggi, F. M., Mecella, M.,

and Mendling, J. (2014). Log-based understanding

of business processes through temporal logic query

checking. In OTM Conferences, volume 8841, pages

75–92. Springer.

Sch

onig, S., Cabanillas, C., Jablonski, S., and Mendling, J.

(2016). A Framework for Efﬁciently Mining the Or-

ganisational Perspective of Business Processes. Deci-

sion Support Systems.

Sch

onig, S., Di Ciccio, C., Maggi, F. M., and Mendling,

J. (2016). Discovery of multi-perspective declara-

tive process models. In Service-Oriented Computing,

ICSOC, Banff, Canada, pages 87–103.

Sturm, C., Sch

onig, S. S., and Ciccio, C. D. (2017). Dis-

tributed multi-perspective declare discovery. In BPM

Demos.

van der Aalst, W. (2011). Process Mining: Discovery,

Conformance and Enhancement of Business Proces-

ses. Springer.

Westergaard, M. and Maggi, F. M. (2012). Looking into the

future: Using timed automata to provide a priori ad-

vice about timed declarative process models. In OTM,

volume 7565 of LNCS, pages 250–267. Springer.

Westergaard, M., Stahl, C., and Reijers, H. (2013). Un-

constrainedMiner: Efﬁcient Discovery of Generalized

Declarative Process Models. BPM CR, No. BPM-13-

28.

Zeising, M., Sch

onig, S., and Jablonski, S. (2014). Towards

a Common Platform for the Support of Routine and

Agile Business Processes. In Collaborative Compu-

ting: Networking, Applications and Worksharing.

A MapReduce Approach for Mining Multi-Perspective Declarative Process Models

595