
Encryption Schemes based on a Single Permutation: PCBC, POFB,
PCFB and PCTR
Kaiyan Zheng
1,2,3
and Peng Wang
1,2,3
1
Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China
2
Data Assurance and Communication Security Research Center, Chinese Academy of Sciences, Beijing 100093, China
3
School of Cyber Security, University of Chinese Academy of Sciences, Beijing 100049, China
Keywords:
Encryption Scheme, Blockwise Adaptive Attack, Related-key Attack, Even-Mansour.
Abstract:
In this paper we discuss how to construct encryption schemes from permutations. Firstly we discuss an in-
tuitive way to design permutation-based encryption schemes, that is by combining mainstream blockcipher-
based encryption modes (such as CBC, OFB, CFB, CTR) with the Even-Mansour cipher, which is an elegant
permutation-based blockcipher. Unfortunately, most of encryption schemes produced by the combination stra-
tegy are not secure enough. Then we propose 4 permutation-based encryption schemes - PCBC, POFB, PCFB
and PCTR, which can resist both the blockwise adaptive attack and the Φ
⊕
-related-key attack when using a
non-repeated nonce. To illustrate it, we give a definition of the indistinguishability from random bits against
blockwise adaptive chosen plaintext attack in the Φ
⊕
-related-key setting, and then prove the security of PCBC
in such definition. The other 3 schemes have similar results. Constructing from a single permutation, these 4
encryption schemes are practical, in the sense that they are less prone to misuse, bring less pressure on the key-
management in real world, and apply to blockwise adaptive scenarios including real-time applications, on-line
settings, memory-restricted devices, etc. Moreover they are more efficient than the Sponge construction.
1 INTRODUCTION
The winner of SHA-3 competition, a permutation-
based hash function, inspires a great many studies on
cryptographic permutations and permutation-based
cryptographic schemes. Lots of cryptographic permu-
tations were designed, including KECCAK (Dworkin,
2015), Prφst (Kavun et al., 2014), PRIMATEs (An-
dreeva et al., 2014), Minalpher-P (Sasaki et al., 2014)
- just to name a few. Numerous cryptographic sche-
mes are designed to be based on cryptographic per-
mutations, especially a large number of authenti-
cated encryption schemes submitted to the CAE-
SAR competition, including Ascon (Dobraunig et al.,
2014), PAEQ (Biryukov and Khovratovich, 2014),
KETJE (Bertoni et al., 2014), APE (Sasaki et al.,
2014), OTR (Kavun et al., 2014), and so on. More ot-
her permutation-based cryptographic schemes are stu-
died, including lightweight hash functions like SPON-
GENT (Bogdanov et al., 2011) and Quark (Aumas-
son et al., 2013), streamciphers like Salsa (Bern-
stein, 2008), tweakable blockciphers like XPX (Men-
nink, 2016) and TEM (Cogliati and Seurin, 2015),
blockciphers like Even-Mansour (Even and Mansour,
1997), etc. However there are little solo studies on
permutation-based encryption schemes, which moti-
vates us to discuss how to construct encryption sche-
mes from a single cryptographic permutation.
1.1 Background
Encryption scheme. Encryption schemes are designed
to provide data confidentiality, and common encryp-
tion modes of operation are based on blockcipher, in-
cluding CBC (Cipher Block Chaining), OFB (Output
Feedback), CFB (Cipher Feedback) and CTR (Coun-
ter), etc. When using a random IV (Initialization Vec-
tor), these 4 modes are proved to be secure in the
single-key chosen plaintext attack (CPA for short) set-
ting (Bellare et al., 1997; Alkassar et al., 2001; Sung
et al., 2001).
Unfortunately, it is a great challenge to imple-
ment random IVs in real world, and once the IV is
predictable, these encryption modes, excluding CTR,
are no longer secure (Duong and Rizzo, 2011; Bard,
2004; Dai, 2002; Moeller et al., 2004; Rogaway,
1996). In (Rogaway, 2004), Rogaway discussed the
case when the IV is guaranteed to be a nonce which
452
Zheng, K. and Wang, P.
Encryption Schemes based on a Single Permutation: PCBC, POFB, PCFB and PCTR.
DOI: 10.5220/0006713804520460
In Proceedings of the 4th International Conference on Information Systems Security and Privacy (ICISSP 2018), pages 452-460
ISBN: 978-989-758-282-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

takes fresh values in each encryption and even can
be chosen by the adversary. Rogaway believed that
nonce-based symmetric encryptions are less prone to
misuse.
Blockwise adaptive attack. In some practical appli-
cation environments like real-time applications, on-
line settings, memory-restricted devices, etc., the
data is processed and outputted block by block, rat-
her than as an atomic object, arising the blockwise
adaptive attack (Bellare et al., 2002; Fouque et al.,
2003; Fouque et al., 2004; Joux et al., 2002; Bard,
2006; Bard, 2007), which assumes that the adver-
sary can adaptively choose subsequent input blocks
based on the preceding output blocks. The bloc-
kwise adaptive attack is not only of theoretical inte-
rest, owing to its operational feasibility in the Secure
Shell (SSH) (Bellare et al., 2002) and the Secure Soc-
kets Layer (SSL) (Bard, 2006).
Some encryption schemes that are secure against
the traditional chosen plaintext attack turn out to suf-
fer the blockwise adaptive attack, like CBC, while
some still maintain the confidentiality against such
stronger attack, like OFB, CFB and CTR using a
random IV (Fouque et al., 2003; Fouque et al., 2004).
Related-key attack. The related-key attack has stu-
died extensively for various cryptographic applicati-
ons (Biham, 1993; Biryukov et al., 2009; Karpman,
2015; Bellare and Kohno, 2003; Biryukov and Kho-
vratovich, 2009; Albrecht et al., 2011), which assu-
mes that the adversary has the capability to query not
only the scheme with the secret key K but also ϕ(K)
where ϕ is a key-deriving-function that can be cho-
sen. Though this stronger attack is not far-fetched in
practical scenarios, it is not covered by the classic se-
curity notions, and we have to take it into considera-
tion when analyzing encryption schemes (no matter
already designed or new).
Even-Mansour cipher. The Even-Mansour cip-
her (Even and Mansour, 1997), designed from a sin-
gle permutation by eXclusive-ORing(XOR) two in-
dependent keys into its input and output respectively,
attracts a great interest due to its elegant structure, and
lots of related studies were published (Daemen, 1991;
Chen and Steinberger, 2014; Dunkelman et al., 2012;
Dobraunig et al., 2015). It can be simplified to the
single-key version by using the same key in both the
input and output (Dunkelman et al., 2012; Chen and
Steinberger, 2014).
Assuming the underlying permutation be a
random one that the adversary can query, both versi-
ons, though are proven to be PRP-CPA in the single-
key model (Dunkelman et al., 2012; Even and Man-
sour, 1997; Chen and Steinberger, 2014), suffer
the related-key attack (Dobraunig et al., 2015), which
makes the Even-Mansour construction fail to be a
well-suited blockcipher for many modes of operation,
such as OTR (Dobraunig et al., 2015).
1.2 Motivation
How can we provide confidential protection when
there is only a cryptographic permutation in hand?
The notable Sponge construction designed in SHA-
3 (Dworkin, 2015) is a convenient approach. Howe-
ver in contrast to mainstream encryption schemes de-
signed from blockcipher, which in every call, process
the message that is as large as the blocksize of the un-
derlying blockcipher, the Sponge construction can’t
achieve the optimal efficiency, as the message it pro-
cesses during each call of the underlying primitive is
far less than the bandwidth (part of which interacts
with the outer while the remaining is reserved to gua-
rantee secure).
Another direct way to get permutation-based en-
cryption schemes that achieve the optimal efficiency
is to combine mainstream confidential modes (like
CBC, OFB, CFB, CTR, etc) with the Even-Mansour
construction. Nevertheless these specific schemes are
not secure enough. When using a non-repeated nonce,
most of these schemes suffer the blockwise adaptive
attack, and then fail to provide confidentiality in lots
of practical scenarios like real-time application, on-
line settings, memory-restricted devices, etc. Due
to the inability in the Even-Mansour construction to
resist related-key attacks, these schemes are prone
to suffer related-key attacks (Dobraunig et al., 2015;
Karpman, 2015). In addition, once large permutations
are used, the keys used in these schemes are also large
(no smaller than the bandwidth of the permutations),
which brings a great pressure on the key-management
in real world.
Based on the above observations, we study how
to design practical encryption schemes from a sin-
gle cryptographic permutation. We aim at propo-
sing nonce-respected efficient encryption schemes
that, when using a key with an appropriate length,
can resist both the blockwise adaptive attack and the
related-key attack.
By the way, though (online) authenticated en-
cryption schemes can meet these requirements easily,
there are lots of applications where unauthenticated
encryption is needed. For example, a certain propor-
tion of errors in the recovered plaintext may be accep-
table in the digitised voice or video service. Without
regard to the integrity, encryption schemes are
Encryption Schemes based on a Single Permutation: PCBC, POFB, PCFB and PCTR
453

capable to run sufficiently fast to reduce latency
time, which are vital in real-time applications and
on-line settings.
1.3 Our Contribution
Firstly in Section 3, we analyze 4 specific
permutation-based encryption schemes, i.e. SEM-
CBC, SEM-OFB, SEM-CFB and SEM-CTR, produ-
ced by combining 4 commonly-used encryption mo-
des, i.e. CBC, OFB, CFB and CTR, with the single-
key Even-Mansour cipher (SEM for short). With a
random IV, these 4 schemes can provide some con-
fidential protection, but most fail when using a non-
repeated nonce, not to mention the inability to resist
the blockwise adaptive attack, which restricts their
usage in practical on-line/real-time scenarios. The re-
sults are concluded in Table 1. It’s obvious that the di-
rect combination strategy may fail to construct practi-
cal permutation-based encryption schemes.
In Section 4 we propose 4 permutation-based en-
cryption schemes - PCBC, POFB, PCFB and PCTR,
improved from SEM-CBC, SEM-OFB, SEM-CFB
and SEM-CTR respectively. Based on a single ideal
permutation, all these 4 schemes can provide confi-
dential protection against the blockwise adaptive cho-
sen plaintext attack in the Φ
⊕
-related-key setting,
even when using a non-repeated nonce. We give a
detail proof of PCBC, and the other 3 schemes can
be proved similarly. We claim that these 4 encryp-
tion schemes are very practical, because they are less
prone to misuse, apply to practical blockwise adap-
tive scenarios, and bring less pressure on the key-
management in real world. Besides, they are more
efficient than the Sponge construction since the plain-
text block they process during each call of the under-
lying permutation is as large as the bandwidth.
2 PRELIMINARIES AND
SECURITY MODELS
Notations. By {0,1}
n
we denote the set of n binary
bits for any n > 0, and {0,1}
n+
=
S
∞
l=1
{0,1}
nl
. Let
S be some finite set, s
R
←− S denotes selecting an ele-
ment at uniformly random from S and assign it to s.
|S| is the cardinality of S while |s| is the length of s. k
denotes the string concatenation operation. Perm(n)
denotes the set of all permutations on {0, 1}
n
, and
Func(n
1
,n
2
) denotes the set of all functions mapping
{0,1}
n
1
to {0,1}
n
2
.
Encryption Scheme. Let SE : {0,1}
k
×{0,1}
n
×
{0,1}
n+
→ {0, 1}
n+
be any encryption scheme,
where {0,1}
k
,{0,1}
n
,{0,1}
n+
denote the space of
keys, IVs and plaintexts/ciphertexts, respectively.
For any K ∈ {0,1}
k
, SE
K
denotes the encryption
function and SE
−1
K
denotes its inverse, which satis-
fies that for any IV ∈ {0,1}
n
,M ∈ {0,1}
n+
, M =
SE
−1
K
(IV,SE
K
(IV,M)).
Here IV denotes either a random one or a non-
repeated nonce. In the former case, i.e. IV
R
←−{0,1}
n
,
IV acts as part of the ciphertext, while in the latter IV
is assumed to be controlled by the adversary. In the
remaining, we misuse the notation SE
K
to denote the
encryption oracle of SE, which takes in a single input
M when using a random IV, but a pair input (N,M)
when using a non-repeated nonce. We won’t empha-
size it unless it causes any confusion.
Besides, we assume that the message which SE
processes is already padded as need, i.e. a non-zero
multiple of n, since the discussion of padding rules
is out of the scope of our paper. Most of encryption
schemes provide the CPA confidentiality only, and
thus we focus on the CPA setting in this paper.
To define the confidentiality of SE, we use the in-
distinguishability from random bits in the remaining.
Denote $ the function which can produce sufficient
random bits on demand. Since SE discussed in our
paper is based on permutations, we assume that the
underlying ideal permutation is P
R
←−Perm(n) and the
adversary has access to P
±
.
The CPA setting. In the single-key model, we assume
that K
R
←− {0,1}
k
, and the CPA oracle is either SE
K
or $. Let D be any CPA adversary that makes at most
q non-duplicate encryption queries and at most r non-
duplicate bi-directional queries to P
±
.
Thus the CPA indistinguishability (IND-CPA for
short) of SE is defined by the maximum advantage at
distinguishing
{
SE
K
,P
±
}
with
{
$,P
±
}
, that is, for
q,r ≥ 0,
Adv
ind−cpa
SE
(q,r) = (1)
max
D
Pr
h
K
R
←− {0,1}
k
: D
SE
K
,P
±
= 1
i
−Pr
h
D
$,P
±
= 1
i
.
Related-key setting. The indistinguishability defini-
tion in the related-key model used in our paper follows
the theoretical framework of Bellare and Kohno (Bel-
lare and Kohno, 2003) and Albrecht et al. (Albrecht
et al., 2011). In the related-key setting, the CPA ad-
versary has access to not only the encryption ora-
cle SE
K
but also SE
ϕ(K)
where ϕ is a key-deriving-
function chosen from a pre-described set Φ where
Φ ⊆ Func(k,k).
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
454

Table 1: The security conclusion of encryption schemes appeared in this paper.
Encryption Schemes IV Assumption
Security Definitions
IND-CPA IND-BW-CPA Φ
⊕
-IND-CPA Φ
⊕
-IND-BW-CPA
SEM-CBC
random
√
×
√
×
nonce × × × ×
SEM-OFB
random
√ √ √ √
nonce × × × ×
SEM-CFB
random
√ √ √ √
nonce × × × ×
SEM-CTR
random
√ √ √ √
nonce
√ √
× ×
PCBC
random or nonce
√ √ √ √
POFB
√ √ √ √
PCFB
√ √ √ √
PCTR
√ √ √ √
In this paper, we target the Φ
⊕
-related-key secu-
rity only, where Φ
⊕
= {ϕ
∆
| ∆ ∈ {0,1}
k
} and ϕ
∆
de-
notes the canonical function K 7→ K ⊕∆. We will mi-
suse ∆,ϕ
∆
in the remaining unless it is confused.
For any SE, we define a Φ
⊕
-related-key ora-
cle RK[SE ] : {0,1}
k
× Φ
⊕
× {0,1}
n
× {0,1}
n+
→
{0,1}
n+
. For any ∆ ∈ Φ
⊕
, RK[SE]
K
computes as
SE
K⊕∆
. Similarly, we define a Φ
⊕
-related-key oracle
of $ as RK[$], which denotes the set of |Φ
⊕
| indepen-
dent functions that produce random bits.
Let D be any Φ
⊕
-related-key CPA adversary that
makes at most q non-duplicate queries to the Φ
⊕
-
related-key oracle and at most r bi-directional non-
duplicate queries to P
±
. Thus the Φ
⊕
-related-key
CPA indistinguishability (Φ
⊕
-IND-CPA for short) of
SE is defined by the maximum advantage at distin-
guishing
{
RK[SE]
K
,P
±
}
with
{
RK[$],P
±
}
, that is,
for q,r > 0,
Adv
Φ
⊕
−ind−cpa
SE
(q,r) = (2)
max
D
Pr
h
K
R
←− {0,1}
k
: D
RK[SE]
K
,P
±
= 1
i
−Pr
h
D
RK[$],P
±
= 1
i
.
Blockwise adaptive setting. The adversary in the
blockwise adaptive setting has the capability to ob-
serve the output blocks that are already computed, be-
fore deciding subsequent input blocks, and insert any
blocks as it likes based on those observations, during
a single query.
Without loss of generality, let the adversary in
the blockwise adaptive chosen plaintext attack (BW-
CPA for short) query block-by-block. Take the CPA
encryption oracle SE
K
as an example, we describe
briefly how the CPA adversary interacts with its ora-
cle in the blockwise adaptive setting, and other ora-
cles perform similarly.
Let SE be the blockwise adaptive oracle of
SE, and during any i
th
encryption query, after kno-
wing the corresponding ciphertext blocks by que-
rying SE
K
(M
i
0
),SE
K
(M
i
1
),··· ,SE
K
(M
i
j−1
), the BW-
CPA adversary chooses the j
th
block M
i
j
and que-
ries SE
K
(M
i
j
), where M
i
0
denotes the IV, i.e. M
i
0
=
IV
i
, and M
i
is the i
th
queried plaintext that M
i
=
M
i
1
···M
i
l
i
and j = 1,··· ,l
i
. Note that the computation
of SE
K
(M
i
0
) may be different from that of SE
K
(M
i
j
),
according to the specific SE scheme.
Moreover, denote the blockwise adaptive oracle of
$ as $, and $(M
i
j
) will return a random bit string that
has the same length of SE
K
(M
i
j
). Similarly, define
RK[SE]
K
, RK[$] as the blockwise adaptive oracle of
RK[SE]
K
, RK[$], respectively. Let D be some BW-
CPA adversary who makes at most q encryption que-
ries to the blockwise adaptive oracle, and at most r
bi-directional queries to the public oracle P
±
.
IND-BW-CPA. The BW-CPA indistinguishability
(IND-BW-CPA for short) of SE is defined by the max-
imum advantage at distinguishing
SE
K
,P
±
from
n
$,P
±
o
, that is, for q,r > 0,
Adv
ind−bw−cpa
SE
(q,r) = (3)
max
D
Pr
h
K
R
←− {0,1}
k
: D
SE
K
,P
±
= 1
i
−Pr
h
D
$,P
±
= 1
i
.
Encryption Schemes based on a Single Permutation: PCBC, POFB, PCFB and PCTR
455
Φ
⊕
-IND-BW-CPA. The Φ
⊕
-related-key BW-CPA
indistinguishability (Φ
⊕
-IND-BW-CPA for short) of
SE is defined by the maximum advantage at distin-
guishing
RK[SE]
K
,P
±
from
n
RK[$],P
±
o
, that is,
for q,r > 0,
Adv
Φ
⊕
−ind−bw−cpa
SE
(q,r) = (4)
max
D
Pr
h
K
R
←− {0,1}
k
: D
RK[SE]
K
,P
±
= 1
i
−Pr
h
D
RK[$],P
±
= 1
i
.
3 THE COMBINATION
STRATEGY
In this section, we discuss 4 specific permutation-
based encryption schemes - SEM-CBC, SEM-OFB,
SEM-CFB and SEM-CTR - produced by combining
4 commonly-used encryption modes, i.e. CBC, OFB,
CFB and CTR, with SEM. Due to the chain structure
of the modes (except CTR), nearly half of the key-⊕-
operations are cancelled and these schemes turn out
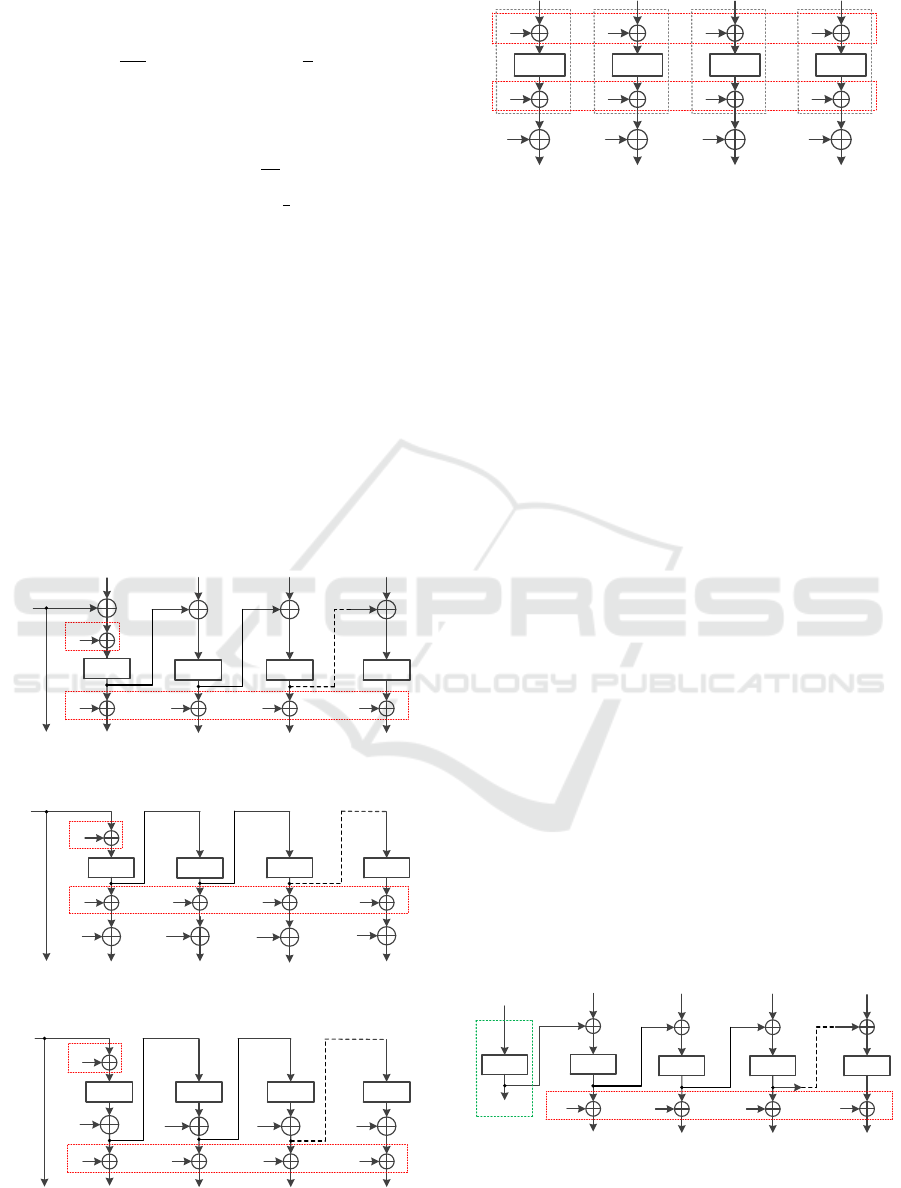
to be very compact, showed in Fig.1 - Fig.4.
P
K
K
IV
M
1
C
1
P
K
M
2
C
2
P
K
M
3
C
3
P
K
M
l
C
l
C
0
…
…
…
…
Figure 1: SEM-CBC.
P
K
K
C
1
P
K
C
2
P
K
C
3
P
K
C
l
M
1
M
2
M
3
M
l
IV
C
0
…
…
…
…
Figure 2: SEM-OFB.
P
K
C
1
P
C
2
P
C
3
P
C
l
M
1
M
2
M
3
M
l
K
K
K
K
IV
C
0
…
…
…
…
Figure 3: SEM-CFB.
P
K
K
C
1
M
1
N || 1
…
…
P
K
K
C
2
M
2
N || 2
P
K
K
C
3
M
3
N || 3
P
K
K
C
l
M
l
N || l
…
…
…
…
…
…
Figure 4: SEM-CTR.
The analyses of these 4 schemes are deduced from
CBC, OFB, CFB and CTR directly (Bellare et al.,
1997; Sung et al., 2001; Alkassar et al., 2001; Joux
et al., 2002; Moeller et al., 2004; Bard, 2006; Bard,
2007), as all these 4 schemes are actually the specific
cases when the underlying blockcipher is exactly the
SEM blockcipher. We omit the details since the ana-
lyses are quite trivial, and the results are concluded in
Table 1.
4 PERMUTATION-BASED
ENCRYPTION SCHEMES:
PCBC, POFB, PCFB AND PCTR
With a single cryptographic permutation in hand, how
can we provide confidential protection? From above,
we know that both direct ways -the Sponge con-
struction and the combination strategy- have some de-
ficiencies.
In this section we, inspired by the common
blockcipher-based modes of operation i.e. CBC,
OFB, CFB and CTR, propose 4 permutation-based
encryption schemes -PCBC, POFB, PCFB and PCTR,
showed in Fig.5-Fig.8. Note that in PCBC, the finite
multiplication by 2 (see the red dashed in Fig. 5) in
each block process is essential to resist the blockwise
adaptive attack, which is unnecessary in the other 3
schemes (see the red dashed in Fig. 6-8) since the ori-
ginal OFB, CFB, and CTR can resist the blockwise
adaptive attack, when using a random IV.
P
M
1
C
1
P
M
2
C
2
P
M
3
C
3
P
M
l
C
l
2L
2
2
L 2
3
L 2
l
L
L
K||N
P
…
…
…
…
…
…
Figure 5: PCBC.
Based on a single cryptographic permutation and
two simple kinds of operations - XOR and the finite
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
456
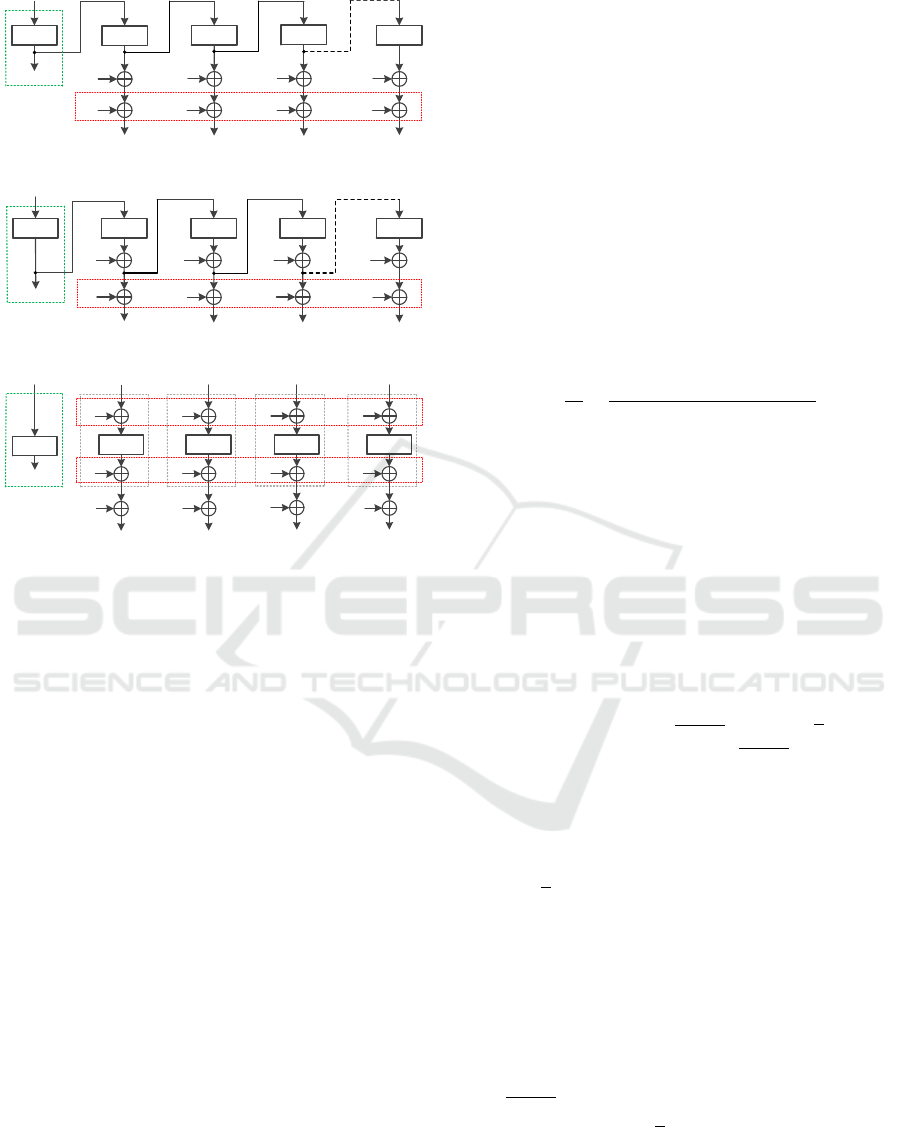
P
C
1
P
C
2
P
C
3
P
C
l
M
1
M
2
M
3
M
l
P
L
K||N
2L 2L
2L
2L
…
…
…
…
…
…
Figure 6: POFB.
P
C
1
P
C
2
P
C
3
P
C
l
M
1
M
2
M
3
M
l
P
L
K||N
2L
2L 2L
2L
…
…
…
…
…
…
Figure 7: PCFB.
P
L
K||N
P
C
1
P
C
2
P
C
3
P
C
l
M
1
M
2
M
3
M
l
1 2 3 l
2L
2L
2L
2L
2L
2L
2L
2L
…
…
…
…
…
…
Figure 8: PCTR.
multiplication, these 4 encryption schemes are practi-
cal. Since these 4 schemes, no matter using a random
IV no a non-repeated nonce, achieve Φ
⊕
-IND-BW-
CPA, which is concluded in Table 1, they are less
prone to misuse, and apply to lots of practical bloc-
kwise adaptive scenarios including real-time appli-
cations, on-line settings, memory-restricted devices,
etc. These schemes bring less pressure on the key-
management in real world, and the key length can
be chosen as need even though large permutations
are used. Moreover they are more efficient than the
Sponge construction, since the plaintext block proces-
sed by one call of the permutation equals exactly the
bandwidth of the permutation.
In the remaining, we take PCBC as an example to
prove that using a non-repeated nonce, PCBC can re-
sist the blockwise adaptive attack in Φ
⊕
-related-key
setting, which is described formally in Theorem 1.
Similar results can be deduced in POFB, PCFB and
PCTR.
4.1 Φ
⊕
-IND-BW-CPA of PCBC
Specification of PCBC. Let P
R
←− Perm(n) be a n-bit
ideal cryptographic permutation, and k is the wan-
ted key length, and PCBC : {0,1}
k
× {0, 1}
n−k
×
{0,1}
n+
→ {0, 1}
n+
represents the PCBC scheme.
For K ∈{0,1}
k
,N ∈{0,1}
n−k
,M ∈{0,1}
n+
and C ∈
{0,1}
n+
where M = M
1
···M
l
, C = C
1
···C
l
and
|M
j
| = |C
j
| = n for j = 1, ··· ,l, the encryption
function C = PCBC
K
(N,M) is defined as following:
Encryption: C = PCBC
K
(N,M)
L = P (KkN); T = 2L; S = T ;
for j = 1 to l do
T = 2T ;
S = P (M
j
⊕S);
C
j
= S ⊕T ;
Theorem 1. To PCBC, assuming that P
R
←− Perm(n)
and that the Φ
⊕
-related-key BW-CPA adversary ma-
kes q Φ
⊕
-related-key queries including at most total
σ blocks and at most r queries to P
±
,
Adv
Φ
⊕
−ind−bw−cpa
PCBC
(q,r)
≤
qr
2
k
+
σ(σ −1) + qr + 2σ(q + r)
2
n
. (5)
Proof. Define the Φ
⊕
-related-key oracle of PCBC
as RK[PCBC] : {0, 1}
k
×Φ
⊕
×{0,1}
n−k
×{0,1}
n+
→
{0,1}
n+
. Without loss of generality, let D be any
Φ
⊕
-related-key BW-CPA adversary that makes ex-
actly q non-duplicated related-key queries, denoted as
(∆
i
,N
i
,M
i
,C
i
), where M
i
= M
i
1
···M
i
l
i
, C
i
= C
i
1
···C
i
l
i
and l
i
is the total blocks of M
i
, for i = 1, ··· ,q. Let
∑
q
i=1
l
i
= σ.
In the blockwise adaptive setting, during any i
th
related-key query, D can delay choosing M
i
j
until
it knows C
i
1
,··· ,C
i
j−1
for j = 1,··· ,l
i
, i = 1, ··· ,q.
Denote the Φ
⊕
-related-key oracles in the blockwise
adaptive setting as RK[PCBC] and RK[$]. Thus
for any (∆
i
,N
i
,M
i
j
) queried, RK[PCBC]
K
(∆
i
,N
i
,M
i
j
)
computes: (1) if j = 1 the initialization is proces-
sed firstly as L
i
= P ((K ⊕∆
i
)kN
i
);T
i
= 2L
i
;S
i
= T
i
;
(2) for any j, the computation is processed as T
i
=
2T
i
;S
i
= P (M
i
j
⊕S
i
);C
i
j
= S
i
⊕T
i
, and C
i
j
is returned.
Let $ be the random function defined as before,
and RK[$](∆
i
,N
i
,M
i
j
) always returns a n-bit random
string. Besides D also has access to the public per-
mutation P
±
. Let D makes exactly r bi-directional
queries to P
±
, denoted as (X
u
,Y
u
) for u = 1,··· ,r.
Refer to (Chen and Steinberger, 2014), let D paly
the “enhanced” game here, that is D is revealed the
key after it has made all its queries but before ma-
king its final decision. Moreover in this specific case
D is revealed more q values. More specifically, in
RK[PCBC] the secret key K as well as all truly L
i
s are
revealed, while in RK[$] a dummy key K
0
R
←− {0, 1}
k
and q distinct dummy values L
0i
s randomly chosen
from {0,1}
n
are given instead. Note that this game
gives no disadvantage to the adversary since it can
neglect the revealed information anyway.
Encryption Schemes based on a Single Permutation: PCBC, POFB, PCFB and PCTR
457

Denote τ the transcript that D creates to record the
queries it made and the answers it received. In more
detail, let τ = (τ
0
,τ
1
,τ
2
), and τ
0
,τ
1
,τ
2
are defined as
following:
• τ
0
=
((K ⊕∆
i
)kN
i
,L
i
) | i = 1,··· ,q
;
• τ
1
=
n
(I
i
j
,O
i
j
) | j = 1,··· , l
i
;i = 1, ··· ,q
o
, where O
i
0
=
L
i
, I
i
j
= M
i
j
⊕ O
i
j−1
and O
i
j
= C
i
j
⊕ (2
j
L
i
) for j =
1,··· ,l
i
;i = 1, ··· ,q;
• τ
2
=
{
(X
u
,Y
u
) |Y
u
= P (X
u
),u = 1, ··· , r
}
.
Obviously, τ
0
mainly denotes the revealed infor-
mation which in PCBC satisfies that L
i
= P ((K ⊕
∆
i
)kN
i
) for i = 1,··· ,q, τ
1
denotes the rewritten form
of all (M
i
j
,C
i
j
) pairs, which -in PCBC- are actually the
input-output pairs of P called by RK[PCBC], and τ
2
denotes the r public bi-directional queries to P
±
.
According to τ, D will make its final decision,
which can be regarded as a (deterministic) function of
the transcript τ. Let T denote all possible transcripts,
and X denotes the transcript variable when D inte-
racts with RK[PCBC] while Y denotes the transcript
variable when D interacts with RK[$]. And then
Adv
Φ
⊕
−ind−bw−cpa
PCBC
(q,r) ≤ ∆(X,Y ), (6)
where ∆(X,Y ) denotes the statistic distance between
X and Y .
Next we play the H-Coefficient technique, which
is of greatly useful in proving various results on ideal
cryptographic primitives such as PRP/PRF (Mennink,
2016; Hoang and Tessaro, 2016; Mouha and Luykx,
2015), to upper bound ∆(X,Y ). The central idea of the
H-Coefficient technique is described as following:
Lemma 1. Let T participate into two disjoint sub-
sets T
good
and T
bad
, and ∃ε ≥ 0 such that ∀τ ∈ T
good
,
Pr[X = τ]/Pr[Y = τ] ≥1−ε. When T
good
with a small
ε is large and T
bad
is small,
∆(X,Y ) ≤ Pr[Y ∈ T
bad
] + ε. (7)
According to Lemma 1, to upper bound ∆(X ,Y )
is to upper bound Pr[Y ∈ T
bad
] and to low bound the
ratio of Pr[X = τ]/Pr[Y = τ] when τ ∈ T
good
.
UPPER BOUND Pr[Y ∈ T
bad
]. Denote the collision
happened between two sets S,S
0
as Col[S,S
0
] =
{
∃(e
1
,e
2
)∈S,∃(e
0
1
,e
0
2
)∈S
0
,e
1
=e
0
1
∨e
2
=e
0
2
}
,
and Col[S] = Col[S,S]. Thus τ is defined
as “bad” if any collision event, Col[τ
0
,τ
2
],
Col[τ
1
] or Col[τ
1
,τ
0
∪ τ
2
], happens. That is
T
bad
=
{
τ∈T | Col[τ
0
,τ
2
] ∨Col[τ
1
] ∨Col[τ
1
,τ
0
∪τ
2
]
}
and T
good
= T \T
bad
.
In the following, we classify the collisions of T
bad
that happens in Y into 4 types: (let u = 1,··· , r; j =
1,··· ,l
i
, j
0
= 1,··· ,l
i
0
;i,i
0
= 1,··· ,q)
• Col[τ
0
,τ
2
]: for any i, u, since both K and L
i
are rand-
omly chosen,
Pr
h
Col[τ
0
,τ
2
]
i
≤
q
∑
i=1
r
∑
u=1
Pr
(K ⊕∆
i
)kN
i
= X
u
+Pr
L
i
= Y
u
≤
qr
2
k
+
qr
2
n
.
• Col[τ
1
]: for any (i, j) 6= (i
0
, j
0
), since L
i
, L
i
0
, C
i
j
and C
i
0
j
0
are randomly chosen,
Pr
h
Col[τ
1
]
i
≤
∑
i,i
0
=1,···,q;
j=1,···,l
i
,
j
0
=1,···,l
i
0
;
(i, j)6=(i
0
, j
0
)
Pr[I
i
j
= I
i
0
j
0
]
+Pr[O
i
j
=O
i
0
j
0
]
!
≤
σ
2
2
n−1
=
σ(σ −1)
2
n
,
where
Pr
h
I
i
j
= I
i
0
j
0
i
= Pr
"
M
i
j
⊕C
i
j−1
⊕2
j−1
L
i
= M
i
0
j
0
⊕C
i
0
j
0
−1
⊕2
j
0
−1
L
i
0
#
=
1
2
n
,
Pr
h
O
i
j
= O
i
0
j
0
i
= Pr
"
C
i
j
⊕2
j
L
i
= C
i
0
j
0
⊕2
j
0
L
i
0
#
=
1
2
n
.
(Actually when i = i
0
the collision probability
here in the BW-CPA case is totally different from
that in the CPA case. Let j < j
0
, the BW-CPA
adversary is capable to choose M
i
0
j
0
to maximize
Pr[M
i
j
⊕C
i
j−1
⊕2
j−1
L
i
= M
i
0
j
0
⊕C
i
0
j
0
−1
⊕2
j
0
−1
L
i
0
] since
it knows M
i
j
,C
i
j−1
,C
i
0
j
0
−1
, while the CPA adversary
isn’t capable to. Thus without the finite multiplication
by 2 in each block process, the BW-CPA adversary can
choose M
i
0
j
0
= M
i
j
⊕C
i
j−1
⊕C
i
0
j
0
−1
which allows I
i
j
= I
i
0
j
0
.)
• Col[τ
1
,τ
0
]: for any i, j,i
0
, since L
i
, L
i
0
and C
i
j
are rand-
omly chosen,
Pr
h
Col[τ
1
,τ
0
] | ¬
Col[τ
1
]
i
≤
∑
i=1,···,q;
j=1,···,l
i
q
∑
i
0
=1
Pr
h
I
i
j
= (K ⊕∆
i
0
)kN
i
0
i
+Pr
h
O
i
j
= L
i
0
i
≤
σq
2
n−1
.
• Col[τ
1
,τ
2
]: for any i, j,u, since both L
i
and C
i
j
are rand-
omly chosen,
Pr
h
Col[τ
1
,τ
2
] | ¬
Col[τ
1
]
i
≤
∑
i=1,···,q;
j=1,···,l
i
r
∑
u=1
Pr[I
i
j
= X
u
]
+Pr[O
i
j
= Y
u
]
!!
≤
σr
2
n−1
.
Therefore,
Pr[τ ∈ T
bad
] (8)
=Pr
h
Col[τ
0
,τ
2
] ∨Col[τ
1
] ∨Col[τ
1
,τ
0
∪τ
2
]
i
≤
qr
2
k
+
σ(σ −1) + qr + 2σ(q + r)
2
n
.
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
458

LOW BOUND Pr[X = τ]/Pr[Y = τ] WHEN τ ∈ T
good
.
When τ ∈ T
good
, all pairs in τ are distinct. In X,
τ mainly records the randomly chosen secret key as
well as the total (q + σ + r) fresh calls to P (or P
±
) ,
that is
Pr[X = τ] =
1
2
k
·
1
2
n
q+σ+r
(2
n
−q −σ −r)!
, (9)
while in Y , τ records the dummy key, q distinct
randomly-chosen L
i
s, σ blocks of random bits and r
calls to P
±
, that is
Pr[Y = τ] =
1
2
k
·
1
2
n
q
·
1
2
nσ
·
1
2
n
r
(2
n
−r)!
. (10)
Obviously, according to (9) (10), when τ ∈ T
good
,
Pr[X = τ] > Pr [Y = τ].
According to Lemma 1, (6), (8),
Adv
Φ
⊕
−ind−bw−cpa
PCBC
(q,r) (11)
≤
qr
2
k
+
σ(σ −1) + qr + 2σ(q + r)
2
n
.
By so far, Theorem 1 is proved.
5 CONCLUSION
In this paper, we study how to provide confidential
protection with a single cryptographic permutation,
and propose 4 practical encryption schemes - PCBC,
POFB, PCFB and PCTR, by adding two simple kinds
of operations - XOR and the finite multiplication.
And we prove that, when using a non-repeated nonce,
these 4 permutation-based encryption schemes are in-
distinguishable from the random function against the
blockwise adaptive chosen plaintext attack in the Φ
⊕
-
related-key setting. Meanwhile they are more effi-
cient than the Sponge construction.
ACKNOWLEDGEMENTS
The work of this paper is supported by the Funda-
mental Theory and Cutting Edge Technology Rese-
arch Program of Institute of Information Engineering,
CAS (Grant No. Y7Z0251103), and the National Na-
tural Science Foundation of China (Grants 61472415,
61732021, 61772519).
REFERENCES
Albrecht, M. R., Farshim, P., Paterson, K. G., and Watson,
G. J. (2011). On cipher-dependent related-key attacks
in the ideal-cipher model. In FSE’11, Fast Software
Encryption - 18th International Workshop. Springer.
Alkassar, A., Geraldy, A., Pfitzmann, B., and Sadeghi, A.
(2001). Optimized self-synchronizing mode of opera-
tion. In FSE’01, Fast Software Encryption - 8th Inter-
national Workshop. Springer.
Andreeva, E., Bilgin, B., Bogdanov, A., Luykx, A., Mendel,
F., Mennink, B., Mouha, N., Wang, Q., and Yasuda, K.
(2014). PRIMATEs v1. Submission to the CAESAR
competition.
Aumasson, J., Henzen, L., Meier, W., and Naya-Plasencia,
M. (2013). Quark: A lightweight hash. J. Cryptology.
Bard, G. V. (2004). The vulnerability of SSL to chosen
plaintext attack. IACR Cryptology ePrint Archive.
Bard, G. V. (2006). A challenging but feasible blockwise-
adaptive chosen-plaintext attack on SSL. In SE-
CRYPT’06, Proceedings of the International Confe-
rence on Security and Cryptography. INSTICC Press.
Bard, G. V. (2007). Blockwise-adaptive chosen-plaintext
attack and online modes of encryption. In IMACC’07,
Cryptography and Coding - 11th IMA International
Conference. Springer.
Bellare, M., Desai, A., Jokipii, E., and Rogaway, P. (1997).
A concrete security treatment of symmetric encryp-
tion. In FOCS’97, 38th Annual Symposium on Foun-
dations of Computer Science. IEEE Computer So-
ciety.
Bellare, M. and Kohno, T. (2003). A theoretical treatment
of related-key attacks: RKA-PRPs, RKA-PRFs, and
applications. In EUROCRYPT’03, International Con-
ference on the Theory and Applications of Crypto-
graphic Techniques. Springer.
Bellare, M., Kohno, T., and Namprempre, C. (2002). Au-
thenticated encryption in SSH: provably fixing the
SSH binary packet protocol. In CCS’02, Proceedings
of the 9th ACM Conference on Computer and Com-
munications Security. ACM.
Bernstein, D. J. (2008). The Salsa20 family of stream cip-
hers. In New Stream Cipher Designs - The eSTREAM
Finalists. Springer.
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G., and
Van Keer, R. (2014). CAESAR submission: Ketje v1.
CAESAR First Round Submission, March.
Biham, E. (1993). New types of cryptanalytic attacks using
related keys (extended abstract). In EUROCRYPT’93,
Workshop on the Theory and Application of of Cryp-
tographic Techniques.
Biryukov, A. and Khovratovich, D. (2009). Related-key
cryptanalysis of the full AES-192 and AES-256. In
ASIACRYPT’09, 15th International Conference on the
Theory and Application of Cryptology and Informa-
tion Security. Springer.
Biryukov, A. and Khovratovich, D. (2014). PAEQ: paral-
lelizable permutation-based authenticated encryption.
In ISC’14, Information Security - 17th International
Conference. Springer.
Biryukov, A., Khovratovich, D., and Nikolic, I. (2009). Dis-
tinguisher and related-key attack on the full AES-256.
In CRYPTO’09, 29th Annual International Crypto-
logy Conference. Springer.
Bogdanov, A., Knezevic, M., Leander, G., Toz, D., Va-
rici, K., and Verbauwhede, I. (2011). SPONGENT:
Encryption Schemes based on a Single Permutation: PCBC, POFB, PCFB and PCTR
459

A lightweight hash function. In CHES 2011, Crypto-
graphic Hardware and Embedded Systems - 13th In-
ternational Workshop. Springer.
Chen, S. and Steinberger, J. P. (2014). Tight security bounds
for key-alternating ciphers. In EUROCRYPT’14, 33rd
Annual International Conference on the Theory and
Applications of Cryptographic Techniques. Springer.
Cogliati, B. and Seurin, Y. (2015). Beyond-birthday-bound
security for tweakable Even-Mansour ciphers with li-
near tweak and key mixing. In ASIACRYPT’15, 21st
International Conference on the Theory and Applica-
tion of Cryptology and Information Security. Springer.
Daemen, J. (1991). Limitations of the Even-Mansour con-
struction. In ASIACRYPT’91, International Confe-
rence on the Theory and Applications of Cryptology.
Springer.
Dai, W. (2002). An attack against SSH2 protocol. Email
to the SECSH Working Group ietf-ssh@ netbsd.
org ftp://ftp. ietf. org/ietf-mail-archive/secsh/2002-02.
mail.
Dobraunig, C., Eichlseder, M., and Mendel, F. (2015).
Related-key forgeries for Prøst-OTR. In FSE’15, Fast
Software Encryption - 22nd International Workshop.
Springer.
Dobraunig, C., Eichlseder, M., Mendel, F., and Schl
¨
affer,
M. (2014). Ascon v1–submission to the CAESAR
competition. CAESAR First Round Submission,
March.
Dunkelman, O., Keller, N., and Shamir, A. (2012). Mini-
malism in cryptography: The Even-Mansour scheme
revisited. In EUROCRYPT’12, 31st Annual Interna-
tional Conference on the Theory and Applications of
Cryptographic Techniques. Springer.
Duong, T. and Rizzo, J. (2011). Here come the xor ninjas.
White paper, Netifera.
Dworkin, M. J. (2015). Sha-3 standard: Permutation-based
hash and extendable-output functions.
Even, S. and Mansour, Y. (1997). A construction of a cipher
from a single pseudorandom permutation. J. Crypto-
logy.
Fouque, P., Joux, A., and Poupard, G. (2004). Blockwise
adversarial model for on-line ciphers and symmetric
encryption schemes. In SAC’04, Selected Areas in
Cryptography - 11th International Workshop. Sprin-
ger.
Fouque, P., Martinet, G., and Poupard, G. (2003). Practi-
cal symmetric on-line encryption. In FSE’03, Fast
Software Encryption - 10th International Workshop.
Springer.
Hoang, V. T. and Tessaro, S. (2016). Key-alternating ciphers
and key-length extension: Exact bounds and multi-
user security. In CRYPTO’16, 36th Annual Interna-
tional Cryptology Conference. Springer.
Joux, A., Martinet, G., and Valette, F. (2002). Blockwise-
adaptive attackers: Revisiting the (in)security of some
provably secure encryption models: CBC, GEM, IA-
CBC. In CRYPTO’02, 22nd Annual International
Cryptology Conference. Springer.
Karpman, P. (2015). From distinguishers to key reco-
very: Improved related-key attacks on even-mansour.
In ISC’15, Information Security - 18th International
Conference. Springer.
Kavun, E. B., Lauridsen, M. M., Leander, G., Rechberger,
C., Schwabe, P., and Yalc¸ın, T. (2014). Prøst. CAE-
SAR Proposal.
Mennink, B. (2016). XPX: generalized tweakable Even-
Mansour with improved security guarantees. In
CRYPTO’16, 36th Annual International Cryptology
Conference. Springer.
Moeller, B. et al. (2004). Security of CBC ciphersuites in
SSL/TLS: Problems and countermeasures. Unpublis-
hed manuscript, May.
Mouha, N. and Luykx, A. (2015). Multi-key security: The
Even-Mansour construction revisited. In CRYPTO’15,
35th Annual International Cryptology Conference.
Springer.
Rogaway, P. (1996). Problems with proposed IP
cryptography. Unpublished paper http://www.
cs. ucdavis. edu/rogaway/papers/draftrogaway-ipsec-
comments-00. txt.
Rogaway, P. (2004). Nonce-based symmetric encryption.
In FSE’04, Fast Software Encryption - 11th Internati-
onal Workshop. Springer.
Sasaki, Y., Todo, Y., Aoki, K., Naito, Y., Sugawara, T., Mu-
rakami, Y., Matsui, M., and Hirose, S. (2014). Mi-
nalpher v1. Submission to the CAESAR competition.
Sung, J., Lee, S., Lim, J. I., Lee, W., and Yi, O. (2001). Con-
crete security analysis of CTR-OFB and CTR-CFB
modes of operation. In ICISC 2001, Information Se-
curity and Cryptology - 4th International Conference.
Springer.
ICISSP 2018 - 4th International Conference on Information Systems Security and Privacy
460
