Electricity Consumption Model Analysis based on Sparse Principal

Components

Bo Yao

, Yiming Xu

, Yue Pang

, Chaoyi Jin

, Zijing Tan

, Xiangdong Zhou

and Yun Su

School of Computer Science, Fudan University, No.220, Handan Road, Shanghai, China

State Grid Shanghai Municipal Electric Power Company, Shanghai, China

Keywords: Electricity Time Series, Sparse Principal Components Analysis, Clustering and Categorization.

Abstract: The well-being of people, industry and economy depends on reliable, sustainable and affordable energy. The

analysis on energy consumption model, especially on electricity consumption model, plays an important role

in providing guidance that makes energy system stable and economical. In this paper, clustering based on

electricity consumption model is imposed to categorize consumers, and Sparse Principal Components

Analysis (SPCA) is employed to analyse electricity consumption model for each group clustered.

Experimental results show that our methods can automatically divide a day into peak times and off-peak

times, so as to reveal in detail the electricity consumption model of different types of consumers. Additionally,

we study the relationships between social background of consumers and their electricity consumption model.

Our experimental results show that social background of consumers has impact on their consumption model,

as expected, but cannot fully determine it.

1 INTRODUCTION

Energy is the life blood of our society. The well-being

of people, industry and economy depends on secure,

sustainable and affordable energy (European Union,

2011). However, our energy system faces a number

of challenges as existing infrastructures close,

domestic fossil fuel reserves decline and old systems

are required to meet new low-carbon objectives

(OFGEM, 2010).

To make sure that energy systems have adequate

capacity and are reliable and economical, effective

adjustments in policies of energy supply department

and in consumption strategies of end consumers are

necessary. The research on energy consumption

model, especially on electricity consumption model,

is a corner stone of these adjustments.

For instance, Time Of Use (TOU) Tariffs set

different prices for electricity at different times of the

day. Time is divided into peak and off-peak periods

that reflect the different levels of demand on the

electricity network. Cheaper electricity prices during

off-peak periods will guide consumers to use power

at that time so as to balance the demand. This

approach benefits electricity supply department in

balancing power supply and benefits end consumers

in reducing costs. However, peak and off-peak times

vary in different seasons of a year, and vary for

different types of consumers. Effective adjustments

of TOU Tariffs for different seasons and consumers

depend on a clear understanding of electricity

consumption model of consumers.

In this paper, we impose K-Means clustering and

Affinity Propagation clustering (AP) (Brendan and

Delbert, 2007) to divide consumers according to their

electricity consumption model. And Sparse Principal

Component Analysis (SPCA) (Hui et al., 2006) is

then employed to analyse electricity consumption

model for each group clustered. Experimental results

show that our method can, for different types of

consumers, automatically divide a day into peak

times and off-peak times.

Principal component analysis (PCA) (Pearson,

1901; Hotelling, 1930s; Jolliffe, 2002) is widely used

in data-processing and dimensionality reduction.

However, PCA suffers from the fact that each

principal component (PC) is a linear combination of

all the original variables, thus it is often difficult to

interpret the results. SPCA utilize the lasso (elastic

net) to produce modified PCs with sparse loadings. In

this case each modified PC is a linear combination of

some significant original variables rather than all.

Thus SPCA provides more interpretation and can be

applied to analyse electricity time series of

590

Yao, B., Xu, Y., Pang, Y., Jin, C., Tan, Z., Zhou, X. and Su, Y.

Electricity Consumption Model Analysis based on Sparse Principal Components.

DOI: 10.5220/0006715405900596

In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 590-596

ISBN: 978-989-758-276-9

consumers. By tuning the sparsity parameter

properly, sparse PCs derived can indicate the

significant time intervals in a day (that is, peak times),

so as to divide a day into different times

automatically.

Additionally, to study the relationships between

social background and electricity consumption model

of consumers, we use ACORN (CACI, 2010) to

categorize consumers and apply SPCA to analyse

electricity consumption model for each category. The

ACORN provides precise information and an in-

depth understanding of different types of people (that

is, social background of these people). Based on the

experiments, we find that social background of

consumers influences the consumption model but

cannot fully determine it. That reveals that it is

insufficient to consider only social background of

consumers, when adjusting policies.

2 RELATED WORK

Data analysis of daily load data generated by smart

meters can beneﬁt both electricity suppliers and end

consumers. A two-stage clustering based on multi-

level 1D discrete wavelet transform and K-means

algorithm is applied to perform daily load curve

clustering and load pattern clustering (Zigui et al.,

2017). Additionally, to obtain distinct consumer

categories, method of category identification based

on association rule mining and characteristic

similarity is also proposed in the paper. Zigui et al.

study the relationships between the natural types of

consumers and the consumer categorization based on

load pattern similarity; they find that the types cannot

full determine the categorization.

A hybrid fuzzy-stochastic technique proposed by

Yu et al., (2017) develops an interval-fuzzy chance-

constrained programming (IFCCP) method to reflect

multiple uncertainties expressed as interval-fuzzy-

random (integration of interval values, fuzzy sets, and

probability distributions). IFCCP has advantages in

uncertainty reflection and policy analysis, while

avoiding complicated intermediate models with high

computational efficiency. Considering the peak

power demand problem, the developed IFCCP

method is used to plan a regional-scale electric power

system (EPS).

In contrast to dividing a day manually relying on

experience, segmenting automatically by our SPCA

provides more convenience and rationality, since the

peak times and off-peak times derived are consistent

with the real consuming habits of consumers.

3 ANALYSING ELECTRICITY

CONSUMPTION MODEL

The process of electricity consumption model

analysis consists of two stages. First, we impose

clustering to divide consumers into groups according

to their consumption model, and meanwhile,

categorize consumers by their social background for

further study. Then, SPCA is employed to analyse

electricity consumption model for each group.

3.1 Clustering and Categorization

To obtain a better understanding of electricity

consumption model, we impose K-Means clustering

and AP clustering to gather consumers with similar

consumption model. K-Means clustering is a method

of vector quantization, originating from signal

processing, and is popular for cluster analysis in data

mining. It aims to partition n observations into k

clusters where each observation belongs to the cluster

with the nearest centroid. Affinity propagation (AP)

clustering is an algorithm based on the concept of

"message passing" between data points. Unlike K-

Means, Affinity Propagation does not require the

number of clusters to be determined before clustering.

Let  denote a    data matrix consisting of

electricity time series of consumers. Herein,  is the

number of consumers,  is the number of time

intervals, and 



is the electricity consumption of

the th consumer in the th time interval. Clustering

is applied to divide data matrix  into K sub-matrices





in the form of 



 , where











 . Each

sub-matrix is composed of electricity time series of

consumers with similar consumption model. After

that, meaningful results can be obtained when

analysing these sub-matrices by SPCA.

Additionally, to study the relationships between

social background and electricity consumption model

of consumers, we use ACORN to categorize

consumers. Similarly, given a    data matrix 

that consists of electricity time series of consumers,

we divide it into Q sub-matrices 



in the form of





  , where











  . Each sub-matrix is

composed of electricity time series of consumers in a

same category. Analysing these sub-matrices by

SPCA may reveal another side of the electricity

consumption model of consumers.

Electricity Consumption Model Analysis based on Sparse Principal Components

591

3.2 Analysing Electricity Time Series

with SPCA

To understand the electricity consumption model of

consumers, we employ SPCA (Hui et al., 2006) to

analyse every sub-matrix 



derived from clustering.

Besides, we also analyse every sub-matrix 



derived

from categorization to understand the relationships

between social background and electricity

consumption model. SPCA is a specialized technique

used in statistical analysis, and in particular, in the

analysis of multivariate data sets. It extends the

classic method of PCA for the reduction of

dimensionality of data by adding sparsity constraints

on the loadings of PCs.

Specifically, PCA can be formulated as a

regression-type optimization problem: Let  denote a

   data matrix, where  and  are the number of

observations and the number of variables,

respectively. And for each  , let 



denote the  th

principal component. Consider the ridge estimates







given by:







 







 



 



(1)

Let  















, then   



, which is the loading

of the th principal component. SPCA adds the 



penalty to equation (1) and fits the following

optimization problem:





 







 



 



 







(2)

That 

















is a sparse approximation to 



, and







is the th sparse principal component. With the

sparsity constraint (that is, the 



penalty) on the

loadings of PCs, a sparse PC derived is a linear

combination of some significant original variables. In

contrast to PCA whose every PC is a linear

combination of all the original variables, SPCA can

provide more meaningful interpretations.

We employ SPCA to analyse those sub-matrices





derived from clustering and 



derived from

categorization. Recall that a sub-matrix derived is

composed of electricity time series of consumers in a

same group, in the form of 



  (



 ). Herein,





(



) is the number of consumers in the group and

 is the number of time intervals in the time series.

By tuning the sparsity parameter 



properly, a sparse

PC derived from the sub-matrix is a linear

combination of some significant time intervals (that

is, based on the experimental results, a daily peak

times). And then we can segment a day into peak

times and off-peak times automatically according to

these sparse PCs derived. Since the peak times are

directly derived from the electricity time series of

consumers, this segmentation is consistent with the

real consuming habits of these consumers. In contrast

to dividing a day manually relying on experience, our

method provides more convenience and rationality.

4 EXPERIMENTS

We first introduce the experiment data in section 4.1,

and then in section 4.2, describe the experiments

where K-Means and AP clustering are imposed to

divide consumers and SPCA is applied to analyse

electricity consumption model for each group. Finally,

a detailed discussion about the relationships between

social background and electricity consumption model

is presented in section 4.3.

4.1 Data

We analysed electricity time series collected by the

Energy Demand Research Project (EDRP) (AECOM,

2011), which was designed to help better understand

how domestic consumers in UK react to improved

information about their energy consumption over the

long term. The data set used in our experiments

include 3118 consumers and their half-hourly

electricity time series from May 9, 2009 to August 24,

2009. Additionally, for each consumer in the data set,

there is an ACORN label which indicates the social

background of the consumer. We utilize these labels

to study the relationships between social background

and electricity consumption model of consumers.

4.2 Electricity Consumption Model

Analysis

4.2.1 Analysing by K-Means and SPCA

We start with an experiment where the electricity

time series were clustered by K-Means. The number

of clusters was set to 8 by adjusting the within-cluster

distance, between-cluster distance and numbers of

consumers in each group. We only chose the first

three groups with sufficient samples. Other groups do

not have enough consumers; this makes deriving

sparse PCs impractical. The sparse principal

components of the first three groups and their

corresponding daily peak times in a week are shown

in table 1(a).

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

592

Table 1(a): The sparse principal components of groups 0, 1 and 2 (K-Means) and their corresponding daily peak times in a

week.

Group

Counts of

consumers

PC1

PC2

PC3

PC4

649

1043

902

19:00-2:30

5:00-16:00

17:00-24:00

8:30-15:30

18:00-24:00

8:00-15:30

15:00-18:00

15:00-17:30

5:30-8:30

5:00-9:00

Table 1(b): The sparse principal components of groups 0, 1 and 2 (AP) and their corresponding daily peak times in a week.

Group

Counts of

consumers

PC1

PC2

PC3

PC4

1006

1165

511

18:00-6:00

17:00-1:00

15:00-22:30

7:30-16:30

7:30-15:30

6:30-7:30

5:00-8:30

5:30-8:00

Figure 1(a): Average electricity time series of groups 0, 1

and 2 (K-Means) in a week. The vertical axis represents the

electricity consumption (kilowatt per hour), and the

horizontal axis represents the time intervals every half hour

(totally 48 * 7 = 336 intervals).

To verify the validity of our method, we plotted

average electricity time series of groups 0, 1 and 2 in

the week. The results are presented in figure 1(a).

Note that the harmonization of daily peak times

derived by our SPCA and those real ones in figure

1(a) demonstrates the validity of our method.

For a better understanding of the electricity

consumption model, we categorized consumers by

ACORN in groups 0, 1 and 2. The results are shown

in figure 2(a) (categories whose count of consumers

is less than 5% were omitted for space limitation).

Category A, B and C of ACORN represent wealthy

households, category H and I of ACORN represent

bourgeois, and category L, M, N, O and P consist of

relatively low-income families. Note that group 0 is

mainly composed of wealthy households and

bourgeois, incurring the highest average electricity

consumption per consumer per day (about 12 kilowatt

per hour), compared to groups 1 and 2. Daily peak

times of this group almost span all day except 3:00 to

5:00; this indicates that consumers in the group have

a habit of using electricity nearly all the day except

the short time after midnight. Group 1 has a more

balanced categorization result, with a less mean value

per consumer per day (about 8 kilowatt per hour).

Figure 1(b): Average electricity time series of groups 0, 1

and 2 (AP) in a week. The vertical axis represents the

electricity consumption (kilowatt per hour), and the

horizontal axis represents the time intervals every half hour

(totally 48 * 7 = 336 intervals).

Accordingly, daily peak times of this group are

shorter, and electricity consumption of these

households is mostly in daytime and in the first half

of the night. Group 2 is mostly composed of relatively

low-income families and bourgeois, with the lowest

average value per consumer per day (about 5 kilowatt

per hour). And the daily peak times of this group are

the shortest among the three groups; the consumers

only use electricity in the morning and in the first half

of the night. In a word, we find the social background

of consumers influences their consumption model

and richer consumers tend to use more electricity in

longer peak times, as expected.

0,1

0,2

0,3

0,4

0,5

117

140

163

186

209

232

255

278

301

324

group 0 group 1 group 2

0,1

0,2

0,3

0,4

0,5

117

140

163

186

209

232

255

278

301

324

group 0 group 1 group 2

Electricity Consumption Model Analysis based on Sparse Principal Components

593

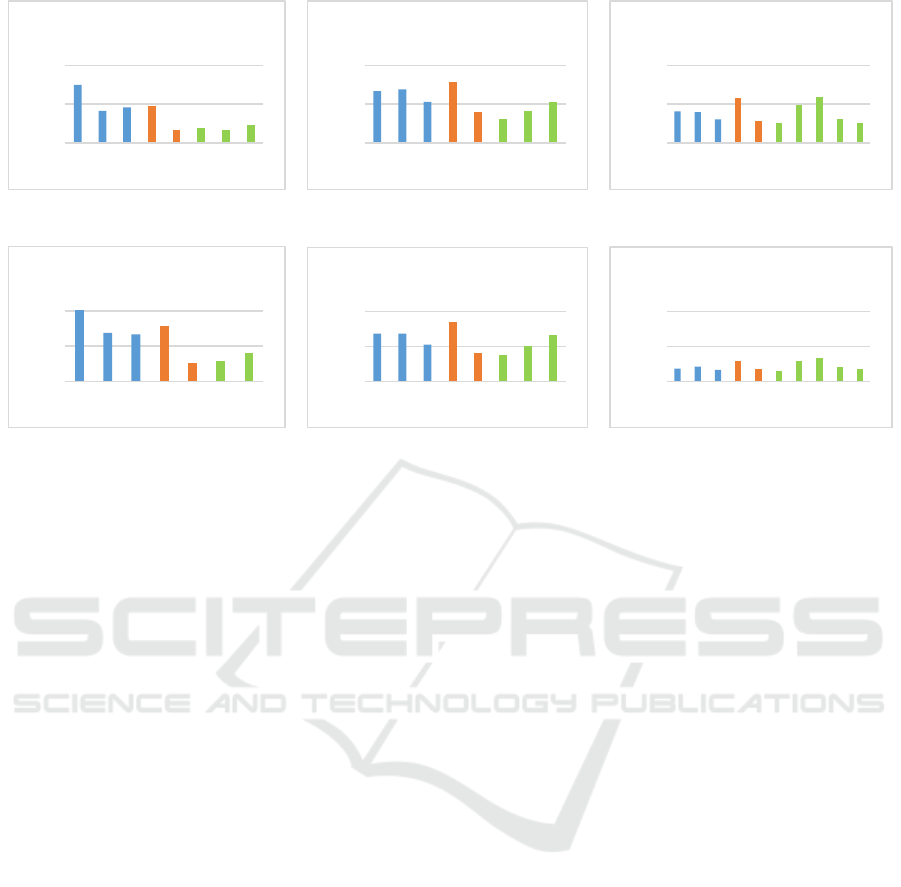
Figure 2(a): Results of categorization for groups 0, 1 and 2 of K-Means.

Figure 2(b): Results of categorization for groups 0, 1 and 2 of AP.

4.2.2 Analysing by AP and SPCA

Experiments in which the electricity time series were

clustered by AP show similar results as those of K-

Means. By trading off the within-cluster distance,

between-cluster distance and numbers of consumers

in each cluster, we selected results with 8 clusters.

Similarly, the first three groups with sufficient

consumers were chosen and their sparse PCs with

corresponding daily peak times in a week are shown

in table 1(b). To clearly show the validity of our

method, we also plotted average electricity time

series of groups 0, 1 and 2 in the week. The results are

presented in figure 1(b). Note that these obtained

daily peak times coincide with those real ones in

figure 1(b).

Similarly, consumers in groups 0, 1 and 2 were

categorized by ACORN for a clear understanding of

electricity consumption model; the results are shown

in figure 2(b) (categories whose count of consumers

is less than 5% were omitted). Category A, B and C

of ACORN represent wealthy households, category H

and I of ACORN represent bourgeois while category

L, M, N, O and P consist of relatively low-income

families. Interestingly, the first three groups with

sufficient consumers of the AP clustering resemble

those of K-Means. Group 0 also mainly consists of

wealthy households and bourgeois, which has the

highest average power consumption per consumer per

day. Consumers in this group tend to use electricity

nearly all the day. Again, group 1 has balanced

categorization results with a middle mean value per

consumer per day, and households in this group are

apt to use power in daytime and in the first half of the

night. Compared to groups 0 and 1, group 2 mostly

consists of relatively low-income families and

bourgeois, having the lowest mean power usage per

consumer per day. Electricity consumption of its

households is mostly in the morning and in the first

half of the night.

4.3 Discussion

To study the relationships between social background

and electricity consumption model of consumers, we

use ACORN to categorize consumers and apply

SPCA to analyse electricity consumption model for

each category. The consumers were categorized into

5 categories and the results are shown in table 3. We

neglected category 2, since the scarcity of consumers

will incur troubles in deriving sparse PCs.

This experiment produced mixed results. We can

find that a category may include both low-electricity-

consumption households and high-electricity-

consumption households. The power consumption

models of lower ones are covered by those of higher

ones, or reversely, the electricity consumption models

of higher ones are weakened by those of lower ones.

To further study the mutual interference in

analysing by categorization and SPCA, firstly, in a

typical category 5, we counted the number of

consumers for each group derived by K-Means and

AP clustering. The results are presented in table 4.

Note that even if category 5 is composed of relatively

low-income families, there are still some families

with high power consumption in the category. And

100

200

A B C H I L M N

group 0

100

200

A B C H I L M N

group 1

100

200

A B C H I L M N O P

group 2

100

200

A B C H I M N

group 0

100

200

A B C H I L M N

group 1

100

200

A B C H I L M N O P

group 2

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

594

Table 2: The sparse principal components of category 5 whose count of consumers is 505 and the corresponding daily peak

times.

Week

PC1

PC2

PC3

PC4

May 9, 2009 - May 15, 2009

May 16, 2009 - May 22, 2009

May23, 2009 - May 29, 2009

17:30-23:30

18:00-23:30

8:00-16:30

15:00-18:00

17:00-18:30

18:00-23:30

7:00-9:30

15:00-17:00

15:30-18:00

6:00-7:00

6:00-7:30

Table 3: Results of categorization by ACORN. Category 1

and 2 represent wealthy households and category 3

represents bourgeois while category 4 and 5 consist of

relatively low-income families.