
Comparative Study of the Behavior of Feature Reduction Methods in
Person Re-identification Task
Bahram Lavi
1
, Mehdi Fatan Serj
2
and Domenec Puig Valls
2
1
Dept. of Electrical and Electronic Engineering, University of Cagliari, Piazza d’Armi, 09123, Cagliari, Italy
2
Dept. of Computer Engineering and Maths School of Engineering, Universitat Rovira i Virgili, Tarragona, Spain
Keywords:
Person Re-Identification, Video Surveillance Systems, Dimensional Reduction Methods.
Abstract:
One of the goals of person re-identification systems is to support video-surveillance operators and forensic
investigators to find an individual of interest in videos acquired by a network of non-overlapping cameras. This
is attained by sorting images of previously observed individuals for decreasing values of their similarity with
a given probe individual. Existing appearance descriptors, together with their similarity measures, are mostly
aimed at improving ranking quality. Many of these descriptors generate a high feature vector represented
as an image signature. To tackle person re-identification in real-world scenario the processing time will be
crucial, so an individual of interest within a network camera should be found out swiftly. We therefore study
some feature reduction methods to achieve a significant trade-off between processing time and ranking quality.
Although, observing some redundancies on the generated patterns of a given descriptor are not deniable, we
suggest to employ a feature reduction method before use of it in real-world scenarios. In particular, we have
tested three reduction methods: PCA, KPCA, and Isomap. We then evaluate our study on two benchmark data
sets (VIPeR, and i-LIDS), by using two state-of-the-art descriptors on person re-identification task. The results
presented in this paper, after applying the feature reduction step, are very promising in terms of recognition
rate.
1 INTRODUCTION
Person re-identification is a computer vision task con-
sisting of recognizing an individual who had previ-
ously been observed over a network of cameras with
non-overlapping fields of view (Bedagkar-Gala and
Shah, 2014). One of its applications consists of sup-
porting video surveillance operators and forensic in-
vestigators in retrieving all the videos showing an in-
dividual of interest, given an image of him/her as a
query (aka probe). In this application scenario, the
goal of a person re-identification system is returning
to the user the frames or videos of all the individuals
recorded by the camera network (aka template gal-
lery) sorted for decreasing similarity to the probe, so
that the user can find the occurrences (if any) of the in-
dividual of interest, ideally in the first positions. This
task is challenging due to several issues typical of vi-
deo surveillance footage, like low resolution, uncon-
strained pose, illumination changes, and occlusions,
which do not allow to exploit strong biometrics like
face. Clothing appearance is therefore one of the most
widely used cues. Other cues like gait and anthropo-
metric measures have also been investigated.
Many of the existing similarity measures (either
hand-crafted or learnt from data) are indeed rather
complex, and require a relatively high processing
time, e.g., (Farenzena et al., 2010; Ma et al., 2014;
Liao et al., 2015). On the other hand, in real-world ap-
plications the template gallery can be very large, and
even if the processing time for a single matching score
is low (e.g., the Euclidean distance between fixed-
length feature vectors (Ma et al., 2014)), evaluating
the matching scores for all the templates can be time-
consuming.
During the past few years, many descriptors have
been proposed in the literature based on clothing ap-
pearance. The existing descriptors are typically con-
structed based on either colour information, texture
information, or combination of both. Despite the dif-
ferences among them, the final descriptor is typically
generated in high-dimension feature-size. In some
cases, the operator intends to attain the result much
faster, because of existing too many templates to be
checked by him/her. We clearly disccused this issue
in (Lavi et al., 2016) by proposing multi-stage sy-
614
Lavi, B., Serj, M. and Valls, D.
Comparative Study of the Behavior of Feature Reduction Methods in Person Re-identification Task.
DOI: 10.5220/0006717906140621
In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 614-621
ISBN: 978-989-758-276-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

stem to attain a significant trad-off between proces-
sing time with the expense of low recognition rate.
To construct such method, one should consider on
couple of simplified versions of a given descriptor to
obtain a faster version. As a simple guideline, that
we suggested, was to employ a feature reduction met-
hod on this purpose. However, apart from existence
of many feature reduction methods, at this paper, we
aim to study the behavior of some of them in person
re-identification problem.
In this paper, three of the most popular feature
reduction methods in machine learning is presented,
and a comparison among all of them is constructed
for person re-identification task. These three met-
hods are principal component analysis (PCA), ker-
nel principal component analysis (KPCA), and Iso-
map. PCA (Hotelling, 1933) is a well-known met-
hod in terms of compressing data pattern which con-
sists of calculating the Eigenvectors of the covari-
ance matrix of the original feature space, and des-
cribe the variation of a set of variables in terms of
a reduced set of uncorrelated linear space of such va-
riables with maximum variance (aka principal com-
ponents (PCs)). KPCA (Sch
¨
olkopf et al., 1999) is the
nonlinear version of PCA in which the original fea-
ture space is mapped to a higher-dimensional features
space using a kernel function, and then PCA is cal-
culated. Isomap (aka isometric feature mapping) is
popular in terms of computing quasi-isometric from a
high-dimensional feature space to a low-dimensional
feature space . Isomap is highly efficient and applica-
ble to a wide range of data points and dimensions (Ba-
lasubramanian and Schwartz, 2002). The isometric
feature space can be supposed as a kernel function
and so this method can also be known as a type of
KPCA technique.
This paper is structured as follows. We first sum-
marize related work in Sect. 2. In Sect. 3, we de-
fine the problem by explaining a standard person re-
identification system. Then, in Sect. 4, we explain the
employed feature reduction methods in our study. Fi-
nally, in Sect. 5 ,we present our experimental results
and discuss on behaviour the feature reduction met-
hods by using two well-known descriptors in person
re-identification task on two benchmark data sets.
2 BACKGROUND
In this section we first describe some standard per-
son re-identification techniques. We then summarize
person re-identification techniques aimed at reducing
processing time in the computation of matching sco-
res.
2.1 Overview on Person
Re-Identification Methods
The recent state-of-the-art abound descriptor for per-
son re-identification task. These descriptors can be
categorised by considering their cue on generating
image signature; colour information (Cheng et al.,
2011; Dikmen et al., 2010), and many of existing
works used as combination of different colour and
texture information to help in attaining a better per-
formance (Farenzena et al., 2010; Prosser et al., 2010;
Ma et al., 2014; Zheng et al., 2013). For person re-
identification task, both processing time and recog-
nition accuracy play an important role to tackle this
problem in online applications. In this respect, some
existing approaches are time consuming due to com-
putation of matching scores for a target image against
the templates in the gallery set. This may be caused
of large number of feature elements generated as an
image signature. Farenzena et al. proposed (Faren-
zena et al., 2010) symmetry driven accumulation of
local features (SDALF) descriptor which consists of
subdividing body into four parts: left and right, torso
and legs. Three kinds of features are extracted from
each part: maximally stable color regions (MSCR),
i.e., elliptical regions (blobs) exhibiting distinct color
patterns (their number depends on the specific image);
a weighted HSV color histogram (wHSV); and recur-
rent high-structured patches (RHSP) that characterize
texture. A specific similarity measure is defined for
each feature; the matching score is computed as their
linear combination. Despite from the small feature
size vectors generated by a descriptor, the whole pro-
cesses for such three descriptors are very time con-
suming. The final descriptor in terms of the feature-
size is variant for different individuals. In (Satta et al.,
2012), a dissimilarity-based approach proposed to de-
sign descriptors made up of bags of local features,
possibly extracted from different body parts. It con-
sists in finding a set of M representative local fea-
tures (called prototypes) from all individuals of the
template gallery, and in representing each template
and probe image as a vector of M dissimilarity va-
lues between the corresponding bag of local features
and the templates. This allows the matching score to
be computed as a distance between feature vectors,
rather than using a more complex similarity measure
between bags of local features.
2.2 Reducing Processing Time in Person
Re-Identification
To our knowledge, the issue of processing time has
been explicitly addressed so far in the context of per-
Comparative Study of the Behavior of Feature Reduction Methods in Person Re-identification Task
615

son re-identification only in (Dutra et al., 2013; Khed-
her and El Yacoubi, 2015). Only in (Dutra et al.,
2013) the proposed solution is a multi-stage system:
the first stage selects a subset of templates using a des-
criptor which is built upon a bag-of-words feature re-
presentation and an indexing scheme based on inver-
ted lists, and requires a low processing time for com-
puting matching scores; the second stage ranks only
the selected templates using a different, more com-
plex descriptor based on mean Riemann covariance.
In (Dutra et al., 2013) only two stages are considered,
and only a subset of templates is ranked by the whole
system, possibly losing the correct identity. The met-
hod of (Khedher and El Yacoubi, 2015) reduces pro-
cessing time in the specific multi-shot setting (when
several images per individual are available), and for
specific descriptors based on local feature matching,
e.g., interest points. It first filters out irrelevant inte-
rest points, then it builds a sparse representation of the
remaining ones.
3 PROBLEM DEFINITION
The existing person re-identification descriptors can
be subdivided into two main categories: fixed-size
feature vectors (e.g., (Ma et al., 2014; Liao et al.,
2015)), and descriptor with variable size (e.g., (Fa-
renzena et al., 2010)). Note that, at this paper, we
study only the descriptors with fixed-size feature vec-
tors. For fixed-size descriptors, an unsupervised fea-
ture reduction technique like PCA can be used. The
suitability of PCA to person re-identification tasks is
witnessed to its use in the pre-processing step of gBi-
Cov (Ma et al., 2014). However, we aim to study
also some other feature reduction methods regarding
to our motivation of our work.
In standard person re-identification systems, X
T
and X
P
are the generated features by a descriptor
for a template and probe image, respectively, m(·, ·)
the similarity measure between two descriptors, and
G = {X
T
1
, . . . , X
T
n
} the template gallery. For a given
X
P
, a standard re-identification system computes the
matching scores m(X
P
, X
T
i
), i = 1, . . . , n, and returns
the list of template images ranked for decreasing va-
lues of the score. Ranking accuracy is typically eva-
luated using the cumulative matching characteristic
(CMC) curve, i.e., the probability (recognition rate)
that the correct identity is within the first ranks. He-
reinafter we consider only the generated fixed-size fe-
ature vector (e.g. X) by a specific descriptor. Fig. 1
presents the whole scheme of our strategy; aiming to
employing a feature reduction method on person re-
identification task
Apparently, some redundancies of patterns can be
occurred within a feature vector, which are intuiti-
vely effected on processing time on real-time applica-
tions. It is worth to remind the readers that the issue
of processing time in person re-identification can be
categorized from two point of views: the processing
time of constructing descriptor ( aka descriptor ge-
neration); which can be done off-line for the gallery
set, and the processing time of computing matching
score between pair of descriptors ( aka descriptors
matching); which has to be done on-line for investiga-
ting an individual of interest (i.e. probe image) as the
procedure of the real-time application. At this the-
sis work, whereas a feature reduction method needs
a training phase to project the proper patterns into
the low-dimensional space as same as a step of the
re-identification system which needs to construct the
descriptor for each individual. We consider, instead,
the issue of the matching processing time of a sin-
gle probe image and a template image. We therefore
study on the feature vectors generated by the descrip-
tors, and investigate an empirical procedure to attain a
significant trade-off between processing time and ran-
king quality in person re-identification task.
Moreover, having redundant and irrelevant pat-
terns from the feature vectors might be caused in over-
fitting problem. Removing these irrelevant pattern
from the feature space before tacking them in real-
world application scenarios is know as prepare data
step in machine learning processes. To sum up, there
might be three key advantages of feature reduction
methods:
1. decrease the risk of overfitting; which allows the
algorithm to make a decision in less redundant
data.
2. improve the recognition accuracy; which avoid
the algorithm by occurrence of misleading those
irrelevant data.
3. decrease the processing time; which leads the
method to be faster.
We therefore study on the feature vector gene-
rated by the descriptors, and investigate an empi-
rical procedure to attain a significant trade-off bet-
ween processing time and ranking quality in person
re-identification task.
4 FEATURE REDUCTION
METHODS
At this paper, we discuss on three feature re-
duction methods and their behaviours in person re-
identification task.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
616

Descriptor
generation
computing
similarity scores
generating the
ranked list
probe image
Descriptor
generation
feature reduction
method
Figure 1: Application of a feature reduction method in per-
son re-identification.
4.1 Principal Component Analysis
(PCA)
PCA (Diamantaras and Kung, 1996) is pretty a well-
known method for linear dimensional reduction. This
method leads to identify important patterns within a
data, and express the data in low-dimensional pat-
terns by keeping the nature of the data at the same
time(aka compressing data). PCA, typically, employs
Singular Value Decomposition (SVD) of the features
to project a feature vector into a lower dimensional
space. SVD can be more fundamental in the concept
of feature reduction method, since not only it provi-
des direct approach to compute the principle compo-
nents(PCs), but also simultaneously helpful to obtain
row and column spaces (Zhang et al., 2007). At the
following, we go through some brief introductions of
the mathematical point of views of SVD.
Let X = {x
1
, x
2
, . . . , x
n
} be the given feature vec-
tor of size n to be compressed. While X is denoted as
X ∈ R
N
, where R represents the real numbers within
the corresponding feature vector. The SVD of X is
defined as
X = USV
H
(1)
where U ∈ F
N×N
and V ∈ F
N×N
are unitary ma-
trices, and S ∈ F
N×N
as a diagonal matrix, S =
diag(α
1
, . . . , α
r
, 0, . . . , 0). The singular values are in
the decreasing order, α
1
≥ . . . ≥ α
r
≥ 0. Accordingly,
in many applications, it can be useful to approximate
X with low-rank matrix
X =
U
r
U
n−r
S
r
0
0 0
V
H
r
V
H
n−r
(2)
Then, we have
¯
X = U
r
S
r
V
H
r
(3)
4.2 Kernel Principal Component
Analysis (KPCA)
Kernel-PCA (KPCA) is an improved theory of tradi-
tional linear PCA in a high-dimensional space which
is constructed by employing a kernel function. On
the other words, KPCA is a non-linear dimensional
reduction for the features to project a lower dimensio-
nal space using the kernel method, and then compute
PCA on the high-dimensional feature space. Howe-
ver, KPCA can be applied based on a specific kernel
of k, this leads the application to choose a proper ker-
nel function (Sch
¨
olkopf et al., 1999). Given a data set
X of input samples {x
1
, x
2
, . . . , x
N
}, a kernel is defined
as follows
k : X × X →R
(x
i
, x
j
) 7→ k(x
i
, x
j
),
(4)
where the kernel k(., .) gives a scalar that describes
the similarity of the samples x
i
and x
j
. In this work,
the Gaussian kernel (RBF) is employed as follow
k(x
i
, x
j
) = exp
−
x
i
− x
j
2
2σ
2
!
(5)
Using the obtained kernel, the originally linear ope-
rations of PCA are performed (as explained in 4.1) to
reduce the dimensionality of the kernel feature space.
The Gaussian kernel (RBF) is chosen in this studying
because the linear kernel function gives the same per-
formance as applying the normal PCA in the original
feature space.
4.3 Isomap
Isomap is a non-linear dimensional reduction through
isometric feature mapping which consists of calcu-
lating quasi-isometric to obtain low-dimensional em-
bedding of a set of high-dimensional data points. The
algorithm is based on estimating of geometry featu-
res of data distribution, and then mapping data to a
new space. Isomap is quite straightforward technique
that resolves feature reduction problem by computing
geodesic distances between each data point. Geode-
sic distance basically computes between two points
over the manifold. In order to compute the distan-
ces between data points x
i
, i = 1, 2, . . . , N, a neighbor-
hood graph of G is constructed in which each data
point x
i
is connected with its k nearest neighbors x
i j
,
j = 1, 2, . . . , k, within a data set, and forming an es-
timation of the geodesic distance between two points
by taking into account the shortest path between them.
One can compute the shortest-path between all the
data points by employing Dijkstras (Dijkstra, 1959) or
Comparative Study of the Behavior of Feature Reduction Methods in Person Re-identification Task
617

Floyds algorithms (Fisher, 1936), and form into a pai-
rwise geodesic distance matrix. The computational
complexity of this method, only when the algorithm
measures the shortest path on the neighborhood graph
and creates a graph distances matrix, is the most time
consuming and it is performed in O(N
3
) operations.
4.4 Error Estimation
The performance of a re-identification system is typi-
cally measured using the CMC curve, defined as the
probability that the correct identity is within the first
rnk ranks, for rnk = 1, . . . , n. By definition, the CMC
curve increases with rnk, and equals 1 for rnk = n.
Whereas, this work aims to reduce the feature space
of the original descriptor, we employ reconstruction
error to estimate the variances the projected feature
space. However, this could be simply identified from
the behaviour of corresponding CMC curve, but for
sake of comparison of different reduction methods,
the reconstruction error is computed between the ori-
ginal feature space and the projected feature space. In
order to estimate the reconstruction error of the pro-
jected feature vector, We employ Frobenius norm. To
this aim, by recalling the projected feature space (
¯
X)
and the original feature vector(X), the reconstruction
error is estimated as
E =
k
X −
¯
X
k
2
F
kXk
(6)
5 EXPERIMENTAL EVALUATION
We carried out our comparison with two well-known
descriptors in person re-identification problem: gBi-
Cov and LOMO, on two benchmark data sets: VIPeR
and i-LIDS. At the following, we give some explana-
tion of the used descriptors as well as the data sets.
5.1 Descriptors and Data Sets
We used the gBiCov, and LOMO descriptors, and
obtained reduced versions of each of them by using
PCA, KPCA, and Isomap feature reduction methods.
gBiCov (Ma et al., 2014) is based on biologically-
inspired features (BIF) obtained by Gabor filters with
different scales over the HSV color channels. The re-
sulting images are subdivided into overlapping regi-
ons of 16 × 16 pixels; each region is represented by
a covariance descriptor that encodes shape, location
and color information. BIF and covariance descrip-
tors are concatenated, and PCA is used to reduce its
dimension. The final generate image signature con-
tains ≈ 6000 elements. LOMO (Liao et al., 2015)
extracts an 8 × 8 × 8-bins HSV histogram and two
scales of the Scale Invariant Local Ternary Pattern
histogram (characterizing texture) from overlapping
windows of 10 × 10 pixels; it then retains one only
histogram from all windows at the same horizontal
location, obtained as the maximum value among all
the corresponding bins. These histograms are conca-
tenated with the ones computed on a down-sampled
image. The final generated image signature contains
≈ 27000 elements.
We evaluated our experimental results on two ben-
chmark data sets: VIPeR, and i-LIDS. VIPeR (Gray
and Tao, 2008) is a challenging data set for person
re-identification; it is made up of two images of 632
individuals from two camera views, with pose and il-
lumination changes, cropped and scaled to 128 × 48
pixels. i-LIDS contains 476 images of 119 pedestri-
ans taken at an airport hall from non-overlapping ca-
meras, with pose and lightning variations and strong
occlusions.
5.2 Experimental Setup
One image for each person was randomly selected
to build the template gallery; the other images
formed the probe gallery. As in (Farenzena et al.,
2010), for each data set we repeated our experiments
on ten different subsets of individuals, using one
image of each individual as template and one as
probe, and reported the average CMC curve over
the ten runs. We used an Intel Core i5 2.6 GHz
CPU. We applied the above-mentioned feature
reduction methods on two well-known descrip-
tors on VIPeR data set in person re-identification
task. The original feature generated by a given
descriptor (X), are reduced for different sizes in r =
{2, 5, 20, 50, 80, 100, 130, 150, 200, 300, 500, 800, 1000,
1200, 2000, 2500, 3500}. For KPCA, we have chosen
the Gaussian kernel because of its good performance.
For Isomap, we set the number of neighborhoods to
k = 5.
5.3 Experimental Results
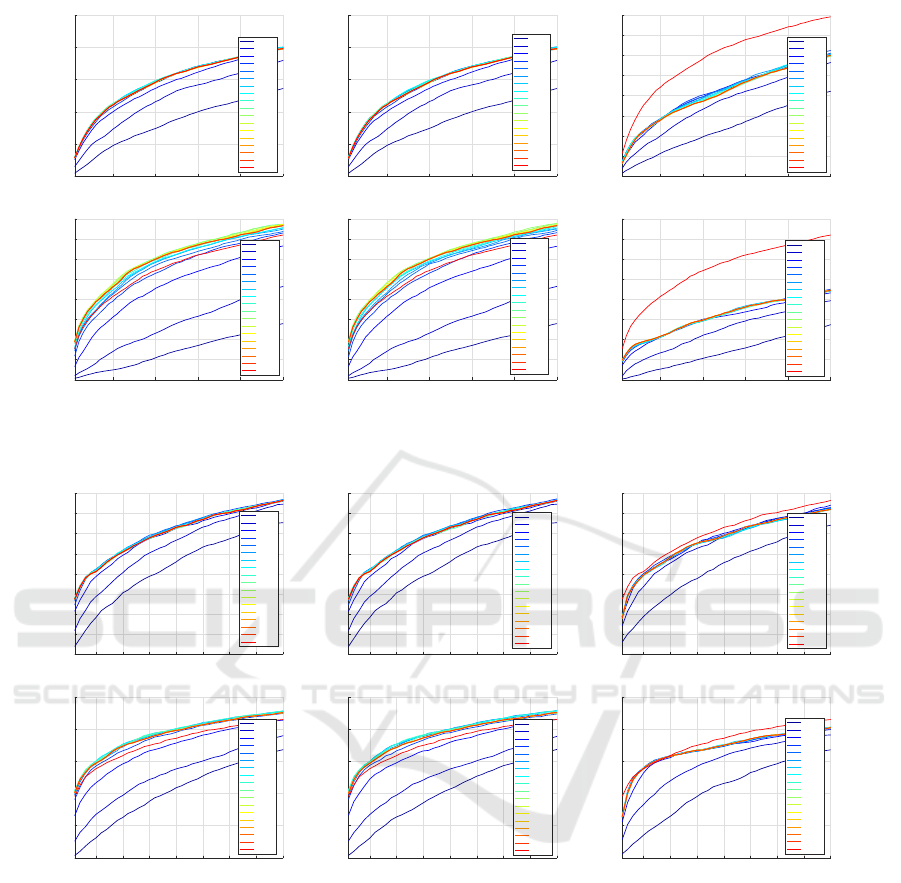
Figures 2 and 3 present the corresponding CMC cur-
ves obtained by using different descriptors as well as
different feature reduction methods on VIPeR, and
i-LIDS data sets, respectively. PCA as a standard
technique, which the new techniques are still unable
to outperform it. KPCA also has a very similar beha-
viour in terms of the recognition accuracy in person
re-identification. Also, in both techniques, the recog-
nition accuracy outperformed the original CMC curve
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
618
10 20 30 40 50
Rank
0
20
40
60
80
100
Recognition rate(%)
CMC, gBiCov, VIPeR, PCA
r=2
r=25
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
10 20 30 40 50
Rank
0
20
40
60
80
100
Recognition rate(%)
CMC, gBiCov, VIPeR, KPCA
r=2
r=25
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
10 20 30 40 50
Rank
0
10
20
30
40
50
60
70
80
Recognition rate(%)
CMC, gBiCov, VIPeR, ISOMAP
r=2
r=25
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
10 20 30 40 50
Rank
0
10
20
30
40
50
60
70
80
Recognition rate(%)
CMC, LOMO, VIPeR, PCA
r=2
r=25
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
10 20 30 40 50
Rank
0
10
20
30
40
50
60
70
80
Recognition rate(%)
CMC, LOMO, VIPeR, KPCA
r=2
r=25
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
10 20 30 40 50
Rank
0
10
20
30
40
50
60
70
80
Recognition rate(%)
CMC, LOMO, VIPeR, ISOMAP
r=2
r=25
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
Figure 2: CMC curves obtained by gBiCov and LOMO descriptors on VIPeR data set in which the feature reduction methods
have been employed. Figure is best viewed in color and under zoom.
5 10 15 20 25 30 35 40
Rank
0
10
20
30
40
50
60
70
80
Recognition rate(%)
CMC, gBiCov, i-LIDS, PCA
r=2
r=5
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
5 10 15 20 25 30 35 40
Rank
0
10
20
30
40
50
60
70
80
Recognition rate(%)
CMC, gBiCov, i-LIDS, KPCA
r=2
r=5
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
5 10 15 20 25 30 35 40
Rank
0
10
20
30
40
50
60
70
80
Recognition rate(%)
CMC, gBiCov, i-LIDS, ISOMAP
r=2
r=5
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
5 10 15 20 25 30 35 40
Rank
0
20
40
60
80
100
Recognition rate(%)
CMC, LOMO, i-LIDS, PCA
r=2
r=5
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
5 10 15 20 25 30 35 40
Rank
0
20
40
60
80
100
Recognition rate(%)
CMC, LOMO, i-LIDS, KPCA
r=2
r=5
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
5 10 15 20 25 30 35 40
Rank
0
20
40
60
80
100
Recognition rate(%)
CMC, LOMO, i-LIDS, ISOMAP
r=2
r=5
r=20
r=50
r=80
r=100
r=130
r=150
r=200
r=300
r=500
r=800
r=1000
r=1200
r=2000
r=2500
r=3500
orginal
Figure 3: CMC curves obtained by gBiCov and LOMO descriptors on i-LIDS data set in which the feature reduction methods
have been employed. Figure is best viewed in color and under zoom.
on LOMO descriptor when PCA and KPCA are app-
lied for the original feature vector, and in the same
way, with slightly better performance by using gBi-
Cov on VIPeR and i-LIDS data sets. In contrast,
KPCA is very time consuming because of the com-
putational complexity when the feature vector is rela-
tively larger in comparison to the other methods. The
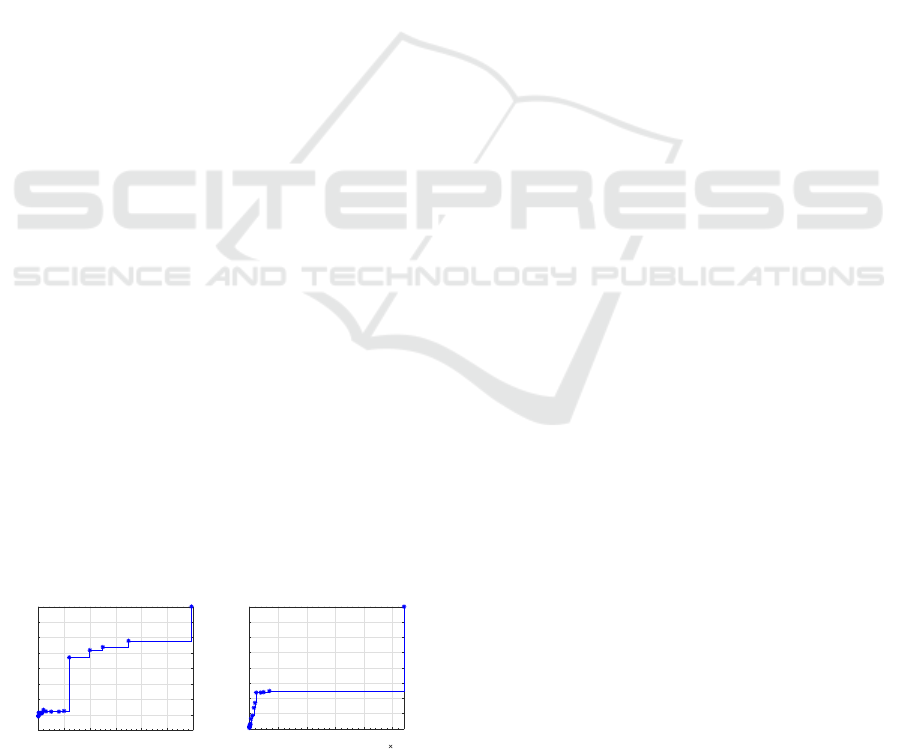
average processing time for computing one matching
score, evaluated on VIPeR and i-LIDS, are reported
in Fig. 4. Similar processing times were observed in
all data sets, due to the use of the same image size.
Moreover, figures 5 and 6 demonstrate the estimated
errors among different feature reduction methods for
different values of r. Apparently from the presented
figures, the error estimation using LOMO and gBicov
descriptors with PCA and KPCA lead to be zero at
the certain value of r > 1000 on VIPeR, and r > 500
on i-LIDS data set with different descriptors. Howe-
ver, Isomap has better behaviour only on i-LIDS data
set with respect to its performance on VIPeR data set,
and this is also obvious from the estimated error in
which the error leads to be zero for r > 500.
To sum up, if one needs to achieve a significant
trade-off between processing time and recognition
rate, PCA could be a good solution in this regard.
Despite from the processing time, one could also em-
Comparative Study of the Behavior of Feature Reduction Methods in Person Re-identification Task
619
ploy KPCA to gain higher recognition rate with ex-
pense of the higher processing time. This is due to
KPCA is more time consuming than traditional PCA
because of its mapping kernel function, as well as op-
timization of the kernel parameters.
6 CONCLUSIONS AND FUTURE
WORK
At this paper we compared the performances of
the most popular fundamental dimensional reduction
methods, PCA, KPCA, and Isomap, on person re-
identification data sets. The comparison is done
through the experiments conducted by using two des-
criptors on two benchmark data sets. The experi-
mental results evidenced that generated features by
these descriptors might be not well-optimum. PCA
and KPCA outperformed the original CMC curve on
LOMO and gBiCov descriptors on VIPeR and i-LIDS
data sets. This was apparent also from their error es-
timation of projected feature space using two descrip-
tors on two data sets. Both these reduction methods
achieve better performances rather than Isomap met-
hod in person re-identification task. The reason relies
in the fact that PCA and KPCA can explore higher
order information of the original inputs than Isomap.
It is worth to point out that, at this work, PCA was
better than others in terms of the computational cost,
while KPCA was more time consuming with respect
to the other two reduction methods. It therefore can be
stated that PCA achieved promising performance for
handling of optimization of raw data and projection of
it to low-dimensional feature space. We studied this
only for the descriptors with fixed-size feature vector.
Finally, we point out that the optimization of the di-
mensional reduction methods analyzed in this paper
is computationally and numerically practical in real-
time applications. As the future work, we aim at ca-
refully study the behavior of these feature reduction
methods by concerning on some analytical terms, and
visualize the projected data on the actual feature space
to get better prospective on those behaviours.
2 1000 2000 3000 4000 5000 6000
r
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.037
t
M
Maching processing time of gBiCov
0 0.5 1 1.5 2 2.5
r
10
4
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
t
M
Maching processing time of LOMO
Figure 4: Average processing time t
M
(in sec.) for com-
puting a matching score for a single probe image and one
template, for each of the two descriptors with different fea-
ture sizes r.
ACKNOWLEDGMENT
We gratefully acknowledge Prof. Giuseppe Rodri-
guez of Dipartimento di Matematica e Informatica at
University of Cagliari, for his initial analysis on the
data and experimental evaluation of this paper.
REFERENCES
Balasubramanian, M. and Schwartz, E. L. (2002). The
isomap algorithm and topological stability. Science,
295(5552):7–7.
Bedagkar-Gala, A. and Shah, S. K. (2014). A survey of ap-
proaches and trends in person re-identification. Image
and Vision Computing, 32(4):270–286.
Cheng, D. S., Cristani, M., Stoppa, M., Bazzani, L., and
Murino, V. (2011). Custom pictorial structures for re-
identification. In BMVC, page 6.
Diamantaras, K. I. and Kung, S. Y. (1996). Principal
component neural networks: theory and applications.
John Wiley & Sons, Inc.
Dijkstra, E. W. (1959). A note on two problems in connex-
ion with graphs. Numerische mathematik, 1(1):269–
271.
Dikmen, M., Akbas, E., Huang, T. S., and Ahuja, N. (2010).
Pedestrian recognition with a learned metric. In Com-
puter Vision–ACCV 2010, pages 501–512. Springer.
Dutra, C. R., Schwartz, W. R., Souza, T., Alves, R.,
and Oliveira, L. (2013). Re-identifying people
based on indexing structure and manifold appea-
rance modeling. In Graphics, Patterns and Images
(SIBGRAPI), 2013 26th SIBGRAPI-Conference on,
pages 218–225. IEEE.
Farenzena, M., Bazzani, L., Perina, A., Murino, V., and
Cristani, M. (2010). Person re-identification by
symmetry-driven accumulation of local features. In
Computer Vision and Pattern Recognition (CVPR),
2010 IEEE Conference on, pages 2360–2367. IEEE.
Fisher, R. A. (1936). The use of multiple measurements
in taxonomic problems. Annals of human genetics,
7(2):179–188.
Gray, D. and Tao, H. (2008). Viewpoint invariant pedestrian
recognition with an ensemble of localized features. In
Computer Vision–ECCV 2008, pages 262–275. Sprin-
ger.
Hotelling, H. (1933). Analysis of a complex of statistical
variables into principal components. Journal of edu-
cational psychology, 24(6):417.
Khedher, M. I. and El Yacoubi, M. A. (2015). Two-stage
filtering scheme for sparse representation based inte-
rest point matching for person re-identification. In Ad-
vanced Concepts for Intelligent Vision Systems, pages
345–356. Springer.
Lavi, B., Fumera, G., and Roli, F. (2016). A multi-stage
approach for fast person re-identification. In Joint
IAPR International Workshops on Statistical Techni-
ques in Pattern Recognition (SPR) and Structural and
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
620

0 500 1000 1500 2000 2500 3000 3500
r
0
1
2
3
4
5
6
7
Error estimation
10
-6
gBiCov, VIPeR, PCA
0 500 1000 1500 2000 2500 3000 3500
r
0
1
2
3
4
5
6
7
Error estimation
10
-9
gBiCov, VIPeR, KPCA
0 500 1000 1500 2000 2500 3000 3500
r
0
0.05
0.1
0.15
Error estimation
gBiCov, VIPeR, ISOMAP
0 500 1000 1500 2000 2500 3000 3500
r
0
1
2
3
4
5
Error estimation
10
-5
LOMO, VIPeR, PCA
0 500 1000 1500 2000 2500 3000 3500
r
0
1
2
3
4
5
Error estimation
10
-8
LOMO, VIPeR, KPCA
0 500 1000 1500 2000 2500 3000 3500
r
0
1
2
3
4
5
6
7
Error estimation
LOMO, VIPeR, ISOMAP
Figure 5: Error estimation by using gBiCov and LOMO descriptors on VIPeR data set for different feature reduction methods.
0 500 1000 1500 2000 2500 3000 3500
r
0
1
2
3
4
5
6
7
Error estimation
10
-6
gBiCov, i-LIDS, PCA
0 500 1000 1500 2000 2500 3000 3500
r
0
1
2
3
4
5
6
7
Error estimation
10
-9
gBiCov, i-LIDS, KPCA
0 500 1000 1500 2000 2500 3000 3500
r
0
0.02
0.04
0.06
0.08
0.1
0.12
Error estimation
gBiCov, i-LIDS, ISOMAP
0 500 1000 1500 2000 2500 3000 3500
r
0
1
2
3
4
5
Error estimation
10
-5
LOMO, i-LIDS, PCA
0 500 1000 1500 2000 2500 3000 3500
r
0
1
2
3
4
5
Error estimation
10
-8
LOMO, i-LIDS, KPCA
0 500 1000 1500 2000 2500 3000 3500
r
0
1
2
3
4
5
Error estimation
LOMO, i-LIDS, ISOMAP
Figure 6: Error estimation by using gBiCov and LOMO descriptors on i-LIDS data set for different feature reduction methods.
Syntactic Pattern Recognition (SSPR), pages 63–73.
Springer.
Liao, S., Hu, Y., Zhu, X., and Li, S. Z. (2015). Person re-
identification by local maximal occurrence represen-
tation and metric learning. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recogni-
tion, pages 2197–2206.
Ma, B., Su, Y., and Jurie, F. (2014). Covariance des-
criptor based on bio-inspired features for person re-
identification and face verification. Image and Vision
Computing, 32(6):379–390.
Prosser, B., Zheng, W.-S., Gong, S., Xiang, T., and Mary,
Q. (2010). Person re-identification by support vector
ranking. In BMVC, page 6.
Satta, R., Fumera, G., and Roli, F. (2012). Fast person re-
identification based on dissimilarity representations.
Pattern Recognition Letters, 33(14):1838–1848.
Sch
¨
olkopf, B., Burges, C. J., and Smola, A. J. (1999). Ad-
vances in kernel methods: support vector learning.
MIT press.
Zhang, L., Marron, J., Shen, H., and Zhu, Z. (2007).
Singular value decomposition and its visualization.
Journal of Computational and Graphical Statistics,
16(4):833–854.
Zheng, W.-S., Gong, S., and Xiang, T. (2013). Reidentifica-
tion by relative distance comparison. Pattern Analysis
and Machine Intelligence, IEEE Transactions on, pa-
ges 653–668.
Comparative Study of the Behavior of Feature Reduction Methods in Person Re-identification Task
621
