
Using Goal Programming on Estimated Pareto Fronts to Solve
Multiobjective Problems
Rodrigo Lankaites Pinheiro
1,2
, Dario Landa-Silva
2
, Wasakorn Laesanklang
3
and Ademir Aparecido Constantino
4
1
Webroster Ltd., PE1 5NB, Peterborough, U.K.
2
ASAP Research Group, School of Computer Science, The University of Nottingham, U.K.
3
Department of Mathematics, Faculty of Science, Mahidol University, Thailand
4
Departamento de Inform
´
atica, Universidade Estadual de Maring
´
a, Maring
´
a, Brazil
Keywords:
Multi-criteria Decision Making, Goal Programming, Pareto Optimisation.
Abstract:
Modern multiobjective algorithms can be computationally inefficient in producing good approximation sets
for highly constrained many-objective problems. Such problems are common in real-world applications where
decision-makers need to assess multiple conflicting objectives. Also, different instances of real-world pro-
blems often share similar fitness landscapes because key parts of the data are the same across these instances.
We we propose a novel methodology that consists of solving one instance of a given problem scenario using
computationally expensive multiobjective algorithms to obtain a good approximation set and then using Goal
Programming with efficient single-objective algorithms to solve other instances of the same problem scena-
rio. We propose three goal-based objective functions and show that on a real-world home healthcare planning
problem the methodology can produce improved results in a shorter computation time.
1 INTRODUCTION
Modern multiobjective algorithms struggle to find
good approximation sets on highly constrained pro-
blems or when the number of objectives is high Gi-
agkiozis and Fleming (2012). Decision-makers of-
ten require a single solution and the Pareto front is
only useful to enable them to choose the preferred so-
lution(s). There are a few techniques that use dom-
ain knowledge to estimate Pareto fronts. Giagkio-
zis and Fleming (2014) propose a technique to es-
timate the Pareto front of continuous multiobjective
problems and then use the estimated front to obtain
values for the decision variables of interesting soluti-
ons. Their technique is particularly useful because it
can be applied to subregions of the objective space.
Another technique is Bayesian multiobjective optimi-
sation, which consists of using a Bayesian model to
learn computationally expensive objective functions
and use the estimation model to quickly explore the
search space Feliot et al. (2016).
In this research we tackle a workforce scheduling
and routing problem (WSRP). A WSRP solution is a
plan in which skilled mobile workers are scheduled to
visit locations that are geographically scattered. Real-
world applications of WSRP usually involve multiple
objectives. However, most approaches in the litera-
ture tackle this problem using a weighted sum to com-
bine the multiple objectives into one. Even genera-
ting single-objective solutions for the WSRP has been
shown to be difficult for problem instances of consi-
derable size Castillo-Salazar et al. (2014, 2016); Lae-
sanklang et al. (2015a). The WSRP arises in several
domains, for example when scheduling home healt-
hcare workers, technicians, and security personnel
among others. Here, we consider the problem of sche-
duling nurses and care workers to visit and provide
care services to patients in their homes. Works in the
literature tackling home healthcare planning problems
usually use data from real-world scenarios Fikar and
Hirsch (2017). This is also the case in the present
work. We employ data from six distinct home healt-
hcare scenarios provided by Webroster Ltd., who pro-
vides enterprise resource planning software for home
healthcare companies.
The quality of solutions to the WSRP considered
here can be measured using several criteria like: in-
curred costs, travel distance, satisfaction of staff pre-
132
Pinheiro, R., Landa-Silva, D., Laesanklang, W. and Constantino, A.
Using Goal Programming on Estimated Pareto Fronts to Solve Multiobjective Problems.
DOI: 10.5220/0006718901320143
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 132-143
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ferences, satisfaction of patients preferences, etc. Due
to the high number of constraints and objectives in
this problem, even state-of-the-art multiobjective al-
gorithms struggle to find good approximations to the
Pareto front within reasonable computation time. In
problems like this where each instance is a repetition
of the same situation but in different days, parts of
the data repeat across multiple instances of the same
problem scenario. For example, the same set of staff
is available for different days with only minor chan-
ges regarding staff avilability. Also, there is a set of
recurring visits that need to be scheduled in each in-
stance of the problem scenario. This happens in other
problems like vehicle routing and nurse scheduling
where instances of the same problem scenario exhi-
bit similar fitness landscapes (η-dimensional surface
representing the Pareto front, where η is the number
of objectives). This issue was investigated in Pinheiro
et al. (2015, 2017) which proposed a technique to ana-
lyse and visualise complex objective relationships and
fitness landscapes in multiobjective problems. Thus,
this paper proposes a methodology that exploits this
similarity between instances of a multiobjetive opti-
misaton problem, in order to solve instances of the
problem more efficiently.
The proposed methodology works as follows. For
a given dataset consisting of multiple instances of the
problem scenario, a single pilot instance is solved
using multiobjective algorithms or the best available
method in order to produce an approximation to the
Pareto optimal set. A decision-maker uses this ap-
proximation set to choose target solutions for the re-
maining instances of the dataset. The chosen target
solutions represent the desired trade-off between the
multiple objectives. Then, goal programming is app-
lied with an efficient single-objective solving method
to obtain solutions that in quality are close enough to
(or better than) the chosen target solutions. Hence,
the main contributions of this work are:
1. A novel methodology that employs an approxi-
mation to the Pareto optimal front of a pilot pro-
blem instance, to solve other similar instances of
the same problem with goal programming and ef-
ficient single-objective algorithms.
2. The assessment of three approaches to define the
goal programming objective function, one uses
a Chebyshev objective function, another uses a
weighted function derived from the target solu-
tion, and the third one uses an objective function
that seeks to minimise the largest deviation to ob-
jective values in the target solution.
The remaining of this paper is structured as fol-
lows. Section 2 outlines the Workforce Schedu-
ling and Routing Problems Project, which is used
to illustrate the application of the proposed metho-
dology. Section 3 presents the proposed methodo-
logy. Section 4 presents the experimental configu-
ration while section 5 presents the results. Finally,
section 7 concludes this work.
2 THE WORKFORCE
SCHEDULING AND ROUTING
PROBLEM
The WSRP is an optimisation problem that combines
a scheduling and a routing problem. A set of m wor-
kers {w
1
,w
2
,... ,w
m
}, must perform tasks on a set of
n visits {v
1
,v
2
,. .. ,v
n
}, which are distributed across
distinct geographical locations. This work considers
a specific case of this problem: the home healthcare
planning problem, where workers are nurses, doctors
and care workers and the purpose of the visits is to
provide care to patients in their homes. For more in-
formation about this WSRP, please refer to Castillo-
Salazar et al. (2012, 2016).
The WSRP studied in this work contemplates the
planning of a single day. Several hard constraints are
considered in the problem: visits require a set of skills
and only workers possessing the required skills can be
assigned; workers can only be assigned to visits if al-
lowed by their respective contracts; every visit must
commence at a specified time in which workers must
already be at the visits’ premises; no time clashes are
allowed, i.e. a worker cannot be assigned to simulta-
neous visits and there must be enough time for a wor-
ker to travel between visits. Also, two soft constraints
are considered: workers may have a list of time inter-
vals in which they are available; locations are grouped
by geographical areas and workers may have a list of
areas in which they are available.
The objectives considered in the problem are:
Z
1
denotes the sum of the distances travelled by the
workers, including commuting from their home
to the first assignment, between each assignment,
and from the final assignment back to their home;
Z
2
denotes the sum of monetary assignment costs
(workers wages for the assigned visits);
Z
3
denotes the sum of skill preferences in respect of
assigning workers with skills that are desirable but
not necessary;
Z
4
denotes the sum of patients preferences in respect
of assigning preferred workers; and
Z
5
denotes the sum of workers preferences in respect
of assigning workers to visits in their preferred
area.
Using Goal Programming on Estimated Pareto Fronts to Solve Multiobjective Problems
133
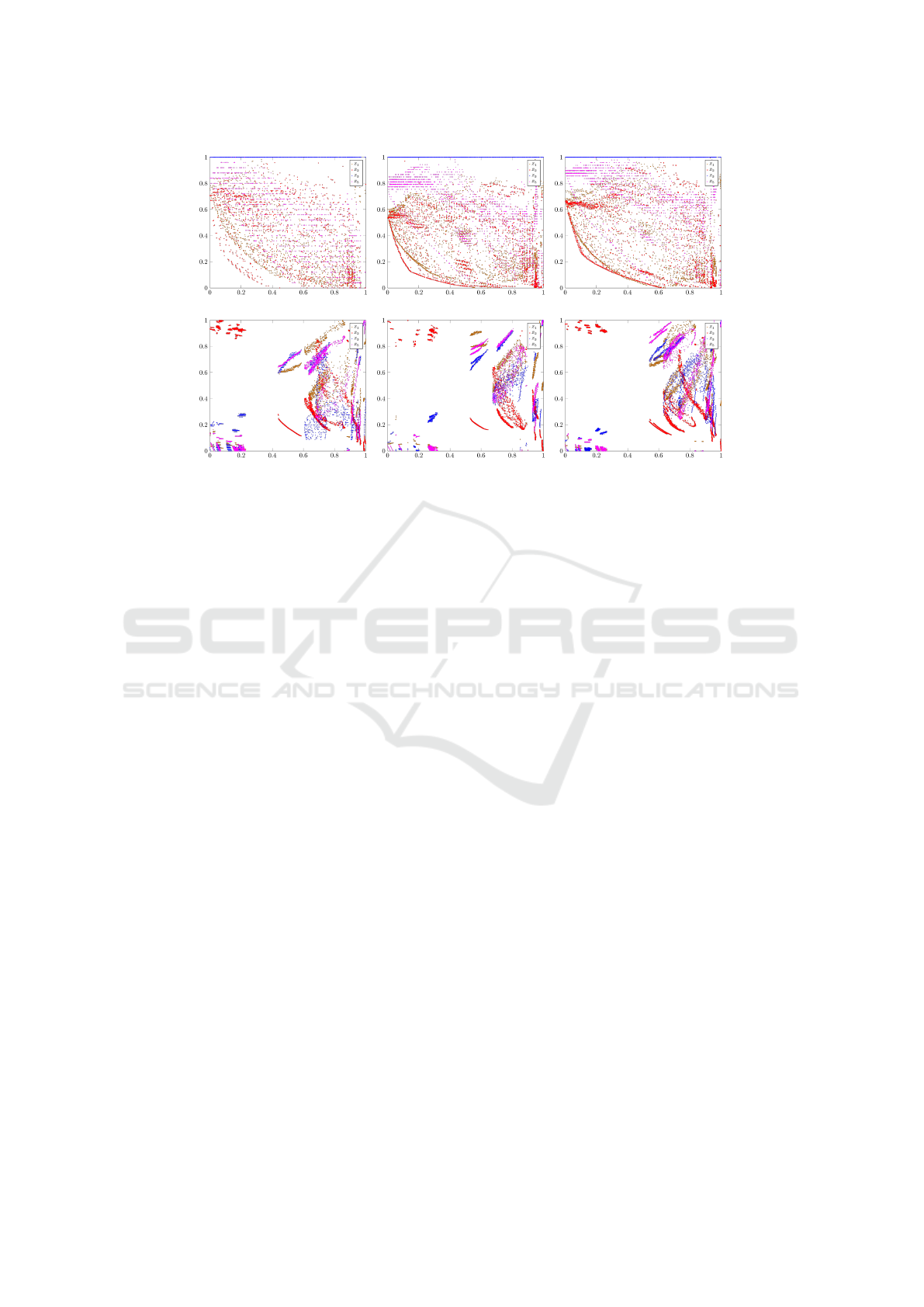
(a) Instance B1 (b) Instance B3 (c) Instance B5
(d) Instance D2 (e) Instance D4 (f) Instance D6
Figure 1: Scatter plots of three instances of datasets B and D. In each case, the x axis shows the value of objective Z
4
and the
y axis shows the values of each of the other objectives in different colours.
Data from four different home healthcare compa-
nies of different sizes and characteristics was provi-
ded and six problem scenarios or dataset were gene-
rated. Each dataset (A, B, C, D, E and F) is composed
of 7 instances for a total of 42 problem instances. Set
A has small instances (number of visits and workers)
while set F has the largest instances.
Other works in the literature have also tackled the
WSRP datasets considered here:
• Laesanklang et al. (2015a) presented a computa-
tional study on the suitability of using exact met-
hods to solve the problem. It was concluded that
only the smaller instances can be solved to opti-
mality by a mathematical solver. Later, Laesan-
klang et al. (2015b) proposed to decompose the
problem by geographical locations in order to em-
ploy the mathematical solver on the sub-problems
and then use heuristic algorithms to integrate the
partial solutions.
• Algethami and Landa-Silva (2015) conducted a
study of various genetic operators applied to this
problem. It was observed that the high number of
constraints and large size of the instances presen-
ted a considerable challenge to the standard ge-
netic algorithm implemented. Later, Algethami
et al. (2016) proposed a knowledge-based indirect
representation and genetic operators to improve
the efficiency of the genetic algorithm for tackling
the problem.
• More recently, Pinheiro et al. (2016) presented a
Variable Neighbourhood Search (VNS) metaheu-
ristic to tackle the WSRP, incorporating two no-
vel heuristics tailored to the problem-domain. The
first heuristic restricts the search space using a pri-
ority list of candidate workers and the second heu-
ristic seeks to reduce the violation of specific soft
constraints. Also, two greedy constructive heuris-
tics were used to give the VNS a good starting
point. Since that VNS is the best-known algo-
rithm to tackle these WSRP instances, that algo-
rithm is employed here within the proposed goal
programming framework.
As preliminary work, we applied the analysis
technique proposed by Pinheiro et al. (2015, 2017) on
all instances considered here. The technique consists
of performing four steps: first the global pairwise re-
lationships are analysed using the Kendall correlation
method; then the ranges of the values found on the gi-
ven approximation front are estimated and assessed;
next these ranges are used to plot a map using Gray
code, similar to Karnaugh maps, that has the ability
to highlight the trade-offs between multiple objecti-
ves; and finally local relationships are identified using
scatter plots. The conclusion is that in the studied da-
tasets, instances of the same datset indeed present si-
milar fitness landscapes. Figure 1 provides evidence
of that and shows the scatter plots of instances B-01,
B-03, B-05, D-02, D-04, and D-06 (arbitrarily cho-
sen). Each datapoint corresponds to normalised ob-
jective values. For reasons of space, we omit the other
datasets and the scatter plots of all instances. The re-
semblance between the fitness landscapes of the pre-
sented instances of datasets B and D is evident. Also,
it is clear that different datasets present distinct fitness
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
134
landscapes, even though they correspond to the same
problem formulation. Finally, it is important to emp-
hasise that datasets A, B and C present similar fitness
landscapes with solutions well spread throughout the
objective space while datasets D, E and F present dis-
tinct fitness landscapes with complex objective relati-
onships and gaps.
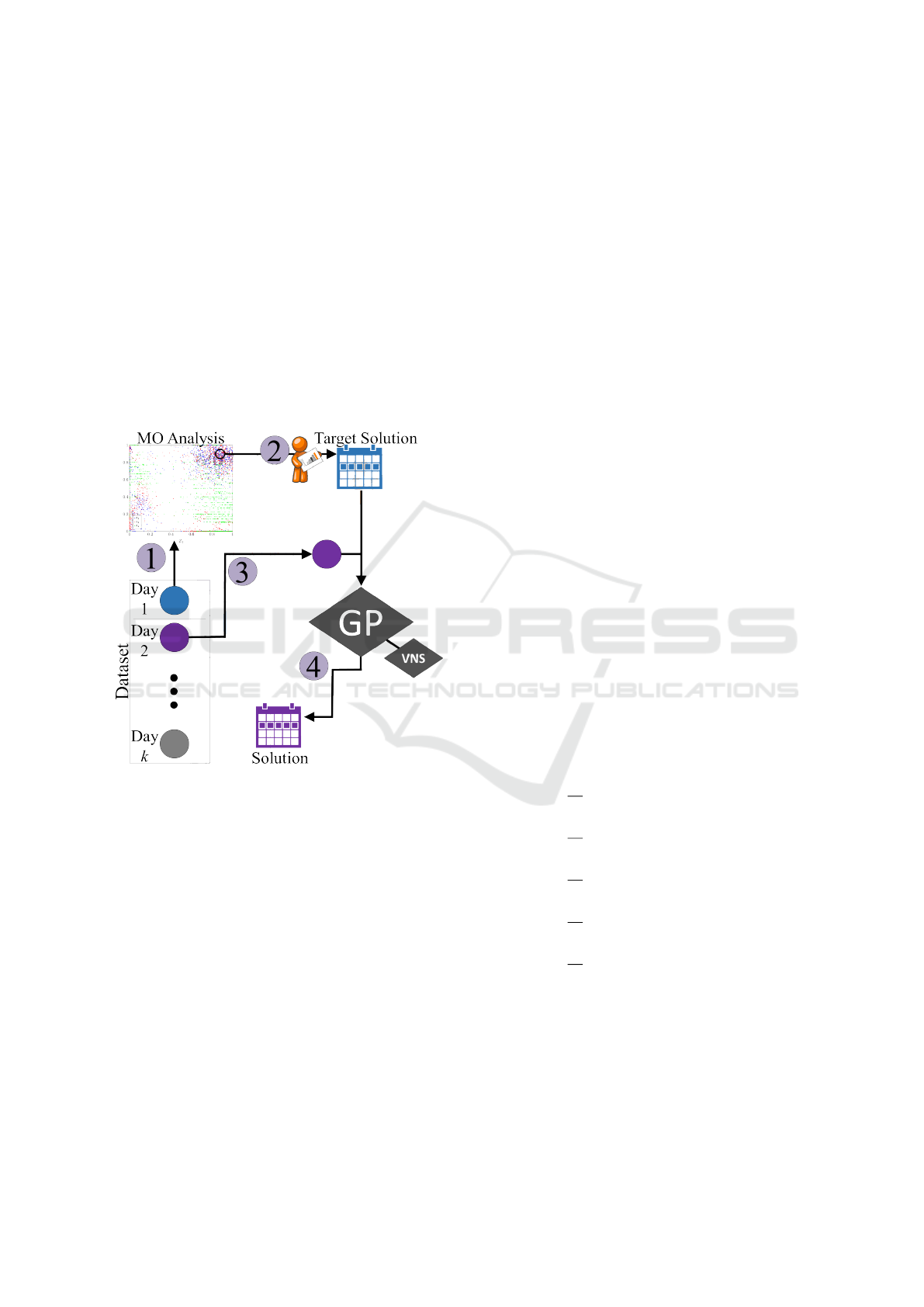
3 PROPOSED METHODOLOGY
Figure 2 presents the overall concept of the proposed
methodology. We use the aforementioned WSRP to
illustrate the concept. Following, we explain each of
the four numbered steps indicated.
Figure 2: Overview of the proposed methodology. The
numbered steps are explained below.
1. A pilot instance within the dataset is selected
by the decision-maker and solved using multiob-
jective algorithms to obtain the best possible non-
dominated approximation set. The pilot instance
must be representative and present similar featu-
res to other instances.
2. The decision-maker chooses an appropriate solu-
tion t from the obtained non-dominated set. This
chosen solution is known as the target solution
and its objective-vector is denoted by
~
Z
t
= (Z
t
1
,Z
t
2
,Z
t
3
,Z
t
4
,Z
t
5
).
3. Each remaining instance in the dataset may now
be solved by the VNS (Pinheiro et al., 2016) using
a modified objective function (goal programming
variant) that attempts to reach the target objective
vector in the current dataset.
4. The final solution obtained by the modified VNS
is presented.
The modified objective function of step 3 has
an important role in the methodology. Following,
we present three approaches for determining the ob-
jective function. The first is the well known Cheby-
shev approach. The second aims to derive a weight-
vector from the target solution and the approximation
set of the pilot instance. The third approach mini-
mises the Euclidean distances to the target objective-
vector.
3.1 Chebyshev Goal Programming
Chebyshev goal programming (Flavell, 1976) is one
of the most widely employed goal programming
techniques that does not necessarily rely on the deci-
sion maker to set priorities between objectives (Jones
and Tamiz, 2016). The technique aims to obtain a ba-
lanced solution by minimising the gap to the target of
the objective that presents the highest gap. Hence, if
the target goals for the objectives are similarly diffi-
cult to be reached, the Chebychev GP technique can
obtain a balanced solution. However, if at least one
target objective value is more difficult to achieve (i.e.
the target goal is too optimistic), the quality of that
objective can be a bottleneck for the remaining ob-
jectives because the search will solely focus on im-
proving that objective. We define the Chebyshev ob-
jective function for the WSRP as follows:
Minimise λ (1)
Subject to
Z
1
Z
t
1
≤ λ (2)
Z
2
Z
t
2
≤ λ (3)
Z
3
Z
t
3
≤ λ (4)
Z
4
Z
t
4
≤ λ (5)
Z
5
Z
t
5
≤ λ (6)
The Chebyshev objective function given by Eq.
(1) is used as the objective function for the WSRP.
The main objective is now to minimise λ, thus fin-
ding a well-balanced solution regarding reaching the
target values. If all targets are reached, λ can assume
fractional values and a solution that shows balanced
improvements on all objectives may be obtained.
Using Goal Programming on Estimated Pareto Fronts to Solve Multiobjective Problems
135

3.2 Derived Weight Vector
One problem with the Chebyshev approach is that it
does not guarantee Pareto efficiency. However, the
optimal solution of a weighted sum (where weights
are not simultaneously null) objective function is al-
ways Pareto efficient. To derive a weight vector from
the target solution, we first convert the approxima-
tion set of the pilot instance into a system of linear
inequalities. Considering that the approximation set
is composed of n objective-vectors (
~
Z
1
,
~
Z
2
, .. .,
~
Z
n
),
the linear inequalities system can be defined as fol-
lows where the aim is to determine the values of
~w = (w
1
,w
2
,w
3
,w
4
,w
5
):
~w
~
Z
t
≤ ~w
~
Z
1
~w
~
Z
t
≤ ~w
~
Z
2
.
.
.
~w
~
Z
t
≤ ~w
~
Z
n
(7)
There is no guarantee that the system of linear in-
equalities has a solution because the fitness landscape
is non-convex, meaning that no set of weights can be
set to achieve some points in the front. Therefore,
instead of finding a solution for the system, we aim to
find a weight vector ~w that satisfies the largest num-
ber of inequalities. Hence, we define the problem of
finding the best weight vector as the following MIP
(mixed-integer programming) minimisation problem.
Minimise
n
∑
j=1
x
j
(8)
subject to
~w
~
Z
t
−~w
~
Z
j
≤ Mx
j
, j = 1,. .. ,n (9)
w
i
∈ (0, 1], x
j
binary ,
(
i = 1, .. ., 5
j = 1, .. ., n
(10)
Note that M is a very large constant.
The objective function given by Eq. (8) aims to
find a weight vector ~w that minimises the number of
linear inequalities in the system (7) which do not ful-
fill the condition ~w
~
Z
t
≤ ~w
~
Z
i
expressed by constraint
(9). Note that constraint (10) guarantees that zero can-
not be chosen as a weight-value as we do not want
criteria to be removed.
Finally, the weight vector ~w obtained from the
MIP model is used in the objective function for the
WSRP as given by Eq. (11).
Minimise
5
∑
i=1
w
i
Z
i
(11)
3.3 Euclidean Distances
We propose an alternative based on the Euclidean dis-
tances to the target vector. In essence, this is a met-
hod that considers all objectives as equally impor-
tant. Hence, minimising the Euclidean distances al-
one does not guarantee Pareto efficiency. In order to
reduce this issue, the proposed method consists of mi-
nimising the distances to the target vector for the ob-
jectives that are worse than the target. If the current
distance for the objectives that are worse than the tar-
get vector is small (< ε), then the aim is to maximise
the distances of the objectives that are better than the
target vector.
Henceforth, the objective function in Eq. (12) be-
comes the objective function for the WSRP.
Minimize
(
z ,if z > ε
−z
0
,otherwise
(12)
where
z =
v
u
u
t
5
∑
i=1
z
i
(13)
z
0
=
v
u
u
t
5
∑
i=1
z
0
i
(14)
z
i
=
(
(Z
i
− Z
t
i
)
2
,if Z
i
> Z
t
i
0 ,otherwise
(15)
z
0
i
=
(
(Z
i
− Z
t
i
)
2
,if Z
i
≤ Z
t
i
0 ,otherwise
(16)
In summary, when the Euclidean distances of the
objectives that are worse than the target vector are lar-
ger than the given parameter ε, the objective function
consists of minimising the Euclidean distances (z).
Otherwise, when z ≤ ε, the objective consists of max-
imising the distances for the objectives that are better
than the target solution (z
0
). Thus, if the solution has
not reached the target, the objective function attempts
to close the gap to the target. If the solution is close or
better than the target, the objective function attempts
to further improve it.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
136
4 EXPERIMENTAL
CONFIGURATION
We applied the proposed methodology to the WSRP
datasets mentioned previously. The first instance of
each dataset (A-01, B-01, C-01, D-01, E-01 and F-
01) was selected as the pilot instance of its respective
dataset. We used the approximation sets obtained as
described next. Fifteen target vectors were randomly
selected (uniformly distributed) from each approxi-
mation set and the same target vectors were used for
the Derived Weight Vector (WV) objective function,
the Euclidean Distances (ED) objective function, and
the Chebyshev (CV) objective function.
For each remaining instance in each dataset,
the Full-VNS algorithm proposed by Pinheiro et al.
(2016) was applied to the fifteen selected target vec-
tors from the pilot instance of its respective dataset
using all three objective functions. For each target
vector of each instance, we ran the Full-VNS algo-
rithm eight times for one minute each. The results
shown comprise the aggregate data.
Multiobjective algorithms struggle to find good
approximation sets in combinatorial problems with
many objectives (more than three) (Giagkiozis and
Fleming, 2012). Hence, we resort to a tailored pro-
cedure to obtain an improved approximation set. Gi-
agkiozis and Fleming (2014) state that most multiob-
jective algorithms can be classified as either Pareto-
based or decomposition-based. This study utilises
NSGA-II (Deb et al., 2002) as the Pareto-based al-
gorithm and MOEA/D (Zhang and Li, 2007) as the
decomposition-based. Thus, for each problem in-
stance the approximation set was obtained as follows:
1. run both the NSGA-II and MOEA/D for one mil-
lion objective evaluations on each possible bi-
objective vector (Z
1
, Z
2
), (Z
1
, Z
3
), .. . (Z
4
, Z
5
);
2. run both the NSGA-II and MOEA/D for one mil-
lion objective evaluations on each possible three-
objective vector (Z
1
, Z
2
, Z
3
), (Z
1
, Z
2
, Z
4
), . .. (Z
3
,
Z
4
, Z
5
);
3. run both the NSGA-II and MOEA/D for one mil-
lion objective evaluations on each possible four-
objective vector (Z
1
, Z
2
, Z
3
, Z
4
), (Z
1
, Z
2
, Z
3
, Z
5
),
.. . (Z
2
, Z
3
, Z
4
, Z
5
);
4. create an archive composed of the non-dominated
solutions found in the previous three steps;
5. generate a population of individuals where half of
the elements are randomly generated and the other
half are randomly drawn from the archive built in
the previous step;
6. run both the NSGA-II and MOEA/D four times
each, for two million objective evaluations, using
the initial population generated in the previous
step and the five-objective vector; and
7. compile an approximation set with all non-
dominated solutions found in all steps.
The number of solution vectors obtained for each
pilot instance was as follows: 1162 for A-01, 1302
for B-01, 1830 for C-01, 2470 for D-01, 3689 for E-
01 and 1500 for F-01.
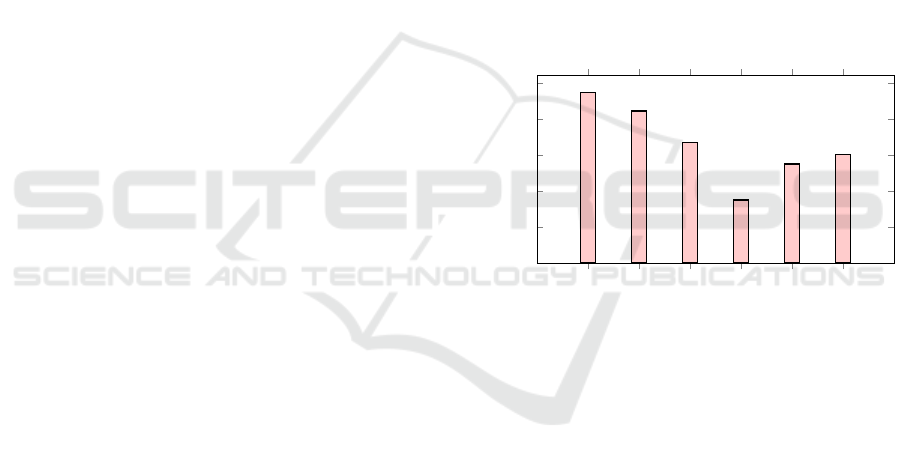
5 EXPERIMENTAL RESULTS
First, we show the effectiveness of the derived weight
vector obtained from the MIP model presented in Eq.
(8)–(10). The effectiveness of a weight vector ~w is
given by the percentage of solutions (in the pilot in-
stance of the approximation set) in which ~w
~
Z
t
≤ ~w
~
Z
i
,
i = 1,. .. ,5. Hence, if the effectiveness is 100%, it
means that the MIP model found a solution for the
inequalities system in Eq. (7).
A-01 B-01 C-01 D-01 E-01 F-01
90%
92%
94%
96%
98%
100%
Dataset
Weigth Vector Effectiveness
Figure 3: Average percentage of the solutions in the approx-
imation set of each target instance such that ~w
~
Z
t
≤ ~w
~
Z
i
.
Figure 3 presents the results of the effectiveness
analysis of the weight vectors obtained. In all pilot in-
stances, the effectiveness surpassed 90% on average.
Pilot instance D-01 presented the worst overall ef-
fectiveness, with an average of 93.5%, while pilot in-
stance A-01 presented the most effective weight vec-
tors averaging 99.5%. In all cases, the MIP model
provided good weight vectors and these were applied
to the WV objective function in Eq. (8).
Next, we show the results for each dataset in three
charts. The target achievement chart displays the per-
centage of solutions, in the given dataset, that achie-
ved the target value in each objective. The gap to tar-
get chart contains the average gap to the target so-
lutions for the solutions that did not reach the tar-
get. Finally, the overall comparison chart displays the
average quality of solutions where positive values in-
dicate that, on average, the solutions found are better
than the target solution and negative values indicate
that the solutions are worse than the target solution.
Using Goal Programming on Estimated Pareto Fronts to Solve Multiobjective Problems
137
Z
1
Z
2
Z
3
Z
4
Z
5
0%
20%
40%
60%
80%
100%
WV ED
CV
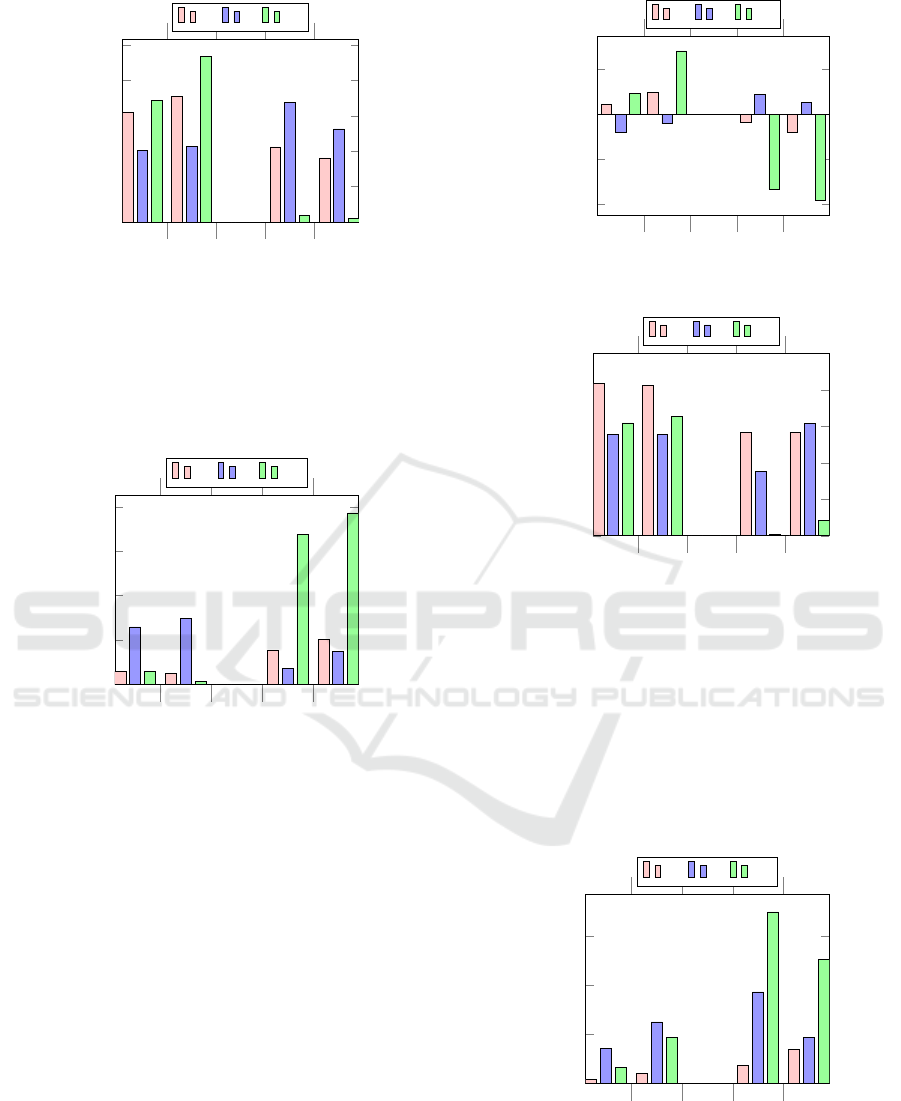
Figure 4: Dataset A – target achievement.
Figures 4–6 present the results of applying the
VNS algorithm with the WV, ED and CV objective
functions to the remaining instances of dataset A. Re-
sults comprise the average values of eight runs for
each target vector of each problem instance for each
objective function.
Z
1
Z
2
Z
3
Z
4
Z
5
0%
10%
20%
30%
40%
WV ED
CV
Figure 5: Dataset A – gap to the target.
In Figure 4, the percentage of achievement of in-
dividual target objective is shown. Note that there are
no values for Z
3
because dataset A does not present
preferred skills information. It is clear that the CV ob-
jective function presented better overall target achie-
vement on Z
1
and Z
2
, followed by WV, while the ED
objective function is better on Z
4
and Z
5
, whilst CV
clearly underperforms.
Figure 5 shows that the average gap of the solu-
tions that did not reach the target is always smaller
than 16% for WV and ED, but high for CV. Also, in
conformity with the previous chart, the CV objective
function presented better values for the objectives Z
1
and Z
2
while the ED objective function obtained bet-
ter values for Z
4
and Z
5
. The CV objective function
presented large gaps on the two latter objectives. Fi-
nally, in Figure 6, it is clear that on average solutions
are at most 10% off the target for WV and ED, but
the CV approach clearly presents a stronger bias to-
wards Z
1
and Z
2
causing the quality of Z
4
and Z
5
to
deteriorate.
Z
1
Z
2
Z
3
Z
4
Z
5
−40%
−20%
0%
20%
WV ED
CV
Figure 6: Dataset A – overall comparison.
Z
1
Z
2
Z
3
Z
4
Z
5
0%
20%
40%
60%
80%
100%
WV ED
CV
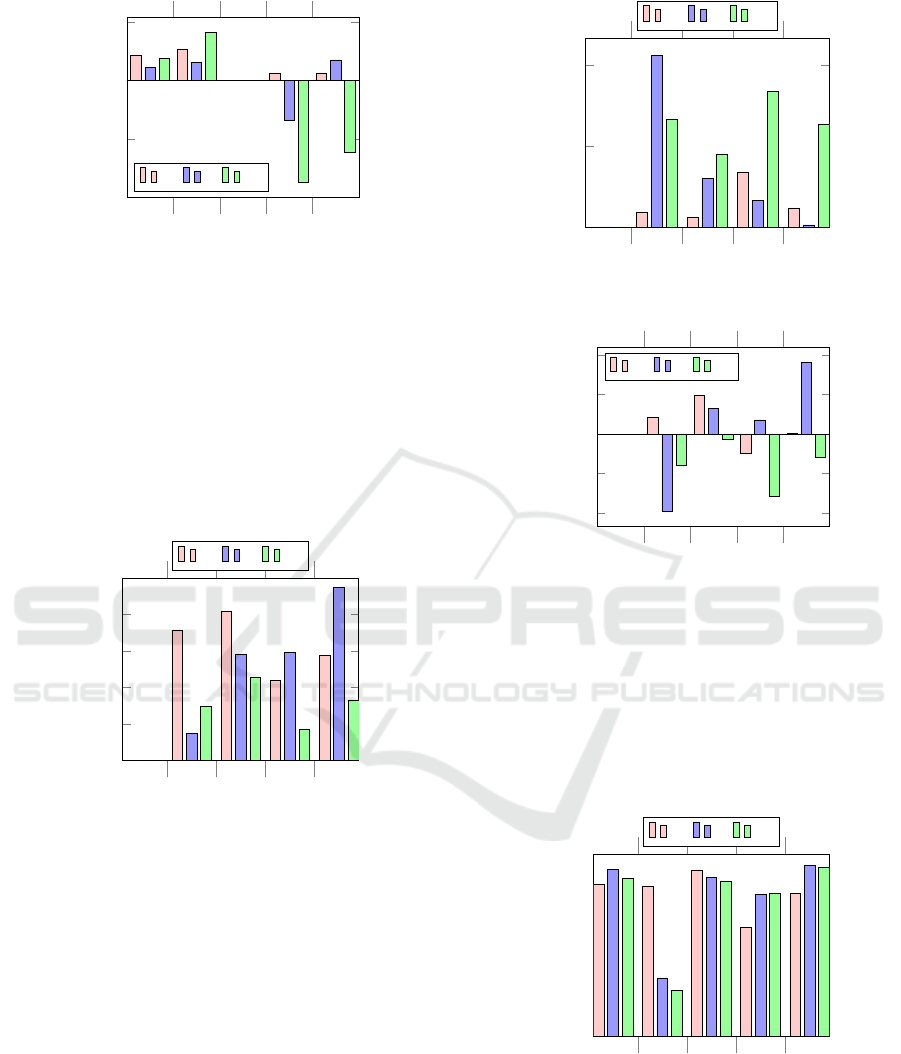
Figure 7: Dataset B – target achievement.
The results for dataset B are presented in Figures
7–9. In Figure 7, it is clear that the WV objective
function obtains better target achievement than the
ED on Z
1
, Z
2
and Z
3
. On Z
4
the ED has a small advan-
tage. Also, when compared to dataset A, the average
overall achievement of the targets is higher for WV
and ED, but not for CV. The CV objective function
shows competitive results on Z
1
and Z
2
, but presents
extremely low achievement rates on Z
4
and Z
5
.
Z
1
Z
2
Z
3
Z
4
Z
5
0%
10%
20%
30%
WV ED
CV
Figure 8: Dataset B – gap to the target.
Figure 8 shows that on all objectives, the WV ob-
jective function obtained smaller average gaps for the
solutions that have not met the target. Conversely, the
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
138
Z
1
Z
2
Z
3
Z
4
Z
5
−20%
0%
20%
WV ED
CV
Figure 9: Dataset B – overall comparison.
CV objective function presents large gaps on Z
4
and
Z
5
. Figure 9 displays that on average, the objective
function WV can provide improved objective-values
on all objectives. However, the objective function ED
presents improved results on Z
1
, Z
2
and Z
5
only, fai-
ling to deliver good results on Z
4
, while CV presents a
similar behaviour as on dataset A: good performance
on Z
1
and Z
2
but bad performance on Z
4
and Z
5
. Thus,
in this dataset, the WV objective function presents a
better alternative to solve the problem.
Z
1
Z
2
Z
3
Z
4
Z
5
0%
20%
40%
60%
80%
100%
WV ED
CV
Figure 10: Dataset C – target achievement.
Figures 10–12 present the results for dataset C.
Note that since that dataset does not have distances in-
formation, Z
1
is always zero. In Figure 10, it is clear
both the objective functions WV and ED are balan-
ced, with WV presenting better results for Z
2
and Z
3
while the ED has the edge on Z
4
and Z
5
. However, the
ED objective function presents deteriorated results on
Z
2
and exceptional results on Z
5
. The CV objective
function underperforms compared to the other met-
hods.
On Figure 11, it is clear that the ED objective
function not only struggles to reach the target for Z
2
,
but it also misses it by 40% on average. This infor-
mation is also reflected in Figure 12. Overall, the WV
objective function presents a more consistent choice
for this dataset as only on Z
4
the overall results are
negative and the average overall performance is su-
Z
1
Z
2
Z
3
Z
4
Z
5
0%
20%
40%
WV ED
CV
Figure 11: Dataset C – gap to the target.
Z
1
Z
2
Z
3
Z
4
Z
5
−40%
−20%
0%
20%
40%
WV ED
CV
Figure 12: Dataset C – overall comparison.
perior. Again, the CV objective function presents the
worst results as it can be seen that for every objective
there is a deficit in the overall quality obtained.
Also, it is important to notice that this dataset pre-
sents a high variance in the sizes of the instances.
Therefore, because C-01 is a large instance, the tar-
get solution simply cannot be achieved on the smaller
instances of that dataset (C-02, C-04, C-05 and C-07).
Z
1
Z
2
Z
3
Z
4
Z
5
0%
20%
40%
60%
80%
100%
WV ED
CV
Figure 13: Dataset D – target achievement.
The results for dataset D are presented by Figu-
res 13–15. In Figure 13 we see an overall increase on
the target achievement when compared to the previ-
ous datasets (A, B and C). As with dataset C, the ED
objective function displayed poor performance for Z
2
Using Goal Programming on Estimated Pareto Fronts to Solve Multiobjective Problems
139
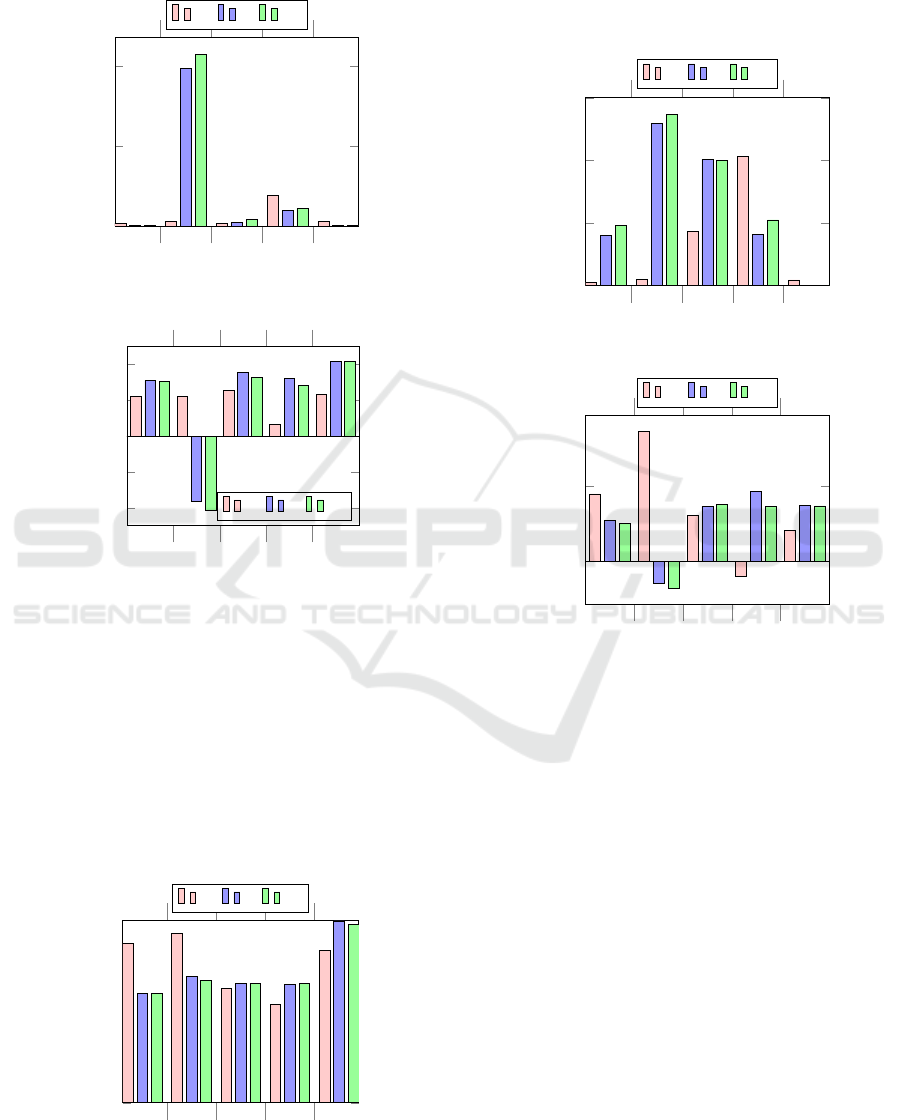
but had better performance on three other objectives
(Z
1
, Z
4
and Z
5
). The CV objective function presented
competitive results on this dataset.
Z
1
Z
2
Z
3
Z
4
Z
5
0%
20%
40%
WV ED
CV
Figure 14: Dataset D – gap to the target.
Z
1
Z
2
Z
3
Z
4
Z
5
−40%
−20%
0%
20%
40%
WV ED
CV
Figure 15: Dataset D – overall comparison.
Figure 14 shows that, except for the ED and CV
objective functions on Z
2
, the gap for the solutions
that have not met the target is small. Also, except for
that objective, the overall average results (Figure 15)
show that all three objective functions present good
results, with the ED surpassing the WV on all ob-
jectives except on Z
2
and the CV presenting results
slightly worse than the ED. Still, the WV objective
function manages to present a higher consistency than
the other objective functions, and it also manages to
present good results for all objectives.
Z
1
Z
2
Z
3
Z
4
Z
5
0%
20%
40%
60%
80%
100%
WV ED
CV
Figure 16: Dataset E – target achievement.
Dataset E results are presented in Figures 16–18.
Like with dataset D, a high overall target achievement
rate is shown (Figure 16). The WV objective function
present exceptional results on Z
1
and Z
2
, but fail to
beat the other objective functions on the remaining
objectives.
Z
1
Z
2
Z
3
Z
4
Z
5
0%
5%
10%
15%
WV ED
CV
Figure 17: Dataset E – gap to the target.
Z
1
Z
2
Z
3
Z
4
Z
5
0%
20%
WV ED
CV
Figure 18: Dataset E – overall comparison.
It is clear from Figure 17 that the ED and CV
objective functions present higher gaps to the target
solutions. Figure 18 shows that all objective functi-
ons perform well on this dataset. The WV objective
function presents better performance on Z
1
and Z
2
,
while the ED objective function presents better results
on Z
4
. The CV objective function presents the best re-
sults on Z
3
.
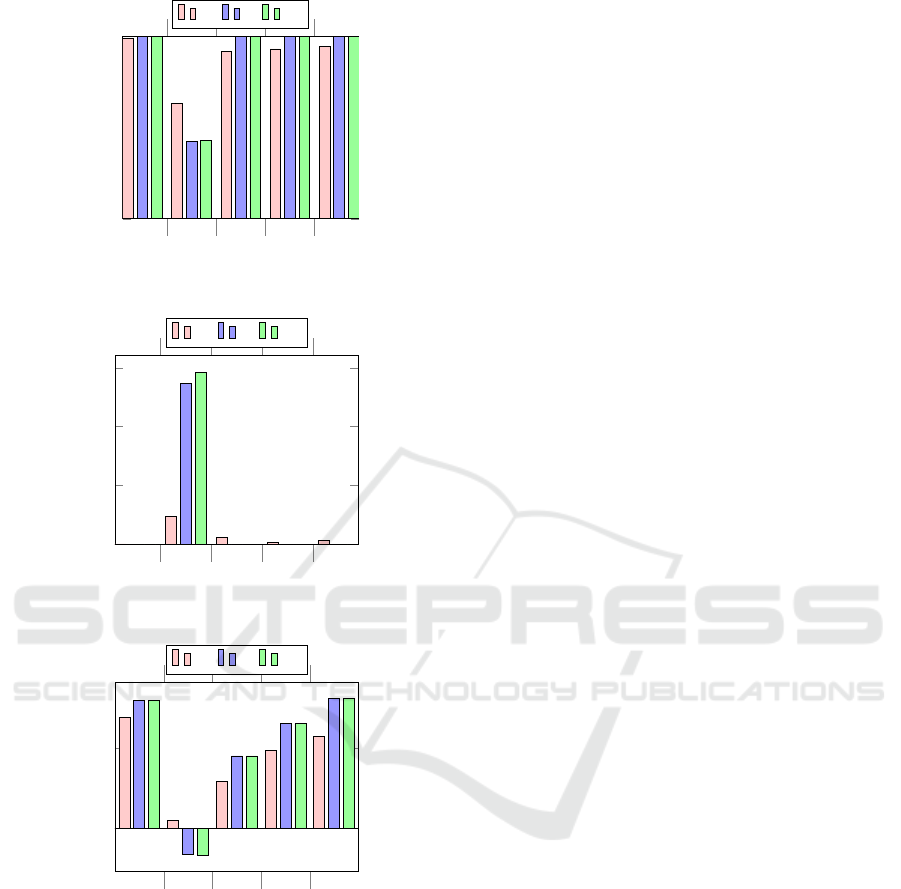
Lastly, the results for dataset F are presented in Fi-
gures 19–21. The target achievement rates (Figure 19)
show that all three objective functions perform well
on this dataset. However, on Z
2
the WV objective
function is noticeably better.
Figure 20 reinforces that claim as the gap for ob-
jective Z
2
is much larger for the ED and CV objective
functions. Finally, Figure 21 shows that on average,
the solutions provided by the WV objective function
are better than the target solutions for all objectives,
and, while the ED and CV objective functions present
better results than the WV on Z
1
, Z
3
, Z
4
and Z
5
, on Z
2
the average results are worse than the target values.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
140
Z
1
Z
2
Z
3
Z
4
Z
5
0%
20%
40%
60%
80%
100%
WV ED
CV
Figure 19: Dataset F – target achievement.
Z
1
Z
2
Z
3
Z
4
Z
5
0%
10%
20%
30%
WV ED
CV
Figure 20: Dataset F – gap to the target.
Z
1
Z
2
Z
3
Z
4
Z
5
0%
50%
WV ED
CV
Figure 21: Dataset F – overall comparison.
6 DISCUSSION
It was shown that both the WV (derived weighted vec-
tor) and ED (Euclidean distances) objective functions
provide good results on the majority of the scenarios,
with the WV objective function being slightly bet-
ter than the ED objective function on average. Also,
for the first three scenarios, the CV objective function
clearly presented inferior results. It is noticeable that
the results were better on the largest datasets D, E and
F. In Section 2 we explained that the smallest datasets
are also the ones with solutions well spread throug-
hout the objective space. Also, it was mentioned that
datasets D, E and F present unique fitness landsca-
pes with several regions containing no solutions and
several local relationships. Therefore, in the smal-
lest datasets, if the objective function is not accurate
enough (regarding reaching the target solution), the
search can deviate from the region of interest more
easily because the objective space is smoother. On the
largest datasets, because the objective space contains
gaps and local relationships, it may be enough for the
search (driven by the objective function) to reach the
same region as the target solution.
Take for instance the example in Figure 22. The
blue dots represent the Pareto front, the green dot is
the target solution, the red dot is the solution found by
the search and the yellow arrow is the search direction
given by the objective function. Note that the search
direction is not accurate, hence it does not point to-
wards the target solution (this is a valid assumption
given that we are either estimating the weight vector
or approximating the Euclidean distances). In Figure
22a, we have a well spread Pareto front and because
there exists a solution aligned with the search vector
(red dot), that solution is taken as the best solution. In
the given example, the chosen solution is better than
the target regarding the objective presented in the x
axis, but it is worse than the target regarding the ob-
jective represented by the y axis.
In Figure 22b, we have a Pareto front with gaps
and local relationships. The search direction is the
same as before but in that direction, there are no so-
lutions, hence the search seeks a closer solution that,
in this case, is one that dominates the target solution
(surpasses the target in all objectives).
A reason for the ED objective function to under-
perform when compared to the WV is the different
ranges of objective-values. Distances and costs can
range from about a few thousand units while the pre-
ferences are measured in dozens of units. This would
lead us to believe that the ED objective function
would provide better results on objectives Z
1
and Z
2
because those are the objectives with high ranges, but
that does not happen, and the algorithm frequently
provides better results on Z
3
, Z
4
and Z
5
. An explana-
tion for this phenomenon lies in Eq. (15). When the
search reaches local optima, it becomes very difficult
for the algorithm to escape it because of the condition
in that equation. If the search reaches local optima
and a few (but not all) objectives fulfil the condition
Z
i
> Z
t
i
, then, slightly disturbing the solution to escape
local optima might result in other objectives fulfil-
ling the condition and making the new solution much
worse. In summary, the VNS used was tailored for the
Using Goal Programming on Estimated Pareto Fronts to Solve Multiobjective Problems
141
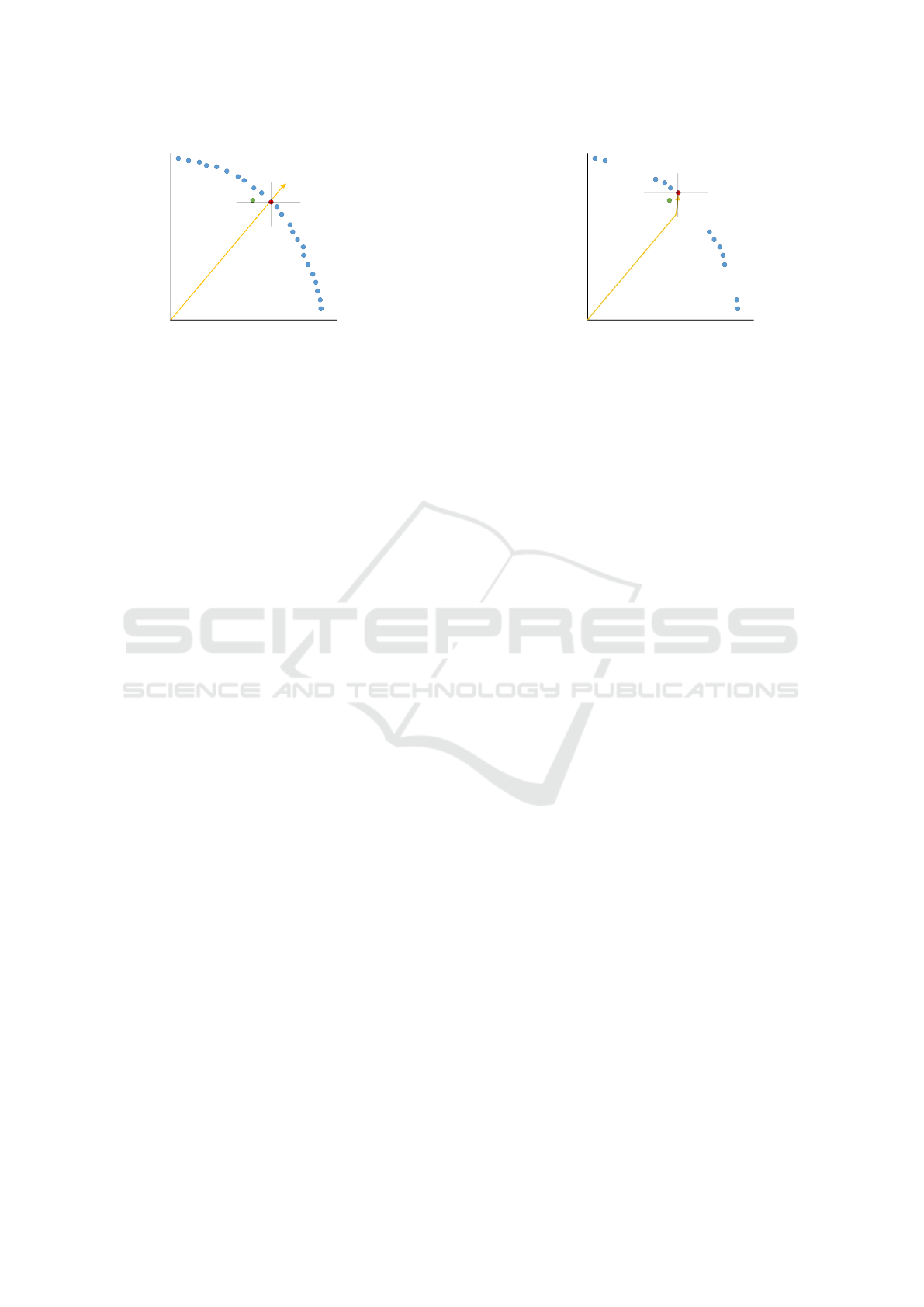
(a) Well-spread Pareto front. (b) Pareto front with gaps.
Figure 22: Example of an inaccurate objective-function on a Pareto front that is well-spread (a) and on a Pareto front with
gaps (b).
WSRP using a weighted function. The ED objective
function drastically changes the objective space and
the algorithm loses performance. The phenomenon is
even worse for the CV objective function.
Additionally, the overall target achievement rate
for all objective functions was higher on the larger
datasets. This happened because the size of those da-
tasets was probably too large for the multiobjective
algorithms to find near-optimal solutions while the
VNS was able to provide improved solutions.
Nonetheless, it is clear that estimating the Pareto
front for problem instances that have similar fitness
landscape to the pilot instance in the same dataset,
is an effective way to tackle the problem. While the
multiobjective algorithms required up to four hours to
obtain the approximation set for hepilot instance of a
dataset, the VNS managed to find competitive solu-
tions in five minutes. For the majority of the experi-
ments, targets were achieved and the overall quality
of results was high.
7 CONCLUSION
In this work we proposed a solving methodology to
use efficient single-objective algorithms to solve a
multiobjective WSRP problem. The methodology
consists of solving an instance of the WSRP using
multiobjective techniques (which are typically com-
putationally expensive) to obtain an approximation
set and then having the decision-maker to choose
adequate target compromise solutions. Then, em-
ploy goal programming to solve other instances of the
same dataset using the selected solution as target. Ad-
ditionally, we used three different objective functions
to guide the algorithms to reach the target. The first
one is the well-known Chebychev approach. The se-
cond one attempts to obtain a weight vector from the
target solution. The third on uses Euclidean distances
to the target solution.
The proposed methodology can potentially be ap-
plied to other multiobjective problems where instan-
ces present similar fitness landscapes. In other real-
world problems, instances of the same scenario have
the same partial data as each instance is a repeti-
tion of the same situation for a different time frame.
For example, instances of a give vehicle routing pro-
blem may have the same fleet every day and recur-
ring deliveries. Similarly, instances of a given edu-
cational timetabling scenario may have the same fa-
cilities and teachers for different terms. Hence, the
technique proposed i this paper can be of practical
use in that type of problems. In addition, the mul-
tiobjective analysis technique proposed by (Pinheiro
et al., 2015, 2017) offers an effective tool to evaluate
whether using goal programming to solve the problem
is applicable or not.
We showed that the methodology proposed here
is capable of finding good trade-off solutions in a
fraction of the time required by multiobjective algo-
rithms to process the approximation set. Also, be-
cause of the strong performance by the chosen single-
objective algorithm in this case, it was common for
solutions to present better objective values than the
target solution.
The fact that instances of the same dataset present
similar fitness landscapes in the WSRP tackled here is
not surprising because many features are recurring in
these home healthcare planning scenarios. The same
or very similar pool of workers is used for different
days and many visits are recurring each day (patients
need daily help to get out of bed, take baths, take me-
dications, etc).
Proposed future work could investigate adaptive
objective functions that can change the search di-
rection according to the current state of the search and
possibly reach improved results.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
142

REFERENCES
Algethami, H. and Landa-Silva, D. (2015). A study of gene-
tic operators for the workforce scheduling and routing
problem. In Proceedings of the XI Metaheuristics In-
ternational Conference (MIC 2015).
Algethami, H., Pinheiro, R. L., and Landa-Silva, D. (2016).
A genetic algorithm for a workforce scheduling and
routing problem. Proceedings of the 2016 IEEE Con-
gress on Evolutionary Computation (CEC 2016).
Castillo-Salazar, J. A., Landa-Silva, D., and Qu, R. (2012).
A survey on workforce scheduling and routing pro-
blems. In Proceedings of the 9th International Confe-
rence on the Practice and Theory of Automated Time-
tabling (PATAT 2012), pages 283–302, Son, Norway.
Castillo-Salazar, J. A., Landa-Silva, D., and Qu, R. (2014).
Computational study for workforce scheduling and
routing problems. In ICORES 2014 - Proceedings of
the 3rd International Conference on Operations Rese-
arch and Enterprise Systems, pages 434–444.
Castillo-Salazar, J. A., Landa-Silva, D., and Qu, R. (2016).
Workforce scheduling and routing problems: litera-
ture survey and computational study. Annals of Ope-
rations Research, 239(1):39–67.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).
A fast and elitist multiobjective genetic algorithm:
NSGA-II. Evolutionary Computation, IEEE Tran-
sactions on, 6(2):182–197.
Feliot, P., Bect, J., and Vazquez, E. (2016). A bayesian ap-
proach to constrained single- and multi-objective op-
timization. Journal of Global Optimization, pages 1–
37.
Fikar, C. and Hirsch, P. (2017). Home health care routing
and scheduling: A review. Computers & Operations
Research, 77(Supplement C):86 – 95.
Flavell, R. B. (1976). A new goal programming formula-
tion. Omega, 4(6):731 – 732.
Giagkiozis, I. and Fleming, P. (2012). Methods for many-
objective optimization: An analysis. Research Report
No. 1030.
Giagkiozis, I. and Fleming, P. (2014). Pareto front estima-
tion for decision making. Evolutionary Computation,
MIT Press.
Jones, D. and Tamiz, M. (2016). A Review of Goal Pro-
gramming, pages 903–926. Springer New York, New
York, NY.
Laesanklang, W., Landa-Silva, D., and Salazar, J. A. C.
(2015a). Mixed integer programming with decom-
position to solve a workforce scheduling and routing
problem. In Proceedings of the International Con-
ference on Operations Research and Enterprise Sys-
tems, pages 283–293.
Laesanklang, W., Pinheiro, R. L., Algethami, H., and
Landa-Silva, D. (2015b). Extended decomposition
for mixed integer programming to solve a workforce
scheduling and routing problem. In de Werra, D., Par-
lier, G. H., and Vitoriano, B., editors, Operations Re-
search and Enterprise Systems, volume 577 of Com-
munications in Computer and Information Science,
pages 191–211. Springer International Publishing.
Pinheiro, R. L., Landa-Silva, D., and Atkin, J. (2015). Ana-
lysis of objectives relationships in multiobjective pro-
blems using trade-off region maps. In Proceedings of
the 2015 Annual Conference on Genetic and Evolutio-
nary Computation, GECCO ’15, pages 735–742, New
York, NY, USA. ACM.
Pinheiro, R. L., Landa-Silva, D., and Atkin, J. (2016). A va-
riable neighbourhood search for the workforce sche-
duling and routing problem. In Advances in Nature
and Biologically Inspired Computing: Proceedings
of the 7th World Congress on Nature and Biologi-
cally Inspired Computing (NaBIC2015), pages 247–
259. Springer International Publishing.
Pinheiro, R. L., Landa-Silva, D., and Atkin, J. (2017). A
technique based on trade-off maps to visualise and
analyse relationships between objectives in optimi-
sation problems. Journal of Multi-Criteria Decision
Analysis, 24(1-2):37–56.
Zhang, Q. and Li, H. (2007). MOEA/D: A multiob-
jective evolutionary algorithm based on decomposi-
tion. Evolutionary Computation, IEEE Transactions
on, 11(6):712–731.
Using Goal Programming on Estimated Pareto Fronts to Solve Multiobjective Problems
143
