The Mapping Distance – a Generalization of the Edit Distance – and its

Application to Trees

Kilho Shin

and Taro Niiyama

University of Hyogo, Kobe, Japan

NTT DoCoMo, Tokyo, Japan

Keywords:

Edit Distance, Kernel, Mapping, Tree.

Abstract:

The edit distances has been widely used as an effective method to analyze similarity of compound data, which

consist of multiple components, such as strings, trees and graphs. For example, the Levenshtein distance for

strings is known to be effective to analyze DNA and proteins, and the Ta

ı distance and its variations are at-

tracting wide attention of researchers who study tree-type data such as glycan, HTML-DOM-trees, parse trees

of natural language processing and so on. The problem that we recognize here is that the way of engineering

new edit distances was ad-hoc and lacked a uniﬁed view. To solve the problem, we introduce the concept

of the mapping distance. The mapping distance framework can provide a uniﬁed view over various distance

measures for compound data focusing on partial one-to-one mappings between data. These partial one-to-one

mappings are a generalization of what are known as traces in the legacy study of edit distances. This is a clear

contrast to the legacy edit distance framework, which deﬁne distances between compound data through edit

operations and edit paths. Our framework enables us to design new distance measures consistently, and also,

various distance measures can be described using a small number of parameters. In fact, in this paper, we

take rooted trees as an example and introduce three independent dimensions to parameterize mapping distance

measures. As a result, we deﬁne 16 mapping distance measures, 13 of which are novel. In experiments, we

discover that some novel measures outperform the others including the legacy edit distances in accuracy when

used with the k-NN classiﬁer.

1 INTRODUCTION

Edit distances have proven to be effective to measure

similarity of compound data such as strings, trees and

graphs. By a compound datum, we mean a datum that

consists of one or more components: a string consists

of letters, and a tree and a graph consist of vertices

and edges.

The Levenshtein distance for strings (Levensh-

tein, 1966) is a well-known example of edit distance

measures. Ta

ı extended the Levenshtein distance to

trees and introduced the ﬁrst instance of edit distance

measures that measure similarity between trees (Ta

ı,

1979). Since computing Ta

ı distances requires he-

avy computation, a number of its variations have been

proposed in the literature including the constrained

distance (Zhang, 1995), the less-constrained distance

(Lu et al., 2001) and the degree-two distances (Zhang

et al., 1996). Their deﬁnitions are all stemmed from

the Ta

ı distance, and they have succeeded in reducing

computational complexity of the Ta

ı distance. On the

other hand, Wang and Zhang (Wang and Zhang, 2001)

introduced the alignment distance to extend the con-

cept of string alignments to trees. In fact, the align-

ment distance has turned out to be identical to the less

constrained distance (Kuboyama et al., 2005). For

graphs, a deﬁnition of edit distances is given in (Neu-

haus and Bunke, 2007).

When we survey the study history of the tree edit

distance, we see that many different deﬁnitions have

been introduced in the literature, but the ways to in-

troduce them appeared ad-hoc rather than being ame-

nable to discipline. Therefore, we cannot deny the

possibility that we have missed instances of the edit

distance measure that have good performance in accu-

racy or time-efﬁciency or both.

Two of the important contributions of this paper

are to introduce the notion of the mapping distance,

which generalizes the legacy edit distance with a con-

sistent view, and to engineer new distance measures

for trees through three novel parameters obtained by

leveraging the mapping distance framework.

In the following sections, we introduce the notion

of mapping distances and clarify their advantages. To

266

Shin, K. and Niiyama, T.

The Mapping Distance – a Generalization of the Edit Distance – and its Application to Trees.

DOI: 10.5220/0006721902660275

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 266-275

ISBN: 978-989-758-275-2

illustrate, we develop our discussion focusing on ap-

plication to trees. In fact, we introduce 16 instances of

mapping distance measures for trees. Although three

of them are well-known in the literature, the remain-

der are novel and are not investigated in the literature.

In addition, we report the results of experiments that

we run to compare these mapping distance measures.

As a result, we have discovered that the distance me-

asures that exhibit the best accuracy performance are

novel measures.

2 LEGACY EDIT DISTANCES

FOR TREES

Just for convenience of explanation, we mean rooted

trees by “trees”. Therefore, in this paper, a tree has

always a root vertex, and all of the other vertices are

its descendants.

In the traditional way, edit distances are deﬁned

based on edit operations, edit paths and edit costs. To

illustrate, we let X and Y be two trees. An edit path

from X to Y is a sequence of edit operations, which is

one of (1) to substitute a vertex y of Y for a vertex x

of X (denoted by (x, y)); (2) to delete a vertex x of X

(denoted by (x, ⊥)); the children of x is re-deﬁned as

children of the parent of x; (3) to insert a vertex y of Y

below a vertex in the relevant tree as a child (denoted

by (⊥, y)); an arbitrary subset of the child vertices of

the vertex below which y is inserted can be selected

and re-deﬁned as child vertices of y.

Example 1. Fig. 1 exempliﬁes an edit path for the Ta

distance. The leftmost tree is X , while the rightmost

tree is Y. We ﬁrst delete the vertex x

(the vertex with

label “b”) from X. The children of x

is re-deﬁned as

children of the root x

. Next, we substitute the ver-

tices y

, y

and y

of Y for the vertices x

, x

and x

, and obtain X

. Finally, we insert the vertex y

below the root y

of X

. To determine children of the

new vertex y

, we select y

and y

. Hence, the edit

path here is represented by

,⊥)(x

)(x

)(⊥,y

= X

= Y

Figure 1: An edit path and a trace (dotted arrows) of the Ta

distance: (x

,⊥)(x

)(x

)(⊥,y

To each edit operation is assigned a cost, which

is usually a non-negative real number. We let γ(v,w),

γ(v,⊥) and γ(⊥,w) denote the costs of substituting w

for v, deleting v and inserting w. When `(v) denotes

the label of a vertex v, the most common setting of

costs is:

γ(v,w) =

(

0, if `(v) = `(w);

1, if `(v) 6= `(w).

γ(v,⊥) = γ(⊥, w) = 1. (1)

Then, the cost of an edit path is the sum of the costs

of the operations that comprise the path: for example,

the cost of the path of Fig. 1 is 3. The Ta

ı distance

(X,Y ) is the minimum cost across all possible edit

paths from X to Y (Ta

ı, 1979).

Many variations of the Ta

ı distance are known in

the literature. The degree-two distance (Zhang et al.,

1996) is an example and poses the constraint that only

vertices with degree one and two can be deleted and

inserted. The degree of a vertex is the number of ed-

ges that the vertex has, and the degree-two distance is

the minimum cost of edit paths under this constraint.

= X

= Y

Figure 2: An edit path and a trace of the degree-two dis-

tance: (x

,⊥)(x

,⊥)(⊥,y

)(x

)(⊥,y

Example 2. In Fig. 2, the vertex x

is of degree one,

and hence, we can delete it. The degree of x

has

changed from three to two after deleting x

, we can

delete it. On the other hand, we can insert y

between

and x

, because its degree is two. In the same way

as Example 1, we substitute the vertices y

, y

and y

of Y for the vertices x

, x

and x

. Then, we obtain

. Finally, we insert y

, whose degree is one. The

corresponding edit script is

,⊥)(x

,⊥)(⊥,y

)(x

)(⊥,y

and its cost is ﬁve.

The trace of an edit path is a partial one-to-one

mapping between the vertex sets of X and Y , deter-

mined by the substitution operations included in the

path. For the edit path of Example 1, the trace deter-

mines (x

→ y

), while that

of Example 2 does (x

→ y

). The

domain and the range of a trace τ are those of τ as a

partial mapping. For example, when we denote the

trace of Example 1 by τ, the domain Dom(τ) and the

range Ran(τ) are {x

} and {y

respectively.

The constrained distance (Zhang, 1995), on the ot-

her hand, poses a constrain on traces.

The Mapping Distance – a Generalization of the Edit Distance – and its Application to Trees

267

In the remainder of this paper, we denote the nea-

rest common ancestor (NCA) of vertices v and w in a

tree X by v ` w. More generally, for a set S of vertices

of X, S

denotes the nearest common ancestor of all

of the vertices of S.

Deﬁnition 1. Two sets S and T of vertices are separa-

ble, iff S

and T

are not in the ancestor-descendent

relation.

Deﬁnition 2 . A trace τ of an edit path is said to be

separable, when S ⊆ Dom(τ) and T ⊆ Dom(τ) are

separable in X, iff τ(S) and τ(T ) are separable in Y .

The constrained distance requires that traces are

always separable and is the minimum cost of edit

paths under this constraint.

Example 3 . The trace of the edit path of Exam-

ple 1 is not separable. In fact, we let S = {x

}

and T = {x

}. Since S

= x

and T

= x

, S and T

are separable in X . By contrast, τ(S)

= y

is the root

of Y , and hence, τ(S) and τ(T ) are not separable.

3 MAPPING DISTANCES

The conditions that determine the edit paths of the Ta

and degree-two distances can be equivalently descri-

bed as constraints on their associated traces. To be

speciﬁc, an edit path complies to the Ta

ı or degree-

two distance, if, and only if, its associated trace meets

the following condition.

ı: A trace preserves the relation of ancestors and

descendants: x

is an ancestor of x

in Dom(τ) ⊆

X, iff τ(x

) is an ancestor of τ(x

) in Y .

Degree-two: A trace preserves the relation of NCA:

if x

and x

are in Dom(τ) ⊆ X, then x

` x

∈

Dom(τ) and τ(x

` x

) = τ(x

) ` τ(x

) hold.

These constraints on traces require that traces as

mappings preserve particular intrinsic structures of

trees.

ı: If a vertex v is an ancestor of a vertex w in a tree

X, we denote v > w. This makes X a partial orde-

red set (poset). Hence, the condition stated above

requires v > w ⇔ τ(v) > τ(w). In other words, τ

and τ

−1

are homomorphisms of posets.

Degree-two: A tree X can be deﬁned as an

algebraic structure (X, `) so that v

v = v,

w = w

v,(v

u = v

u) and v

u ∈

w,w

u,u

v} hold for any {v,w,u} ⊆ X. The

condition stated above means that τ and τ

−1

are

homomorphisms, that is, τ(v

w) = τ(v)

τ(w)

holds for any {v, w} ⊆ Dom(τ) ⊆ X.

On the other hand, given an edit path π and the

associated trace τ, the cost γ(π) is calculated by

γ(π) =

∑

v∈X\Dom(τ)

γ(v,⊥) +

∑

w∈X\Ran(τ)

γ(⊥,w) +

∑

v∈Dom(τ)

γ(v,τ(v)).

Since the left-hand side is a function of τ, we also

denote it by γ(τ).

To determine a mapping distance d(X,Y ) between

X and Y , we ﬁrst determine a set M

X,Y

per pair (X,Y )

that consists of partial one-to-one mappings from X

to Y , and then, we let d(X,Y ) = min

µ∈M

X,Y

γ(µ).

Furthermore, we let X be a set of trees for which

distances are to be computed and assume that a set

of mapping M

X,Y

is uniquely assigned to each pair

(X,Y ) ∈ M

. By requiring µ ∈ M

X,Y

⇒ µ

−1

∈ M

Y,X

and symmetry of the cost function γ, that is, γ(v, w) =

γ(w,v) and γ(v,⊥) = γ(⊥, v), the resulting distance

measure has symmetry. Hence, d(X,Y ) = d(Y,X)

holds. Regarding the triangle inequality d(X,Y ) +

d(Y, Z) ≥ d(X , Z), we have the following theorem.

Theorem 1 . If a family of sets of partial mappings

M = {M

X,Y

| (X,Y ) ∈ X

} is transitive, that is, if

µ ∈ M

X,Y

and ν ∈ M

Y,Z

, ν ◦ µ ∈ M

X,Z

, the triangle in-

equality holds for the resulting mapping distance.

4 PARAMETERIZING TRACES

The framework of the mapping distance also suits

parameterizing mapping distance measures. In this

section, we introduce a set of parameters that describe

a certain class of mapping distances for trees. Once

such parameters are given, by testing all of the combi-

nations of parameter values, we can ﬁnd the distance

measure that ﬁts to the relevant application the best.

For simplicity, we pose two premises on the partial

mappings (traces) to investigate.

• We focus on rooted trees: the relation of ancestor

and descendants is given among vertices.

• Traces preserve the relation of ancestors and des-

cendants: v > w ⇔ τ(v) > τ(w) always holds.

The parameters we introduce below are shape

type, inter-vertex gap and exact label match.

4.1 Shape Type

This parameter determines domains and ranges of

traces. In this paper, we determine ﬁve possible

values for this parameter, namely, Forest, Tree,

Agreement, Path and Separable.

Forest: This value speciﬁes that Dom(τ) and Ran(τ)

can be arbitrary subsets of trees X and Y , and

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

268

τ does not require anything more than that τ is

a homomorphism of posets with respect to the

ancestor-descendent order. This value applies to

the Ta

ı edit distance.

Tree: This value speciﬁes that Dom(τ) and Ran(τ)

have the maximum vertices with respect to the

ancestor-descendent relation, and τ does not re-

quire anything more than that τ is a homomor-

phism of posets with respect to the ancestor-

descendent order.

Agreement: This value speciﬁes that Dom(τ) and

Ran(τ) are closed under the NCA operation, and

τ is a homomorphism of algebraic structures with

respect to the NCA operator. This value applies to

the degree-two edit distance.

Path: This value speciﬁes that Dom(τ) and Ran(τ)

are totally ordered sets with respect to the

ancestor-descendent relation, and τ is a homomor-

phism of posets.

Separable: Deﬁnition 2 deﬁnes this value. Dom(τ)

and Ran(τ) can be arbitrary subsets of trees X and

Y , and τ is separable. This value applies to the

constrained edit distance.

4.2 Inter-vertex Gap

The parse-tree kernel (Collins and Duffy, 2001)

counts the number of so-called co-rooted subtrees

shared between two trees. The basic idea of the ker-

nel is that, the more co-rooted subtrees the trees share,

the more similar are the trees. What we should note

here is that a co-rooted subtree does not allow gaps

between their vertices: If two vertices are in the re-

lation of parent and child in a co-rooted subtree, they

are also a parent and a child in the original tree.

Gaps are not allowed, Gaps are allowed.

Figure 3: Inter-vertex gaps: vertices in gray determines a

subtree.

By contrast, the distances that we saw in Section 1

all allow gaps. Hence, the second parameter inter-

vertex gap determines whether Dom(τ) and Ran(τ)

allow gaps between their adjacent vertices.

4.3 Exact Label Match

In (Shin, 2015), a method to convert edit distance pro-

blems into pattern extraction problems is shown. In

particular, the author of the paper has derived Mos-

tly Adjusted Agreement Sub-Tree (MAAST) problem

from the degree-two distance, which relaxes the con-

straint of exact match of labels of the well-known

MAST problem (Kao et al., 2007).

First, we brieﬂy review MAST problem. To make

the explanation simple, we take two rooted trees

and X

and consider agreement subtrees between

them. In Fig. 4, Y is an agreement subtree with em-

beddings ε

: Y → X

and ε

: Y → X

. The embed-

dings are required to preserve the relation of ancestors

and descendants, the NCA relation and vertex labels.

The MAST problem is a problem to ﬁnd the largest

agreement subtree in size. In other words, the ob-

jective function of optimization is the size |Y |.

c e

Figure 4: An agreement subtree and the MAST problem.

On the other hand, Fig. 5 depicts a trace τ of the

edit path of Fig. 2. Actually, ε

◦ ε

−1

is comparable

with τ, and the only difference is that τ does not ne-

cessarily preserve labels of vertices. In fact, in Fig. 5,

τ maps the vertex labeled “e” of X

to the vertex labe-

led “g” of X

Figure 5: A trace of the degree-two distance.

In (Shin, 2015), a non-negative penalty function p

is introduced, and the MAAST problem is deﬁned as

a problem to maximize the objective function of the

form of |Dom(τ)| − p(τ). p(τ) = 0, iff τ preserves

vertex labels.

The author has also proven that the τ that maximi-

zes this objective function also yields the degree-two

distance.

The signiﬁcance of (Shin, 2015) consists in deﬁ-

ning a new type of pattern extraction problems relax-

ing the constraint of the exact label match and having

shown the equivalence between solving the MAAST

problem and computing the degree-two distance.

Reversely, this inspires us to introduce a new class

of edit distances by requiring exact label match for

traces. Thus, the last parameter that we introduce de-

termines whether or not exact label match is required

for traces.

The Mapping Distance – a Generalization of the Edit Distance – and its Application to Trees

269

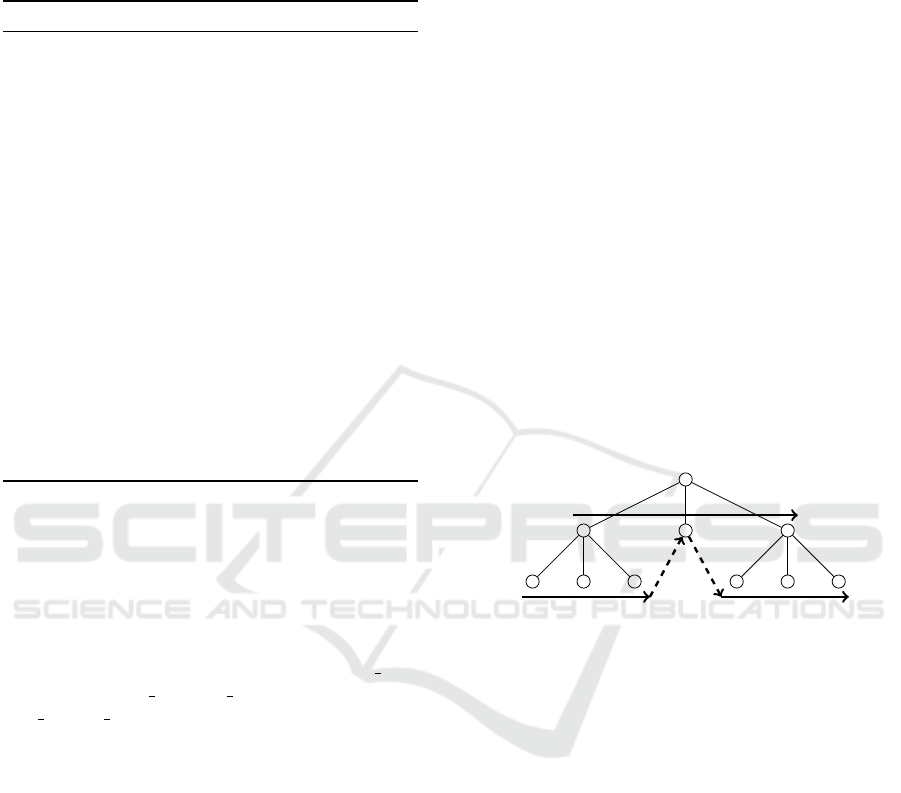
Table 1: Possible combinations of parameters. In the

SHAPE column: F = Forest; T = Tree; S = Separable; A =

Agreement; P = Path; In the GAP and MATCH columns: T

= True; F = False.

SHAPE GAP MATCH DESCRIPTION

F T F Ta

ı (Ta

ı, 1979)

F T T

F F F

F F T

T T F Identical to Ta

ı distance.

T T T

T F F Identical to A-F-F.

T F T Identical to A-F-T.

S T F Constrained

(Zhang, 1995)

S T T

S F F

S F T

A T F Degree-two

(Zhang et al., 1996)

A T T

A F F Identical to T-F-F.

A F T Identical to T-F-T.

P T F

P T T

P F F

P F T

4.4 Combinations of Parameters

Table 1 shows the possible combinations of para-

meter values. For convenience of expression, we

represent each combination by the three capitals

of the parameter values selected. For example,

F-F-T represents the combination of SHAPE TYPE

= Forest, INTER VERTEX GAP = False and EX-

ACT LABEL MATCH = True.

Three of the distances in Table 1 are known

in the literature: F-T-F represents the Ta

ı distance

(Ta

ı, 1979); S-T-F represents the constrained distance

(Zhang, 1995); A-T-F represents the degree-two dis-

tance (Zhang et al., 1996). The remainder are novel

edit distances ﬁrst introduced in this paper.

Also, some of them are identical to each other. To

be precise, since trees that do not allow inter-vertex

gaps are always agreement trees, T-F-F and T-F-T

are identical to A-F-F and A-F-F, respectively.

5 A COMPREHENSIVE

COMPARISON OF THE

MAPPING DISTANCE

MEASURES

5.1 Rooted Ordered Trees

To compute mapping distances efﬁciently, we further

assume that trees are rooted ordered trees.

When an total order is given to the children of

every parent vertex of a tree, the tree is called an roo-

ted ordered tree. The order is called a sibling order.

The sibling order can be easily extended to a left-right

order so that, given two vertices in a rooted ordered

tree, they are either in the ancestor-descendant rela-

tion or the left-right relation (Fig. 6).

When considering mapping distances between

rooted ordered trees, partial one-to=one mappings

(traces) that we consider must preserve not only the

ancestor-descendant order but also the left-right or-

der: x

is located left to x

in Dom(τ) ⊆ X, iff τ(x

) is

located left to τ(x

) in Y .

Figure 6: A rooted ordered tree: A sibling order (solid ar-

rows) and an extended left-right order (dashed arrows).

When trees are not ordered, in other words, when

they are rooted but unordered trees, it is known that

computing their edit distances is not necessarily trac-

table (Yamamoto et al., 2014).

On the other hand, when we assume that trees are

ordered, for all of the edit distances listed in Table 1,

there are efﬁcient algorithms to compute them.

In the literature, the problem of computing

ı edit distances has been known to have heavy

computational complexity, and much effort has been

made to improve efﬁciency. Zhang and Shasha

(Zhang and Shasha, 1989) proposed an algorithm of

O(|X||Y |min{w(X), h(X)}min{w(Y ),h(Y )})-time,

where |X |, w(X ) and h(X) denote the number of

vertices, the width (the number of leaves) and the

height (the length of the longest path from the

root to a leaf) of X. Klein (Klein, 1998) improved

the efﬁciency to O(|X|

|Y | log |Y |)-time by taking

advantage of decomposition strategies (Dulucq and

Touzet, 2003). Demaine et al. (Demaine et al., 2006)

further optimized this technique and presented an

algorithm of O(|X|

)-time. When we only look at

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

270

the asymptotic evaluations, Demaine’s algorithm

looks the fastest, but it easily lapses into the worst

case. Therefore, the algorithm of Zhang and Shasha

in fact outperforms Demaine’s algorithm in many

practical cases. In this regard, RTED, an algorithm

that Pawlik and Augsten (Pawlik and Augsten, 2011)

have developed, not only has the same asymptotic

complexity as Demaine’s algorithm but also almost

always outperforms the competitors in practice.

For the constrained distance (Zhang, 1995) and

the degree-two distance (Zhang et al., 1996), efﬁ-

cient algorithms to compute them in O(|X||Y |)-time

are presented in their original papers.

5.2 Algorithms

Fig. 7 to 11 give algorithms to compute the edit

distances listed in Table 1 except for those already

known.

The function c(x, y) for trees x and y is deﬁned as

follows:

c(x, y) =











0, if `(rt(x)) = `(rt(y));

1, if `(rt(x)) 6= `(rt(y))

and ELM = False;

∞, if `(rt(x)) 6= `(rt(y))

and ELM = True.

`(rt(x)) denotes the label of the root of x and ELM

stands for EXACT LABEL MATCH.

In the diagrams of the ﬁgures, for a tree, the met-

hod .children takes the children of the root of the

tree and return as an array of trees. The order in the

array is identical to the sibling order.

The algorithm is expressed as pseudo-codes

using an imaginary programming language similar to

SCALA (https://scala-lang.org). For example, for an

array of trees the method .head returns the ﬁrst tree

of the array, while the method .tail returns the new

array of trees after eliminating the ﬁrst tree. Also,

the operator ++ indicates a simple concatenation of ar-

rays. The function ff* computes edit distances of the

types of F-F-F and F-F-T. The difference between

them as algorithms is only the value of c(x,y) used

when the labels `(rt(x)) and `(rt(y)) are different.

The asymptotic estimations of the time complex-

ity of these algorithms are O(|X|

|Y |

) for ff*, tt*

and tf* and O(|X||Y |) for the others. These complex-

ities might be improved taking advantages of the met-

hod used in (Pawlik and Augsten, 2011) and (Kimura

and Kashima, 2012). In (Kimura and Kashima, 2012),

a linear-time algorithm to compute subpath kernels is

presented. The algorithm leverages a list of all the

sufﬁxes ordered in the lexicographical order: A sufﬁx

ff*(x: Array[Tree], y: Array[Tree]): Int = {

if(x.isEmpty) return y.size

if(y.isEmpty) return x.size

t = x.head; u = y.head

v0 = c(t, u) + sub(t.children, u.children)

+ ff*(x.tail, y.tail)

v1 = ff*(t.children ++ x.tail, y) + 1

v2 = ff*(x, u.children ++ y.tail) + 1

return min(v0, v1, v2)

}

sub(x: Array[Tree], y: Array[Tree]): Int = {

if(x.isEmpty) return y.size

if(y.isEmpty) return x.size

t = x.head; u = y.head

v0 = c(t, u) + sub(t.children, u.children)

+ ff*(x.tail, y.tail)

v1 = e(x.tail, y) + t.size

v2 = e(x, y.tail) + u.size

return min(v0, v1, v2)

}

Figure 7: Algorithms for F-F-F and F-F-T.

tt*(x: Tree, y: Tree) => Int = {

v0 = c(x, y) + tt*(x.children, y.children)

v1 = x.children.map(t => sub(t, y) + x.size - t.size)

v2 = y.children.map(t => sub(x, t) + y.size - t.size)

v3 = x.size + y.size

return min(v0, min(v1), min(v2), v3)

}

sub(x: Array[Tree], y: Array[Tree]): Int = {

if(x.isEmpty) return y.size

if(y.isEmpty) return x.size

t = x.head; u = y.head

v0 = c(t, u) + sub(t.children, u.children)

+ sub(x.tail, y.tail)

v1 = sub(t.children ++ x.tail, y) + 1

v2 = sub(x, u.children ++ y.tail) + 1

return min(v0, v1, v2).min

}

Figure 8: Algorithms for T-T-F and T-T-T.

tf*(x: Tree, y: Tree) => Int = {

v0 = c(x, y) + sub (x.children, y.children)

v1 = x.children.map(t => tf*(t, y) + x.size - t.size)

++ Array(x.size + y.size)

v2 = y.children.map(t => tf*(x, t) + y.size - t.size)

++ Array(x.size + y.size)

return min(v0, min(v1), min(v2))

}

sub(x: Array[Tree], y: Array[Tree]): Int = {

if(x.isEmpty) return y.size

if(y.isEmpty) return x.size

t = x.head; u = y.head

v0 = c(t, u) + sub(t.children, u.children)

+ sub(x.tail, y.tail)

v1 = d(x.tail, y) + t.size

v2 = d(x, y.tail) + u.size

return min(v0, v1, v2)

}

Figure 9: Algorithms for T-F-F and T-F-T.

The Mapping Distance – a Generalization of the Edit Distance – and its Application to Trees

271

pt*(x: Tree, y: Tree) => Int = {

v0 = c(x, y) + x.size + y.size - 2 +

(Array(0) +: x.children.flatMap(t =>

y.children.map(u => pt*(t, u) - t.size - u.size)))

v1 = x.children.map(t => pttf(t, y) + x.size - t.size)

++ Array(x.size + y.size)

v2 = y.children.map(t => pttf(x, t) + y.size - t.size)

++ Array(x.size + y.size)

return min(min(v0), min(v1), min(v2))

}

Figure 10: Algorithms for P-T-F and P-T-T.

pf*: (x: Tree, y: Tree): Int = {

v0 = sub(x, y)

v1 = x.children.map(t => pf*(t, y) + x.size - t.size)

v2 = y.children.map(t => pf*(x, t) + y.size - t.size)

v3 = x.size + y.size

return min(v0, min(v1), min(v2), v3)

}

sub(x: Tree, y: Tree): Int = {

return c(x, y) + x.size + y.size - 2 +

min((Array(0) ++ x.children.flatMap(t =>

y.children.map(u => sub(t, u) - t.size - u.size))))

Figure 11: Algorithms for P-F-F and P-F-T.

is a string of labels of a contiguous path from a vertex

to the root of the tree.

5.3 Comparison Results

In the following, we see the results of experiments

using six datasets. We ran ﬁve-fold cross validation

with the k-NN algorithm changing k from 1 to 10, and

then, measured accuracy scores (

TP+TN

TP+FP+FN+TN

). The

edit distance measures whose SHAPE TYPE parameter

is PATH did not show good results for all the datasets

tested, we exclude them from the explanation.

5.3.1 Colon-Cancer Dataset

The COLON-CANCER dataset was retrieved from the

KEGG/GLYCAN database (Hashimoto et al., 2006),

and speciﬁes 134 glycan trees annotated relating to

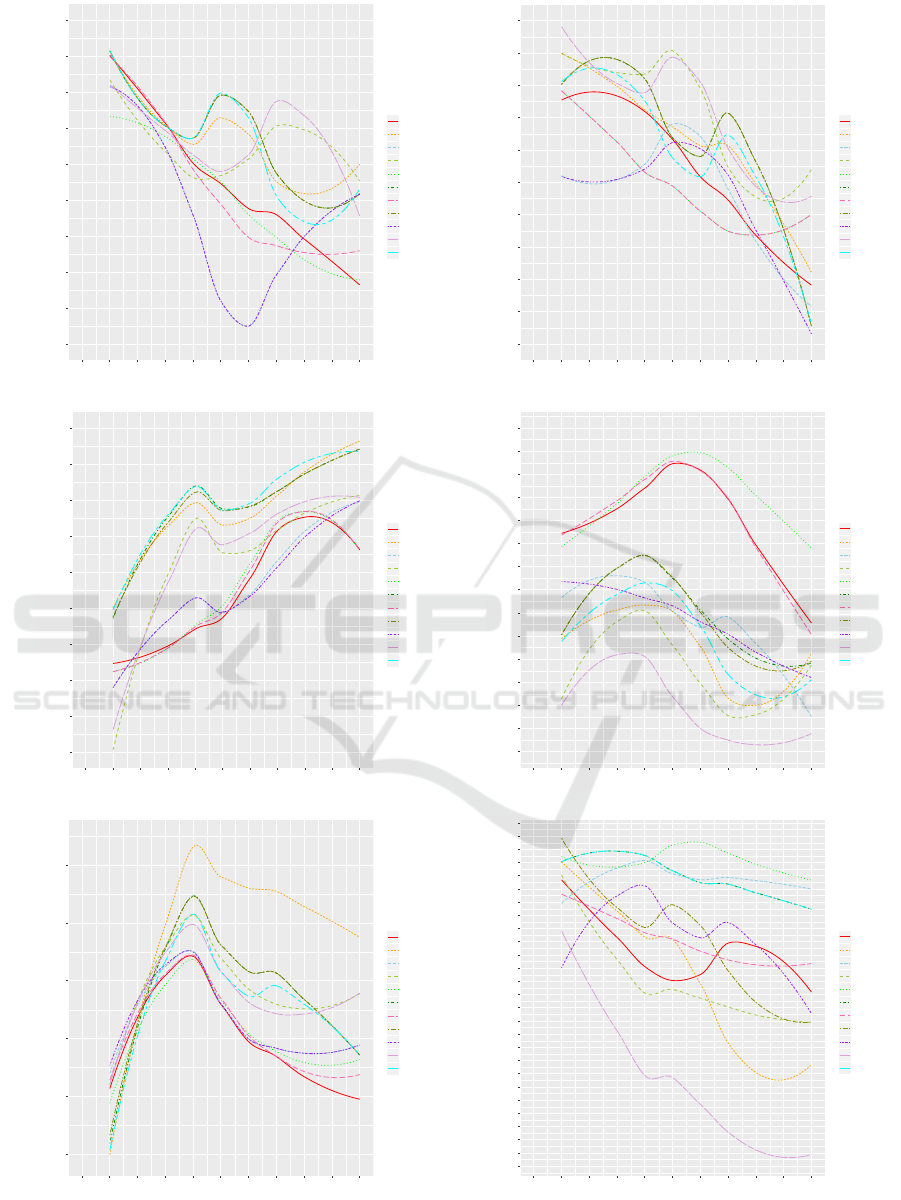
the disease of colon cancer. As Fig. 12 (a) shows,

although the T-T-T, A-T-T, A-T-F (degree-two) and

S-T-F (constrained) distances show the highest accu-

racy, the novel two outperform the known two on

average across all k.

5.3.2 Cystic-Fibrosis Dataset

This dataset was also retrieved from the

KEGG/GLYCAN database. It contains 160 gly-

can trees annotated relating to the disease of

cystic-ﬁbrosis. As Fig. 12 (b) shows, the T-F-T

distance shows the highest accuracy, which is novel

introduced in this paper.

5.3.3 Leukemia Dataset

This dataset was also retrieved from the

KEGG/GLYCAN database. It contains 422 trees

annotated relating to the disease of leukemia. As

Fig. 12 (c) shows, the A-T-T, T-T-T and L-T-T

distances show the highest accuracy. All of them

require exact label match, and therefore, are novel.

5.3.4 Syntactic Dataset

This dataset is the dataset PropBank provided

in (Moschitti, ). It contains 225 parse trees labeled

with two syntactic role classes for modeling the syn-

tactic/semantic relation between a predicate and the

semantic roles of its arguments in a sentence. As

Fig. 12 (d) shows, the F-T-F (Ta

ı) distance shows

the highest accuracy, and the S-T-F (constrained) and

A-T-F (degree-two) distances follow. All of them are

known in the literature.

5.3.5 Web Access Dataset

This dataset was the one used in (Zaki and Aggarwal,

2006), and consists of 810 trees representing web-

page accesses by users, and the annotation is based

on whether the user is from a .edu site or not. As

Fig. 12 (e) shows, the A-T-T distance outperforms the

others in terms of both the highest accuracy and the

average. The A-T-T distance has been introduced in

this paper.

5.3.6 Phishing Dataset

We generated this dataset for this experiment. We

collected 73 URL of phishing sites from PhishTank,

(https://www.phishtank.com/), and 65 URL of au-

thentic sites independently. From the collected URL,

we generated DOM trees to form this dataset. As

Fig. 12 (f) shows, the F-T-F (Ta

ı) distance shows the

highest accuracy, and the F-F-F and T-T-T distances

follow.

5.4 Summary

The table below shows the averaged ranks with re-

spect to the highest accuracy scores across the six da-

tasets.

We should remark that the distances of the *-T-T

type monopolize the top four. Hence, distances with

traces that allow gaps between vertices and require

exact match between labels can be more accurate. Of

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

272

A A

B B

C C

D D

D D D D

D D

E E

F F

F F F F

K K

K K K K

L L

L L L L

M M

N N

P P

0.84

0.85

0.86

0.87

0.88

0.89

0.90

0.91

0.92

0.93

0 1 2 3 4 5 6 7 8 9 10

accuracy

metric

atf

att

fff

fft

ftf

ftt

stf

stt

tff

tft

ttt

(a) COLON-CANCER

A A A A

A A

B B

C C C C

C C

D D

E E

F F

K K

L L

M M M M

M M

N N

P P P P

P P

0.63

0.64

0.65

0.66

0.67

0.68

0.69

0.70

0.71

0.72

0.73

0 1 2 3 4 5 6 7 8 9 10

accuracy

metric

atf

att

fff

fft

ftf

ftt

stf

stt

tff

tft

ttt

(b) CYSTIC-FIBROSIS

A A

B B

C C

D D

E E

F F

K K

L L

M M

N N

N N N N

N N

P P

0.785

0.795

0.805

0.815

0.825

0.835

0.845

0.855

0.865

0.875

0 1 2 3 4 5 6 7 8 9 10

accuracy

metric

atf

att

fff

fft

ftf

ftt

stf

stt

tff

tft

ttt

A A

B B

C C

C C C C

C C

D D

E E

F F

K K

K KL L

L L

L L L L

M M

N N

P P

0.70

0.71

0.72

0.73

0.74

0.75

0.76

0.77

0.78

0.79

0.80

0.81

0.82

0.83

0.84

0 1 2 3 4 5 6 7 8 9 10

accuracy

metric

atf

att

fff

fft

ftf

ftt

stf

stt

tff

tft

ttt

(d) Syntactic

A A

B B

C C

D D

E E

E E E E

F F

K K

L L

L LM M

M M

N N

P P

P P P P

P P

0.80

0.81

0.82

0.83

0.84

0.85

0 1 2 3 4 5 6 7 8 9 10

accuracy

metric

atf

att

fff

fft

ftf

ftt

stf

stt

tff

tft

ttt

(e) Web-Access

A A

B B

B B B B

C C

C C C C

C CD D

D D

E E

F F

K K

K K K K

L L

M M

N N

P P

0.55

0.56

0.57

0.58

0.59

0.60

0.61

0.62

0.63

0.64

0.65

0.66

0.67

0.68

0.69

0.70

0.71

0.72

0.73

0.74

0.75

0.76

0.77

0.78

0.79

0.80

0.81

0 1 2 3 4 5 6 7 8 9 10

accuracy

metric

atf

att

fff

fft

ftf

ftt

stf

stt

tff

tft

ttt

(f) Phishing

Figure 12: Comparison in accuracy.

The Mapping Distance – a Generalization of the Edit Distance – and its Application to Trees

273

FTT STT ATT TTT TFT ATF

3.2 3.2 3.6 4.6 6.9 6.9

FFT STF FTF FFF TFF

6.9 7.2 7.4 7.7 8.4

course, all of them are novel distance measures intro-

duced in this paper. Furthermore, the following shows

the p-values when we perform the Hommel test let-

ting F-T-T be the control.

FTT STT ATT TTT TFT ATF

– 1.00 0.81 0.84 0.16 0.16

FFT STF FTF FFF TFF

0.14 0.10 0.10 0.07 0.04

We see that there is a clear line between the *-T-T

type and the others: with the signiﬁcance level of

10%, the superiority of the F-T-T (and S-T-T) dis-

tance to the S-T-F (constrained), F-T-F (Ta

ı), F-F-F

and T-F-F distances is proven statistically signiﬁcant;

For the A-T-F (degree-two) and T-F-T distances, alt-

hough we cannot reject the null hypothesis, the p-

values are as small as 16%, much smaller than 84%

for the T-T-T distance.

6 CONCLUSION

We have shown that viewing edit distance measures

from a view point of properties of their associated tra-

ces is useful. In particular, by using particular proper-

ties of traces as parameters to describe edit distance

measures, we not only can deal with edit distances

measures consistently but also can engineer new me-

asures systematically. In fact, taking rooted trees as an

example, we have introduced three independent para-

meters, and have shown that the parameters determine

16 edit distance measures. Surprisingly, only three

among them had been known in the literature, and

all the remainder were novel. Furthermore, through

experiments to measure predictive accuracy of each

combination of one of the 16 measures and the k-

NN classiﬁer, we have discovered that a certain novel

class of edit distance measures can perform the best.

The measures belonging to the class are signiﬁcantly

different from the edit distance measures known in

the literature, since the cost to replace a label with a

different label is set as inﬁnity. This mandates the as-

sociated traces to preserve labels of vertices.

7 ACKNOWLEDGMENTS

This work was partially supported by the Grant-in-

Aid for Scientiﬁc Research (JSPS KAKENHI Grant

Number 16K12491 and 17H00762) from the Japan

Society for the Promotion of Science.

REFERENCES

Collins, M. and Duffy, N. (2001). Convolution kernels for

natural language. In Advances in Neural Information

Processing Systems 14 [Neural Information Proces-

sing Systems: Natural and Synthetic, NIPS 2001], pa-

ges 625–632. MIT Press.

Demaine, E. D., Mozes, S., Rossman, B., and Weimann, O.

(2006). An optimal decomposition algorithm for tree

edit distance. ACM Trans. Algo., 6.

Dulucq, S. and Touzet, H. (2003). Analysis of tree edit

distance algorithms. In the 14th annual symposium on

Combinatorial Pattern Matching (CPM), pages 83 –

95.

Hashimoto, K., Goto, S., Kawano, S., Aoki-Kinoshita,

K. F., and Ueda, N. (2006). KEGG as a glycome in-

formatics resource. Glycobiology, 16:63R – 70R.

Kao, M.-Y., Lam, T.-W., Sung, W.-K., and Ting, H.-F.

(2007). An even faster and more unifying algorithm

for comparing trees via unbalanced bipartite matc-

hings.

Kimura, D. and Kashima, H. (2012). Fast computation of

subpath kernel for trees. In ICML.

Klein, P. N. (1998). Computing the edit-distance between

unrooted ordered trees. LNCS, 1461:91–102. ESA’98.

Kuboyama, T., Shin, K., Miyahara, T., and Yasuda, H.

(2005). A theoretical analysis of alignment and edit

problems for trees. In Proc. of Theoretical Computer

Science, The 9th Italian Conference, Lecture Notes in

Computer Science 3701, pages 323–337.

Levenshtein, V. I. (1966). Binary codes capable of cor-

recting deletions, insertions, and reversals. Soviet

Physics Doklady, 10(8):707 – 710.

Lu, C. L., Su, Z. Y., and Tang, G. Y. (2001). A New Measure

of Edit Distance between Labeled Trees. In LNCS, vo-

lume 2108, pages pp. 338–348. Springer-Verlag Hei-

delberg.

Moschitti, A. Example data for TREE KERNELS

IN SVM-LIGHT. http://disi.unitn.it/moschitti/Tree-

Kernel.htm.

Neuhaus, M. and Bunke, H. (2007). Bridging the gap bet-

ween graph edit distance and kernel machines. World

Scientiﬁc.

Pawlik, M. and Augsten, N. (2011). Rted: A robust algo-

rithm for the tree edit distance. In Proceedings of the

VLDB Endowment, volume 5, pages 334–345.

Shin, K. (2015). Tree edit distance and maximum

agreement subtree. Inf. Process. Lett., 115(1):69–73.

ı, K. C. (1979). The tree-to-tree correction problem. jour-

nal of the ACM, 26(3):422–433.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

274

Wang, J. T. L. and Zhang, K. (2001). Finding similar con-

sensus between trees: an algorithm and a distance

hierarchy. Pattern Recognition, 34:127–137.

Yamamoto, Y., Hirata, K., and Kuboyama, T. (2014). Trac-

table and intractable variations of unordered tree edit

distance. Int. J. Found. Comput. Sci, 25(3):307–330.

Zaki, M. J. and Aggarwal, C. C. (2006). XRules: An ef-

fective algorithm for structural classiﬁcation of XML

data. Machine Learning, 62:137–170.

Zhang, K. (1995). Algorithms for the constrained edi-

ting distance between ordered labeled trees and related

problems. Pattern Recognition, 28(3):463–474.

Zhang, K. and Shasha, D. (1989). Simple fast algorithms

for the editing distance between trees and related pro-

blems. SIAM journal of Computing, 18(6):1245 –

1262.

Zhang, K., Wang, J. T. L., and Shasha, D. (1996). On the

editing distance between undirected acyclic graphs.

International Journal of Foundations of Computer

Science, 7(1):43–58.

The Mapping Distance – a Generalization of the Edit Distance – and its Application to Trees

275