Automatic Counting and Classiﬁcation of Microplastic Particles

Javier Lorenzo-Navarro

, Modesto Castrill

on-Santana

, May G

omez

, Alicia Herrera

and Pedro A. Mar

ın-Reyes

Instituto Universitario Sistemas Inteligentes y Aplicaciones Num

ericas en Ingenier

ıa (SIANI),

Universidad de Las Palmas de Gran Canaria, Las Palmas de Gran Canaria, Spain

Marine Ecophysiology Group (EOMAR), Instituto Universitario ECOAQUA,

Universidad de Las Palmas de Gran Canaria, Las Palmas de Gran Canaria, Spain

Keywords:

Microplastics, Beach Pollution, Automatic Counting, Microplastics Classiﬁcation.

Abstract:

Microplastic particles have become an important ecological problem due to the huge amount of plastics debris

that ends up in the sea. An additional impact is the ingestion of microplastics by marine species, and thus

microplastics enter into the food chain with unpredictable effects on humans. In addition to the exploration of

their presence in ﬁshes, researchers are studying the presence of microplastics in coastal areas. The workload

is therefore time consuming, due to the need to carry out regular campaigns to quantify their presence in the

samples. So, in this work a method for automatic counting and classifying microplastic particles is presented.

To the best of our knowledge, this is the ﬁrst proposal to address this challenging problem. The method makes

use of Computer Vision techniques for analyzing the acquired images of the samples; and Machine Learning

techniques to develop accurate classiﬁers of the different types of microplastic particles that are considered.

The obtained results show that making use of color based and shape based features along with a Random

Forest classiﬁer, an accuracy of 96.6% is achieved recognizing four types of particles: pellets, fragments, tar

and line.

1 INTRODUCTION

The use of plastics is very widespread in our society

due to the properties that make them superior to other

materials in many applications. The worldwide pro-

duction of plastics without including PET-, PA-, PP-

and polyacryl-ﬁbers was 322 million tonnes in 2015

(Plastic Europe, 2016). Among those properties, the

plastics in general have good resistance to corrosion

and chemicals, low costs and good durability. How-

ever, those properties make the plastics one of the

most difﬁcult debris to treat; and a part of this debris

ends up in the sea, producing an ecological problem

(Galgani et al., 2013). An estimation due to Jambeck

et al. (Jambeck et al., 2015) establishes that over 8

million tonnes of plastic enter the marine environment

annually.

The plastics in the sea can be categorized accord-

ing to their size. One category is the ”microplas-

tics” which correspond to small microplastic parti-

cles (Thompson et al., 2004; Arthur et al., 2009).

Microplastics can also be subdivided into two sub-

categories: primary microplastics which are those

that are produced as micron-sized particles; and sec-

ondary microplastics that correspond to fragments of

the breakdown of larger plastics debris (Besley et al.,

2017). As it was stated before, the good durability of

plastics results in an accumulation in the marine envi-

ronment of the microplastics that due to their reduced

size can be ingested by a wide variety of organisms

(Set

a et al., 2014).

An indirect measure of the amount of microplas-

tics in the sea is measuring the number and type

of particles that arrive to the beaches, that is also a

source of beach pollution by itself. This topic has

received a growing attention in the biology literature

(Van Cauwenberghe et al., 2015). In order to com-

pare results from different studies, it is necessary to

deﬁne a common protocol in sampling, extraction and

quantiﬁcation of the microplastics particles (Shim and

Thomposon, 2015). It is in the quantiﬁcation task

where this work proposes an automatic approach that

not only counts the number of microplastics particles,

but it also classiﬁes into different categories. After re-

vieweing the literature, to the best of our knowledge,

this paper proposes the ﬁrst attempt to automatically

address this challenging problem.

Due to the recent interest that has received the

646

Lorenzo-Navarro, J., Castrillón-Santana, M., Gómez, M., Herrera, A. and Marín-Reyes, P.

Automatic Counting and Classiﬁcation of Microplastic Particles.

DOI: 10.5220/0006725006460652

In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 646-652

ISBN: 978-989-758-276-9

Figure 1: Sample of microplastics obtained in a beach of

Canary Islands.

study of microplastics in the sand, and the lack of a

standardized protocol in the quantiﬁcation of the par-

ticles, we are not aware of any automatic approach to

solve this task. Currently, researchers count and iden-

tify manually the particles that appears in a sample

(Figure 1) that is a very time consuming process. In

some cases, the use of image processing software can

be used to alleviate this task, but in the end the re-

searchers have to classify the particles using the met-

rics obtained with the image processing tool.

A similar task to the microplastics analysis is the

study of the zooplankton which is also very time con-

suming because it requires to count and classify the

different species that appear in a sample; in the same

way that must be done with microplastics samples.

In the zooplankton analysis, ZooImage tool (Gros-

jean and Denis, 2014) has been used to the automated

classiﬁcation of zooplankton species (Irigoien et al.,

2008; Bachiller et al., 2012; Medellin-Mora and Es-

cribano, 2013). ZooImage is an opensource solution

written in R and that makes use of ImageJ image

analysis tool to obtain different statistics of the zoo-

plankton samples as abundances, total and partial size

spectra or biomasses, etc. The accuracy of the ﬁrst

version of ZooImage was evaluated in (L. Bell and

R. Hopcroft, 2008), reporting an accuracy over 70%,

but it varies depending of the species and the size of

them. Similar evaluations have not been reported for

recent versions of the software. ZOOSCAN (Gros-

jean et al., 2004) is another software that allows the

automatic counting of zooplankton samples and the

semi-automatic identiﬁcation of taxa with accuracy

rates about 75% similar to ZooImage.

Some researchers have applied ZooImage to mi-

croplastics with poor results due to the fact that this

tool compute a set of features mainly based on optical

density. Those features are well suited for identifying

zooplankton species but they are not the best ones for

Figure 2: Sample of microplastics obtained in a beach of

Canary Islands.

microplastic particles that are mainly opaque. Thus,

researchers must do the work manually, while de-

manding a simple and adopted solution for this prob-

lem.

In this paper, an approach for counting and clas-

sifying microplastic particles is presented integrat-

ing both Computer Vision as Machine Learning tech-

niques. The main contributions of the paper can be

summarized as: 1) automatic counting detection of

microplastic particles in a sample image, and 2) auto-

matic classiﬁcation of the particles into four types of

interest.

2 METHODOLOGY

In recent years, the use of the Deep Learning ap-

proaches for object classiﬁcation (Krizhevsky et al.,

2012; Simonyan and Zisserman, 2014; Girshick,

2015; Szegedy et al., 2015) have exhibited a perfor-

mance in complex tasks like never before. Obviously,

the problem of microplastics classiﬁcation could be

solved with a Deep Learning approach but the lack of

thousands of labeled samples hinders the training pro-

cess. Thus, the proposed approach follows the clas-

sical pattern recognition pipeline (Duda et al., 2001)

with the following stages: image acquisition, image

segmentation, feature extraction and classiﬁcation.

2.1 Image Acquisition

Images acquisition is performed using a high deﬁni-

tion scanner due to the small size of the microplas-

tic particles (0.3-5 mm) after distributing the particles

over the scanning platform (Figure 2). This is done

similarly to the requirements imposed by ZooImage.

These images have a high resolution that goes from

Automatic Counting and Classiﬁcation of Microplastic Particles

647

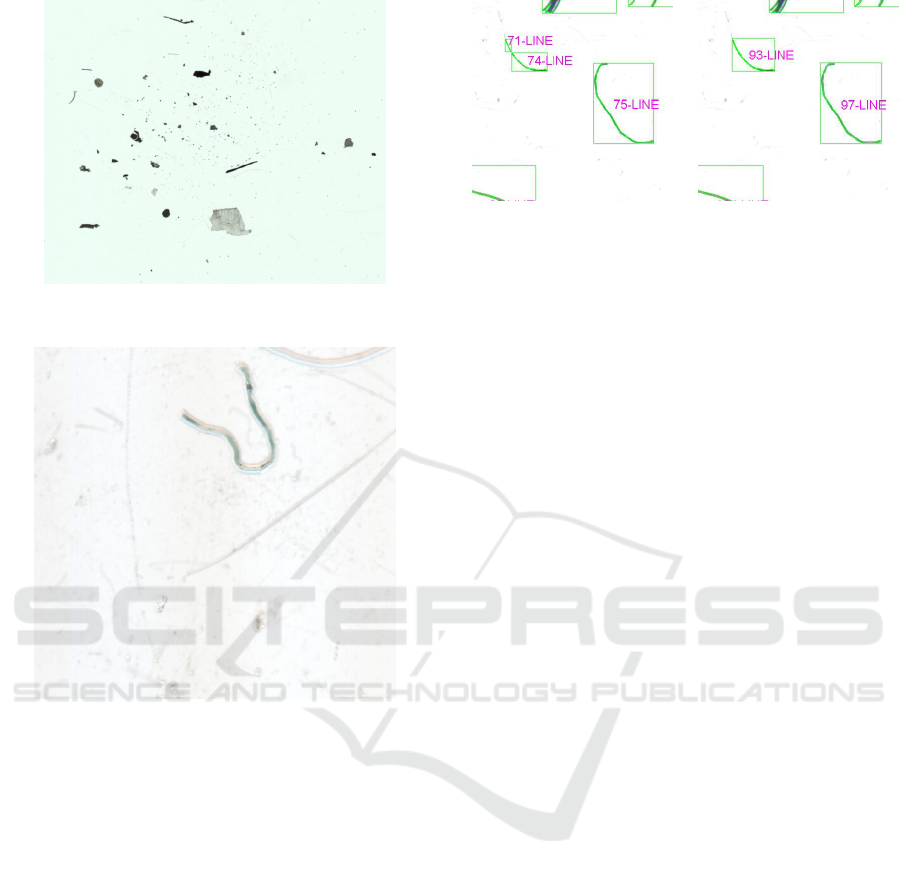
Figure 3: Crop of an image of a microplastics sample.

Figure 4: Background detail with creases and a line mi-

croplastic particle.

aproximately 4800x6900 pixels to 9700x13800 pixels

depending on the scanner conﬁguration. These high

resolution images avoid the loss of details in the par-

ticles but it has the drawback that reveals any imper-

fection of the background. Figure 4 shows this effect

where some creases can be mixed up with the line that

appear in the image. This fact introduced a source of

noise in the identiﬁcation of some types of microplas-

tics, speciﬁcally the lines.

2.2 Image Segmentation

Due to the nature of the images that are obtained by

means of a scanner, the background is clear and the

particles are normally darker as can be seen in Figure

3. The ﬁrst task is to obtain the connected components

(blobs) that are candidate to be microplastic particles.

This task can be carried out by means of a threshold-

ing technique where pixels with a value higher than

a threshold are considered background. In the liter-

ature, there are a bunch of thresholding algorithms

Figure 5: Fishing line

segmentation using Otsu’s

method.

Figure 6: Fishing line seg-

mentation using Sauvola’s

method.

(Sezgin and Sankur, 2004). They can be grouped

into global methods when a single threshold value is

used in the whole image; and adaptive methods when

the threshold value is calculated at each pixel, which

depends on some local statistics. Among the global

methods, one of the most widely used is the Otsu’s

method (Otsu, 1979) that gives good results when the

regions are not linear. In the problem of microplastic

particles, one type is due to the breakdown of ﬁsh-

ing lines or nets and their shape is very linear. For

this kind of particles, Otsu’s method does not pro-

duce good results because it is prone to divide lin-

ear blobs into several parts. To avoid this drawback

the adaptive threshold method proposed by Sauvola

and Pietik

ainen (Sauvola and Pietik

ainen, 2000) has

been used. A comparison between the results of both

methods applied to a ﬁshing line particle are shown

in Figures 5 and 6. It is observed that the particle

93-LINE of Figure 6, in Figure 5 appears as two par-

ticles, 71-LINE and 74-LINE.

2.3 Feature Extraction

The features obtained for each blob can be grouped

into two categories: color and geometric features.

Into the ﬁrst category, the features are computed over

each blob pixel and those are:

• Average and variance of the gray level of the blob

pixels.

• Average and variance of the RGB components of

the blob pixels.

• Average and variance of the HSV components of

the blob pixels.

The second category of features includes all those

features that are related with the shape of the blob.

Those features are:

• Compactness of the blob computed as

perimeter

/area.

• Ratio between the area of the blob and its bound-

ing box.

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

648

a) Pellet. b) Fragment.

c) Tar.

d) Line.

Figure 7: Details of microplastics and tar particles captures.

• Ratio between the width and the height of the blob

bounding box.

• Ratio between the major and minor axis of the ﬁt-

ted ellipse.

• Ratio between the major and minor radius deﬁned

as the distance from the furthest and closest pixel

of the contour to the centroid of the blob.

2.4 Classiﬁcation

As it was stated before, the lack of a huge amount of

labeled images makes difﬁcult to train a deep learn-

ing based approach as a Convolutional Neural Net-

work (Lecun et al., 1998). For this reason, some well

known Machine Learning supervised methods are go-

ing to be used, speciﬁcally K Nearest-Neighbor, C4.5,

Random Forest, Adaptive Boosting and Support Vec-

tor Machine. In the following paragraphs, a brief de-

scription of each method is given.

K Nearest-Neighbor (K-NN). This method belongs

to the case-based classiﬁers (Aha et al., 1991)

which store all the training instances. Later, the

classiﬁcation of a new sample is performed con-

sidering the K nearest training samples to it. The

class assigned to the test sample is given using a

voting strategy among the K nearest training sam-

ples. Different values of K, distances measures

to get the nearest neighbors and voting strategies

have been proposed in the literature.

C4.5. This classiﬁer is a decision tree (Quinlan,

1993) which is built in a top-down manner. Train-

ing samples are divided in each node according to

the best attribute of the subset of training samples

that correspond to the node. The stopping crite-

ria is when all samples that correspond to a node

belong to the same class or the best split of the

node does not surpass a ﬁxed Chi-square signiﬁ-

cant threshold. After the growing stage, a pruning

phase is realized to avoid overﬁtting.

Random Forest (RF). This classiﬁer is made up of

several decision trees which are built using sub-

sets of the training samples randomly selected

with replacement (Breiman, 2001). In the grow-

ing stage of each tree, in each node a set of ran-

domly attributes is considered obtaining in this

way uncorrelated trees. To classify a new sam-

ple, after feeding it into all the trees, a majority

strategy is used to assign the class to the sample.

Support Vector Machine (SVM). This classiﬁer ob-

tains the hyperplanes that separate the training

samples of different classes minimizing the ex-

pected error (Vapnik, 1999). The support vec-

tor are those samples that deﬁne the hyperplanes.

For non linear separables classes, the original

Automatic Counting and Classiﬁcation of Microplastic Particles

649

space is transformed using kernels where the most

frequently used are polynomial and radial based

(RBF).

Adaptive Boosting (AdaBoost). Boosting is an ap-

proach in Machine Learning that builds high ac-

curate classiﬁers based on weak ones. Adaptive

Boosting (Freund, 2001) is one of the most widely

used boosting algorithms. In AdaBoost algo-

rithms, the weak classiﬁers are iteratively trained

using the misclassiﬁed samples of the previous

classiﬁer, in this way, each classiﬁer reﬁnes the

outcome of the previous one.

3 EXPERIMENTS AND RESULTS

In this work, four categories of microplastics are con-

sidered (see Figure 7). A brief description of them is

given below.

Pellet. This category corresponds to small beads of

primary microplastics.

Fragment. This category corresponds to small frag-

ments derived from the breakdown of larger plas-

tic debris.

Line. This category corresponds to small part of ﬁsh

lines or nets.

Tar. Although it is not a plastic polymer, this cat-

egory is included because it represents an im-

portant fraction of marine debris in coastal areas

(Herrera et al., 2017). These tar wastes are likely

to come from ships that discharge bunker oil at

sea, or from old oil spills deposited on rocks and

fragmented by action of waves, producing small

solid tar fragments.

For the experimental setup, the particles are ob-

tained from four images containing a total of 844 in-

stances: 342 pellet particles, 227 fragment particles,

174 tar particles and 101 line particles. For each par-

ticle, the 19 features described in section 2.3 are com-

puted, and the ﬁve classiﬁers are trained using a 10-

fold cross validation setup.

For the AdaBoost classiﬁer, a simple linear regres-

sion logistic was used as weak classiﬁer. The number

of neighbors in the K-NN classiﬁer was set to 1 (K=1)

via cross validation and euclidean distance as distance

function. The SVM classiﬁer was trained with RBF

kernel and with parameter C=12 whose value was

tuned by cross-validation.

The accuracy obtained for each classiﬁer is shown

in Table 1. According to the results, the classiﬁer with

the lowest performance is the SVM with 91.1 of ac-

curacy. AdaBoost, K-NN and C4.5 give similar ac-

curacy around 93 and the classiﬁer with the highest

a) Fragment classiﬁed as

tar.

b) Line classiﬁed as tar.

c) Pellet classiﬁed as frag-

ment.

Figure 8: Examples of classiﬁcation errors.

accuracy is the Random Forest that yields 96.6. In

Table 1, it can be also observed that for all the clas-

siﬁers, the values of recall and precision are close to

the accuracy which implies a similar performance of

the classiﬁers for the four classes.

In order to assess if there exists redundancy

among the computed features, a feature selection and

feature projection processes prior to train the Ran-

dom Forest were carried out. For feature selection

we adopted the ReliefF method (Kononenko, 1994)

which tries to ﬁnd those features that maximize the

separation of the classes. The best result was obtained

using 17 features, two less than the original feature

set, with an accuracy of 96.6. Those removed were

Ratio between the width and the height of the blob

bounding box and Ratio between the major and minor

axis of the ﬁtted ellipse. The projection of the feature

set was done with the Principal Component Analysis

keeping the 95 of the initial variability, resulting in a

7-dimension space. The accuracy of the Random For-

est using the projected features was 95.5.

The confusion matrix for the Randon Forest with

the selected features is shown in Figure 9. Though

the Random Forest in general does not produce too

much missclassiﬁcation, it can be observed that the

most are with the fragment category. This is due to the

high variability in shape and color of this kind of mi-

croplastics because they come from large plastic de-

bris. In Figure 8, some missclassiﬁcations are shown.

In most cases, these misclassiﬁcation errors are dif-

ﬁcult to overcome even for experts. In this sense,

texture descriptors may introduce additional informa-

tion. The computation of these descriptors was done

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

650

Table 1: Results of microplastics classiﬁcation (%)

Classiﬁer Accuracy Precision Recall

AdaBoost 93.5 93.5 93.5

K-NN (K=1) 93.7 93.9 93.7

C4.5 92.4 92.4 92.4

Random Forest 96.4 96.5 96.4

SVM (C=12) 91.1 91.1 91.1

ReliefF + Random Forest 96.6 96.6 96.6

PCA + Random Forest 95.5 95.6 95.5

using the same blobs that those used for computing

the color features. As a prospective test, the Weber

Local Descriptor (Chen et al., 2010) was computed

for the classes Fragment, Pellet and Tar; and a Ran-

dom Forest was trained in a 10 cross-validation setup

obtaining an accuracy of 88.5%. If this kind of texture

descriptors are combined with those presented in this

paper, we expect that the overall performance could

improve.

Figure 9: Confusion matrix for the Random Forest.

Classiﬁed as

Pellet Fragment Tar Line

Pellet 338 4 0 0

Fragment 10 206 10 0

Tar 0 3 171 0

Line 0 1 0 100

4 CONCLUSIONS

In this paper, a method for counting and classi-

fying microplastic particles has been presented ex-

hibiting promising results. The method makes use

of both Computer Vision techniques and Machine

Learning algorithms. The use of a adaptive thresh-

olding method that takes into account the linear shape

of one type of microplastic particle has improved the

segmentation results.

Five different classiﬁcation methods were tested

to assess their performance in classifying the four

types of microplastics considered in this work. To

train and test the classiﬁers, 14 color-based and 5

shape-based features were computed on each detected

particle. This feature set has proved to have enough

discrimination ability to differentiate among the mi-

croplastics under consideration because for all the

classiﬁers the accuracy was higher than 90%. The

best result was obtained with the Random Forest clas-

siﬁer, using the 17 most informative features, that

yields an accuracy of 96.6%.

After this preliminary results, even when there is

no study about the acceptable error measuring the

presence of microplastics, experts seem to be more

interested in having an automatic tool that saves lots

of time, even if classiﬁcation errors would be around

10%. As already mentioned, manual counting is a

time consuming task affected seriously by fatigue,

therefore not free of errors even if done by human

experts. However, in order to increase this accuracy,

a transfer learning approach can be used with pre-

trained convolutional network and doing a ﬁne tuning

with the microplastics labeled samples.

ACKNOWLEDGEMENTS

This work has been partially funded by the Departa-

mento de Inform

atica y Sistemas of the Universidad

de Las Palmas de Gran Canaria.

REFERENCES

Aha, D. W., Kibler, D., and Albert, M. K. (1991). Instance-

based learning algorithms. Machine Learning, 6:37–

66.

Arthur, C., Baker, J., and Bamford, H., editors (2009). Pro-

ceedings of the International Research Workshop on

the Occurrence, Effects and Fate of Microplastic Ma-

rine Debris, number NOS-OR&R-30 in NOAA Tech-

nical Memorandum.

Bachiller, E., Fernandes, J., and Irigoien, X. (2012). Im-

proving semiautomated zooplankton classiﬁcation us-

ing an internal control and different imaging devices.

Limnology and oceanography, methods, 10:1–9.

Besley, A., Vijver, M. G., Behrens, P., and Bosker, T.

(2017). A standardized method for sampling and

extraction methods for quantifying microplastics in

beach sand. Marine Pollution Bulletin, 114(1):77 –

83.

Breiman, L. (2001). Random forests. Machine Learning,

45(1):5–32.

Chen, J., Shan, S., He, C., Zhao, G., Pietik

ainen, M., Chen,

X., Gao, W. (2010). WLD: A Robust Local Image

Descriptor. IEEE Transactions on Pattern Analysis

and Machine Intelligence,32(9), 1705–1720.

Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Pattern

Classiﬁcation (2nd Edition). Wiley-Interscience.

Automatic Counting and Classiﬁcation of Microplastic Particles

651

Freund, Y. (2001). An adaptive version of the boost by ma-

jority algorithm. Machine Learning, 43(3):293–318.

Galgani, F., Hanke, G., Werner, S., and De Vrees, L.

(2013). Marine litter within the european marine strat-

egy framework directive. ICES Journal of Marine Sci-

ence, 70(6):1055–1064.

Girshick, R. (2015). Fast r-cnn. In Proceedings of the 2015

IEEE International Conference on Computer Vision

(ICCV), ICCV ’15, pages 1440–1448, Washington,

DC, USA. IEEE Computer Society.

Grosjean, P. and Denis, K. (2014). zooimage: Analysis of

numerical zooplankton images.

Grosjean, P., Picheral, M., Warembourg, C., and Gorsky,

G. (2004). Enumeration, measurement, and identiﬁ-

cation of net zooplankton samples using the zooscan

digital imaging system. ICES Journal of Marine Sci-

ence, 61(4):518–525.

Herrera, A., Asensio, M., Mart

ınez, I., Santana, A.,

Packard, T., and G

omez, M. (2017). Microplastic and

tar pollution on three canary islands beaches: An an-

nual study. Marine Pollution Bulletin. In press.

Irigoien, X., Fernandes, J., Grosjean, P., Denis, K., Albaina,

A., and Santos, M. (2008). Spring zooplankton distri-

bution in the bay of biscay from 1998 to 2006 in re-

lation with anchovy recruitment. Journal of Plankton

Research, 31.

Jambeck, J. R., Geyer, R., Wilcox, C., Siegler, T. R., Per-

ryman, M., Andrady, A., Narayan, R., and Law, K. L.

(2015). Plastic waste inputs from land into the ocean.

Science, 347(6223):768–771.

Kononenko, I. (1994). Estimating attributes: Analysis and

extensions of RELIEF. In Bergadano, F. and de Raedt,

L., editors, Machine Learning: ECML-94, pages 171–

182, Berlin. Springer.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. In Proceedings of the 25th International

Conference on Neural Information Processing Sys-

tems - Volume 1, NIPS’12, pages 1097–1105, USA.

Curran Associates Inc.

L. Bell, J. and R. Hopcroft, R. (2008). Assessment of

zooimage as a tool for the classiﬁcation of zooplank-

ton. Journal of Plankton Research, 30.

Lecun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).

Gradient-based learning applied to document recogni-

tion. In Proceedings of the IEEE, volume 86, pages

2278 – 2324.

Medellin-Mora, J. and Escribano, R. (2013). Automatic

analysis of zooplankton using digitized images: State

of the art and perspectives for latin america. Latin

American Journal of Aquatic Research, 41:29–41.

Otsu, N. (1979). A Threshold Selection Method from Gray-

level Histograms. IEEE Transactions on Systems,

Man and Cybernetics, 9(1):62–66.

Plastic Europe (2016). Plastics - the facts 2016.

Quinlan, J. R. (1993). C4.5: Programs for Machine Learn-

ing. Morgan Kauffman Pub., Inc., Los Altos, Califor-

nia.

Sauvola, J. and Pietik

ainen, M. (2000). Adaptive document

image binarization. Pattern Recognition, 33:225–236.

Set

a, O., Fleming-Lehtinen, V., and Lehtiniemi, M.

(2014). Ingestion and transfer of microplastics in

the planktonic food web. Environmental Pollution,

185(Supplement C):77 – 83.

Sezgin, M. and Sankur, B. (2004). Survey over image

thresholding techniques and quantitative performance

evaluation. Journal of Electronic Imaging, 13(1):146–

168.

Shim, W. J. and Thomposon, R. C. (2015). Microplastics in

the ocean. Archives of Environmental Contamination

and Toxicology, 69(3):265–268.

Simonyan, K. and Zisserman, A. (2014). Very deep con-

volutional networks for large-scale image recognition.

CoRR, abs/1409.1556.

Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S. E.,

Anguelov, D., Erhan, D., Vanhoucke, V., and Rabi-

novich, A. (2015). Going deeper with convolutions.

In CVPR, pages 1–9. IEEE Computer Society.

Thompson, R. C., Olsen, Y., Mitchell, R. P., Davis, A.,

Rowland, S. J., John, A. W. G., McGonigle, D., and

Russell, A. E. (2004). Lost at sea: Where is all the

plastic? Science, 304(5672):838–838.

Van Cauwenberghe, L., Devriese, L., Galgani, F., Robbens,

J., and Janssen, C. R. (2015). Microplastics in sed-

iments: A review of techniques, occurrence and ef-

fects. Marine Environmental Research, 111(Supple-

ment C):5 – 17. Particles in the Oceans: Implication

for a safe marine environment.

Vapnik, V. (1999). The Nature of Statistical Learning The-

ory. Springer-Verlag.

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

652