
Photopolymerizable Nanoparticle-polymer Composite Materials
for Light and Neutron Beam Manipulations
Yasuo Tomita
1,†
, Kohta Nagaya
1
, Toshi Aoi
1
, Yuko Iso
1
, Akihisa Kageyama
1
, Naoya Nishimura
2
,
Keisuke Odoi
2
, Koichi Umemoto
3
, J¨urgen Klepp
4
, Christian Pruner
5
and Martin Fally
4
1
Department of Engineering Science, University of Electro-Communications, Chofu, Tokyo 182-8585, Japan
2
Materials Research Laboratories, Nissan Chemical Industries, LTD., Funabashi, Chiba 274-0052, Japan
3
Central Research Center, Daicel Corp., Himeji, Hyogo 671-1283, Japan
4
Faculty of Physics, University of Vienna, Vienna, Austria
5
Department of Materials Science and Physics, University of Salzburg, Salzburg, Austria
Keywords:
Nanocomposite Materials, Photonic Nanostructured Materials, Nanoparticles, Photopolymer, Volume Holo-
graphic Grating, Holographic Data Storage, Nonlinear Optics, Neutron Optics.
Abstract:
We report on a recent progress in a new class of photopolymerizable nanostructured materials, the so-called
photopolymerizable nanoparticle-polymer composites (NPCs). They consist of photoreactive monomer (pho-
topolymer) dispersed with inorganic or organic nanoparticles at high concentrations. The initially uniform
distribution of nanoparticles in a neat monomer host is spatially assembled under holographic exposure, pro-
viding the single step formation of large scale and multi-dimensional photonic lattice structures in NPC films.
This property can be used for versatile applications in photonics and neutron optics such as holographic data
storage, holographic optical elements, nonlinear photonic crystals and slow-neutron beam control. Here we
describe applications of NPCs dispersed with new organic and inorganic nanoparticles to holographic data
storage and holographic diffractive elements for light and neutron beams.
1 INTRODUCTION
Photonic nanostructured materials having spatially
ordered arrangements such as photonic crystals and
metamaterials have been of considerable interest for
their tailored linear and nonlinear optical properties
that cannot be usually available by natural materi-
als (Lourtioz et al., 2005; Smith et al., 2004). An-
other type of nanostructured materials involves ei-
ther random arrangements of nanoscale materials,
i.e., nanoparticles (nanocrystals), embedded in a host
material or different materials finely interspersed
with/altered one another. Such nanocomposite ma-
terials exhibit the local-field effect that can be also
used to control the linear and nonlinear optical prop-
erties by various types of spatial arrangements in-
cluding Maxwell-Garnett, Bruggeman and layered
composite geometries (Dolgaleva and Boyd, 2012).
However, these nanostructured materials are usually
photo-insensitive so that no light control of their ar-
rangement is possible.
As a novel photo-configurable nanostructured
material, in 2002 we demonstrated volume holo-
graphic recording in a new type of photopolymeriz-
able organic-inorganic nanocomposite material, the
so-called photopolymerizable nanoparticle-polymer
composite (NPC) (Tomita et al., 2016a), in which
inorganic TiO
2
nanoparticles were highly dispersed
in methacrylate photopolymer (Suzuki et al., 2002).
The idea of using inorganic nanoparticles possessing
a wide variety of refractive indices in the visible is to
employ them as transporting species under spatially
inhomogeneous illumination (holographic exposure),
so that nanoparticles and monomer species mutually
diffuse and phase-separate each other to form the spa-
tial density modulation of nanoparticles according to
the light-intensity distribution. It would induce large
refractive index modulation provided that refractive
indices between nanoparticles and the formed poly-
mer are large enough to form higher contrast pho-
tonic lattice structures (phase gratings) than those
formed in conventional all-organic photopolymer ma-
terials under holographic exposure. In addition, the
inclusion of inorganic nanoparticles contributes to
the improvement of mechanical and thermal stabil-
ity of the formed photonic lattice structure. Sub-
Tomita, Y., Nagaya, K., Aoi, T., Iso, Y., Kageyama, A., Nishimura, N., Odoi, K., Umemoto, K., Klepp, J., Pruner, C. and Fally, M.
Photopolymerizable Nanoparticle-polymer Composite Materials for Light and Neutron Beam Manipulations.
DOI: 10.5220/0006728803130322
In Proceedings of the 6th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2018), pages 313-322
ISBN: 978-989-758-286-8
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
313

sequently, we reported volume holographic record-
ing in NPCs using other SiO
2
and ZrO
2
nanopar-
ticles dispersed in (meth)acrylate monomer capable
of the chain-growth polymerization. It was shown
that the saturated refractive index modulation am-
plitude (∆n
sat
) as large as 1 × 10
−2
was possible
in the blue and the green with reduced polymeriza-
tion shrinkage and high thermal stability (Suzuki and
Tomita, 2004; Suzuki et al., 2006; Tomita et al.,
2008; Omura and Tomita, 2010). In order to use inor-
ganic nanoparticle dispersed NPCs for optical record-
ing media in holographic data storage (HDS) (Co-
ufal et al., 2000; Curtis et al., 2010), we proposed
NPCs with thiol-ene/thiol-yne monomers capable of
the step-growth polymerization (Hata et al., 2011;
Mitsube et al., 2014; Kawana et al., 2015). It
was shown that a plane-wave holographic grating
recorded in such thiol-ene/thiol-yne based NPCs sat-
isfied all the requirements for HDS media, that is,
∆n
sat
≥ 5 × 10
−3
, the material recording sensitivity
higher than 500 cm/J and polymerization shrinkage
lower than 0.5 %. We then successfully demonstrated
shift-multiplexed holographic digital data page stor-
age in thiol-ene/thiol-yne based NPCs by using a two-
beam interference setup (Momose et al., 2012; Mit-
sube et al., 2014; Takayama et al., 2014).
High dispersion (>20vol.%) of inorganic
nanoparticles in host monomer always requires
careful surface treatment for their uniform dispersion
without any aggregation. In order to relax this severe
requirement, we proposed NPCs dispersed with
hyperbranched polymers (HBPs) (Gao and Yan,
2004), nanostructured polymer possessing highly
branched main chains, as organic nanoparticles.
Indeed, HBPs are preferable because of the ease
of their preparation and the controllability of the
size and refractive index. Until now we have re-
ported NPCs dispersed with various types of HBPs.
These include low refractive index hyperbranched
poly(ethyl methacrylate) (HPEMA) and high re-
fractive index hyperbranched polystyrene (HPS)
having their refractive indices of 1.51and 1.61 at a
wavelength of 589 nm, respectively (Tomita et al.,
2006b). They could be dispersed in multifunctional
(meth)acrylate monomer without any aggregation at
their concentrations up to 40 vol.%. They gave ∆n
sat
as large as 8 × 10
−3
and 7× 10
−3
, respectively, at a
recording intensity of 100 mW/cm
2
and at recording
and readout wavelengths of 532 nm. Recently, we
also introduced newly developed HBP having the
ultrahigh refractive index of 1.82 to increase ∆n
sat
further (Tomita et al., 2016b). An NPC grating
incorporated with such an HBP gave ∆n
sat
as large
as 2.2 × 10
−2
at 532 nm with good optical quality,
suggesting its application to a holographic diffractive
element for wearable eyeglasses to be used for
augmented and mixed reality by which the real-time
and ubiquitous access of virtual 2D/3D images is
possible in free space.
One can also utilize the composite nature of NPCs
for developing artificial nonlinear optical materials
when either guest or both guest and host have dis-
tinct optical nonlinearities. So far, optical nonlineari-
ties of metal-dielectric nanocomposites were reported
by many workers (Hache et al., 1988), where the sur-
face plasmon resonance (SPR) (Klar et al., 1998) tak-
ing place at the interface between metallic nanoparti-
cles and a dielectric host was used to induce the op-
tical nonlinearity due to the coherent oscillation of
free electrons occupying states near the Fermi level
in the conduction band. This SPR resulted in the
local-field enhancement (Dolgaleva and Boyd, 2012),
leading to the enhancement of the optical nonlinear-
ities of metal-dielectric nanocomposites. We stud-
ied the nonlinear optical properties of holographically
recordable NPCs dispersed with HBP-metallic (Au or
Pt) nanoparticle complex (Liu et al., 2010). It was
shown that they exhibited the dielectric confinement
effect near SPR and that the magnitude of their effec-
tive third-order nonlinear optical susceptibility was of
the order of 10
−10
esu at a wavelength of 532 nm. We
also investigated the optical nonlinearity in a semi-
conductorCdSe quantumdot dispersed NPC film (Liu
et al., 2012). Because of the composite structure cas-
caded high order optical nonlinearitieswere observed.
Associated nonlinear Bragg diffraction from the1D
photonic lattice structure recorded in the NPC film
were also observed.
Volume gratings recorded in NPCs can find com-
pletely different applications from those in optics and
photonics. Namely, matter waves can be manipulated
by diffraction from gratings, where such an incoming
beam interacts with periodically assembled nuclei via
the strong (nuclear) force. Neutrons have been ex-
tensively used for scientific and engineering studies.
In particular, neutron optics and spectroscopy have
been deployed for nuclear physics, quantum physics,
condensed matter physics, biology, life and medical
sciences, materials science and engineering (Sears,
1989; Rauch and Werner, 2015; Klepp et al., 2014;
Willis and Carlile, 2013). For some of these purposes
efficient neutron optical elements such as mirrors and
beam splitters are essential, for example, to construct
a neutron interferometer. A perfect silicon crystal is
employed to diffract a thermal neutron beam at neu-
tron wavelengths λ
neu
shorter than 0.4 nm. Because
the phase in neutron interferometer is proportional to
λ
neu
(Rauch and Werner, 2015), as opposed to the in-
AOMatSens 2018 - Special Session in Advanced Optical Materials, Sensors and Devices
314

verse wavelength law in optics, slow neutrons (cold
and very cold neutrons) at longer wavelengths(0.4 nm
< λ
neu
< 10 nm) are advantageous. However, slow-
neutron optics requires other neutron optical elements
as Bragg’s law cannot be satisfied for slow neutron
beams with perfect silicon crystals. For this reason
Rupp et al. demonstrated the diffraction of a cold
neutron beam (λ
neu
= 1.5 nm) by a holographic vol-
ume grating optically recorded in PMMA-based pho-
topolymer with deuterium substitution (Rupp et al.,
1990). Despite their successful proof-of-principle
demonstration the diffraction efficiency was severely
limited by the Pendell¨osung oscillation (Klepp et al.,
2012a) that averaged out the diffraction efficiency due
to the very thick film (∼2 mm) and the limited colli-
mation of an incident slow neutron beam. By taking
advantage of the composite nature of NPCs, we de-
veloped neutron optical elements by use of a volume
grating optically recorded in a 100-µm thick NPC film
dispersed with SiO
2
nanoparticles that have substan-
tive interaction strength with slow neutrons. We suc-
cessfully demonstrated manipulation of slow neutron
beams such as beam splitting, triple beam division
and mirror operations (Fally et al., 2010; Klepp et al.,
2011; Klepp et al., 2012b; Klepp et al., 2012c).
In this paper we first describe the grating forma-
tion mechanism in NPCs and discuss material’s de-
sign parameters governing ∆n
sat
. Then we describe
applications of NPCs dispersed with new organic and
inorganic nanoparticles to holographic data storage
and holographic diffractive elements for light and
neutron beams.
2 GRATING FORMATION
MECHANISM
Here we describe the grating formation in an NPC
film where nanoparticles are uniformly dispersed in
host monomer capable of radical photopolymeriza-
tion, as shown in Fig.1(a). Photoinitiator species lo-
cally generate free radicals by their dissociation un-
der two-beam interfering exposure and the subsequent
reaction of free radicals with monomer leads to the
polymerization reaction between monomer radicals
and unreacted monomer in the bright regions. This
polymerization process lowers the chemical potential
of unreacted monomer in the bright regions, leading
to the diffusion of unreacted monomer from the dark
to the bright illuminated regions. Because nanopar-
ticles are photo-insensitive and their chemical poten-
tial increases as a result of the monomer consump-
tion in the bright illuminated regions, nanoparticles
counter-diffusefrom the bright to the dark illuminated
regions. In this way the mutual diffusion and the
phase separation of monomer and nanoparticles lead
to the spatial density modulation of nanoparticles dur-
ing holographic exposure [see Fig.1(b)]. Such holo-
graphic assembly of nanoparticles in the formed poly-
mer host (Tomita et al., 2005) results in the formation
of a refractive index grating due to the density and
compositional differences between the bright and the
dark illuminated regions. This model was confirmed
experimentally as shown in Figs. 1(c) and 1(d) that
show electron-probe micro-analyzer (EPMA) images
of density distributions of Si and S atoms, respec-
tively (Tomita et al., 2006a), where Si and S atoms
correspond to constituents of nanoparticles and the
formed polymer.
monomer
nanoparticle
recording
beams
(a)
(b)
(c)
(d)
Figure 1: Holographic assembly of nanoparticles in an
NPC material (a) before and (b) after holographic expo-
sure. EPMA images of (c) Si (nanoparticles) and (d) S (the
formed polymer) atomic density distributions after holo-
graphic exposure.
It can be shown that ∆n
sat
for the 1st-order peri-
odic spatial modulation of the refractive index in an
NPC as a multi-component photopolymer system is
approximately given by (Tomita et al., 2016a)
∆n
sat
= a∆f (n
n
− n
p
), (1)
where a is a form factor depending on a waveform
of the density modulation of nanoparticles and ∆ f
is a difference in the volume fraction of dispersed
nanoparticles between the peak and the average vol-
ume fraction f of the nanoparticles. Also, n
n
(n
p
) is
the refractive index of the nanoparticle (the formed
host polymer), respectively. The value for a is unity
for a sinusoidal waveform and is 2sin(rπ)/π for a
rectangular waveform with the duty ratio r. It can be
seen that ∆f and |n
n
− n
p
| are major material’s de-
sign parameters that determine ∆n
sat
. It is easy to find
that ∆f takes values between 0 and f at 0 ≤ f ≤ 0.5
and between 0 and 1 − f at 0.5 ≤ f ≤ 1. Thus, ∆ f
is maximized to be 0.5 at f = 0.5 and the density
modulation index of nanoparticles defined as ∆f/ f is
unity. In practice, however, an increase in f larger
than, say, 0.4 causes substantive holographic light
scattering (Suzuki and Tomita, 2007) during record-
ing when |n
n
− n
p
| is very large for a very thick NPC
Photopolymerizable Nanoparticle-polymer Composite Materials for Light and Neutron Beam Manipulations
315

film dispersed with nanoparticles having ∼10 nm in
size. This situation would reduce ∆n
sat
. For this rea-
son ∆ f = f ∼ 0.4 would be a practical maximum
limit.
3 HOLOGRAPHIC DATA
STORAGE
As described in the introduction part, we developed
thoil-ene/thiol-yen based NPCs for HDS media and
employed them in shift-multiplexed holographic dig-
ital data page storage by using a two-beam interfer-
ence method (Momose et al., 2012; Mitsube et al.,
2014; Takayama et al., 2014). Here we describe their
use in coaxial holographic recording setup (Horimai
et al., 2005). Figure 2 illustrates our optical setup for
a holographic digital data page recording using the
coaxial holographic recording setup. The linearly po-
larized laser beam at a recording and readout wave-
length of 532 nm was expanded and collimated to
encode a circular and concentric input page pattern
for digital signal and reference data with the 9:16
symbol modulation coding format (Takayama et al.,
2014) [see Fig. 3(a)] via a transmission-type liquid
crystal spatial light modulator (HOLOEYE Photonics
LC2002) with 1024 768 pixels and a pixel pitch of
36 µm. The size of one data page [the circular por-
tion in Fig. 3(a)] had 12969 bits that corresponded to
14441 symbol data of information. No error correc-
tion coding (ECC) was made. The transmitted data-
bearing beam was loosely focused on an NPC film
sample of 100-µm thickness via two relay lenses and
an objective lens. For thiol-ene based NPC film sam-
ples we employed the stoichiometric thiol-ene for-
mulation of commercial secondary dithiol monomer,
1,4-bis(3-mercaptobutyryloxy)butane (Showa Denko
K.K.), and triene monomer, 1, 3, 5–triallyl–
triazine-2,4,6(1H,3H,5H)-trione (Sigma-Aldrich), to-
Figure 2: Setup for coaxial holographic digital data page
recording.
gether with the dispersion of 25 vol.% SiO
2
nanoparticles (the average size of 13 nm) and a
photoinitiator/green-sensitizer system consisting of
Irgacure 784 (Ciba) and BzO
2
(Sigma-Aldrich) at
1 and 1.25 wt.%, respectively, with respect to the
thiol-ene monomer blend. For thiol-yne based
NPC film samples we employed the stoichiomet-
ric thiol-yne monomer blend consisting of com-
mercial trithiol monomer, trimethylolpropane tris(3-
mercaptopropionate) (Sigma-Aldrich), and diyne
monomer, 1, 7-octadiyne (Sigma-Aldrich). It was
mixed with a co-monomer at 15 wt.% with respect to
the thol-yne monomer blend, N-vinyl-2-pyrrolidone
(Sigma-Aldrich), acting as a plasticizer for the uni-
form dispersion of 25 vol.% SiO
2
nanoparticles. A
photoinitiator/green-sensitizer system consisting of
Irgacure 784 and BzO
2
at 1 and 1.25 wt.%, respec-
tively, with respect to the thiol-yne monomer blend
were also mixed. The reconstructed straight-through
image through a uniformly cured thiol-ene NPC film
sample by an incoherent LED is shown in Fig. 3(b).
the symbol error rate (SER) and the signal-to-noise
ratio (SNR) are found to be 7.7×10
−5
and 14, respec-
tively. The reconstructed image from a recorded thiol-
ene based NPC film sample is shown in Fig. 3(c) by
which SER and SNR are found to be 7.7×10
−5
and
12, respectively. Figure 3(d) shows the reconstructed
(a) (b)
(c) (d)
Figure 3: (a) Digital data page pattern with the 9:16 sym-
bol modulation code. (b) Magnified image of the straight-
through image via a uniformly cured thiol-ene based NPC
film. (c) Magnified image of the reconstructed digital data
page pattern from a recorded thiol-ene based NPC film. (d)
Magnified image of the reconstructed digital data page pat-
tern from a recorded thiol-yne based NPC film.
AOMatSens 2018 - Special Session in Advanced Optical Materials, Sensors and Devices
316

image from a recorded thiol-yne NPC film sample,
giving SER and SNR of 7.7×10
−5
and 11, respec-
tively. It is known that error-free retrieval of data
pages with an SER of lower than 1×10
−1
is possible
with ECC (Tanaka et al., 2007). Therefore, the mea-
sured performance suggests that error-free retrieval of
digital data pages is possible with our thiol-ene/thiol-
yne based NPCs.
4 HOLOGRAPHIC DIFFRACTIVE
ELEMENTS
4.1 Light Beams
Holographic diffractive elements usually require high
diffraction efficiencies near 100%. This is possible
when a volume phase grating is thick enough to meet
the conditions that the product of the coupling con-
stant κ(≡ π∆n
sat
/λcosθ
B
) and the grating thickness
L be near (2m− 1)π/2(m = 1, 2,···) for a transmis-
sion grating and be larger than, say, 2 for a reflec-
tion grating in light optics (Yeh, 1993). Here λ is a
readout wavelength in vacuum and θ
B
is the Bragg
angle in the volume grating. The latter is measured
from the optical axis for an incident readout beam.
There is often another requirement for wide angular
and/or wavelength selectivities (i.e., the angular aper-
ture and/or spectral bandwidth of the Bragg diffrac-
tion) for specific applications. In this case the selec-
tivity of a volume grating is inversely proportional to
L. For narrowband optical filters, holographic sen-
sors, and holographic data storage a thick volume
grating of the order of 100 µm is preferable. On
the other hand, a thin volume grating near 10 µm is
desired for applications such as wearable eyeglasses
used for augmented and mixed reality, which requires
high diffraction efficiencies at wide acceptable angles
(i.e., with a wide Bragg aperture). In such a case
the diffraction efficiency near 100% requires ∆n
sat
to
be larger than ∼ 2.5 × 10
−2
for transmission and re-
flection volume gratings of 10 µm thickness at a vis-
ible wavelength. NPCs would be suitable for such
an application because of the ease of their coating on
curved eyeglass surfaces and the potentiality of in-
creasing ∆n
sat
by a suitable choice of nanoparticles
according to the material’s design strategy based on
Eq. (1).
Here we show our recent result of transmis-
sion NPC volume gratings dispersed with HBP or-
ganic nanoparticles with the ultrahigh refractive in-
dex. We synthesized HBP containing triazine and
aromatic ring units [see Fig. 4(a)] and the average
size was approximately 12 nm estimated by a small
angle X-ray scattering method. The refractive in-
dex was found to be 1.82 at a wavelength of 532
nm, which was much higher than those of HPEMA
and HPS used for NPCs in our past work (Tomita
et al., 2006b). Such an ultrahigh value can be at-
tributed to the incorporation of triazine and aromatic
ring units to the HBP structure. We mixed this HBP
with single functional monomers, tetrahydrofurfuryl
acrylate (THF-A, TCI) and N-vinyl-2-pyrrolidone
(NVP, Sigma-Aldrich), used as plasticizers. In this
work we employed multifunctional acrylate monomer
(n
D
=1.48), di-pentaerythritol polyacrylate (A-DPH-
12E, Shin-Nakamura Chem. Co. Ltd) [see Fig.
4(b)], to the mixture to form the high cross-linked
structure after curing and increase the recording sen-
sitivity as compared to that of more viscous mul-
tifunctional monomer, dipentaerythritol penta-/hexa-
acrylate (DPHA, TOAGOSEI Co., Ltd.), used in our
previous work (Tomita et al., 2016b). The resultant
concentration ratio of THF-A: NVP: A-DPH-12E in
vol.% was 63:5:5 when the HBP concentration was
fixed to be 27 vol.%, the maximum doping concen-
tration of HBP. A green photosensitizer Irgacure 784
(Ciba) was also added to the monomer blend of THF-
A, NVP, and A-DPH-12E. at 1.5 wt.% with respect
to A-DPH. The mixed syrup was cast on a glass plate
loaded with a 10-µm thick spacer and was finally cov-
ered with another glass plate for holographic record-
ing.
(a) (b)
Figure 4: Chemical structures of (a) HBP and (b) A-DPH-
12E.
We used a two-beam interference setup to write an
unslanted and plane-wave transmission volume grat-
ing at 1-µm grating spacing by two mutually coher-
ent beams of equal intensities at a wavelength of
532 nm. A low-intensity He-Ne laser beam operat-
ing at a photoinitiator-insensitive wavelength of 633
nm was employed as a readout beam to monitor the
buildup dynamics of the grating. All the beams were
s-polarized. Figure 5 shows photographs of a vol-
ume grating recorded in an NPC sample. Good uni-
formity and high transparency of the volume grating
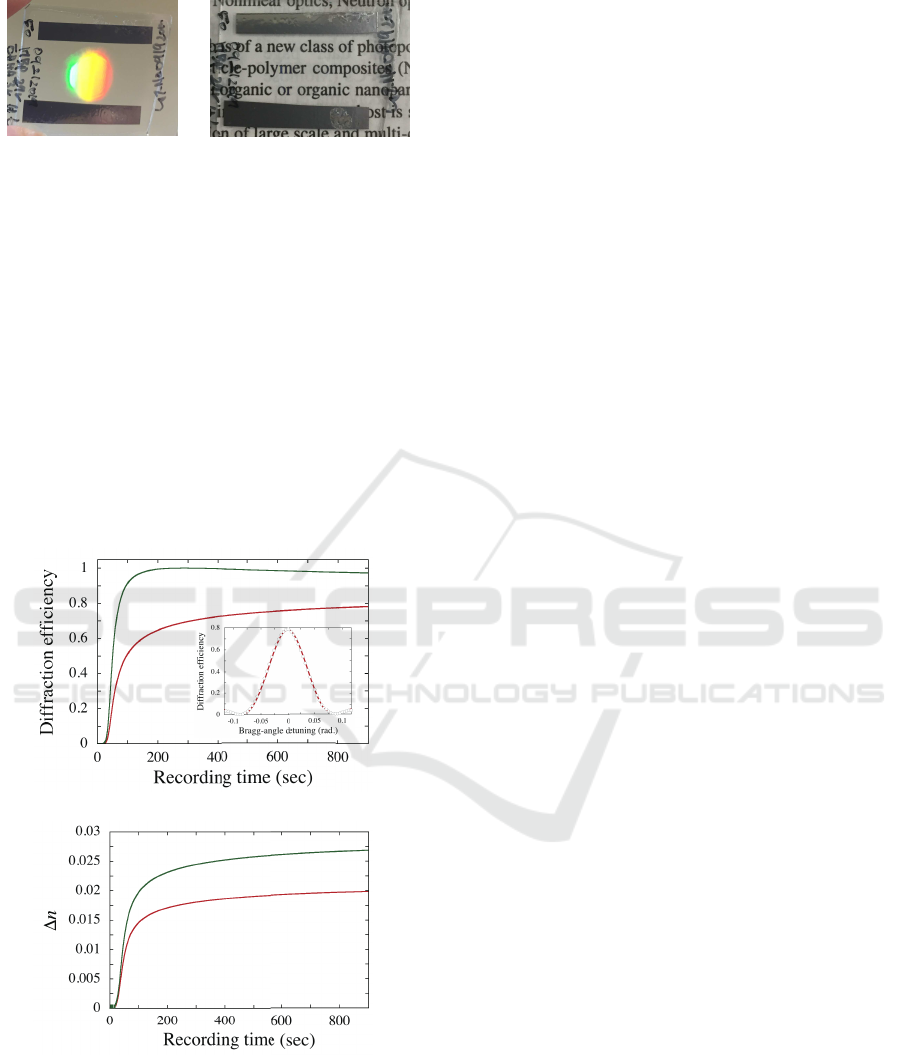
are seen. Figure 6(a) shows the recording dynam-
ics of the diffraction efficiency, defined as the ratio
Photopolymerizable Nanoparticle-polymer Composite Materials for Light and Neutron Beam Manipulations
317
(a) (b)
Figure 5: (a) Photograph of an NPC volume grating under
white light illumination from a fluorescent lamp. (b) Photo-
graph of the same grating viewed from the top.
of the 1st-order diffracted signal power to the sum
of the transmitted and the 1st-order diffracted beam
powers, at a readout wavelength of 633 nm and at
a recording intensity of 75 mW/cm
2
. The inset is
a Bragg-angle detuning dependence of the saturated
diffraction efficiency probed at 633 nm. The solid
curve denotes the least-squares curve fit of the data
to Kogelnik’s formula (Kogelnik, 1969). A good fit
of the data to the formula with the correlation coeffi-
cient higher than 0.99 indicates the uniformity of the
recorded NPC volume grating along the thickness di-
(a)
(b)
Figure 6: (a) Recording dynamics of the diffraction effi-
ciency probed by a 633-nm laser beam at a recording inten-
sity of 75 mW/cm
2
. The curve in green is the extrapolated
recording dynamics of the diffraction efficiency at 532 nm
as described in the text. The inset is a Bragg-angle detun-
ing dependence of the diffraction efficiency probed at 633
nm. (b) Buildup dynamics of ∆n at wavelengths of 532 nm
(green) and 633 nm (red).
rection. It was determined that the effective thick-
ness ℓ
eff
of the recorded NPC volume grating was
10.8 µm. The extrapolated recording dynamics of the
diffraction efficiency at 532 nm (the curve in green)
was also plotted in Fig. 6(a) by measuring the sat-
urated diffraction efficiency at 532 nm together with
∆n
sat
at 532 nm and ℓ
eff
as described below. It can be
seen that the diffraction efficiency at 532 nm finally
saturates below 100% due to the overmodulation ef-
fect. Figure 6(b) shows the corresponding buildup dy-
namics of the refractive index modulation amplitude
∆n that was extracted from measured diffraction ef-
ficiency data by ℓ
eff
and Kogelnik’s formula. In this
extraction procedure estimated values for ∆n at 633
nm were converted to those at 532 nm by multiplying
the former by a factor being the ratio of ∆n
sat
mea-
sured at 532 nm to that measured at 633 nm. We
found that ∆n
sat
at 532 nm was 2.7×10
−2
, larger than
2.2×10
−2
obtained by our previous NPC composition
with DPHA (Tomita et al., 2016b). Furthermore, the
recording intensity (75 mW/cm
2
) was lower than a
half of that with the previous one (200 mW/cm
2
) due
to the use of A-DPH having higher photochemical re-
activity and lower viscosity than those of DPHA. Us-
ing Eq. (1), we could estimate ∆f to be 0.09 at a=1
(the sinusoidal modulation) and 0.14 at a = π/2 (the
rectangular modulation at r = 0.5). Therefore, further
increase in ∆n
sat
would be possible.
4.2 Neutron Beams
Until now we have successfully demonstrated various
manipulation schemes for slow-neutron beams (e.g.,
beam splitting, triple beam division and total beam
deflection) via transmission volume gratings recorded
in NPCs dispersed with SiO
2
and ZrO
2
nanoparti-
cles (Fally et al., 2010; Klepp et al., 2012b; Klepp
et al., 2012c). As shown in Fig. 7, however, it was
necessary to effectively increase the interaction length
of an NPC transmission grating by tilting it at a large
angle ζ (∼ 70
◦
) so that the diffraction efficiency can
approach near 100% due to the Pendell¨osung inter-
ference effect [see, for example, (Sears, 1989) and for
the particular method see (Somenkov et al., 1978)].
Note that the tilt at ∼ 70
◦
corresponds to an effective
increase in L by a factor of 1/cos70
◦
∼ 2.9. Such a
large increase in thickness by the grating tilt is detri-
mental in device applications owing to a substantive
increase in incoherent scattering and absorption loss
for a slow-neutron beam propagating in supporting
glass substrates and an NPC material.
In order to avoid such a grating tilt, we need to
increase ∆n
sat
for neutrons. In neutron optics n
n
and
n
p
in Eq. (1) must be given at slow-neutron wave-
AOMatSens 2018 - Special Session in Advanced Optical Materials, Sensors and Devices
318
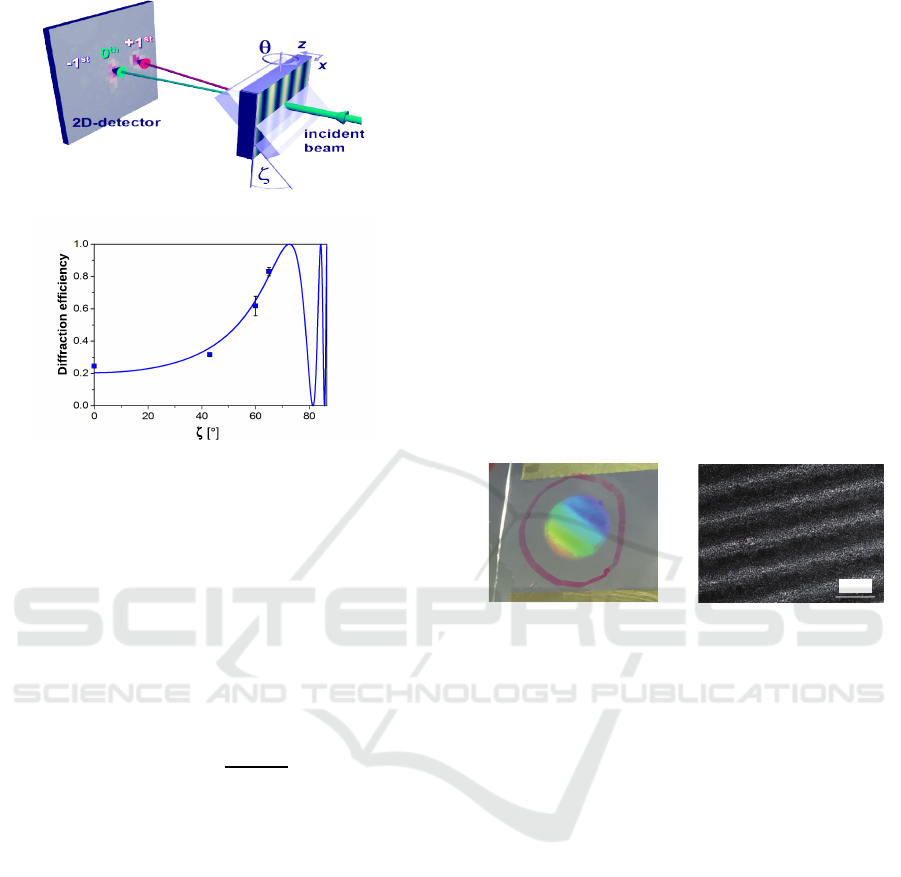
(a)
(b)
Figure 7: (a) Recording dynamics of the diffraction effi-
ciency probed by a 633-nm laser beam at a recording in-
tensity of 75 mW/cm
2
. (a) Schematic of the slow-neutron
beam diffraction via an NPC transmission grating. (b) Peak
(Bragg-matched) diffraction efficiencies η
P
as a function of
NPC grating’s tilt angle ζ for an incident very cold neutron
beam at a neutron wavelength of 3.76 nm, while the solid
curve is a theoretical plot (Klepp et al., 2011).
lengths. The neutron refractive index n
neu
of a non-
magnetic material is approximately given by (Klepp
et al., 2012a)
n
neu
= 1−
λ
2
neu
b
c
ρ
2π
, (2)
where b
c
is the average mean coherent scattering
length for a particular isotope and ρ is the atomic
number density of the material. Therefore, the fac-
tor n
n
− n
p
in Eq. (1) is determined by a differ-
ence in b
c
ρ between dispersed nanoparticles and host
monomer. For the core SiO
2
material of nanoparticles
used in our measurement [see Fig. 7(b)] b
c
ρ is given
by 3.64 × 10
−6
/
˚
A
2
. It is well known that diamond
possesses very high coherent and very low incoherent
scattering cross sections with low absorption for neu-
trons as compared with other materials. Diamond has
b
c
ρ of 1.17× 10
−5
/
˚
A
2
, which is approximately three
times larger than that of SiO
2
. It implies that ∆n
sat
of
NPC gratings dispersed with nanodiamonds is three
times larger than that of NPC gratings dispersed with
SiO
2
nanoparticles. It follows immediately that no
grating tilt is necessary to obtain high diffraction effi-
ciency.
Recently, we have investigated the possibility of
using nanodiamond for NPC volume gratings. Here
we describe our proof-of-principle result below. Nan-
odiamonds were prepared by the explosion method
and then were made some surface treatment on the
core of a nanodiamond (4 nm in diameter) for good
dispersion in host monomer. We could successfully
disperse nanodiamonds at the concentration of 19
vol.% in an acrylate monomer blend. A green pho-
tosensitizer Irgacure 784 (Ciba) was also added at the
concentration of 4.3 wt.%. Figure 8(a) illustrates a
photograph of an NPC transmission plane-wave grat-
ing at grating spacing of 1 µm recorded by two 532-
nm lasers at the total intensity of 100 mW/cm
2
. The
definite diffraction from an area (∼ 1 cm in diame-
ter) can be seen. Figure 8(b) shows a transmission-
electron microscope image of the cross section of the
grating. The dark (bright) banded areas correspond
to high concentration portions of nanodiamonds (the
formed polymer), showing holographic assembly of
nanodiamonds in the formed polymer.
1
μ
m
(a) (b)
Figure 8: (a) A photograph of an NPC transmission plane-
wave grating at grating spacing of 1 µm under white light
illumination from a fluorescent lamp. (b) A transmission-
electron microscope image of the cross section of the grat-
ing.
Figure 9(a) shows the Bragg-angle detuning curve
probed at 633 nm for the saturated NPC grating.
The solid curve denotes the least-squares curve fit
of the data to Kogelnik’s formula, giving ℓ
eff
to be
33 µm. Figure 9(b) shows the buildup dynamics of
∆n at 532 nm, which was extracted as similar to
the way described above. We found that ∆n
sat
was
2.7×10
−3
. We estimated the density modulation of
nanodiamonds by using the measured value for ∆n
sat
and the refractive indices of nanodiamonds and the
formed monomer blends. We found ∆f to be 0.006
at a = 1 and 0.010 at a = π/2 and r = 0.5, approx-
imately one order smaller than that of the HBP dis-
persed NPC grating shown in Fig. 6. This result
suggests that the mutual diffusion of nanodiamonds
and monomer needs to be facilitated much more for
an increase of ∆ f. Our investigation is underway to
increase ∆f in nanodiamond-dispersed NPC gratings
and apply them to neutron diffraction experiments. It
would also be expected that nanodiamonds dispersed
NPC gratings are useful for holographic applications
Photopolymerizable Nanoparticle-polymer Composite Materials for Light and Neutron Beam Manipulations
319

(a)
(b)
Figure 9: (a) Bragg-angle detuning dependence of the
diffraction efficiency at 633 nm. (b) Buildup dynamics of
∆n at wavelengths of 532 nm.
in light optics because of very high refractive index
(n
D
=2.417) of bulk diamond in the visible spectral re-
gion.
Finally, it should be noted that we have recently
succeeded volume holographic recording in NPCs
dispersed with superparamagnetic Fe
3
O
4
nanoparti-
cles. Such magnetic nanoparticle dispersed NPC grat-
ings have potential applications such as slow-neutron
beam’s spin control (Klepp et al., 2012a; Tomita et al.,
2016a; Li˘cen et al., 2017) as well as magneto-optic
devices in light optics (Tomita et al., 2005).
5 CONCLUSIONS
We have described the mechanism of the holographic
grating formation in NPCs and our recent results for
holographic applications to holographic data storage
and to holographic diffractive elements in light and
neutron optics. It has been shown that thiol-ene/thiol-
yne based NPCs provide excellent performance with
satisfactorily low SERs and high SNRs in a coaxial
holographic digital data page recording system. It has
also been shown that transmission gratings recorded
in NPCs dispersed ultrahigh refractive index HBP
give ∆n
sat
close to 3× 10
−2
at moderate grating spac-
ing, promising for holographic diffractive elements in
light optics. In addition, we have successfully demon-
strated volume holographic recording in NPCs dis-
persed with nanodiamonds that possess very high co-
herent and very low incoherent scattering cross sec-
tions with low absorption for neutrons. It can be ex-
pected that nanodiamondsdispersed NPC grating pro-
vide a new possibility of slow-neutron beam control.
ACKNOWLEDGEMENTS
The authors would like to thank a number of col-
laborators, including E. Hata, K. Mitsube, K. Mo-
mose, S. Takayama, K. Chikama, P. Geltenbort (ILL,
Grenoble, France), and J. Kohlbrecher (PSI, Villigen,
Switzerland) for their contribution to this work. This
work was supported by the Ministry of Education,
Culture, Sports, Science and Technology of Japan un-
der the grant numbers 15H03576 and 17K19072.
REFERENCES
Coufal, H. J., Psaltis, D., and Sincerbox, G. T., editors
(2000). Holographic Data Storage. Springer, Berlin.
Curtis, K., Dhar, L., Hill, A. J., Wilson, W. L., and Ayres,
M. R., editors (2010). Holographic Data Storage
From Theory to Practical Systems. Wiley, West Sus-
sex.
Dolgaleva, K. and Boyd, R. W. (2012). Local-field effects
in nanostructured photonic materials. Advances in Op-
tics and Photonics, 4:1–77.
Fally, M., Klepp, J., Tomita, Y., Nakamura, T., Pruner,
C., Ellabban, M. A., Rupp, R. A., Bichler, M.,
Drevenˇsek-Olenik, I., Kohlbrecher, J., Eckerlebe, H.,
Lemmel, H., and Rauch, H. (2010). Neutron op-
tical beam splitter from holographically structured
nanoparticle-polymer composites. Physical Review
Letters, 105:123904–1–123904–4.
Gao, C. and Yan, D. (2004). Hyperbranched polymers:
from synthesis to applications. Progress in Polymer
Science, 29:183–275.
Hache, F., Ricard, D., Flytzanis, C., and Kreibig, U. (1988).
The optical kerr effect in small metal particles and
metal colloids: The case of gold. Applied Physics A,
47:347–357.
Hata, E., Mitsube, K., Momose, K., and Tomita, Y. (2011).
Holographic nanoparticle-polymer composites based
on step-growth thiol-ene photopolymerization. Opti-
cal Materials Express, 1:207–222.
Horimai, H., Tan, X., and Li, J. (2005). Collinear hologra-
phy. Applied Optics, 24:16196–16209.
Kawana, M., Takahashi, J., Yasui, S., and Tomita, Y. (2015).
Characterization of volume holographic recording in
photopolymerizable nanoparticle-(thiol-ene) polymer
composites at 404 nm. Journal of Applied Physics,
117:053105–1–053105–6.
AOMatSens 2018 - Special Session in Advanced Optical Materials, Sensors and Devices
320

Klar, T., Perner, M., Grosse, S., von Plessen, G., Spirkl, W.,
and Feldmann, J. (1998). Surface-plasmon resonances
in single metallic nanoparticles. Physical Review Let-
ters, 80:4249–4252.
Klepp, J., Pruner, C., Tomita, Y., Geltenbort, P., Drevenˇsek-
Olenik, I., Gyergyek, S., Kohlbrecher, J., and Fally,
M. (2012a). Holographic gratings for slow-neutron
optics. Materials, 2012:2788–2815.
Klepp, J., Pruner, C., Tomita, Y., Mitsube, K., Geltenbort,
P., and Fally, M. (2012b). Mirrors for slow neutrons
from holographic nanoparticle-polymer free-standing
film-gratings. Applied Physics Letters, 100:214104–
1–214104–3.
Klepp, J., Pruner, C., Tomita, Y., Plonka-Spehr, C.,
Ivanov, S., Geltenbort, P., Kohlbrecher, J., Ellabban,
M. A., and Fally, M. (2011). Neutron diffraction by
holographic gratings recorded in SiO
2
nanoparticle-
polymer composites. Physical Review A, 84:013621–
1–013621–7.
Klepp, J., Sponar, S., and Hasegawa, Y. (2014). Fundamen-
tal phenomena of quantum mechanics explored with
neutron interferometers. Progress of Theoretical and
Experimental Physics, 2014:082A01–1–082A01–61.
Klepp, J., Tomita, Y., Pruner, C., Kohlbrecher, J., and Fally,
M. (2012c). Three-port beam splitter for cold neu-
trons using holographic nanoparticle-polymer com-
posite diffraction gratings. Applied Physics Letters,
101:154104–1–154104–3.
Kogelnik, H. (1969). Coupled wave theory for thick holo-
gram gratings. The Bell System Technical Journal,
48:2909–2947.
Liu, X., Adachi, Y., Tomita, Y., Oshima, J., Nakashima,
T., and Kawai, T. (2012). High-order nonlinear opti-
cal response of a polymer nanocomposite film incor-
porating semiconducotor CdSe quantum dots. Optics
Express, 20:13457–13469.
Liu, X., Matsumura, K., Tomita, Y., Yasui, K., Kojima, K.,
and Chikama, K. (2010). Nonlinear optical responses
of nanoparticle-polymer composites incorporating or-
ganic (hyperbranched polymer)-metallic nanoparticle
complex. Journal of Applied Physics, 108:073102–1–
073102–9.
Li˘cen, M., D.-Olenik, I.,
˘
Coga, L., Gyergyek, S., Kralj, S.,
Fally, M., C.Pruner, P.Geltenbort, Gasser, U., Nagy,
G., and Klepp, J. (2017). Neutron diffraction from su-
perparamagnetic colloidal crystals. Journal of Physics
and Chemistry of Solids, 110:234–240.
Lourtioz, J.-M., Benisty, H., Berger, V., G´erard, J.-M., and
Mystre, D. (2005). Photonic Crystals. Springer,
Berlin.
Mitsube, K., Nishimura, Y., Nagaya, K., Takayama, S.,
and Tomita, Y. (2014). Holographic nanoparticle-
polymer composites based on radical-mediated thiol-
yne photopolymerizations: Characterization and shift-
multiplexed holographic digital data page storage.
Optical Materials Express, 4:982–996.
Momose, K., Takayama, S., Hata, E., and Tomita, Y. (2012).
Shift-multiplexed holographic digital data page stor-
age in a nanoparticle-(thiol-ene) polymer composite
film. Optics Letters, 37:2250–2252.
Omura, K. and Tomita, Y. (2010). Photopolymerization
kinetics and volume holographic recording in ZrO
2
nanoparticle-polymer composites at 404 nm. Journal
of Applied Physics, 107:023107–1–023107–6.
Rauch, H. and Werner, S. A. (2015). Neutron Interferome-
try. Oxford University Press, Oxford, 2nd edition.
Rupp, R. A., Hehmann, J., Matull, R., and Ibel, K. (1990).
Neutron diffraction from photoinduced gratings in a
PMMA matrix. Physical Review Letters, 64:301–302.
Sears, V. F. (1989). Neutron Optics. Oxford University
Press, Oxford.
Smith, D. R., Pendry, J. B., and Wiltshire, M. C. K. (2004).
Metamaterials and negative refractive index. Science,
305:788–792.
Somenkov, V. A., Shilstein, S. S., Belova, N. E., and
Utemisov, K. (1978). Observation of dynamical os-
cillations for neutron scattering by Ge crystals using
the inclination method. Solid State Communications,
25:593–595.
Suzuki, N. and Tomita, Y. (2004). Silica nanoparticles-
dispersed methacrylate photopolymer with net diffrac-
tion efficiency near 100%. Applied Optics, 43:2125–
2129.
Suzuki, N. and Tomita, Y. (2007). Holographic scattering
in SiO
2
nanoparticles-dispersed photopolymer films.
Applied Optics, 46:6809–6814.
Suzuki, N., Tomita, Y., and Kojima, T. (2002). Holographic
recording in TiO
2
nanoparticle-dispersed methacry-
late photopolymer films. Applied Physics Letters,
81:4142–4123.
Suzuki, N., Tomita, Y., Ohmori, K., Hidaka, M., and
Chikama, K. (2006). Highly transparent ZrO
2
nanoparticle-dispersed acrylate photopolymers for
volume holographic recording. Optics Express,
14:12712–12719.
Takayama, S., Nagaya, K., Momose, K., and Tomita,
Y. (2014). Effects of symbol modulation coding
on readout fidelity of shift-multiplexed holographic
digital data page storage in a photopolymerizable
nanoparticle-(thiol-ene)polymer composite film. Ap-
plied Optics, 53:B53–B59.
Tanaka, K., Hara, M., Tokuyama, K., Hirooka, K., Ish-
ioka, K., Fukumoto, A., and Watanabe, K. (2007).
Improved performance in coaxial holographic data
recording. Optics Express, 15:16196–16209.
Tomita, Y., Chikama, K., Nohara, Y., Suzuki, N., Fu-
rushima, K., and Endoh, Y. (2006a). Two-dimensional
imaging of atomic distribution morphology cre-
ated by holographically induced mass transfer of
monomer molecules and nanoparticles in a silica-
nanoparticle-dispersed photopolymer film. Optics
Letters, 31:1402–1404.
Tomita, Y., Furushima, K., Ochi, K., Ishizu, K.,
Tanaka, A., Ozawa, M., Hidaka, M., and Chikama,
K. (2006b). Organic nanoparticle (hyperbranched
polymer)-dispersed photopolymers for volume holo-
graphic storage. Applied Physics Letters, 88:071103–
1– 071103–3.
Tomita, Y., Hata, E., Momose, K., Takayama, S., Liu,
X., Chikama, K., Klepp, J., Pruner, C., and Fally,
Photopolymerizable Nanoparticle-polymer Composite Materials for Light and Neutron Beam Manipulations
321

M. (2016a). Photopolymerizable nanocomposite pho-
tonic materials and their holographic applications in
light and neutron optics. Journal of Modern Optics,
63:S1–S31.
Tomita, Y., Nakamura, T., and Tago, A. (2008). Improved
thermal stability of volume holograms recorded in
nanoparticle-polymer composite films. Optics Letters,
33:1750–1752.
Tomita, Y., Suzuki, N., and Chikama, K. (2005). Holo-
graphic manipulation of nanoparticle-distribution
morphology in nanoparticle-dispersed photopoly-
mers. Optics Letters, 30:839–841.
Tomita, Y., Urano, H., Fukamizu, T., Kametani, Y.,
Nishimura, N., and Odoi, K. (2016b). Nanoparticle-
polymer composite volume holographic gratings dis-
persed with ultrahigh-refractive-index hyperbranched
polymer as organic nanoparticles. Optics Letters,
41:1281–12884.
Willis, B. T. M. and Carlile, C. J. (2013). Experimental
Neutron Scattering. Oxford University Press, Oxford.
Yeh, P. (1993). Introduction to Photorefractive Nonlinear
Optics. Wiley, New York.
AOMatSens 2018 - Special Session in Advanced Optical Materials, Sensors and Devices
322
