Dynamic Movement Monitoring
Algorithms for Real Time Exercise Movement Feedback
Marcel Tiator, Fabian B
¨
untig and Christian Geiger
University of Applied Sciences D
¨
usseldorf, M
¨
unsterstrae 156, 40476 D
¨
usseldorf, Germany
Keywords:
Movement Monitoring, Home Rehabilitation, Exergames.
Abstract:
Following to an implantation of an artificial knee joint, patients have to perform rehabilitation exercises at
home. The motivation to exercise can be low and if the exercises are not executed, an extended rehabilitation
time or a follow-up operation is possibly required. Moreover, incorrect exercise executions over a long period
can lead to injuries. Therefore, we present two Programming by Demonstration (PbD) algorithms, a Nearest-
Neighbour (NN) model and the Alpha Algorithm (AlpAl), for measuring the quality of exercise executions,
which can be used in order to give feedback in exergames. The models can locate an ideal posture depending
on a patient’s posture in a dynamic movement. Furthermore, they work in real time and independent of
the execution speed, in order to suggest the correct exercise movement. To validate the functionality of the
algorithms, four correct and incorrect test movements of four persons were analyzed from the monitoring
algorithms. Each localized ideal movement from the algorithms as well as each ground truth movement were
compared with an imitated test movement by a Dynamic Time Warping (DTW) algorithm. Since we expect
a linear dependency between the DTW-distances, we calculated the linear correlation, which was significant
high. Hence, we think that the proposed algorithms are appropriate to monitor physiotherapeutic exercises
while playing an exergame.
1 INTRODUCTION
As a result of terminal arthritis in the knee, an arti-
ficial knee joint implantation is performed (Ayoade
and Baillie, 2014; Mistry et al., 2016). In Germany
alone, about 130 of 100.000 inhabitants get this im-
plant and the number of follow-up operations after
the implantation has increased in recent years (Ra-
ten, 2013). After the knee-operation, the full range
of motion is attempted to be restored by rehabilitation
measures, partly consisting of physiotherapeutic exe-
rcises (Mistry et al., 2016). These exercises are taught
in a clinical area, which should be continued at home
independently (Pachoulakis and Tsilidi, 2016) as well
as regularly for a fast completion of the rehabilitation.
However, these are often not performed properly
and there are several reasons for this: the patient does
not know the purpose of the exercise, lack of moti-
vation or little time in everyday life (Chandra et al.,
2012). According to a visit to the ambulant rehabili-
tation centre M
¨
unster, it was confirmed through dis-
cussions with physiotherapists, that the patients often
do not continue their exercises at home sufficiently,
because some of them have no motivation to do their
exercises. Additionally, patients do not receive pro-
fessional feedback on movements at home (Anantha-
narayan et al., 2013). Moreover, the clinical exercise
time is short compared to the home exercise time (Da
Gama et al., 2015; Laerhoven and Lo, 2004). Finally,
while a patient is exercising, incorrect exercise exe-
cutions over a long period can lead to injuries (Su,
2013). This is not only the case with the physiothera-
peutic exercises movements (Kowsar et al., 2016).
Therefore, several approaches incorporating a Re-
habilitation System (ReSys) to increase exercise mo-
tivation at home and to give feedback on movements
exist. To implement such a system, motion capturing
technologies, which acquire data for analysis of mo-
vements, can be used (Crocher et al., 2013; Su et al.,
2014; Chandra et al., 2012; Da Gama et al., 2016).
Such a ReSys should not replace a physiotherapist,
but should serve as a supportive measure when the pa-
tient is exercising at home (Benettazzo et al., 2015).
Among other things, the information about the entire
rehabilitation status and feedback on trajectories as
well as on postures of exercises should influence the
motivation positively, too (Maclean et al., 2000; Vel-
loso et al., 2013b; Gal et al., 2015). If this informa-
tion is communicated to the user in an exergame, the
exercise motivation can be increased. Thus, a faster
184
Tiator, M., Büntig, F. and Geiger, C.
Dynamic Movement Monitoring.
DOI: 10.5220/0006735001840191
In Proceedings of the 4th International Conference on Information and Communication Technologies for Ageing Well and e-Health (ICT4AWE 2018), pages 184-191
ISBN: 978-989-758-299-8
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: The user moves a huge tree trunk when doing the
marching exercise from figure 3. While the user is exerci-
sing, coins have to be collected and flying pigs have to be
avoided. The aim of the game is to get the most points.
More collected coins and less time for the route will incre-
ase the score, whereas collisions with the pigs will decrease
the score. The movement feedback as well as the movement
monitoring is not yet integrated. Furthermore, the game is
developed by the TA cooperation partner University Duis-
burg Essen.
rehabilitation can be achieved.
Therefore, the Therapy-Assist (TA) project aims
to develop a home ReSys, which allows rehabilita-
tion patients with an artificial knee joint, to exercise
and receive feedback on movements while playing an
exergame. A sensor platform, consisting of a Kinect
and Inertial Measurement Units (IMUs), is developed,
to acquire data for analysis of movements in order to
give appropriate feedback. In the end, patients should
exercise regularly when using the ReSys. A game
from the TA project is depicted in figure 1, which ga-
mifies the marching exercise in figure 3 b).
In this context we propose algorithms, which
check the orientation of joints in real time, such that
direct feedback can be given. In order to do so, pos-
tures are compared with ideal corresponding postures
in a dynamic movement. In addition, the real time
analysis allows a trainee to learn and execute mo-
vements independent of movement execution speed.
Ultimately, it is possible to identify incorrect joint
orientations in a dynamic movement. Two Program-
ming by Demonstration (PbD) approaches are pre-
sented, namely a Nearest-Neighbour (NN) model and
a self-developed algorithm, called Alpha Algorithm
(AlpAl).
The document is structured as follows: Existing
methods for the analysis of movements are described
in section 2. In section 3 the NN model and the AlpAl
are presented and examined by a correlation analysis.
The method as well as the results are discussed and
concluded in section 4. Finally, an outlook on future
possibilities and investigations is given in section 5.
Figure 2: The upper two figures (a) show a correct execution
of the marching exercise, whereas the lower two figures (b)
show an incorrect execution, since the leg is twisted.
2 RELATED WORK
Appropriate feedback can increase the exercise mo-
tivation when it depends on a movement monitoring,
which adapts to patients of different rehabilitation sta-
tes (Benettazzo et al., 2015). Adaption can be imple-
mented by parameterized models. Camporesi et al.
parameterized dynamic movements by using plane-
constraints (Camporesi et al., 2014). After a princi-
pal component analysis of a PbD recording, the max-
imum amplitude or the hold time of an exercise can
be set. Due to the distance calculation from a joint
position to the plane, twists of joints, where the joint
position is still the same, cannot be detected. But this
is a general problem, when using position based data
for monitoring a joint orientation. If the monitoring
uses position data of joints, a normalization of joint
lengths can avoid a false feedback, in consequence of
people with limbs of different length (Ruttkay and van
Welbergen, 2008).
Besides that, parameters for describing mo-
vements, which are known by the user group, can
make a monitoring system more user friendly. For
example, Zhao et al. used the anatomical angles of
a joint in a body plane (Zhao et al., 2014a). The
choice of the anatomical angle as the monitoring para-
meter can be advantageous in the physiotherapy con-
text, since physiotherapists measure in some cases the
range of motion with a goniometer (Martin-Moreno
et al., 2008).
The inclusion of temporal features (e.g. fixed exe-
rcise execution speed) in the movement monitoring
(Ruttkay and van Welbergen, 2008; Anderson et al.,
2013) could be disadvantageous when playing an exe-
rgame, because the user should focus more on the
game than on the exercise execution at a fixed speed.
In order to avoid temporal features in the monitoring,
a Dynamic Time Warping (DTW) algorithm for com-
parison of movements can be used (Su, 2013). But
Dynamic Movement Monitoring
185

this has the disadvantage, that a movement has to be
executed and extracted in order to do the DTW analy-
sis. Hence, there is at least a feedback latency of one
exercise execution. This is also the case, if a sliding
window is used (Velloso et al., 2013a).
In contrast to that, direct feedback can be given,
when using a classifier for monitoring an exercise
execution (Velloso et al., 2013a). Mistakes in an exe-
rcise could be summarized as classes. Obviously this
technique can provide real time feedback, the training
data has to be acquired and the classifiers have to be
trained. This process can be very time consuming,
which can make the creation of new exercises hard.
Movements can also be monitored by the defi-
nition of fixed rules. For example, Pachoulakis et
al. have implemented a monitoring of a knee bend,
among which one parameter of the exercise is the dis-
tance of the hip joint to the ground (Pachoulakis et al.,
2015). Since the PbD approach was not used here,
the monitoring of new movements means defining and
implementing new rules. Apart from that, via a static
rule it is difficult to monitor the postures of a dyna-
mic movement, for instance, a limit value operation
of a property (e.g. checking the hip height) enables
adopting incorrect postures.
Another way to monitor dynamic movements wit-
hout temporal dependency and give feedback in real
time is the usage of a Finite State Machine (FSM),
where parts of the movement define the states (Zhao
et al., 2014b). The implementation of the FSM from
Zhao et al. is unidirectional, such that only forward
movements can be monitored. Such a monitoring
could be inappropriate, when unpredictable forward
as well as backward movements are executed in the
exergame.
Instead of analyzing a movement to suggest a cor-
rect movement, it is also possible to combine mo-
vements with interactions and the achievement of go-
als, such that a patient executes a movement in a cer-
tain way. For this purpose, Anderson et al. have de-
signed a game, that measures an activity score, which
is measured by parameters of a Wii controller, the
completion of tasks in the game and balance values
from a Wii balance board (Anderson et al., 2010). If
one player moves more than another, he receives a
higher score. Thereby, the motivation to move more
could be increased when playing a game.
Motivation and suggestion of certain movement
can also be created by gesture recognition. Pachou-
lakis and Tsilidi developed a game, in which it is ne-
cessary to lead a ball by hand gestures over wooden
planks (Pachoulakis and Tsilidi, 2016). The player
risks a fall down of the ball, if the ball control gestu-
res are not recognized. In other ways, patients have
to move in an application of Yu et al. in order to ca-
tch stars, which are falling from the sky (Yu et al.,
2011). Beyond that, audio-visual signs are used to
support the movements. In an application of Assad et
al., one have to follow a star trajectory, what comes
close to the execution of a certain movement (Assad
et al., 2011). This is also the case in a modified Fruit-
Ninja variant developed by Khademi et al., in which
the player has to carry out a cutting movement with
the index finger (Khademi et al., 2014). These inte-
ractive methods of suggesting movements in a playful
way allow that incorrect postures can be adopted and
no monitoring algorithm is recognizing this.
3 MONITORING
Five different rehabilitation exercises were selected
for the development of the ReSys in the TA project.
In one exercise, a practitioner lies down on the back
in a seated position and presses the feet against the
wall (figure 3 a)). Since the joints do not move in this
exercise, it is possible to compare the current pose of
the practitioner with a reference pose. Furthermore,
dynamic movements are also performed in some exe-
rcises. In figure 3 b) an exercise is shown in which a
practitioner raises his legs by 90
◦
in a marching mo-
vement on the spot alternately. During this exercise,
some patients twist their legs (figure 2 b)), whereby a
physiotherapist would apply a correction, if he would
detect this twist. Therefore, a monitoring algorithm
should analyze the motions in real time, such that the
ReSys can provide real time feedback on incorrectly
executed movements.
Additionally, the monitoring should depend on
the PbD approach, in order to easily create new mo-
vements. Furthermore, dependence on temporal fea-
tures should be avoided, such that the movements can
be potentially learned in rest by a trainee. Moreo-
ver, the user should be able to focus on the exergame
while he is exercising and the monitoring is analyzing
his movements in order to give feedback. Apart from
that, forward as well as backward movements
1
should
be monitored equally. Finally, the monitoring mecha-
nism should localize the ideal orientation of a joint.
For example, if someone twists the leg in the mar-
ching exercise (figure 2 b)), it should be possible to
determine the ideal corresponding orientation of the
leg (figure 2 a)).
1
A forward movement refers to the phase of leg lifting
from the machinery exercise in figure 2.
ICT4AWE 2018 - 4th International Conference on Information and Communication Technologies for Ageing Well and e-Health
186

Figure 3: a) shows a knee rehabilitation exercise, in which a
practitioner presses with his feet against the wall while lying
in a sitting position. b) shows another exercise, in which a
practitioner marches on the spot and lifts the legs about 90
◦
in the sagittal plane.
3.1 Nearest-Neighbour
The unweighted NN model searches for the nearest
reference orientation
2
q
r
∈ H by iteration of a PbD list
(see algorithm 1). A reference pose p
r
in a motion M
can belong to the found orientation q
r
in order to de-
termine the orientations of all joints of the body. Since
the NN model determines the nearest neighbour via
distances, a suitable distance measurement for orien-
tations has to be used.
Quaternion SearchNN(q
n
)
1 dist = max
2 Quaternion q
nn
3 foreach Quaternion q
r
∈
ReferenceOrientations do
4 tmp dist = ComputeDistance(q
n
, q
r
)
5 if tmp dist < dist then
6 dist = tmp dist
7 q
nn
= q
r
end
8 return q
nn
Algorithm 1: Pseudo-Code of the NN implementation.
q
nn
indicates the found nearest neighbour orientation.
dist is the nearest neighbour distance and tmp dist is a
temporary distance for a neighbour.
This could be the rotation difference q
nr
in eq. 1,
i.e. a rotation from a current orientation q
n
to a refe-
rence orientation q
r
.
2
In this contribution, all variables with a q indicate a
quaternion.
q
n
∗ q
nr
= q
r
⇔ q
nr
= q
−1
n
∗ q
r
(1)
This rotational difference can be converted into an
euler vector and the amount of the euler vector can
serve as a distance measurement (algorithm 1 at line
4 in function ComputeDistance (q
n
, q
r
)). Exclusive
use of orientations results in a temporal independent
localization. Furthermore, the PbD data has to be re-
corded once in order to create the list of reference
orientations.
3.2 Alpha Algorithm
This algorithm uses the body planes, which got the
same transformation as the stem joint. Beyond that,
a PbD recording with the forward movement of the
exercise should be present. When a movement is exe-
cuted, the vector of the joint deflection is projected
on a chosen body plane
3
(eq. 2), resulting in a vector
~u
j,p
∈ R
2
. The normal ~n
p
of the body plane results
from the cross product of two coordinate axes of the
stem joint, which span the plane. Additionally, the
3D projected vector
4
~v
j,p
is rotated around the inverse
root joint orientation q
−1
root
in eq. 3, so that the joint
deflection is axes aligned with the world coordinate
system. Consequently, ~u
j,p
obtains non-zero vector
coordinates of q
0
v, j,p
(eq. 3) in the axes that span the
planes.
~v
j,p
= ~v
j
0
−
~v
j
0
∗ ~n
p
|n
p
|
2
∗ ~n
p
(2)
q
0
v, j,p
= q
−1
root
∗ q
v, j,p
∗ (q
−1
root
)
−1
= q
−1
root
∗ q
v, j,p
∗ q
root
(3)
The vector of the projected minimum joint de-
flection should correspond to a fixed reference vec-
tor ~u
re f , j,p
. This can be realized by a 2D rotation
of ~u
min, j,p
(eq. 4 to 7) with an angle of α
min,p
=
∠ ~u
min, j,p
~u
re f , j,p
.
R
α
min,p
∗ ~u
min, j,p
= (4)

cos(α
min,p
) −sin(α
min,p
)
sin(α
min,p
) cos(α
min,p
)

∗ ~u
min, j,p
= (5)
~u
re f , j,p
= (6)
~u
min, j,p
0
(7)
In order to get the maximum deflection, a vector
~u
max, j,p
is rotated by R
α
min,p
, whereby the operation
results in ~u
max, j,p
0
. After that, the angle α
max,p
can
be calculated
5
. At runtime, an angle of α
p
(apply 2D
3
~u indicates a vector in the 2D body plane. The index j
stands for joint and p stands for a certain body plane.
4
~v stands for a vector of a joint deflection. .
5
The α-angles are calculated via ∠ ~u
j,p
~u
re f , j,p
.
Dynamic Movement Monitoring
187

rotation and α-angle calculation to ~u
j,p
) has to be de-
termined and it must be proofed, if α
p
is within the
range of 0
◦
to α
max,p
. Since the angle calculation ∠~x~y
only represents values from 0
◦
to 180
◦
, the function
a(α
p
) (eq. 8) is used to model movements, which in-
clude a deflection more than 180
◦
in a body plane
6
.
α
0
p
= a(α
p
) =

360
◦
− α
p
, if ~u
j,p
0
x
< 0
α
p
, else
(8)
However, this presupposes a sense of rotation in
the 2D plane, whereby a clockwise rotation is chosen
as in figure 4.
Figure 4: The right turn in the body planes is symbolized
by a yellow arrow. In contrast, a turn in the other direction
is a left-hand turn. Moreover, a) shows the frontal plane, b)
the sagittal plane and c) the transverse plane.
The next step is to interpolate joint orientations
of the previously made PbD recording from sampling
point to sampling point via the spherical linear inter-
polation function. Each resulting interpolated joint
movement is processed according to the equations eq.
2 to 8, so that an angle of α
0
p
is calculated. An interpo-
lated orientation is stored as a reference orientation, if
a certain sampling rate of α
s,p
± α
f ,p
is fulfilled (α
f ,p
is a tolerance for the non-compliance of the sampling
rate α
s,p
). At the end of this interpolation process,
an array of reference orientations is available for the
runtime, whereby poses can be also assigned to the
orientations as well. At runtime, a α
0
p
must be clam-
ped to the range of motion by eq. 9 to 11, since these
orientations were only stored in the interpolation pro-
cess.
α
00
p
=
c(α
0
p
) =

f (α
0
p
) , if α
0
p
> α
0
max,p
α
0
p
, else
(9)
with
f (α
0
p
) =

α
0
max,p
, if α
0
p
< α
0
g,p
0
◦
, else
(10)
α
g,p
= 180
◦
+
α
0
max,p
2
(11)
Finally, an index is obtained from the angle α
00
p
,
which is assigned to a reference orientation. This is
6
~u
j,p
0
x
stands for the x-component of ~u
j,p
0
.
done by dividing the angle α
00
p
by the sampling rate
α
s,p
. This quotient is rounded down to the next integer
by eq. 12.
i = b
α
00
p
α
s,p
c (12)
Finally, by inserting the index i in the array of
orientations, which were created in the interpolation
process, the reference orientation is localized. After
the ideal pose localization, the joint orientations of
the current reference posture can be compared by eq.
1.
3.3 Method
We want to validate the functionality of the proposed
algorithms. Motions can be compared by pearson cor-
relation (Velloso et al., 2017), but repetitions of exe-
rcises can have different durations. This means, that
an interpolation of the movement data is necessary. In
order to avoid an interpolation, the DTW algorithm is
used to compare two sequences of movements with
different durations in the euler domain. Furthermore,
a correctly imitated test movement is expected to have
a low DTW distance to a reference movement. Simi-
larly, a localized movement should have a low DTW
distance to a correctly imitated test movement. The
DTW distances from test to a localized movement and
test to a reference movement should have a high posi-
tive linear correlation coefficient. This correlation is
then checked for significance by a directed t-test. The
null hypothesis H
0
: ρ ≤ 0 and the alternative hypot-
hesis H
1
: ρ > 0 were examined.
For this purpose, four test movements were defi-
ned, which were executed by four test persons cor-
rectly and incorrectly from their perspective. The
subjects were healthy adults in the age of 20 to 27.
They were instructed about the movements and trai-
ned them a few times. After that, a recording of the
exercises was made. Thus, for each movement ex-
ist N = 8 different versions. The movement of lif-
ting the left leg was chosen from the marching exer-
cise (Ex11, figure 2). The spreading of the right leg
of a hip abduction (Ex12) was monitored. In order
to monitor more complex movements, two capoeira
kicks (Ex13, Ex14) of the right leg were monitored,
which include the main deflection in more than one
degree of freedom. Since the sensor platform from
the TA project has not yet been developed, the mo-
vement data was acquired by an IMU suit. The sen-
sors of the suit are differently attracted from subject
to subject. Therefore, a certain deviation from the ba-
sic IMU-orientations of the person who has made the
PbD recording was taken into account.
ICT4AWE 2018 - 4th International Conference on Information and Communication Technologies for Ageing Well and e-Health
188

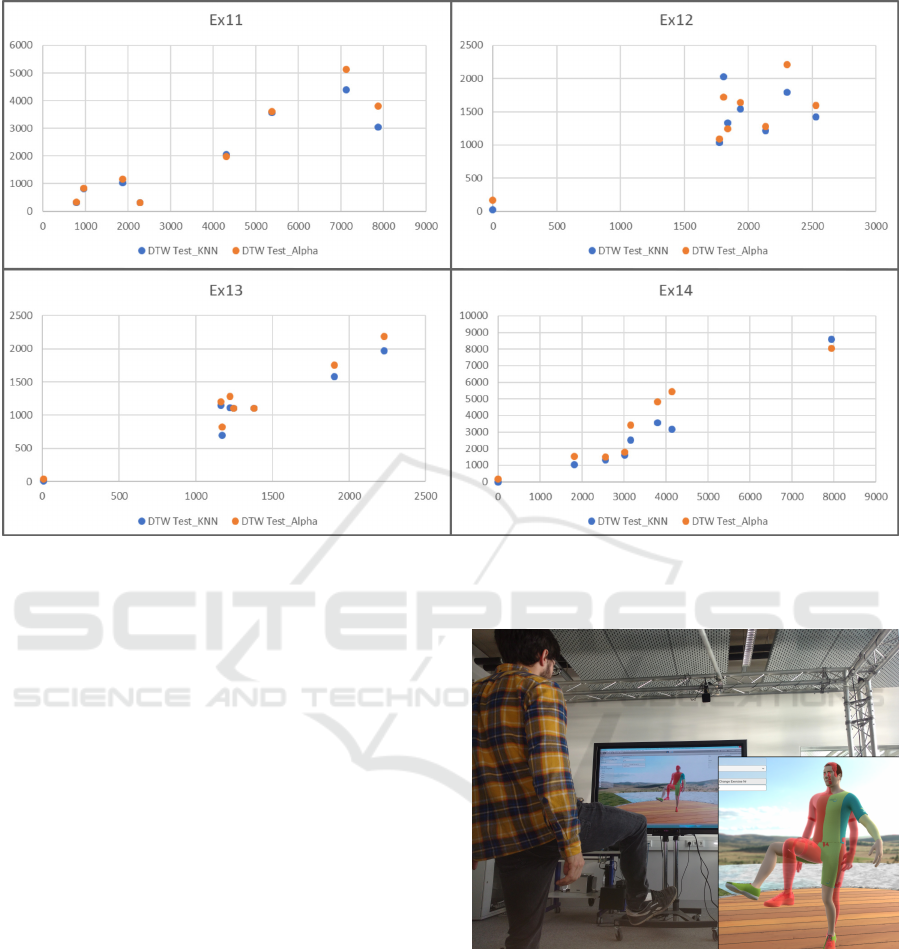
Figure 5: The DTW distances from the test to reference movements are plotted on the x-axis, whereas the distances from test
to localized movements are plotted on the y-Axis. The blue dots represent the NN-model and the orange dots represent the
AlpAl.
3.4 Results
The linear correlation coefficients of all movements
are significant (p < 0.05). The explicit correlation
coefficients are given in table 1. The correlation coef-
ficients of the DTW distances from test to reference
movement and test to NN localization data are given
under ρ
NN
(The same principle applies to the AlpAl).
Table 1: Linear correlation coefficients of the DTW dis-
tances from the reference and localized movements to test
movements.
Exercise ρ
NN
ρ
Al pAl
11 ≈ 0.908 ≈ 0.931
12 ≈ 0.814 ≈ 0.858
13 ≈ 0.970 ≈ 0.972
14 ≈ 0.972 ≈ 0.944
According to the significant results, there is a non-
random correlation between a localized motion se-
quence of the two models and the reference to the test
motion sequences. Therefore, the localization models
can indicate where a joint of a person should be lo-
cated, if an incorrect posture is taken in a dynamic
movement.
Additionally, the requirements from section 3 are
fulfilled. A new movement can be adapted via a PbD
Figure 6: This figure shows a silhouette of the ideal posture
of the body depending on the posture of a practitioner.
recording. The monitoring of the joints in a dyna-
mic movement is independent of a certain execution
speed or temporal window. Furthermore, direct feed-
back can be given, since the methods do not require
any extraction of an exercise repetition.
The localization can be exemplary visualized as
feedback by a transparent silhouette (ghost) in rela-
tion to the own body movement (figure 6). The color
of the ghost changes, depending on the deviation from
the reference orientation. Red stands for an inappro-
Dynamic Movement Monitoring
189

priate imitation of the movement and green stands for
an appropriate imitation.
4 DISCUSSION & CONCLUSION
The DTW algorithm for the comparison of two mo-
tions uses the euclidean distance. This has the disad-
vantage, that two obvious euler angles can be far away
when euler jumps occur. For example, one coordinate
of a degree of freedom can be 358
◦
and the next could
be 2
◦
, resulting in the absolute euclidean distance of
356
◦
, even though the shortest way is only 4
◦
. Since
there are no euler jumps in the data, this disadvantage
can be neglected for the evaluation.
Figure 5 shows the DTW distances, whereby the
reference data was also used as test data. Here, the
NN model has a zero DTW distance, but the AlpAl
has produced a small deviation due to the interpola-
tion process of the reference movement. The interpo-
lation process of the two capoeira kicks ends in half
of the movement, since the maximum leg deflection
is already reached in half of the movement. Unfor-
tunately, the hip cannot be chosen as an observable
joint, because it represents the stem joint of the body
and has a globally dependent hip deflection. This pre-
vents an influence of the localization from the align-
ment of a patient in the room. The NN algorithm has
the advantage over the AlpAl, that it can be used wit-
hout parameters, except for the choice of a joint to be
monitored. In contrast to this, parameters have to be
selected in the interpolation process of the AlpAl. On
the other hand, the AlpAl comes with a constant run-
time complexity of O = 1 and offers a motion inde-
pendent calculation duration for the movement moni-
toring. The NN algorithm is associated with a linear
runtime complexity in the length of the PbD recor-
ding. According to the constant runtime complexity,
the AlpAl can be used to develop a graphically or rat-
her logically elaborated exergame. Thus, developers
can plan the system resources in the temporal execu-
tion independent of the PbD recording. These algo-
rithms can be used with any motion capturing system,
which measure local joint orientations in a hierarchi-
cal way, such that at least one parent joint exist.
The proposed algorithms enable monitoring of
movements in an exergame, in which feedback to the
movements can be given. This can increase exercise
motivation, but further investigations are necessary in
order to find out, how the movement feedback is rela-
ted to the exercise motivation. However, the feedback
based on the monitoring can ensure, that inappropri-
ate movements are detected and possible injuries be
avoided. Moreover, patients can re-learn exercises
(e.g. with the ghost feedback), if they have forgotten
them.
5 FUTURE WORK
Since it is still unclear, how fast a feedback should
react and which movement analysis in an exergame
is most suitable for certain movements to increase
exercise motivation, we want to compare several mo-
vement analysis methods with the user group from the
TA project. Being able to define the maximum ampli-
tude of an exercise like Camporesi et al. (Camporesi
et al., 2014) may be a sensible addition of the moni-
toring algorithms. This could be done in the AlpAl
by modifying the α
max,p
parameter. In addition, the
search of the NN algorithm could be sped up by star-
ting the search at the last found neighbour and setting
a threshold to localize the nearest neighbour. Supple-
mentary to this, we want to extend both models, such
that more complex movements can be monitored (e.g.
a dance performance).
REFERENCES
Ananthanarayan, S., Sheh, M., Chien, A., Profita, H., and
Siek, K. (2013). Pt Viz: Towards a Wearable Device
for Visualizing Knee Rehabilitation Exercises. Pro-
ceedings of the SIGCHI Conference on Human Fac-
tors in Computing Systems, pages 1247–1250.
Anderson, F., Annett, M., and Bischof, W. F. (2010). Lean
on Wii: Physical rehabilitation with virtua reality Wii
peripherals. Studies in Health Technology and Infor-
matics, 154:229–234.
Anderson, F., Grossman, T., Matejka, J., and Fitzmaurice,
G. (2013). YouMove: Enhancing Movement Training
with an Augmented Reality Mirror. Proceedings of
the 26th annual ACM symposium on User interface
software and technology - UIST ’13, pages 311–320.
Assad, O., Hermann, R., Lilla, D., Mellies, B., Meyer, R.,
Shevach, L., Siegel, S., Springer, M., Tiemkeo, S., Vo-
ges, J., Wieferich, J., Herrlich, M., Krause, M., and
Malaka, R. (2011). Motion-Based Games for Parkin-
son’s Disease Patients. pages 47–58. Springer, Berlin,
Heidelberg.
Ayoade, M. and Baillie, L. (2014). A novel knee rehabili-
tation system for the home. Proceedings of the 32nd
annual ACM conference on Human factors in compu-
ting systems - CHI ’14, pages 2521–2530.
Benettazzo, F., Iarlori, S., Ferracuti, F., Giantomassi, A.,
Ortenzi, D., Freddi, A., Monteriu, A., Innocenzi, S.,
Capecci, M., Ceravolo, M. G., and Longhi, S. (2015).
Low Cost RGB-D Vision Based System to Support
Motor Disabilities Rehabilitation at Home. Ambient
Assisted Living: Italian Forum 2014, (August):449–
461.
ICT4AWE 2018 - 4th International Conference on Information and Communication Technologies for Ageing Well and e-Health
190

Camporesi, C., Popelar, A., Kallmann, M., and Han, J.
(2014). Motion parameterization and adaptation stra-
tegies for virtual therapists. Lecture Notes in Com-
puter Science (including subseries Lecture Notes in
Artificial Intelligence and Lecture Notes in Bioinfor-
matics), 8637 LNAI:99–108.
Chandra, H., Oakley, I., and Silva, H. (2012). Designing
to support prescribed home exercises. Proceedings of
the 7th Nordic Conference on Human-Computer In-
teraction Making Sense Through Design - NordiCHI
’12, page 607.
Crocher, V., Hur, P., and Seo, N. J. (2013). Low-cost virtual
rehabilitation games: House of quality to meet patient
expectations. 2013 International Conference on Vir-
tual Rehabilitation, ICVR 2013, pages 94–100.
Da Gama, A., Fallavollita, P., Teichrieb, V., and Navab, N.
(2015). Motor Rehabilitation Using Kinect: A Syste-
matic Review. Games for Health Journal, 4(2):123–
135.
Da Gama, A. E. F., Chaves, T. M., Figueiredo, L. S., Baltar,
A., Meng, M., Navab, N., Teichrieb, V., and Fallavol-
lita, P. (2016). MirrARbilitation: A clinically-related
gesture recognition interactive tool for an AR rehabi-
litation system. Computer Methods and Programs in
Biomedicine, 135(July):105–114.
Gal, N., Andrei, D., Nemes¸ D. I., Nd
ˇ
as¸an, E., and Stoicu-
Tivadar, V. (2015). A Kinect based intelligent e-
rehabilitation system in physical therapy. Studies in
Health Technology and Informatics, 210:489–493.
Khademi, M., Mousavi Hondori, H., McKenzie, A., Doda-
kian, L., Lopes, C. V., and Cramer, S. C. (2014). Free-
hand interaction with leap motion controller for stroke
rehabilitation. Proceedings of the extended abstracts
of the 32nd annual ACM conference on Human fac-
tors in computing systems - CHI EA ’14, (November
2015):1663–1668.
Kowsar, Y., Moshtaghi, M., Velloso, E., Kulik, L., and
Leckie, C. (2016). Detecting Unseen Anomalies in
Weight Training Exercises. OzCHI Proceedings of the
28th Australian Conference on Computer-Human In-
teraction, pages 517–526.
Laerhoven, K. V. and Lo, B. (2004). Medical healthcare
monitoring with wearable and implantable sensors.
Proc. of the 3rd International Workshop on Ubiqui-
tous Computing for Healthcare Applications, (Janu-
ary):11.
Maclean, N., Pound, P., Wolfe, C., and Rudd, A. (2000).
Qualitative analysis of stroke patients’ motivation for
rehabilitation. Bmj, 321(7268):1051–1054.
Martin-Moreno, J., Ruiz-Fernandez, D., Soriano-Paya, A.,
and Jesus Berenguer-Miralles, V. (2008). Monitoring
3D movements for the rehabilitation of joints in phy-
siotherapy. Conference proceedings : ... Annual Inter-
national Conference of the IEEE Engineering in Me-
dicine and Biology Society. IEEE Engineering in Me-
dicine and Biology Society. Conference, 2008:4836–9.
Mistry, J. B., Elmallah, R. D., Bhave, A., Chughtai, M.,
Cherian, J. J., McGinn, T., Harwin, S. F., and Mont,
M. A. (2016). Rehabilitative Guidelines after Total
Knee Arthroplasty: A Review. Journal of Knee Sur-
gery, 29(3):201–217.
Pachoulakis, I. and Tsilidi, D. (2016). Technology-assisted
Carpal Tunnel Syndrome Rehabilitation using serious
games: the Roller Ball example. Advances in Image
and Video Processing, (August 2016).
Pachoulakis, I., Xilourgos, N., Papadopoulos, N., and Ana-
lyti, A. (2015). A Kinect-based Physiotherapy and As-
sessment Platform for Parkinson ’ s disease Patients.
Physiotherapy, 2016.
Raten, A. (2013). Knieoperationen : Große regionale Un-
terschiede bei der Versorgung mit k
¨
unstlichen Knie-
gelenken.
Ruttkay, Z. and van Welbergen, H. (2008). Elbows Higher!
Performing, Observing and Correcting Exercises by a
Virtual Trainer. pages 409–416. Springer Verlag.
Su, C.-J. (2013). Personal Rehabilitation Exercise Assistant
with Kinect and Dynamic Time Warping. Internatio-
nal Journal of Information and Education Technology,
3(4):448.
Su, C.-J., Chiang, C.-Y., and Huang, J.-Y. (2014). Kinect-
enabled home-based rehabilitation system using Dy-
namic Time Warping and fuzzy logic. Applied Soft
Computing, 22(November 2010):652–666.
Velloso, E., Bulling, A., and Gellersen, H. (2013a). Moti-
onMA: motion modelling and analysis by demonstra-
tion. CHI ’13: Proceedings of the SIGCHI Conference
on Human Factors in Computing Systems, page 1309.
Velloso, E., Bulling, A., Gellersen, H., Ugulino, W., and
Fuks, H. (2013b). Qualitative activity recognition of
weight lifting exercises. Proceeding AH ’13 Procee-
dings of the 4th Augmented Human International Con-
ference, pages 116–123.
Velloso, E., Carter, M., Newn, J., Esteves, A., Clarke,
C., and Gellersen, H. (2017). Motion Correlation.
ACM Transactions on Computer-Human Interaction,
24(3):1–35.
Yu, W., Vuong, C., and Ingalls, T. (2011). An Interactive
Multimedia System for Parkinson s Patient Rehabili-
tation. Virtual and Mixed Reality - Systems and Appli-
cations, Part II, HCI 2011, pages 129–137.
Zhao, W., Feng, H., Lun, R., Espy, D. D., and Reinthal,
M. A. (2014a). A Kinect-based rehabilitation exercise
monitoring and guidance system. Proceedings of the
IEEE International Conference on Software Engineer-
ing and Service Sciences, ICSESS, pages 762–765.
Zhao, W., Lun, R., Espy, D. D., Ann Reinthal, M., and
Reinthal, M. A. (2014b). Realtime Motion Asses-
sment For Rehabilitation Exercises: Integration Of
Kinematic Modeling With Fuzzy Inference. Journal
of Artificial Intelligence and Soft Computing Rese-
arch, 4(4):267–285.
Dynamic Movement Monitoring
191