Supporting CPS Modeling Through a New Method for Solving Complex
Non-holomorphic Equations
Giulio Masetti
1,2
, Simone Dutto
1
, Silvano Chiaradonna
1
and Felicita Di Giandomenico
1
1
ISTI-CNR, Pisa, Italy
2
Department of Computer Science, University of Pisa, Italy
Keywords:
Generative Programming, Newton-raphson, Complex System of Equations, Non-holomorphic Functions,
Wirtinger Derivatives.
Abstract:
Modeling cyber-physical systems (CPSs) for assessment or design support purposes is a complex activity.
Capturing all relevant physical, structural or behavioral aspects of the system at hand is a crucial task, which
often implies representation of peculiar features/constraints through non-linear equations. Values that fulfill
the constraints, described with a domain specific language, are obtained solving the equations through a prop-
erly developed solution tool. Only for a limited set of CPSs it is possible to find a straightforward strategy
to design the software that solves the constraints equations. In the general case, instead, the modeler has to
develop an ad-hoc artifact for each different system. This is the case of non-holomorphic but real analytic
complex equations, adopted to represent system components with wave behaviors. In this paper, we present a
new approach to develop a software for solving such complex equations following a generative programming
strategy, based on Wirtinger derivatives within the Newton-Raphson method.
1 INTRODUCTION AND
RELATED WORK
Modern cyber-physical systems (CPSs) are smart sys-
tems that include engineered interacting networks
of physical and computational components (NIST,
2015).
Several layers of abstraction are commonly used
to characterize a CPS: components level, network of
physical components, network of computational com-
ponents, network of interactions among physical and
cyber components, etc, each one possibly described
with a different formalism or domain specific lan-
guage.
Focusing on a model-based design perspective, a
comprehensive model of the system is typically as-
sembled at the beginning of the system design pro-
cess, to assist the designer in making choices on the
system under development. Refinements of the ini-
tially defined model can be performed in later stages,
e.g triggered by observations emerging during the im-
plementation phase.
Models represent at a suitable detailed level (that
depends on the objective of the analysis carried on
through modeling) both the structure of the system
and its behavior during lifetime, subject to the envi-
ronmental context it operates in and related phenom-
ena, such as faults.
In CPS, the modeling of control units requires a
fairly detailed description of the physical component
that has to be controlled, of the adopted control poli-
cies and of related fault-tolerance mechanisms, if any.
There exists a vast literature, in particular for em-
bedded systems (Rizano et al., 2011), about archi-
tectural choices, dependability-related concepts, pro-
gramming paradigms, etc, when dealing with model
creation and model-guided software implementation
phases. However, when defining the physical part of
the system state within a model, it is common prac-
tice not to follow a general strategy but an ad-hoc se-
quence of steps. This results in additional work for
the modeler, as well as request for higher expertise in
the specific adopted formalisms.
Inside a model, the state of the controlled com-
ponents is often represented via a set of constraints
upon the physical elements of the controlled system.
These constraints characterize the nature and evolu-
tion of the controlled system and are modeled using
some sort of declarative formalism, typically alge-
braic equations. This implies that one essential as-
pect of the modeling process is the availability of a
(semi-automatic) procedure to generate the software
680
Masetti, G., Dutto, S., Chiaradonna, S. and Giandomenico, F.
Supporting CPS Modeling Through a New Method for Solving Complex Non-holomorphic Equations.
DOI: 10.5220/0006752306800688
In Proceedings of the 6th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2018), pages 680-688
ISBN: 978-989-758-283-7
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

that is responsible, within the model, for the compu-
tation of the components state by numerically solving
the given equations.
Depending on the characteristics of the con-
straints, general methods have been considered
(Broyden, 1965), (Kelley, 1995), (Khalil, 2002), but
when their conditions are not satisfied, specific meth-
ods (ad hoc, i.e., depending on the CPS studied) have
to be found (Bejarano and S
´
anchez, 1989), (Avargel
and Cohen, 2010).
In this paper, the focus is on physical components
subject to state changes following a periodic motion
governed by equations that are not sufficiently smooth
(complex non-holomorphic) to allow straightforward
implementation of standard equation solution meth-
ods. Physical components governed by this class of
equations can be found in several real-world systems,
such as:
• electrical circuits in Alternating Current, where
the steady-state is represented by the Power Flow
Equations (Wang et al., 2017);
• calibration of antennas, where Radio Interferome-
try Measurement Equations (Tasse, 2014) are em-
ployed;
• wave profile shaping, where convolution of pha-
sors equations (Arrillaga, 2003) define the con-
structive/destructive superimposition of periodic
waves within a (non)-linear medium.
In all the mentioned scenarios, the physical part
of the component state that appears in the model is
represented using complex numbers and resorting to
non-smooth equations. As an help to modelers, the
contribution of this paper is the definition and imple-
mentation of a new general solution method, able to
compute solution for this class of equations.
Specifically, the new implemented method, called
WNR, takes the constraint equations and calculates
their solution. The mathematical details are briefly
discussed and each step of the method is described
providing a runnable MATLAB (MathWorks, 2017)
function.
The rest of the paper has the following structure.
After the description of the mathematical context in
Section 2, the new method is discussed in Section 3.
A simple but representative case study, adopted to il-
lustrate how the method works, is depicted in Sec-
tion 4. Finally, conclusions and directions for future
work are briefly drawn in Section 5.
2 CONTEXT
The evolution of a CPS is modeled by states and tran-
sitions among states. Each state is commonly de-
scribed as a list of state variables. Depending on their
characteristics, the state variables belong to real num-
bers (R) or, more generally, to complex numbers (C).
The state transitions of a system are ruled by theoreti-
cal relations and practical aspects, that are collected in
a set of constraints, implemented with a list of equa-
tions in which some state variables are known while
others are unknown.
Considering the array z = (z
1
,z
2
,...,z
n
) ∈ C
n
containing all unknowns, the system constraints are
given by f(z) = 0 ∈ C
m
, i.e., a shorter notation for the
list of equations:











f
1
(z
1
,z
2
,...,z
n
) = 0
f
2
(z
1
,z
2
,...,z
n
) = 0
.
.
.
f
m
(z
1
,z
2
,...,z
n
) = 0
(1)
It is important to observe that, even when the sys-
tem variables and constraints are described in C, real
formulations and implementations are preferred. This
is because nowadays computer architectures work
with real numbers. In fact, since they consider each
complex number as a couple of real numbers, com-
plex calculus involves more calculations and, conse-
quently, it is less precise and slower with respect to
the real one.
Depending on the characteristics of the functions
f
i
, a problem like (1) belongs to one of the two fol-
lowing classes: linear problems and non-linear prob-
lems. As can be seen in the following subsections,
while the first type of problems can be easily studied,
solution approaches exist only for a little part of the
second ones.
2.1 Linear Problems
The problem (1) is called linear if it can be written as:











a
11
z
1
+ a
12
z
2
+ ···+ a
1n
z
n
= b
1
a
21
z
1
+ a
22
z
2
+ ···+ a
2n
z
n
= b
2
.
.
.
a
m1
z
1
+ a
m2
z
2
+ ···+ a
mn
z
n
= b
n
(2)
It is possible to use a matricial form to collect, in a
single contracted equation, the system (2). The result
is given by:
A ·z = b (3)
where A is a matrix containing all the numbers a
i j
and
· is the matrix-vector product.
Supporting CPS Modeling Through a New Method for Solving Complex Non-holomorphic Equations
681

Provided that the equations in (2) are linearly in-
dependent, there are three possible cases:
1. if m < n, i.e., there are less equations than un-
knowns, the problem has infinite solutions;
2. if m = n, i.e., the number of equations is equal to
the number of unknowns, and A is non-singular,
the problem has exactly one solution;
3. if m > n, i.e., there are more equations than un-
knowns, the problem has no solutions.
If the problem admits at least one solution, it can be
solved by considering the inverse of the matrix A, be-
cause z = A
−1
·b. The implementation of the inverse
matrix computation has been widely studied and op-
timized, and can be found in most of mathematical
software, e.g. MATLAB (MathWorks, 2017).
2.2 Non-linear Problems
All problems like (1) that can not be written as in (2)
are classified as non-linear problems. Rarely direct
approaches can solve this kind of problems and some-
times it is impossible to know if a solution exists. For-
tunately, there exist iterative approaches that allow to
find approximations of one of the problem solutions.
When in (1) m = n, one of the most used
and implemented iterative solution approaches is the
Newton-Raphson method (NR) (Kelley, 1995). In its
steps, starting from an initial guess of z, the new ap-
proximation is determined using the Jacobian J of
the initial non-linear problem. However, since the
Jacobian of a set of real (or, respectively, complex)
equations is the matrix containing all their real (com-
plex) derivatives, in order to use NR, the problem has
to contain all derivable (holomorphic, i.e., complex
derivable) equations (Kreutz-Delgado, 2009).
An implementation of NR with MATLAB (Math-
Works, 2017) can be given by:
function [z, conv] = NR(z, par, max_it, tol)
conv = 0; i = 0; % initialize
F = feval(z, par); % evaluate f(z)
normF = norm(F, inf);
if normF < tol % check tolerance
conv = 1; exit;
end
while(conv==0 && i<max_it) % do NR iterations
i = i + 1; % update it.counter
J = jeval(z, F, par); % evaluate J
dz = -(J \ F); % calc. update step
z = z + dz; % update z
F = feval(z, par); % evaluate f(z)
normF = norm(F, inf);
if normF < tol % check convergence
conv = 1;
end
end
where the inputs are: (i) the initial guess z, (ii)
a list of parameters par containing all known val-
ues, (iii) the maximum number of iterations max_it
and (iv) the tolerance tol. The evaluation of f and J
is performed by the functions feval and jeval, re-
spectively. The functions feval and jeval are de-
fined and implemented by the modeler. feval has
inputs z and par; jeval has inputs z, par and F, i.e.,
the result of the current evaluation of f. The defini-
tion of jeval can include built-in automatic deriva-
tive operators provided by MATLAB. The solution
dz = -(J \ F) of the linear system J ·dz = −f(z)
determined by the Jacobian is used to approximate z
(z = z + dz).
Despite NR is a powerful and fast method, for
some problems it does not converge (conv = 0) and
hence the solution cannot be found.
When the functions f
i
of f are not complex deriv-
able, and then NR is not applicable, solutions can be
found only using an ad-hoc method.
3 THE NEW APPROACH: WNR
Our aim is to improve NR in order to obtain a method
that can find solutions when classic NR fails or can
not be used. The proposed method is called Wirtinger
Newton Raphson (WNR) because of the particular
derivatives used. WNR applies to systems described
by real derivable complex equations that can be holo-
morphic or non-holomorphic.
In fact, each function f
i
: C
n
→ C in f can be
seen as
˜
f
i
: R
2n
→ C when the cartesian coordinates
z
j
= x
j
+ıy
j
are considered. If all
˜
f
i
are derivable with
respect to x
j
and y
j
(as real variables), then the fol-
lowing method, here implemented in MATLAB, can
be used:
function [z, conv] = WNR(z, par, max_it, tol)
conv = 0; i = 0; % initialize
F = feval(z, par); % evaluate f(z)
normF = norm(F, inf);
if normF < tol % check tolerance
conv = 1; exit;
end
while(conv==0 && i<max_it) % do WNR iterations
i = i + 1; % update it.counter
G = wfunc(F); % NEW function
J = wjeval(z, F, par); % NEW Jacobian
dw = -(J \ G); % NEW update step
dz = wstep(dw); % calc. update step
z = z + dz; % update z
F = feval(z, par); % evaluate f(z)
normF = norm(F, inf);
if normF < tol % check convergence
conv = 1;
end
end
AMARETTO 2018 - Special Session on domAin specific Model-based AppRoaches to vErificaTion and validaTiOn
682

The theoretical steps behind the new functions
wfunc, wjeval and wstep are described in the Sub-
section 3.1, while their implementation in MATLAB
is presented in Subsection 3.2.
3.1 Mathematical Process
After writing the functions
˜
f
i
: R
2n
→ C
n
by consid-
ering the complex variables in f
i
as z
j
= x
j
+ ıy
j
, if
all the
˜
f
i
are real derivable, a new kind of complex
derivatives can be defined. They are called Wirtinger
derivatives (Kreutz-Delgado, 2009) and are the fol-
lowing partial differential operators:
∂
W
f
i
∂z
j
=
1
2

∂
˜
f
i
∂x
j
−ı
∂
˜
f
i
∂y
j

∂
W
f
i
∂z
j
=
1
2

∂
˜
f
i
∂x
j
+ ı
∂
˜
f
i
∂y
j

(4)
where z
j
= x
j
−ıy
j
is the complex conjugate of z
j
.
Despite their formal definition, Wirtinger deriva-
tives of f
i
can be calculated as complex derivatives
with respect to z
j
(or, respectively, z
j
) while consider-
ing z
j
(z
j
) constant, so that the passage to
˜
f
i
is merely
formal.
The Wirtinger Jacobian (Kreutz-Delgado, 2009)
of f is defined analogously to the classic complex
one. However, since there are 2n Wirtinger deriva-
tives for each of the n functions f
i
, considering only
the Wirtinger derivatives of f returns a rectangular ma-
trix. Hence, in order to make square the Wirtinger
Jacobian, the Wirtinger derivatives of f, i.e., the com-
plex conjugate of f, are also considered. The resulting
structure of the Wirtinger Jacobian is given by:
J
W
=



∂
W
f
∂z
∂
W
f
∂z
∂
W
f
∂z
∂
W
f
∂z



∈ C
2n,2n
(5)
where the entries of its submatrices are:

∂
W
f
∂z

i j
=
∂
W
f
i
∂z
j

∂
W
f
∂z

i j
=
∂
W
f
i
∂z
j

∂
W
f
∂z

i j
=
∂
W
f
i
∂z
j
=

∂
W
f
i
∂z
j


∂
W
f
∂z

i j
=
∂
W
f
i
∂z
j
=

∂
W
f
i
∂z
j

(6)
It is important to observe that the Wirtinger deriva-
tives of f can be calculated as complex conjugates of
the Wirtinger derivatives of f, so that the number of
computations needed can be halved.
The innovative idea in WNR is to use in each
step of NR the Wirtinger derivatives and Wirtinger
Jacobian instead of their classic derivatives and Ja-
cobian. Consequently, instead of the linear system
J ·dz = −f(z), the new system solved in each step
of WNR is:
J
W
·
dz
dz
!
= −
f(z)
f(z)
!
(7)
Moreover, exploiting the particular structure of
J
W
, we manage to obtain a new formulation of the
linear system based on real numbers (7). Thanks to
this real formulation the new approach can be easily
implemented and the results can be achieved with less
calculations than using the complex version. Here are
the steps to get the final formulation used in WNR:
1. following by (6), J
W
can be written as:
J
W
=



∂
W
f
∂z
∂
W
f
∂z

∂
W
f
∂z
 
∂
W
f
∂z




=
A
B
B A
!
(8)
2. if a matrix presents a structure like the one de-
scribed in (8), it can be transformed into a centro-
hermitian matrix (Lee, 1980), defined as:
M ∈ C
m,m
|M
i j
= M
m+1−i,m+1−j
, for 1 ≤i, j ≤ m
(9)
The transformation passes through the indexes
permutation:
π : i 7→ 3n + 1 −i for n < i ≤ 2n (10)
that inverts the order of the last n rows or columns.
In order to transform J
W
into a centrohermitian
matrix, π has to be applied to both its rows and
columns. The best way to do that is considering
the matrix associated to the permutation π, given
by:
P
π
=
I
n
0
n
0
n
J
n
!
∈ R
2n,2n
(11)
where I
n
and J
n
are the identity and exchange ma-
trix, respectively, defined as follows:
I
n
=
1
0
.
.
.
0
1
!
, J
n
=
0
1
.
.
.
1
0
!
∈R
n,n
(12)
Hence, the centrohermitian transformation of J
W
is obtained by left and right multiplying J
W
by the
permutation matrix P
π
, so that:
P
π
A
B
B A
!
P
π
=
A
BJ
n
J
n
B J
n
AJ
n
!
(13)
that is a matrix satisfying (2) and, consequently, a
centrohermitian matrix;
Supporting CPS Modeling Through a New Method for Solving Complex Non-holomorphic Equations
683

3. every centrohermitian matrix M ∈C
m,m
is similar
to a real matrix (Lee, 1980), i.e., there exists a
matrix Q ∈ C
m,m
that is unitary (Q
−1
= Q
t
) and
for which Q
t
MQ ∈ R
m,m
.
Therefore, it is possible to find a real version of
the centrohermitian Wirtinger Jacobian obtained
in (13). In fact, when considering the unitary ma-
trix given by:
Q =
1
√
2
I
n
ıI
n
J
n
−ıJ
n
!
∈ C
2n,2n
(14)
the complex matrix described in (13) is similar to
the following real matrix:
Q
t


A
BJ
n
J
n
B
J
n
AJ
n


Q=


ℜ(A+B) ℑ(B−A)
ℑ(A+B) ℜ(A−B)


(15)
where ℜ(...) and ℑ(. . . ) indicate respectively the
real and imaginary part of a complex number;
4. the formulation based on real numbers of the sys-
tem (7) solved in each step of WNR can be ob-
tained by the transformations of J
W
described in
(13) and (3).
Starting from (7) written as:
A
B
B A
!
·
dz
dz
!
= −
F
F
!
(16)
where F = f(z), applying (13) to (16) gives:
A
BJ
n
J
n
B J
n
AJ
n
!
·
dz
J
n
dz
!
= −
F
J
n
F
!
(17)
Finally, the similitude introduced in (3) applied
to (4) returns:
ℜ(A+B) ℑ(B−A)
ℑ(A+B) ℜ(A−B)
!
·dw = −G (18)
where:
dw =
ℜ(dz)
ℑ(dz)
!
, G =
ℜ(F)
ℑ(F)
!
(19)
Hence, (18) can be used as real formulation of the
linear system in each step of WNR that, consequently,
can be described using only real quantities.
3.2 MATLAB Functions for WNR
The modeler can ignore the mathematical details pre-
sented in Subsection 3.1 since they are all collected
in the functions wfunc, wjeval and wstep of WNR.
In fact, these functions can be implemented directly
using the results of Section 3.1 and in particular the
matricial equation (18).
Their descriptions and MATLAB implementa-
tions are given by:
• wfunc: this function takes the current evaluation
F of f and returns the vector G that appears in the
right-hand side of (18) and that is described in
(19), so that:
function G = wfunc(F)
G = [real(F);
imag(F) ];
• wjeval: calling J the real Wirtinger Jacobian de-
fined in (3) and used in (18) , wjeval is defined
as:
function J = wjeval(z, F, par)
n = length(z);
W = wJ(z,F,par);
A = W(1:n, 1:n);
B = W(1:n, n+1:2*n);
J = [real(A+B), imag(B-A);
imag(A+B), real(A-B) ];
The function wJ evaluates the Wirtinger Jacobian
by computing the Wirtinger derivatives, that can
be implemented in two different ways:
(i) by using the definition (4) with MATLAB
built-in real derivatives, after writing the variables
with their real and imaginary parts;
(ii) by exploiting built-in complex derivatives with
respect to the variables while considering their
conjugates constant and vice versa;
• wstep: this function converts back to dz the result
dw = -(J \ G) of the linear system (18), and is
given by:
function dz = wstep(dw)
n = length(dw)/2;
dz = dw(1:n) + 1i*dw(n+1:2*n);
This is because dw, as described in (19), contains
ℜ(dz) and ℑ(dz).
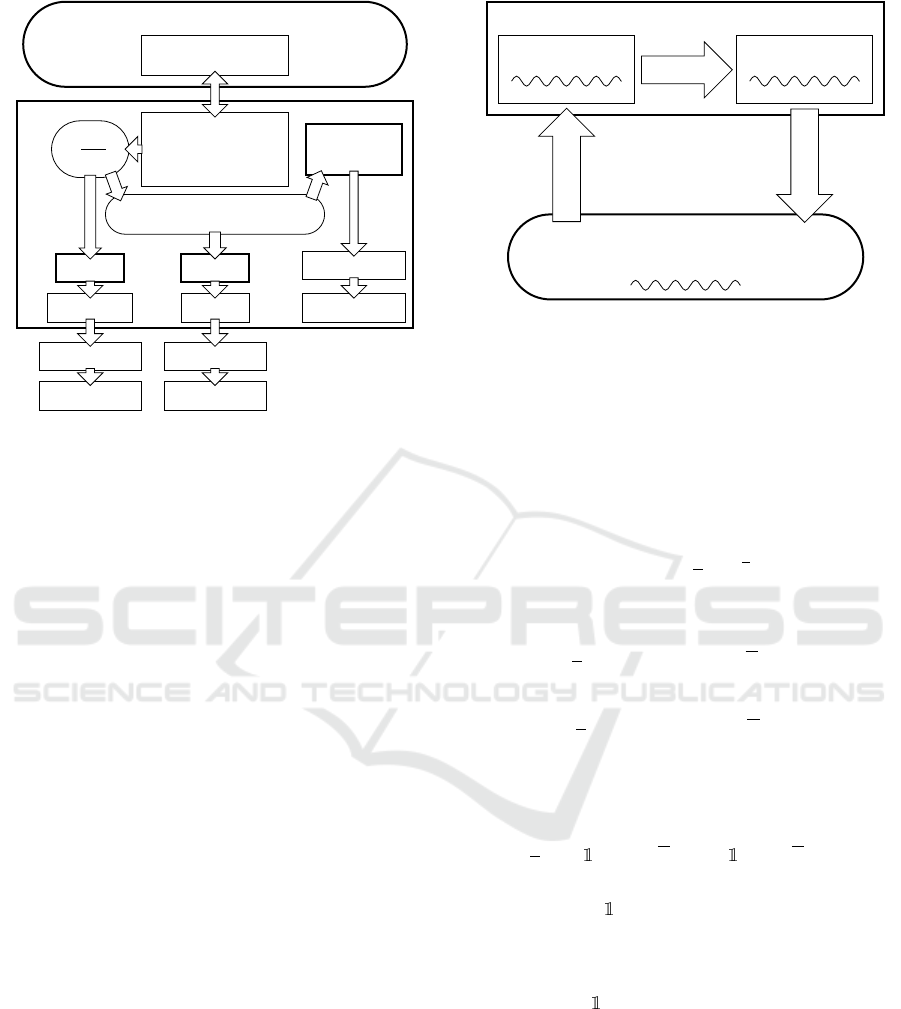
In Figure 1 the possible choices of the modeler
are schematically presented. It is important to ob-
serve that, when NR or WNR can be used, the mod-
eler has only to define the functions that evaluate f and
its (classical or Wirtinger) derivatives. Conversely, if
the modeler chooses or is obliged to use an ad hoc
method, a specific formulation for the constraints has
to be found and the corresponding ad-hoc solving pro-
cedure has to be developed and implemented.
4 CASE STUDY
The CPS adopted as case study to illustrate the pro-
posed method is presented in the following. In order
to deal with a simple, and at the same time general,
scenario, the focus here is only on the cyber part of
AMARETTO 2018 - Special Session on domAin specific Model-based AppRoaches to vErificaTion and validaTiOn
684

Cyber Physical System
Constraints
Modeler Intervention







f
1
(z
1
, z
2
, . . . , z
n
) = 0
.
.
.
f
m
(z
1
, z
2
, . . . , z
n
) = 0
∃
∂f
i
∂z
j
?
f
i
non-holomorphic real analytic?
NR
feval, jeval
Formulation
Implementation
WNR
feval, wJ
Formulation
Implementation
Ad hoc
method
Formulation
Implementation
YES
NO
YES
NO
Figure 1: Diagram describing how the the modeler is sup-
ported by the proposed WNR approach, compared with NR
and ad hoc methods, in the overall process of modeling and
solving constraints of CPSs.
the system, abstracting away the details of the physi-
cal part. The high level logical architecture, depicted
in Figure 2, includes a sensor, the control unit and an
actuator.
The sensor collects those data coming from the
environment that show periodic behavior and it is as-
sumed that the control unit receives a signal described
as a function of time t of the form:
u(t) =
n−1
∑
h=0
u
h
sin(hωt +φ
h
) = ℑ
n−1
∑
h=0
P
u,h
e
ıhωt
!
(20)
where P
u,h
= u
h
e
ıφ
h
∈ C is the phasor of module u
h
and phase φ
h
, as presented in (Arrillaga, 2003). Sup-
pose that u(t) is related but not equal to the actual
state of the controlled component, that is described
by a signal expressed as:
v(t) =
n−1
∑
h=0
v
h
sin(hωt +ψ
h
) = ℑ
n−1
∑
h=0
P
v,h
e
ıhωt
!
(21)
However, u
h
and φ
h
can change their values and
the aim of the control unit is to compute an estima-
tion ˜v(t) of v(t), i.e., new values of P
v,h
= v
h
e
ıψ
h
. If
˜v(t) is out of bounds, the control unit has to bring the
system back in a safe state sending instructions to the
actuator.
This case study is commonly encountered when
dealing with non-linear physical systems whose non-
linearities have to follow a prescribed behavior. The
control unit consists of an iterative process in which,
whenever the input signal is found to be unsafe, a new
Control Unit
u(t)
WNR
˜v(t)
Physical Component
v(t)
Sensor
Actuator
Figure 2: Simple diagram describing the case study.
setting of the parameters that describe v(t) has to be
found.
For the case study, the input signal u(t) and the
unknown state v(t) are related by:
u(t) = v(t)v(t) (22)
Since the imaginary part of a complex number z
can be calculated as:
ℑ(z) = −
ı
2
(z −z) (23)
the expressions in (20) and (21) can be written as:
u(t) = −
ı
2

n−1
∑
h=0
P
u,h
e
ıhωt
−
n−1
∑
h=0
P
u,h
e
−ıhωt

(24)
v(t) = −
ı
2

n−1
∑
h=0
P
v,h
e
ıhωt
−
n−1
∑
h=0
P
v,h
e
−ıhωt

(25)
Using (24) and (25) in (22), the phasors of u(t) in
relation to those of v(t) are given by:
P
u,h
=
ı
2
n−1
∑
k=0
h
k≥h

P
v,k
P
v,k−h
+
h>0
P
v,k
P
v,k−h

−
k≤h
P
v,k
P
v,h−k
i
(26)
where:
aQb
=
(
1 if a Q b
0 elsewhere
(27)
For h = 0,...,n −1, the n variables z
h
of z are the
phasors P
v,h
, while the n functions f
h
of f are:
f
h
(z) = f
h
(P
v,0
,...,P
v,n−1
) = P
u,h
−u
h
e
ıφ
h
(28)
where u
h
,φ
h
are constants and P
u,h
are given by (26).
The constraints f(z) = 0 originated assembly (26)
and (28), are non-linear non-holomorphic complex
equations.
Supporting CPS Modeling Through a New Method for Solving Complex Non-holomorphic Equations
685

0 5 10 15 20
0
1
2
3
t
u(t)
Figure 3: Input signal u(t) received from the sensor.
Notice that equation (26) can be directly translated
in MATLAB so that the implementation of WNR de-
scribed in Section 3 can be used.
In particular, as said in Subsection 3.2 and de-
picted in Figure 1, the modeler can ignore all the
mathematical passages and use directly the MAT-
LAB implementation presented. The only functions
to be determined to obtain the working solver WNR are
feval and wJ. feval can be directly obtained from
(26), so that the resulting implementation is given by:
function F = feval(z, par)
n = length(par);
Pu = par; % par = [P_{u,0};...;P_{u,n-1}]
Pv = z; % z = [P_{v,0};...;P_{v,n-1}]
F = zeros(n,1);
for h = 0:n-1
for k = 0:n-1
if (h <= k)
F(h+1) += Pv(k+1)*conj(Pv(k-h+1));
if (0 < h)
F(h+1) += Pv(k+1)*conj(Pv(k-h+1));
end
end
if (k <= h)
F(h+1) -= Pv(k+1)*Pv(h-k+1);
end
end
end
F = .5*i*F;
F = F - Pu;
end
The implementation of wJ needs to calculate
Wirtinger derivatives of f. As said in Subsection
3.1 Wirtinger derivatives can be computed by simply
deriving the function f with respect to the variables
z
h
= P
v,h
while considering their conjugates constant
and with respect to the variables z
h
= P
v,h
while con-
sidering P
v,h
constant. Starting from (26) and follow-
ing these instructions, the results are given by:
∂
W
P
u,h
∂P
v,k
=
ı
2

k≥h

P
v,k−h
+
h>0
P
v,k−h

−
k≤h
2P
v,h−k

∂
W
P
u,h
∂P
v,k
=
ı
2
k≤n−1−h
(P
v,k+h
+
h>0
P
v,k+h
)
(29)
0 5 10 15 20
0
1
2
3
t
v
0
(t)
Figure 4: Initial guess of the controlled component signal.
so that the implementation of wJ in MATLAB is:
function W = wJ(z,F,par)
n = length(par);
Pu = par; % par = [P_{u,0};...;P_{u,n-1}]
Pv = z; % z = [P_{v,0};...;P_{v,n-1}]
W = zeros(n,2*n);
for h=0:n-1
for k=0:n-1
if (h <= k)
W(h+1,k+1) += conj(Pv(k-h+1));
if (0 < h)
W(h+1,k+1) += conj(Pv(k-h+1));
end
end
if (k <= h)
W(h+1,k+1) -= 2*Pv(h-k+1);
end
if (k <= n-1-h)
W(h+1,n+k+1) += Pv(k+h+1);
if (0 < h)
W(h+1,n+k+1) += Pv(k+h+1);
end
end
end
end
W = .5*i*W;
end
In order to exercise the case study in a concrete
scenario, we consider the event in which n = 4 and the
input signal u(t) received from the sensor, as shown
in Figure 3, is given by:
P
u,0
= 1ı , P
u,1
= 0.5 ,
P
u,2
= −0.1ı , P
u,3
= 0.01
(30)
The initial guess v
0
(t) of the controlled compo-
nent signal is depicted in Figure 4 and characterized
by:
P
v
0
,0
= 1ı , P
v
0
,1
= 1 ,
P
v
0
,2
= 0.5ı , P
v
0
,3
= 1
(31)
Starting from v
0
(t) an estimation ˜v(t) of the com-
ponent signal has to be computed. Running WNR as
described in Section 3, with an imposed tolerance of
AMARETTO 2018 - Special Session on domAin specific Model-based AppRoaches to vErificaTion and validaTiOn
686

0 5 10 15 20
0
1
2
3
t
˜v(t)
Figure 5: Estimation of v(t) obtained with WNR.
0 5 10 15 20
0
1
2
3
t
˜v(t)˜v(t)
Figure 6: Plot showing that ˜v(t) ˜v(t) = u(t).
10
−6
, we obtain the new estimation ˜v(t) of v(t), with
parameters:
P
v,0
= 0.98394ı , P
v,1
= 0.24967 ,
P
v,2
= −0.03621ı , P
v,3
= 0.00968
(32)
so that the resulting signal is depicted in Figure 5.
As correctness proof, Figure 6 shows that the
product ˜v(t) ˜v(t) is a signal equal to u(t). WNR
reaches the correct estimation ˜v(t) in 8 steps, as
shown in Figure 7, that describes the behavior until
convergence of the error of each step of WNR, given
by the infinite norm of f(z).
5 CONCLUSIONS AND
FUTURE WORK
When numerically computing the physical part of a
CPS state, it could be needed to solve complex non-
holomorphic equations. This paper addressed this
class of equations and developed: i) a novel semiau-
tomatic procedure to transform their original formula-
tion into a new and more tractable form, and ii) a so-
lution method for this new formulation, implemented
in MATLAB.
The major principles the new solution is based on
are: Wirtinger calculus application and centrohermi-
0 1 2 3 4 5 6 7 8
10
−10
10
−7
10
−4
10
−1
10
2
iteration
||f(z)||
∞
Figure 7: Plot in logaritmic scale of the descending error in
WNR iterations.
tian structure exploitation. The idea is to define a gen-
eral procedure that can be followed by the modeler,
without concentrating on mathematical details except
for the definition of function f and derivatives compu-
tation, that can in many cases be performed symboli-
cally by MATLAB itself.
The advantage of the new proposed approach is
that the evolution of the states of the modeled CPS can
be described by changing the values of the parameters
of f, thus avoiding the complicated redefinition of the
solver.
Extensions of the presented study are foreseen in
several directions, including:
• performance of the new solution method has to
be investigated in comparison with other, ad-hoc,
strategies;
• automatic symbolic derivatives in the context of
Wirtinger calculus is a promising line of research
and can further automatize the approach presented
in this paper;
• the centrohermitian symmetry is not the only
structure that the Wirtinger Jacobian matrix
presents, thus a careful investigation of the prop-
erties of this matrix can lead to improved perfor-
mance of the proposed approach;
• the new solver can be customized to fulfill particu-
lar implementation needs, such as a reduced mem-
ory consumption. For example, the discussed case
study offers a sparse Jacobian matrix with a struc-
ture that can be further exploited using the native
sparse representation capabilities of MATLAB.
REFERENCES
Arrillaga, J. (2003). Power system harmonics. J. Wiley &
Sons, West Sussex, England Hoboken, NJ.
Avargel, Y. and Cohen, I. (2010). Modeling and identifi-
cation of nonlinear systems in the short-time fourier
Supporting CPS Modeling Through a New Method for Solving Complex Non-holomorphic Equations
687

transform domain. IEEE Transactions on Signal Pro-
cessing, 58(1):291–304.
Bejarano, J. D. and S
´
anchez, A. M. (1989). Generalized
fourier transforms for nonlinear systems. Journal of
Mathematical Physics, 30(8):1871–1876.
Broyden, C. G. (1965). A class of methods for solving non-
linear simultaneous equations. Mathematics of Com-
putation, 19(92):577–593.
Kelley, C. (1995). Iterative Methods for Linear and Non-
linear Equations. Society for Industrial and Applied
Mathematics.
Khalil, H. (2002). Nonlinear Systems. Pearson Education.
Prentice Hall.
Kreutz-Delgado, K. (2009). The Complex Gradient Opera-
tor and the CR-Calculus. ArXiv e-prints.
Lee, A. (1980). Centrohermitian and skew-centrohermitian
matrices. Linear Algebra and its Applications,
29(Supplement C):205 – 210. Special Volume Ded-
icated to Alson S. Householder.
MathWorks (2017). MATLAB version 9.3.0.713579
(R2017b). The Mathworks, Inc., Natick, Mas-
sachusetts.
NIST (2015). Framework for Cyber-Physical Systems.
Rizano, T., Passerone, R., Macii, D., and Palopoli, L.
(2011). Model-based design of embedded control
software for hybrid vehicles. In 2011 6th IEEE In-
ternational Symposium on Industrial and Embedded
Systems, pages 75–78.
Tasse, C. (2014). Applying wirtinger derivatives to the radio
interferometry calibration problem.
Wang, Z., Cui, B., and Wang, J. (2017). A necessary condi-
tion for power flow insolvability in power distribution
systems with distributed generators. IEEE Transac-
tions on Power Systems, 32(2):1440–1450.
AMARETTO 2018 - Special Session on domAin specific Model-based AppRoaches to vErificaTion and validaTiOn
688