Isolation Forest for Anomaly Detection in Raw Vehicle Sensor Data

Julia Hofmockel

and Eric Sax

Audi Electronics Venture GmbH, Gaimersheim, Germany

Institute for Information Processing Technologies, Karlsruher Institute of Technology, Karlsruhe, Germany

Keywords:

Anomaly Detection, Data Transfer, Isolation Forest.

Abstract:

A vehicle generates data describing its condition and the driver’s behavior. Sending data from many vehicles

to a backend costs money and therefore needs to be reduced. The limitation to relevant data is inescapable.

When using data collected from a vehicle ﬂeet, the normality can be learned and deviations from it identiﬁed

as abnormal and thus relevant. The idea of learning the normality with the Replicator Neural Network and

the Isolation Forest is applied to the identiﬁcation of anomalies and the reduction of data transfer. It is com-

pared how good the methods are in detecting anomalies and what it means for the trafﬁc between vehicle and

backend. It can be shown that the Isolation Forest beats the Replicator Neural Network. When reducing the

transfered amount of data to 7%, in average more than 80.63% of the given anomalies are included.

1 INTRODUCTION

In the automotive industry, the usage of data gener-

ated by vehicles offers new potential for the future.

By collecting and processing the data from many ve-

hicles on a backend, functions like autonomous driv-

ing or the improvement of the product in a technical

or costumer orientated way can be realized (see Fig.

1) (Gadatsch, 2017).

One challenge in this context is the amount of

data. Only in the internal communication system, one

vehicle alone produces up to 750 kilobytes per sec-

ond. Extrapolated to a ﬂeet of 150 vehicles, each driv-

ing one hour per day, up to 2.8 terabytes are produced

in one week. Transmitting all data from vehicle to

backed over air and store it there is not feasible, be-

cause of the transmission costs, data loss and the re-

quired preprocessing steps in the vehicle. One idea

to solve this issue is the focus on anomalies, because

they might represent interesting events and they bring

new information to the backend. An anomaly can be

deﬁned as an observation that deviates so much from

other observations as to arouse suspicion that it was

generated by a different mechanism (Hawkins, 1980).

This paper applies the idea of ﬁnding unusual ve-

hicle behavior as deviation from the normality deﬁned

by the raw vehicle sensor data from a vehicle ﬂeet.

The focus is in the application of the Isolation Forest

approach.

The paper is organized as follows: In Sect. 2

vehicle data

Figure 1: Collection of data via vehicle ﬂeet.

different methods for detecting anomalies are intro-

duced. Section 3 explains how the idea of anomaly

detection is applied on the vehicles sensor data. Ex-

periments and results are demonstrated in Sect. 4.

The paper ends with a conclusion and the description

of further research in Sect. 5.

2 STATE OF THE ART

Anomalies are detected in various domains as for

example to recognize attacks on a network (intru-

sion detection) or some kind of fraud regarding credit

card transactions. It is also applied in medicine to

detect diseases and unusual symptoms. Comparable

to anomalies in the vehicle sensor data is the detec-

tion of a defect sensor before the system breaks down

(Pahuja and Yadav, 2013; Pimentel et al., 2014; Gold-

stein and Uchida, 2016).

Model-based methods for anomaly detection are

one-class Support Vector Machines (SVMs) or Repli-

cator Neural Networks (ReplNN) (Chandola et al.,

2009). A newer method is the Isolation Forest (Ifor-

est) (Liu et al., 2008; Liu et al., 2012).

Hofmockel, J. and Sax, E.

Isolation Forest for Anomaly Detection in Raw Vehicle Sensor Data.

DOI: 10.5220/0006758004110416

In Proceedings of the 4th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2018), pages 411-416

ISBN: 978-989-758-293-6

411

In the one-class SVM, the smallest possible sphere

including all the normal data is found during train-

ing. In the application, data points outside of the

sphere are detected as abnormal (Tax and Duin, 2004;

Sch

olkopf et al., 2000).

While training a Replicator Neural Network, a

prediction function f (x) is learned, such that the dif-

ference between training point x ∈ R

, and its recon-

structed output f (x) =

x ∈ R

is minimized for all

x ∈ T , with T describing the training data and d the

number of features. The weights are learned with nor-

mal data and in the application the reconstruction er-

ror of test data point x

test

characterizes its anomaly

score. The reconstruction error is calculated as the

mean squared difference between the original value

and its reconstruction (Dau et al., 2014; Hawkins

et al., 2002):

||x

test

−

test

. (1)

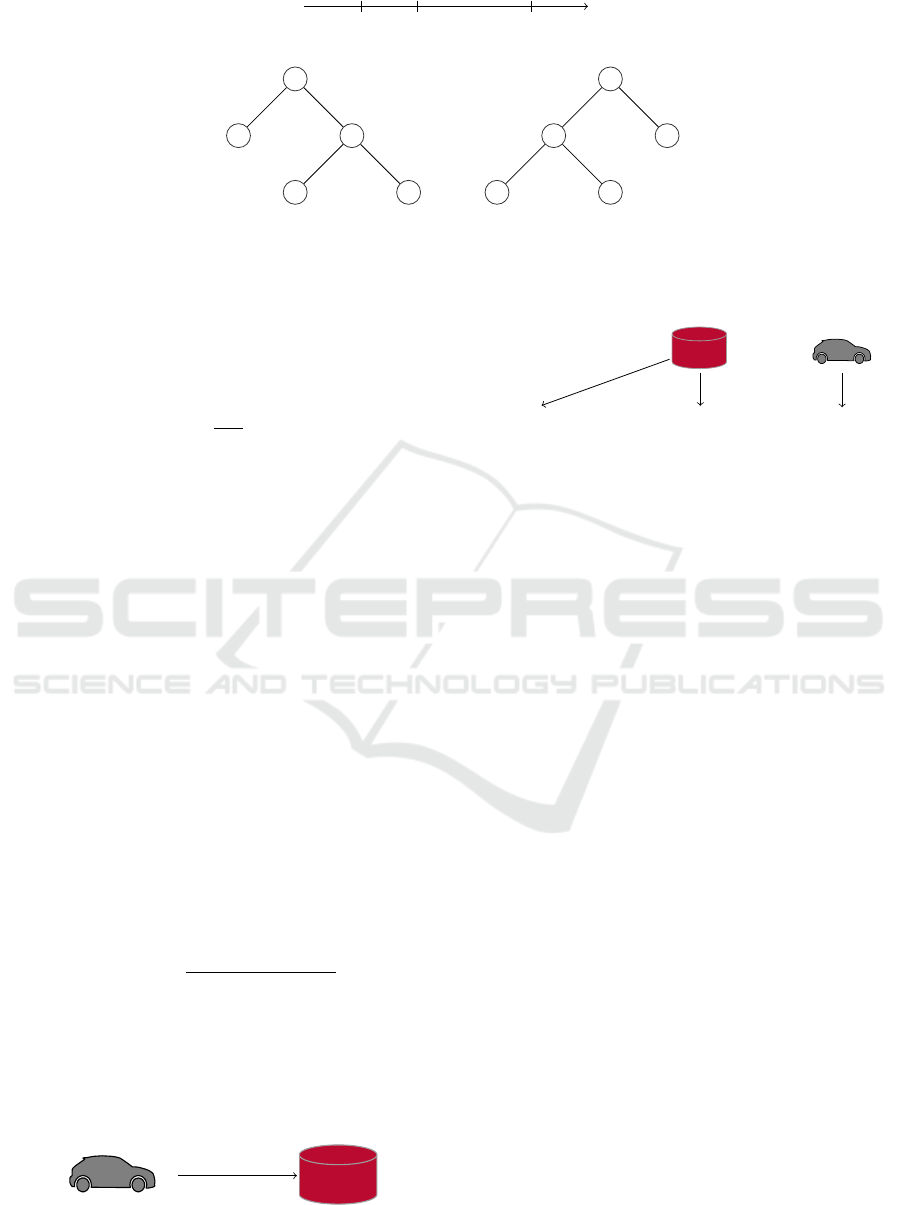
The Isolation Forest approach assumes that

anomalies are easier to isolate from the rest of the data

than normal instances (see Fig. 2) (Liu et al., 2008;

Liu et al., 2012).

Many binary trees are generated using different

subsamples of the training data T . Hereby splitting

feature and splitting value are chosen randomly (uni-

form distribution). The only parameters to deﬁne are

the number of trees (t) and the subsampling size (ψ).

As exemplary shown in Fig. 3, the tree where the

splitting value differentiates between normal and ab-

normal is more likely to be generated. That is why

the expected path length of an abnormal data point is

shorter than the path length of normal instances. Ac-

cordingly for the example (Liu et al., 2008; Liu et al.,

2012):

P(T

) < P(T

) =⇒ E(h

) < E(h

), (2)

with P(T

) describing the probability of tree T

and

E(h

) as the expected path length (h

) of data point x

i ∈ {0,1,2}:

E(h

) = P(h(x

) = 1) · 1 + P(h(x

) = 2) · 2. (3)

The average path length of the test data point

test

overall generated trees is used to calculate the

anomaly score. The smaller the score, the higher the

probability of being an anomaly (Liu et al., 2008; Liu

et al., 2012).

3 OUR CONTRIBUTION

For the anomaly detection in vehicle sensor data,

the concept of one-class classiﬁcation is employed.

Therefore data items are collected on the backend and

Figure 2: Isolation approach.

by assuming that most of them are normal, a refer-

ence model is learned (compare Fig. 1). In the ap-

plication phase, the model is applied in the vehicle to

detect deviations from the normal behavior as anoma-

lies (Chandola et al., 2009). This approach ensures

that after the training phase, data transfered between

vehicle and backend is restricted to unusual situations

not or rarely seen on the backend (see Fig. 4).

The paper analyses if the Isolation Forest is suit-

able to detect anomalies in raw vehicle sensor data

with the aim of reducing data transfer. For compari-

son, a Replicator Neural Network is trained and tested

additionally.

4 EXPERIMENTS AND RESULTS

To evaluate the methods for detecting anomalies in

raw vehicle sensor data, different datasets are used.

Based on data collected by a vehicle ﬂeet, the model

describing the normality is trained. Hereby it is as-

sumed that most of the data are normal, but the ground

truth is not known. For evaluation, different rides with

enforced anomalies like an accident, full breaking or

overspeed are under consideration. These rides are

completely labeled.

The analyzed data are the signals transfered

via the internal communication system in the vehi-

cle, more concrete via the Controller Area Network

(CAN-bus) (Winzker, 2017). These signals like ve-

locity, longitudinal/lateral acceleration, steering an-

gle/velocity, information about opened windows or

brake pressure describe driving and vehicle behavior.

4.1 Evaluation criteria

For the comparison of the Replicator Neural Network

and the Isolation Forest, the database X is split as

shown in Fig. 5. The training data T ⊂ X are as-

sumed to be normal and used to learn the reference

model. The validation data V ⊂ X\T is sampled from

the same database as the training data and is there-

fore also meant to be mostly normal. The proportion

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

412

(a) exempary dataset with three instances,

most unusual

(b) Tree T

, P(T

) = D

, P(T

) =

Figure 3: Example for understanding Isolation Forest, D

i j

is the distance from data point x

to point x

with D

< D

, (Liu

et al., 2012).

of detected anomalies in the validation data (γ) shows

how good the model generalizes and if it can be used

to reduce the data transfer:

γ =

|V |

, (4)

with V

describing the validation data detected as

anomaly.

Based on its anomaly score, an instance is pre-

dicted as abnormal if the score succeeds a deﬁned bor-

der τ.:

score > τ → anomaly. (5)

For τ, the 95%-quantile of the anomaly scores of the

training data (S(T )) is used because it ensures that

95% of the training data are classiﬁed as normal,

while the 5% most exceptional training data get ig-

nored. Thus, the assumption of exclusively normal

training data gets defused:

= Q

(S(T )). (6)

The border is also applied to classify the labeled test

data and to calculate Recall (fraction of correctly de-

tected anomalies among real anomalies) and Preci-

sion (fraction of correctly detected anomalies among

detected anomalies). Their harmonic mean is the F-

Score (Bekkar et al., 2013):

F-Score = 2

Recall · Precision

Recall + Precision

. (7)

Additionally, the Area Under the Curve (AUC) result-

ing from the Receiver-Operating-Characteristic curve

(ROC-curve) is calculated, because for this purpose

no concrete border needs to be set (Fawcett, 2006).

It can be evaluated if the anomaly score in general is

abnormal data

Figure 4: Reduction to anomalies in application phase.

training data (T )

validation data (V )

test data

Figure 5: Usage of given data.

suitable to sort the data points by normality and the

methods can be compared. The analysis is limited to

the test data completely labeled (see Fig. 5).

4.2 Database

Different datasets are used for evaluation. Table 1

clariﬁes that the nine test cases differentiate in the

amount of given data for training, the number of ana-

lyzed signals d and the enforced anomalies within the

test ride. The sampling rate is 100 milliseconds.

4.3 Results

The following section compares the Replicator Neu-

ral Network with the Isolation Forest. The Replicator

Neural Network consists of one hidden layer with d

neurons (T

oth and Gosztolya, 2004; Dau et al., 2014).

Our experiments have revealed that for the Isolation

Forest, t = 256 and ψ = 256 are the settings which

can’t be improved by further increase.

Table 2 shows the AUC for the different use cases

presented in Table 1. It can be identiﬁed that espe-

cially the accidents can be perfectly separated from

the remaining data due to an AUC equals 1. The Ta-

ble clariﬁes that the Isolation Forest has an high av-

erage AUC of 0.9080 which beats the ReplNN. In all

test cases the Isolation Forest achieves an AUC above

0.83. The only exception is test case K8. Here the

Replicator Neural Network performs better, but also

not well. Reason could be that for the high dimension

(d = 353), the amount of training data is not enough.

Isolation Forest for Anomaly Detection in Raw Vehicle Sensor Data

413

Table 1: Database for evaluation.

Driving time for

training [h]

Anomalies in test ride

137

accident

239

accident

enforced anomalies as drive with open doors, full

breaking, overspeed, ...

106

enforced anomalies as drive with open doors, full

breaking, close window with pinched book, ...

353

Electronic Stability Control (ESC) intervention

353

ESC intervention

161

Antilock Braking System (ABS) intervention

Shown by the remaining test cases, the Isolation For-

est provides a score, which is a suitable measurement

to sort data points by their normality.

When regarding the proportion of detected

anomalies in the validation data (γ), the Isolation For-

est sticks out to generalize quite well. The value of

γ = 0.0696 ﬁts the border τ

. When 95% of the

training data are classiﬁed as normal, 94.1% of the

validation data are also predicted to be normal. The

Replicator Neural Network with γ = 0.237 tends to

overﬁt and can not generally be applied to different

data than the training data. Accordingly, when ap-

plying the trained Isolation Forest in vehicles, only

6.96% of the data are identiﬁed as abnormal and

transmitted to the backend. The reduction of data

transfer is guaranteed. Recall and Precision explain

that in average 80% of the anomalies are detected and

transfered, but only 31.45% of the data are really ab-

normal. The classiﬁcation with the ﬁxed threshold

is not reliable and additionally the anomaly score

needs to be taken into account.

Figure 6 in the Appendix demonstrates which

anomalies are detected by the Isolation Forest with

threshold τ

. It can be seen that especially the ac-

cidents and safety interventions are identiﬁed. Less

extreme driving situations (e.g. full braking or over-

speed) are not categorized to be abnormal. Events like

window opening rear left are predicted as anomaly be-

cause they are rare in the training data T .

In summary, the results show that the amount of

data transfered from vehicle to backend can be re-

duced while ensuring that most of the abnormal sit-

uations are included. Furthermore, when considering

the anomaly score, the most abnormal situations can

directly be identiﬁed.

5 CONCLUSION

The paper introduces the idea of anomaly detection to

reduce the data transfer between vehicle and backend.

The investigations show that the anomaly score yield

by the Isolation Forest can be used to identify very

unusual situations and delivers better results than the

Replicator Neural Network. The deﬁnition of a score-

based border distinguishing between normal and ab-

normal is difﬁcult and depends on the use case.

By reducing data transfer to data detected as ab-

normal, up to 93% of trafﬁc can be saved. Hereby it

is ensured that most of the actual anomalies are trans-

mitted as well. The wrongly classiﬁed data points

can then be separated on the backend by their smaller

anomaly score.

The next steps will be further improvements of the

model. The investigation so far was reduced to static

events. Since the vehicle produces time dependent

data, an extension is necessary. Features describing

the time series need to be extracted.

REFERENCES

Bekkar, M., Djemaa, H. K., and Alitouche, T. A. (2013).

Evaluation measures for models assessment over im-

balanced data sets. Journal Of Information Engineer-

ing and Applications, 3(10).

Chandola, V., Banerjee, A., and Kumar, V. (2009).

Anomaly detection: A survey. ACM Comput. Surv.,

41(3):15:1–15:58.

Dau, H. A., Ciesielski, V., and Song, A. (2014). Anomaly

detection using replicator neural networks trained on

examples of one class. In Dick, G. and Browne,

Will N., e. a., editors, Simulated Evolution and Learn-

ing. SEAL 2014. Lecture Notes in Computer Science,

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

414

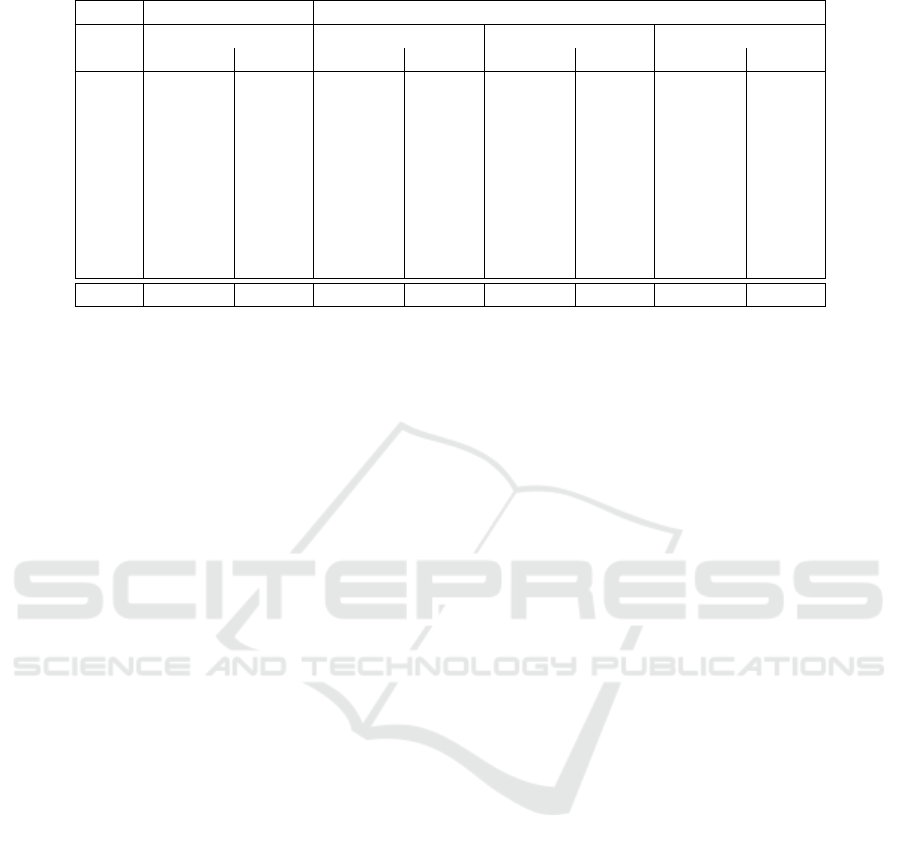
Table 2: Comparison: Replicator Neural Network vs. Isolation Forest.

τ = Q

(S(X))

AUC γ Recall Precision

ReplNN Iforest ReplNN Iforest ReplNN Iforest ReplNN Iforest

K1 1.0000 1.0000 0.2762 0.0444 1.0000 1.0000 0.0167 0.0270

K2 1.0000 1.0000 0.0912 0.1347 1.0000 1.0000 0.0909 0.0769

K3 1.0000 1.0000 0.5634 0.1773 1.0000 1.0000 0.0182 0.1429

K4 1.0000 0.9895 0.0699 0.0103 1.0000 1.0000 0.0400 0.3333

K5 0.7500 0.9356 0.1249 0.0833 0.7500 0.5833 0.6000 0.7778

K6 0.8126 0.8813 0.1192 0.0266 0.8182 0.5455 0.1765 0.5455

K7 0.8600 1.0000 0.6716 0.0693 1.0000 1.0000 0.3846 0.4545

K8 0.6690 0.5267 0.0998 0.0372 0.3590 0.1282 0.1458 0.4167

K9 0.8065 0.8387 0.1138 0.0430 1.0000 1.0000 0.0476 0.0556

mean 0.8776 0.9080 0.2367 0.0696 0.8808 0.8063 0.1689 0.3145

pages 311–322, Cham. Springer International Pub-

lishing.

Fawcett, T. (2006). An introduction to roc analysis. Pattern

Recogn. Lett., 27(8):861–874.

Gadatsch, A. (2017). Big Data – Datenanalyse als Ein-

trittskarte in die Zukunft, pages 1–10. Springer

Fachmedien Wiesbaden, Wiesbaden.

Goldstein, M. and Uchida, S. (2016). A comparative eval-

uation of unsupervised anomaly detection algorithms

for multivariate data. PLoS ONE, 11(4):1–31.

Hawkins, D. (1980). Identiﬁcation of Outliers. Springer

Netherlands.

Hawkins, S., He, H., Williams, G., and Baxter, R. (2002).

Outlier detection using replicator neural networks. In

Kambayashi, Y. and Winiwarter, Werner, e. a., editors,

4th International Conference on Data Warehousing

and Knowledge Discovery, pages 170–180, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Liu, F. T., Ting, K. M., and Zhou, Z.-H. (2008). Isolation

forest. In IEEE International Conference on Data

Mining 2008, ICDM ’08, pages 413–422, Washing-

ton, DC, USA. IEEE Computer Society.

Liu, F. T., Ting, K. M., and Zhou, Z.-H. (2012). Isolation-

based anomaly detection. ACM Trans. Knowl. Discov.

Data, 6(1):3:1–3:39.

Pahuja, D. and Yadav, R. (2013). Outlier detection for dif-

ferent applications:review. International Journal of

Engineering Research & Technology, 2.

Pimentel, M. A. F., Clifton, D. A., Clifton, L., and

Tarassenko, L. (2014). Review: A review of novelty

detection. Signal Process., 99:215–249.

Sch

olkopf, B., Williamson, R. C., Smola, A. J., Shawe-

Taylor, J., and Platt, J. C. (2000). Support vector

method for novelty detection. In Solla, S. A., Leen,

T. K., and M

uller, K., editors, Advances in Neural

Information Processing Systems 12, pages 582–588.

MIT Press.

Tax, D. M. J. and Duin, R. P. W. (2004). Support vector data

description. Mach. Learn., 54(1):45–66.

oth, L. and Gosztolya, G. (2004). Replicator neural net-

works for outlier modeling in segmental speech recog-

nition. In Yin, F.-L., Wang, J., and Guo, C., editors,

Advances in Neural Networks – ISNN 2004, pages

996–1001, Berlin, Heidelberg. Springer.

Winzker, M. (2017). Bussysteme in der Automobiltech-

nik, pages 175–179. Springer Fachmedien Wiesbaden,

Wiesbaden.

Isolation Forest for Anomaly Detection in Raw Vehicle Sensor Data

415

APPENDIX

Figure 6: Detected anomalies sorted by anomaly score.

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

416