Using Machine Learning for Recommending Service Demand Estimation

Approaches - Position Paper

Johannes Grohmann, Nikolas Herbst, Simon Spinner and Samuel Kounev

Universit

at W

urzburg, Am Hubland, 97074 W

urzburg, Germany

Keywords:

Service Demand Estimation, Machine Learning, Approach Selection, Service Modeling.

Abstract:

Service demands are key parameters in service and performance modeling. Hence, a variety of different

approaches to service demand estimation exist in the literature. However, given a speciﬁc scenario, it is not

trivial to select the currently best approach, since deep expertise in statistical estimation techniques is required

and the requirements and characteristics of the application scenario might change over time (e.g., by varying

load patterns). To tackle this problem, we propose the use of machine learning techniques to automatically

recommend the best suitable approach for the target scenario. The approach works in an online fashion and

can incorporate new measurement data and changing characteristics on-the-ﬂy. Preliminary results show that

executing only the recommended estimation approach achieves 99.6% accuracy compared to executing all

approaches available, while speeding up the estimation time by 57%.

1 INTRODUCTION

Optimizing performance of applications in modern

day cloud environments usually aims at minimizing

the allocated resources while still complying with cer-

tain Service Level Objectives (SLOs). Service de-

mands (also known as resource demands) can help to

reach that goal. A service demand is the average time

a unit of work (e.g., request or transaction) spends

obtaining service from a resource (e.g., CPU or hard

disk) in a system over all visits excluding any wait-

ing times (Menasc

e et al., 2004). Requests can be

grouped into different workload classes with similar

service demands.

Timely and precise service demands can be uti-

lized by other tools optimizing the resource alloca-

tion in a cloud environment, including proactive auto-

scaling mechanisms used for elastic resource provi-

sioning (Bauer et al., 2017), stochastic performance

models such as Queueing Networks (QN) (Bolch

et al., 1998), Queueing Petri Nets (QPN) (Bause,

1993), or architecture-level performance models such

as the Descartes Modeling Language (DML) (Kounev

et al., 2016).

Over the years, a number of approaches to Service

Demand Estimation (SDE) have been proposed using

different statistical estimation techniques (e.g., linear

regression (Rolia and Vetland, 1995; Brosig et al.,

2009) or Kalman ﬁlters (Wang et al., 2012; Zheng

et al., 2008) and based on different laws from queue-

ing theory. When selecting an appropriate approach

for a given scenario, a user has to consider different

characteristics of the estimation approach, such as the

expected input parameters, its accuracy and its robust-

ness to measurement anomalies. Depending on the

constraints of the application context, only a subset of

the estimation approaches may be applicable (Spinner

et al., 2015).

Naturally, one wants to select the suitable (e.g.,

best, fastest or a combination of both) approach for

a given scenario. This is especially challenging in

online settings, where the load patterns, the system

structure and even the application architecture and

therefore the characteristics of the service demand es-

timates may not be known in advance and may change

frequently. This also eliminates the possibility for an

expert guess, since this guess has to be repeated in

certain periods.

We therefore propose the use of machine learn-

ing techniques to select the suitable approach in this

context. Given a representative data set, we can train

different Machine Learning Algorithms (MLAs) with

the performance and the time-to-result of different

estimators. During live production, the pre-trained

MLA can be used to predict the most suitable ap-

proach (subject to certain criteria) in the current sce-

nario.

This work aims at providing a proof-of-concept.

Our contributions in this paper are:

1. We list the features that proved to be useful for the

Grohmann, J., Herbst, N., Spinner, S. and Kounev, S.

Using Machine Learning for Recommending Service Demand Estimation Approaches - Position Paper.

DOI: 10.5220/0006761104730480

In Proceedings of the 8th International Conference on Cloud Computing and Services Science (CLOSER 2018), pages 473-480

ISBN: 978-989-758-295-0

473

recommendation of SDE approaches.

2. We evaluate three MLAs (Decision Tree (DT),

Support Vector Machine (SVM), Neural Network

(NN)) with regard to their recommendation capa-

bilities.

3. We show the beneﬁt (time saving) and the draw-

back (accuracy loss) of recommendation for SDE.

The remainder of the paper is structured as fol-

lows. We list the related work and the approaches

considered in this paper in Section 2. Section 3 ex-

plains our approach in more detail. We present pre-

liminary results in the ofﬂine scenario in Section 4

and give a small outlook into our future planned work

in Section 5. We summarize our statements in Sec-

tion 6

2 RELATED WORK

Next to Filling-the-Gap (Wang et al., 2015), the only

publicly available tool providing different ready-to-

use approaches to service demand estimation is the

Library for Resource Demand Estimation (LibReDE)

by (Spinner et al., 2014).

LibReDE currently sup-

ports implementations of the following eight estima-

tion approaches:

• Service Demand Law (Brosig et al., 2009)

• Approximation with response times (Brosig et al.,

2009)

• Least Squares (LSQ) regression using queue-

lengths and response times (Kraft et al., 2009)

• LSQ regression using utilization law (Rolia and

Vetland, 1995)

• Kalman Filter (KF) using utilization law (Wang

et al., 2012; Wang et al., 2011)

• KF using response times and utilization (Zheng

et al., 2008; Kumar et al., 2009)

• Recursive optimization using response

times (Menasc

e, 2008)

• Recursive optimization using response times and

utilization (Liu et al., 2006)

Further approaches for SDE can be found in this

survey (Spinner et al., 2015). For lack of space,

we can not go into detail about the used approaches

and refer to the original papers or the LibReDE user

guide (Spinner et al., 2014).

LibReDE: Available for download at

http://descartes.tools/librede.

Note that there are different methodologies (sim-

ple approximation, LSQ regession, KF and mathe-

matical optimization) involved. This leads to a wide

diversity in terms of run-time and estimation quality

in different scenarios. This was established by com-

paring the performance of the estimators in different

scenarios, e.g. by varying resource utilization or the

number of workload classes (Spinner et al., 2015).

Linear Regression (LR) techniques were quite

thoroughly investigated in literature, including the im-

pact of different factors and limitations of LR in ser-

vice demand estimation (Rolia and Vetland, 1995;

Rolia and Vetland, 1998; Paciﬁci et al., 2008; Casale

et al., 2008; Casale et al., 2007; Stewart et al., 2007).

Other works compare LSQ regression with Maximum

Likelihood Estimation (MLE) (Kraft et al., 2009)

or Independent Component Analysis (ICA) (Sharma

et al., 2008). The performance of KFs for service

demand estimation is investigated by (Zheng et al.,

2005; Zheng et al., 2008; Kumar et al., 2009).

In our prior work (Grohmann et al., 2017), we

used generic optimization methods to optimize the

parameter settings of the aforementioned approaches

for the given target scenario. Our work in this paper

can be seen as orthogonal and complementary to this,

since the recommendation uses the approaches as-is.

3 APPROACH SELECTION

METHODOLOGY

This section describes our idea for using MLAs for

the selection of SDE approaches at run-time.

In order to be able to predict the best SDE ap-

proach, we need to create a model on a labeled train-

ing set. This training set consists of time series of sys-

tem metrics. We use these traces to estimate service

demands using the different approaches and validate

the results via cross-validation.

After running all estimation approaches, we can

extract several features about each trace. These fea-

tures can be used to characterize and categorize the

traces. The MLAs are fed with the extracted features,

as well as with the approach that worked best on the

respective trace. After the training is completed, the

deﬁned features can also be extracted for new and

so far unseen traces. With these, the trained MLAs

model can predict the approach that should work best

on the respective trace.

We deﬁne the machine learning problem as a

classiﬁcation problem. We have a labeled data set

{(x

),...,(x

)} assigning each feature vector

a label y

. The label represents the best SDE ap-

proach in the given situation (based on the minimum

CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science

474

cross-validation error). Given that we consider 8 dif-

ferent SDE approaches in our experiments, we dis-

tinguish between 8 different classes. The vectors x

contain one real number for each feature, i.e. x

∈ R

where k is the number of features.

After the training is complete, the obtained model

can be used to select the best suitable SDE approach

at run-time. The training set can consist of an ofﬂine

data set, which was collected beforehand or it can

be extended dynamically in an online fashion. If

the training set is augmented during live production,

training processes can be repeated arbitrarily often al-

though this might take up some time depending on the

size of the training set and the complexity of the used

features.

The intervals of when a current trace should be

archived to the training set, when the model should

be retrained and when the selection of the current ap-

proach should be executed are variable. This opens

room for conﬁguration and experimentation.

Note that due to the use of cross-validation to rank

the different SDE approaches, no manual labeling or

interaction is required during the creation of the train-

ing set. (Since all approaches can be tried and the

one with the highest score is chosen.) Hence, large

amounts of data from different computing clusters of

the cloud can be used as training set very easily. Also,

the model is able to increase it’s training set continu-

ously during production and therefore learn from its

own mistakes.

We list the features, we consider in Section 3.1 and

describe different MLAs we use for recommendation

in Section 3.2

3.1 Features

This section contains the list of features we extract to

train the algorithms. Features are certain characteris-

tics of the input traces used by the system to extract

knowledge about the traces.

The MLAs are heavily dependent on those fea-

tures and a careful selection as well as the right

amount is crucial for a satisfactory outcome. Since

the MLAs try to distinguish between different classes

of traces, too many features can actually be harm-

ful. However, it is generally a good idea to collect

as many features as possible at ﬁrst and then decide

later, which are the most informative. In some cases,

this decision can even be left to the MLA itself.

In the following, trace refers to one training ex-

ample of our data set. A trace usually consists a time

series of the CPU-utilization of each resource, the re-

sponse time and the arrival rate of each request of

the respective workload classes for feature generation.

The CPU-utilization measures the average utilization

of the CPU for a certain interval, the response time

contains the response time of each request and the ar-

rival rate holds the number of incoming requests for

a certain interval. These traces are given to the SDE

approaches for their estimations. For each trace, we

want to create a feature representation y

(see previous

section) that captures the characteristics of this trace.

Furthermore, we have some general meta-

information about the traces holding the number of

resources (e.g. number of CPUs and/or CPU cores)

and the number of different workload classes (i.e. dif-

ferent request types/methods). The number of work-

load classes already has a direct impact on the perfor-

mance of the estimators as shown by (Spinner et al.,

2015). Therefore, we include this meta-information

as features.

Additionally, we extract statistical information

about the traces as features. (Spinner et al., 2015)

show for example that the utilization has a signiﬁcant

impact on some of the estimators. It is therefore use-

ful to include information about the average utiliza-

tion of the available resources as well as the minimum

and the maximum utilization.

However, it does not seem useful to average this

information over all resources. Especially the differ-

ent workload classes are characteristic for having dif-

ferent values. We therefore deﬁne a set of statistical

features, extract those for each resource (utilization

features) and workload class (arrival rate and response

time features) and concatenate them to one feature

vector y

This limits the number of maximum resources and

workload classes to process. In order to be able to

concatenate all features to one vector, we need to de-

ﬁne a maximum number of resources and workload

classes used for training. If a trace has less statisti-

cal features, the remaining values can be ﬁlled with

zeros.

The extracted statistical features for the set of data

points d = (d

,...,d

) are:

The number of samples n per trace.

The arithmetic average: d =

∑

i=1

The geometric average:

d = (

∏

i=1

)

The standard deviation: σ =

∑

i=1

− d)

The quadratic average or Root Mean Square (RMS):

rms



+ d

+ ··· + d



The minimum value in d.

The maximum value in d.

Using Machine Learning for Recommending Service Demand Estimation Approaches - Position Paper

475

The kurtosis of d, a measure for the tailed-

ness of the graph of d, see (Westfall, 2014):

k =

∑

i=1

−d)



∑

i=1

−d)



− 3.

The skewness of d, a measure for asymme-

try. See (Joanes and Gill, 1998): s =

∑

i=1

−d)

n−1

∑

i=1

−d)

3/2

The 10

percentile. Below this point are 10% of the

total points in d.

The 90

percentile. Below this point are 90% of the

total points in d.

Omitted features: Furthermore, it seems useful

to include correlation information about the traces.

However, as the whole idea of the online selection is

to improve the speed of the SDE, the feature calcula-

tion (which is done online as well) has to be reason-

ably fast as well.

We experimented with features regarding the cor-

relations and the covariances between the traces, the

Variance Inﬂation Factor (VIF) and information about

the statistical distributions. However, those are costly

to calculate and as they did not show any improve-

ments in our experiments, we decided not to include

them in the feature set. Instead, we focus on the fea-

tures mentioned above. For the results of the aug-

mented feature set, see (Grohmann, 2016).

The total number of features is therefore k = 2 +

11 · r + 22 · w, with r being the number of resources

and w being the number of workload classes in the

training set.

3.2 Algorithms

For our proof-of-concept, we limit ourselves to im-

plement three MLAs..

Decision Tree: DTs are a well-known and intuitive

way to cluster information that is quite easy to under-

stand for a human supervisor (Breiman et al., 1984).

For splitting decisions we use the Gini impurity I

by (Breiman et al., 1984). It measures how pure a

split is, i.e. the average probability of an an element

of the node to be labeled wrong if it was randomly

classiﬁed according to the relative frequencies of the

node. It is calculated with

( f ) =

∑

i=1

(1 − f

), (1)

if J is the number of classes and f

the fraction of

classes labeled with label i, i.e. the probability to ran-

domly draw class i for a given element. Note that I

reaches its minimum value at zero if all the elements

belong to the same class. The Gini impurity has there-

fore to be minimized, in order to create pure trees.

To avoid over-ﬁtting, we limit the amount of nodes

in the DT to 100.

Support Vector Machines: SVMs have many pa-

rameters and conﬁguration options (Russell and

Norvig, 2009). The correct conﬁguration of them

poses an optimization problem itself. For our experi-

ments we use a Gaussian kernel function

K(x,y) = exp

kx + yk

, (2)

with σ = 8 and a soft-margin penalty of 5. We face the

multi-class problem with the one-vs-all strategy. Ac-

cording to a small grid-search, this proved to perform

best on our data set.

Neural Networks: Our implementation of a NN

is a multi-layer sigmoid-perceptron with its nodes

fully connected by acyclic arcs, prohibiting feedback

loops. We decided to use two inner layers (since two

inner layers are enough to represent any kind of func-

tion (Cybenko, 1988)), resulting in a total of four lay-

ers if we add the input and the output layer. We limit

ourselves to 100 neurons excluding the input layer in

order to ensure the fast processing of the recommen-

dation algorithm. Therefore, we kept the number or

neurons (and especially the number of layers) reason-

ably small.

The output layer consists of one node for each

available estimator (currently eight), resulting in 46

fully connected nodes for each of the inner layers.

We use the back-propagation algorithm (Bryson

and Ho, 1969) with ﬁve epochs for training. LSQ

serves as error function and the sigmoid function in

equation 3 as activation function for each neuron:

S(t) =

1 + e

−t

. (3)

The sigmoid function is a popular choice in the litera-

ture as it offers nice mathematical properties (Russell

and Norvig, 2009).

For selection, every output neuron represents one

approach. The NN recommends the approach with

the highest value of its respective output node.

CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science

476

4 EXPERIMENTS IN OFFLINE

SCENARIO

In this section, we evaluate the performance of the dif-

ferent MLAs selecting or recommending SDE tech-

niques. We compare the estimation error as well as

the run-time when running all approaches in parallel

vs recommending one approach and running just this

one. We distinguish between the utilization error E

and the response time error E

as deﬁned in the fol-

lowing section, since different use cases stress both

errors differently.

Note that the experiments in this section just con-

sider the ofﬂine case (existing non-changing data set)

which leads to better replicability and transparency.

However, the result are still transferable to an online

scenario.

4.1 Experiment Design

Our training set consists of measurements obtained

from running micro-benchmarks on a real system.

The micro-benchmarks generate a closed workload

with exponentially distributed think times and service

demands. As mean values for the service demands,

we selected 14 different subsets of the base set [0.02s,

0.25s, 0.5s, 0.125s, 0.13s] with number of workload

classes C = {1,2,3}. The subsets were arbitrarily

chosen from the base set so that the service demands

are not linearly growing across workload classes. The

subsets intentionally also contained cases where two

or three workload classes had the same mean value

as service demand. The mean think times were deter-

mined according to the targeted load level of an exper-

iment. We varied the number of workload classes C =

{1,2,3} and the load level U = {20%, 50%, 80%}

between experiments. The traces were already used

by (Spinner et al., 2015), where a more detailed de-

scription of the test environment can be found.

In total, 210 traces of approximately one hour run-

time were collected: They were randomly split into

training (80%) and validation set (20%), resulting in

a total of 168 training traces and 42 validation traces.

Therefore, we execute all estimation algorithms on

the 168 training traces, extract the features and use

those pairs to train the different MLAs. After that,

we show the trained algorithm one of the 42 valida-

tion traces and compare its prediction with the actual

performance of the different estimators.

The run-time measurements include feature ex-

traction, MLA execution and SDE of the selected ap-

proach. The training, the recommendation and the es-

timations are performed on a virtual machine hosted

on a XenServer hypervisor. The VM i srunning Win-

dows 10 (64 Bit), assigned with 6 Cores of an Intel



Xeon



E5-2640 v3 @ 2,6 GHz processor and 32 GB

of RAM.

For error analysis we separate between the relative

response time error E

and the absolute utilization er-

ror E

shown in Equation 4:

∑

c=1



− R



∑

c=1

) −U



(4)

with C being the number of workload classes, R

the average measured response time of workload class

c over all resources,

the predicted average response

time based on the estimated service demands, X

the

measured throughput of workload class c,

the esti-

mated service demand of workload class c and U the

average measured utilization over all resources.

4.2 Experiment Results

Table 1 shows the results of the different MLAs. We

compare the three approaches DT, SVM and NN in-

troduced in Section 3.2 with the default variant. The

default executes all approaches at the same time and

chooses the one with the best accuracy (after all ap-

proaches ﬁnish) based on their cross-validation re-

sults. In practice, this is a reasonable approach,

since the use of parallelization makes this feasible and

wrong/worse predictions can be quite costly. We refer

to this method as a-posteriori and use it as baseline.

Next to the time spent training, the improvements

of error and estimation time, we show the hit-rate of

each algorithm. By hit-rate we refer to the ratio of

traces in which the MLA actually recommended the

approach that proved to be the one with the best accu-

racy, i.e., the one chosen by a-posteriori.

If we ﬁrst look at the training times of all three

algorithms, we see that the required training time is

comparable along the algorithms. Surprisingly, NN is

notably faster than the other two approaches. How-

ever, the training times are all acceptable in an online

scenario (given that the training can actually run in

the background).

After the training is complete, all recommendation

algorithms run faster than the a-posteriori algorithm,

since they only execute one algorithm instead of all.

This is not very surprising. However, it is nice to con-

ﬁrm that the feature generation and the execution of

the algorithm does not generate unsustainable over-

head. Again DT, SVM and NN behave comparably,

with NN in the lead.

Using Machine Learning for Recommending Service Demand Estimation Approaches - Position Paper

477

Table 1: Comparison of different recommendation approaches with the a-posteriori approach.

Algorithm A-posteriori DT SVM NN

Train time (hh:mm:ss) – 00:07:58 00:07:51 00:06:28

Avg. estimation time (ms) 1 751.21 914.05 997.69 746.26

Std. deviation of est. time 328.87 428.68 344.63 267.82

Rel. improvement to a-posteriori – 47.80% 43.03% 57.39%

Avg. estimation error 0.18 0.19 0.18 0.18

Std. deviation of est. error 0.07 0.08 0.07 0.07

Rel. improvement to a-posteriori – −3.51% −0.37% −0.37%

Hit-rate 1 0.74 0.62 0.62

However, the gain in estimation time is not as

great as one might expect. This is due to mainly

three reasons: First, as already mentioned, the fea-

ture generation and the actual recommendation intro-

duce some overhead in the estimation process. Sec-

ondly, the optimization approaches (see Section 2) are

considered to be the more accurate, but at the same

time the most expensive estimators. Due to its good

results, the MLAs tend to choose the optimization

approaches. Therefore, only the fast estimators are

saved which of course decreases the gain.

Lastly, while the relative gain of around 57% (for

NN) is quite notable, the short overall run-time of un-

der two seconds for the a-posteriori algorithm leads

to a relatively small absolute improvement of around

1 second. Note that the execution of all estimators

is usually much faster than the sum of all individual

estimation times, due to the use of multi-threading

and caching effects. However, with bigger or more

complex traces this gain will most probably increase,

since the fraction of time used for feature generation

decreases and the penalty for unnecessary estimation

runs increases due to increasing estimation time.

If we look at the estimation error, we observe

that all of our MLAs performed worse than the a-

posteriori algorithm. This is not surprising, as we

do not expect to be able to make a perfect predic-

tion for every trace. However, the relative errors are

quite small compared to the gain in estimation time.

The DT has an average estimation error of under 0.19

which is less than 4% worse than the baseline ap-

proach. SVM and NN perform even better. Their

average estimation error is only 0.4% higher than the

baseline error.

This is especially interesting, since DT actually

has a higher hit-rate than SVM and NN. It selects the

best approach in 76% of all cases, while the other two

approaches select only 62% times the best approach.

Nevertheless, performances of SVM and NN are bet-

ter. We conclude that both techniques make less fatal

mistakes: While DT makes less mistakes, the ones

it does are more severe and choose estimators that are

way worse than the best ones for the respective traces.

In contradiction, most cases where SVM and NN do

not choose the best estimator, they choose one that is

almost as good as the best for the analyzed scenario.

It is also interesting that NN and SVM perform

exactly identical on this test set. They probably learn

the same function, since our training set is very lim-

ited. To summarize, we can say that the NN esti-

mates more than twice as fast than the a-posteriori

algorithm, while delivering comparable results.

4.3 Threats to Validity

Although the presented results are quite promising,

we only showed analyses on one type of trace. We

want to increase variability (number and type of re-

sources or workloads) in future work, but believe this

preliminary results still prove our point.

We included only one individual train-

ing/recommendation run in Table 1. We repeated

the experiments several times with shufﬂed training

and validation data sets in order to validate the

results. However, the random shufﬂing of training

and validation data set made it impractical to add

different runs to our evaluation.

We did very limited amounts of feature engineer-

ing as well as algorithm parameter tuning. However,

we think that in this stage of the experiments and for

the limited amount of training data, this could very

easily lead to overﬁt to this kind of data.

5 NEXT STEPS

Our experiments show the applicability of the SDE

selection approach. We now address challenges for

the implementation of those approaches in an online

scenario with a distributed micro-service based appli-

cation architecture.

CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science

478

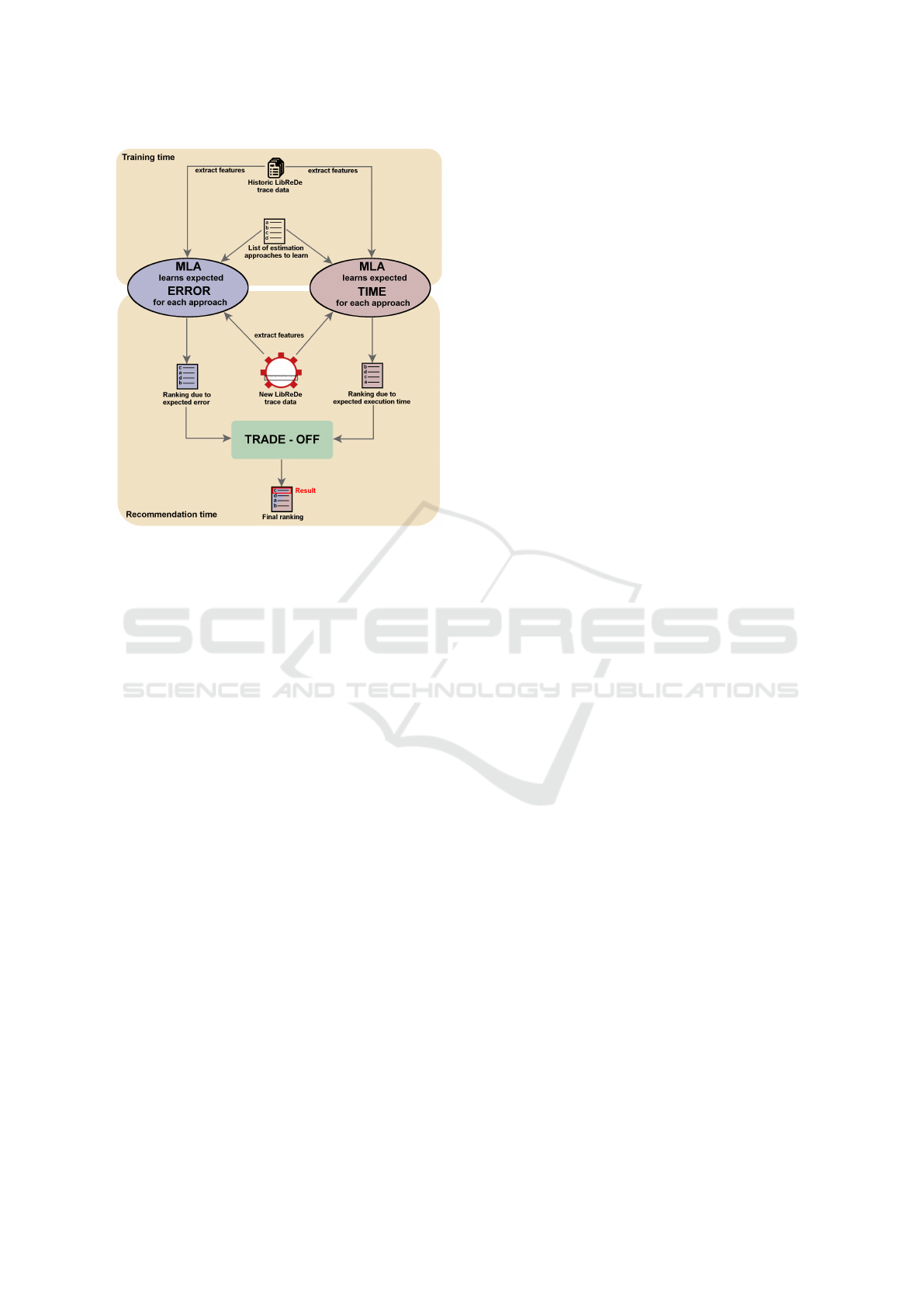
Figure 1: Conceptional overview over the envisioned trade-

off algorithm.

5.1 Trade-off Support

Section 4.2 shows that the best approach in terms

of accuracy is sometimes also the slowest approach.

Therefore, selecting the suitable approach poses a dif-

ferent challenge. What if the slowest approach is too

slow? What if the estimation is needed faster than

a given threshold or the second best (but way faster)

approach might work well enough for a speciﬁc sce-

nario?

To tackle this, we want to incorporate a trade-off

algorithm as shown in Figure 1. This algorithm basi-

cally consists of two complementary MLA, basically

regressing or ranking the different approaches by er-

ror and the run-time. (They in turn might consist of

multiple MLAs internally.) After doing so, an arbi-

trary decision process can be inserted to select be suit-

able approach based on the user.

However, this requires that both algorithms are ac-

curate enough to be trustworthy.

5.2 Towards Online SDE Selection

Some other challenges arise, when applying SDE in

an online fashion. As already mentioned in Sec-

tion 3, further questions have to be answered when

live data is incorporated into the training set: What

length should the traces be? How often should the

MLA be retrained? In which intervals should the se-

lection be repeated?

Further technical challenges involve proper par-

allelization (in order to train the MLAs in the back-

ground) as well as memory management and cut-off,

to avoid ever-increasing run-times.

We further plan to include the integration with

our optimization algorithms (Grohmann et al., 2017).

They optimize the parameter conﬁgurations based on

a historical data set. Although both approaches can

be used independently from each other, they comple-

ment each other really well. The optimization can

run in parallel to the recommendations and trigger a

retraining, if improved parameter settings have been

found.

6 SUMMARY

This paper introduces the use of Machine Learning

Algorithms in order to recommend or select the best

Service Demand Estimation approach. We develop a

feature set and evaluate the performance of Decision

Trees, Support Vector Machines and Neural Networks

on an ofﬂine data set.

The main takeaways are:

• The use of machine learning for the selection of a

Service Demand Estimation (SDE) approach can

improve the estimation time by more than 57%.

The resulting accuracy decrease is less than 0.5%.

• A relatively small set of statistical features is

enough to enable the selection algorithm of pro-

ducing reasonable selections.

• Our experiments show that NN and SVM are ca-

pable of producing excellent result, with NN be-

ing superior in run-time.

• Further work may support a treshold or trade-

off algorithm to recommend the best suitable ap-

proach in a time-critical scenario.

ACKNOWLEDGEMENTS

This work was co-funded by the German Research

Foundation (DFG) under grant No. (KO 3445/11-1)

and by Google Inc. (Faculty Research Award).

REFERENCES

Bauer, A., Herbst, N., and Kounev, S. (2017). Design and

Evaluation of a Proactive, Application-Aware Auto-

Scaler. In ACM/SPEC ICPE 2017.

Using Machine Learning for Recommending Service Demand Estimation Approaches - Position Paper

479

Bause, F. (1993). Queueing petri nets-a formalism for the

combined qualitative and quantitative analysis of sys-

tems. In Proceedings of the 5th International Work-

shop on Petri Nets and Performance Models, pages 14

– 23.

Bolch, G., Greiner, S., de Meer, H., and Trivedi, K. S.

(1998). Queueing Networks and Markov Chains:

Modeling and Performance Evaluation with Com-

puter Science Applications. Wiley-Interscience, New

York.

Breiman, L., Friedman, J., Olshen, R., and Stone, C. (1984).

Classiﬁcation and Regression Trees. Wadsworth and

Brooks, Monterey, CA.

Brosig, F., Kounev, S., and Krogmann, K. (2009). Auto-

mated Extraction of Palladio Component Models from

Running Enterprise Java Applications. In VALUE-

TOOLS ’09, pages 1–10.

Bryson, A. E. and Ho, Y.-C. (1969). Applied optimal con-

trol : optimization, estimation, and control.

Casale, G., Cremonesi, P., and Turrin, R. (2007). How to

Select Signiﬁcant Workloads in Performance Models.

In CMG Conference Proceedings.

Casale, G., Cremonesi, P., and Turrin, R. (2008). Robust

Workload Estimation in Queueing Network Perfor-

mance Models. In Euromicro PDP 2018, pages 183–

187.

Cybenko, G. (1988). Continuous valued neural networks

with two hidden layers are sufﬁcient. Technical re-

port, Department of Computer Science, Tufts Univer-

sity, Medford, MA.

Grohmann, J. (2016). Reliable Resource Demand Estima-

tion. Master Thesis, University of W

urzburg.

Grohmann, J., Herbst, N., Spinner, S., and Kounev, S.

(2017). Self-Tuning Resource Demand Estimation. In

IEEE ICAC 2017.

Joanes, D. and Gill, C. (1998). Comparing measures

of sample skewness and kurtosis. Journal of the

Royal Statistical Society: Series D (The Statistician),

47(1):183–189.

Kounev, S., Huber, N., Brosig, F., and Zhu, X. (2016).

A Model-Based Approach to Designing Self-Aware

IT Systems and Infrastructures. IEEE Computer,

49(7):53–61.

Kraft, S., Pacheco-Sanchez, S., Casale, G., and Dawson,

S. (2009). Estimating service resource consumption

from response time measurements. In VALUETOOLS

’09, pages 1–10.

Kumar, D., Tantawi, A., and Zhang, L. (2009). Real-time

performance modeling for adaptive software systems.

In VALUETOOLS ’09, pages 1–10.

Liu, Z., Wynter, L., Xia, C. H., and Zhang, F. (2006). Pa-

rameter inference of queueing models for IT systems

using end-to-end measurements. Perform. Evaluation,

63(1):36–60.

Menasc

e, D. (2008). Computing missing service demand

parameters for performance models. In CMG Confer-

ence Proceedings, pages 241–248.

Menasc

e, D. A., Dowdy, L. W., and Almeida, V. A. F.

(2004). Performance by Design: Computer Capac-

ity Planning By Example. Prentice Hall PTR, Upper

Saddle River, NJ, USA.

Paciﬁci, G., Segmuller, W., Spreitzer, M., and Tantawi, A.

(2008). CPU demand for web serving: Measurement

analysis and dynamic estimation. Perform. Evalua-

tion, 65(6-7):531–553.

Rolia, J. and Vetland, V. (1995). Parameter estimation

for performance models of distributed application sys-

tems. In CASCON ’95, page 54. IBM Press.

Rolia, J. and Vetland, V. (1998). Correlating resource de-

mand information with ARM data for application ser-

vices. In Proceedings of the 1st international work-

shop on Software and performance, pages 219–230.

ACM.

Russell, S. and Norvig, P. (2009). Artiﬁcial Intelligence:

A Modern Approach (3rd Edition). Prentice Hall, 3

edition.

Sharma, A. B., Bhagwan, R., Choudhury, M., Golubchik,

L., Govindan, R., and Voelker, G. M. (2008). Auto-

matic request categorization in internet services. SIG-

METRICS Perform. Eval. Rev., 36:16–25.

Spinner, S., Casale, G., Brosig, F., and Kounev, S. (2015).

Evaluating Approaches to Resource Demand Estima-

tion. Perform. Evaluation, 92:51 – 71.

Spinner, S., Casale, G., Zhu, X., and Kounev, S. (2014).

Librede: A library for resource demand estimation.

In ACM/SPEC ICPE 2014, ICPE ’14, pages 227–228,

New York, NY, USA. ACM.

Stewart, C., Kelly, T., and Zhang, A. (2007). Exploiting

nonstationarity for performance prediction. SIGOPS

Oper. Syst. Rev., 41:31–44.

Wang, W., Huang, X., Qin, X., Zhang, W., Wei, J., and

Zhong, H. (2012). Application-Level CPU Consump-

tion Estimation: Towards Performance Isolation of

Multi-tenancy Web Applications. In IEEE CLOUD

2012, pages 439 –446.

Wang, W., Huang, X., Song, Y., Zhang, W., Wei, J., Zhong,

H., and Huang, T. (2011). A statistical approach for

estimating cpu consumption in shared java middle-

ware server. In IEEE COMPSAC, 2011, pages 541–

546. IEEE.

Wang, W., P

erez, J. F., and Casale, G. (2015). Filling the

gap: A tool to automate parameter estimation for soft-

ware performance models. In Proceedings of QUDOS

2015, pages 31–32, New York, NY, USA. ACM.

Westfall, P. H. (2014). Kurtosis as peakedness, 1905–2014.

rip. The American Statistician, 68(3):191–195.

Zheng, T., Woodside, C., and Litoiu, M. (2008). Perfor-

mance Model Estimation and Tracking Using Optimal

Filters. IEEE TSE, 34(3):391–406.

Zheng, T., Yang, J., Woodside, M., Litoiu, M., and Iszlai, G.

(2005). Tracking time-varying parameters in software

systems with extended Kalman ﬁlters. In CASCON

’05, pages 334–345. IBM Press.

CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science

480