An Alternative Raster Display Model

Titusz Bugya and G

abor Farkas

Department of Cartography and Geoinformatics, University of P

ecs, H-7624 P

ecs, Hungary

Keywords:

Data Visualization, Raster Data Model.

Abstract:

In this paper we present an alternative, vector based coverage model, which could extend the traditional raster

model. As the coverage model only changes the representation model behind rasters, it needs minimal effort to

implement, mitigates current raster limitations, and has minimal performance impact due to modern comput-

ers’ increased computing capacities. Moreover, coverages could still get the beneﬁts of the traditional raster

model. As the data model remains the same, traditional raster based operations can still be applied on rect-

angular coverages, while other patterns can still beneﬁt at least from matrix algebra. Finally, not only current

raster operations could be kept, but there would not be any limitations of developing new ones optimized for

different coverage patterns (e.g. hexagonal operations).

1 INTRODUCTION

It is basic knowledge, Geographic Information Sys-

tems (GIS) work with two distinct data types: rasters

and vectors. There are essential differences between

the two models, converting them into each other re-

sults in data loss most of the time. These models are

still used in parallel since not only their characteris-

tics, but their typical use cases also differ. A fun-

damental attribute of the 2D raster model (hereafter

raster model) is it can be created and used without

interpreting the represented phenomenon. That is,

a raster – for example a land cover image – can be

created without excessive knowledge of the surveyed

area. On the other hand, the vector model requires in-

terpretation. Vectors can only be created, if one can

choose and delimit the mapped entities, while the ef-

fective use of attributes also requires being familiar

with the mapped phenomenon.

Additionally, the two models differ in the types

of mapped phenomena. Usually, rasters are used for

continuous data (e.g. temperature), while vectors are

used for discrete entities (e.g. administrative divi-

sions, infrastructure). This duality in GIS caused by

the distinct characteristics of– and use cases for the

two speciﬁc data models create a seemingly irresolv-

able disagreement when both of them are needed. In

this study we argue, this duality is not really neces-

sary, and the conversions between the two models can

be neglected. Furthermore, by loosening the restric-

tions of the traditional raster model, new, interest-

ing raster-vector cross products could be developed,

which might be more appropriate for a given task than

choosing a traditional model.

2 THE RESTRICTIVE RASTER

MODEL

Since our current raster model is a heritage of an

old computing era (Lim, 2008), it is still burdened

with technological limitations of those times. No

matter how those limitations are eased or vanished

(Chrisman, 1987), our raster model still consists of

a strongly coupled data–, and representation model.

That is, rasters are matrices seamlessly ﬁlling a rect-

angular extent in a projected raster space (Ritter and

Ruth, 1997). As common GIS software suggest,

they must be represented with rectangular, coincident

cells.

2.1 Strengths and Weaknesses

Despite of the limitations, the beneﬁts of the raster

model make it a useful, and widely used data model

even in modern GIS analyses. However, by group-

ing some of its major characteristics (Huisman and

De By, 2009; Bolstad, 2016; Farkas, 2017) by the

level of conceptuality (i.e. data and representation),

one can see, most of its strongest, most enduring mer-

its are coming from the data model (Table 1).

Most of the strengths are coming from the model’s

simplicity. Since the majority of a traditional raster

262

Bugya, T. and Farkas, G.

An Alternative Raster Display Model.

DOI: 10.5220/0006762402620268

In Proceedings of the 4th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2018), pages 262-268

ISBN: 978-989-758-294-3

Table 1: Characteristics of the raster data model without

being exhaustive.

Data model

Continuous coverage

Small size, good

compressibility

Advantages

Simple data structure

Good for parallel computing

Easy to overlay when aligned

Disadvantages Quadratic growth in raster size

Representation model

Easy to create textures

Fast rendering (textures,

pyramids)

Advantages

Easy to resample and

interpolate

Georeferencing is unequivocal

Hard to reproject

Rotation needs resampling

Disadvantages

Precision depends on latitude

Sampling bias

ﬁle consists of cell values, rasters have good com-

pressibility, as matrices can be easily encoded in a

binary format. Furthermore, as subsetting a matrix

is trivial, tiling up a raster layer for saving bandwidth,

making operations faster, or parallelizing an analysis

is easy.

On the other hand, advantages bound to the repre-

sentation model are not huge, while the disadvantages

are severe. Most of the restrictions of the raster model

are coming from its disadvantages, and can be origi-

nated to the shapes of individual cells. As they are

restricted to be rectangular and coincident, reprojec-

tion needs resampling and interpolation in most of the

time. Furthermore, if cells are used for representing

their centroids (i.e. sampling), a bias is unavoidably

introduced, as diagonals are longer than sides.

2.2 Evolution of the Raster Model

In order to overcome a few disadvantages of the raster

model, it has undergone some changes. First, when

the raster model was introduced to aid plotting and vi-

sualization on digital displays (Lim, 2008), cells had

a good reason to be squares. This initial property is

still carried by some of the old, but popular formats,

like the ArcInfo ASCII Grid (Yu and Custer, 2006).

Next, the classical raster model took the opportu-

nity to extend rasters in the only possible way: per-

mitting different resolutions on different axes. The

GeoTIFF data exchange format is a prime example

for this. It creates a raster grid with rectangular cells

from a regular TIFF image with a tie point and an

afﬁne transformation matrix (Ritter and Ruth, 1997).

Since there were demands for various new raster

capabilities, and the current, restrictive raster model

could not incorporate them, theoretical and practi-

cal raster concepts parted. Now the theoretical con-

cept capable of ﬁlling an extent with different shapes,

called regular–, and irregular tessellation (Huisman

and De By, 2009), is taught as GIS theory. Rasters,

on the other hand, are the widely implemented subset

of regular tessellations using rectangular grids.

Some of the more popular demands, like the

hexagonal grid (Birch et al., 2007) are slowly mak-

ing their way into various GIS software in form of

tools (Ramakrishna et al., 2013; Esri, 2017), how-

ever they are generated and stored as polygon layers.

The problem with this approach is almost every ad-

vantage of the raster data model is lost. For example,

after the grid is generated, the continuity is not en-

forced anymore, making space for a variety of user

errors. Another potential concept for geomorpholo-

gists, the Multiresolution Image Format (Bugya and

Halmai, 2013) does not have a straightforward way

of getting implemented, as it relies on the raster data

model.

3 DISPLAYING RASTERS AS

VECTORS

Since most limitations of the raster model are com-

ing from the representation model, we propose an al-

ternative display model for rasters, and other regular

tessellations: the coverage model. Rendering raster

grids as vectors would need minimal modiﬁcations to

popular data exchange formats, and minor modiﬁca-

tions in GIS software. On the other hand, it would

mitigate current raster limitations, making space for

improvement.

3.1 A Permissive Coverage Model

The main aspect in deﬁning our coverage model was

making it as permissive as possible. That is, its sole

requirement is continuous coverage in a spatial extent.

Speciﬁcally, elements of the coverage must not have

gaps between them, nor overlap each other. We real-

ize that such a strong criterion should be enforced by

the model itself. Consequently, having an unequivo-

cal, direct mapping between the coverage pattern and

the data matrix is unavoidable. If no such mapping

could be established in a practical way, the coverage

should be treated as an irregular tessellation (e.g. TIN

An Alternative Raster Display Model

263

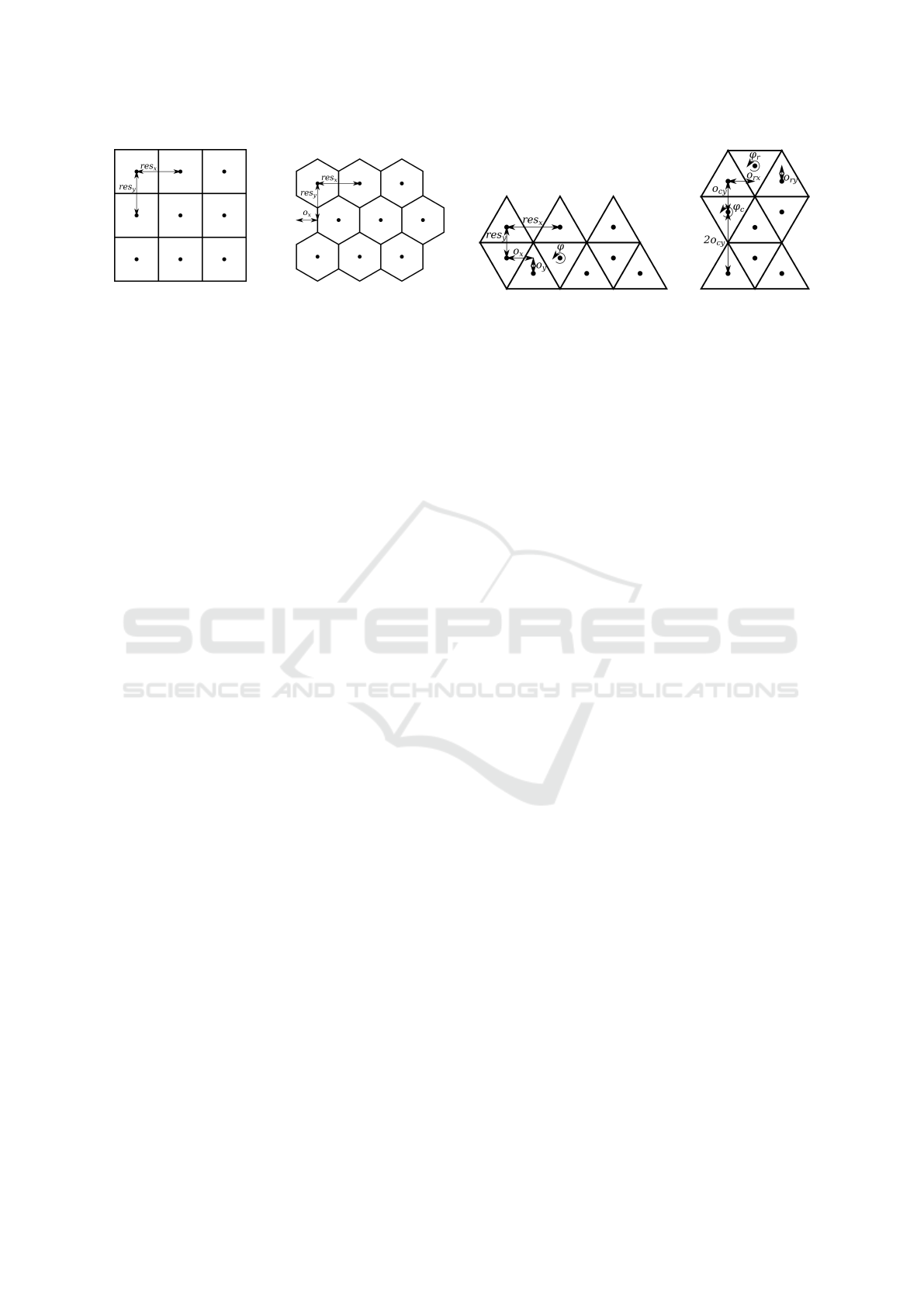
(a) (b)

Figure 1: Required attributes for describing rectangular (a)

and hexagonal (b) coverages. Vertical and horizontal reso-

lution (res

, res

), and horizontal offset (o

), which can be

negative.

model). Using such a model could enable an imple-

mentation to apply more heuristics as the regularity

of the pattern increases. This way, traditional rasters

would be treated in a more ﬂexible way; as an edge

case of the vector model.

The amount of information needed to describe a

regular pattern is minimal, while for more complex

patterns it can gradually increase. In case of rectangu-

lar coverages, users could not experience any differ-

ences. They would look very similar to texture-based

representations, while – as the data model behind the

coverage model is the same – traditional raster and

image tools can be used on them. Furthermore, ex-

isting and new compression algorithms for raster data

can also be used on every coverage. By considering

the rectangular pattern as the trivial one-to-one map-

ping to the underlying matrix, hexagonal tessellations

can be described with only a few attributes (Figure

1), assuming the orientation of individual cells are

horizontal (i.e. points-up or honeycomb). Develop-

ers could implement another set of tools optimized

for hexagonal coverages (and rectangular coverages

with an offset), as computations on hexagonal grids

are well-founded (Her, 1995), while there are also po-

tential use cases of them in GIS (Birch et al., 2007).

The third regular tessellation in euclidean space –

a triangular pattern – has no trivial mapping to a ma-

trix. Such a mapping can be deﬁned in various ways,

but grouped into two distinct categories; row-to-row

mapping, where each row consist of cells with the

same attributes, and element-to-cell mapping, where

neighboring cells are changing periodically (Figure

2). No matter which method is used, there will al-

ways be a periodicity included, which needs to be

considered. Such ambiguous coverages can make lit-

tle use of traditional raster tools, although the conti-

nuity is granted, and matrix algebra can be used on

a single coverage, or when the patterns of two cov-

erages match. Furthermore, as they would be treated

like vectors, vector tools could be used on such cov-

erages.

(a) (b)

Figure 2: Two different matrix mapping techniques in a 3x3

triangular tessellation. In row-to-row mapping (a), the hor-

izontal resolution (res

) is constant in a row, while the ver-

tical resolution (res

) and offsets (o

, o

) are periodically

changing in new rows. The rotation (ϕ) is always applied

on a new row. In element-to-cell mapping (b), there are off-

sets and a rotation for cells in a row (o

, o

, ϕ

), and for

cells in new rows (o

, 2o

, ϕ

). The vertical offset for new

rows is periodically changing.

In order to describe arbitrary patterns, there is one

ﬁnal consideration left: the way pattern geometries

are stored. As there are numerous ways to tessellate

an extent with irregular shapes, we do not think the

coverage model should be restricted to euclidean

regular tessellations (i.e. rectangular, hexagonal, tri-

angular). If one can describe an arbitrary pattern with

an unequivocal mapping to the underlying matrix,

that pattern should be able to used as a coverage.

While there are numerous ways to describe such a

shape, we argue, it should be done in a normalized

coordinate system enclosing the axis-oriented bound-

ing box of the shape (Figure 3). This way shapes

could be automatically scaled with the resolution of

the coverage. Shape coordinates should be relative

to the anchor point, as it would decrease the number

of calculations required for visualizing the pattern,

as in the following pseudo-code of a straightforward

implementation (assuming hardware-acceleration is

used):

Input: Cell shape S, Pattern P, First

centroid C

, Resolution R.

Output: Coverage triangulation T .

1. Calculate S

by scaling S with R.

2. Calculate triangulation S

from S

3. do

4. Get current cell’s rotation ϕ from P.

5. Calculate cell S

by offsetting S

by C

6. Rotate S

by ϕ around C

7. Add S

to T .

8. Calculate next centroid C

using P.

9. until There are no cells remaining.

Storing the ﬁrst anchor point or centroid is im-

portant, as it serves as the starting point of the pat-

tern, a reference to absolute shape coordinates, and

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

264

ID X Y

1 0.4 -0.2

2 0.5 -0.1

3 0.4 0

4 0.45 -0.03

5 0.25 0.25

6 -0.05 0.25

7 0 0.38

8 -0.13 0.5

9 -0.25 0.38

10 -0.2 0.25

Figure 3: An arbitrary pattern described with a minimal

number of attributes. Coordinates of the shape are stored in

a normalized coordinate system, therefore it can be linearly

scaled with the resolution of the coverage. As this pattern is

based on a rectangular coverage, only one offset is needed

for cells in the same row (o

), and one for new rows (o

which also agree with the resolution.

a basis to offset, and rotate the shape in the pattern.

On the other hand, storing the topology of neighbor-

ing shapes could be also considered, since that way

a GIS could validate a coverage more easily and ac-

curately (i.e. without false positives from arbitrary

ﬂoating point calculations, and without the overhead

of calculating the ﬁrst period of the pattern). Simi-

larly to triangular tessellations, these arbitrary cover-

ages could neither be used for traditional raster analy-

ses, although they would still get the other beneﬁts of

the raster data model.

The complexity of a pattern can be gradually in-

creased by deﬁning multi-shape patterns (e.g. eu-

clidean projections of spherical tessellations), how-

ever assessing the feasibility of such coverages is out

of the scope of this study.

3.2 Required Modiﬁcations

For effective coverage storage and retrieval, a stan-

dardized set of parameters should be worked out. As

mentioned before, a regular pattern can be described

with periodically changing translations and rotations,

while an arbitrary pattern should contain the shape,

and optionally its topological relationship with its

neighbors. These are just additional metadata, which

need to be stored in a coverage ﬁle. Some of the cur-

rent formats can be extended to hold such informa-

tion, while for others, it can be safely assumed, their

contents are rectangular grids.

Moreover, formats supporting coverages should

store the lower left cell’s center (or anchor point).

While currently it is very popular to store the lower

left corner of a raster layer, for non-rectangular pat-

terns it can be ambiguous. Finally, despite of storing

the lower left corner of the ﬁrst cell’s bounding box is

trivial, a calculation can be saved by not doing so.

A concise description of the triangular pattern in

Figure 2b in JavaScript Object Notation could be the

following:

{

origin: [46.07, 18.21],

shape: [[-0.5, -0.5], [0.5, -0.5], [0, 0.5],

[-0.5, -0.5]],

row_pattern: {

rotation: [180deg],

offset: [

[0.5, 1/3],

[0.5, -1/3]

]

col_pattern: {

rotation: [180deg],

offset: [

[0, 4/3],

[0, 2/3]

]

}

The second part of the implementation would be

a coverage interpreter. As every adequate GIS soft-

ware is capable of rendering vectors, it would take

minimal effort to extend the rendering engine to draw

patterns. Besides the pattern drawing algorithm de-

scribed before, only vector rendering methods need

to be used (e.g. drawing cells as polygons, or trian-

gulating and creating vertex buffers). The underlying

low-level rendering engine can take care of the rest.

Due to the vector nature of coverages, resampling

for display purposes would be rarely needed, although

current raster resampling algorithms could be used

for rectangular coverages. Pyramids, however, would

need to be stored as resampled coverages with dif-

ferent resolutions instead of textures. If pyramids are

really needed for arbitrary patterns, a simple approach

could be converting the pattern to a rectangular cover-

age ﬁrst (rasterization), then building pyramids from

the result.

3.3 Advantages and Limitations

While the coverage model only differs from the raster

model in visualization, it is easier to see its beneﬁts,

if compared directly with the traditional raster model.

Since the coverage–, and raster models share their

data model, changes can only be found in its represen-

tation model. Furthermore, as the coverage model en-

courages additional heuristics applied to edge cases,

the characteristics (Table 2) can depend on the pat-

tern. There are some independent advantages, on the

other hand. As coverages are rendered as vectors, ro-

An Alternative Raster Display Model

265

Table 2: Characteristics of the coverage representation

model using different patterns.

Common charactersitics

Easy to reproject

Advantages Easy to rotate

Variable cell size

Disadvantages Slower than textures

Rectangular coverage

Easily convertible to textures

Advantages Easy to interpolate and resample

Georeferencing is unequivocal

Disadvantages Sampling bias

Hexagonal coverage

Easy to interpolate

Advantages

Less sampling bias

Hard to resample

Slower than rectangular

Disadvantages

Hard to create textures

No lower left corner

Arbitrary coverage

Advantages Pattern can be tailored to use case

Performance depends on pattern

Hard to interpolate and resample

Disadvantages

Hard to create textures

Georeferencing is not trivial

tation and reprojection are trivial operations. More-

over, since no textures are used, cell size can vary

in a single coverage, allowing constant precision in

projected coordinate systems. The sole common dis-

advantage is the performance impact. While perfor-

mance depends on the complexity of the pattern, even

rectangular coverages are outperformed by textures.

Rectangular coverages have the most advantages,

since they inherit the advantages of the raster model,

while most of their disadvantages are mitigated by the

vector based visualization of the coverage model. The

only disadvantage, which cannot be resolved by the

coverage model is the sampling bias, since it is com-

ing from the rectangular cells. On the other hand, this

can be solved by choosing a hexagonal pattern. On

hexagonal coverages less heuristics can be applied,

therefore they have more disadvantages. For example,

it is simple to interpolate in a hexagonal coverage, as

centroids of neighboring cells can be calculated eas-

ily. However, resampling one is hard, as hexagons

cannot be partitioned into smaller hexagons. Finally,

ass hexagons do not have lower left corners, hexago-

nal coverages need to supply the centroid of the origin

cell, or the lower left corner of its bounding box.

Since arbitrary coverages group patterns which do

not have any heuristics applied, those are the most dis-

advantageous ones. Apart from the common advan-

tages, they have only one; the freedom of choosing the

best pattern for the task. However, – depending on the

complexity of cell geometries – they have worse ren-

dering performance. Moreover, since a general algo-

rithm for interpolating and resampling must be vector

based (i.e. laying down the whole pattern is a require-

ment), those operations would be hard and slow. As

follows, general operations on these coverages could

only be written on a vector basis, therefore they would

rather act as a large vector layers with many small

polygons than a raster layer. On the other hand, op-

erations modifying cell values only (e.g. raster calcu-

lator) could still be fast, as they can run against the

underlying matrix without considering the pattern.

3.4 Performance Impact

There is only one aspect the current, restrictive raster

model excels at: performance. It was created with

performance in mind, therefore it offers the quickest

representation model possible in GIS. However, the

computing capacity of modern computers (even hand-

held devices) surpassed the need for such optimiza-

tions long ago. Since one can enjoy the beneﬁts of

hardware-acceleration even in a browser (Nogueira,

2012), there is no reason to stick with the faster model

on the expense of usability.

On the other hand, the performance impact of such

a change should still be considered. There are – and

in the near future there will be – good reasons for such

optimizations. There are cases, where the amount

of transmitted data or battery life matters (e.g. ﬁeld

devices), or where there is only limited computing

power (e.g. embedded systems). In order to take

those cases into consideration, the current raster dis-

play model should be kept as is. This way, desktop

users with more computing power could be granted

a permissive coverage model, while developers could

still build applications using traditional, texture based

rasters.

Another, less trivial implication is due to the ﬂexi-

bility of the vector model. As coverages display cells

as polygons, cell geometries can be stored, if needed.

This way, one can freely adjust the ratio of stored

and calculated data. As spatial Database Management

Systems (DBMSs) are optimized for effective storing,

and quick retrieval of geometries and attributes, the

performance of dynamically subsetting, and even an-

alyzing large coverages could be increased on the ex-

pense of disk usage. This grants scalability to users,

as they could freely choose tradeoffs. For example,

a rectangular coverage can be stored as a GeoTIFF

ﬁle, in a relational database, or in an array database

(Baumann, 2001) as a georeferenced matrix. On the

other hand, it can also be stored in a database as vec-

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

266

tor data by storing the center of each cell, or storing

the geometries of the cells. In this scenario – with

proper indexing – not only subsetting could be faster,

but sparse matrices and multiresolution images could

also be stored with ease.

Similarly, developers can choose the best ratio

of memory consumption and rendering performance.

For example, if hardware-acceleration is used, the tri-

angulation of the whole layer can be stored, gradu-

ally increasing performance on the expense of mem-

ory consumption. However, additional memory re-

quirement can also be ﬁne-tuned. For example, one

must store at least two ﬂoating point values per ver-

tex, which can be complemented with four byte val-

ues (RGBA colors) for maximum performance. On

the other hand, colors can be deﬁned dynamically, on

the ﬂy, in order to decrease memory consumption. In

cases when memory footprint should be kept at min-

imum, the tessellation can be triangulated on every

drawn frame. Alternatively, if both the rendering en-

gine and the application requirements permit it, the

coverage can be rendered on a texture, and reused un-

til the map scale changes.

4 CONCLUSIONS

The raster model is still a dominant, widely used

model in GIS, although it has numerous limitations.

Its fundamental advantage comes from its matrix na-

ture, as it has well-optimized, fast algorithms, which

can effectively be parallelized. On the other hand, its

disadvantages – mostly coming from its representa-

tion model – are also severe. Its rectangular grid is

based on euclidean geometry, therefore it can only

map spherical surfaces and volumes with distortions.

It is also vulnerable to transformations, and hard to

reproject.

On the other hand, the vector data model does not

have these limitations; vectors can be arbitrarily and

accurately reprojected or interpolated. They require

more computing power for those operations, however,

modern personal computers have the computing ca-

pacity required for a vector-based coverage model.

Furthermore, vectors have the unique ability of stor-

ing many attributes linked to a single entity, and well-

optimized spatial Database Management Systems ca-

pable of analyzing them.

The coverage model we are proposing in this pa-

per makes possible to use non-rectangular tessella-

tions similarly to traditional rasters. Its practical im-

plementation seems straightforward, as it does not

collide with database standards, and can be integrated

into raster data exchange formats with minimal mod-

iﬁcations. On the software side, as the simple form of

the proposed model would only require afﬁne trans-

formations and a vector rendering engine, thus adding

it to modern GIS software would have no conceptual,

nor practical limits.

ACKNOWLEDGEMENTS

This study was supported by the

UNKP-17-3-I New

National Excellence Program of the Ministry of Hu-

man Capacities, Hungary. The authors would like

to thank the ﬁve anonymous reviewers for their con-

structive comments on the ﬁrst version of this article.

REFERENCES

Baumann, P. (2001). Web-enabled raster gis services for

large image and map databases. In 12th International

Workshop on Database and Expert Systems Applica-

tions, 2001. Proceedings., pages 870–874. IEEE.

Birch, C. P., Oom, S. P., and Beecham, J. A. (2007). Rect-

angular and hexagonal grids used for observation, ex-

periment and simulation in ecology. Ecological Mod-

elling, 206(3):347–359.

Bolstad, P. (2016). GIS Fundamentals: A First Text on Ge-

ographic Information Systems, Fifth Edition.

Bugya, T. and Halmai,

A. (2013). The multiresolution im-

age format. Journal of Geographic Information Sys-

tem, 5(1):87–95.

Chrisman, N. (1987). Fundamental principles of geographic

information systems. In Proceedings of Auto-Carto,

volume 8, pages 32–41.

Esri (2017). Generate Tessellation.

https://pro.arcgis.com/en/pro-app/tool-

reference/data-management/generatetesellation.htm.

Accessed: 2017-11-17.

Farkas, G. (2017). Practical GIS. Packt Publishing, Birm-

ingham, UK.

Her, I. (1995). Geometric transformations on the hexag-

onal grid. IEEE Transactions on Image Processing,

4(9):1213–1222.

Huisman, O. and De By, R. A. (2009). Principles of geo-

graphic information systems. ITC Educational Text-

book Series, 1.

Lim, H. (2008). Raster Data. In Shekhar, S. and Xiong,

H., editors, Encyclopedia of GIS, pages 949–955.

Springer, NY, USA.

Nogueira, E. T. (2012). WebGL: a new standard for devel-

oping 3D applications. Virtual Reality and Scientiﬁc

Visualization Journal, 5(2):40–60.

Ramakrishna, A., Chang, Y., and Maheswaran, R. (2013).

An interactive web based spatio-temporal visualiza-

tion system. In Bebis, G., Boyle, R., Parvin, B., Ko-

racin, D., Li, B., Porikli, F., Zordan, V., Klosowski, J.,

An Alternative Raster Display Model

267

Coquillart, S., Luo, X., Chen, M., and Gotz, D., edi-

tors, Advances in Visual Computing: 9th international

symposium, ISVC 2013, Part II., pages 673–680.

Ritter, N. and Ruth, M. (1997). The GeoTiff data inter-

change standard for raster geographic images. In-

ternational Journal of Remote Sensing, 18(7):1637–

1647.

Yu, E. and Custer, A. (2006). ArcInfo ASCII Grid

format. http://old.geotools.org/ArcInfo-ASCII-Grid-

format 5250.html. Accessed: 2017-11-13.

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

268