Interactive Fuzzy Decision Support to Adjust Human Resource

Structures

Peter Rausch and Michael Stumpf

Technische Hochschule N

urnberg Georg Simon Ohm, Keßlerplatz 12, 90489 Nuremberg, Germany

Keywords:

Human Resource Planning, Human Resource Management, Manpower Planning, Fuzzy Decision Support,

Fuzzy Linear Optimization, Uncertainty, Fuzzy Set Theory.

Abstract:

Human resource planning plays a key role for enterprises’ and organizations’ sustainable success. This paper

focuses on issues and challenges in the ﬁeld of human resource planning in hierarchical organizations. Due to

current challenges, like digital transformation, progress in artiﬁcial intelligence, etc., a fundamental structural

transformation of workforce is initiated in many companies and organizations. Especially, huge enterprises

in many industries and the service sector as well as organizations in the public sector have to review their

mid-term and long-term desired human resource (HR) target structures. Based on an organization’s target

structure, a strategy to transfer the actual HR structure to a desired new target structure is needed. This step

is a big challenge because of many uncertainties of system parameters and complex structures of the planning

approaches with many constraints and conﬂicting goals. To bridge gaps in this ﬁeld, an interactive fuzzy

approach which supports the development of strategies for actual-target structural adjustments (ATSA) in big

organizations will be presented. This approach manages conﬂicting goals and is based on experience gained

in an organization of the public sector, but it can also be transferred to non-governmental industry and service

companies.

1 INTRODUCTION

Digital transformation, progress in artiﬁcial intelli-

gence, globalization and process reengineering trig-

ger fundamental structural transformations of work-

force, both in enterprises and in the public sector.

Considering that human resource planning is a key

factor for enterprises’ and organizations’ sustainable

success, this issue is a serious challenge. Thus, espe-

cially, huge enterprises in many industries and service

sectors as well as organizations in the public sector,

like public authorities, the army, and the police, have

to manage transformation processes of their human

resource (HR) structures. For this reason, decision

support systems in the ﬁeld of HR planning are es-

sential. Despite all progress in research, some serious

issues have not been addressed in an appropriate man-

ner yet. For instance, the complexity of staff planning

issues causes a lot of effort since all the necessary data

for the planning tools has to be gathered. Especially

in case of medium- and long-term oriented planning,

approaches additionally struggle with uncertainties of

planning parameters. Most tools are not able to cope

with a lack of data precision and reduce vague data

to (unrealistic) crisp values. Moreover, procedures

to manage conﬂicting goals, for instance, minimizing

costs versus fast stafﬁng of open positions, have to be

provided, which is not always the case.

To analyze these issues in detail, the paper is ar-

ranged as follows: At ﬁrst, we give a brief survey

on HR planning. We will outline the issue of actual-

target structural adjustments (ATSA) and classify it

in the ﬁeld of HR planning. Afterwards, related work

and open challenges will be discussed. The presented

approach addresses open issues and provides interac-

tively generated strategies for future staff alignments.

It is designed for medium-sized or big organizations

and can be used by industry and service companies

as well as by other organizations. We will brieﬂy

describe the sources of data input, namely, an HR

system providing the actual headcount and a decision

support system, which computes an HR target struc-

ture. Subsequently, the interactive fuzzy approach to

explore the solution space and to identify actual-target

adjustment strategies is presented. Details of the re-

lated planning procedure will be given, including a

solution to solve conﬂicting goals. Finally, we discuss

the impacts of our approach and provide conclusions

for further developments.

Rausch, P. and Stumpf, M.

Interactive Fuzzy Decision Support to Adjust Human Resource Structures.

DOI: 10.5220/0006765204410447

In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 441-447

ISBN: 978-989-758-298-1

441

2 OPEN ISSUES, CHALLENGES,

AND RELATED WORK

Since HR planning covers a broad range of issues,

it is important to classify the subject of this re-

search. There are many different interpretations of

the term HR planning with varying scope. For in-

stance, Geisler regards HR planning as a ”process

including forecasting, developing and controlling by

which a ﬁrm ensures that it has the right number of

people and the right kind of people at the right places

at the right time doing work for which they are eco-

nomically most useful” (Geisler, 1967). Others like

Koltnerov

a et al. follow Geisler and explicitly em-

phasize the aspect of forecasting the future manpower

requirements respectively the number and the type of

employees required by an enterprise in the near future

(Koltnerov

a et al., 2013). Stainer deﬁnes HR plan-

ning ”as a strategy for the procurement, development,

allocation, and utilization of an enterprise’s human re-

sources” (Stainer, 1971). Kacha

akov

a et al. distin-

guish a wider view in terms of planning the personnel

development and a narrow meaning covering plans of

employees and plans of stafﬁng jobs (Kacha

akov

et al., 2008).

In the following sections we address the issue of

planning a series of steps to eliminate differences be-

tween the actual and desired quantitative and quali-

tative HR structure of an organization on a medium-

term or a long-term timeline. This includes process

steps to determine how an organization should move

from its current manpower position to its desired man-

power position which can be called manpower plan-

ning according to Vetter (Vetter, 1967). The presented

approach can also be used to support gap analysis

which aims to asses human capital readiness in an or-

ganization (Snell et al., 2016).

As already mentioned in the introduction, big

companies and organizations have to cope with pro-

found structural transformations of the workforce. In

our case, we consider an organization in the pub-

lic sector which also tries hard to manage this is-

sue. In terms of above mentioned HR planning sub-

jects which are being analyzed here, the planning of

actual-target structure adjustments (ATSA) of the re-

garded organization was challenging. Due to conﬁ-

dentiality reasons we can only outline the basic re-

quirements here. Nevertheless, we will see that the

challenges and issues are also representative for other

huge organizations and enterprises. In our case, a lin-

ear optimization approach was used which should be

part of the new solution. In general, huge organiza-

tion’s workforce planning involves many constraints

and is based on complex planning approaches (Spen-

gler, 2006). Thus, it is generally almost impossible

to anticipate all effects of ATSA strategies, for in-

stance, the impacts of adjustment strategies to digest

a merger.

Additionally, many HR planning parameters and

their relationships cannot be represented by determin-

istic elements. For instance, in a huge organization

it is usually not mission-critical to be slightly un-

derstaffed in a certain department for a limited time.

Hence, the amount of the necessary headcount for this

department is fuzzy. If a planning system is only ca-

pable of handling crisp data, it is likely that valid op-

tions in the solution space which might be appreciated

by the decision maker are not considered. Meanwhile,

the issue of fuzziness in the ﬁeld of HR planning is al-

ready recognized. A lot of scientiﬁc research can be

found, for instance (Jana et al., 2017a), (Jana et al.,

2017b), (Doka et al., 2015), (Xu et al., 2005), and

(Nobari et al., 2012). Nevertheless, these approaches

do not cover the aspect of planning actual-target struc-

ture adjustments. Yamchi et al. compare determin-

istic and fuzzy approaches in the ﬁeld of manpower

planning, but they just provide a deterministic equiv-

alent of a model which represents a fuzzy system

according to their statement (Yamchi et al., 2016).

The original fuzzy model is not described and proce-

dures to explicitly manage conﬂicting goals are not re-

garded. For instance, rapid actual-target adjustments

can cause higher expenses for redundancy pay-outs in

case of headcount reductions. Therefore, in our case,

it was necessary to develop a new solution which ad-

dresses all the above mentioned issues.

Before a detailed presentation of the interactive

fuzzy solution, we will brieﬂy outline the necessary

data sources of the approach as far as it serves com-

prehension.

3 ACTUAL HEADCOUNT DATA

AND ORGANIZATIONAL

TARGET STRUCTURE (OTS)

Most enterprise resource planning systems contain

an HR component which can be used to provide ac-

tual headcount data accessible via software interfaces.

The provided data can also include information about

the expiration of contracts. Other companies or or-

ganizations deploy standalone HR software which is

more or less integrated with other components. In our

case, the necessary headcount data for actual-target

adjustments is generated by a tailor-made software.

Another custom software component supports

the calculation of an organization’s target structure,

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

442

namely, the quantitative and qualitative structure of

the staff depending on the function, educational back-

ground (professional trainings) and the (sub-) organi-

zation. The staff structure of organizational units and

their age-speciﬁc compositions are determined. The

results are based on decision makers’ speciﬁcations,

for instance, required unit volumes or replenishment

needs as well as educational and professional back-

grounds.

Based on the computed results and the data of the

HR administration system, actual-target adjustment

strategies can be derived like described in the next

sections.

4 ACTUAL-TARGET

STRUCTURAL ADJUSTMENTS

(ATSA)

To analyze adjustment strategies in terms of transfer-

ring the actual HR structure to the target structure

within a certain timespan the planning model has to

reﬂect:

• Flows from one hierarchy level to another

• Opportunities in terms of ”the chance to graduate

from one level to the next is x %”

• Constant relations between headcounts in certain

units of the organization

• Objectives minimizing the target-actual distance

within a certain timespan

As already mentioned in Section 2, challenges such

as potentially conﬂicting goals, for instance, ”rapid

actual-target adjustments versus higher expenses for

swift promotions”, have to be considered. Addition-

ally, fuzziness of planning parameters has to be an-

ticipated. For example, future headcount volumes of

organizational units, ﬂow coefﬁcients, opportunities

and failure rates (regarding trainings as prerequisite

for a promotion) often can’t exactly be quantiﬁable in

advance. With the help of fuzziﬁcation decision mak-

ers get a certain degree of freedom which can be used

to ﬁnd a good solution according to the linear equa-

tion system, the conﬂicting goals and the subjective

appreciation of compromises.

5 INTERACTIVE FUZZY

SOLUTION FOR THE ATSA

PROBLEM

To solve the problem outlined in Section 4 an iterative

solution ﬁnding technique named FULPAL (FUzzy

Linear Programming based on Aspiration Levels) is

used. FULPAL allows decision makers to explore the

vast solution space step by step regarding multiple ob-

jectives. In each iteration decision makers are able

to adjust their subjective aspiration levels concerning

goals and also regarding the adherence of fuzzy con-

straints. For this purpose, they are allowed to mod-

ify the underlying model parameters of the planning

problem step by step. The idea of this procedure is to

ﬁnd a satisfying solution in the sense of bounded ra-

tionality, see (Simon, 1955) and (Becker and Siegel,

1958). The underlying theory is acknowledged by re-

cent research, see (Senf, 2017) and (Shinkle, 2012),

and is useful to manage complexity in our case. Due

to the complexity of the decision problem, it is as-

sumed that the decision maker’s value system can

change when the solution space is explored.

Before the iterative planning process is thoroughly

explained, it is necessary to understand the model and

its parameters in detail.

5.1 Modeling the Hierarchical HR

Structure with FULPAL

In order to model the planning problem the domain

has to be described. To reduce complexity in our case

and to simplify our example some assumptions will

be made:

• The hierarchical organization consists of N hier-

archy levels and only aggregated headcounts per

level are considered.

• The planning period covers T periods.

• In order to be promoted to a higher level training

over Y years has to be completed.

• Hierarchy levels cannot be skipped.

• Demotion is not allowed.

• Entire hiring starts at the lowest level.

• Discharges are not allowed in training.

Taking these assumptions into account, variables

to represent the states (headcount) for all possible per-

mutations of planning periods, hierarchy levels, and

training years are required. So, a state variable L [n]

represents the headcount in the model for planning

period t and hierarchy level n with y years of training.

Interactive Fuzzy Decision Support to Adjust Human Resource Structures

443

Flow variables have to be introduced to represent

ﬁnished training steps and promotions. UP[n]

de-

notes the number of employees which ﬂow after plan-

ning period t from hierarchy level n with y years of

training towards their next state variable. This can ei-

ther be the next year y + 1 in training or a promotion

to the next hierarchy level n + 1 with training year

y = 0. Additional ﬂow variables are needed to repre-

sent external inﬂuences, either inbound for hiring in

the lowest hierarchy level A: IN [A]

or outbound for

discharges OUT[n]

in planning period t for hierarchy

level n without being in training (y = 0).

An example illustration of the hierarchic structure

is depicted in Figure 1, where the different variables

are shown. To model the structure of the hierarchical

problem over multiple periods relationships between

state and ﬂow variables have to be established. This

is done by adding constraints to the linear program.

Figure 1: Example Illustration for n =

{

A, B, C, . . .

}

, Y = 1.

For hiring and discharges the state change for

training year y = 0 can be written as Equation 1. This

means, that headcounts at hierarchy level n in period t

are equal to headcounts at the same hierarchy level

of the previous period t − 1 minus the number of em-

ployees which began a training after the previous pe-

riod plus the number of hired employees minus the

number of discharged employees in period t.

L[n]

= L [n]

t−1

− UP [n]

t−1

+ IN [n]

− OUT [n]

(1)

To model trainings for subsequent training years y ≥ 1

Equation 2 is introduced. L[n]

is determined by the

state variable of the previous year minus the employ-

ees which advanced one year in training after the pre-

vious period (away from this state variable) plus the

employees which advanced one year in training after

the previous period (towards this state variable).

L[n]

= L [n]

t−1

− UP [n]

t−1

+ UP [n]

t−1

y−1

(2)

To represent promotions, only state variables with

y = 0 are considered. Equation 3 establishes the con-

nection between different periods. As denoted in

Equation 3, the state variable in period t is equal to

the corresponding state variable in period t − 1 mi-

nus the employees which advanced one year in train-

ing after the previous period plus UP[n − 1]

t−1

which

represents the number of promoted employees from

hierarchy level n − 1 to n minus discharges in hierar-

chy level n in period t.

L[n]

= L [n]

t−1

− UP [n]

t−1

+ UP [n − 1]

t−1

− OUT [n]

(3)

By means of this part of the model, the ﬂows from

one hierarchy level to the next are established, see

Section 4. Since this just represents the determinis-

tic version of the constraints, we will look at fuzzy

parameters for the constraints and the objective func-

tions of the linear program in the following sections.

5.2 Fuzzy Parameters

To put the model into action, actual data from HR

components, see Section 3, for the headcount at dif-

ferent hierarchy levels has to be added. This can

be achieved by adding further constraints which at-

tach actual values to the corresponding state variables

L[n]

, see Equation 4.

L[n]

= Actual value for hierarchy level n (4)

Usually, these numbers will be crisp values. How-

ever, values for the target structure after T years, are

uncertain and can be speciﬁed as fuzzy parameters.

So, instead of adding crisp constraints to the model

fuzzy constraints are used, see Equations 5 and 6.

L[n]

≤

[n]

(5)

L[n]

≥

i+1

[n]

(6)

The ﬁrst fuzzy constraint, see Equation 5, repre-

sents the upper bound for the headcount in hierarchy

level n in the last period T as a fuzzy constraint bor-

der

[n]

, where i denotes the i-th fuzzy parameter.

To do this, a good subjective representation for the

upper bound (denoted as b

[n]

in Figure 2) has to be

deﬁned. Afterwards, the decision maker has to deter-

mine a higher value which isn’t a good representation

for the upper bound anymore (denoted as b

[n]

Figure 2).

To control the planning process the decision

maker is able to adjust the aspiration level AL

[n]

to these bounds. It has to be an element of the inter-

val

[n]

, b

[n]

and represents an acceptable level

of utilizing a resource. Equation 6 represents a lower

bound accordingly.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

444

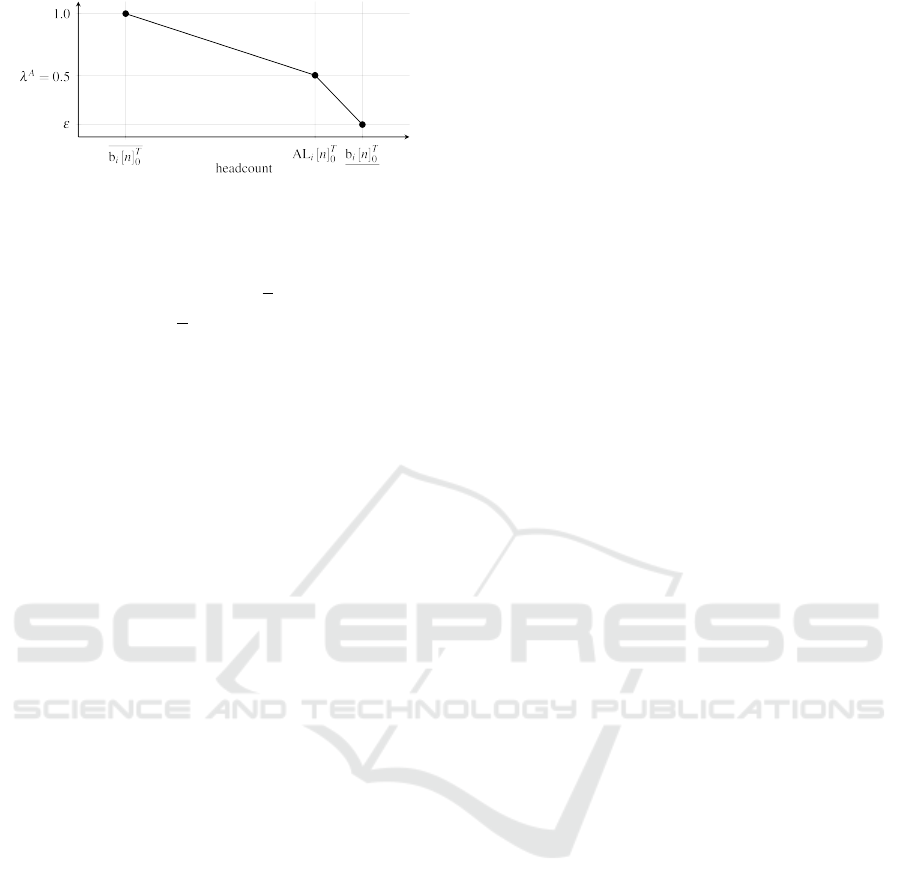
Figure 2: Fuzzy constraint border with aspiration level of

target value for y = 0.

If intermediate milestones are needed it is possible

to add more constraints to the model. For example, if

a speciﬁc target value in period

is desired, a fuzzy

constraint with

i+2





can be added to meet this

requirement.

In the same way other restrictions can be im-

posed, for instance, opportunities, see Section 4, are

established by adding constraints as in Equation 7.

i+3

represents a minimum percentage as fuzzy value

for those who are able to graduate from one hierar-

chy level (state variables L[n]

) to the next (via ﬂow

variables UP[n]

i+3

· L [n]

≥ UP[n]

(7)

As mentioned in Section 4 constant relations be-

tween headcounts of different hierarchy levels can

also be modeled in this manner. To make sure that a

particular ratio between two hierarchy levels is main-

tained in all periods constraints like Equation 8 can be

added. For this purpose, it has to be considered that

employees who take part in a training are also mem-

bers of this hierarchy level. So, the ratio

i+4

be-

tween two different (n

6= n

) hierarchy levels relates

the sums of all state variables for each hierarchy level

(

∑

L[n

]

and

∑

L[n

]

) to another one. For

every period t this ratio should hold a constraint and

has to be added separately.

i+4

∑

L[n

]

∑

L[n

]

(8)

5.3 Objective Functions

Concerning the constraints, the regarded organization

intends to minimize the cost of the overall ATSA, see

Equation 9. The cost factors for each hierarchy level

can also be fuzzy values.

∑

n=0

∑

t=0

∑

y=0

Cost[n]

· L [n]

→ min (9)

Furthermore, FULPAL allows to specify multiple

objectives which can be contradictory. As an exam-

ple for a conﬂicting goal it could be desired, that a

speciﬁc hierarchy level is staffed as fast as possible.

For instance, setting up the middle management be-

fore a massive hiring initiative can be necessary. This

is contradictory to the objective minimizing costs.

Options to handle conﬂicting objectives by means

of aspiration levels are described in the next section.

5.4 Iterative Planning Process

The planning process, see Figure 3, begins with im-

porting the actual data and the target structure from

the HR systems as described in Section 3. After-

wards the decision maker can specify his subjective

aspiration levels and an overall value λ

∗

is computed.

∗

represents the achieved result, namely the maxi-

mized minimal degree of satisfaction concerning all

constraints and the goals (Rausch et al., 2013). The

goal for the decision maker is to reach a solution with

∗

slightly above λ

where λ

is arbitrarily set to 0.5

in FULPAL and represents the assigned membership

value for the aspiration levels. Details on the assign-

ment of aspiration levels to membership values can be

found in (Rausch et al., 2013). In case a solution does

not satisfy the aspiration level concerning at least one

objective or constraint, a λ

value below 0.5 occurs,

and the solution is not acceptable. The decision pro-

cess does not necessarily end at this point. The de-

cision maker is allowed to explore the solution space

further and may modify his aspiration levels for a new

iteration. In case λ

∗

surpluses 0.5 signiﬁcantly, plan-

ning parameters may be tightened for a new iteration.

If the decision maker does not want to use this free-

dom, he can also accept the solution, and the planning

process ends.

6 EVALUATION

The interactive solution process based on the concept

of satisfying aspiration levels ensures that the sub-

jective preferences and goals of the decision maker,

which can dynamically change during the decision

process, are met. It turned out that this approach is

congruent with human thinking while testing the sys-

tem. Besides, the complexity of the planning problem

could be signiﬁcantly reduced. The decision maker

can start the planning process without a fully devel-

oped or only vaguely describable system of objec-

tives and information about the planning parameters.

Imprecise system parameters, for instance, headcount

limits for departments, can be entered fuzzy in accor-

dance to reality, and no artiﬁcial level of precision is

enforced to provide system inputs. By anticipating

real world’s fuzziness a wider range of valid options

of the solution space which may be interesting for the

Interactive Fuzzy Decision Support to Adjust Human Resource Structures

445

Figure 3: Iterative planning process with FULPAL, based on (Rausch et al., 2012).

decision maker are taken into account during the plan-

ning process. Thus, it is likely that the quality of the

planning results is better in many cases. This effect

is also enforced by taking the decision makers’ inter-

nal knowledge during the planning process into ac-

count. If necessary, implicit knowledge can be made

explicit by adding additional constraints or objectives

to a model during the interactive process. So, the in-

teractive exploration fosters also the acceptance of the

generated solutions and helps the decision maker to

cope with the complexity of the system and its so-

lution space. The presented approach is also useful

in terms of managing conﬂicting goals in the ﬁeld of

ATSA problems.

7 CONCLUSIONS AND FUTURE

WORK

It has been shown that fuzzy optimization models sig-

niﬁcantly contribute to manage uncertainties in the

ﬁeld of human resource planning. Of course, the pre-

sented approach cannot handle unforeseen disruptive

events. Nonetheless, it is resilient regarding stress

which inﬂuences system parameters, for instance, in

case of workforce bottlenecks due to external factors.

Additionally, by allowing fuzziness more or less valid

solutions can be taken into account. This can be bene-

ﬁcial, because a compromise solution, which violates

a constraint slightly could be better from a decision

maker’s point of view in terms of all goals and con-

straints. At ﬁrst sight, the impression can emerge that

more effort is needed for setting up the fuzzy model

compared to modeling a crisp system. But in our case,

we had a different impression. System parameters can

be entered in accordance with reality and there were

no discussions how to reduce fuzzy values to a crisp

number.

The veriﬁcation of this observation and analysis

of the general effects on modeling effort would be

an interesting subject for a future study. In particu-

lar, it should be examined to what extent users can

change model parameters, like constraint borders, be-

tween individual steps in practice, for instance, to ex-

ternalize their implicit knowledge. Furthermore, it

would be interesting to deploy the presented approach

in other sectors and to get more experience with dif-

ferent industries. Since in our case a linear optimiza-

tion approach had to be a part of the new solution,

a comparison with other approaches like fuzzy soft

computing could be also an interesting subject for fur-

ther research.

In summary, the presented fuzzy approach pro-

vides a powerful instrument to manage structural

transformations of the workforce and to master the

related challenges. Organizations in the public sec-

tor, big companies as well as large institutions, like

churches, can beneﬁt from the approach and become

more successful in the important ﬁeld of human re-

source planning.

ICEIS 2018 - 20th International Conference on Enterprise Information Systems

446

REFERENCES

Becker, S. and Siegel, S. (1958). Utility of grades: level of

aspiration in a decision theory context. J. Exp. Psy-

chol., 55:81–85.

Doka, K., Ahmad, F., Shamsuddin, S., Awang, W., and

Ghazali, N. (2015). Integrated decision support sys-

tem for human resource selection using topsis based

models. Applied Mathematical Sciences, 9:6403–

6414.

Geisler, E. (1967). Manpower planning: An Emerging Staff

Function. American Management Association, New

York.

Jana, R., Sanyal, M., and Chakrabarti, S. (2017a). Bi-

nary fuzzy goal programming for effective utiliza-

tion of it professionals. In Mandal, J., Satapathy, S.,

Sanyal, M., and Bhateja, V., editors, Proceedings of

the First International Conference on Intelligent Com-

puting and Communication, volume 458 of Advances

in Intelligent Systems and Computing, pages 395–405.

Springer.

Jana, R., Sanyal, M., and Chakrabarti, S. (2017b). Multi-

objective it professionals’ utilization problems using

fuzzy goal programming. In Satapathy, S., Bhateja,

V., Udgata, S., and Pattnaik, P., editors, Proceedings of

the 5th International Conference on Frontiers in Intel-

ligent Computing: Theory and Applications, volume

526 of Advances in Intelligent Systems and Comput-

ing, pages 199–208. Springer.

Kacha

akov

a, A., Nachtmannov

a, O., and Joniakov

a, Z.

(2008). Personnel management. IURA Edition.

Koltnerov

a, K., Chlpekov

a, A., and Sam

akov

a, J. (2013).

Personnel planning reﬂecting the requirements of

sustainable performance of industrial enterprises.

In Semmelrock-Picej, M. and Novak, A., editors,

ECMLG 2013: The Proceedings of The 9th European

Conference on Management Leadership and Gover-

nance, pages 136–143. Academic Conferences and

Publishing International Limited.

Nobari, S., Jabrailova, Z., and Nobari, A. (2012). Us-

ing fuzzy decision support systems in human resource

management. In ICIIM 2012: International Con-

ference on Innovation and Information Management,

volume 36, pages 204–207. IACSIT Press.

Rausch, P., Rommelfanger, H., Stumpf, M., and Jehle, B.

(2012). Managing uncertainties in the ﬁeld of plan-

ning and budgeting - an interactive fuzzy approach. In

Bramer, M. and Petridis, M., editors, Proceedings of

AI-2012, The Thirty-second SGAI International Con-

ference on Innovative Techniques and Applications of

Artiﬁcial Intelligence, Research and Development in

Intelligent Systems XXIX, pages 375–388. Springer.

Rausch, P., Stahl, F., and Stumpf, M. (2013). Efﬁcient inter-

active budget planning and adjusting under ﬁnancial

stress. In Bramer, M. and Petridis, M., editors, Pro-

ceedings of AI-2013, The Thirty-third SGAI Interna-

tional Conference on Innovative Techniques and Ap-

plications of Artiﬁcial Intelligence, Research and De-

velopment in Intelligent Systems XXX, pages 375–

388. Springer.

Senf, N. N. (2017). Organisationale Anspruchsniveaus.

SpringerGabler, Wiesbaden.

Shinkle, G. A. (2012). Organizational aspirations, reference

points, and goals: Building on the past and aiming for

the future. Journal of Management, 38:415–455.

Simon, H. (1955). Behavioral model of rational choice. Q.

J. Econ., 69:99–118.

Snell, S., Morris, S., and Bohlander, G. (2016). Manag-

ing Human Resources. Cengage Learning, Boston, 17

edition.

Spengler, T. (2006). Modellgest

utzte Personal-

planung, working paper no. 10, url:

http://tinyurl.com/y7sybvpx, last access: 2017-11-20.

Stainer, G. (1971). Manpower planning: The Management

of Human Resources. Heinemann, London.

Vetter, E. (1967). Manpower Planning for High Talent Per-

sonnel. Michigan Univ., Ann Arbor.

Xu, Z., Song, B., and Chen, L. (2005). Fuzzy logic ex-

perience model in human resource management. In

Khosla, R., Howlett, R., and Jain, L., editors, KES

2005: Knowledge-Based Intelligent Information and

Engineering Systems, volume 3682 of Lecture Notes

in Computer Science, pages 204–207. Springer.

Yamchi, H. G., Azar, A., Alvani, M., and Javadin, R. S.

(2016). Comparison of the deterministic and fuzzy ap-

proaches in HR planning. Journal of Industrial Strate-

gic Management, 1:39–50.

Interactive Fuzzy Decision Support to Adjust Human Resource Structures

447