When Should the Chicken Cross the Road?

Game Theory for Autonomous Vehicle - Human Interactions

C. W. Fox

1,2,3

, F. Camara

3,2

, G. Markkula

, R. A. Romano

, R. Madigan

and N. Merat

Ibex Automation Ltd, U.K.

School of Computer Science, University of Lincoln, U.K.

Institute for Transport Studies, University of Leeds, U.K.

Keywords:

Autonomous Vehicles, Human Factors, Game Theory.

Abstract:

Autonomous vehicle localization, mapping and planning in un-reactive environments are well-understood, but

the human factors of complex interactions with other road users are not yet developed. This study presents an

initial model for negotiation between an autonomous vehicle and another vehicle at an unsigned intersections

or (equivalently) with a pedestrian at an unsigned road-crossing (jaywalking), using discrete sequential game

theory. The model is intended as a basic framework for more realistic and data-driven future extensions. The

model shows that when only vehicle position is used to signal intent, the optimal behaviors for both agents

must include a non-zero probability of allowing a collision to occur. This suggests extensions to reduce this

probability in future, such as other forms of signaling and control. Unlike most Game Theory applications in

Economics, active vehicle control requires real-time selection from multiple equilibria with no history, and we

present and argue for a novel solution concept, meta-strategy convergence, suited to this task.

1 INTRODUCTION

Automated vehicle (AV) localization, mapping, and

planning have recently become practically feasible

due to price falls in computer processing power. The

problem of simultaneous localization and mapping

(SLAM) is well understood (Thrun et al., 2005),

and despite its exact solution being NP-hard (Soto-

Alvarez and Honkamaa, 2014), good approximati-

ons exist such as particle ﬁltering, which make use

of large compute power to draw samples near soluti-

ons. Route planning in non-interactive environments

also has well known tractable solutions such as the

A-star algorithm. Given a route, localizing and cont-

rol to follow that route then becomes a similar task to

that performed by the 1959 General Motors Firebird-

III self-driving car (Bidwell et al., 1959), which used

electromagnetic sensing to follow a wire built into the

road. Such path following, using wires or SLAM, can

then be augmented with simple safety logic to stop

the vehicle if any obstacle is in its way, as detected by

any range sensor. Free and open source systems for

this level of ‘self-driving’ are now widely available

(Kato et al., 2015).

In contrast, problems that these vehicles will face

around interacting with other road users are much har-

der both to formulate and solve. Autonomous vehi-

cles do not just have to deal with inanimate objects,

sensors, and maps. They have to deal with other

agents, currently human drivers and pedestrians and

eventually other autonomous vehicles, all of which

may be at least as “intelligent” and “rational” as they

are, and in competition with them for space, time and

priority on the road. Recent studies have shown (Ma-

digan et al., tion) that in trials of autonomous mi-

nibuses, pedestrians knowingly obstruct autonomous

vehicles around once every three hours – enough to

occur once every day on a long commute. Once hu-

man road users know that AV safety systems are pro-

grammed to stop if any obstacle is in their path, they

can quickly take advantage of this to push in front of

the AV and take priority. If this becomes common

knowledge across a whole city, AVs will make little

or no progress because they will be forced to yield at

every single interaction.

Understanding and predicting other agents’ beha-

vior, especially when that includes understanding and

predicting their understandings and predictions of on-

eself, and of one’s understanding and predictions of

them, ad inﬁnitum, is a massively more complex pro-

blem than inferring locations and maps. It may even

be formally uncomputable as it requires predictions

of and actions based on one’s future behavior (via the

other party’s models of it), which are well known in

Computer Science to lead to paradox and uncomputa-

bility as in G

odel’s theorem and the Halting problem

Fox, C., Camara, F., Markkula, G., Romano, R., Madigan, R. and Merat, N.

When Should the Chicken Cross the Road?.

DOI: 10.5220/0006765404310439

In Proceedings of the 4th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2018), pages 431-439

ISBN: 978-989-758-293-6

431

(Velupillai, 2009).

Game Theory provides some framework for ma-

naging such self-referential decisions, but appears to

be incomplete as a prescriptive theory when multiple

equilibria are present. Solutions may be formally

computationally intractable (NP-hard) in some cases

(Papadimitriou and Roughgarden, 2005). And when

multiple equilibria are present, it is not clear whether

game theory or any other rational line of argument

will ever be able to even formulate the problems, let

alone solve them. A simple example of game theory

is the classic game ‘Chicken’, in which two cars

each drive straight towards each other at speed or

swerve away, and the nominal loser (the ‘chicken’)

is the one to swerve, but both players are much

bigger losers if they both do not swerve, and collide.

The classic formal Chicken model makes the strong

and unrealistic assumption that the straight/swerve

decision is made as a pair of simultaneous action

selections, (a

) by both players (Y and X) so that

the payoff values given the actions can be represented

as a 2×2 matrix of pairs (v

) :

Y \ X a

=swerve a

=straight

=swerve (0,0) (-1, +1)

=straight (+1, -1) (-100,-100)

The central concept of game theory is equilibrium

(Nash et al., 1950) which for a 2×2 matrix game as

above describes any pair of strategies for the two play-

ers such that if either player knew the other’s they

would not change their own. Conceptually, if equili-

bria exist then one can usually be found via ‘ﬁctitious

play’, i.e. each player simulates her and her oppo-

nent’s behaviour in a virtual world where they know

each other’s strategies, until they converge. Strategies

are probability distributions over actions. If a game

has only one equilibrium then it is optimal for both

players to play its strategies. When there are multi-

ple equilibria, the question of what to do is less clear.

Historically, Game Theory has focused on description

of observed behaviors (how do people act? Why did

the chicken cross the road?) and mechanism design

(how can government make them act?) rather than

prescription (when should we act? When should the

chicken cross the road?) of real-time action selection

by agents. This is due to its roots in economics and

mathematics rather than robotics. This distinction be-

comes crucial when multiple equilibria are present in

a game. The descriptive school would say that any

of the equilibria are valid descriptions of what might

be observed in human behavior data (Ciliberto and

Tamer, 2009). The ‘mechanism design’ school typi-

cally argues (Palfrey, 1990) that the problem of equi-

librium selection is ‘unpleasant’ and should be avoi-

ded by changing the rules of the game to produce

a single unambiguous equilibrium which all players

can usefully use. For cases where the equilibrium

selection problem cannot be avoided in these ways,

many different solution concepts (aka. ‘equilibrium

reﬁnements’) have been proposed and debated (Bin-

more, 2007) for choosing between them. Two of these

are widely acknowledged to be ‘rational’ when app-

lied in order: 1. Dominance - Clearly, if an equili-

brium is worse for all players than at least one other,

then we discard it without question; 2. Evolutionary

stability / symmetry (ESS) - Assume everyone in the

world was to use the same equilibrium as me. Discard

equilibria where this would not work. These concepts

help to reduce the number of potential multiple equi-

libria but do not guarantee reduction to a unique one.

To discard further equilibria, more controversial con-

cepts have been debated (Binmore, 2007) including:

1. Trembling hand stability - Assume other player has

a small epsilon probability of making a mistake; pre-

fer equilibria that we converge back to if that happens;

2. Basin size (aka. ‘risk dominance’). Assume both

players use ﬁctitious play starting from maximum en-

tropy strategies. Consider which equilibrium attracts

from the most start points, and this thus most likely

to occur. 3. Social maximum (aka. ‘payoff domi-

nance’) Choose the equilibrium with the largest sum

of payoffs to all players (even if I am worse off than

in others). 4. Other arbitrary conventions. Such as

using the action with the ﬁrst letter in the alphabet.

These work only if all players agree to use them in

advance or can be argued to possess social knowledge

to make them conﬁdent that others will choose the

same ones as them. This appears to be the point where

the mathematics of Game Theory ends, and philoso-

phical debate about the meaning of ‘rationality’ takes

its place (Binmore, 2007). However, as autonomous

vehicle engineers building real-time control systems,

we must make some action selection in these situati-

ons, somehow.

Chicken is intended as a simple educational exam-

ple game and not as a model of real vehicles. This

study modiﬁes it into a general and more realistic

vehicle interaction problem, where an AV competes

for priority with another vehicle or a pedestrian step-

ping out in front of it, and allowing them to negotiate

with one another by observing each others’ behaviour

over time. Initially we consider the simplest possible

model of this class of problems, of an AV and another

similar vehicle approaching an unmarked intersection

at speed as in ﬁg. 1(left). This would also apply to the

case of two pedestrians meeting each other and nego-

tiating for space. We then extend it to cases where the

two players have asymmetric penalties in the event of

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

432

Figure 1: Scenario and model.

collision – modeling an AV encountering a potential

jaywalker stepping into the road, or an AV encounte-

ring a physically larger or smaller vehicle such as an

armored SUV or cyclist at an intersection. The model

proposed here is intended to be the simplest possible

which captures the dynamics of interest common to

these cases, but which can also serve as a foundation

for many more complex ones.

Game theory is used extensively in macroscopic

trafﬁc modeling via Wardrop equilibrium in ﬂow net-

works (Bolland et al., 1979) with focus on route se-

lection in large, economy-like, markets of many road

users rather than microscopic pairwise interactions.

Where game theory has been applied to pairwise traf-

ﬁc decisions, it has mostly been at the level of simple

single-shot games as reviewed in (Elvik, 2014). In a

few cases such as lane-changing (Meng et al., 2016;

Kim and Langari, 2014) and merging (Kita, 1999) it

has been extended to sequential games as used here,

but not for AV-pedestrian interactions as here. The

meta-strategy convergence concept used here is no-

vel to our knowledge, as is the use of the sequential

model as a foundation for AV-human intersection and

jaywalking control.

2 METHODS

Turn-taking model. In the simplest possible model we

set up two symmetric agents (vehicles or pedestrians)

approaching an intersection as a chess-like, discrete

space, discrete speed, and discrete time, turn-taking

game, as in ﬁg. 1(right). This does not yet use any

Game Theory because the players’ decisions are not

made at the same time. We will use it to introduce

notation and as a base to grow more detailed models.

We assume a (1 meter) grid world, with two straight

roads at right angles meeting at the intersection.

Assume one vehicle on each road, labeled

Y and X.

(We will later consider one player to be a pedestrian

We use the convention of writing Y before X, and

the orientation of the grid world of ﬁg. 1, to match

(row,column) matrix notation.

or different types of vehicle.) Assume discrete alter-

nating turns one per second, in which one vehicle can

choose either a 1m/s or 2m/s speed, i.e. move either

one box forward or two boxes forward. (This ensures

a ﬁnite game, because the vehicles are guaranteed

to move closer to the intersection at each step.

Formally, y and x are decreasing variants.) 2m/s is a

slow real world speed but is chosen to coincide with

simple integer movements of 1 or 2 boxes per turn.

(The reader may wish to multiply all distances and

speeds by 10 if they wish to think in more real-world

units.) Write y for Y’s distance in meters to the

intersection, x for X’s distance in meters. Assume a

crash occurs if the vehicles are in the same square

or if one vehicle is in the intersection square and the

other moves through it in a single step. (This may

be implemented by treating (y,x) ∈ {(0,0), (1,1)} as

crash states, and all other states with one agent at 0

or 1 as non-crash endgame states, avoiding the need

to model negative positions beyond the intersection.)

We assign (negative) utility U

crash

to each player for

a crash; otherwise −U

time

T where T is the number

of seconds it takes to reach the intersection from the

start of the game, and U

time

is the (positive) value of

saving one second of travel time. Assume that both

players have identical utility functions, and know this

to be the case. This game can be played, for example,

as a board game between two human players. The

turn-taking model can be solved by a standard (Rich

and Knight, 1991) backward induction max-max

tree search as in algorithm 1, where the boolean b

represents which player’s turn is current, t is time

elapsed, y and x are the two players’ positions,

and the results are expected value pairs for the two

players, v

y,x,t,b

=(v

y,x,t,b

Sequential chicken model. If we replace turn-

taking by simultaneous action selection by both

players at each discrete 1s turn, the model transforms

into a sequence of Game Theoretic matrix games

(“sub-games”). This is equivalent to a board game

where both players write down their speed choice (1

or 2) in secret then reveal them and make the moves

together rather than in turns. The payoffs of any

sub-game at state (y > 1,x > 1,t) become recursive

functions of the next states, (y − a

,x − a

,t + 1),

where a

∈ {1, 2} are the speed selection actions

for speeds of 1m/s and 2m/s. As in the turn-taking

model, these inductive values are based on the end-

game states when one or both vehicles have reached

the intersection (considered to occur at square 0 or

1). Consider the value v

y,x,t

= (v

y,x,t

) of the

sub-game when the game is in state (y,x,t). The in-

duction relation for this sub-game’s payoff matrix is,

When Should the Chicken Cross the Road?

433

y,x,t

= v(



v(y − 1,x − 1,t + 1) v(y − 1,x − 2,t + 1)

v(y − 2,x − 1,t + 1) v(y − 2,x − 2,t + 1)



)

and is computable via standard matrix Game Theory.

Optimal mixed strategies, where they exist, and re-

sulting state probabilities given an initial start state,

for this model are shown in ﬁg. 2.

Algorithm 1

world_value((y,x,t,b)) =

if y==x==0 or y==x==1

or (y==1 and x==0) or (y==0 and x==1)

or (y==0 and x==-1) or (y==-1 and x==0):

(-100,-100) #crash

if y<=0 or x<=0:

(-t-y/2 , -t-x/2) #someone arrives

if b: #recursion

mymax(world_value((y-2,x,t+1,False)),

world_value((y-1,x,t+1,False)))

if not b: #recursion

yourmax(world_value((y, x-2, t+1, True)),

world_value((y, x-1, t+1, True)))

Asymmetric utility model. A ﬁnal model asks what

happens if the two players have different collision uti-

lities. This occurs for example if one player has a he-

avier/safer car than the other, such as an SUV (Sports

Utility Vehicle). Or if one player is a weaker road user

such as a cyclist, or a pedestrian negotiating to cross

the road in a conﬂict zone in front of our AV. Will

even a small change in these utilities break the sym-

metry of the sequential chicken model and tip the ba-

lance of who yields? If so, this would give a rational

justiﬁcation for the purchase of heavy vehicles such

as SUVs: the intent of such purchases is not to actu-

ally get into collisions and beneﬁt from reduced da-

mage, but rather to maintain the possibility, however

remote, of such a disaster, and exploit the backward

induction from it to obtain concessions in more be-

nign possible worlds, namely of the other player yiel-

ding. Purchase of an SUV would then be rational,

reducing the cost of time delays to the owner. (There

is of course then a higher level game when the other

road users can buy similar vehicles, beyond the scope

of our present model.) For simplicity we retain the as-

sumption that both players have the same time delay

utilities, U

time

as in the previous model, but we now

consider scenarios where one player is stronger than

the other, as (U

crash

) = (U

crash

,rU

crash

), for ra-

tios r ∈ [1,100]. When utilities become asymmetric it

is possible that more equilibria will be present, so we

switch to numerical computation of them using the

Lemke-Howson algorithm.

Meta-strategy convergence. The asymmetric chic-

ken model may have multiple equilibria which are

not fully disambiguated by dominance and ESS so-

lutions concepts. We propose a novel (to our know-

ledge) solution concept for use in solving this and ot-

her models, which we call meta-strategy convergence.

This is based on everything we currently know about

the ‘rational’ process of equilibrium pruning and se-

lection, including the absence of information in some

cases, and on a temporal ordering of rational reaso-

ning. After removing dominated and non-ESS equili-

bria, we know of no good remaining solution concepts

under the assumption that the other player is also ra-

tional. (Trembling hand, basins etc. make a diffe-

rent assumption about a fallible opponent, but for AVs

which will eventually interact with other autonomous

vehicles, we want all players to be completely mecha-

nized and rational.) In the absence of any other way

to select from the remaining equilibria’s strategies, we

form a new meta-strategy which chooses one of them

from a ﬂat (maximum entropy) prior. By symmetry,

there is no way to prefer any over any other, hence

their selection probabilities must be equal, given this

state of knowledge. Curiously, this is equivalent to a

new strategy which averages the action probabilities

from each remaining strategy, yet is not itself in that

set, because it is an average between them. Hence,

it is not a member of any equilibrium and cannot be

an optimal strategy itself. However, we have deri-

ved it step-by-step over time in a completely rational

way. It is our best solution so far at this new point in

time. As it is our best rational solution at this time,

the other player will also compute that we have re-

ached it. We then consider, as in standard ﬁctitious

play, what the other player will do next. They will ap-

ply ﬁctitious play to modify their strategy in response.

Then we will modify ours, and they will modify theirs

again. This will iterate until we converge, unambigu-

ously, onto a speciﬁc and uniquely deﬁned one of the

original equilibria. This contains the rational strate-

gies for both players, and can be reached determinis-

tically by both of them without the need for any pre-

established conventions or communications. Like all

solution concepts, this is something of a philosophi-

cal rather than purely mathematical argument. It is

the best argument currently known to us so we consi-

der it to be rational for the AV control tasks.

Temporal gauge invariance. The state values of

the game theoretic models above are presented as

functions of (y,x,t) but our current implementation

makes use of an approximation to reduce the num-

ber of sub-games to be solved and thus the compu-

tation time. Because both player’s utilities are li-

near functions of time, we may (up to a small er-

ror in the ratio of crash to delay utilities) choose dif-

ferent gauges to measure time, such as considering

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

434

P(a

= 1|y,x,t) =

y−1,x−2,t+1

− v

y−2,x−2,t+1

y−1,x−2,t+1

+ v

y−2,x−1,t+1

− v

y−1,x−1,t+1

− v

y−2,x−2,t+1

P(y

init

) = 1,P(y

init

,x 6= x

init

) = 0,P(y 6= y

init

) = 0

P(y, x,t) =

∑

∆y∈1,2

∑

∆x∈1,2

P(a

= ∆y, a

= ∆x|y − ∆y,x − ∆x,t − 1)P(y − ∆y, x − ∆x,t −1)

Figure 2: Strategy selection (1) and backward induction state probability (2-3) equations.

the time of every turn game to be t = 0. When the

ﬁrst player, say Y , reaches the intersection, we as-

sign values (v

0,x

) = (0, −U

time

x/2) as it will take

X a further x/2 seconds to reach the intersection at

maximum speed 2m/s now the road is clear. (Also

1,x

) = (0, −U

time

(x − 1)/2) to handle the other

required end states in the same way.) This simpliﬁes

all state values and functions of them to be functions

only of (y,x). Removing dependence on t also makes

it simpler to visualize results as 2D (y, x) matrices.

3 RESULTS

Assume U

crash

= −20 and U

time

= 1 throughout. (This

values a crash as being equally bad as a 100 second

delay reaching the intersection. In the real world the

crash penalty would be much larger, but smaller ones

produce more easily visualizable results for our pre-

sent purpose.)

Turn-taking model. The value function for Y in

the turn-taking model is shown in ﬁg. 3. The game

is symmetric so X has the same function when the

player’s names are swapped. The turn taking mo-

del is fully deterministic, because full information is

available to each player when it is their turn. Fig. 4

and 5 show simulated runs beginning at asymmetric

(y 6= x) and symmetric (y = x) starting states.When

the vehicles start with very different differences, e.g.

(y = 12,x = 8) they both proceed at full speed (2m/s)

and avoid each other. When started at identical dis-

tances, such as (y = 10,x = 10), the initial turn-taking

advantage becomes the tie-breaker, in both parties in-

terests. Collisions never occur in the turn-taking mo-

del due to its determinism.

Sequential chicken model. Fig. 6 shows the value

matrix for games with vehicles at up to 20m from the

intersection, and ﬁg. 7 show the optimal strategies.

Fig. 8 shows the state space probabilities and ﬁg.

9 shows a stochastic sample, starting with large time

(2 seconds) gap between the vehicles. All probabili-

ties in the state space are very close to 0 or 1, so the

outcome is almost deterministic as in the turn-taking

model of the same setting.

Fig. 10 shows state space probabilities when the

Figure 3: State values for turn-taking game.

Figure 4: Simulation of turn taking game, differing starts.

Figure 5: Simulation of turn taking game, equal starts.

vehicles start at identical distances y = x = 10. In this

case, the outcome is different from the turn-taking

model, because the game is fully symmetric but the

symmetry is no longer broken by turn-taking. This

means that both players must employ a policy consis-

ting of mixed strategies until the symmetry is broken

When Should the Chicken Cross the Road?

435

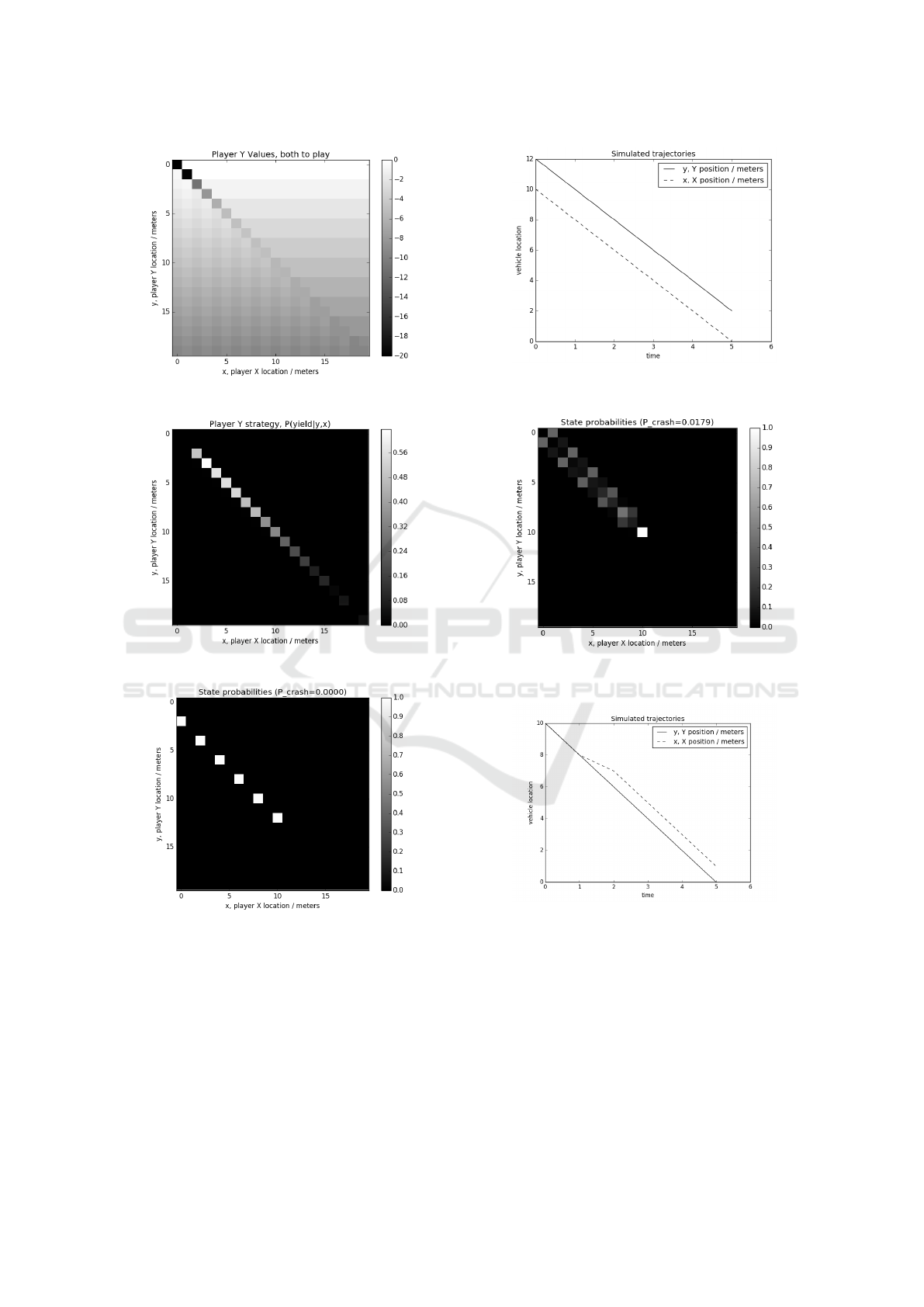
Figure 6: Sequential chicken state values.

Figure 7: Sequential chicken optimal strategy.

Figure 8: Sequential chicken state probabilities, from asym-

metric start (12,10).

by one of them. The optimal policy is to yield with

an increasing probability as distance to collision de-

creases, as seen in ﬁg. 7. Fig. 11 is a typical sample

simulation drawn from the above state probabilities.

The most common outcome is for one vehicle to yield

at a random time, with yield probability increasing as

the vehicles draw closer.

Occasionally, as in ﬁg. 12, both players choose

Figure 9: Sequential chicken simulation, from asymmetric

start (12,10).

Figure 10: Sequential chicken state probabilities, from sym-

metric start (10,10).

Figure 11: Sequential chicken typical simulation, from

symmetric start (10,10).

to yield at the same time, prolonging the conﬂict and

costing them both a delay. Very occasionally a col-

lision will occur as a result of this process, when the

players fail to negotiate priority before both reaching

the intersection together. This is rare, but must have a

non-zero probability, computed and denoted as P

crash

The collision probability with U

crash

= −20 is

1.79%, and with U

crash

= −100 it lowers to 0.7%. It

is interesting to test how choice of this scaling (versus

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

436

Figure 12: Sequential chicken atypical simulation, from

symmetric start (10,10).

Figure 13.

Figure 14.

the ﬁxed U

time

=1) affects the residual collision proba-

bility, because if it has a large effect then any realis-

tic model will require scaling calibration against some

empirical data. Assuming that both players continue

to share the same utility function, and know this to

be the case, ﬁg. 12 shows the effect of varying the

collision utility scale while keeping the time utilities

ﬁxed.

This suggests that choices in range [-1000,0] do

have large effects on the collision probability, but pen-

alties worse than -1000 are much the same as each ot-

her in this effect. In real life, the cost of crashing a car

(even very slightly) is almost always vastly larger than

that of losing a few seconds journey time. This graph

suggests that for these realistic penalties, the precise

choice of shared collision penalty values is unimpor-

tant as long as it is over 1000 times worse than a 1

second time delay penalty.

Asymmetric utility model. As hypothesized, asym-

metric collision penalties (such as our AV encounte-

ring a strong SUV or a weak cyclist or pedestrian)

have a large effect on who must yield, and with a

very small change in the probability of actual colli-

sion. This small change is the key to breaking sym-

metry and ensuring strong probability of the weaker

player yielding ﬁg. 12.

4 CONCLUSION

In all the models, when one agent has any small ad-

vantage it is usually – but probabilistically – optimal

for both agents for the strong one to take the priority

and the weak one to yield.

It is essential that there is some small but strictly

non-zero probability of collision being allowed to

occur as a consequence of both sides’ optimal strate-

gies. It is impossible for an AV to make any progress

at all if this is not the case, because given this kno-

wledge, every single other road user could dominate

them in any conﬂict - even pedestrians jumping out in

front of them for fun as seen in real-world trials (Ma-

digan et al., tion). Under these models, it is essential

that AVs are programmed with a non-zero probability

of deliberately causing a collision. This may be le-

gally difﬁcult, as such programming may be argued

to constitute not only manslaughter but also murder,

being rationally pre-meditated by the software engi-

neer.

These results are interesting as they suggests that

purchasing SUVs, or armoring our autonomous vehi-

cle like an SUV, is a very rational strategy, not in order

to better survive the rare collisions that do occur, but

to ensure a high probability of other vehicles getting

out of our way to save our time and money on delays.

By adding armor to our own vehicle we can make the

optimal strategy for the other player yielding tend to-

wards certainty at every encounter. This also models

what will happen when our AV encounters a pede-

strian. The larger cost of collision to the pedestrian

than to our AV gives us a strong position, from which

we can act aggressively and be conﬁdent that the pe-

destrian will yield. The answer to ‘When should the

chicken cross then road?’ is ‘quite rarely if there is a

car coming, but with non-zero probability’.

We found that the way in which the models quan-

tize time is important. The turn-taking model arti-

ﬁcially removed most of the subtly of game theory

When Should the Chicken Cross the Road?

437

by breaking its symmetry via the turn taking mecha-

nism itself. This suggests that such a quantization is

not a good model for the real world, it hides the main

problem of the scenario from the start. A related mo-

deling issue around time relates to Zeno’s Paradox. In

the models presented here, time ticks are discrete and

of equal length. It might be argued that two Zeno-like

players could choose to deﬁne each of their ticks to

have half the duration of the previous one, and thus

create an inﬁnite number of ticks which would be cer-

tain to eventually lead to an asymmetric yield and

avoidance of collision. Formal mathematical analy-

sis of this claim could form future work, though in

practice, any human or machine compute system has

some ﬁnite limit on its computation speed.

Extended models should handle speed more re-

alistically. Rather than just two discrete speeds, a

continuum of speeds should be available, including

stopping at a complete halt. Continuous speeds may

require sampling approximations to compute over,

while complete halts allow for potentially inﬁnite

time games which require further consideration to

model. Human drivers when faced with, for example,

a busy motorway merge, may gradually slow down

towards a halt at the end of the slip-road, while dri-

vers in their path may do the same. Perhaps under a

continuous speed model this behavior can be shown

to converge safely as everyone slows down towards a

halt and reduces both the probability and penalty of

collisions. Nevertheless, the underlying logic must

still hold - that there must be a credible threat of

a non-zero probability of causing some collision, in

order that the other party cannot take advantage of

the AV every time. Future models should add furt-

her realistic details to the framework. Real drivers

do not know each other’s utility functions and must

infer them in an information game during the inte-

raction. This could include giving and reading signals

about utility such as the model, age, colour and clean-

liness of their cars, their lateral positions on the road,

their facial expressions and hand gestures as well as

more formal car signaling via light ﬂashing and horn

usage. Real drivers may not have Markovian time de-

lay utilities and more detailed models should allow for

time dimensioned value functions v(y,x,t) rather than

than simpler v(y, x) used here. Trafﬁc regulations and

conventions such as legally binding and non-binding

signs and lights, and the cost of public humiliation or

legal action for being seen or recorded breaking them

should be added to modify utilities. Such models sug-

gest new signaling conventions for autonomous vehi-

cles, such as use of V2V radio communications and

virtual currencies to aid negotiations; or the use of

small AV-mounted water-pistols to induce small ne-

gative utilities in assertive pedestrians in place of ac-

tually hitting them.

ACKNOWLEDGEMENTS

This project has received funding from the European

Union’s Horizon 2020 Research and Innovation pro-

gramme under grant agreement InterACT No 723395.

REFERENCES

Bidwell, J., Cataldo, R., and Van House, R. (1959). Chassis

and control details of Firebird III. Technical report,

SAE Technical Paper.

Binmore, K. (2007). Playing for real: a text on game the-

ory. Oxford university press.

Bolland, J., Hall, M., Van Vliet, D., and Willumsen, L.

(1979). Saturn: Simulation and assignment of trafﬁc

in urban road networks. In Proceedings of the Inter-

national Symposium on Trafﬁc Control Systems, Ber-

keley, Calif. D, volume 2, pages 99–114.

Ciliberto, F. and Tamer, E. (2009). Market structure and

multiple equilibria in airline markets. Econometrica,

77(6):1791–1828.

Elvik, R. (2014). A review of game-theoretic models of

road user behaviour. Accident Analysis & Prevention,

62:388–396.

Kato, S., Takeuchi, E., Ishiguro, Y., Ninomiya, Y., Takeda,

K., and Hamada, T. (2015). An open approach to au-

tonomous vehicles. IEEE Micro, 35(6):60–68.

Kim, C. and Langari, R. (2014). Game theory based auto-

nomous vehicles operation. International Journal of

Vehicle Design, 65(4):360–383.

Kita, H. (1999). A merging–giveway interaction model of

cars in a merging section: a game theoretic analysis.

Transportation Research Part A: Policy and Practice,

33(3):305–312.

Madigan, R., Nordhoff, S., Fox, C., Ezzati Amini, R.,

Louw, T., Wilbrink, M., Schieben, A., and Merat, N.

(in preparation). Understanding interactions between

automated vehicles and other road users. Manuscript

in preparation.

Meng, F., su, J., Liu, C., and Chen, W.-H. (2016). Dyn-

amic decision making in lane change: Game theory

with receding horizon. In Conference: 11th UKACC

International Conference on Control.

Nash, J. F. et al. (1950). Equilibrium points in n-person ga-

mes. Proceedings of the national academy of sciences,

36(1):48–49.

Palfrey, T. R. (1990). Implementation in Bayesian equili-

brium: the multiple equilibrium problem in mecha-

nism design.

Papadimitriou, C. H. and Roughgarden, T. (2005). Com-

puting equilibria in multi-player games. In Procee-

dings of the sixteenth annual ACM-SIAM symposium

on Discrete algorithms, pages 82–91. Society for In-

dustrial and Applied Mathematics.

VEHITS 2018 - 4th International Conference on Vehicle Technology and Intelligent Transport Systems

438

Rich, E. and Knight, K. (1991). Artiﬁcial intelligence.

McGraw-Hill, New.

Soto-Alvarez, M. and Honkamaa, P. (2014). Multi-

ple hypotheses data association propagation for ro-

bust monocular-based SLAM algorithms. In Acou-

stics, Speech and Signal Processing (ICASSP), 2014

IEEE International Conference on, pages 6543–6547.

IEEE.

Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic

robotics. MIT press.

Velupillai, K. V. (2009). Uncomputability and undecida-

bility in economic theory. Applied Mathematics and

Computation, 215(4):1404–1416.

When Should the Chicken Cross the Road?

439