
Scalable Data Placement of Data-intensive Services in Geo-distributed
Clouds
Ankita Atrey, Gregory Van Seghbroeck, Bruno Volckaert and Filip De Turck
IDLAB-imec, Technologie Park, UGent, Gent, Belgium
Keywords:
Data Placement, Geo-distributed Clouds, Location-based Services, Online Social Networks, Scalability,
Spectral Clustering, Hypergraphs, Approximation.
Abstract:
The advent of big data analytics and cloud computing technologies has resulted in wide-spread research in
finding solutions to the data placement problem, which aims at properly placing the data items into distributed
datacenters. Although traditional schemes of uniformly partitioning the data into distributed nodes is the de-
facto standard for many popular distributed data stores like HDFS or Cassandra, these methods may cause
network congestion for data-intensive services, thereby affecting the system throughput. This is because as
opposed to MapReduce style workloads, data-intensive services require access to multiple datasets within
each transaction. In this paper, we propose a scalable method for performing data placement of data-intensive
services into geographically distributed clouds. The proposed algorithm partitions a set of data-items into geo-
distributed clouds using spectral clustering on hypergraphs. Additionally, our spectral clustering algorithm
leverages randomized techniques for obtaining low-rank approximations of the hypergraph matrix, thereby
facilitating superior scalability for computation of the spectra of the hypergraph laplacian. Experiments on a
real-world trace-based online social network dataset show that the proposed algorithm is effective, efficient,
and scalable. Empirically, it is comparable or even better (in certain scenarios) in efficacy on the evaluated
metrics, while being up to 10 times faster in running time when compared to state-of-the-art techniques.
1 MOTIVATION
Since the advent of the Internet, the scale at which
data is being generated and processed is increasing
at an exponential rate (ins, 2017). Today, we live
in a world that is data-rich or what is also referred
to as the Information age. For instance, the amount
of data managed by Internet giants like Google and
Facebook is of the order of thousands of petabytes
(sca, 2015). The advancements in big data and cloud
computing technologies have definitely enriched the
field of scalable data management with state-of-the-
art distributed data processing systems like Hadoop
and more recently Apache Spark. The main idea
employed in these systems is to uniformly distribute
data across servers and perform parallel computations
on the so-constructed small subsets of data on each
server independently. While uniform data partition-
ing schemes using hashing work well for MapReduce
style workloads that can be easily parallelized, they
are not suitable for data-intensive workloads that re-
quire access to multiple datasets within each trans-
action (Yu and Pan, 2015; Golab et al., 2014). In
these scenarios uniform partitioning may result in a
huge volume of data migrations thereby leading to
network congestion and eventually reduced system
throughput, especially in the case of geographically
distributed datacenters where inter-datacenter com-
munication latencies and costs are high. Having said
that, there is a need for specialized data placement
strategies capable of addressing the previously dis-
cussed deficiencies for data-intensive services.
Data-intensive services are becoming increasingly
common in a plethora of real-world scenarios, namely
– online social networks (OSNs), content distribu-
tion networks (CDNs) etc. Additionally, ubiquity of
the cloud and increased reliance of people across the
globe on online services like OSNs and CDNs, re-
quires data to be stored in datacenters that are geo-
graphically distributed. The workload generated by
these services present two niche challenges that are
non-existent in MapReduce style workloads. (1) In
the case of CDN services like YouTube the hosted con-
tent is stored in datacenters situated around the world.
It is highly likely that the set of contents retrieved
by a user query may be stored in different datacen-
Atrey, A., Van Seghbroeck, G., Volckaer t, B. and De Turck, F.
Scalable Data Placement of Data-intensive Services in Geo-distributed Clouds.
DOI: 10.5220/0006767504970508
In Proceedings of the 8th International Conference on Cloud Computing and Services Science (CLOSER 2018), pages 497-508
ISBN: 978-989-758-295-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
497

!
"
!
#
!
$
!
%
!
&
!
'
!
(
)*+,
-.*/
0123,.+45*
!
(
!
"
62!
#
62!
'
62!
&
62!
%
62!
$
!
"
!
(
62!
#
!
#
!
(
62!
"
!
'
!
(
62!
&
!
&
!
(
62!
'
!
%
!
(
62!
$
!
$
!
(
62!
%
!
(
!
"
!
&
!
$
!
#
!
(
!.,7.4.8
98:.10,4.8
;0<=0
3,84<1>,/
?=54+=
Figure 1: Use Case: A Location-based OSN service.
ters across the globe. Similar is the case for OSNs
as well. (2) Moving ahead, since the users of OSN
services like Facebook may register check-ins at vari-
ous locations across the world, not only the data-items
but also the source locations of data requests are geo-
graphically distributed.
Motivated by the above discussions, the problem
of data placement for data-intensive services in data-
centers that are distributed geographically across the
world is the topic of research detailed in this pa-
per. The use case under investigation is a location-
based OSN service as portrayed in Fig 1. A sample
Facebook social network is represented using a graph
where each vertex corresponds to a user and undi-
rected edges between two vertices represent friend-
ship. In this network, users {v
1
,v
5
} are friends of the
user v
4
. Similarly {v
6
,v
1
} are friends of v
7
. Addi-
tionally, the list of all the friends of every user is also
portrayed in the table presented right above the social
network. Each user can register a check-in, which is
denoted by her user-id assigned to a datacenter near-
est to her check-in location. In Fig. 1, the user v
1
has registered two check-ins, at datacenters located
in Virginia and Tokyo respectively, while user v
2
has
checked-in at Frankfurt. Moreover, each user check-
in requires data-items corresponding to all her friends,
which constitutes the data request pattern triggered
by this check-in. For example, a check-in by user v
5
in Sydney would trigger a data request requiring the
data-items corresponding to her friends {v
1
,v
4
} to be
transferred to that location.
While data placement has been studied exten-
sively (Golab et al., 2014; Yuan et al., 2010; Ebrahimi
et al., 2015; Jiao et al., 2014), literature on geo-
distributed data-intensive services is relatively scarce
(Yu and Pan, 2017). Any successful solution to this
problem should provide two capabilities, namely –
capturing and improving (1) data-item – data-item
associations; and (2) data-item – datacenter associa-
tions. State-of-the-art methods proposed in (Nishtala
et al., 2013) and (Agarwal et al., 2010) are capable
of improving data-item – data-item, and data-item –
datacenter associations respectively, however, these
methods cannot jointly handle both aspects. To jointly
incorporate both aspects, (Yu and Pan, 2015; Yu
and Pan, 2017) recently proposed a multi-objective
data placement algorithm using hypergraphs. Hy-
pergraphs offer a powerful representation by present-
ing a natural way of capturing multi-way relation-
ships. Similar to graph partitioning however, hyper-
graph partitioning is NP-Hard. To this end, the au-
thors use heuristic partitioning algorithms available in
a publicly available tool – PaToH (Catalyurek, 2011),
to efficiently partition large hypergraphs. However,
as shown in Sec. 6, PaToH lacks scalability under cer-
tain scenarios while also suffering in terms of efficacy.
To bridge this gap, in this paper, we propose a novel
scalable method for data placement through Spectral
Clustering on Hypergraphs.
Owing to their strong mathematical properties
spectral methods have been shown to be promising
in a plethora of areas of machine learning with semi-
nal research by (Shi and Malik, 2000; Spielmat, 1996;
Meila and Shi, 2001; Ng et al., 2001). Despite the ad-
vantages offered by spectral methods: superior effi-
cacy, strong mathematical properties etc., they are not
usually efficient and scalable on large scale data. We
mitigate the issue of lack of scalability by proposing
an approximate spectral clustering algorithm, thereby
bringing the power of spectral methods to perform ef-
fective hypergraph clustering. To summarize, the key
contributions of this work are as follows.
• We study the data placement problem in a chal-
lenging and close to real-world setting of data-
intensive services in geo-distributed datacenters
(Sec. 3), where traditional methods of hash based
partitioning that are prominent in systems like
Hadoop and Spark do not perform well.
• We propose a novel scalable algorithm to solve
the data placement problem for geo-distributed
data-intensive services through Spectral Cluster-
ing on Hypergraphs (Sec. 4).
• Through extensive experiments on a real-world
trace-based social network dataset (Secs. 5 and 6),
we show that the proposed spectral clustering al-
gorithm is scalable, and provides a speed-up of
up to 10 times over the state-of-the-art hyper-
graph partitioning method while portraying sim-
ilar (or in some cases even better) efficacy on sev-
eral evaluation metrics.
2 RELATED WORK
The data placement problem has been studied ex-
tensively in the literature spanning a wide-variety of
CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science
498

research areas, both from the perspective of execu-
tion environments: ranging from distributed systems
(Chervenak et al., 2007; Golab et al., 2014) to cloud
computing environments (Yuan et al., 2010; Li et al.,
2017; Ebrahimi et al., 2015; Liu and Datta, 2011); ap-
plication areas: online social network services (Jiao
et al., 2014; Han et al., 2017), location aware data
placement for geo-distributed cloud services (Yu and
Pan, 2017; Zhang et al., 2016; Yu and Pan, 2015; Yu
and Pan, 2016; Agarwal et al., 2010), and many more.
Here, we provide an overview the existing works that
overlap with our problem.
Research on data placement in geo-distributed
clouds has increasingly gained popularity over the
years. Owing to multiple niche challenges as dis-
cussed in Sec. 1, specialized solutions have been de-
vised to solve this problem. The biggest challenge
for data placement algorithms in such scenarios is that
data migrations from one location to another is signif-
icantly more expensive and problematic when com-
pared to other real-world scenarios like grids, clusters,
or private clouds where distance between data-centers
is not significant.
(Agarwal et al., 2010) proposed a system: Volley,
to perform automatic data placement in geographi-
cally distributed datacenters. The proposed system
possesses the capability to capture data-item – dat-
acenter associations, however, it lacked the capabil-
ity for handling data-item – data-item associations.
(Jiao et al., 2014) formulates a multi-objective so-
cial network aware optimization problem that per-
forms data placement by building a model frame-
work, which takes multiple objectives into consider-
ation. (Han et al., 2017) introduce an adaptive data
placement algorithm for social network services in a
multicloud environment, which adapts to the chang-
ing data traffic for performing intelligent data migra-
tion decisions. (Rochman et al., 2013) have focused
on placing data in a distributed environment to en-
sure that a large fraction of region specific requests
are served at a lower cost. In (Huguenin et al., 2012),
a user generated content (UGC) dataset (with more
than 650000 YouTube videos) is used to show the cor-
relation between the content locality and geographic
locality. (Zhang et al., 2016) propose an integer pro-
gramming based data placement algorithm capable of
minimizing the data communication cost while honor-
ing the storage capacity of geo-distributed datacenters
as well.
Researchers have also focused on the design of
specialized replication strategies for geo-distributed
services. (Kayaaslan et al., 2013) have proposed a
document replication framework to deal with the scal-
ability issues. In this replication framework, docu-
Table 1: Summary of notations used.
Item Definition
V The set of users in the social network V = {v
1
,v
2
,..., v
n
}.
E The set of edges in the social network ∀e = (v
x
,v
y
) ∈ E.
Adj(v) The set of friends of the user v | v ∈ V.
D The set of data-items D = {d
v
1
,d
v
2
,..., d
v
n
}.
L The set of datacenters and their locations L = {L
1
,L
2
,..., L
l
}.
R The set of request patterns R = {R
1
,R
2
,..., R
r
}.
C The set of user check-ins C = {C
k
= (R
i
,L
j
) | ∃R
i
∈ R , L
j
∈ L}.
Π The hypergraph incidence matrix.
W
Π
The hyperedge weight matrix.
Φ The desired datacenter storage distribution.
P (D) A partition on the set of data-items D.
Γ(L
j
) Cost (per unit) of outgoing traffic from datacenter L
j
.
κ(L
j
,L
j
0
) Inter datacenter latency (directed) between L
j
and L
j
0
.
S(L
j
) Storage cost (per unit) of datacenter L
j
.
N (R
i
) Average number of datacenters accessed by request R
i
.
ments are replicated on datacenters based on region
specific user interests. (Shankaranarayanan et al.,
2014) propose replication strategies for a class of
cloud storage systems denoted as quorum-based sys-
tems (viz. Cassandra, Dynamo) capable of solv-
ing the data placement problem cognizant of var-
ious location-aware metrics like location of geo-
distributed datacenters, inter-datacenter communica-
tion costs etc.
(Golab et al., 2014) prove the reduction of data
placement problem to the well known graph parti-
tioning problem and propose an integer linear pro-
gramming solution. The authors also propose two
scalable heuristics to reduce the data communication
cost for data-intensive scientific workflows and join-
intensive queries in distributed systems. In (Qua-
mar et al., 2013), the authors study the problem of
OLTP workloads in cloud computing environments,
and propose a scalable workload aware data partition-
ing and data placement approach called SWORD to
reduce the partitioning overhead. SWORD is pro-
posed as a two phase approach: in the first phase a
workload is modeled as a hypergraph which is further
compressed by using hash partitioning, and later the
compressed hypergraph is partitioned to get the place-
ment output. Hypergraph based partitioning solutions
(Catalyurek et al., 2007) have also been used in grid
and distributed computing environments previously.
Recently, (Yu and Pan, 2015; Yu and Pan, 2016;
Yu and Pan, 2017) propose data placement strategies
using hypergraph modeling and publicly available
partitioning heuristics (Catalyurek, 2011) for data-
intensive services, which constitutes the current state-
of-the-art for location-aware data placement in geo-
distributed clouds. The research presented in this pa-
per proposes a novel hypergraph partitioning scheme
using spectral clustering and enjoys strong mathemat-
ical properties and improved efficacy when compared
to the competing techniques. Moreover, it enjoys su-
perior efficiency and scalability by employing low-
rank matrix approximations while retaining the same
efficacy as portrayed by the state-of-the-art.
Scalable Data Placement of Data-intensive Services in Geo-distributed Clouds
499

Virginia
Frankfurt
California
Tokyo
Sydney
|
|
|
d
V3
Datacenters
Data)Request)Patterns
Data)item
Data)Request)pattern
Data)Request)- Datacenter)Edge
d
V2
d
V4
d
V5
d
V6
d
V7
d
V1
d
V3
d
V5
d
V7
d
V6
d
V4
d
V2
d
V3
d
V1
R
1
R
2
R
3
R
1
R
3
R
2
L
1
L
2
L
3
L
4
L
5
d
V1
d
V2
Figure 2: Mapping of different requests to geo-distributed
datacenters.
3 PROBLEM STATEMENT
In this section, we formally define the data placement
problem for data-intensive services in geo-distributed
datacenters. Table 1 summarizes the notations used in
the rest of the paper.
A location based online social network (Fig. 1)
is represented using a graph G(V, E), where V rep-
resents the set of users, and E represents the set of
edges (denoting friendship) between any two users of
the social network. The set D contains n data-items
corresponding to each user v ∈ V of the social net-
work. Each user v ∈ V can register a check-in, where
a check-in is a tuple C
k
= (R
i
,L
j
) ∈ C composed of
a data request pattern R
i
∈ R and a datacenter loca-
tion L
j
∈ L. Each data request pattern R
i
is com-
prised of a set of data-items D ⊆ D requested by a
user v ∈ V . As discussed in Sec. 1, considering the lo-
cation based social networks use-case, a data request
pattern R
i
belonging to a check-in C
k
registered by
a user v would comprise the data-items correspond-
ing to all the friends of v, i.e. R
i
= {d
u
| u ∈ Adj(v)}.
Moving ahead, L
j
∈ L represents the location of a dat-
acenter capable of serving user requests. The location
of a check-in C
k
is decided as the datacenter location
L
j
closest (in distance) to the actual physical location
of the user check-in. In other words, the check-in C
k
signifies a request for data-items contained in R
i
trig-
gered from the datacenter located at L
j
.
Next, we discuss the basic concepts described
above in the context of the location based online so-
cial networks use-case presented in Sec. 1. Fig. 2
builds upon the example portrayed in Fig. 1 to show-
case the data request patterns corresponding to the
check-ins registered by users v
1
,v
2
, and v
3
. Let us
denote the data request patterns as R
1
,R
2
, and R
3
respectively, where R
1
= {d
v
2
,d
v
3
,d
v
4
,d
v
5
,d
v
6
,d
v
7
},
R
2
= {d
v
1
,d
v
3
}, and R
3
= {d
v
1
,d
v
2
}. Let us also la-
bel the datacenter locations as L
1
= Virginia,L
2
=
Cali f ornia,L
3
= Frank f urt,L
4
= Sydney, and L
5
=
Tokyo. Recall that the user v
1
registered two check-
ins: one in Virginia and the other in Tokyo. Simi-
larly, v
2
registered a check-in in Frankfurt, while v
3
checked-in in Tokyo. Thus, in total there are four
check-ins: two (C
1
and C
2
) for the user v
1
, and one
each (C
3
and C
4
respectively) for users v
2
and v
3
,
where C
1
= (R
1
,L
1
), C
2
= (R
1
,L
5
), C
3
= (R
2
,L
3
), and
C
4
= (R
3
,L
5
).
Having defined the basic concepts and their nota-
tions, we formally define the problem as:
Problem. Given a set of n data-items D, m user
check-ins C
k
= (R
i
,L
j
) ∈ C , each comprising a data
request pattern R
i
being originated from a datacen-
ter located at L
j
, a set of l datacenters with loca-
tions in L, with the per unit cost of outgoing traf-
fic from each datacenter ∀L
j
∈ L,Γ(L
j
), the per unit
storage cost of each datacenter ∀L
j
∈ L,S (L
j
), the
inter datacenter latency (directed) for each pair of
datacenters ∀L
j
,L
j
0
∈ L,κ(L
j
,L
j
0
), and the average
number of datacenters accessed by the data-items re-
quested in each request pattern R
i
being N (R
i
), per-
form data placement to minimize the optimization ob-
jective O, which is defined as the weighted average of
Γ(·),κ(·,·),S(·), and N (·).
4 SPECTRAL CLUSTERING ON
HYPERGRAPHS
To effectively solve the data placement problem, we
propose a technique as outlined in Algorithm 1. Given
the set of data items D, and the set of user check-ins C
comprising the set of data request patterns R and their
locations L, we first construct a hypergraph. As dis-
cussed in Sec. 1, hypergraphs provide the capability
to capture multi-way relationships, thereby facilitat-
ing modeling of data-item – data-item and data-item –
datacenter location associations. With the hypergraph
incidence matrix Π constructed, next, we partition the
set of data-items D into l parts corresponding to the L
datacenters according to the desired storage distribu-
tion Φ, using the proposed scalable spectral clustering
algorithm. Fig. 3 portrays the overall scheme of our
method.
We next explain each of the fundamental steps in
detail.
Workload
Set+of+User+
Check-ins+
($)
Hypergraph+
Modelling
Hypergraph+
Incidence+
Matrix+(")
Spectral+
Clustering
Data+
Placement+
Output
Figure 3: Overview of our Approach.
CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science
500

4.1 Hypergraph Modeling
Continuing our discussion in Sec. 1, hypergraphs pro-
vide the ideal representation to solve the data place-
ment problem in geo-distributed datacenters owing
to their capability of capturing multi-way relation-
ships. A hypergraph H(V
H
,E
H
) is a more sophis-
ticated graph construct and a generalization over a
graph G(V,E), where (hyper)edges are capable of
capturing relationships between several vertices as
opposed to just a pair of vertices in graphs. This abil-
ity of hyperedges to capture higher order relationships
between data points facilitates the hypergraph model
to manage both data-item – data-item and data-item –
datacenter locations associations.
Algorithm 1: Data Placement Algorithm.
Input: D, C , R , L, G(V,E), Φ
Output: Partitioning of the set of data-items P (D) into l
datacenters
1: (Π, W
Π
) ← ConstructHypergraph(D,C , G(V,E))
2: P (D) ← SpectralClustering(Π, W
Π
,l, Φ)
3: return P (D)
In the context of our problem statement, every
user check-in C
k
∈ C consists of a datacenter loca-
tion L
j
∈ L and a data request pattern R
i
∈ R . Note
that for a check-in by a user v, R
i
is a set of data-
items corresponding to all the friends of v, i.e. Adj(v),
as portrayed by the social network G(V,E). Since a
data request pattern involves data-items correspond-
ing to multiple vertices of G(V,E), hyperedges pro-
vide a better way to model data-item – data-item as-
sociations by linking/connecting multiple data-items
via the same hyperedge. Additionally, hyperedges
also facilitate modeling of data-item – datacenter lo-
cation associations by connecting a data-item with a
datacenter location when a data-item d
V
i
is requested
from a datacenter location L
j
.
The hypergraph vertex set V
H
comprises of all the
data-items D and the datacenter locations L. Thus,
the number of vertices in the hypergraph are |V
H
| =
n
0
= n + l. Formally,
V
H
= D ∪ L (1)
Let R
L
= {∀d ∈ R
i
,∀L
j
∈ L|∃C
k
= (R
i
,L
j
) ∈
C ,R
d j
} denote the set of edges connecting data-items
with datacenter locations corresponding to all the data
request patterns R
i
∈ R triggered by user check-ins
C
k
∈ C at datacenter locations L
j
∈ L. The hyper-
graph edge set E
H
consists of hyperedges correspond-
ing to all the data request patterns R and all the data-
item – datacenter location edges R
L
. Thus, the num-
ber of hyperedges in the hypergraph are |E
H
| = m
0
=
r + nl. Formally,
E
H
= R ∪ R
L
(2)
Fig. 4a portrays the hypergraph representation of
the data-items and request patterns as presented in
Fig. 2. The data-items {d
v1
,. ..,d
v7
} and the dat-
acenter locations {L
1
,L
3
,L
5
} constitute the hyper-
graph vertex set. The hyperedges corresponding to
the data request patterns {R
1
,R
2
,R
3
} are labeled as
he1,he2, he3 respectively and are denoted using a
dashed ellipse, while the hyperedges connecting each
data-item – datacenter location pair are labeled as
he4,. ..,he17. Since v
2
,v
3
,v
4
,v
5
,v
6
,v
7
are friends
of v
1
, the data-items d
v2
,. ..,d
v7
belonging to the
request pattern R
1
are connected by the hyperedge
he1. Similarly, since v
7
is a friend of v
1
, who reg-
istered two check-ins: one at Virginia (L
1
) and the
other at Tokyo (L
5
), the hyperedge he4 = (d
v
7
,L
1
) and
he10 = (d
v
7
,L
5
) represents the relationship between
the data-item d
v
7
and the datacenter locations where
it was requested, namely – Virginia (L
1
) and Tokyo
(L
5
). Fig. 4b portrays the incidence matrix Π corre-
sponding to the hypergraph H presented in Fig. 4a.
As can be seen, the rows of this matrix are the ver-
tex set of the hypergraph, while the columns are the
hyperedges. Moreover, if a vertex participates in a hy-
peredge then the row corresponding to it contains a 1
in the column corresponding to that hyperedge, and
0 otherwise. Since the hyperedge he1 (corresponding
to the data request pattern R
1
) connects the data-items
d
v2
,. ..,d
v7
the entries in Π corresponding to them are
filled with 1 while all other entries are 0.
4.1.1 Calculating Hyperedge Weights
Having constructed the hypergraph H(V
H
,E
H
) and
discussed its representation using a hypergraph in-
cidence matrix Π, we next discuss ways to assign
weights to hyperedges. There are two major types
of hyperedges constructed in the representation dis-
cussed above: (1) Data request pattern hyperedges,
and (2) Data-item – Datacenter hyperedges, and both
of them capture different properties required by a data
placement algorithm in geo-distributed datacenters.
The weight of a data request pattern hyperedge W
R
is set using the request rate of that pattern, which is
defined as the number of times a data request pattern
is triggered by a user check-in. The weight W
R
fa-
cilitates prioritization of data-items that are usually
requested together, to be placed together by the data
placement algorithm, thereby helping optimize (min-
imize) N (R
i
): the average number of datacenters ac-
cessed by a data request pattern R
i
. On the other hand,
the weights (W
κ
R
L
,W
S
R
L
,W
Γ
R
L
) corresponding to data-
item – datacenter hyperedges (R
L
) facilitate mini-
mization of inter datacenter latency κ(L
j
,L
j
0
), storage
cost S (L
j
), and cost of outgoing traffic Γ(L
j
) respec-
Scalable Data Placement of Data-intensive Services in Geo-distributed Clouds
501

!
"#
!
"$
"%&'%(%)
*+,-+
.&)(,/0&1
Vertex&Set
Data&item
Datacenter
Hyperedge Set
Data&item&– Datacenter&edge
Data&Request&pattern&edge
!
"2
!
"3
!
"4
5
6
789:6
!
";
<
6
<
4
5
4
789:4
5
;
789:;
9:#8= 9:>
9:6?8= 9:63
9:6@
9:62
<
$
(a) Hypergraph Representation
0 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0
1 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0
1 1 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1
1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0
1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0
1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0
0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0
he1
he2% he3% he4%
he5% he6% he7
he8%
he9
he10%
he11%he12%
he13%
d
V1
d
V2
d
V3
d
V4
d
V5
d
V6
d
V7
L
1
L
3
L
5
he14%
he15%
he16%he17%
Hypergraph%Incidence%Matrix%(")
he18%
(b) Hypergraph Incidence Matrix
Figure 4: Modeling the data request patterns triggered by user check-ins as a Hypergraph.
tively, by giving priority to placing data-items at data-
center locations from where they have been requested
more frequently.
The resultant hyperedge weight matrix W
Π
of Π is
a diagonal matrix of size m
0
× m
0
, which is defined as
the weighted sum of W
R
, W
κ
R
L
, W
S
R
L
, and W
Γ
R
L
. Math-
ematically,
W
Π
= W · (W
R
,W
κ
R
L
,W
S
R
L
,W
Γ
R
L
). (3)
where, W is the weight vector for deciding the priori-
ties of the previously discussed hyperedge weighting
strategies.
4.2 Spectral Clustering
Spectral methods have been shown to be promising
in a plethora of machine learning research areas: im-
age segmentation (Shi and Malik, 2000; Meila and
Shi, 2001), data clustering (Ng et al., 2001), web
search (Gibson et al., 1998), and information retrieval
(Deerwester et al., 1990). The power of these algo-
rithms is that they possess both sound mathematical
properties and strong empirical prowess. They are
named spectral algorithms as they use the information
manifested within the spectra (both eigen-values and
eigen-vectors) of a similarity/affinity matrix. More
fundamentally, for a graph G represented using a sim-
ilarity matrix containing node-node similarities, these
methods use the spectra of the graph laplacian to un-
derstand the intrinsic data properties like structure,
connectivity etc. Interestingly, the laplacian for hy-
pergraph was derived in (Zhou et al., 2006), where it
is shown to be analogous to the simple graph lapla-
cian. This result facilitates application of spectral
methods on hypergraphs.
Having discussed about the importance of spec-
tral methods, we next describe the proposed algo-
rithm for performing spectral clustering on hyper-
graphs. The first step in spectral clustering on hyper-
graphs is to construct the hypergraph laplacian ma-
trix L
H
. The output of the hypergraph construction
step is a n
0
× m
0
dimensional hypergraph incidence
matrix Π and a m
0
× m
0
dimensional diagonal hyper-
edge weight matrix W
Π
. As discussed previously, the
hypergraph incidence matrix Π = [he
1
,he
2
,. ..,he
m
0
]
possesses m
0
hyperedges, where each hyperedge he
i
=
[he
1,i
,he
2,i
,. ..,he
n
0
,i
] is a n
0
-dimensional binary vec-
tor. The entry he
j,i
= 1 indicates that the j
th
vertex
in the hypergraph vertex set is participating in the i
th
hyperedge, while he
j,i
= 0 indicates otherwise. With
this, the hypergraph laplacian L
H
is defined as:
L
H
= I − (D
−1/2
v
ΠW
Π
D
−1
he
Π
T
D
−1/2
v
) (4)
where, I is a n
0
× n
0
identity matrix;
D
v
is a n
0
× n
0
diagonal vertex degree matrix defined
as D
v
= diag(
∑
Π);
D
he
is a m
0
×m
0
diagonal hyperedge degree matrix de-
fined as D
he
= diag(
∑
Π
T
);
W
Π
is a m
0
× m
0
diagonal hyperedge weight ma-
trix defined as W
Π
= diag([W
1
,W
2
,. ..,W
0
m
]), and
W
1
,. ..,W
0
m
are calculated as described in Eq. 3. Thus,
L
H
becomes a n
0
× n
0
matrix.
The next step is to perform eigen-decomposition
of the hypergraph laplacian matrix L
H
, in order
to identify its spectra: the eigen-values and eigen-
vectors. The eigen-decomposition of L
H
is written
as:
L
H
= UΛV (5)
where,
U = [u
1
,. ..,u
n
0
] is a n
0
× n
0
matrix formed by the
eigen-vectors of L
H
;
Λ = diag(λ
1
,. ..,λ
n
0
) is a diagonal n
0
× n
0
matrix
formed by the eigen-values of L
H
and,
V = U
T
since L
H
is a square symmetric matrix.
The eigen-vectors U and eigen-values Λ collec-
tively define the spectra for the hypergraph laplacian
L
H
.
As discussed in Sec. 1, despite their strong theo-
retical and mathematical properties, spectral methods
are usually not scalable. This is mainly due to the
CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science
502

complex operation of performing a full eigen decom-
position of a large matrix, which is cubic O(n
0
3
) in
the dimensionality of L
H
in the worst case. Having
said that, it is shown in the literature (Zhou et al.,
2006) that it is not required to use all the eigen-
vectors and thus, in practice one may work with just
a small fraction of n
0
. To this end, we work with a
low-rank approximation of L
H
, thereby restricting the
eigen decomposition to just calculate the 100 small-
est eigen vectors of L
H
. To scale this operation fur-
ther, we employ the use of randomized methods to
perform approximate partial matrix decompositions
(Halko et al., 2011), which again works very well in
practice without any significant loss in accuracy. As
will be explained later in Sec. 6, these randomized
methods facilitate the proposed spectral clustering al-
gorithm to achieve superior efficiency and scalability,
without any loss in the efficacy.
The last step involves performing k-means clus-
tering on the eigen-vectors U of the hypergraph lapla-
cian matrix L
H
. Since we know the number of dat-
acenter locations a priori, which is l = |L|, we par-
tition U into l clusters. This operation partitions
the set of data-items D into l different sets, thereby
forming P (D), which is used as the placement de-
cision recommended by the proposed data placement
algorithm. The clustering approach used here is not
a vanilla k-means, rather it includes multiple exten-
sions. First, to ensure load balancing we modify
the objective function of k-means to honor the de-
sired storage distribution Φ, which provides informa-
tion about the expected capacity of each datacenter
location. Second, we employ the use of k-means++
initialization as proposed in (Arthur and Vassilvitskii,
2007) and parallelization to scale-up the clustering al-
gorithm to very large datasets.
The three step process: (1) Hypergraph Laplacian
construction, (2) Eigen decomposition of the hyper-
graph laplacian, and (3) k-means clustering on the
eigen-vectors, with added extensions and modifica-
tions constitutes the proposed scalable spectral clus-
tering algorithm.
Note that the approach discussed above is capable
of solving the data placement problem without con-
sidering the possibility of replicas. Since replication
may be important in real-world settings for ensuring
fault-tolerance and load-balancing, we briefly discuss
an extension to allow for the scenarios with replica-
tion as well. To this end, we use the proposed data
placement algorithm to get a placement without repli-
cation, however, we change the capacity of each dat-
acenter from s
L
j
to s
L
j
/r, where r is the desired repli-
cation factor. We then execute the same algorithm r
times on different permutations of the set of datacen-
ters L. This allows the same data-item to be stored (in
the expected sense) on r datacenters, thereby meeting
the desired replication factor. With this, the proposed
algorithm is extended to handle scenarios where repli-
cation is allowed as well. For the sake of brevity, we
keep this discussion around extensions to scenarios
with replication short. A detailed analysis and eval-
uation of various replication strategies will constitute
as future work.
5 EVALUATION SETUP
5.1 Geo-distributed Datacenters
To simulate a real-world geo-distributed cloud envi-
ronment, we employ the use of l = 9 geo-distributed
datacenters based on the regions provided by AWS
global infrastructure (aws, 2017). Note that the AWS
infrastructure evolves continuously and for the sake
of standardization and reproducible comparison with
previous work (Yu and Pan, 2015), we only chose
the 9 oldest and prominent regions, namely: Vir-
ginia, California, Oregon, Ireland, Frankfurt, Singa-
pore, Tokyo, Sydney, and Sao Paulo, for our exper-
imental setup. Our experimental setup closely mir-
rors the actual AWS setup, as the costs involved for
storage and outgoing traffic as indicated in Table 2a
are as advertised by Amazon. Moreover, the inter-
datacenter latencies(aws, 2016) are also measured by
the packet transfer latency between the chosen regions
using the Linux ping command. Table 2b presents
the average inter-datacenter latency values (in ms) be-
tween the 9 chosen datacenter regions. It is evident
from the values portrayed in Table 2 that the proper-
ties exhibited by datacenters vary significantly with
the region, and hence, any data placement strategy
should incorporate this knowledge while performing
placement decisions.
5.2 Data
The dataset used in our experiments is a trace of
a location-based online social network – Gowalla
1
,
available publicly from the SNAP (sna, 2017) repos-
itory. The Gowalla dataset has been used extensively
(Yu and Pan, 2015; Yu and Pan, 2017) for data place-
ment research in geo-distributed cloud services. The
social network contains 196591 vertices and 950327
edges. The vertices are the users in the social network,
while the edges represent friend relationship between
1
http://snap.stanford.edu/data/loc-gowalla.html
Scalable Data Placement of Data-intensive Services in Geo-distributed Clouds
503

Table 2: (a) Traffic and Storage Costs, and (b) Inter Datacenter Latency (in ms) based on Geo-distributed Amazon Clouds.
(a) Costs (in $)
Region
Storage Outgoing
($/GB-month) Traffic ($/GB)
Virginia 0.023 0.02
California 0.026 0.02
Oregon 0.023 0.02
Ireland 0.023 0.02
Frankfurt 0.025 0.02
Singapore 0.025 0.02
Tokyo 0.025 0.09
Sydney 0.025 0.14
Sao Paulo 0.041 0.16
(b) Latency (in ms)
Region Virginia California Oregon Ireland Frankfurt Singapore Tokyo Sydney Sao-Paulo
Virginia 0.0 72.738 86.981 80.546 88.657 216.719 145.255 229.972 119.531
California 71.632 0.0 19.464 153.202 166.609 174.010 102.504 157.463 192.670
Oregon 88.683 19.204 0.0 136.979 159.523 161.367 89.095 162.175 182.716
Ireland 80.524 153.220 136.976 0.0 19.560 239.023 212.388 309.562 191.292
Frankfurt 88.624 166.590 159.542 19.533 0.0 325.934 236.537 323.483 194.905
Singapore 216.680 173.946 161.423 238.130 325.918 0.0 73.807 175.328 328.080
Tokyo 145.261 102.523 89.157 212.388 236.558 73.785 0.0 103.907 256.763
Sydney 229.748 157.843 161.932 309.562 323.152 175.355 103.900 0.0 322.494
Sao Paulo 119.542 192.700 181.665 191.559 194.900 327.924 256.665 322.523 0.0
two users. The trace provides 6442890 user check-
ins logged over the period of February, 2009 to Octo-
ber, 2010. As described in Sec. 3, each user check-in
consists of a data request pattern and a location. In
continuation to our discussions in Sections 1 and 3,
a request (indicated by a check-in) by a user v would
involve pulling the data of all his/her friends. Thus,
the data request pattern corresponding to a check-in
by a user v is the set of data-items corresponding to
all the friends of v, i.e. Adj(v). The location field of
a user check-in are the GPS coordinates of the place
from where the check-in was triggered. These GPS
coordinates were mapped to the closest (in terms of
distance) datacenter region to identify the source lo-
cation of a data request pattern, and can thus, be one
of the 9 datacenter regions as described in Sec. 5.1.
With this pre-processing, we obtain a use-case sce-
nario consisting of 196591 data-items and 102314
data request patterns.
Moving ahead, we present certain dataset statis-
tics. Fig. 5 portrays the distribution of user check-ins
across the 9 datacenter regions discussed above. It is
evident that Virginia and Frankfurt register the high-
est (≈ 40%) and the second highest (≈ 30%) number
of user check-ins. On the other hand, Tokyo, Syd-
ney, and SaoPaulo get the fewest (≈ 10% combined)
number of user check-ins. This clearly shows a huge
disparity in the check-in distribution. Based on the
user check-in distribution, we extract the storage size
distribution Φ of the datacenter regions, which is de-
pendent upon both the number of check-ins registered
in a region and the size of data request pattern trig-
gered by the check-in. As is clear from Fig. 6, the
desired storage distribution portrays a similar trend
as that of the check-in distribution. Note that this
storage distribution Φ also serves as an input to the
data placement algorithm, thereby facilitating load-
balancing among the 9 datacenter regions. More fun-
damentally, the load-balancing factor is calculated as
the expected storage size at each datacenter region us-
ing the storage distribution Φ.
0
0.1
0.2
0.3
0.4
0.5
Virginia
California
Oregon
Ireland
Frankfurt
Singapore
Tokyo
Sydney
SaoPaulo
Distribution of Check-ins
Figure 5: Distribution of user check-ins across geo-
distributed datacenters.
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Virginia
California
Oregon
Ireland
Frankfurt
Singapore
Tokyo
Sydney
SaoPaulo
Distribution of Expected Storage Size
Figure 6: Distribution of expected datacenter storage size.
5.3 Algorithms
We compare the proposed data placement algorithm
using spectral clustering on hypergraphs for effective-
ness, efficiency, and scalability against a number of
baselines – Random and Nearest, and the state-of-the-
art hypergraph partitioning technique (Yu and Pan,
2015; Yu and Pan, 2017). All the algorithms were
implemented in C++. To perform hypergraph parti-
tioning for the technique proposed by (Yu and Pan,
2015) and reproduce their results we use the PaToH
(Catalyurek, 2011) toolkit. Next, we give brief de-
CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science
504

scriptions of the compared techniques:
• Random: partitions the set of data-items D ran-
domly into |L| = l datacenters. To distribute the
data-items according to the datacenter storage size
distribution Φ, we ensure that random partitioning
samples data-items based on Φ thereby ensuring
load-balancing.
• Nearest: assigns each data-item to the datacen-
ter from where it has been requested the highest
number of times. Similar to random, to ensure
load-balancing this technique follows the datacen-
ter storage distribution Φ. Thus, once the dat-
center with the highest number of requests for a
particular data-item has reached its capacity, we
randomly choose a datacenter location capable of
serving new requests.
• Hypergraph Partitioning: is the data placement
algorithm proposed by (Yu and Pan, 2015; Yu and
Pan, 2017). After the hypergraph modeling step
discussed in Sec. 4, it uses the hypergraph parti-
tioning algorithms available in the PaToH toolkit.
The partitioning algorithms maintain the datacen-
ter storage size distribution Φ, thereby ensuring
load-balancing.
5.4 Parameters
As discussed in Sec. 4, different hyperedge weights
(W
R
,W
κ
R
L
,W
S
R
L
,W
Γ
R
L
) facilitate optimization of dif-
ferent objectives. As stated in Eq. 3, a weight vector
W facilitates prioritization of these objectives based
on the assigned weights. In our study, we incorporate
the use of specific weight vector W settings: W
1
:
{100,1, 1,1}, W
2
: {1,100,1,1}, W
3
: {1,1,100,1},
and W
4
: {1,1,1,100}, which represent different pref-
erences or importance of the considered evaluation
metrics, such as, higher priority of collocating the as-
sociated data-items thereby minimizing the datacenter
span N (·), lower inter-datacenter traffic Γ(·), lower
inter-datacenter latency κ(·), and lower storage cost
S(·) respectively. Note that in all the weight-vector
settings, the value 100 is just used to indicate higher
relative importance of the corresponding metric. The
results portrayed are not dependent on the specific
value of 100, rather the weight-vectors can work with
any value as long as it is >> 1.
5.5 Evaluation Metrics
• Span (N (·)): of a data request pattern R
i
is de-
fined as the average number of datacenters re-
quired to be accessed to fetch the data-items re-
quested in R
i
. Further, the span for the entire
workload is calculated as the average of the dat-
acenter spans of each request pattern R
i
∈ R .
• Traffic (Γ(·)): The total traffic cost of a data re-
quest pattern R
i
is defined as the sum of outgoing
traffic prices of the datacenters involved in out-
going requests for the data-items in R
i
. Further,
the traffic cost of the entire workload is calculated
as the sum of traffic costs of each request pattern
R
i
∈ R .
• Latency (κ(·)): The inter-datacenter latency of a
data request pattern R
i
is calculated as the sum
of access latencies required to fetch all the data-
items requested in R
i
from the datacenter where
they are placed to the datacenter from where the
request was triggered. Further, the latency of the
workload is calculated as the sum of the latencies
of each request pattern R
i
∈ R .
• Storage (S(·)): The sum of the total cost on stor-
ing all of the data-items corresponding to every
data request pattern R
i
∈ R in datacenters L pre-
scribed by the data placement algorithm.
• Balance: is calculated as the pearson’s correla-
tion coefficient between the expected storage size
distribution Φ, and the actual storage size distri-
bution obtained after performing data placement.
If the value is close to 1, it means that the two dis-
tributions are highly similar, while they are dis-
similar if the value is close to −1.
• Objective. (Obj.): is defined as the weighted sum
of the considered performance metrics, where the
weights are described using the weight vector W.
6 EVALUATION RESULTS
All the experiments were done using codes written in
C++ on an Intel(R) Xeon(R) E5-2698 28-core ma-
chine with 2.3 GHz CPU and 256 GB RAM run-
ning Linux Ubuntu 16.04. Owing to their non-
deterministic nature, results for the random and hy-
pergraph partitioning methods are averaged over 10
runs. Note that the results portrayed corresponding to
each evaluation metric (barring Balance) are normal-
ized in the scale of [0,1] by dividing each value by
the highest observed value in that particular metric.
Normalization ensures that all the values lie in a com-
mon range ([0,1]), thereby facilitating joint analysis
of all the considered evaluation metrics for all the al-
gorithms. Since the problem formulation in this study
is concerned with the minimization of the evaluation
metrics, the smaller the portrayed values the better the
performance is. Additionally, note that the results for
Scalable Data Placement of Data-intensive Services in Geo-distributed Clouds
505
0
0.2
0.4
0.6
0.8
1
Obj
Span
Traffic
Latency
Storage
Balance
Normalized Evaluation Metrics
Random
Nearest
Hyper
Spectral
Figure 7: W
1
= {100, 1, 1,1}: Higher priority towards min-
imizing the datacenter span N (·).
the balance evaluation metric are close to 1 for all the
techniques considered in this study. This is because
every technique possesses the capability to honor the
desired storage size distribution Φ.
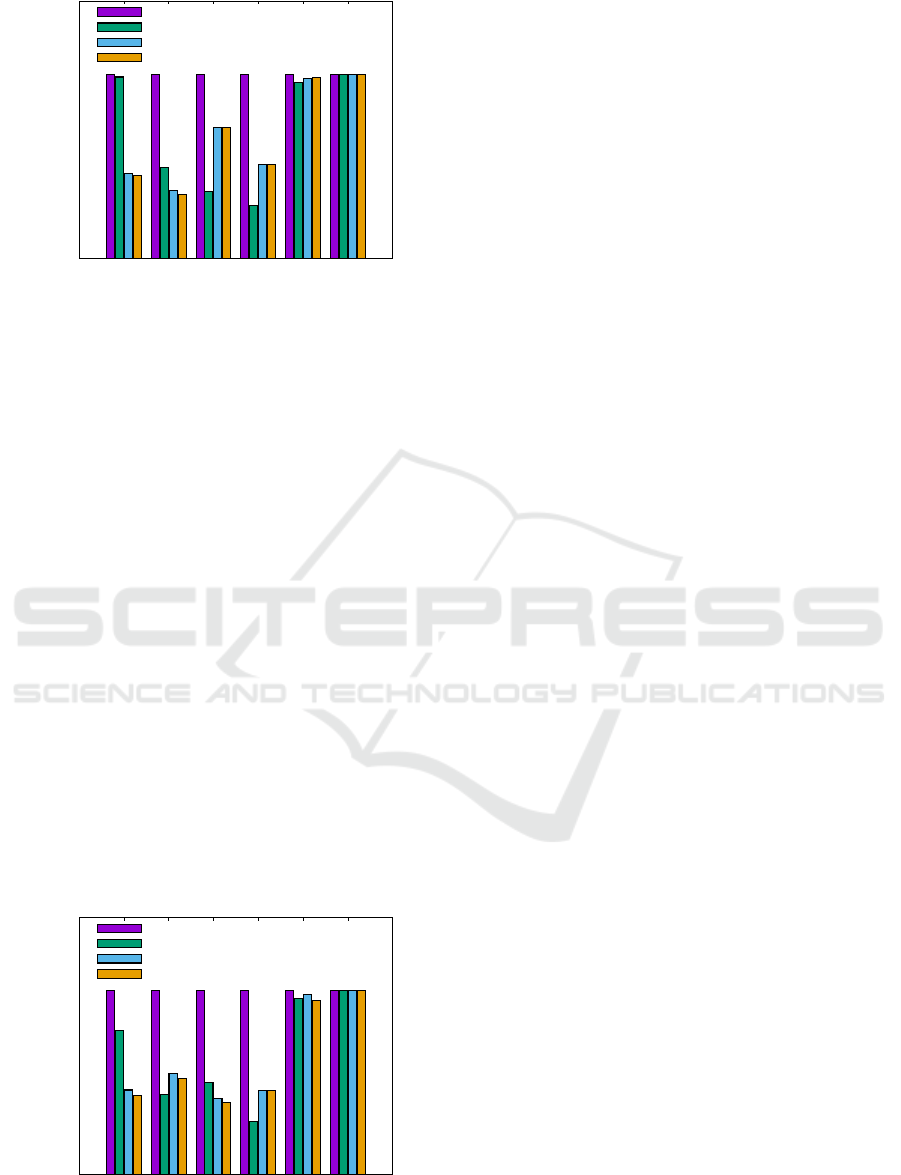
Fig. 7 presents the results corresponding to the
weight-vector setting W
1
, where minimizing the data-
center span holds the highest priority in the optimiza-
tion objective. It is evident that both, the proposed
spectral clustering algorithm (Spectral), and the state-
of-the-art hypergraph partitioning algorithm (Hyper)
achieve a low value on the overall optimization ob-
jective (Obj), while being significantly better than the
random and nearest methods. This is because of their
capability to preferentially minimize the datacenter
span, which possesses the highest priority in the opti-
mization under W
1
. Note that Nearest outperforms
both Hyper and Spectral on the traffic and latency
metrics, as they have lower weights in the optimiza-
tion objective under W
1
. However, both Spectral and
Hyper are still significantly better than the Random
method.
A similar behavior is observed in Figs. 8, 9, and
10 corresponding to the other three weight vector set-
0
0.2
0.4
0.6
0.8
1
Obj
Span
Traffic
Latency
Storage
Balance
Normalized Evaluation Metrics
Random
Nearest
Hyper
Spectral
Figure 8: W
2
= {1, 100, 1,1}: Higher priority towards min-
imizing the inter-datacenter traffic Γ(·).
tings W
2
, W
3
, and W
4
respectively. Both Spectral
and Hyper outperform the other methods significantly
on the overall optimization (Obj), while also being
significantly better on the corresponding evaluation
metric that the weight-vector setting is tuned to op-
timize. More fundamentally, in addition to being bet-
ter on Obj., both Spectral and Hyper outperform the
other methods in minimizing inter-datacenter traffic
cost Γ(·), inter-datacenter latency κ(·), and storage
cost S(·), when a higher preference is given to these
metrics under the weight-vector settings W
2
, W
3
, and
W
4
respectively.
The main limitation of Nearest is that it tries to
assign each data-item to a datacenter with the high-
est number of accesses to that data-item, thereby aim-
ing to minimize (on an average) the geographical dis-
tance between the data-item and the source location
of the data request oblivious to the fact that the ac-
tual traffic or storage costs might not be proportional
to the distance. The main advantage of both Spectral
and Hyper over Nearest is that owing to their higher-
order modeling capabilities they are capable of better
addressing multi-objective optimizations, and possess
the capability to adapt their performance based on dif-
ferent weight-vector settings. This is evident from the
results portrayed in Figs. 7– 10. To further empha-
size on the capability to adapt the optimization based
on different weight-vector settings, we discuss the re-
sults portrayed in Fig. 10. It is clear that according
to W
4
, the optimization objective gives more prefer-
ence towards minimizing the storage cost. Note that
storage cost and other parameters like inter-datacenter
traffic and latency might be inversely related to each
other, i.e., a lower storage cost might lead to higher
latencies or traffic cost. This behavior is also evident
from Fig. 10, where both Spectral and Hyper achieve
lower storage costs, thereby also achieving better per-
formance on Obj, however, suffer slightly on other
metrics. Thus, methods like Nearest would find diffi-
culty in handling such cases, while both Spectral and
Hyper possess the capability to adapt the optimization
based on the weight-vector.
Figs. 7– 10 show that the performance of both
Spectral and Hyper are quite similar on the evaluated
metrics. While Spectral is always marginally better in
efficacy when compared to Hyper, the major advan-
tage of Spectral over Hyper comes from its capabil-
ity to scale gracefully and efficiently to large datasets.
It is intuitive that scalability is a paramount property
for any data placement algorithm, since the scale of
real-world social networks or for that matter any real-
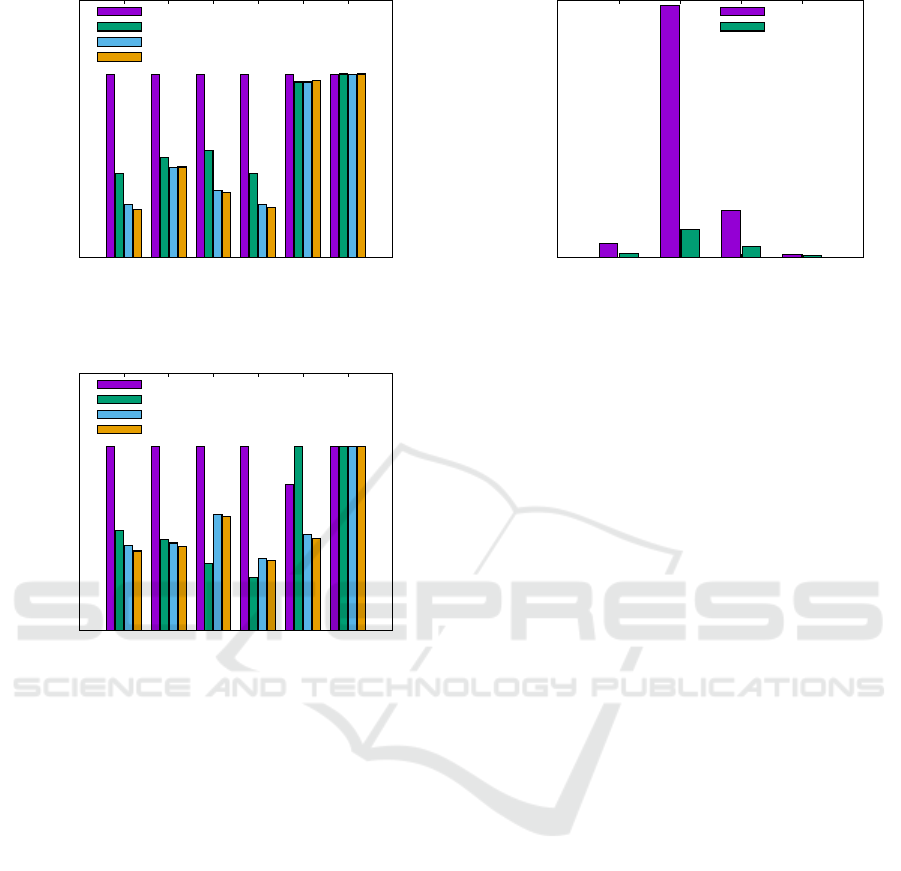
world data-intensive services is humongous. Fig. 11
shows that Spectral is up to 10 times (≈ 3–4 times on
average) faster when compared to Hyper, while also
CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science
506
0
0.2
0.4
0.6
0.8
1
Obj
Span
Traffic
Latency
Storage
Balance
Normalized Evaluation Metrics
Random
Nearest
Hyper
Spectral
Figure 9: W
3
= {1, 1, 100,1}: Higher priority towards min-
imizing the inter-datacenter latency κ(·).
0
0.2
0.4
0.6
0.8
1
Obj
Span
Traffic
Latency
Storage
Balance
Normalized Evaluation Metrics
Random
Nearest
Hyper
Spectral
Figure 10: W
4
= {1,1, 1,100}: Higher priority towards
minimizing the storage cost S(·).
being slightly better in all evaluated metrics for the
majority of the considered weight-vector settings.
In summary, through extensive experiments we
verify that the proposed spectral clustering algorithm
is efficient, scalable, and effective. Although Spectral
is not always the best on every evaluated metric, it
serves to be the most effective technique in terms of
improving Obj, which is the main target of our multi-
objective optimization. Additionally, it possesses the
capability to adapt to the change in weight vector set-
tings W, which facilitates handling of a variety of
real-world scenarios as described by different weight
vectors.
7 CONCLUSIONS
In this paper, we have addressed the problem of
data placement of data-intensive services into geo-
distributed clouds. We identified the need for spe-
cialized methods to perform data placement for data-
intensive services, as contrary to MapReduce style
0
500
1000
1500
2000
2500
3000
W
1
W
2
W
3
W
4
Running Time (in secs.)
Hyper
Spectral
Figure 11: Efficiency of spectral clustering over hypergraph
partitioning.
workloads, these workloads require access to multi-
ple datasets within a single transaction, thus, render-
ing traditional methods of hash based partitioning in-
adequate. Consequently, we devised a scalable spec-
tral clustering algorithm for hypergraph partitioning,
thereby facilitating data placement. Experiments on
a real-world trace-based social network dataset por-
trayed the effectiveness, efficiency, and scalability of
the proposed algorithm. In the future, we would like
to design and develop a distributed version of our al-
gorithms and implement the entire system on state-of-
the-art big data technologies like Apache Spark. Ad-
ditionally, we would also like to include the notion of
replicas directly in the data placement problem for-
mulation.
ACKNOWLEDGEMENTS
This research is partly funded by the IWT SBO De-
CoMAdS project.
REFERENCES
(2015). How much data does X store? https://
techexpectations.org/2015/03/28/how-much-data-
does-x-store/.
(2016). Latency Between AWS Global Regions. http://
zhiguang.me/2016/05/10/latency-between-aws-
global-regions/.
(2017). AWS Global Infrastructure. https://aws.
amazon.com/about-aws/global-infrastructure/.
(2017). SNAP Datasets. https://snap.stanford.edu/data/.
(2017). The Exponential Growth of Data.
https://insidebigdata.com/2017/02/16/the-
exponential-growth-of-data/.
Agarwal, S., Dunagan, J., Jain, N., Saroiu, S., Wolman,
A., and Bhogan, H. (2010). Volley: Automated Data
Scalable Data Placement of Data-intensive Services in Geo-distributed Clouds
507

Placement for Geo-distributed Cloud Services. In
NSDI.
Arthur, D. and Vassilvitskii, S. (2007). k-means++: The
Advantages of Careful Seeding. In SODA, pages
1027–1035.
Catalyurek, U. V. (2011). PaToH (Partitioning Tool for
Hypergraphs). http://bmi.osu.edu/umit/PaToH/ man-
ual.pdf.
Catalyurek, U. V., Boman, E. G., Devine, K. D.,
Bozdag, D., Heaphy, R., and Riesen, L. A. (2007).
Hypergraph-based Dynamic Load Balancing for
Adaptive Scientific Computations. In IPDPS, pages
1–11.
Chervenak, A., Deelman, E., Livny, M., Su, M., Schuler,
R., Bharathi, S., Mehta, G., and Vahi, K. (2007). Data
Placement for Scientific Applications in Distributed
Environments. In GRID.
Deerwester, S. C., Ziff, D. A., and Waclena, K. (1990).
An Architecture for Full Text Retrieval Systems. In
DEXA, pages 22–29.
Ebrahimi, M., Mohan, A., Kashlev, A., and Lu, S. (2015).
BDAP: A Big Data Placement Strategy for Cloud-
Based Scientific Workflows. In BigDataService,
pages 105–114.
Gibson, D., Kleinberg, J., and Raghavan, P. (1998). Infer-
ring Web Communities from Link Topology. In HY-
PERTEXT, pages 225–234.
Golab, L., Hadjieleftheriou, M., Karloff, H., and Saha,
B. (2014). Distributed Data Placement to Minimize
Communication Costs via Graph Partitioning. In SS-
DBM, pages 1–12.
Halko, N., Martinsson, P., and Tropp, J. A. (2011). Find-
ing Structure with Randomness: Probabilistic Algo-
rithms for Constructing Approximate Matrix Decom-
positions. SIAM Review, 53(2):217–288.
Han, S., Kim, B., Han, J., K.Kim, and Song, J. (2017).
Adaptive Data Placement for Improving Performance
of Online Social Network Services in a Multicloud
Environment. In Scientific Programming, pages 1–17.
Huguenin, K., Kermarrec, A. M., Kloudas, K., and Ta
¨
ıani,
F. (2012). Content and Geographical Locality in User-
generated Content Sharing Systems. In NOSSDAV,
pages 77–82.
Jiao, L., Li, J., Du, W., and Fu, X. (2014). Multi-objective
data placement for multi-cloud socially aware ser-
vices. In INFOCOM, pages 28–36.
Kayaaslan, E., Cambazoglu, B. B., and Aykanat, C. (2013).
Document Replication Strategies for Geographically
Distributed Web Search Engines. Inf. Process. Man-
age., 49(1):51–66.
Li, X., Zhang, L., Wu, Y., Liu, X., Zhu, E., Yi, H., Wang, F.,
Zhang, C., and Yang, Y. (2017). A Novel Workflow-
Level Data Placement Strategy for Data-Sharing Sci-
entific Cloud Workflows. IEEE TSC, PP(99):1–14.
Liu, X. and Datta, A. (2011). Towards Intelligent Data
Placement for Scientific Workflows in Collaborative
Cloud Environment. In IPDPSW, pages 1052–1061.
Meila, M. and Shi, J. (2001). Learning Segmentation by
Random Walks. In NIPS, pages 873–879.
Ng, A. Y., Jordan, M. I., and Weiss, Y. (2001). On Spec-
tral Clustering: Analysis and an Algorithm. In NIPS,
pages 849–856.
Nishtala, R., Fugal, H., Grimm, S., Kwiatkowski, M., Lee,
H., Li, H. C., McElroy, R., Paleczny, M., Peek, D.,
Saab, P., Stafford, D., Tung, T., and Venkataramani,
V. (2013). Scaling Memcache at Facebook. In NSDI,
pages 385–398.
Quamar, A., Kumar, K. A., and Deshpande, A. (2013).
SWORD: Scalable Workload-aware Data Placement
for Transactional Workloads. In EDBT, pages 430–
441.
Rochman, Y., Levy, H., and Brosh, E. (2013). Re-
source placement and assignment in distributed net-
work topologies. In INFOCOM, pages 1914–1922.
Shankaranarayanan, P. N., Sivakumar, A., Rao, S., and
Tawarmalani, M. (2014). Performance Sensitive
Replication in Geo-distributed Cloud Datastores. In
DSN, pages 240–251.
Shi, J. and Malik, J. (2000). Normalized Cuts and Image
Segmentation. PAMI, 22(8):888–905.
Spielmat, D. A. (1996). Spectral Partitioning Works: Planar
Graphs and Finite Element Meshes. In FOCS, pages
96–105.
Yu, B. and Pan, J. (2015). Location-aware associated data
placement for geo-distributed data-intensive applica-
tions. In 2015 IEEE Conference on Computer Com-
munications (INFOCOM), pages 603–611.
Yu, B. and Pan, J. (2016). Sketch-based data placement
among geo-distributed datacenters for cloud storages.
In INFOCOM, pages 1–9.
Yu, B. and Pan, J. (2017). A Framework of Hypergraph-
based Data Placement among Geo-distributed Data-
centers. IEEE TSC, PP(99):1–14.
Yuan, D., Yang, Y., Liu, X., and Chen, J. (2010). A
data placement strategy in scientific cloud workflows.
FGCS, 26(8):1200 – 1214.
Zhang, J., Chen, J., Luo, J., and Song, A. (2016). Effi-
cient location-aware data placement for data-intensive
applications in geo-distributed scientific data centers.
Tsinghua Science and Technology, 21(5):471–481.
Zhou, D., Huang, J., and Sch
¨
olkopf, B. (2006). Learn-
ing with Hypergraphs: Clustering, Classification, and
Embedding. In NIPS, pages 1601–1608.
CLOSER 2018 - 8th International Conference on Cloud Computing and Services Science
508
