
Composite Alternative Pareto Optimal Recommendation System
with Individual Utility Extraction (CAPORS-IUX)
William Jeffries and Alexander Brodsky
George Mason University, 4400 University Drive 4A4, Fairfax, VA 22030, U.S.A.
Keywords: Recommender Systems, Decision Guidance, Decision Optimization, Pareto Optimum.
Abstract: We propose a methodology and develop a system for generating composite alternative recommendations
combining user-guided continuous improvement with Pareto optimal trade-off considerations and for
extracting individual utility. The methodology describes a way to (1) construct a set of Pareto optimal
recommendations given a selected metric and the user’s current utility, (2) explore the feasibility space by
relaxing the Pareto optimal constraint in a given dimension, and (3) extract the utility for an individual user
by capturing the interactions between the user and the system. The system itself consists of (1) a mechanism
for generating feasible recommendations, (2) implementation of the key algorithms of the methodology, and
(3) user interface for enabling interaction with the user.
1 INTRODUCTION
Composite alternative recommender systems
recommend a combination of products and services,
based on multiple criteria such as price, availability,
and user ratings. They include recommenders for
vacation packages, investment portfolios, healthcare
plans, product bundles, and more.
Consider an example of a sourcing
recommender. In this case, a recommendation is a
set of orders, where an order contains a set of item
quantities to be purchased from a particular supplier.
Sourcing recommendations are associated with
multiple criteria such as cost, carbon emissions, and
fulfillment time. These recommendations are
composite since they contain multiple suppliers with
multiple items, and they are multi-criteria because of
the three metrics mentioned previously. The result of
generated recommendations must be Pareto-optimal.
There has been extensive research conducted on
composite alternative recommenders in recent years.
This research comprises proposed methods and
presented systems, addressing both domain specific
and domain-independent recommenders.Interdonato
et al (2013) propose a graph-based framework that
uses Page Rank-style algorithm to learn packages
that conform to a user preference model. The
framework is ultimately based on user rankings and
identifies domain-independence as its key feature.
CARD (Brodsky, Henshaw and Whittle, 2008) is a
proposed framework for generating optimal
composite alternative recommendations. CARD
utilizes a SQL-based data model for generating the
recommendation space. It also extends the SQL
language in order to provide diverse
recommendations and to provide a mechanism for
learning user preferences. CARD is a generic
framework capable of being applied across domains.
There is no current implementation of the CARD
framework. FlexRecs (Koutrika, Bercovitz and
Garcia-Molina, 2009) is a proposed framework for
providing domain-independent recommendations.
The recommendation space in FlexRecs is generated
using workflows designed by system implementers.
As with CARD, the FlexRecs framework is built on
top of relational data models and extended relational
operators.
These three frameworks address composite
recommendations, but do not offer a system that
implements the framework, nor use methodology on
which the system functionality can be based.
Xie, Lakshmanan and Wood (2010) present a
generic package recommender system that uses a
variation of the knapsack problem to generate
optimal top-k recommendations. The
recommendation space in their system is generated
using individual component recommenders.
Furthermore, ratings are the only metric used to
calculate recommendations. TopRecs+ (Khabbaz,
328
Jeffries, W. and Brodsky, A.
Composite Alternative Pareto Optimal Recommendation System with Individual Utility Extraction (CAPORS-IUX).
DOI: 10.5220/0006770403280335
In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 328-335
ISBN: 978-989-758-298-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Xie and Lakshmanan, 2011) is another generic
package recommender that uses a variation of the
knapsack problem to find optimal top-k package
recommendations. As with Xie et al above,
TopRecs+ leverages individual item recommenders
to generate the composite alternative recommender
space. CompRec-Trip (Xie, Lakshmanan and Wood,
2011) is a system for recommending travel packages
by finding the optimal alternatives using user-
supplied preferences and constraints. As Xie et al’s
other work mentioned above, the system uses
component recommender systems for generating the
recommendation space. The system is narrowly
focused, but allows flexibility through interaction
with the user.
These three systems generate composite
recommendations by aggregating single-item
recommenders. However, this aggregation does not
take into account interaction among the components
of the composite recommendation. Therefore,
neither offers an integrated composite alternative
methodology, which is often required when
components have a non-trivial interaction among
them. Also, in the case of CompRec-Trip, the system
is domain-specific and not designed to accommodate
general recommendation problems.
Ribeiro, et al (2015) propose two Pareto-efficient
approaches for recommender systems. In both
approaches, they propose using recommendation
accuracy, novelty, and diversity as the objectives to
consider when generating a Pareto-efficient list of
recommendations. One approach creates a Pareto-
efficient ranked list from multiple competing
recommendation algorithms. Their second approach
creates Pareto-efficient hybrid recommenders built
from individual recommender algorithms. While
both approaches apply Pareto-efficiency to their
recommendations, it is limited to the criteria of
accuracy, diversity, and novelty. However, many
package recommendations require diverse user-
defined criteria, such as cost, risk, benefit, etc.,
which is outside the scope of (Ribeiro et al, 2015).
Neither approach considers continuous user
feedback. Furthermore, both approaches are
proposed algorithms that do not include a system to
implement their methodology.
To the best of our knowledge, there are no
proposed recommender systems that combined
Pareto optimal solutions for arbitrary user-defined
criteria with continuous user guidance. Nor is there a
system with this combination of features designed
for composite alternatives that have complex
interactions between them.
To address these limitations, CAPORS (Jeffries
and Brodsky) was developed. CAPORS introduced a
methodology and system for recommending Pareto-
optimal composite alternatives based on (1) multi-
criteria optimization and (2) continuous user-guided
feedback.
In CAPORS, the trade-off consideration is
explicitly expressed between designated cost and
benefit metrics, but not with arbitrary metrics. And,
while CAPORS allows a user to explore the
feasibility space to find an optimal recommendation,
CAPORS was not designed to learn the user’s
utility.
Addressing these two limitations of CAPORS is
the exact focus of this paper.
First, we propose a methodology for (1)
generating Pareto optimal recommendations using
arbitrary metrics and (2) extracting the utility of an
individual user. The methodology first generates an
initial set of recommendations based on Pareto-
optimal curve by comparing one of the metrics (the
default metric) against the default user utility. Then,
the user iteratively improves the alternatives through
critique of additional metrics and re-optimizations to
iteratively discover a feasible recommendation
closest to that user’s utility. Finally, the user accepts
the most desired recommendation and a final utility
for that user is extracted.
Second, we develop Composite Alternative
Pareto Optimal Recommender System with
Individual Utility Extraction (CAPORS-IUX) to
implement this methodology. CAPORS-IUX is
implemented using Unity Decision Guidance
Management System (DGMS) (Brodsky, Luo, and
Nachawati). CAPORS-IUX also uses the same
notion of an Analytic Model as CAPORS. An
analytical model formally describes feasibility
constraints and metrics of interest as a function of
parameter and control variables. With the help of
Unity DGMS, CAPORS-IUX manages the
workflow of recommendations improvement based
on three key algorithms.
Third we have developed algorithms for (1)
generation of Pareto-optimal curve for the
recommendation Analytic Model along a selected
metric and the current user utility, (2) generation of
Pareto-optimal improvement along a different metric
and the updated user utility, and (3) calculation of
the updated user utility.
Finally, we conduct an experiment using
synthetic users to demonstrate the ability of
CAPORS-IUX to find a recommendation that is
optimal, or very close to optimal, for a given user
utility.
Composite Alternative Pareto Optimal Recommendation System with Individual Utility Extraction (CAPORS-IUX)
329

This paper is organized into the following
sections. Section 2 demonstrates composite
alternative recommendation using a supply chain
sourcing example. Section 3 describes the core
algorithms of the system. Section 4 illustrates the
system architecture. Section 5 details an
experimental study conducted to demonstrate utility
convergence. Section 6 concludes and offers ideas
for future extensions.
2 UTILITY EXTRACTION BY
SOURCING EXAMPLE
We return to the sourcing example from the original
paper in order to explain the utility extraction
methodology. Supply chain sourcing is the process
of constructing orders for goods to be purchased
from some universe of suppliers such that
constraints such as demand are met. For a more
detailed explanation on supply chain sourcing,
please refer to Section 2 of the original paper.
In this scenario, CAPORS-IUX is used to
generate an order configuration stipulating which
items are to be ordered from which suppliers and at
what quantities. As with any recommender system,
the goal is to generate recommendations with the
highest predicted utility to the individual user.
The methodology used by CAPORS-IUX to
generate the optimal recommended order
configuration is shown in Figure 1.
Figure 1: State Diagram.
To generate an initial set of recommendations, an
initial data structure is used. This data structure
includes (1) metrics definitions used to evaluate each
recommendation, (2) an analytic model for
computing metrics and constraints of a given
recommendation, (3) variable input for exploring the
feasible space of composite alternatives, (4)
configuration setting for maximum number of
recommendations to generate, (5) configuration
setting for default metric for user to consider, and
(6) configuration setting for default utility weights
(e.g. equal weights for all metrics).
The system generates an initial set of
recommendations and displays to the user. The user
is presented with four main user interface sections
(explained in greater detail below and shown in
Appendix A): (1) a graph, called the Current Trade-
off Graph of recommendations with current utility
along the x-axis and the metric to consider along the
y-axis, (2) a table of all current recommendations to
consider with each of the computed metrics and a
mechanism for choosing the best recommendation in
the set, (3) a graph, called the Best-So-Far Graph
displaying all of the recommendations chosen by the
user as best in each iterative Current Trade-off
Graph, and (4) a table of all the best
recommendations so far chosen by the user.
The Current Trade-off Graph allows the user to
consider recommendations by comparing a set of
recommendations projected onto the Pareto front of
the feasibility space against a single metric of
interest. That is, there does not exist a
recommendation that improves on one metric
without sacrificing another. Initially, the current
utility is computed using equal weights for each
metric and the metric of interest is defined in the
configuration setting of the initial data structure.
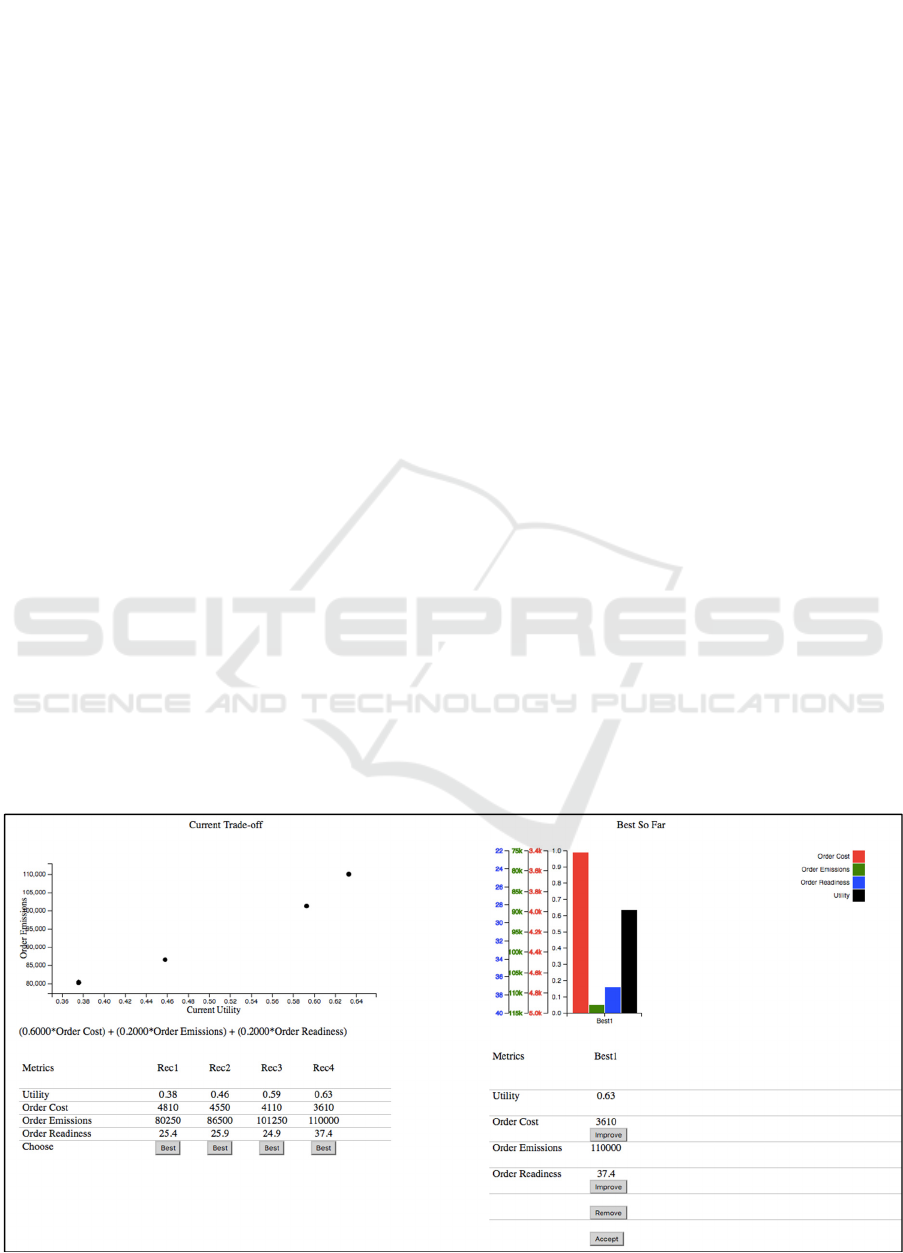
Figure 2: Current Trade-off Graph and Table.
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
330
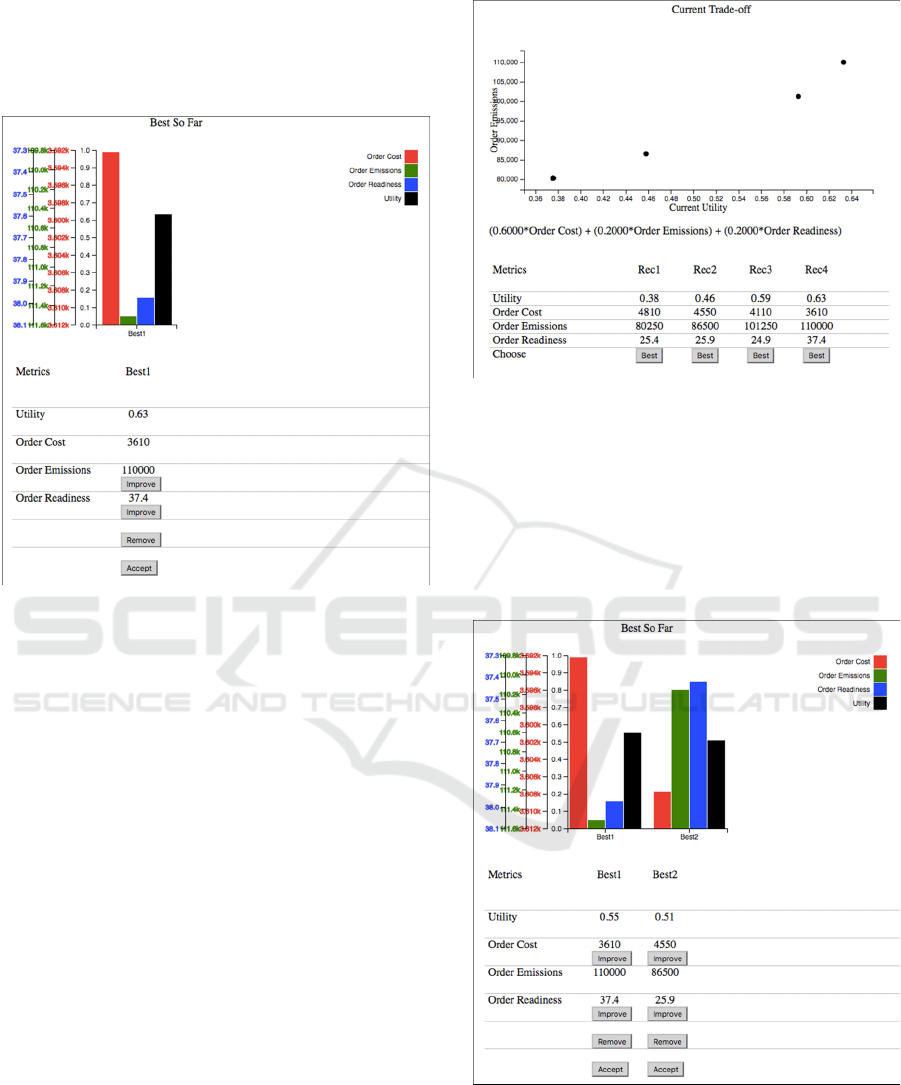
For example, the user selects “Rec 2” as the best
of the currently displayed set of recommendations.
Upon selection the preferred recommendation is
added to the Best Recs Graph and Best Recs Table.
Figure 3: Best-So-Far Graph.
Also, the current utility is updated based on the
selection, and the Current Trade-off Graph and
Current Trade-off Table are updated to reflect the
new utility calculations.
Next, the user can (1) generate a new set of
recommendations by improving upon one of the
metrics for the recommendation, (2) remove the
recommendation from the list, or (3) accept the
recommendation as the final, best overall
recommendation.
In our example, the user selects the column
containing the recommendation and then the row
containing the Order Emissions metric. The Improve
button is pressed and the Current Trade-off Graph
and Table are updated with a new set of
recommendations. The y-axis of the Current Trade-
off Graph will be the selected metric to improve, and
the x-axis will be the current utility that was
calculated the last time the user selected a Best
recommendation.
Figure 4: Updated Current Trade-off.
Now, the user selects new Rec 2 as the new best
recommendation so far. The recommendation is
added to the Best So Far graph and table, and the
utilities are all recalculated and updated in the
graphs and tables. The Best So Far graph always
displays recommendations from highest utility to
lowest utility, left to right.
Figure 5: Updated Best-So-Far.
To finalize the process this example, the user
chooses Best 1 as the most optimal recommendation
by selecting the Best 1 column and pressing the
Accept button. A final user utility is then calculated.
Composite Alternative Pareto Optimal Recommendation System with Individual Utility Extraction (CAPORS-IUX)
331

3 KEY ALGORITHMS
CAPORS-IUX is implemented using three main
algorithms. These algorithms are responsible for
generating a set of recommendations for considera-
tion and for updating the user-specific utility.
The first algorithm is the paretoOptimal
algorithm for generating recommendations. This
algorithm takes as input (1) an analytic model am,
(2) variable input vi, (3) metrics definitions m, (4)
metric weights for y-dimension y-dim, (5) metric
weights for x-dimension x-dim, (6) number of points
to generate L, and (7) epsilon e.
A two-dimensional space is created using a
linear combination of metrics in the y direction and a
linear combination of metrics in the x direction.
These linear combinations are determined by the
weights passed in for each dimension. Both
dimensions are normalized to [0, 1].
L unit vectors are then generated for the space.
The directions of the vectors are evenly spaced from
the x-axis to the y-axis.
Figure 6: Candidate Utility Vectors.
A point on each vector is then produced by using
the linear combination of the weighted x-axis
metrics for the x component of the point, and a
linear combination of the weighted y-axis metrics
for the y component of the point. This point captures
the preferred recommendation by the user for the
associated vector direction.
However, this point might not represent a point
in the space of feasible recommendations. Therefore,
a final step is performed that projects this point onto
the Pareto-front.
Figure 7: Projection onto Utility Vector.
paretoOptimal(am, vi, m, y-dim, x-dim, L, e)
recs []
for i=0 to L-1 do {
alpha_i e + [((π/2 – 2e) / L) * i]
w_xi cos(alpha_i)
w_yi sin(alpha_i)
rec_i max_utility(am, vi, m, w_xi, w_yi, x-dim, y-dim, e)
recs recs + {w_xi, w_yi, rec_i}
}
return recs
function max_utility(am, vi, m, w_x, w_y, x-dim, y-dim, e)
optimal_rec argmax{rec_utility}(compute_rec)
return optimal_rec
function compute_rec(am, vi, m, w_x, w_y, x-dim, y-dim, e)
model_output am(vi)
model_constraints model_output.constraints
num_metrics m.length
sum_x 0
sum_y 0
for i in num_metrics do {
weight_i x-dim[i]
value_i model_output.metrics[i]
sum_x sum_x + (weight_i * value_i)
for i in num_metrics do {
weight_i y-dim[i]
value_i model_output.metrics[i]
sum_y sum_y + (weight_i * value_i)
rec_utility (w_x * sum_x) + (w_y * sum_y)
return {model_output, rec_utility}
The second algorithm, improveMetric, is used
to generate a new set of recommendations based on
improving one metric while relaxing the Pareto-
optimal constraints of the others. This algorithm
takes as input (1) an analytic model am, (2) variable
input vi, (3) metrics m, (4) current utility cu, (5)
metric to improve mp, (6) number of points to
generate L, and (7) epsilon e.
This algorithm simply leverages the
paretoOptimal algorithm by setting the y-dim to 1
for the metric corresponding to mp, and the x-dim to
the weight of current utility for all metrics not mp.
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
332

improveMetric(am, vi, m, cu, mp, L, e)
num_metrics m.length
x-dim[1,…,num_metrics] 0
y-dim[1,…,num_metrics] 0
y-dim[mp] 1
for i=0 to num_metrics-1 do{
x-dim[i] = cu[i]
return paretoOptimal(am, vi, m, y-dim, x-dim, L, e)
Finally, the extractUtility algorithm, calculates
the user’s utility using the x and y components of the
underlying vector for the user’s preferred
recommendation point. This algorithm takes as input
(1) selected recommendation srec and (2) the current
utility cu. The output is the normalized user utility.
The mechanism for extracting the utility involves
recovering the underlying vector that was projected
onto the Pareto-front by the paretoOptimal
algorithm. This algorithm takes as input (1) selected
recommendation srec, (2) current utility cu, (3)
metrics m, and (4) current metric-to-consider mp.
extractUtility(srec, cu, m, mp)
axis srec.axis
w_x axis.x
w_y axis.y
y_weight 1
num_metrics m.length
user_utility []
sum_utility 0
for i=0 to num_metrics do {
if i==mp then {
user_utility user_utility + w_yi
sum_utility sum_utility + w_yi
}
else {
x_weight = cu[i]
user_utility user_utility + (x_weight * w_xi)
sum_utility sum_utility + (x_weight * w_xi)
}
normalized_utility []
for i=0 to num_metrics-1 do {
normalized_utility user_utility[i] / sum_utility
}
return normalized_utility
4 SYSTEM ARCHITECTURE
The system consists of two core internal
components: (1) Recommendation Engine, which
implements paretoOptimal, improveRec, and
extractUtility algorithms, and (2) Recommendation
User Interface for displaying results and enabling
user-guided improvement of recommendations. The
Recommendation Engine is further integrated with
Unity DGMS for: (1) generating recommendation
space and computing metrics, and (2) executing
argmin and argmax functions.
Figure 8: System Architecture.
The Recommendation Engine must be initialized
with a data structure that contains (1) metrics
definitions used to evaluate each recommendation,
(2) an analytic model for computing metrics and
constraints of a given recommendation, (3) variable
input for exploring the feasible space of composite
alternatives, (4) configuration setting for maximum
number of recommendations to generate and (5)
configuration setting for default metric for user to
consider, and (6) configuration setting for default
utility weights (e.g. equal weights for all metrics).
The Recommendation Engine integrates with
Unity DGMS in order to generate the domain-
specific recommendations based on the input model.
Furthermore, Unity DGMS provides the capability
of calculating metrics on each recommendation.
The JSON output of the recommendation engine
is fed directly to the user interface. The user
interface is written in HTML and JavaScript. The
JavaScript functions of the user interface perform
the following: (1) load the recommendation JSON
records; (2) bind JSON data to D3JS (Data Driven
Documents, 2016) charting library; (3) format the
Current Tradeoff Graph; (4) display Current
Tradeoff Table; (5) format the Best So Far Graph;
(6) display Best So Far Table; (7) load improved
recommendations from Unity DGMS; (8) handle all
user interactions (best, remove, improve, accept).
5 EXPERIMENTAL STUDY
We conduct an experimental study using synthentic
users, in order to measure the performance of the
system. Performance is measured by how fast, and
to what degree, the system converges in presenting
the user with the most optimal recommendation,
based on the user’s known utility. For this
experiment, we use the sourcing example from
Section 2.
Composite Alternative Pareto Optimal Recommendation System with Individual Utility Extraction (CAPORS-IUX)
333

To initialize the experiment, a set of ten
synthetic users is created by generating a random
utility for each user. The random utility is an array
of random weights, one for each metric.
User 1 [0.54636, 0.1495, 0.3041]
User 2 [0.3393, 0.0763, 0.5844]
User 3 [0.2262, 0.0862, 0.6876]
User 4 [0.1378, 0.3556, 0.5066]
User 5 [0.7261, 0.2243, 0.0495]
Figure 9: First 5 Synthetic User Utilities.
The experiment is run by iterating through each
synthetic user and executing the system’s algorithms
until convergence between the system recommended
alternative and the preferred user alternative is
reached. Convergence is defined as when the
distance between the system recommended
alternative and the preferred user alternative stops
improving.
At the start of a user iteration, the optimal
recommendation is calculated using DGMS, given
the assigned user utility. This recommendation
serves as ground truth when measuring convergence.
Next, a first set of Pareto-optimal
recommendations are generated using default utility
of [0.33, 0.33, 0.33] with the cost metric as the first
metric to consider. A utility gap is then generated.
We define utility gap UG by
=
− ()
BUU=best user utility and UU(srec) is the user
utility of the system recommendation. If the utility
gap is zero, indicating that the system found the
optimal recommendation, the user iteration is
complete.
Otherwise, the best-so-far recommendation is
chosen based on the assigned user utility. This
causes the system to extract an updated system
utility for the user. The next metric to consider is
then determined by computing the gap between the
system utility and user utility for each metric. The
metric with the largest gap is chosen as the next
metric to consider.
The improveMetric algorithm is then called
with the new metric to consider and the updated
system utility, to generate a new set of
recommendations. A new utility gap is calculated
and the experiment checks for convergence. If
convergence is not reached, another cycle of
recommendations begins.
runExperiment(num_users, num_metrics)
convergences = []
for i=1 to num_users do {
utility_gap Inf
last_utility_gap Inf
done false
step 1
user_convergence = {}
user_utility randomizeWeights(num_metrics)
system_utility [0.33, 0.33, 0.33]
bestUserUtility findBestRecommendation(user_utility)
recs paretoOptimal(…)
while done == false do {
bestSystemUtility max(recs.utility)
utility_gap abs(bestUserUtility – bestSystemUtility) /
bestUserUtility
user_convergence[step] = utility_gap
if (utility_gap == 0) or (utility_gap >= last_utility_gap) {
done true
convergences convergences + user_convergence
}
else {
best_so_far findBestSoFar(recs, user_utility)
system_utility extractUtility(best_so_far, …)
next_metric findNextMetric(best_so_far, user_utility
system_utility)
recs improveMetric(next_metric, system_utility, …)
}
step step + 1
last_utility_gap utility_gap
}
}
return convergences
The utility gaps and rates of convergence across
all of the users in the experiment are collected and
plotted. As seen in Figure 10, the system converges
to the optimal recommendation within 3 steps, or the
number of metrics.
Figure 10: Convergence Results.
6 CONCLUSIONS
In this paper we proposed a methodology and present-
ed a system for generating composite alternative
recommendations combining user-guided continuous
improvement with Pareto optimal trade-off
considerations and for extracting individual utility.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
Step 1 Step 2 Step 3
Utility
Gap
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
334
This methodology improves upon earlier
research by providing a way to iteratively construct
Pareto-optimal recommendations such that the
individual user’s utility can be extracted.
Furthermore, we developed a system, CAPORS-
IUX, to implement the methodology. We also
provided experimental results that prove the ability
of CAPORS-IUX to converge on the true utility of
the individual user.
In future work, we will extend the concept of
utility extraction beyond the individual to the group
level.
REFERENCES
Xie, M., Lakshmanan, L.V. and Wood, P.T., 2010,
September. Breaking out of the box of
recommendations: from items to packages. In
Proceedings of the fourth ACM conference on
Recommender systems (pp. 151-158). ACM.
Brodsky, A., Morgan Henshaw, S. and Whittle, J., 2008,
October. CARD: a decision-guidance framework and
application for recommending composite alternatives.
In Proceedings of the 2008 ACM conference on
Recommender systems (pp. 171-178). ACM.
Khabbaz, M., Xie, M. and Lakshmanan, L.V., 2011.
TopRecs+: Pushing the Envelope on Recommender
Systems. IEEE Data Eng. Bull., 34(2), pp.61-68.
Interdonato, R., Romeo, S., Tagarelli, A. and Karypis, G.,
2013, November. A versatile graph-based approach to
package recommendation. In Tools with Artificial
Intelligence (ICTAI), 2013 IEEE 25th International
Conference on (pp. 857-864). IEEE.
Koutrika, G., Bercovitz, B. and Garcia-Molina, H., 2009,
June. FlexRecs: expressing and combining flexible
recommendations. In Proceedings of the 2009 ACM
SIGMOD International Conference on Management of
data (pp. 745-758). ACM.
Xie, M., Lakshmanan, L.V. and Wood, P.T., 2011, April.
Comprec-trip: A composite recommendation system
for travel planning. In Data Engineering (ICDE), 2011
IEEE 27th International Conference on (pp. 1352-
1355). IEEE.
Brodsky, Alexander, Juan Luo and M. Omar Nachawati,
2016. “Toward Decision Guidance Management
Systems: Analytical Language and Knowledge Base.”
Technical Report GMU-CS-TR-2016-1. Extension of:
Brodsky, A. and Luo, J., 2015, April. Decision Guidance
Analytics Language (DGAL)-Toward Reusable
Knowledge Base Centric Modeling. In ICEIS (1) (pp.
67-78).
Ribeiro, M.T., Ziviani, N., Moura, E.S.D., Hata, I.,
Lacerda, A. and Veloso, A., 2015. Multiobjective
pareto-efficient approaches for recommender systems.
ACM Transactions on Intelligent Systems and
Technology (TIST), 5(4), p.53.
Jeffries W. and Brodsky A. (2017). Composite Alternative
Pareto Optimal Recommender System (CAPORS). In
Proceedings of the 19th International Conference on
Enterprise Information Systems - Volume 1: ICEIS,
ISBN 978-989-758-247-9, pages 496-503. DOI:
10.5220/0006277404960503.
Data Driven Documents 2016. Available from
<https://d3js.org>. [9 August 2016]
APPENDIX A: USER INTERFACE
Composite Alternative Pareto Optimal Recommendation System with Individual Utility Extraction (CAPORS-IUX)
335
