
The VideoM@T Project
Engaging Students on Learning Tricky Topics in Mathematics Through Creative
Skills
Sara Cruz, José Alberto Lencastre
and Clara Coutinho
Institute of Education, University of Minho, Campus de Gualtar, 4710-057, Braga, Portugal
Keywords: Threshold Concepts, Tricky Topics, Technology-enhanced Learning, Creative Video Editing.
Abstract: This article presents the VideoM@t project, designed to enhance students' understanding of mathematical
concepts through creative video editing. VideoM@t was founded on the JuxtaLearn process, an eight-stage
pedagogical framework that uses an online platform to assist the students in planning, editing, and sharing
knowledge about threshold concepts in a flipped classroom model. The project involved 52 students from
9
th
grade and three teachers of mathematics. Qualitative and quantitative data were collected to understand
students' level of comprehension on tricky topics in mathematics. The results show that students were able
to overcome their difficulties during the creative video editing process. The comparison between the first
and the final quiz radar charts suggest that students have developed understandable knowledge on tricky
topics in mathematics.
1 INTRODUCTION
VideoM@t was one of the winning projects of the
contest “Ideias com Mérito” [Ideas with Merit]
promoted by the Portuguese Ministry of Education
to encourage schools to develop innovative projects
that use information and knowledge to support the
school curriculum. The prize was used to buy tablets
that students used throughout the project
implementation. In the VideoM@t project, we seek
to stimulate students' understanding of mathematical
threshold concepts through the production of
creative videos. Threshold concepts are reported in
the literature as complex concepts that students have
difficulty in understanding, sometimes taking refuge
in the memorisation of the concept without really
understanding it (Meyer and Land, 2003). For
students, threshold concepts are troublesome
because they are conceptually difficult to
comprehend (Perkins, 2006). An abstract concept
describes something general, but concrete
representations and real-world examples always
describe something specific and are very important
when connecting concrete and abstract mathematical
contexts (Rystedt, Helenius and Kilhamn, 2016).
VideoM@t project was founded on the
JuxtaLearn learning process. The JuxtaLearn process
uses creative video editing by students to get them to
a deeper understanding of a threshold concept or a
tricky topic (Adams, Rogers, Coughlan, Van-der-
Linden, Clough, Martin, and Collins, 2013). In the
JuxtaLearn process, the terminology ‘tricky topic’ is
used to refer to issues identified by teachers as
difficult for their students (Adams and Clough,
2015), even though these difficulties are not the
same as those reported in the literature as core
threshold concepts. In the JuxtaLearn process, to
understand the tricky topic, students have to surpass
some stumbling blocks that are outstripped first
during storyboarding and then in video editing.
During the whole process, CLIPIT coordinates all
user interaction and data such as documents,
storyboards, quizzes and videos.
This article is structured in five sections: in
Section 2, we introduce VideoM@t and the
JuxtaLearn learning process, while Section 3
presents the methods for data collection, then
Section 4 presents our main results and reflections.
We conclude in Section 5 with a synthesis and
proposals for future work.
342
Cruz, S., Alberto Lencastre, J. and Coutinho, C.
The VideoM@T Project.
DOI: 10.5220/0006771703420349
In Proceedings of the 10th International Conference on Computer Supported Education (CSEDU 2018), pages 342-349
ISBN: 978-989-758-291-2
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 BACKGROUND
2.1 VideoM@t Project
The search for solutions that foster academic success
in mathematical subjects for a group of students and
our willingness to implement the JuxtaLearn
learning process led to the elaboration of the
VideoM@t project. VideoM@t is centred on a
taxonomy developed by the JuxtaLearn project that
helps teachers to promote students' interest in
threshold concepts through the creation of original
explanatory videos. With VideoM@t, our primary
goals were to implement methodological alternatives
in which students construct their knowledge through
actions where they develop mathematical literacy to
understand complex math concepts. The project was
funded and the money was used to buy tablets. The
use of tablets, due to their portability, allows higher
efficacy in accessing digital contents (Lencastre,
Bento, and Magalhães, 2016). With this project, we
promote the sharing and involvement of students in
the production of videos that explore the
mathematics curricula. We developed in students a
creative inspiration, as well as an improvement in
their conceptual understanding and their knowledge.
2.2 The JuxtaLearn Learning Process
The JuxtaLearn learning process is founded on a
specific pedagogic framework that aims to identify
and promote knowledge in threshold concepts in
STEM areas (Science, Technology, Engineering,
and Mathematics) through creative video editing.
The JuxtaLearn process involves the students in
eight steps, and is user-centred (Martín, Gértrudix,
Urquiza-Fuentes, Haya, Hernán-Losada and
Castellanos, 2014); i.e., the student is the protagonist
in the learning process, and the teacher is a
facilitator between the student and the knowledge
(Lencastre and Coutinho, 2015).
Figure 1: The JuxtaLearn Process.
Step 1 (Identify) – The teacher identifies the
tricky topics based on their previous experience.
Each tricky topic can be divided into smaller
stumbling blocks.
Step 2 (Demonstrate) – The teacher creates
one or more Standard Teaching Activities (STA)
around the stumbling blocks.
Step 3 (Interpret) – Students perform a
diagnostic quiz to determine their level of
understanding about the tricky topic.
Step 4 (Perform) – Students create a
storyboard to explain the tricky topic.
Step 5 (Compose) – In groups, the students
make a video explaining the tricky topic.
Step 6 (Share) – Videos are shared with the
class via CLIPIT.
Step 7 (Discuss) – Debate among students is
promoted, allowing the social construction of
knowledge while promoting the consolidation of the
concept.
Step 8 (Review) – Students return to the quiz
from Step 3 to re-assess their understanding of the
tricky topic.
The entire process is tracked online on the
CLIPIT platform (see Figure 1). CLIPIT is a web
space that allows collaboration, peer assessment, and
analysis of the learning progression in a flipped
classroom model. The productive failure-based
flipped classroom pedagogical design, allows
students to have more time for thinking and
discovering, and may help to improve students’
problem-solving skills (Song and Kapur, 2017).
CLIPIT was developed to support the JuxtaLearn
learning process by allowing comments and analysis
of the results (Adams and Clough, 2015). CLIPIT
has a database of tricky topics, and their related
stumbling blocks, examples of student’s problems,
quizzes and teaching material. To learn more about
CLIPIT, see the article from Cruz, Lencastre,
Coutinho, Clough, and Adams (2016) - Threshold
Concepts Vs. Tricky Topics - Exploring the Causes
of Student's Misunderstandings with the Problem
Distiller Tool, reported in the references.
3 METHOD
VideoM@t was strongly anchored on JuxtaLearn
learning steps. The study included the identification
of tricky topics in mathematics with three teachers
and the application of the entire process with 52
students. The teachers collaborated voluntarily,
involving three of her own classes.
The VideoM@T Project
343

Diverse methods were used to collect the data: (i)
interviews with the teachers; (ii) system logs on the
platform, (iii) a diary to gather direct observations,
(iv) a final focus group with the students to
understand their perceptions about the whole
process.
3.1 Identifying the Tricky Topics
The first step was to identify the threshold concepts
with the teachers. The three teachers assembled in a
group, reflected on the difficulties of their students
and identified threshold concepts that, from their
teaching experience, are tricky topics. Thus, based
on their knowledge, teachers identified the following
tricky topics: solving equations with denominators,
literal equations, solving 1st-order equations, and
solving equations with parentheses. Then, with the
guidance of the Problem Distiller tool, they divided
each tricky topic into stumbling blocks, and wrote a
brief description of the specific problems. The
Problem Distiller tool displays a set of tabbed panes
prompting teachers to reflect on and select possible
reasons why their students might be having a
particular problem, connecting all the information
entered to the appropriate tricky topic and stumbling
block or blocks (Adams and Clough, 2015). The
gathered tricky topics were then used by the students
to develop their videos.
3.2 Creative Video Editing
The creative video editing process involved six tasks
for each group of students: (1) diagnostic test (initial
quiz available on CLIPIT); (2) create a storyboard;
(3) edit the video, (4) watch the video and discuss it
with peers, (5) post-knowledge test (final quiz
available on CLIPIT) and (6) reflect on the results.
Initially (Identify) with the help of the Tricky
Topic Tool, we identified tricky topics and
mathematical topics that teachers considered
difficult for their students. The data collection was
done through system logs on the platform and a
diary to collect direct observations.
Next, (Demonstrate step) the teachers made
CLIPIT available through students’ activities
(videos, PDFs, links) with relevant information
about the identified tricky topics. The students
accessed the information, clarified doubts and then
completed a diagnostic quiz to determine their level
of understanding about the tricky topic. A diagnostic
quiz is the starting-point for students participating in
the JuxtaLearn Process (Adams and Clough, 2015).
Figure 2 shows a student verifying the result
obtained in the questionnaire.
Figure 2: Students checking the quiz radar charts.
Based on the results obtained in the diagnostic quiz,
the teachers established work groups comprising two
students. The group was set so that a student with
more difficulty in a certain topic would work with a
student who presented less difficulty. So, in pairs,
students drew storyboards to explain one of the
tricky topics or the initially identified stumbling
blocks (Perform step). The storyboards were
scientifically and pedagogically validated by the
teachers and the students created explanatory videos
based on these storyboards (Compose step).
The videos were shared in the class (Share
step) and a discussion was organised around the
work done (Discuss step). Then, the students
performed a final quiz (with the same questions as
the diagnostic quiz) to be able to compare results
and see their evolution.
In the end, with students, we performed a
focus-group to understand their perception of the
JuxtaLearn learning process. After transcribing the
material from the focus-group, a content analysis
was done following the guidelines of Bardin (2013).
A set of dimensions and categories emerged from
data, which are as follows: (i) Students' perception
of the storyboard design process, (ii) Students'
perception of the value of video editing, and (iii)
reflection about the process.
3.3 Participants
Three math teachers (T1, T2, and T3) working in a
public school, all being women aged between 42–50
years old. 52 students (Si, com i∈
1, …, 52
) from
the 9
th
grade, 31 girls and 21 boys, ages from 13–15
years old. Each teacher was responsible for
developing the JuxtaLearn process in her own class.
CSEDU 2018 - 10th International Conference on Computer Supported Education
344

4 RESULTS
The Problem Distiller Tool helps teachers reflect on
the causes of student problems they had identified
(Cruz, Lencastre, Coutinho, Clough, and Adams,
2016). So, based on their teaching practice, teachers
identified the tricky topics in mathematics that are
problematic for their students, and checked if the
tricky topics were already listed in the Tricky Topic
Tool and the database of CLIPIT.
Studies consider that concepts poorly
understood in arithmetic constitutes an obstacle to a
student's understanding of algebra (Guimarães,
Arcavi, Gómez, Ponte, and Silva, 2006). There is a
mathematical connection between algebra and
arithmetic as each is normally taught using
abstraction and generalisation processes. The
teachers identified arithmetical difficulties in
understanding and apprehending the algebraic
process for solving equations. So, teachers identified
the following tricky topics: (i) solving 1st-order
equations, (ii) solving equations with denominators,
(iii) solving equations with parentheses, and (iv)
literal equations.
Then teachers reflected on the difficulties
they usually encounter with their students and tried
to identify stumbling blocks and comprehension
gaps in tricky topics (Table 1). When teachers
expressed problems explaining why their students
had difficulty understanding the tricky topic, they
were guided by the Problem Distiller Tool.
Table 1: Tricky Topics and their stumbling blocks.
Tricky Topic
Stumbling Blocks
Solving 1st-
order
equations
Translation of statements of current
language for symbolic language
Simplification of algebraic
expressions
Principles of equivalence
Verification of solution
Notion of unknown and notion of
solution of an equation
Solving
equations
with
denominators
Distributive property of
multiplication
Priority of elementary operations,
Equivalence principles of equations,
notion of equation
Notion of solution
Simplification of algebraic
expressions and simplification of
fractions
Tricky Topic Stumbling Blocks
Solving
equations
with
parentheses
Distributive property of
multiplication
Distributive property of
multiplication
Property of elementary operations
Principles of equivalence of
equations
Use of rules to solve 1st degree
Equations with a non-denominator
unknown
Notion of unknown
Current language translation to
symbolic language
Simplification of algebraic
expressions and rational numbers
Literal
equations
Principles of equivalence of algebraic
equations
Simplification of algebraic
expressions
Solve a literal equation in order to an
unknown
Notion of solution and notion of
equation
The Problem Distiller tool lists a set of problems that
typically challenge students, helping the teacher to
think and reflect on their experience working with
students. Through this reflection, the teacher is able
to identify the gaps in an understanding of the tricky
topic and associate their own students’ difficulties to
the comprehension problems listed in the Problem
Distiller tool. As they made selections from the
Problem Distiller tool, teachers were identifying
problems that students typically encounter in
understanding tricky topics. At the same time,
teachers were also able to reflect on why these
problems occur and how they can be solved.
Figure 3: Problem Distiller to a 1st grade equation.
The VideoM@T Project
345
For example, on the tricky topic 1
st
-Grade equation
(Figure 3), the teachers reported that students do not
know the principles of equivalence and have
considerable difficulty in simplifying algebraic
expressions, which makes it difficult to work with
equations. Teachers also reported that their students
sometimes cannot verify whether a number is a
solution to a given equation because they cannot
recognise the meaning of unknown. On the Problem
Distiller Tool, teachers also associate possible
causes for difficulties on the tricky topic 1
st
-Grade
equation. They said that the causes for the
difficulties may arise from the students’ incomplete
knowledge of concepts that they should already
know, or a misunderstanding of the method for
solving equations.
The tricky topics identified in Step 1 of the
JuxtaLearn process have been revised. Then,
teachers shared material available in CLIPIT for
students to review the mathematical contents (Step 2
of the JuxtaLearn process). All students had an
initial quiz (Step 3 of the JuxtaLearn process),
previously prepared by the teachers on the Quiz
Tool in CLIPIT. We used the Radar Chart to help
students diagnose their own comprehension
problems in a tricky topic and to help teachers
reflect on ways of aiding the student to overcome
these stumbling blocks. The visualisation by
students of their own radar chart helps them to
identify and to diagnose the stumbling blocks they
encounter when trying to understand the tricky topic
(Hartnett and Adams, 2016); this can assist them to
focus on overcoming these difficulties. The
reflection on one's mistakes is relevant
(Cherepinsky, 2011) to overcoming gaps in
understanding and overcoming difficulties in
learning mathematics. Based on the results obtained
in the initial quiz, each group of two students created
a storyboard (Step 4 of the JuxtaLearn process) on a
mathematical subject in which they had difficulty.
Then, based on the storyboard created, the students
edited a video (Phase 5 of the JuxtaLearn process)
on the following topics: (i) solving a literal equation
in order to an unknown, (ii) the distributive property,
(iii) principles of equivalence between equations,
(iv) check if a value is a solution to an equation, (v)
notion of solving an equation, (vi) notion of
unknown of an equation, (vii) check if an ordered
pair is a solution, notion of unknown, (viii)
simplification of algebraic expressions, and (ix)
properties of the elementary operations. A
storyboard is a set of drawings as a representation of
a film in sequences, and these drawings can contain
elements such as dialogues, pictures, sketches
(Hartnett, Malzahn and Goldsmith, 2014). At the
end of this phase, 25 storyboards and their videos
were created. Storyboards and video scripts are
potential objects that allow the transfer of
knowledge between different students through the
creation of a movie. The creation of storyboards
constitutes a creative step on which students
collaborate, share knowledge and reflect in order to
identify and clarify differences (Hartnett et al.,
2014). The collaborative construction of videos
favours motivation for tasks (Cruz, Lencastre and
Coutinho, 2015). The videos created were shared
(Step 6 of the JuxtaLearn process) in class and a
discussion (Step 7 of the JuxtaLearn process) was
promoted around the results achieved. In the end,
students completed a final quiz (Step 8 of the
JuxtaLearn process) to compare performances. The
visualization of their quiz results as a radar chart
helps students to diagnose their own progress. In the
following image, we present an example of a radar
chart of the initial and final quizzes by one of the
students involved – S4
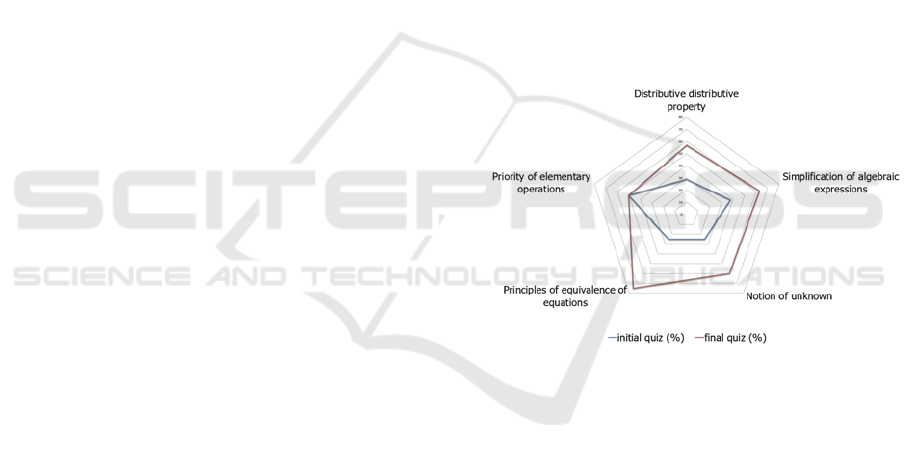
Figure 4: Radar chart with initial and final quizzes.
Comparing the chart radar observations for the
initial and final quizzes, we found that the student
improved in overcoming some stumbling blocks. We
observed that the student increased the number of
correct answers to questions that involve having the
notion of unknown, knowing the equivalence
principles of equations, knowing the distributive
property of multiplication and knowing how to
simplify algebraic expressions. The student kept the
same number of correct answers to questions that
involved knowing the priority of elementary
operations.
Comparing the results obtained on the radar
of the initial quiz with the ones obtained on the final
quiz (Table 2), in all three classes it was found that
most students improved their scores.
CSEDU 2018 - 10th International Conference on Computer Supported Education
346
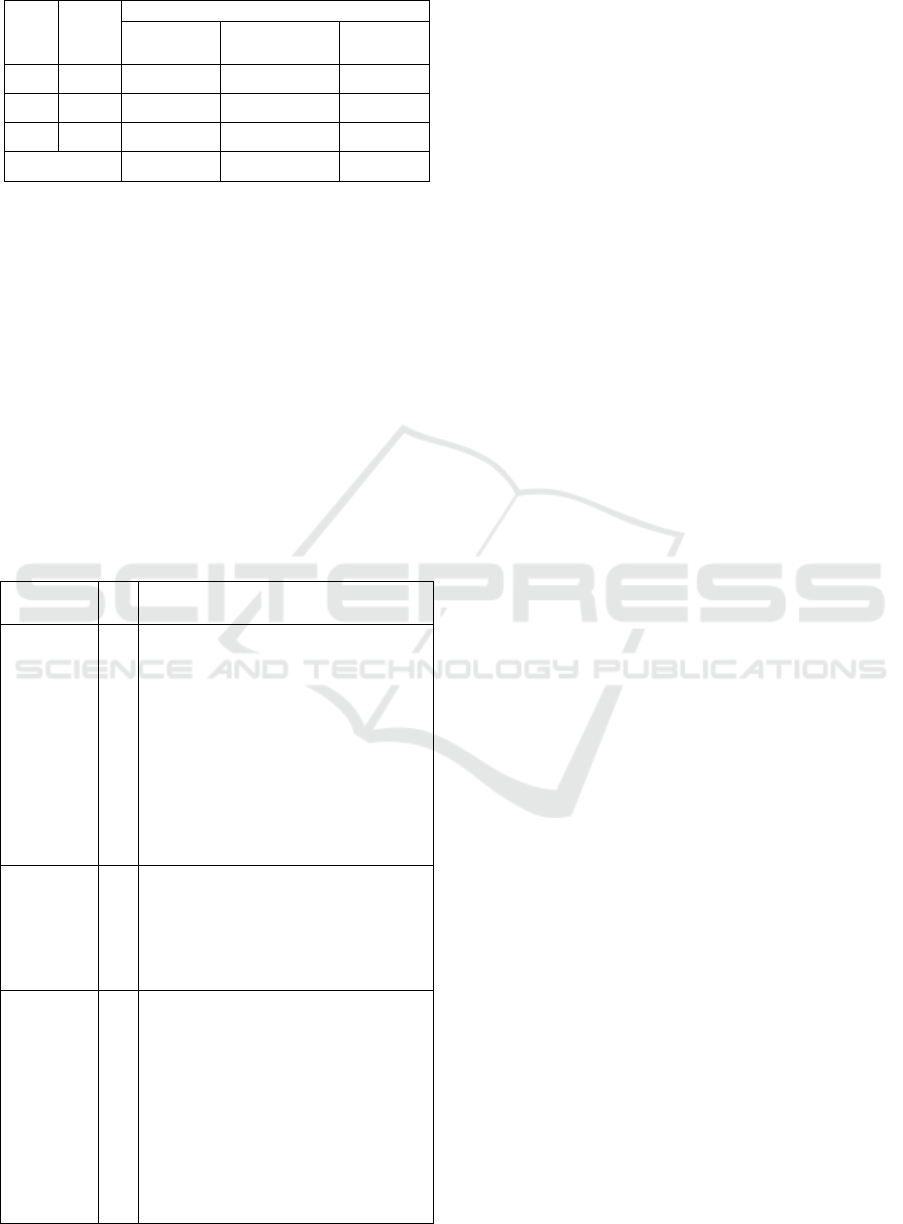
Table 2: Comparison between the initial and final quiz.
Class
Teacher
Variation of the final to the initial quiz
Positive
variation
There was
no variation
Negative
variation
A T1
87% 13% 0%
B T2
50%
28% 22%
C T3
69% 12% 19%
Total
67% 18% 14%
Song and Kapur (2017) in their quasi-experimental
study comparing the “traditional flipped classroom”
pedagogical design to the “productive failure”
pedagogical design in the flipped classroom for a
curriculum in a Secondary school found something
similar. In this study, authors worked in two Grade 7
classes, one of them with “traditional flipped
classroom” and the other class with the “productive
failure-based flipped classroom”, with students who
had more difficulty.
The content analysis was developed
according to the phases suggested by Bardin (2013),
so Table 3 presents students’ voices according to the
three categories considered.
Table 3: Category of analysis.
Tricky
topic
N.º Stumbling Blocks
Students'
perception
of the
storyboard
design
process
5 "The most difficult thing is to have the
idea for the storyboard" (S2).
"Because we had to find a way to
explain an equation and it was
complicated" (S24).
"It is as if we were to teach" (S32).
"Was the one who gave more work, to
have ideas" (S41).
"Was the one that gave more work, to
have ideas" (S41).
Students'
perception
of the
value of
video
editin
g
3 "I enjoyed recording the video" (S13).
"The one I liked the most was making
the video" (S11).
"We did the same job, but on the
computer, so it's more appealing"
(
S32
)
.
Reflection
about the
process
2
"The first problem is that we had to
know the matter, then we had the
problem of perceiving how we are
going to explain that. The third
problem was getting it to the paper,
which was in our head. The fourth
problem was to convey to reality
"(S4).
"This work has clarified some
misunderstandings, almost all of
them" (S51).
Interpreting Table 3, we verified that during
reflection at the end of the cycle, the students
considered that "storyboard phase" (S4) was the
stage of the process they felt to be the most difficult
as they had to "get the idea for the storyboard" (S2).
Finding "a way to explain an equation and it was
complicated" (S24), worked "as if we were
teaching" (S32), so this step "was what worked the
most" (S41).
According to the opinion of the students, the
most enjoyable step in the process was to "record the
video" (C4A13), or "make the video" (C4A11).
They enjoyed doing creative video-editing work and
having the opportunity to work out more exercises
using this method, because "on the computer, then
it's more appealing" (S32). These results are similar
to those obtained by Kearney and Schuck (2006); in
a study with a group of students who had to choose
the content for a video, they wrote their own scripts
and storyboards and proceeded to the creative
edition of the video. During this work, creative
video production has motivated, enveloped, and
enthused students in learning and working with
mathematical concepts. All the students admit that
the process helped them to think differently,
"because it clarified some doubts, almost all of
them" (C4A51). Students need to feel that they can
create and choose their own path in learning through
clear guidelines in order to improve their
understanding and creative performance (Adams et
al., 2013).
In general, students consider that thinking
about and planning the videos helped them to
overcome the stumbling blocks that were obstacles
to learning. However, they admit that they had
difficulties in doing the work: "The first problem is
that they had to know the matter, then they had the
problem of realising how they were going to explain
it. The third problem was getting what was in the
head on to paper. The fourth problem was to convey
the reality" (S4). By awakening students' curiosity in
concepts, the JuxtaLearn learning process is
intended to support students in a deeper
understanding of a specific concept through a
creative process of video editing that is based on a
stimulating and flexible approach (Adams et al.,
2013).
The VideoM@T Project
347

5 CONCLUSIONS
In this article, we described the VideoM@t project
based on the JuxtaLearn learning process. During
the study, we identified and discussed ways in which
the process helped the students to overcome
misunderstandings on mathematical concepts.
Teachers identified the tricky topics that their
students have, and we uploaded them into the Tricky
Topic Tool. Then, with the help of the Problem
Distiller Tool, teachers were led to reflect about
misunderstandings that they usually find among
their students. Teachers were able to put into
practice the whole JuxtaLearn process with their
students, by guiding them in the production of
storyboards and instructional videos in a
collaborative way. Students created 25 explanatory
videos about concepts they had difficulty in. They
considered that producing videos helped them –
“work has clarified some misunderstandings, almost
all of them" (S51). In this phase, they admit to
having experienced increased difficulty, because
they "had to find a way to explain an equation and it
was complicated" (S24). In general, all students
enjoyed doing the work, mainly "recording the
video" (S13), because the process involved students
by making them an active part in their own learning.
The results of Rystedt, Helenius and Kilhamn (2016)
in a case study investigates how a group of 12-year-
old pupils contextualise a task formulated as an
equation expressed in a word problem, showing the
importance of giving pupils opportunities to realise
the position of symbolic mathematical
representations when dealing with mathematical
concepts. In line with Rystedt et al. (2016), our
analysis indicates that engaging students in concrete
activities that involve them helps to improve their
skills.
Data analysis showed that the VideoM@t
involved the majority of the students. All of them
completed the JuxtaLearn learning process and most
improved the results in the post-knowledge test.
According to the results obtained by Rystedt et al.,
2016), the concrete representations (such as real-
world situations) are conceptually different from
abstract mathematical concepts. Pirhonen and Rasib
(2017), in a study about the learning method in
which students produce instructional videos about
the content matter of their learning process, realised
that producing a video combined with the content
approach can be an efficient and motivating way of
learning. A didactical implication of this case study
is that it is difficult to incorporate the rich meaning
of an abstract concept. However, the video creation
involve the students in recreational activities that
allowed them to develop skills around these
concepts. It also seems appropriate to analyse in
future research if the level of reflection achieved
with the use of the Problem Distiller Tool
contributes to changing the teachers' professional
practice.
The radar chart works as a digital tool for
evaluation and visualisation of the results by
students and teachers. The students’ view of the
radar chart, however, should be regarded as a
significant means to support reflection alone.
Although the role of the teacher is also important, it
is a teacher's task to manage the students’ reflection
in order to promote deeper thinking. In line with
Cruz, Lencastre, Coutinho, Clough and Adams
(2016), findings suggest that students are receptive
to making videos and can improve their
mathematical knowledge around complex concepts.
These results are important to foster curiosity around
mathematical topics, but further research is needed
to study the pedagogical relevance of this.
In today's innovation society, mathematical
knowledge becomes ever more relevant in the
development of the next generation of creative
thinkers and innovators. This VideoM@t project
was set out to solve problems in the understanding
of mathematical concepts, through creative video
editing. The ease with which students deal with
video, mobile technology, and digital resources
should be used in the learning process for
educational purposes (Lencastre et al., 2016). Do
teachers conceive the idea of being able to work
remotely, to create digital resources to help the
student and guide a student-centred work in a non-
presentational way? Global connectivity and new
forms of communication are some of the drivers that
reshape the way we think, which influences how we
learn and develop skills. Are schools taking
advantage of the potential of digital technologies,
including the possibility of having personalised
information and open content? Do teachers use the
interactivity that this type of material make possible?
To improve the teaching of mathematics, it is
necessary to establish a new vision for learning. It
would be beneficial if students could learn with
study tools that adapt to their capabilities. CLIPIT
helped students to assess their own knowledge about
a mathematical topic. Students are positively
reinforced during their individual learning processes.
In future research, it would be interesting to create
some courses in a similar way to create the
storyboard and video in the same application, aiming
for a more immediate support to students’ work by
CSEDU 2018 - 10th International Conference on Computer Supported Education
348

the teacher and at the same time broadening the
possibility of online co-production, breaking away
from the traditional way of teaching and learning.
ACKNOWLEDGEMENTS
The VideoM@t project received funding from the
Ministry of Education and the Ministry of Culture,
through a contest promoted by the School Libraries
Network (Portugal). We would like to sincerely
thank all the students and teachers from School of
Palmeira (Portugal), which agreed to participate in
the project.
REFERENCES
Adams, A., Rogers, Y., Coughlan, T., Van-der-Linden, J.,
Clough, G., Martin, E., & Collins, T. (2013). Teenager
needs in technology enhanced learning. In Workshop
on Methods of Working with Teenagers in Interaction
Design, CHI 2013. Paris, France.
Adams, A. & Clough, G. (2015). The E-assessment
burger: Supporting the Before and After in E-
Assessment Systems. Interaction Design and
Architecture(s) Journal - IxD&A, N.25, 39-57.
Bardin, L. (2013). Análise de conteúdo. Lisboa: Ed. 70.
Bívar, A., Grosso, C., Oliveira, F., & Timóteo, M. (2012).
Metas curriculares do ensino básico – matemática.
Lisboa: Ministério da Educação e Ciência (MEC).
Cherepinsky, V. (2011). Self-reflective grading: Getting
students to learn from their mistakes. Primus, 21(3),
294-301.
Cruz, S., Lencastre, J. A., Coutinho, C., Clough, G., &
Adams, A. (2016). Threshold Concepts Vs. Tricky
Topics - Exploring the Causes of Student's
Misunderstandings with the Problem Distiller Tool. In
James Uhomoibhi, et al. (ed.), Proceedings of
CSEDU2016, Vol.1, (pp.205-215). Rome:
SCITEPRESS
Cruz, S., Lencastre, J. A., Coutinho, C., Clough, G., &
Adams, A. (2016). The Problem Distiller Tool:
supporting teachers in uncovering why their students
have problems understanding Threshold Concepts. In
Gennaro Costagliola, et al. (Eds.), Computers
Supported Education (pp. 380–401). Cham: Springer.
Cruz, S., Lencastre, J. A., Coutinho, C., José, R., Clough,
G., & Adams, A. (2017). The JuxtaLearn process in
the learning of maths’ tricky topics: Practices, results
and teacher’s perceptions. In Paula Escudeiro, et al.
(ed), Proceedings of CSEDU2017, Vol.1 (pp.387-
394). Porto: SCITEPRESS.
Guimarães, F., Arcavi, A., Gómez, B., Ponte, J. P., &
Silva, J. (2005). O ensino aprendizagem dos Números
e da Álgebra: Que problemas, que desafios. Encontro
2005, (pp.361-379). Caminha: SPIEM.
Hartnett, E., Malzahn, N., & Goldsmith, R. (2014).
Sharing video making objects to create, reflect &
learn. In Learning through Video Creation and
Sharing (LCVS 2014), September, Graz, Austria.
Kearney, M., & Schuck, S. (2006). Spotlight on authentic
learning: Student developed digital video projects.
Australasian Journal of Educational Technology,
22(2), 189-208.
Lencastre, J. A., & Coutinho, C. (2015). Blended
Learning. In Mehdi Khosrow-Pour (org.)
Encyclopedia of Information Science and Technology,
Third Edition, Volume II (pp. 1360-1368). Hershey
PA: IGI Global.
Lencastre, J. A., Bento, M., & Magalhães, C. (2016).
Mobile Learning: potencial de inovação pedagógica.
In Tânia Maria Hetkowski & Maria Altina Ramos
(orgs.), Tecnologias e processos inovadores na
educação (pp. 159-176). Curitiba: Editora CRV.
Lencastre, J. A., Coutinho, C., Cruz, S., Magalhães, C.,
Casal, J., José, R., Clough, G., & Adams, A. (2015). A
video competition to promote informal engagement
with pedagogical topics in a school community. In
Markus Helfert, et al. (ed.), Proceedings of
CSEDU2015, Vol.1, (pp.334-340), Lisbon:
SCITEPRESS
Martín, E., Gértrudix, M., Urquiza-Fuentes, J., Haya, P.
A., Hernán-Losada, I., & Castellanos, J. (2014).
¡Estudiantes creativos! Creación de vídeos educativos
en redes sociales educativas. In Hernández, J. y
Martín, E. (Eds.), Pedagogía audiovisual:
Monográfico de experiencias docentes multimedia,
(53). Madrid, Servicio de Publicaciones, Universidad
Rey Juan Carlos.
Meyer, J., & Land, R. (2003) Threshold concepts and
troublesome knowledge: linkages to ways of thinking
and practising within the disciplines. In Rust, C. (Ed.)
Improving student Learning - Theory and Practice Ten
Years on, (pp. 412-424). Oxford: OCSLD.
Perkins, D. (2006). Constructivism and troublesome
knowledge. In J. Meyer & R. Land (Eds.),
Overcoming barriers to student understanding:
Threshold concepts and troublesome knowledge (pp.
33–47). Abingdon: Routledge.
Pirhonen, J., & Rasi, P. (2017). Os vídeos instrucionais
gerados por alunos facilitam a aprendizagem através
de emoções positivas. Journal of Biological
Education, 51(3), 215-227.
Rystedt, E., Helenius, O., & Kilhamn, C. (2016). Moving
in and out of contexts in collaborative reasoning about
equations. The Journal of Mathematical Behavior, 44,
50-64.
Song, Y., & Kapur, M. (2017). How to Flip the Classroom
– “Productive Failure or Traditional Flipped
Classroom” Pedagogical Design? Educational
Technology & Society, 20 (1), 292–305.
The VideoM@T Project
349
