Dynamical Creation of Policy Trees for a POMDP-based
Intelligent Tutoring System
Fangju Wang
University of Guelph, 50 Stone Road East, Guelph, Ontario, Canada
Keywords:
Intelligent Tutoring System, Computer Supported Education, Partially Observable Markov Decision Process,
Computational Complexity.
Abstract:
In this paper, we discuss a new technique for creating policy trees in an intelligent tutoring system (ITS) that
is based on a partially observable Markov decision process (POMDP). The POMDP model is a useful tool for
dealing with uncertainties. With a POMDP, an ITS may choose optimal teaching actions even when uncer-
tainties exist. Great computational complexity in solving a POMDP has been a major obstacle to applying the
POMDP model to intelligent tutoring. The technique of policy trees is considered a less expensive approach.
However, policy trees are still too expensive for building ITSs that teach practical subjects. In our research, we
develop a new technique of policy trees, in which trees are grouped and dynamically created. This technique
has advantages of better time and space efficiencies. It enables us to build more efficient ITSs. Particularly
the technique makes it possible to build ITSs on platforms which have limited storage capacity and computing
power.
1 INTRODUCTION
Computational complexity is a key issue in build-
ing an interactive intelligent tutoring system (ITS).
An ITS must be able to reside on a computing plat-
form, and respond to student questions or requests in
a timely fashion. However, many mathematical mod-
els underlying ITSs are computationally intractable.
Huge space consumption and lengthy computing time
have been major obstacles to applying the models to
intelligent tutoring. The partially observable Markov
decision process (POMDP) model is one of them.
The POMDP model may enable an ITS to choose
optimal actions in teaching a student, even when un-
certainties exist. A major goal for building an ITS is
adaptive teaching. To be adaptive, in each tutoring
step a system should be able to choose the action that
is most beneficial to the student it teaches. Mathemat-
ically, adaptive tutoring can be modeled by a Markov
decision process (MDP), in which the agent makes
optimal decisions considering the current states. In an
MDP, the agent observes states clearly and knows ex-
actly what the current states are. However, in a tutor-
ing process, the teacher is often uncertain about stu-
dent states (Woolf, 2009).
A POMDP is an extension of an MDP for deal-
ing with uncertainties. In a POMDP, the task of
choosing an optimal action is referred to as solving
the POMDP. This task is computationally expensive.
A simplified, less expensive technique for POMDP-
solving is to use policy trees, in which decision mak-
ing involves evaluating a set of trees and choosing an
optimal one. However, the technique of policy trees
is still too expensive to be used in practical applica-
tions. In making a decision, the number of trees to
evaluate is exponential, and the number of operations
in evaluating a tree is also exponential. To apply the
POMDP model to intelligent tutoring, we must ad-
dress the problems of computational complexity.
In our research, we develop a new technique of
policy trees for POMDP-solving in an ITS. In this
technique, policy trees are subdivided into small tree
sets. When making a decision, the POMDP agent
evaluates the trees in a set, instead of all the possi-
ble trees. A tree set is dynamically created when the
agent needs to evaluate it. The technique has advan-
tages of better time and space efficiencies.
In this paper, we first introduce the technical back-
ground of the POMDP model that is needed for dis-
cussing our technique, followed by reviewing the ex-
isting work related to our research. Then we present
our techniques for grouping trees and dynamic tree
creation, and discuss some experimental results.
Wang, F.
Dynamical Creation of Policy Trees for a POMDP-based Intelligent Tutoring System.
DOI: 10.5220/0006774601370144
In Proceedings of the 10th International Conference on Computer Supported Education (CSEDU 2018), pages 137-144
ISBN: 978-989-758-291-2
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
137

2 PARTIALLY OBSERVABLE
MARKOV DECISION PROCESS
2.1 MDP and POMDP
A POMDP is an extension of an MDP, as mentioned
in the previous section. An MDP can model a deci-
sion process in which different actions can be chosen
in different states to maximize rewards. The core of
an MDP includes S, A, and ρ, which are a set of states,
a set of actions, and a reward function. In a decision
step, the agent is in s ∈S, takes a ∈A that is available
in s, enters s
0
∈ S, and receives reward ρ(s,a,s
0
). The
MDP model is stochastic. An MDP includes T , which
is a set of state transition probabilities. P(s
0
|s,a) ∈ T
is the probability that the agent enters s
0
after taking
a in s. Another core component in an MDP is policy
π(s). It guides the agent to choose the optimal action
available in s to maximize rewards.
As an extension of an MDP, a POMDP has two
additional core components: O and Z, which are a set
of observations and a set of observation probabilities.
A POMDP can model a decision process in which
the agent is not able to see states completely. In a
POMDP, the agent infers information about states and
represents the information about states by a belief, de-
noted by b. In a decision step, the agent is in s ∈S that
it is not able to see, chooses a ∈A based on its current
belief b, enters s
0
∈ S that it is not able to see either,
observes o ∈O, and infers information about s
0
by us-
ing P(o|a,s
0
) ∈ Z and P(s
0
|s,a) ∈ T .
Belief b is defined as
b = [b(s
1
),b(s
2
),...,b(s
Q
)] (1)
where s
i
∈ S (1 ≤ i ≤ Q) is the ith state in S, Q is the
number of states in S, b(s
i
) is the probability that the
agent is in s
i
, and
∑
Q
i=1
b(s
i
) = 1.
In a POMDP, the policy is π(b). In a decision step,
it guides the agent to choose an action considering the
current belief b to maximize the long term reward.
2.2 Policy Trees for POMDP-Solving
For a given b, an optimal π returns an optimal ac-
tion. In a POMDP, finding the optimal π is referred
to as solving the POMDP. For most practical appli-
cation problems, POMDP-solving is a task of great
complexity (Carlin and Zilberstein, 2008; Rafferty
et al., 2011). A simplified, less expensive technique
for POMDP-solving is to use policy trees.
In a policy tree, nodes are actions, and edges are
observations. The action at the root is called the root
action. An action node has observation edges to ac-
tions at the next level. After an action is taken, the
next action to take is one of the actions at the next
level, depending on what the agent observes. Fig-
ure 1 illustrates the general structure of a policy tree,
in which a
r
is the root action, a is an action, and K
is the number of possible observations. Note that an
action node has edges of all the possible observations
to the next level.
o
1
o
2
o
K
a aa
...
a a
...
o
1
o
2
a
o
K
...
...
... ... ...
a
r
Figure 1: The general structure of a policy tree.
When a technique of policy trees is used for
POMDP-solving, finding the optimal policy is to
identify the optimal tree. In each decision step, the
agent finds the optimal policy tree considering its cur-
rent belief, and takes the root action of the tree. In the
following, we discuss a method to find the optimal
tree.
Each policy tree is associated with a value func-
tion, which evaluates the long term reward of taking
the tree (policy). Let τ be a policy tree. The value
function of state s given τ is
V
τ
(s) = R (s, a)+γ
∑
s
0
∈S
P(s
0
|s,a)
∑
o∈O
P(o|a,s
0
)V
τ(o)
(s
0
)
(2)
where a is the root action of τ, s
0
is the next state,
i.e. the state that the agent enters into after taking a,
γ is a discounting factor (0 ≤ γ ≤ 1), o is the obser-
vation after a is taken, τ(o) is the subtree in τ which
is connected to the root by the edge of o, and R (s,a)
is the expected immediate reward after a is taken in s,
calculated as
R (s,a) =
∑
s
0
∈S
P(s
0
|s,a)R (s, a,s
0
) (3)
where R (s,a, s
0
) is the expected immediate reward
after the agent takes a in s and enters s
0
. The sec-
ond term on the right hand side of Eqn (2) is the dis-
counted expected value.
From Eqns (1) and (2), we have the value function
of belief b given τ:
V
τ
(b) =
∑
s∈S
b(s)V
τ
(s). (4)
CSEDU 2018 - 10th International Conference on Computer Supported Education
138

Thus we have π(b) returning the optimal policy tree
ˆ
τ
for b:
π(b) =
ˆ
τ = argmax
τ∈T
V
τ
(b), (5)
where T is the set of trees to evaluate in making the
decision.
The size of a policy tree depends on the number
of possible observations and the horizon. When the
horizon is H, the number of nodes in a tree is
H−1
∑
t=0
|O|
t
=
|O|
H
−1
|O|−1
(6)
where |O| is the size of O. At each node, the number
of possible actions is |A|. Therefore, the total number
of all possible H-horizon policy trees is
|A|
|O|
H
−1
|O|−1
. (7)
Both numbers are exponential.
3 RELATED WORK
Researchers in the fields of ITSs have seen the great
potential of the POMDP model in building ITSs.
Extensive research has been conducted in applying
POMDPs to intelligent tutoring (Cassandra, 1998;
Williams et al., 2005; Williams and Young, 2007;
Theocharous et al., 2009; Rafferty et al., 2011; Chi-
naei et al., 2012; Folsom-Kovarik et al., 2013). In the
work related to applying the model to ITSs, POMDPs
were used to model student states, and to customize
and optimize teaching. In a commonly used structure,
student states had a boolean attribute for each of the
subject contents, actions available to a tutoring agent
were various types of teaching techniques, and obser-
vations were results of tests given periodically. The
goals were to teach as many of the contents in a fi-
nite amount of time, or to minimize the time required
to learn the entire subject. In the following, we re-
view some work in which policy trees were used for
POMDP-solving in ITSs.
Rafferty and co-workers created a POMDP-based
system for teaching concepts (Rafferty et al., 2011).
A core component of the system was a technique
of fast teaching by POMDP planning. The tech-
nique was for computing approximate POMDP poli-
cies, which selected actions to minimize the expected
time for the learner to understand concepts. The
researchers framed the problem of optimally select-
ing teaching actions by using a decision-theoretic ap-
proach, and formulated teaching as a POMDP plan-
ning problem. In the POMDP, the states represented
the learners’ knowledge, and the transitions mod-
eled how teaching actions stochastically changed the
learners’ knowledge.
For solving the POMDP, the researchers devel-
oped a method of forward trees, which are variations
of policy trees. A forward tree is constructed by in-
terleaving branching on actions and observations. For
the current belief, a forward trees was constructed to
estimate the value of each pedagogical action, and the
best action was chosen. The learner’s response, plus
the action chosen, was used to update the belief, and
then a new forward search tree was constructed for se-
lecting a new action for the updated belief. The cost of
searching the full tree is exponential in the task hori-
zon, and requires an O(|S|
2
) operations at each node.
To reduce the number of nodes to search through, the
researchers restricted the tree by sampling only a few
actions, and limited the horizon to control the depth
of the tree.
In the work reported in (Wang, 2016), an exper-
imental ITS was developed for teaching concepts in
computer science. A POMDP was used in the sys-
tem to model processes of intelligent tutoring. In
the POMDP, states, actions, and observations mod-
eled student knowledge states, system tutoring ac-
tions, and student actions, respectively. A method of
policy trees was proposed for POMDP-solving. In the
method, policy trees were created and stored in a tree
database. To choose an optimal action to respond to a
given student query, the agent searched the database
and evaluated a set of trees. For reducing the costs
in making a decision, techniques were developed to
minimize the tree sizes and decrease the number of
trees to evaluate. A major disadvantage of the pro-
posed policy tree method was its space complexity.
The techniques of policy trees for improving
POMDP-solving have made good progress towards
building practical POMDP-based ITSs. However,
they were still too costly to use. For example, as the
authors of (Rafferty et al., 2011) concluded, computa-
tional challenges existed in their technique of forward
trees, despite sampling only a fraction of possible ac-
tions and using short horizons. Also, how to sample
actions and how to shorten a horizon are challenging
problems. Computational complexity has been a bot-
tleneck in applying the POMDP model to intelligent
tutoring.
4 GROUPING OF POLICY TREES
4.1 An Overview
To address the problems of computational complexity
in applying the method of policy trees in a POMDP-
based ITS, we develop a new technique, in which pol-
icy trees are grouped and trees are dynamically cre-
Dynamical Creation of Policy Trees for a POMDP-based Intelligent Tutoring System
139

ated. With this technique, the agent evaluates a small
set of trees when making a decision. The trees in the
set are dynamically created for better space efficiency.
In this section, we discuss the grouping of trees, and
in the next section, the dynamic tree creation.
The discussion is in the context of an experimen-
tal ITS, which we developed for testing our tech-
niques. The ITS teaches concepts in software basics.
A POMDP helps the ITS choose optimal teaching ac-
tions. We cast the ITS on to the POMDP, by using
POMDP states to represent student knowledge states,
and actions to represent system tutoring actions. We
treat student actions (asking questions, accepting an-
swers, etc ) as observations.
4.2 State Space Partitioning
To have small tree sets, we partition the state space
into subspace, and then group trees in each subspace
into tree sets. Before the tree grouping technique, we
discuss our method for state space partitioning.
We define the states in terms of concepts in the
instructional subject. In software basics, concepts in-
clude program, instruction, algorithm, and many oth-
ers. We associate each state with a state formula,
which is of the form:
(C
1
C
2
C
3
...C
N
), (8)
where C
i
is the variable for the ith concept C
i
, taking
a value
√
C
i
or ¬C
i
(1 ≤i ≤N), and N is the number
of concepts in the subject. We use
√
C
i
to represent
that the student understands C
i
, and ¬C
i
to represent
that the student does not. A formula is a representa-
tion of a student knowledge state. For example, for-
mula (
√
C
1
√
C
2
¬C
3
...) is a representation of the state
in which the student understands C
1
and C
2
, but not
C
3
, ... States thus defined have Markov property.
When there are N concepts in an instructional sub-
ject, the number of state formulae is 2
N
. This implies
that the number of possible states is 2
N
. As can be
seen in Eqn (2), the cost for evaluating a value func-
tion is proportional to the size of state space. To re-
duce the cost, we partition the state space into smaller
subspaces. The partitioning technique is based on
prerequisite relationships between concepts.
Prerequisite relationships are pedagogical orders
of concepts. A concept may have zero or more pre-
requisites, and a concept may serve as a prerequisite
of zero or more concepts. For example, in mathemat-
ics, derivative has prerequisites function, limit and so
on, and function is a prerequisite of derivative, inte-
gral, and so on. To understand a concept well, a stu-
dent should understand all its prerequisites first. For
a set of concepts, the prerequisite relationships can be
represented by a directed acyclic graph (DAG). In this
paper, when a concept is a prerequisite of another, we
call the latter a successor of the former.
In the first step of our space partitioning tech-
nique, we subdivide concepts such that concepts hav-
ing prerequisite relationships are in the same group.
Some very “basic” concepts may be in two or more
groups. In the second step, for each group, we cre-
ate a state subspace by using concepts in the group to
define states, in the way just discussed. In the third
step, we eliminate invalid states. For details of the
partitioning technique, please see (Wang, 2015). Af-
ter space partitioning, we create policy trees for each
subspace. In a tree, the nodes and edges concern con-
cepts in the subspace only.
This partitioning technique is based on our obser-
vation that in a window in a tutoring process, stu-
dent questions likely concern concepts that have pre-
requisite relationships with each other. The observa-
tion suggests that we could localize the computing for
choosing an optimal teaching action within a smaller
state subspace defined by concepts having prerequi-
site relationships.
The total number of states in the subspaces are
much smaller than the number of states in the space
defined by using all the concepts. In addition, the
number and sizes of policy trees in subspaces are
much smaller because the sets of actions and obser-
vations are smaller.
4.3 Policy Tree Grouping
The cost for making a decision depends on the num-
ber of trees to evaluate, that is, the size of T in Eqn
(5). For lower costs, we group the trees in each sub-
space into small tree sets. When choosing an optimal
teaching action, the agent evaluates trees in a single
set. For discussing the grouping method, we first de-
fine optimal action and tutoring session.
In science and mathematics subjects, many con-
cepts have prerequisites. When the student asks about
a concept, the system should decide whether it would
start with teaching a prerequisite for the student to
make up some required knowledge, and, if so, which
one to teach. The optimal action is to teach the con-
cept that the student needs to make up in order to un-
derstand the originally asked concept, and that the stu-
dent can understand it without making up other con-
cepts.
A tutoring session is a sequence of interleaved
student and system actions, starting with a question
about a concept, possibly followed by answers and
questions concerning the concept and its prerequi-
sites, and ending with a student action accepting the
CSEDU 2018 - 10th International Conference on Computer Supported Education
140

answer to the original question. If, before the accep-
tance action, the student asks a concept that has no
prerequisite relationship with the concept originally
asked, we consider that a new tutoring session starts.
We classify questions in a session into the original
question and current questions. The original question
starts the session, concerning the concept the student
originally wants to learn. We denote the original ques-
tion by (?C
o
), where C
o
is the concept concerned in
the question and superscipt o stands for “original”. A
current question is the question to be answered by the
agent at a point in the session, usually for the student
to make up some knowledge. A current question may
be asked by the student, or made by the agent. We
denote a current question by (?C
c
), where C
c
is the
concept concerned in the question, and superscipt c
stands for “current”. Concept C
c
is in (℘
C
o
∪C
o
),
where ℘
C
o
is the set of all the direct and indirect pre-
requisites of C
o
.
In the following, we discuss an example, which
involves concepts database and file. We assume that
file is a prerequisite of database. At a point in a tu-
toring process, the student asks question “What is a
database?” If database has no prerequisite relation-
ship with the concepts asked/taught right before the
question, we consider the question starts a new tu-
toring session, and it is the original question of the
session. If the agent believes that the student already
understands all the prerequisites of database, and an-
swers the question directly, the question is also the
current question when the agent answers it. If the
agent teaches database in terms of file, and then the
student asks question “What is a file?”, the system
action of teaching database is not an optimal because
the student needs to make up a prerequisite. At this
point the question about file is the current question. If
the agent answers the question about file and the stu-
dent satisfies the answer, the system action is optimal.
Now we consider the grouping of trees. When the
agent has current question (?C
c
) to answer, it needs to
choose an optimal action. The optimal action may be
to teach C
c
or teach one of the prerequisites of C
c
,
depending on the agent’s belief about the student’s
knowledge state. Recall that in a tutoring step, the
agent evaluates a set of trees and chooses the root ac-
tion of the tree that has the highest value. The set of
trees to evaluate to answer (?C
c
) should include trees
in which root actions are to teach C
c
or prerequisites
of C
c
. Since the ultimate goal to answer (?C
c
) is to
answer the original question (?C
o
), actions to answer
(?C
o
) should be included in the trees in the set.
Based on the above consideration, we have our
grouping strategy: for each possible pair of (?C
o
)
and (?C
c
), we create tree set T
C
o
C
c
. In a tutoring ses-
sion with original question (?C
o
), to choose an opti-
mal action to answer current question (?C
c
), the agent
evaluates trees in T
C
o
C
c
. Since T
C
o
C
c
is normally much
smaller than the set of all the possible trees, the cost
for choosing an optimal tree can be significantly re-
duced. The tree structure will be discussed in the next
section.
5 DYNAMIC CREATION OF
POLICY TREES
5.1 Structure of the Policy Trees
In the following, we denote the system action for
teaching concept C by (!C), and denote a student ac-
ceptance action by (Θ). An acceptance action can be
something like “I understand”, and “I see”.
As just discussed, in a state subspace, for each
possible pair of original and current questions, de-
noted by (?C
o
) and (?C
c
), we create tree set T
C
o
C
c
. The
optimal action to answer current question (?C
c
) may
be to teach C
c
, or to teach one of the prerequisites
of C
c
. Therefore, the trees in T
C
o
C
c
have root actions
(!C
c
), or (!C) where C ∈℘
C
c
. For each C ∈℘
C
c
, we
have a tree in T
C
o
C
c
, of which the root is (!C). We de-
note a tree in T
C
o
C
c
with root action (!C) by T
C
o
C
c
.τ
C
.
In a tutoring session started by (?C
o
), the ultimate
goal of the agent is to teach C
o
. In a policy tree for
answering a current question, any leaf node must be a
system action to terminate the session, after a student
acceptance action that accepts (!C
o
). A path in the
tree includes possible questions and answers concern-
ing prerequisites of C
o
. Also, since possible student
questions in the session concern prerequisites of C
o
,
we limit the observation set O to questions concern-
ing concepts in ℘
C
o
only. (Student actions are treated
as observations.)
...
...
...
...
o
M
o
i
o
1
... ...
... ......... ...
...
o
′
1
o
′
i
(Θ)
(Θ)
(!C)
a a a a
a
′
a
′
a
′
a
′
o
′
M
′
Figure 2: The general structure of policy tree T
C
o
C
c
.τ
C
.
Figure 2 illustrates the general structure of pol-
icy tree T
C
o
C
c
.τ
C
. The root of T
C
o
C
c
.τ
C
is (!C), i.e. an
Dynamical Creation of Policy Trees for a POMDP-based Intelligent Tutoring System
141

action for teaching C ∈ (℘
C
c
∪C
c
). When C has M
prerequisites C
1
, ... C
M
, the root has M + 1 children.
The observations o
1
,...,o
i
,...,o
M
are student actions
(?C
1
),...,(?C
i
),...,(?C
M
). The first M children are
sub-trees connected by the observation edges. Ac-
tions at the sub-tree roots are (!C
1
),...,(!C
M
). Note
that edge o
i
(1 ≤ i ≤ M) may connect to any one of
them. The last child is a sub-tree rooted by (!C
u
),
where C
u
is one of the direct successors of C. When
C has more than one direct successor, C
u
is the one
on the path from C
o
to C. The semantics of such root-
children structure is that after (!C), if the student ac-
cepts (!C), teach the direct successor C
u
, if the student
asks about a prerequisite of C, teach a prerequisite.
The prerequisite to teach is dynamically selected. The
selection will be discussed in the next subsection.
In a policy tree, each sub-tree is structured in the
same way. That is, the root has edges for prerequisites
of the concept in the root action and an acceptance
edge, illustrated by o
0
1
, ..., o
0
i
, ..., o
0
M
0
and (Θ) in Fig-
ure 2, where M
0
is the number of prerequisites of the
concept in the action connected by o
i
. However, if a
prerequisite has been taught in the path from the tree
root, the edge is not included. If a root is (!C
o
) for
answering the original question, its acceptance edge
connects to an action terminating the session.
5.2 Creation of the Policy Trees
When the student asks question (?C
o
) starting a new
tutoring session, the agent goes to the subspace that
contains C
o
, and contains all the prerequisites of C
o
as well. To answer current question (?C
c
) in the ses-
sion, it evaluates all the trees in tree set T
C
o
C
c
. We have
developed a new technique to dynamically create the
tree set when it is evaluated. This technique has bet-
ter space efficiency than the method of storing a tree
database.
As discussed in the previous subsection, in trees in
T
C
o
C
c
, root actions teach concepts in (℘
C
c
∪C
c
). In the
general structure of a policy tree (illustrated in Fig-
ure 1), each edge (observation) connects to all the
possible actions (in different trees). With this struc-
ture, for each C ∈(℘
C
c
∪C
c
) the number of trees with
root (!C) is exponential in the number of possible ob-
servations (see Eqn (7)). That is, the number of trees
having the same root action is exponential.
To reduce the cost for evaluating policy trees, in
T
C
o
C
c
we create only one tree for each C ∈ (℘
C
c
∪C
c
),
and use it to approximate an exponential number of
trees. To have only one tree for each C ∈ (℘
C
c
∪C
c
),
we connect each edge to one action, instead of all the
possible actions. For example, when creating the tree
in Figure 2, we select one action for edge o
1
, one ac-
tion for o
2
, ... one action for o
0
1
, and so on.
In our research, we discovered that in a state only
a small number of actions have large enough chances
to be taken. In computing Eqn (2) for evaluating trees,
most actions contribute little to tree values. This sug-
gests that we would not lose much information when
ignoring the actions that are less likely to be taken
and contribute less. In the following, we discuss the
selection of an action for each edge by using the tree
in Figure 3.
o
M
o
i
o
1
o
′
1
o
′
i
(Θ)
(Θ)
(!C)
a
a
′
o
′
M
′
b
t
b
t+1
b
t+2
... ...
... ... ... ...
... ...
... ... ... ...
Figure 3: The general structure of policy tree T
C
o
C
c
.τ
C
.
Assume at time step t, the agent has belief b
t
, and
will evaluate tree set T
C
o
C
c
, and assume the tree in Fig-
ure 3 is T
C
o
C
c
.τ
C
. In creating the tree, we select (!C)
as the root, which is a possible action to take at t, and
then select an action for each edge based on an up-
dated belief at the next level, and so on. For example,
we need to select action a for edge o
i
based the up-
dated belief b
t+1
, select a
0
for o
0
i
based on the updated
b
t+2
, and so on.
A belief is a set of probabilities (see Eqn (1)).
To update a belief, we update each of the probabili-
ties. The following is the formula to calculate element
b
0
(s
0
) in updated belief b
0
:
b
0
(s
0
) =
∑
s∈S
b(s)P(s
0
|s,a)P(o|a,s
0
)/P(o|a) (9)
where P(s
0
|s,a) ∈ T and P(o|a,s
0
) ∈ Z transition
probability and observation probability, P(o|a) is the
total probability for the agent to observe o after a is
taken, calculated as
P(o|a) =
∑
s∈S
b(s)
∑
s
0
∈S
P(s
0
|s,a)P(o|a,s
0
). (10)
P(o|a) is used in Eqn (9) as a normalization. Using
Eqn (9) we can calculate b
t+1
from b
t
, (!C), and o
i
.
Let b
t+1
be
b
t+1
= [b
t+1
(s
1
),b
t+1
(s
2
),...,b
t+1
(s
Q
)]. (11)
In b
t+1
we can find the j such that b
t+1
(s
j
) ≥b
t+1
(s
k
)
for all the k 6= j (1 ≤ j,k ≤ Q). Assume the state
formula of s
j
is
(
√
C
1
√
C
2
...
√
C
l−1
¬C
l
...¬C
N
0
). (12)
CSEDU 2018 - 10th International Conference on Computer Supported Education
142

The belief and state formula indicate that most likely
the student does not understand C
l
, but understands all
of its prerequisites. Therefore, ρ(s
j
,(!C
l
)) returns a
high value. Considering a single step, we select (!C
l
)
as an optimal action at b
t+1
. Thus we select (!C
l
) as
a, and connect the edge of o
i
to it.
6 EXPERIMENTAL RESULTS
AND DISCUSSION
In this section, we present two sets of experimental
results. The first set includes the results of evaluating
adaptive teaching of the system, and the second set in-
cludes the results of testing the technique for dynamic
creation of trees. The data set used in the experiments
included 90 concepts in software basics. Each con-
cept had zero to five prerequisites.
We used a two-sample t-test method to evaluate
the system performance in adaptive teaching. The test
method was the independent-samples t-test. 30 stu-
dents participated in the experiment, who were adults
without formal training in computing. The students
were randomly divided into two equal size groups.
Group 1 studied with the ITS with the POMDP turned
off, and Group 2 studied with the POMDP turned on.
Each student studied with the ITS for about 45 min-
utes. The student asked questions about concepts in
the subject, and ITS taught the concepts. The per-
formance parameter was rejection rate, which was
the ratio of the number of system actions rejected by
a student to the total number of system actions for
teaching the student.
For each student, we calculated a rejection rate.
For the two groups, we calculated mean rejection
rates
¯
X
1
and
¯
X
2
. The two sample means were used
to represent population means µ
1
and µ
2
. The alterna-
tive and null hypotheses are:
H
a
: µ
1
−µ
2
6= 0, H
0
: µ
1
−µ
2
= 0
The means and variances calculated for the two
groups are listed in Table 1. In the experiment, n
1
=15
and n
2
=15, thus the degree of freedom is (15 −1) +
(15 −1) = 28. With alpha at 0.05, the two-tailed t
crit
is 2.0484 and we calculated t
obt
= +8.6690. Since
the t
obt
is far beyond the non-reject region defined
by t
crit
= 2.0484, we could reject H
0
and accept H
a
.
The analysis suggested that the POMDP could sig-
nificantly reduce the rejection rate. This implies that
the POMDP helped the system significantly improve
adaptive teaching.
We tested the dynamic tree creation technique
with the same data set of software basics, on a desk-
top computer with an Intel Core i5 3.2 GHz 64 bit
Table 1: Number of students, mean and estimated variance
of each group.
Group 1 Group 2
Number of students n
1
= 15 n
2
= 15
Sample mean
¯
X
1
= 0.5966
¯
X
2
= 0.2284
Estimated variance s
2
1
= 0.0158 s
2
2
= 0.0113
processor and 16GB RAM. For comparison, we also
tested a static tree creation technique. Both the static
and dynamic tree creation techniques have the same
algorithm for grouping trees. The difference is that
in the static technique all the tree sets were created
and stored in a database before the ITS started teach-
ing students, while in the dynamic technique a tree
set was created right before it was evaluated. In both
techniques, the state space was subdivided into six
subspaces. The largest subspace included 27 con-
cepts, 4,970 valid states, 170 tree sets, and 688 trees.
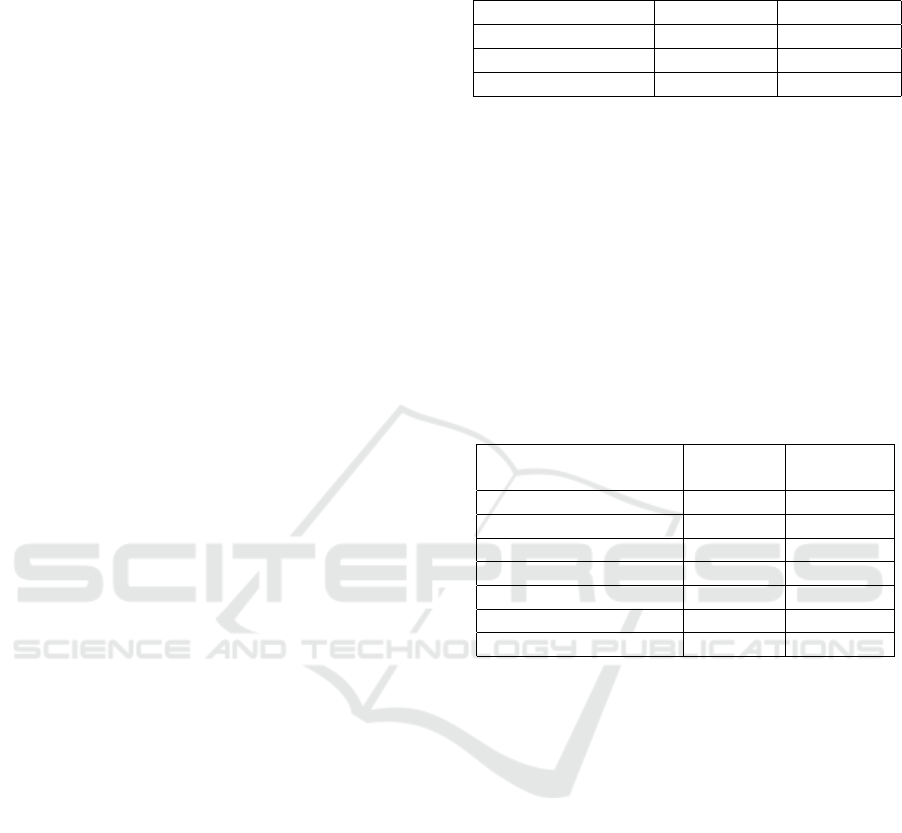
Table 2: Comparison between static and dynamic tree cre-
ation methods.
Static Dynamic
creation creation
Permanent pace usage 1.078GB 0
Max space usage 1.078GB 215.68MB
Database creation time 36,888ms
Max tree creation time 158ms
Belief update time 525ms 518ms
Max decision time 147ms 152ms
Max Response time 669ms 828ms
In Table 2 we list results of the two techniques.
The space usage includes that for the tree database
or tree sets only. The maximum tree creation time
was for creating the largest tree set, of which the size
was 215.68MB. The maximum decision time was for
evaluating trees in the largest tree set and choosing
the optimal tree. Response time included the time for
calculating a new belief, and evaluating a tree set to
choose an optimal tree. The maximum response time
was recorded when the largest tree set was evaluated.
The experimental results suggest that the dynamic
tree creation technique is effective for building space-
efficient ITSs. Its space usage was a small fraction
of that of a static tree creation technique. In terms of
time efficiency, the dynamic technique was compara-
ble to a static technique. Since the time for dynami-
cally creating a tree set is short, the total response time
was only slightly longer than that of the static tech-
nique. As can be seen in Table 2, the maximum re-
sponse time with dynamic tree creation was less than
a second. For a tutoring system, such response time
could be considered acceptable. Time efficiency can
be improved with a cache of tree sets.
Dynamical Creation of Policy Trees for a POMDP-based Intelligent Tutoring System
143

7 CONCLUDING REMARKS
We have developed a new technique to address the
space complexity problem in building POMDP-based
ITSs. In this technique, policy trees are dynamically
created when they are evaluated, and no space is re-
quired to store a tree database. The technique is espe-
cially useful for building ITSs on handheld devices,
which usually have limited storage spaces. While sig-
nificantly improving space efficiency, the technique
does not sacrifice much time efficiency. In some
cases, it may even have advantages in time efficiency.
For example, for system without durable storage, the
technique may largely reduce the time to start, since
the lengthy tree database creation is not needed.
ACKNOWLEDGEMENTS
This research is supported by the Natural Sci-
ences and Engineering Research Council of Canada
(NSERC).
REFERENCES
Carlin, A. and Zilberstein, S. (2008). Observation compres-
sion in DEC-POMDP policy trees. In Proceedings of
the 7th International Joint Conference on Autonomous
Agents and Multi-agent Systems, pages 31–45.
Cassandra, A. (1998). A survey of pomdp applications. In
Working Notes of AAAI 1998 Fall Symposium on Plan-
ning with Partially Observable Markov Decision Pro-
cess, pages 17–24.
Chinaei, H. R., Chaib-draa, B., and Lamontagne, L. (2012).
Learning observation models for dialogue POMDPs.
In Canadian AI’12 Proceedings of the 25th Cana-
dian conference on Advances in Artificial Intelligence,
pages 280–286.
Folsom-Kovarik, J. T., Sukthankar, G., and Schatz, S.
(2013). Tractable POMDP representations for intel-
ligent tutoring systems. ACM Transactions on In-
telligent Systems and Technology (TIST) - Special
section on agent communication, trust in multiagent
systems, intelligent tutoring and coaching systems
archive, 4(2):29.
Rafferty, A. N., Brunskill, E., Thomas, L., Griffiths, T. J.,
and Shafto, P. (2011). Faster teaching by POMDP
planning. In Proceesings of Artificial Intelligence in
Education (AIED 2011), pages 280–287.
Theocharous, G., Beckwith, R., Butko, N., and Philipose,
M. (2009). Tractable POMDP planning algorithms for
optimal teaching in spais. In IJCAI PAIR Workshop
2009.
Wang, F. (2015). Handling exponential state space in a
POMDP-based intelligent tutoring system. In Pro-
ceedings of 6th International Conference on E-Service
and Knowledge Management (IIAI ESKM 2015),
pages 67–72.
Wang, F. (2016). A new technique of policy trees for
building a POMDP based intelligent tutoring system.
In Proceedings of The 8th International Conference
on Computer Supported Education (CSEDU 2016),
pages 85–93.
Williams, J. D., Poupart, P., and Young, S. (2005). Fac-
tored partially observable Markov decision processes
for dialogue management. In Proceedings of Knowl-
edge and Reasoning in Practical Dialogue Systems.
Williams, J. D. and Young, S. (2007). Partially observable
Markov decision processes for spoken dialog systems.
Elsevier Computer Speech and Language, 21:393–
422.
Woolf, B. P. (2009). Building Intelligent Interactive Tutors.
Morgan Kaufmann Publishers, Burlington, MA, USA.
CSEDU 2018 - 10th International Conference on Computer Supported Education
144