An Approach to Extract Proper Implications Set from High-dimension
Formal Contexts using Binary Decision Diagram
Phillip Santos
1
, Julio Neves
1
, Paula Silva
1
, S
´
ergio M. Dias
1,2
, Luis Z
´
arate
1
and Mark Song
1
1
Pontifical Catholic University of Minas Gerais (PUC Minas),
R. Walter Ianni, 255 - S
˜
ao Gabriel - 31.980-110, Belo Horizonte, Minas Gerais, Brazil
2
Federal Service of Data Processing (SERPRO),
Av. Jos
´
e C
ˆ
andido da Silveira, 1.200 - Cidade Nova - 31.035-536, Belo Horizonte, Minas Gerais, Brazil
Keywords:
Formal Concept Analysis, Proper Implications, Binary Decision Diagram.
Abstract:
Formal concept analysis (FCA) is currently used in a large number of applications in different areas. Ho-
wever, in some applications the volume of information that needs to be processed may become infeasible.
Thus, demand for new approaches and algorithms to enable the processing of large amounts of information
is increasing substantially. This paper presents a new algorithm for extracting proper implications from high-
dimensional contexts. The proposed algorithm, ProperImplicBDD, was based on the PropIm algorithm. Using
a data structure called binary decision diagram (BDD) it is possible to simplify the representation of the formal
context and to improve the performance on extracting proper implications. In order to analyze the performance
of the ProperImplicBDD algorithm, we performed tests using synthetic contexts varying the number of attri-
butes and context density. The experiments shown that ProperImplicBDD has a better perfomance – up to 8
times faster – than the original one, regardless of the number of attributes, objetcts and densities.
1 INTRODUCTION
With the advance of technology, the volume of in-
formation collected and stored to attend new requi-
rements from the society has increased significantly.
Due to this large amount of data, it is practically infe-
asible to analyze it without the support of techniques
of extraction and representation of knowledge. One
of the techniques that can be used to process and ana-
lyze this information is the Formal Concept Analysis
(FCA) (Ganter and Wille, 1997).
The FCA is a field of mathematics created for
data analysis where associations and dependencies
between objects and attributes are identified from a
data set (Ganter et al., 2005). One way to represent a
set of data composed of instances is through a formal
context (G, M,I) which is an incidence table compo-
sed by objects G, attributes M and the incidence rela-
tion I between objects and attributes.
A knowledge possible to obtain from the formal
context is the set of implications I among the attri-
butes that characterize the formal context (Taouil and
Bastide, 2001). The implication A → B (A,B ⊆ M)
reveals that every object containing the attributes be-
longing to set A has also the attributes from set B. The
sets A and B are considered, respectively, premise and
conclusion.
Applying different properties to a set I , we can
generate sets of implications with certain constraints
for specific domains. One of these specific sets is the
set of proper implication, which for each implication
the premise is minimal and the conclusion is a single-
ton (unit set).
This set of implications is useful because it provi-
des a kind of minimum representation about the data,
when the goal is to find the minimum set of attributes
to achieve specific purposes. For example, the work
developed in (Silva et al., 2017) had as goal the identi-
fication of relationships between professional skills of
LinkedIn users, which the set of proper implications
was applied to identify the minimum set of skills (pre-
mise) that imply in professional competence (conclu-
sion).
Different challenges have been proposed in FCA
community (Priss, 2006). One of these challenges
is the manipulation of high-dimensional formal con-
texts such as those with 120,000 objects and 70,000
attributes. High-dimensional formal contexts can be
50
Santos, P., Neves, J., Silva, P., Dias, S., Zárate, L. and Song, M.
An Approach to Extract Proper Implications Set from High-dimension Formal Contexts using Binary Decision Diagram.
DOI: 10.5220/0006775400500057
In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 50-57
ISBN: 978-989-758-298-1
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

generated from big data problems and they are com-
putationally difficult to handle - most algorithms do
not perform accordingly in these contexts and they are
usually unable to process large amounts of data.
So, in this paper, we present a new algorithm,
ProperImplicBDD, which is able to handle high-
dimensional formal contexts. It is based on PropIm
algorithm proposed in (Silva et al., 2017), but our al-
gorithm uses a known data structure named binary
decision diagram (BDD) to store and manipulate ef-
ficiently formal contexts (Neto et al., 2018). There-
fore, it can process a greater volume of data if compa-
red to the algorithms proposed in (Silva et al., 2017)
and (Taouil and Bastide, 2001). The main objectives
of this work are:
• to use BDD’s as a data structure in order to ex-
tract proper implications from high dimensional
contexts;
• to process a greater volume of data compared to
the algorithms proposed in (Silva et al., 2017)
and (Taouil and Bastide, 2001);
• to handle contexts in order to partially meet those
proposed by the challenge (Priss, 2006), such as
context containing 120,000 objects and 70,000 at-
tributes.
In order to analyze the performance of the Pro-
perImplicBDD algorithm, we performed tests using
only synthetic contexts. We have decided to use synt-
hetic contexts instead of real ones in order to control
the experiments and produce concrete results. We can
control and vary the number of attributes and context
density to evaluate our approach.
The variation in attributes and densities were used
to analyze the size and time of searches using the
BDD. The number of objects was fixed in 120,000 to
meet partially the challenge proposed in (Priss, 2006).
The experiments shown that ProperImplicBDD
has a better perfomance – up to 8 times faster – than
PropIm, regardless of the number of attributes, obje-
tcts and densities.
This paper is organized as follows: Section II pre-
sents the basic concepts of the FCA and BDD approa-
ches. Section III describes the related works on BDD
and implications. Section IV describes the methodo-
logy. In Section V, the experiments are presented and
discussed. Finally, Section VI presents the conclusi-
ons and future works.
2 BACKGROUND
2.1 Formal Concept Analysis
The formal concept analysis (FCA) is a field of mat-
hematics that allows the identification of associations
(concepts) and dependencies (implications) of a data
set represented as a formal context (Ganter and Wille,
1997).
Details about formal context, formal concept and
implication rules, basic elements of FCA, are descri-
bed in the following subsections.
2.1.1 Formal Context
A formal context is formed by a triple (G, M,I),
where G is a set of objects (rows), M is a set of at-
tributes (columns) and I is defined as the binary rela-
tionship (incidence relation) between objects and at-
tributes where I ⊆ G × M (Ganter et al., 2005).
An example of a context is shown in Table 1. The
objects (rows) are: Whale, Owl, Human, Shark and
Penguin. The attributes (columns) are : Aquatic, Ter-
restrial, Irrational, Feathered. The incidences (“X”)
are the relationship between objects and attributes:
Whale contains Aquatic and Irrational attributes, Owl
contains Terrestrial, Irrational and Feathered attribu-
tes, etc. For example, the owl has the following cha-
racteristics: terrestrial, irrational and feathered.
Table 1: A simple formal context.
Aquatic Terrestrial Irrational Feathered
Whale X . X .
Owl . X X X
Human . X . .
Shark X . X .
Penguin . X X X
2.1.2 Formal Concept
A formal concept is defined by a pair (A,B) where
A ⊆ G is called extension and B ⊆ M is called
intention. This pair must follow the conditions where
A = B
0
and B = A
0
(Ganter et al., 2005). The relation
is defined by the derivation operator (
0
):
A
0
= {m ∈ M | gIm ∀ g ∈ A}
B
0
= {g ∈ G | gIm ∀ m ∈ B}
A formal concept seeks to identify the set of
attributes (intention) that delimit and characterize an
object (extension). Using the Table 1 as an example,
the generated concepts would be:
({Whale, Owl, Human, Shark, Penguin}, {})
An Approach to Extract Proper Implications Set from High-dimension Formal Contexts using Binary Decision Diagram
51

({Owl, Human, Penguin}, {Terrestrial})
({Owl, Penguin}, {Terrestrial, Irrational, Feathered})
({}, {Aquatic, Terrestrial, Irrational, Feathered})
({Whale, Owl, Shark, Penguin}, {Irrational})
({Whale, Shark}, {Aquatic, Irrational})
2.1.3 The Set of Implications
Implications are dependencies between elements of a
set of attributes which were obtained from a formal
context.
Using a formal context (G, M, I) an implication
would be A → B where A, B ⊆ M (A and B are defined,
respectively, premise and conclusion).
An implication rule A → B is considered valid for
the context (G, M, I) if, and only if, every object that
has the attributes of A also has the attributes of B. For-
mally ∀g ∈ G[∀a ∈ A gIa → ∀b ∈ B gIb].
As an example of what an implication is, one can
consider the universe of animals as described in Table
1. In this table, every feathered animal is irrational.
This type of relationship can be described as an im-
plication. The implication “Feathered implies Irratio-
nal” (Feathered → Irrational) is a way to describe that
any animal that has feather is also irrational. Table 2
is an example of implication rules based on the formal
context presented in Table 1.
Implication rules can be obtained through for-
mal concepts (Bertet, 2006), formal contexts (Rys-
sel et al., 2014) and concept lattice (Bertet and Mon-
jardet, 2001). In our work the implication rules ex-
traction is based on formal contexts.
Table 2: Implication rules extracted from the formal context
in Table 1.
A → B
Terrestrial → Irrational, Feathered
Irrational → Terrestrial, Feathered
Feathered → Terrestrial, Irrational
Aquatic → Irrational
Irrational → Aquatic
2.1.4 The Set of Proper Implications
The set of implications is called as the set of proper
implications (Taouil and Bastide, 2001) or unary im-
plication system (UIS) (Bertet and Monjardet, 2001)
when, for each implication, the right side (conclu-
sion) contains only one attribute and the left side (pre-
mise) is reduced: if A → m ∈ I then there is not
any Q → m ∈ I such that Q ⊂ A. The set of pro-
per implications I for (G,M,I) is defined formally
as: {A → m ∈ I |A ⊆ M and m ∈ M \ A and ∀Z ⊂ A :
Z → m /∈ I }.
2.2 Binary Decision Diagram
The binary decision diagram (BDD) is a form to re-
present canonical boolean formulas. It is substanti-
ally more compact than the traditional structure forms
(normal conjunctive and disjunctive form) and It can
be manipulated efficiently (Bryant, 1986).
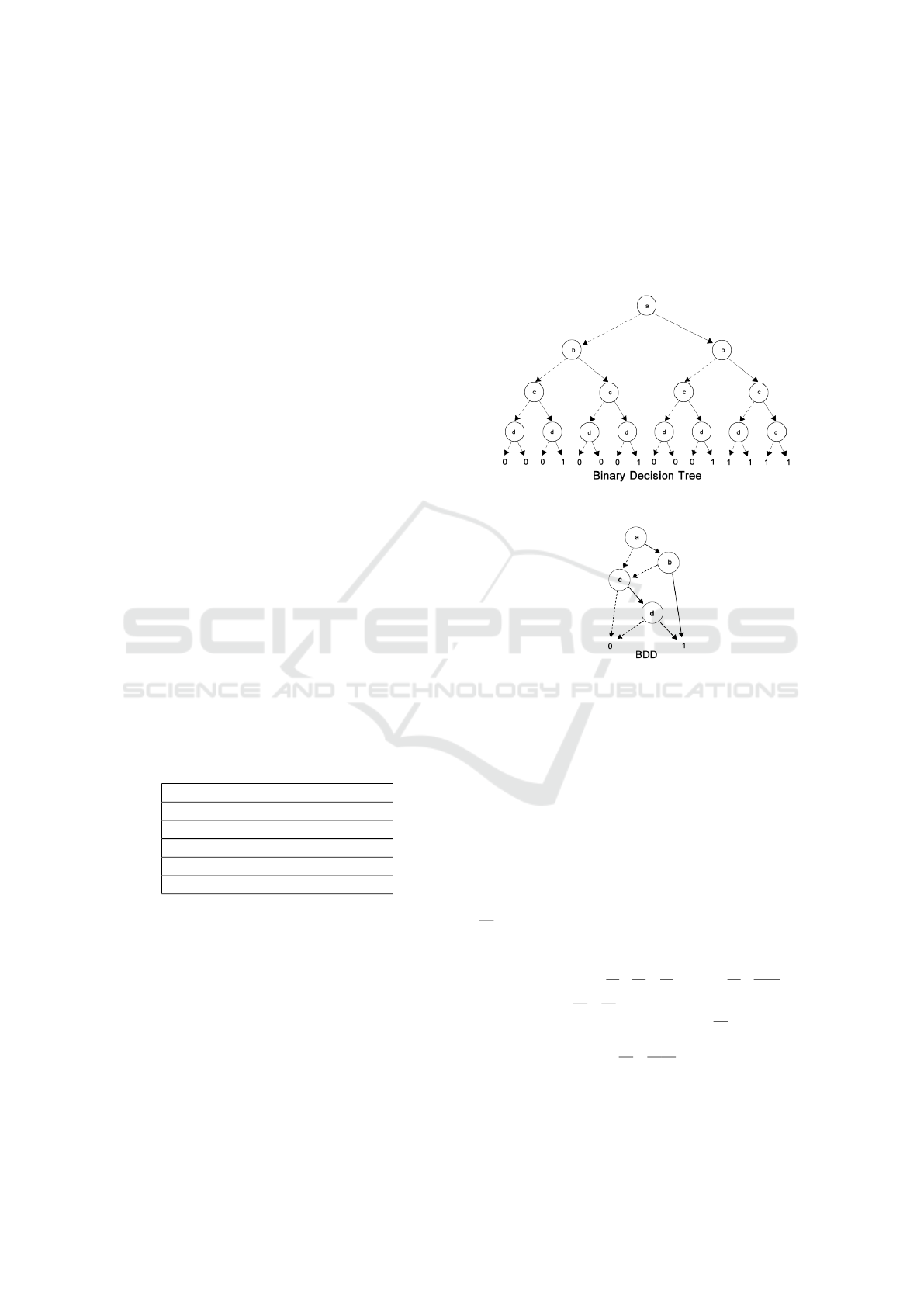
Figure 1: BDD (Binary Decision Tree) Example.
Figure 2: Example of a BDD simplification from the Figure
1.
Figure 2 provides a simple example which the
BDD is used to represent a binary decision tree des-
cribed on the Figure 1. Note that, it is possible to
represent the same information using a structure con-
siderably more compact than the original.
In our approach we use the formal context in order
to create the BDD. Equation (1) represents a boolean
formula correspondent to Table 1.
For a better view of Equation (1), attributes names
have been replaced by letters: Aquatic (a
1
), Terres-
trial (a
2
), Irrational(a
3
), Feathered (a
4
). The attribute
a
1
means that in this part of the function the attribute
is false (an object does not contain such attribute).
f(a
1
,a
2
,a
3
,a
4
) = a
1
a
2
a
3
a
4
+ a
1
a
2
a
3
a
4
+ a
1
a
2
a
3
a
4
(1)
The part a
1
a
2
a
3
a
4
of the equation was created to
validate the Whale and Shark objects, a
1
a
2
a
3
a
4
it was
already created to validate the Penguin and Owl ob-
jects and the last part
a
1
a
2
a
3
a
4
validates the Human
object.
The generated BDD corresponding to the formal
context presented in Table 1 (and described by Equa-
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
52

tion (1)) can be seen in Figure 3. For a better view of
each object in the BDD, object names have been re-
placed by numbers and attributes replaced by letters:
Whale (1), Owl (2), Human (3), Shark (4), Penguin
(5) and Aquatic (a
1
), Terrestrial (a
2
), Irrational(a
3
),
Feathered (a
4
).
Figure 3: BDD that represents the context in the Table 1.
The most relevant BDD libraries were evaluated in
(Rimsa et al., 2009). Among them, the CUDD - Co-
lorado University Decision Diagram was chosen for
providing function packs to work with Binary Deci-
sion Diagrams (BDDs) and to have more recent up-
dates. The CUDD also has functions for Algebraic
Decision Diagrams (ADDs) and Zero-suppressed Bi-
nary Decision Diagrams (ZDDs) that can be used to
represent formal contexts.
3 RELATED WORKS
There are currently several FCA applications to ex-
tract proper implications. However, to the best of
our knowledge, there is no algorithm that can work
in high-dimensional contexts. We found studies that
used BDD in FCA but focusing on extraction of for-
mal concepts, but not on implications.
In (Taouil and Bastide, 2001) the Impec, the state
of the art algorithm to extract proper implication,
was proposed in order to extract all proper implica-
tions with some support from a formal context. But
the algorithm does not perform accordingly in high-
dimensional contexts.
In (Salleb et al., 2002) BDD’s were used to sto-
ring the transaction logs as a truth table and for find
frequent patterns in large transactional data sets.
In (Silva et al., 2017) the authors proposed the
PropIm algorithm to extract proper implications ba-
sed on the Impec algorithm. The algorithm was
used to identify the relationships between professio-
nal skills of LinkedIn users’ profile through appropri-
ate implications. The results presented the minimum
sets of skills that would be required to achieve cer-
tain job positions. Although the algorithm is more
efficient than Impec, but it does not have a good per-
formance in high-dimensional context.
4 METHODOLOGY
This work adopted as methodology, the usage of synt-
hetic contexts randomly generated with densities and
controlled dimensions.
Initially, it was decided to use contexts of 50, 100
and 150 attributes, though adding a new constraint for
the maximum time limit for extracting the implication
rules. This limit has been set up to 14 days and it was
set after tests performed with the algorithm PropIm
which did not return any result or finished after long
periods of processing.
We decided to generate, for each experiment, 10
formal contexts. Note that the randomly generated
incident table can vary between two contexts with the
same dimensions and densities giving rise to different
implication sets. Therefore a differentiated perfor-
mance was obtained for each context. We calculated
an average runtime based on the context size and den-
sity.
The 120,000 objects were combined with sets of
50, 100 and 150 attributes, with densities ranging
from the minimum, 30%, 50%, 70% and the maxi-
mum density for each generated context.
We use the SCGAz tool (Rimsa et al., 2009) to ge-
nerate random contexts within the limits of controlled
densities and sizes.
The experiments with such contexts allows a bet-
ter control regarding the generation of contexts for
analysis. That was the main reason we did not work
on real bases, since we could not control the tests.
4.1 Representing a Formal Context with
the BDD
For the creation of the BDD representing the formal
context, it was used a similar algorithm that was pro-
posed by (Rimsa et al., 2009).
The Algorithm 1 expects as input a file in the Bur-
meister format (Burmeister, 2003), it traverses all at-
tributes of the object and, if it has the attribute (inci-
dence), the BDD variable indicated by index “i” is
An Approach to Extract Proper Implications Set from High-dimension Formal Contexts using Binary Decision Diagram
53

Algorithm 1: Formal context using BDD.
Input: file on format cxt
Output: context on BDD format
1: FileLine =File.ObtainLine();
2: while File.End() do
3: BDDTemp =BDDNew
4: for i ← 0 to NumberAttributes do
5: if FileLine[i] ==’X’ then
6: BDDTemp& =noTrue(i)
7: else
8: BDDTemp& =noFalse(i)
9: end if
10: end for
11: BDDContext =BDDTemp
12: end while
13: return BDDContext
inserted in the objects’s temporary BDD with a “true”
indication. Otherwise, the variable admits a “false”
indication. Finally, the temporary BDD is added to
BDD which represents the context. Thus, by doing
AND operations to insert the attributes and OR for
the objects, the context using BDD is built.
4.2 PropIm Algorithm
For a better analysis of our Algorithm (ProperIm-
plicBDD), we first present the PropIm (Silva et al.,
2017).
Algorithm 2: PropIm.
Input: Formal context (G,M,I)
Output: set of implication imp with support greater
than 1
1: imp =
/
0
2: for all m ∈ M do
3: P =m
00
4: size =1
5: Pa =
/
0
6: while size < |P| do
7: C =

P
size

8: Pc = getCandidate(C,Pa)
9: for all P1 ⊂Pc do
10: if P1
0
6=
/
0 and P1
0
⊂m
0
then
11: Pa = Pa ∪ {P1}
12: imp = imp ∪ {P1 → m}
13: end if
14: end for
15: size++
16: end while
17: end for
18: return imp
The algorithm receives as input a formal context
(G, M, I), and outputs a set of proper implications.
Line 1 initializes the set imp as empty. The following
loop (lines 2-17) analyzes each attribute present in M.
Initially, each attribute m can be a conclusion for a set
of premises. For each m, it calculates the premises
P1.
In line 3, P records all the attributes that contains
the same objects of m. The size counter determines
the size of each premise, as the smallest possible size
is 1 (an implication of type x → z), it is initialized to
1 (Line 4).
Pa stores a set of auxiliary premises that can ge-
nerate an implication using m as a conclusion (in line
5 Pa is initialized as empty).
From lines 6-16, the set of minimum premises is
found and is limited by |P|. In Line 7, the set C
obtains all combinations of size size from elements in
P. In Line 8, the set of candidate premises is formed
through the Algorithm 5.
Each candidate premise P1 ⊂ PC is checked to
ensure if the premise P1 and the conclusion m re-
sults in a valid proper implication. Case P1
0
6= 0
and P1
0
⊂ m
0
, the premise P1 is added to the set of
auxiliary premises Pa and also the implication {P1
→m} is added to the list of implications imp = imp
∪{P1→m}.
4.3 The Proposed Algorithm
ProperImplicBDD
In order to have a better performance than the al-
gorithm PropIm (Silva et al., 2017) and to process
a larger volume of data, all PropIm algorithm met-
hods were previously analyzed. After this analysis,
we verified that the function that returned the objects
in common from a set of attributes was the most cos-
tly part of the algorithm.
In order to optimize this function, we decided to
use BDD’s to represent the formal context in more
compressed form and to obtain a better performance
in context operations with attributes and objects.
The complexity order for the extraction of proper
rules is O(|M||imp|(|G||M| + |imp||M|)). The com-
plexity order of the ProperImplicBDD algorithm is
exponential, however, an heuristic was implemented
to reduce the combinations of attributes in the premi-
ses.
We also created a function – primeAtrSetBDD –
to improve the verification of similarity among attri-
butes and objects (Algorithm 4). This function calcu-
lates the BDD context conjunction with the attributes
informed through parameters and returns a BDD con-
taining all objects of m.
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
54

Algorithm 3: ProperImplicBDD.
Input: Formal context (G,M,I)
Output: set of implication imp with support greater
than 1
1: imp =
/
0
2: for all m ∈ M do
3: bddC = primeAtrSetBDD(m)
4: P =m
00
5: size =1
6: Pa =
/
0
7: while size < |P| do
8: C =

P
size

9: Pc = getCandidate(C,Pa)
10: for all P1 ⊂ Pc do
11: bddP = primeAtrSetBDD(P1)
12: if bddC 6= 0 and bddP 6= 0 and bddC
== bddP then
13: Pa = Pa ∪ {P1}
14: imp = imp ∪ {P1 → m}
15: end if
16: end for
17: size++
18: end while
19: end for
20: return imp
The ProperImplicBDD pseudo-code is described
in the Algorithm 3. The algorithm receives as input a
formal context (G, M, I), and outputs a set of proper
implications.
Line 1 initializes the set imp as empty. The follo-
wing loop (lines 2-19) analyzes each attribute of the
set M. Initially, each attribute m can be a conclusion
for a set of premises. For each m, it calculates the
premises P1.
In line 3, bddC through the Algorithm 4 receives
and stores the BDD containing all objects of the m at-
tribute. This BDD will be used in checking the equa-
lity between the premise BDD (P1) and the conclu-
sion BDD (m).
In line 4, P records all the attributes that contains
the same objects of m. The size counter in Algorithm
3 determines the size of each premise, as the smallest
possible size is 1 (an implication of type x → z), it is
initialized to 1 (Line 5).
Pa stores a set of auxiliary premises that can ge-
nerate an implication using m as a conclusion (in line
6 Pa is initialized as empty). From lines 7-18, the set
of minimum premises is found and is limited by |P|.
In Line 8, the set C obtains all combinations of
size size from elements in P. In Line 9, the set of
candidate premises is formed through the Algorithm
5.
For each candidate premise P1 ⊂ PC the bddP
stores the BDD that contains all objects of the pre-
mise.
In line 12 a check is made between bddC and
bddP to ensure that premise P1 and conclusion m re-
sults in a valid implication. If bddC = bddP the im-
plication is valid.
Considering that, the premise p1 is added to the
hypothesis of local premises Pa and also the impli-
cation {P1 →m} is added to the list of implications
imp = imp ∪ {P1→m}.
4.3.1 PrimeAtrSetBDD Algorithm
The Algorithm 4 presents the primeAtrSetBDD
function, which is responsible for obtaining the BDD
that contains all objects from the list of attributes in-
formed as a parameter.
The function computes the conjunction between
the BDD that represents the entire formal context and
the BDD of each attribute of the list of attributes. It
outputs a BDD containing only the objects that con-
tains all the attributes informed.
Algorithm 4: PrimeAtrSetBDD.
1: procedure PRIMEATRSETBDD(ListAttributes)
2: bddNewExt = bddCxt
3: for all it ∈ ListAttributes do
4: bddNewExt& =bddNewExt.And(it)
5: end for
6: return bddNewExt
7: end procedure
4.3.2 GetCandidate Algorithm
The Algorithm 5 obtains all subsets that do not con-
tain an attribute that belongs to the Pa premise. It
receives, as a parameter, the sets C and Pa and returns
a set D of premises.
Algorithm 5: GetCandidate.
1: procedure GETCANDIDATE(C,Pa)
2: D =
/
0
3: for all a ∈A|A⊂Pa do
4: for all B ⊂C do
5: if a 6∈B then
6: D =Pa/B
7: end if
8: end for
9: end for
10: return D
11: end procedure
An Approach to Extract Proper Implications Set from High-dimension Formal Contexts using Binary Decision Diagram
55

5 EXPERIMENTS
The main goal of our experiments was to evaluate the
performance of ProperImplicBDD algorithm in gene-
rating proper implications set. In order to evaluate the
performance, a comparison was made between Pro-
perImplicBDD and PropIm for extracting the impli-
cations set for several synthetic contexts (Table 3).
Both algorithms were coded in C++ and execu-
ted on a IBM Server with four 2-core Intel Xeon (3.1
GHz) processors, 32 GB of RAM, 1TB of disk storage
and running on Ubuntu 16.04 OS. In all the experi-
ments, we evaluated the performance of ProperImpli-
cBDD and PropIm running the same context with a
maximum time of 14 days in order to obtain the pro-
per implications set.
Table 3: Synthetic Contexts used in the experiments.
Context |G| |M| |I|
Density
(%)
#1 120.000 50 1.799.769 30
#2 120.000 50 2.999.984 50
#3 120.000 50 4.200.545 70
#4 120.000 100 3.600.503 30
#5 120.000 100 6.000.036 50
#6 120.000 100 8.399.916 70
#7 120.000 150 5.399.809 30
#8 120.000 150 8.999.955 50
#9 120.000 150 12.601.449 70
We tested our algorithm and obtained significant
gains in execution time when compared to PropIm
(see Table 4 and Figure 4).
The results showed that ProperImplicBDD impro-
ved the execution time from 46% to 88% in all the
tested scenarios.
Moreover, our proposed algorithm had a speedup
from 1.84 up to 8.07 compared to PropIm applying
the same contexts as input.
It is important to point out that the higher the den-
sity of context is, the greater the gain in the proposed
algorithm will be.
Another very significant result, as presented in Ta-
ble 4, is that the proposed algorithm was able to cal-
culate the proper implications set (output) to contexts
with 150 attributes, while PropIm did not return any
results during a week of execution.
Therefore, the experimental results show that the
algorithm has high performance for very large data.
The confidence interval used is 95%.
Table 4: Results for PropIm and ProperImplicBDD algo-
rithm with 120.000 objects.
Context
(Attributes X
Density(%))
PropIm
(minutes)
ProperImplic
BDD
(minutes)
Speed
-Up
50 x 30% 416 227 1,84
50 x 50% 98 29 3,39
50 x 70% 286 35 8,07
100 x 30% 279 97 2,89
100 x 50% 369 144 2,57
100 x 70% 667 162 4,10
150 x 30% . 17,028 .
150 x 50% . 8,028 .
150 a x 70% . 3,332 .
Figure 4: Time execution comparison.
6 CONCLUSION AND FUTURE
WORKS
This paper proposed a new algorithm, ProperImpli-
cBDD with the goal of extracting proper implications
set with a better performance than PropIm algorithm
in high-dimensional contexts.
Initially, the main objective of our proposed algo-
rithm was to extract proper implications set in con-
texts with large volumes of data. After the experi-
ments, we realized that the algorithm obtained gains
beyond expected.
Our algorithm was faster in all contexts used in
the tests. In contexts with 150 attributes and 120,000
objects, similar to the quantity of objects that was
the challenge in (Priss, 2006), ProperImplicBDD was
able to extract all the proper implications set while the
PropIm algorithm did not return any result during a
week of execution. ProperImplicBDD also presented
speedups from 1,84 to 8,07 in the extraction of proper
implications set.
An important observation of using a Binary De-
cision Diagram (BDD) as the data structure was that
in denser contexts, as more similar objects exists, the
context becomes more optimized and performs better.
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
56

We suggest as a future work a modification in the
algorithm to support distributed computing. Additi-
onally, we suggest that ProperImplicBDD is used in
a context of a real-world problem. Also more tests
can be performed using synthetic contexts, ensuring
that how much more identical objects in a context, the
BDD that will be created based on this context it more
optimized than a context with fewer repeated objects
increasing the performance of ProperImplicBDD. Fi-
nally, we also suggest the exploration of techniques to
reduce a implications set (Dias and Vieira, 2017).
ACKNOWLEDGEMENT
The authors acknowledges the financial support of
CAPES, FAPEMIG, CNPq and the partial support of
SERPRO. The authors would like to warmly thank
PUC-MG researchers for raising important questions
and making relevant suggestions that helped improve
the quality of the paper.
REFERENCES
Bertet, K. (2006). Some algorithmical aspects using the ca-
nonical direct implicationnal basis. page 101–114. In-
ternational Conference on Concept Lattices and their
Applications - CLA.
Bertet, K. and Monjardet, B. (2001). The multiple facets
of the canonical direct unit implicational basis. vo-
lume 411, page 2155 – 2166. Theoretical Computer
Science.
Bryant, R. E. (1986). Graph-based algorithms for bool-
ean function manipulation. IEEE Trans. Comput.,
35(8):677–691.
Burmeister, P. (2003). Formal concept analysis with co-
nimp: Introduction to the basic features. Fachbereich
Mathematik, Technische Universit
¨
at Darmstadt.
Dias, S. M. and Vieira, N. J. (2017). A methodology for
analysis of concept lattice reduction. volume 396, pa-
ges 202–217. Information Sciences.
Ganter, B., Stumme, G., and Wille, R. (2005). Formal con-
cept analysis: foundations and applications. volume
3626. Springer Science & Business Media.
Ganter, B. and Wille, R. (1997). Formal concept analy-
sis: Mathematical foundations. Springer-Verlag New
York, Inc., Secaucus, NJ, USA, 1st edition.
Neto, S. M., Z
´
arate, L. E., and Song, M. A. (2018). Hand-
ling high dimensionality contexts in formal concept
analysis via binary decision diagrams. volume 429,
pages 361–376. Information Sciences.
Priss, U. (2006). Some open problems in formal concept
analysis. International Conference on Formal Concept
Analysis.
Rimsa, A., Z
´
arate, L. E., and Song, M. A. (2009). Eva-
luation of different bdd libraries to extract concepts
in fca–perspectives and limitations. page 367–376.
Computational Science–ICCS, Lyon France.
Ryssel, U., Distel, F., and Borchmann, D. (2014). Fast al-
gorithms for implication using proper premises. vo-
lume 70, page 25–53. Annals of Mathematics and Ar-
tificial Intelligence.
Salleb, A., Maazouzi, Z., and Vrain, C. (2002). Mining
maximal frequent itemsets by a boolean based appro-
ach. page 285–289. European Conf. on Artificial In-
telligence.
Silva, P. R. C., Dias, S. M., Brand
˜
ao, W. C., Song, M. A.,
and Z
´
arate, L. E. (2017). Formal concept analysis
applied to professional social networks analysis. vo-
lume 1, pages 123–134. ICEIS.
Taouil, R. and Bastide, Y. (2001). Computing proper im-
plications. page 46–61. International Conference on
Conceptual Structures-ICCS.
An Approach to Extract Proper Implications Set from High-dimension Formal Contexts using Binary Decision Diagram
57