Towards Rich Sensor Data Representation

Functional Data Analysis Framework for Opportunistic Mobile Monitoring

Ahmad Mustapha, Karine Zeitouni and Yehia Taher

DAVID Laboratory, UVSQ, Paris-Saclay University, 45 Avenue des Etats-Unis, Versailles, France

Keywords:

Functional Data Analysis, Database, Spatiotemporal, Multivariate Time Series, Sensors, Opportunistic

Mobile Monitoring.

Abstract:

The rise of new lightweight and cheap sensors has opened the door wide for new sensing applications. Mobile

opportunistic sensing is one type of these applications which has been adopted in multiple citizen science

projects including air pollution monitoring. However, the opportunistic nature of sensing along with cam-

paigns being mobile and sensors being subjected to noise and missing values leads to asynchronous and un-

clean data. Analyzing this type of data requires cumbersome and time-consuming preprocessing. In this paper,

we introduce a novel framework to treat such type of data by seeing data as functions rather than vectors. The

framework introduces a new data representation model along with a high-level query language and an analysis

module.

1 INTRODUCTION

The rise of new lightweight and cheap environmental

sensors is opening the door wide for more IoT ap-

plications that haven’t been possible years ago. Re-

cently, air quality monitoring has ridden the wave and

shifted towards opportunistic mobile monitoring. Op-

portunistic mobile monitoring takes advantage of peo-

ple daily commuting in order to monitor air pollution

on a ﬁne scale (Van Den Bossche et al., 2016). This

is done by fetching air quality sensors kits on volun-

teers and leaving them to commute while holding the

sensors without restriction on time or space.

In air quality monitoring context, the sensors kits

generate multivariate spatial time series. For exam-

ple, one record of these kits might include Black Car-

bon (BC) concentration, Nitrogen Oxide (NO2) con-

centration, location (latitude, longitude), and a times-

tamp. Such data has always been stored using con-

ventional relational databases as one long table. How-

ever, such representation of time series isn’t the best

representation when it comes to data analysis.

Analyzing multivariate spatial time series requires

a cumbersome preprocessing stage. Especially when

it comes to opportunistic monitoring. The data gen-

erated from multiple individuals won’t be synchro-

nized during opportunistic monitoring because there

exists no restriction on time or space.(Van Den Boss-

che et al., 2016) While one individual is using the sen-

sor the other might not. Moreover, sensors are always

subjected to malfunctioning, noise, and no-signal mo-

ments which results in noisy, and incomplete time se-

ries. Fixing these problems in large datasets is cum-

bersome and time-consuming. In this paper, we aim

to describe a novel multivariate spatial time series rep-

resentation that can solve the aforementioned prob-

lems in a robust and semi-automatic manner.

The proposed representation sees the measured

variables as functions rather than discrete data

records. While sensors can only generate discrete

data, the generated data can always be approximated,

using curve ﬁtting and regression techniques, by

functions with a considerable number of parameters.

These approximate functions are then stored along

with the residuals and other quality indices as they

are. The notion of functionDB (Thiagarajan and Mad-

den, 2008) is borrowed to apply functions storage,

aggregation, transformation, and retrieval through an

extended SQL query language. This proposed repre-

sentation is to be implemented and the supposed ben-

eﬁts will be validated.

The rest of the paper is structured as what fol-

lows. Section 2 illustrates and describes the proposed

framework.Section 3 demonstrates a spatial applica-

tion. Section 4 discusses the beneﬁts of the frame-

work and Section 5 concludes the paper.

290

Mustapha, A., Zeitouni, K. and Taher, Y.

Towards Rich Sensor Data Representation.

DOI: 10.5220/0006788502900295

In Proceedings of the 4th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2018), pages 290-295

ISBN: 978-989-758-294-3

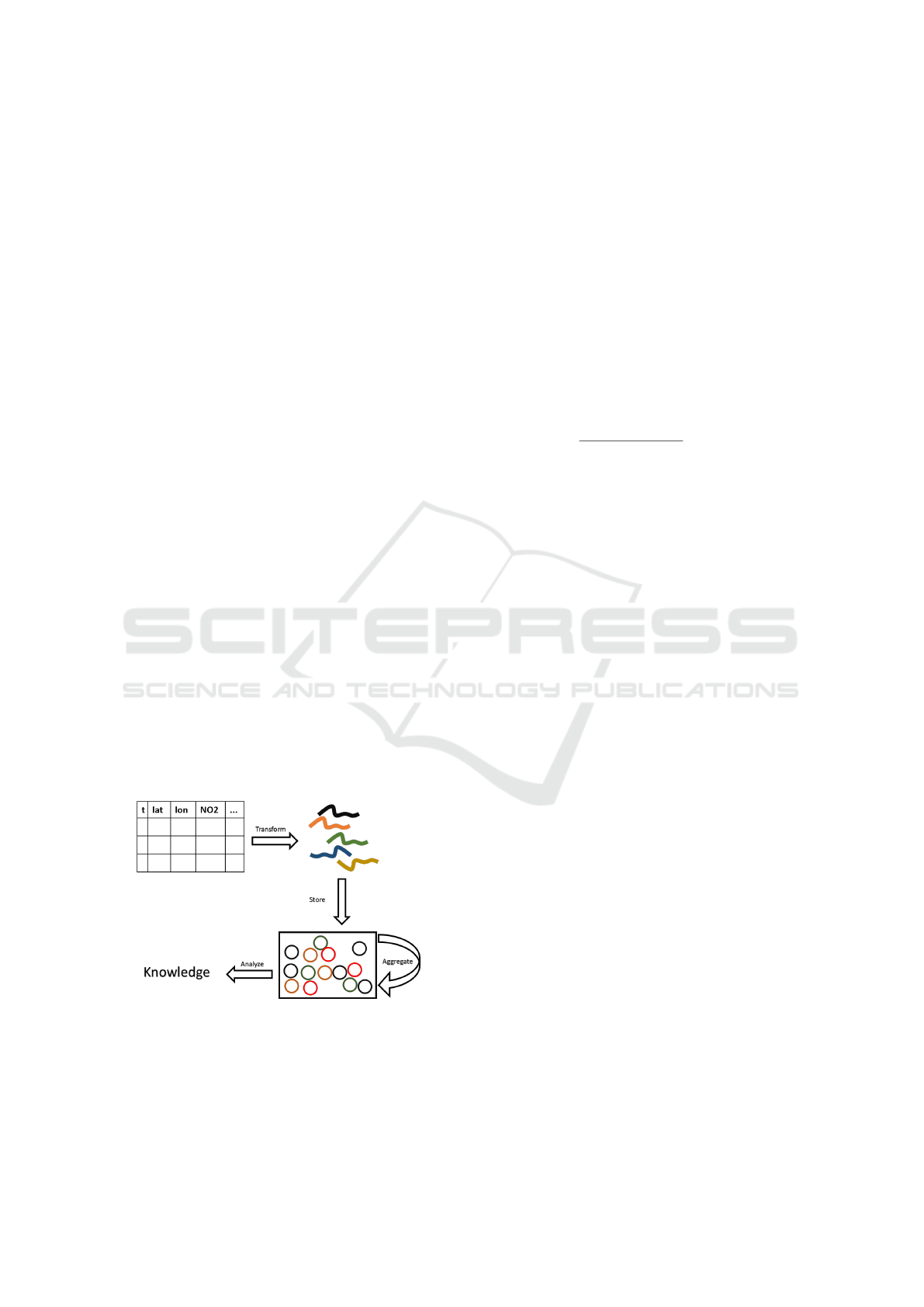
2 THE FRAMEWORK

2.1 Overview

Data scientists and researchers have been approxi-

mating discrete data by functions for several reasons.

However, curve ﬁtting has always been a stage and

not a destination or a ﬁnal structure. In this proposal,

we are willing to go further and establish functions

as a well-deﬁned and more abstract representation of

sensors data.

In order to achieve this representation, a trans-

formation and restructuring process will be applied

to raw and discrete sensors data similar to conven-

tional ETL (Extract, Transform, Load). The initial

step of this process is to read the data which are usu-

ally stored in ASCII formatted ﬁles or as tables in

databases. Curve ﬁtting techniques are then applied

to generate a function for each monitored entity as a

relation to a certain continuum mostly time or space.

After the functions are generated they are stored and

restructured in a specialized database. At this point,

the data is fully represented by a pool of functions.

The power of such representation is not only in over-

coming cumbersome preprocessing but also in the op-

erations that can be applied to the functions. Alge-

braic aggregation and transformation can be applied

to functions in the interest of generating new func-

tions that enrich the initial set. Also, knowledge can

be extracted directly from this pool of functions by

applying functional data analysis techniques (Ramsay

and Silverman, 2013), a ﬁeld of statistics that focuses

on analyzing functions, to serve exploratory, conﬁr-

matory, or predictive objectives. Figure 1 illustrates

an overview of the entire process.

Figure 1: The framework’s data ﬂow.

2.2 Function Generation

Approximating discrete data by functions is achieved

through curve ﬁtting techniques. Let (x

) be a

group of observed discrete data points for a given

physical process where x represents a given contin-

uum and y represents a certain variable. Let f be the

function that is supposed to approximate the discrete

data and be a mapping from x to y. We set f to be a

ﬂexible core function with tweakable parameters vec-

tor C. Hence we end up having:

Y = f (C,X)+ε

Where Y is a vector of all the observed variables, X

the vector of the continuum values corresponding to

each element in Y, and ε

ε is the error between f and

the original data. To approximate the data the error

should be decreased by choosing the right C. C can

be obtained by solving the differential equation:

d(Y − f (C, X))

= 0

This difference represents the sum of the distance be-

tween each original data point and its corresponding

approximated data points.The derivation is because a

function admits its extreme (maximum or minimum)

when its derivative is equal to zero, but since the dif-

ference in our case is open-ended ( it doesn’t have a

maximum) then it certain that it admits a minimum

when the derivative is equal to zero.

One of the most used models for approximating

data is linear expansion where the parametrized func-

tion f is set to be an aggregation of well deﬁned basis

functions each is multiplied by a coefﬁcient and these

coefﬁcients are the tweakable parameters:

f (C,x) =

∑

i=1

(x) = c

(x) + ... + c

(x) (1)

In which B

,...,B

are the basis functions and

,..,c

are the coefﬁcients. One of the heavy used

basis system for periodic data is Fourier Basis:

f (x) = c

+ c

sin(ωx) + c

cos(ωx) + c

sin(2ωx)

+ c

cos(2ωx) + ...

(2)

Where c

,... are the coefﬁcients, the ba-

sis functions B

= 1, B

2r(even)

= cos(rωx), and

2r+1(odd)

= sin(rωx). ω is a parameter that deter-

mines the period of the ﬁtted function 2π/ω. Another

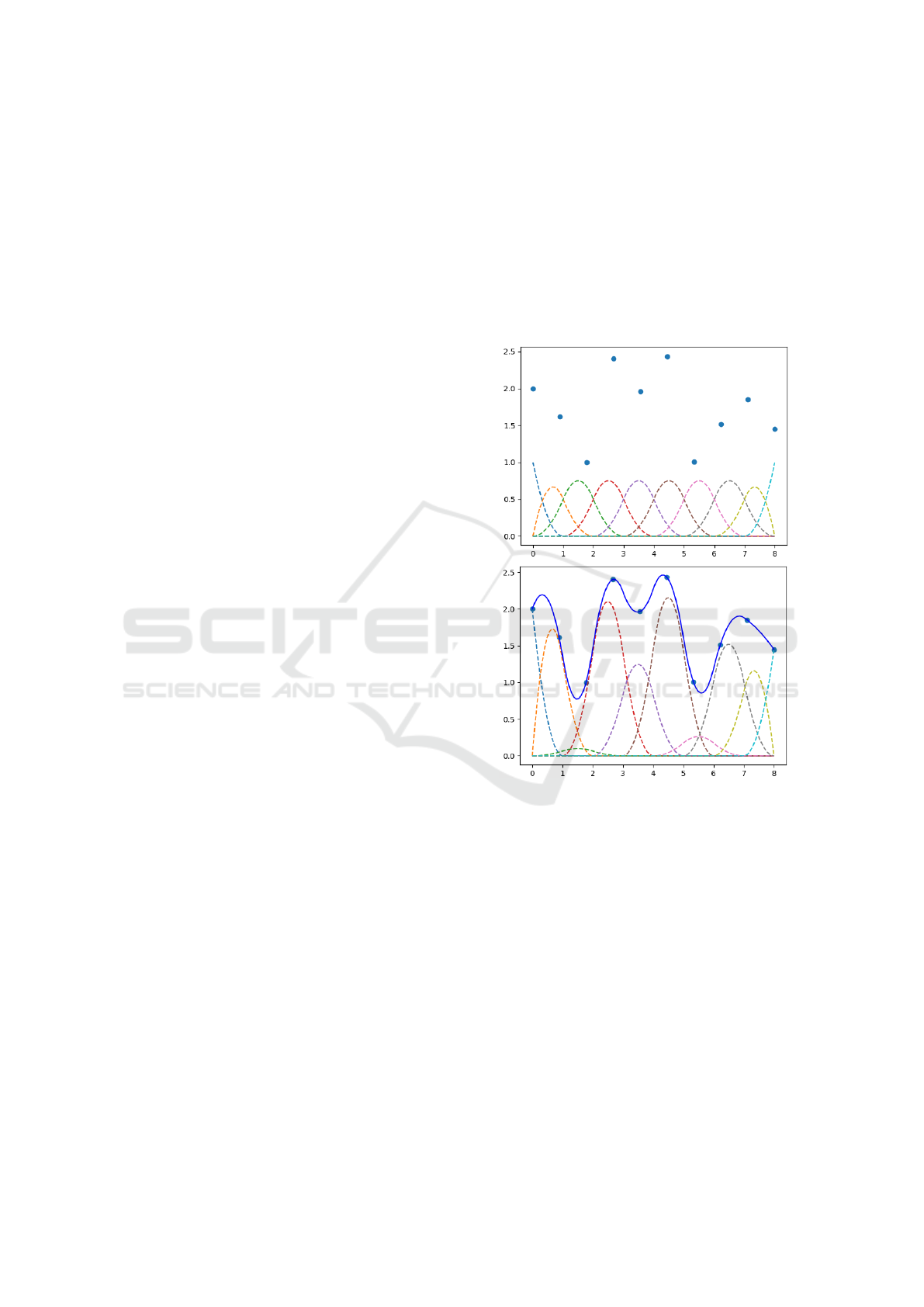
widely used basis is Basis Spline (B-spline). Figure 2

shows the initial set of the Spline basis functions that

is set to approximate the shown data points. After

tweaking the functions with the suitable coefﬁcients

we can see how the summation of them ( the non-

dashed curve in blue ) approximates the data points.

This approach is not only applicable for one-

dimensional interpolation but also for multidimen-

sional interpolation. One important use case is spa-

tial interpolation where a phenomenon is monitored

Towards Rich Sensor Data Representation

291

against space variation i.e. with respect to location

measured using GPS units. In this interpolation case,

there are two independent variables which are geo-

graphical latitude and longitude and the resulting in-

terpolated artifact will be a 2D surface.

The framework we propose can handle such use

case by generalizing linear expansion, particularly

splines, into higher dimensions. Thin Plate Spline

(TPS) is a linear expansion function suitable for spa-

tial and multidimensional interpolation. Equation 3

below represents the TPS function. TPS works by

ﬁnding ﬁrst a 2D plane that captures the data global

trend and then adding 2D splines around the measured

data to formulate the local trend.

f (x,y) = a

+ a

x + a

y +

∑

j=1

R(r,r

) (3)

Where a

are the parameters that deﬁnes

the global trend.

∑

j=1

R(r,r

) represents the lo-

cal variations where N is the number of measured

data points, R(r, r

) is a basis function, λ

,λ

,...,λ

are the to be found coefﬁcients of the basis functions.

Similar to one dimensional interpolation a

and

,λ

,...,λ

can be obtained by solving a certain dif-

ferential equation that ﬁt the function to the data while

imposing a smoothing constraint.

2.3 Function Storage

After generating the functions the next step is to store

them. In our proposal, we will borrow and extend

the idea of FunctionsDB. FunctionsDB is a func-

tion database which permits the storage and retrieval

of continuous functions using a SQL-like declarative

language with the main goal of exploiting the con-

tinuous nature of functions. FunctionDBs query pro-

cessor applies queries directly to the algebraic repre-

sentation of the functions using algebraic operations.

The main enabler in FunctionDB is the function ta-

ble which is a data model that stores function in their

algebraic form. The function table is a normal rela-

tional table where the columns are the parameters of

the regressed or ﬁtted functions along with predicates

(constraints). To emphasize, if a group of data points

that belongs to a certain interval of the independent

variable [p1, p2] is ﬁtted to a 2

degree polynomial

ax2 + bx + c, the result will be stored in a one tuple

in the form of (p1, p2, a, b, c) where the ﬁrst

two columns represent the constraint where the func-

tion is deﬁned and the others represent the function.

However, the authors of functionDB conﬁned func-

tion representation to polynomials only and the pro-

posed table cannot represent different representations

such as Fourier and Splines without adding a ﬂag that

can specify the type of the stored function making

things less open to new models. In our proposal, we

are willing to store functions in a less structured and

more ﬂexible form where functions are stored as al-

gebraic statements along with the residuals (the vec-

tor of the difference between the original values and

the ﬁtted function values) and other indices such as

the Sum of Squared Errors (SSE) and the Root-Mean

Squared Error (RMSE) along with the predicates.

Figure 2: Approximating discrete data using Basis Spline,

before and after multiplying the basis functions with the

corresponding coefﬁcients.

2.4 High Level Query Language

FunctionDB creates, retrieve, and manipulate func-

tions by introducing a set of SQL commands that

wraps regression logic and algebraic operations.

However, the authors of this novel database conﬁned

the regressed functions to only linear and polynomial

ones. We are willing to extend it to cover the usu-

ally used functions for interpolating discrete data such

as B-spline, Fourier, and others. For convenience,

we will point to this language as Functional-SQL or

FSQL.

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

292

2.4.1 Function Creation

FSQL’s function creation logic is a wrapper for inter-

polation and smoothing algorithms used by statisti-

cians to approximate functions to discrete data points.

The listing below introduces the set of commands that

gives a taste of how functional views of discrete data

can be created.

CREATE VIEW NO2Time

AS FIT NO2 OVER Time

USING BASIS Fourier(...)

USING ALGO LSSE(...)

USING PARTITION SplitEqually(...)

TRAINING DATA SELECT * FROM Somedata

In order to generate a functional view of some

data, this data should be already existing in a

relational form or in structured ﬁles. In example

x this data should include NO2 and Time as two

attributes or columns and it is speciﬁed by the key-

word TRAINING DATA CREATE VIEW NO2Time

will create a view of the name NO2Time.

AS FIT NO2 OVER Time speciﬁes the dependent and

independent variable NO2 and Time.USING BASIS

speciﬁes the basis that should be used here Fourier is

chosen that should take arguments such as the number

of basis functions and the period. USING ALGO speci-

ﬁes the algorithm that should be used to approximate

the discrete data. It is mentioned in x that the coef-

ﬁcients that best minimizes the difference between

the original data and the ﬁtting function can be found

by solving a differential equation that expresses

the Least Sum of Squared Error (LSSE). However

multiple algorithms can be used such as weighted

LSSE that increases or decreases the importance

of errors along the ﬁtting interval, penalized LSSE

can also be used to force a penalty over the ﬁtted

function curvature. USING PARTITION speciﬁes

how to segment the data. It is better to ﬁt multiple

functions over large data sets as this achieves a better

ﬁt with increased ﬂexibility. SplitEqually(...)

divides the data set into equal parts of a given size

and then a function will be ﬁtted on each part.

2.4.2 Function Retrieval

Although querying a database to obtain continuous

functions is useful, most of the time the user will need

to discretize the results after obtaining the continuous

function in a read query. That is why FSQL, which

is based on the FunctionDB notion, will support both

types of intentions( continuous or discrete ). And this

will not only satisfy the user’s requirements but will

also permit a database of functions to be integrable

with the current relational databases.

This distinction is achieved by introducing the

Grid keyword. The listings below emphasis this

point.

SELECT NO2 FROM NO2Time

WHERE Time = "12-6-2017 17:30:32"

SELECT NO2 FROM NO2Time

WHERE Time > "12-6-2017 17:30:32"

and Time < "15-6-2017 12:30:00"

SELECT NO2 FROM NO2Time

WHERE Time > "12-6-2017 17:30:32"

and Time < "15-6-2017 12:30:00"

GRID Time 1H

The ﬁrst listing showcase a normal point-wise

query where the user is interested in the value of NO2

at one point of time and it can be achieved under

the hood by substituting the given value in the cor-

responding functional view of NO2Time. On the sec-

ond hand, the second listing will return the algebraic

form of the existing function between the queried

time. Finally the third listing showcase the GRID key-

word. In this example, the returned value will be a

table of columns Time and NO2 where the time col-

umn is projected on an hourly basis.

2.4.3 Function Aggregation

FSQL will also support aggregation clauses similar to

the ones in normal databases. However and because

of the continuous nature of the functions traditional

aggregates are not possible. The aggregation opera-

tions in FunctionDB are applied on inﬁnite bounded

intervals where the traditional aggregates aren’t suit-

able. For example, there is no meaning in having the

aggregate COUNT, which is usually used to return the

number of rows with certain conditions speciﬁed by

WHERE clause, over a continuous function. It doesn’t

make sense to query how many points of NO2 are

above a certain threshold because they are either zero

or inﬁnite. However, you can quantify this by sub-

stituting the COUNT clause with the continuous analo-

gous VOLUME. If we want to quantify how many NO2

data we have in a certain table it will be analogous to

the size of the time interval where the NO2 data is col-

lected in other words the VOLUME of a variable that

depends on one independent variable is the interval

length. While if this variable depends on two inde-

pendent variables the VOLUME will be the area that is

covered by these two variables and so on. The same

can be applied to the sum SUM aggregate. The contin-

uous SUM is the integral of the queried variable along

the intervals where the conditional clause is applied.

For more information about this topic, the reader is

referred to the FunctionDB paper. The following list-

Towards Rich Sensor Data Representation

293

ing provides an example where the SUM aggregate is

used.

SELECT SUM(NO2) FROM NO2Time

WHERE NO2 < 10 and Time < 20-8-2017

It is noteworthy to mention that all the retrieval

and aggregation commands are to be computed in

a symbolic manner wherever possible. We mean

by symbolic, the usage of mathematical calculations

rather numerical ones. For example, the retrieval of a

measurement below a certain threshold, as in the pre-

vious listing WHERE NO2 < 10, is not computed by

re-sampling the ﬁtted function and then ﬁltering it,

but by solving the inequality when the difference be-

tween the function and the threshold is below zero.

The authors of functionDB proved empirically that

using symbolic computation have performed better in

terms of time and resource utilization than using nu-

merical computation. This is one of the reasons that

support our approach.

2.5 Functional Analysis

Functional Data Analysis (FDA) is a ﬁeld of statis-

tics where functions are analyzed to explore, conﬁrm,

or predict certain knowledge statements. Unlike the

conventional data mining techniques that are applied

over vectors of discrete data, FDA works only with

functions; functions are the atomic data structure in

FDA. FDA is widely used for time series, spatial data,

and spatiotemporal data. One of our frameworks main

goals is to fasten and ease the transition from asyn-

chronous discrete data into functional views and ﬁ-

nally into knowledge. For that, one important con-

tribution of our framework is to integrate functional

analysis operations with the high-level FSQL. In our

framework, the set of aggregates in FSQL are ex-

tended to support functional analysis operations. The

number of functional analysis operations is being in-

creased through the years by the continuous research

efforts in the ﬁeld; this shows the importance of our

framework to be a platform that can incubate such ef-

forts. However, there is a group of basic and widely

used operations that are essential in any functional

analysis application.

2.5.1 Basic Operations

Functional data analysis usually starts by applying ba-

sic exploratory operations that permits to understand

the data more. Starting with the very basic statis-

tical operations such as mean, variance, covariance,

and correlation of a group of functional observations

and not ending with different transformation opera-

tions such as derivation, and registration. Derivation

helps in seeing the rate of change in the data which

gives the analyst a deeper sense of the data. Regis-

tration is the process of aligning different functional

observations with respect to function features such as

valleys and peaks; this leads to a better representation

of the data. The following listing showcase how some

of these aggregates might be used.

CREATE VIEW DerivativeMeanABCDE AS

SELECT MEAN(DERIVE(NO2TimeA, NO2TimeB,

NO2TimeC, NO2TimeD, NO2TimeE))

WHERE Time > 10-09-2017

This query creates a new continuous functional view

that represents the mean of the derivative of 5 differ-

ent NO2 observations after a certain time.

2.5.2 Advanced Operations

Advanced functional analysis operations include

Functional Principle Component Analysis (FPCA),

Functional regression and many others used in the

classiﬁcation, clustering, and prediction of functional

data. FPCA is the functional version of the Princi-

ple Component Analysis (PCA) tool which is a well-

known dimensionality reduction tool used in data

mining. With FPCA functions can be projected over a

group of principal components that represents the sys-

tem where the variance between the functions projec-

tion is maximized. This type of operations might get

really complex and divers that is why we didnt con-

sider integrating them into FSQL aggregates. How-

ever, we are willing to build an external module that

acts over the algebraic representation of functions.

This module should be extensible so that researchers

can integrate their own developed algorithms and op-

erations.

3 RELEVANCE

DEMONSTRATION

Polluscope is a multidisciplinary project that aims to

measure individual’s air pollution exposure and re-

late it to health using opportunistic mobile monitor-

ing. One prior task was to asset different air pollutants

sensors. The quality assessment was done through a

novel algorithm introduced in (Fishbain et al., 2017)

that compares sensor time series with an accurate ref-

erence time series. The problem was that the sam-

pling rate of each time series was different and the al-

gorithm couldn’t be applied. To overcome this prob-

lem we developed an R language library that wraps in-

terpolation logic provided by the functional data anal-

ysis library of R fda.R (Ramsay et al., 2017). The de-

veloped library ﬁts two functions one for the sensor

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

294

time series and one for the reference time series and

then re-sample both according to a common sampling

rate. This problem represents a relevance demonstra-

tion for one side of our work as it shows how interpo-

lation is a recurring requirement in mobile monitoring

projects.

4 DISCUSSION

Although this framework was inspired by the need to

resolve the asynchronous, noisy and multivariate na-

ture of data generated in opportunistic mobile sensing

applications, the beneﬁts of such framework can be

generalized to cover a wider area of applications.

• Semi-automation of data preprocessing: curve ﬁt-

ting is usually used to resolve the noise in data

through smoothing, impute the missing values and

normalize asynchronous data through interpola-

tion. Our framework inherits these actions by us-

ing functions as the atomic data structure rather

than vectors. However, curve ﬁtting is not al-

ways straightforward and depends on the data in

hand; thus the framework should provide a bal-

ance between wrapping the ﬁtting logic by high-

level queries and giving more control over the

logic to the user. This way the user can choose

what level of control he needs as the nature of data

diverse.

• Easy and Familiar Query Language: SQL is a

very known standard to the level it became ubiq-

uitous in data and computer scientists daily work.

Extending this language and deploying it in our

framework permits every one to utilize curve ﬁt-

ting and functional analysis power without know-

ing the complex logic underhood. Moreover using

SQL as a wrapper for function storage, retrieval,

and aggregation permits the framework to be in-

tegrable with existing relational databases. This

was integrity was an impactful contribution by

FunctionDB and our framework inherits it.

• Raw Data Abstraction: One of the hidden po-

tentials of our framework is giving semantics to

raw data. When you represent large data sets by

a group of relations ( functions ) between dif-

ferent variables, you implicitly give semantics to

data and rise their abstraction level. The stored

functions can be even exported in a suitable data

formate and then be integrated into knowledge

bases where reasoners can be used to link these

functions with different aspects of the internet of

Things (IoT) semantics.

5 CONCLUSION

To overcome the complexity of asynchronous and

noisy spatiotemporal multivariate data generated from

opportunistic mobile monitoring we have introduced

a high-level framework that can ease the entire pre-

processing and analysis process. The Framework is

based on four cornerstones: curve ﬁtting, algebraic

storage model, high-level query language, and an

analysis module. The introduced model is found to

be useful not only in opportunistic sensing applica-

tions but in a wide set of applications that depends

on functional analysis and deals with spatiotemporal

data. However, the proposed framework might end

to be complex under the hood and will raise multi-

ple challenges in terms of architectural design, robust-

ness, and scalability that should be solved.

ACKNOWLEDGMENT

This work is supported by the grant ANR-15-CE22-

0018 POLLUSCOPE of the French National Re-

search Agency (ANR).

REFERENCES

Fishbain, B. et al. (2017). An evaluation tool kit of air qual-

ity micro-sensing units. Science of The Total Environ-

ment, 575:639 – 648.

Ramsay, J. and Silverman, B. (2013). Functional Data

Analysis. Springer Series in Statistics. Springer New

York.

Ramsay, J. O., Wickham, H., Graves, S., and Hooker, G.

(2017). fda: Functional Data Analysis. R package

version 2.4.7.

Thiagarajan, A. and Madden, S. (2008). Querying continu-

ous functions in a database system. In Proceedings of

the 2008 ACM SIGMOD International Conference on

Management of Data, pages 791–804, New York, NY,

USA. ACM.

Van Den Bossche, J. et al. (2016). Opportunistic mobile air

pollution monitoring: A case study with city wardens

in Antwerp.

Towards Rich Sensor Data Representation

295