Investigating the Use of Primes in Hashing for Volumetric Data

eonie Buckley, Jonathan Byrne and David Moloney

Movidius, Intel, Ireland

Keywords:

Hashing, SLAM, Storage, Indexing, Volumetric Data, Primes, Voxels.

Abstract:

Traditional hashing methods used to store 3D volumetric data utilise large prime numbers. The intention of

this is to achieve well-distributed hash addresses to minimise addressing collisions. Hashing is an attractive

method to store 3D volumetric data, as it provides simple method to store, index and retrieve data. However,

implementations fail to provide theoretical support as to why they utilise large primes which act to create

a hash address through randomising key values. Neither is it speciﬁed what a “large” prime is. 3D data

is inherently well-distributed as each coordinate in 3D space is already unique. It is thus investigated in this

paper whether this randomisation through the use of large primes is necessary. The history of the use of primes

for hashing 3D data is also investigated, as is whether their use has persisted due to habit rather than due to

methodical investigation.

1 INTRODUCTION

Hashing is used to map data of arbitrary size to an

addressing space, and is a popular method to store,

retrieve and delete 3D volumetric data (Teschner

et al., 2003) (Klingensmith et al., 2015) (Niener

et al., 2013) (Eitz and Lixu, 2007) (K

ahler et al.,

2015). In much of the early literature discussing hash-

ing (Knott, 1975) (Knuth, 1998), the common goal

is to achieve distinct mapping addresses. However,

Knuth states that “it is theoretically impossible to de-

ﬁne a hash function that creates truly random data

from nonrandom data in ﬁles” (Knuth, 1998). The

birthday paradox (Good, 1950) highlights the difﬁ-

culty in achieving distinct addresses: if a random

function is selected to map 23 keys to a table of size

365, the probability that no two keys map to the same

location is only 0.4927.

In hashing, the address calculation is generally

achieved by a randomised scrambling of key values,

with many methods using large primes to achieve

this scrambling (Teschner et al., 2003) (Klingensmith

et al., 2015) (Niener et al., 2013) (Eitz and Lixu,

2007) (K

ahler et al., 2015). Hashing is an appropriate

term, as a hash is “a random jumble achieved by hash-

ing”, where hashing means to cut or to chop (Knott,

1975).

Hash coding was ﬁrst described in open liter-

ature by Arnold I. Dumey in the 1950s (Knuth,

1998) (Dumey, 1956) (although the idea of hashing

appears to have been originated by H.P Luhn in an

internal IBM memorandum in January 1953). Dumey

discusses a real life example where the details of eight

machines that are sold to the public must be stored.

To ensure that the details of no two machines would

be stored at the same address, originally the six digit

identiﬁers of the machines were used. However, on

inspection of the identiﬁers, it was found that the

fourth digit of each of them was unique. It was there-

fore sufﬁcient to store only the fourth digit as an iden-

tiﬁer, and release the other ﬁve for other purposes.

Although this analogy is rather extreme, Dumey ex-

plains that an examination of the item description may

reveal built-in redundancy which can be used to re-

duce memory usage.

It is important to note that the choice of Hash func-

tion is dependent on the application. Some applica-

tions are focused on maintaining data integrity (i.e

minimising the number of hashing collisions), while

others are focused on execution speed (Eitz and Lixu,

2007) (speed of data retrieval). As well as minimising

hashing collisions, another consideration is to provide

a technique that allows for an ease of data insertion

and removal, which is paramount when considering

dynamic data.

A hashing algorithm should be selected so that the

addresses are uniformly distributed (Teschner et al.,

2003). An optimal solution is to provide a per-

fect hashing function, which allows the retrieval of

data in a hash table with a single query (Jaeschke,

1981) (Sprugnoli, 1977). This would provide a hash

with no addressing collisions. Intuitively, this could

304

Buckley, L., Byrne, J. and Moloney, D.

Investigating the Use of Primes in Hashing for Volumetric Data.

DOI: 10.5220/0006797803040312

In Proceedings of the 4th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2018), pages 304-312

ISBN: 978-989-758-294-3

be achieved by providing a suitably large hash table.

However, this is not always practical as volumetric

data is often used in memory conﬁned situations, such

as for SLAM (Simultaneous Location And Mapping)

on mobile and robotic platforms using real-time sen-

sors (Klingensmith et al., 2015; K

ahler et al., 2015).

What is apparent however, is that 3D volumetric data

inherently possesses well distributed voxel addresses.

Referring to hashing functions mapping different

data to the same hash address, it has been stated

that “...such collisions cannot be avoided in prac-

tice” (K

ahler et al., 2015). It is true that collisions

cannot be completely avoided, but it is investigated in

this paper whether certain prime values can be chosen

to reduce/minimise the number of collisions.

This paper not only compares the use of different

prime values in 3D volumetric data, but also investi-

gates whether large primes are necessary at all. The

remainder of the paper is structured as follows:

• Section 2 - Related Work

• Section 3 - Hashing Parameters

• Section 4 - Tests administered

• Section 5 - Results

2 RELATED WORK

Anyone who attempts to generate

random numbers by deterministic

means is, of course, living in a state of

sin

John von Neumann

To understand why the use of primes in the hash-

ing of 3D data has persisted, an examination of the

most important classical hashing methods is required.

These methods are explored by Knuth (Knuth, 1998)

in much detail, some of which are described below:

2.1 Division Hashing Method

For certain scenarios, it was found that basic hashing

methods can provide adequate results by providing a

simple mapping for a memory limited map. The divi-

sion method is particularly simple (Knuth, 1998):

H(K) = K%M (1)

Where K is the identiﬁer of the data to be hashed

(or the Key), M is an arbitrary number and % is the

modulus operator. Knuth emphasises the importance

in choosing the value of M, and how this choice can

introduce bias into the results. For example, if M is

an even number, H(K) will be even when K is even,

and odd when K is odd, which would lead to substan-

tial bias. Taking this and further considerations into

account, he suggested choosing M to be a prime num-

ber such that r

6= ±(a%M), where k and a are small

numbers and r is the radix of the character set. Knuth

states that using these prime numbers “has been found

to be quite satisfactory in most cases”, but does not

provide results. Note that Knuth’s recommendation

of the use of primes relates only to the case speciﬁed

above.

2.2 Multi-identiﬁer Hashing Function

The Division Hashing Method above in Section 2.1,

while effective for simple scenarios, is only of use

for data with a single identiﬁer. For data with multi-

ple identiﬁers Knuth suggests utilising multiple inde-

pendent hash functions - one per identiﬁer - and then

combining the results in some way. This idea was

ﬁrst introduced by J. L. Carter and M. N. Wegman

and the equation is given below (Knuth, 1998; Carter

and Wegman, 1979):

H(K) = (h

) + h

) + ... + h

))%N (2)

where l is number of identiﬁers, h

is an indepen-

dent hash function, x

is an identiﬁer and N is the

number of addresses available. This function is espe-

cially efﬁcient when x

is a single character because

a LUT (look up table) can be utilised for h

, which

removes the need for multiplications.

2.3 XOR Hashing Function

Many implementations (Teschner et al., 2003) (Klin-

gensmith et al., 2015) (Niener et al., 2013) (Eitz and

Lixu, 2007)(K

ahler et al., 2015) (K

ahler et al., 2016)

utilise an XOR hashing function to index 3D volu-

metric data into a hash table. This hash address is

retrieved using Equation (3):

hash(x, y, z) = (P

∗ x ⊕ P

∗ y ⊕ P

∗ z)%N (3)

where ⊕ is the XOR operation, (P

, P

) are se-

lected prime values, x, y, z are the 3D coordinates of

the data in the volumetric structure that is to be stored

and N is the size of the hash table. None of (Teschner

et al., 2003) (Klingensmith et al., 2015) (Niener et al.,

2013) (Eitz and Lixu, 2007) (K

ahler et al., 2015) clar-

ify why large primes are utilised. It is not stipulated

in (K

ahler et al., 2016) that (P

, P

), or the “hash

coefﬁcients” be primes.

In the case of hashing for 3D volumetric data,

XOR hashing is the most commonly used, and is thus

examined in further detail.

Investigating the Use of Primes in Hashing for Volumetric Data

305

3 PARAMETERS IN XOR

HASHING

There are many parameters that inﬂuence the results

of the chosen hashing function. As discussed in sec-

tion 1, a “successful” hash function is dependent on

the application. For the purposes of this paper, the fo-

cus is on maintaining data integrity (minimising the

number of voxels that are not stored in the hash ta-

ble due to addressing collisions) while maintaining a

reasonable data footprint. Regardless of the hashing

function chosen, the following parameters can have

an impact on the results of the function.

3.1 Use of Primes

The use of primes is common in hashing func-

tions, with (Teschner et al., 2003) (Klingensmith

et al., 2015) (Niener et al., 2013) (Eitz and Lixu,

2007) (K

ahler et al., 2015) all using large primes.

Knuth (Knuth, 1998) afﬁrms that the ﬁrst mention

of using primes for hashing is by Dumey (Dumey,

1956) in 1956, where taking the remainder of divid-

ing by a prime is discussed as a method of map-

ping data to addresses in a hash table. Dumey

states: “ ...divide this number by a number

slightly less than the number of addressable locations

(the writer prefers the nearest prime)” indicating that

the choice to use primes is a personal preference.

Many factors must to be taken into considera-

tion when choosing constant/prime values in hashing

functions (Knuth, 1998). As discussed in Section 2.1,

Knuth found certain primes to be adequate when us-

ing the Division Hashing Method in Equation (1),

but does not provide a blanket endorsement for using

primes. Why the use of primes in hashing for 3D vol-

umetric data persists may be understood with the help

of a quote from John von Neumann: “Young man, in

mathematics you don’t understand things. You just

get used to them.”

3.2 Hash Table Size

The size of the hash table relates to how many hash

table addresses exist. The size of the hash table is of

importance for a number of reasons. As discussed in

Section 2.1, when the hash address is a modulus of

the hash table size, the choice of hash table size can

introduce biases. However, the focus of this paper is

to investigate the inﬂuence of using primes in hashing,

so the impact of altering the size of the hash table is

not investigated at present.

Figure 1: 4x4x4 voxel block.

3.3 Hash Table Entry Size

When H.P. Luhn ﬁrst suggested hashing, he stressed

the advantage of using hash table entries that store

more than one element, as this reduces the number

of external searches required to ﬁnd the correct en-

try (Knuth, 1998). The hash table entry size equates

to the number of voxels (and any other identifying

data) that can be stored in a single hash table en-

try. The blocks sizes used in other implementa-

tions vary, with some not disclosing the size (Mirtich,

1997) (Teschner et al., 2003), and others using sizes

of up to 512 voxels (8

) (K

ahler et al., 2016) (K

ahler

et al., 2015). This paper represents 64 voxels (4

) per

hash entry, this number is variable.

A reason for not wanting to represent a large num-

ber of voxels per hash entry is due to the sparse nature

of much 3D data - the Dublin City Dataset (Laefer

et al., 2015) was found to have an average occupancy

of 1.36% (98.74% sparse), but with a large distribu-

tion of voxels. This is similar to the typical 93% spar-

sity found in the scenes examined in (Klingensmith

et al., 2015). Representing 64 voxels per entry was

found to be adequate, as if noise is present in the form

of outliers, only a single entry would be allocated for

that noise. The larger the hash entry, the more mem-

ory will be allocated to noisy voxels.

These 64 voxels represent a 4

block, like the

one shown in Figure 1. When it is determined that

a voxel is occupied and must be added to the hash

table, it is ﬁrst determined which block it belongs

to. In a 64

voxel environment, there are 16

blocks. The identiﬁer of the block is taken as the

coordinates of the corner node of the block (i.e. the

red voxel in Figure 1), discretised with respect to the

size of the blocks. This is similar other implementa-

tions (Teschner et al., 2003) (Mirtich, 1997) (K

ahler

et al., 2015) and (K

ahler et al., 2016).

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

306

4 COMPARISON OF PRIME

VALUES FOR HASHING

To adequately determine whether large primes are

required to minimise addressing collisions, various

tests were administered on two datasets, the Stanford

Bunny (Turk and Levoy, 2005) and the Liffey Tile

from the Dublin City Dataset (Laefer et al., 2015).

Parameters for the Stanford Bunny and the Liffey tile

are shown in Table 1.

Further tests were then administered on larger, real

world datasets which are detailed in Appendix A.

Table 1: Parameters for the Stanford Bunny and the Dublin

City Dataset Liffey Tile.

Bunny Liffey Tile

Resolution 64

256

No occupied voxels 11070 234131

% Occupancy 4.2% 1.4%

Max x 63 255

Max y 62 255

Max z 49 153

Hash Table Size (No. Entries) 2040 128000

Hash Table Size (Bytes) 32kB 2MB

The following tests were carried out on the Stan-

ford Bunny and the Liffey Tile:

• Comparison of Prime Values for XOR Hashing

• Comparison of the Ordering of Prime Values for

XOR Hashing

• Comparison of Non Prime Values for XOR Hash-

ing

• Determination of the inﬂuence of the choice of

constant values on the distribution of addressing

collisions

Upon completion of the above tests, the following

were then administered on the larger, real world

datasets:

• Determination of whether “Optimum values” ex-

ist for XOR Hashing

The following actions/events occur when testing

various primes for XOR Hashing on the datasets pre-

viously mentioned:

• Insertion. Insertions into the Hash table are very

simple to perform. Once it is determined that a

voxel is occupied and should be inserted into the

hash table, the hash address of the voxel block

that the voxel belongs to is calculated using Equa-

tion 3. If an addressing collision does not occur,

the bit corresponding to that voxel in the hash en-

try is set to one. If an addressing collisions occurs

the voxel cannot be set. Dealing with collisions is

discussed below.

• Collisions. While (Teschner et al., 2003) dis-

cusses the problem of mapping different data to

the same hash address, and suggests increasing

how many voxels are represented in each hash

entry in an attempt to reduce collisions, it is not

discussed how to deal with these collisions when

they do occur. There are very simple methods in

use to deal with these collisions. (Niener et al.,

2013) deals with collisions through storing the

data to be inserted in the next available sequen-

tial entry. A.D Lin, inspired by Luhn’s early

work (Knuth, 1998), suggested a technique which

could accommodate collisions using “degenera-

tive addresses”. For example, if a collision occurs

in entry 2748, the voxels would be placed in en-

try 274, from which overﬂows would be placed in

entry 27 and so on.

This paper does not implement collision resolu-

tion, as the benchmarking of different prime val-

ues is concerned with the percentage of address-

ing collisions. Resolving these collisions intro-

duces additional overheads, so it is thus preferable

to invest effort into reducing the initial number of

collisions than to focus on accommodating these

collisions. If a collision occurs an attempt is not

made to accommodate the voxel which caused the

collision.

5 RESULTS

The results for the tests detailed in Section 4 are out-

lined below.

5.1 Comparison of Prime Values for

XOR Hashing

As discussed in section 3.1, many implementations

of hashing for 3D volumetric data, such as (Teschner

et al., 2003; Niener et al., 2013; Eitz and Lixu, 2007)

and (K

ahler et al., 2015) utilise speciﬁed large primes

to calculate the hashed address. However, none of the

aforementioned implementations provide evidence as

to why they utilised those large primes. ( (Klingen-

smith et al., 2015) does not specify the prime values,

but uses “arbitrary large primes”)

To determine why the primes in these implemen-

tations were chosen, various prime values were tested

for both the Stanford Bunny (Turk and Levoy, 2005)

and the Liffey Tile from the Dublin City Dataset (Lae-

fer et al., 2015) for XOR Hashing. All prime values

Investigating the Use of Primes in Hashing for Volumetric Data

307

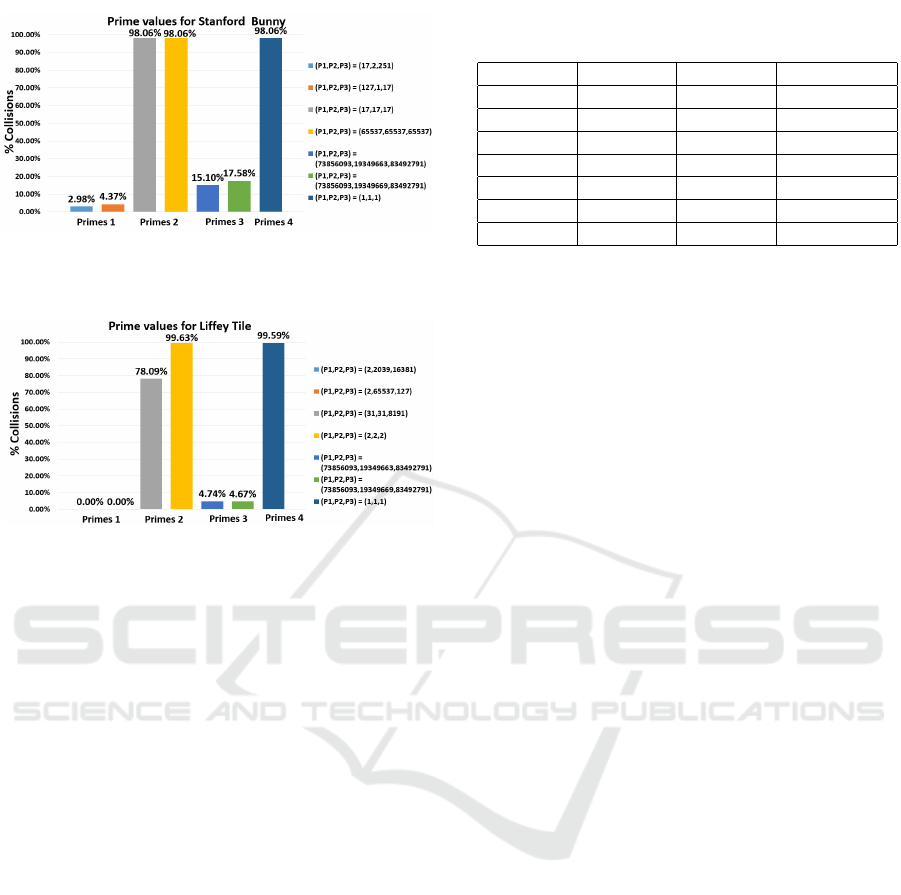
Figure 2: Comparison of Prime Values for the Stanford

Bunny.

Figure 3: Comparison of Prime Values for the Liffey Tile.

less than 83492791, the largest of the primes sug-

gested by (Teschner et al., 2003) were considered.

2040 and 128000 Hash Table Entries were used re-

spectively. These table sizes were chosen as they

equate to roughly half the total number of voxels in

each of these datasets.

A subset of the results obtained from testing vari-

ous primes for the Stanford Bunny and the Liffey Tile

are shown in Figures 2 and 3 respectively. These re-

sults were chosen to demonstrate how the choice of

primes can greatly inﬂuence the addressing collision

rate. The following combinations are displayed:

1. Prime combinations that produced the lowest ad-

dressing collision rates (Primes 1)

2. Prime combinations that produced the highest ad-

dressing collision rates (Primes 2)

3. Prime combinations used in (Teschner et al.,

2003; Eitz and Lixu, 2007; Niener et al., 2013)

and (K

ahler et al., 2015) (Primes 3)

4. All prime values set to one (Primes 4)

It was found that the primes used in (Teschner

et al., 2003) and (Eitz and Lixu, 2007), and those

used in (Niener et al., 2013) and (K

ahler et al.,

2015) achieved an addressing collision rate which was

higher than other combinations of primes. It was

found, as is evident from Figures 2 and 3, that many

combinations of primes provided the minimum num-

ber of addressing collisions, i.e. 0% for the Liffey

Table 2: Testing of various combinations of ordering of

primes on the Stanford Bunny.

Bunny

% Collisions

73856093 19349663 83492791 15.09

73856093 83492791 19349663 17.39

83492791 73856093 19349663 16.81

83492791 19349663 73856093 16.78

19349663 83492791 73856093 16.32

19349663 73856093 83492791 17.51

tile, and very low rates (2.98%) for the Bunny. While

these values are still primes, they are not all “large

primes” as stipulated in (Klingensmith et al., 2015).

These results indicate that “large primes” are not

required to achieve optimal results for XOR hashing

for volumetric data.

5.2 Comparison of the Ordering of

Prime Values for XOR Hashing

Another observation is that none of (Teschner et al.,

2003; Niener et al., 2013; Eitz and Lixu, 2007)

or (K

ahler et al., 2015) discuss the ordering of the

prime utilised, i.e. which of the primes are assigned

to (P

, P

) respectively.

To investigate whether varying the order of the

primes would impact the addressing collision rate,

the order of the primes from (Teschner et al., 2003)

and (Eitz and Lixu, 2007) were varied for the Stanford

Bunny. These results are shown below in Table 2.

While the collision rates did not vary greatly for

the primes used in Table 2, other prime values pro-

duced greater variance. Testing ordering combina-

tions of (P

, P

) = (2, 17, 127) for the Stanford

Bunny produced addressing collision rates of between

6.02% and 16.10%.

These results indicate that not only does the choice

of primes impact the addressing collision rate for

XOR Hashing, so too does the ordering of those

primes.

5.3 Comparison of Non Prime Values

for XOR Hashing

Upon the discovery in Section 5.2 that large primes

are not necessary to optimally hash 3D volumetric

data, it was investigated whether there is a need for

the “prime” values used in XOR Hashing to be primes

at all.

The same methodology as described in Section 5.2

was followed for this test - various non prime values

were used for (P

, P

) from equation 3 for XOR

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

308

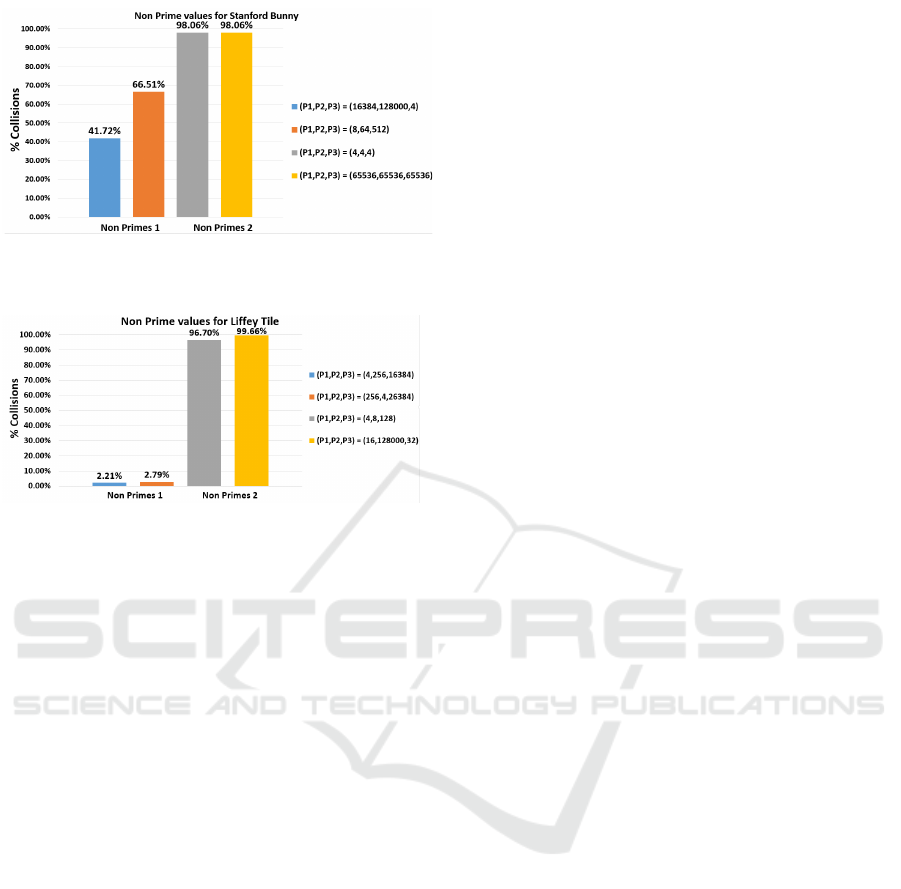
Figure 4: Comparing non prime values on the Stanford

Bunny.

Figure 5: Comparing non prime values on the Dublin City

Dataset Liffey Tile.

Hashing. These were again tested on the Stanford

Bunny (Turk and Levoy, 2005) and the Liffey Tile

from the Dublin City Dataset (Laefer et al., 2015). To

ensure that the values tested were not primes, powers

of 2 were used, up to 2

. A subset of these results

are shown in Figures 4 and 5. These results were cho-

sen to demonstrate how the choice of non primes can

greatly inﬂuence the addressing collision rate. The

following combinations are displayed:

1. Non Prime combinations that produced the lowest

addressing collision rates (Non Primes 1)

2. Prime combinations that produced the highest ad-

dressing collision rates (Non Primes 2)

Testing with non prime values for XOR Hashing

provided mixed results. While addressing collision

rates of < 3% were obtained using non prime values

for the Liffey Tile, the lowest rate obtained for the

Stanford Bunny was 41.72%.

While using non prime values for the Liffey Tile

did not produce addressing collision rates as low as

when using some prime combinations, it produced

better results than using (P

, P

) from (Teschner

et al., 2003; Eitz and Lixu, 2007), and (Niener et al.,

2013; K

ahler et al., 2015). However, non prime val-

ues for the Stanford Bunny did not produce address-

ing collision rates lower than when using (P

, P

)

from (Teschner et al., 2003; Eitz and Lixu, 2007),

and (Niener et al., 2013; K

ahler et al., 2015).

This indicates that while non prime values for

XOR Hashing can provide better results than using

primes for some datasets, one cannot deﬁnitely say

that using primes/non primes is favorable over using

the other.

5.4 Determination of the Inﬂuence of

the Choice of Constant Values on

the Distribution of Addressing

Collisions

The distribution of collisions could be of concern de-

pending on the application. For example, a large con-

centration of collisions in one place could lead to the

loss of say an entire object in an indoor environment

when using hashing for SLAM applications. This

could be problematic for an indoor robot scanning a

living room if collisions occurred for all the voxels

associated with a chair. However, if the collisions are

better distributed, only a number of addressing col-

lisions may occur from a few objects. It is therefore

important to determine if certain combinations of con-

stant values can provide well distributed addressing

collisions for a range of 3D volumetric data.

A visual representation for the collision rates us-

ing the constant values from Section 5.5 are shown

in Figures 6 and 7 for both the Stanford Bunny (Turk

and Levoy, 2005) and the Liffey Tile from the Dublin

City Dataset (Laefer et al., 2015). These ﬁgures indi-

cate the distribution of addressing collisions for both

models, and how these distributions can be inﬂuenced

by the constant values chosen for XOR Hashing. In

Figures 6 and 7 red voxels represent voxels that are

inserted into the hash table successfully. Blue voxels

represent where an addressing collision occurred and

thus the voxels could not be inserted.

What is apparent from these results is not only

does the choice of constants for (P

, P

) signiﬁ-

cantly impact the addressing collision rate of XOR

Hashing, it also impacts the distribution of collisions.

This is more apparent from Figure 6 than Figure 7

as the resolution is smaller (64

voxels v 256

). In

Figures 6a and 6b, the majority of collisions that oc-

cur are grouped together. However, in Figures 6c,

and 6d, while the percentage of addressing collisions

are lower, the collisions that do occur are for the most

part well distributed across the model.

However, one cannot draw deﬁnitive conclusions

from the distribution of collisions in Figure 6, as the

same is not necessarily true in Figure 7. Figure 7c

uses the same constants as in Figure 6c, but with a far

higher addressing collision rate (81.27% v 2.98%),

and thus cannot provide well distributed collisions for

Investigating the Use of Primes in Hashing for Volumetric Data

309

(a) (P

, P

) = (2, 128, 8292)

(b) (P

, P

) = (32, 128, 512)

, P

) = (17, 2, 251)

(d) (P

, P

) =

(73856093, 19349663, 83492791)

Figure 6: Comparing different combinations of constant

values for XOR Hashing on the Stanford Bunny (Turk and

Levoy, 2005).

(a) (P

, P

) =

(2, 128, 8292)

(b) (P

, P

) = (32, 128, 512)

, P

) = (17, 2, 251)

(d) (P

, P

) =

(73856093, 19349663, 83492791)

Figure 7: Comparing different combinations of constant

values for XOR Hashing on the Liffey Tile from the Dublin

City Dataset (Laefer et al., 2015).

the Liffey Tile in Figure 7c as the collision rate is so

high.

While the constants used in Figures 6d and 7d do

provide well distributed addressing collisions, there

are constant value combinations that provide a lower

addressing collision rate for the two models.

It is thus determined that while certain constant

value combinations provide well distributed address-

ing collisions for the two models tested, these val-

ues do not necessarily provide the lowest possible ad-

dressing collision rate.

Figure 8: Comparing different constant values for XOR

Hashing for the Stanford Bunny and the Liffey Tile from

the Dublin City Dataset.

5.5 Determination of Whether

“Optimum Values” Exist for XOR

Hashing

In Section 5.2 it was shown that large primes are

not necessary to minimise addressing collisions for

XOR hashing - smaller primes produced less address-

ing collisions than the large primes recommended

in (Teschner et al., 2003) and (Eitz and Lixu, 2007).

In Section 5.3 it was shown that for the Liffey Tile,

small, non prime values can produce far fewer ad-

dressing collisions for XOR hashing when compared

with the large primes recommended in (Teschner

et al., 2003), (Eitz and Lixu, 2007), (Niener et al.,

2013) and (K

ahler et al., 2015). However, this did

not hold true for the Stanford Bunny.

On the back of both of these ﬁndings, it was then

investigated whether one set of constant values for

, P

) in XOR Hashing can provide optimal re-

sults regardless of the 3D volumetric data being con-

sidered. All of (Teschner et al., 2003; Klingensmith

et al., 2015; Niener et al., 2013; Eitz and Lixu, 2007;

ahler et al., 2015) use large primes for XOR Hash-

ing for 3D volumetric data, but do not consider, in

detail, how the nature of the data could inﬂuence the

choice of constants, be they primes or not.

To determine whether a set of values could be used

in XOR hashing that would provide adequate results

for a diverse range of 3D volumetric data, various

combinations of primes and non primes were tested

for the Stanford Bunny (Turk and Levoy, 2005) and

the Liffey Tile of the Dublin City Dataset (Laefer

et al., 2015). The results are shown below in Figure 8.

These values were also tested on the whole Dublin

City Dataset (Laefer et al., 2015) and the New York

Dataset (of Commerce, 2014a), the results of which

are shown in Figures 9 and 10 respectively in the form

of a box-plot.

From Figure 8 it is clear that constant values

that provide a low addressing collision rate for one

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

310

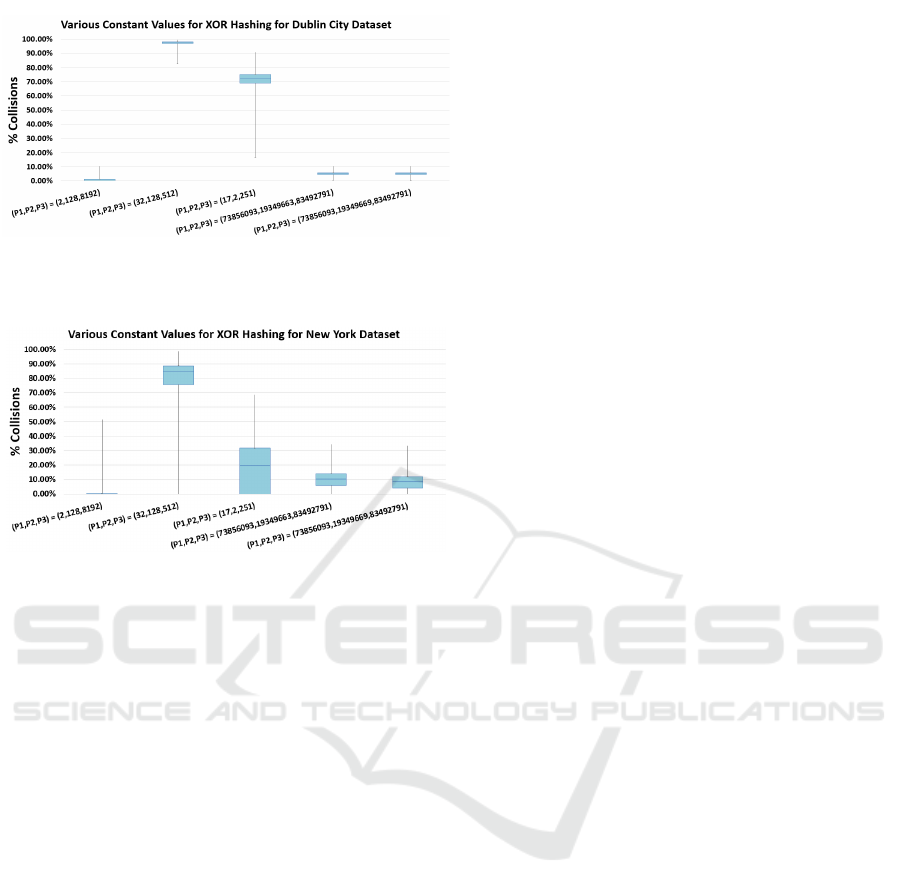
Figure 9: Comparing different constant values for XOR

Hashing for the Dublin City Dataset.

Figure 10: Comparing different constant values for XOR

Hashing for the New York City Dataset.

model do not guarantee a low collision rate for an-

other model. This is of importance as the distribution

of voxels in models being considered is not always

known before hashing.

Figures 9 and 10 indicate again that varying

constant values cannot be guaranteed to provide a

low addressing collision rate for a wide range of

datasets. The results for (P

, P

) = (2, 128, 8192)

and (P

, P

) = (73856093, 19349663, 83492791)

in both Figures 9 and 10 are statistically signiﬁcant as

there is no overlap between the distributions. These

results also indicate that the constant values recom-

mended in (Teschner et al., 2003; Eitz and Lixu, 2007;

Niener et al., 2013) and (K

ahler et al., 2015) do not al-

ways provide the lowest possible addressing collision

rate.

It was thus determined that there is no set of “op-

timum values” that can be used to optimally hash

a wide range of 3D volumetric datasets using XOR

Hashing, and it is unwise to advise the use of certain

values over others without prior knowledge of the data

to be hashed.

6 CONCLUSION

The following have been determined regarding the

use of primes for the hashing of 3D volumetric data

through the research conducted as part of this paper:

• Primes (large or otherwise) are not required in

XOR Hashing for optimal results - non primes can

provide equal and at times better addressing colli-

sion rates.

• The ordering of primes in XOR Hashing impacts

the addressing collision rate.

• When primes are used in XOR hashing, larger

primes do not necessarily produce optimal results.

More speciﬁcally, the primes used in (Teschner

et al., 2003; Klingensmith et al., 2015; Niener

et al., 2013; Eitz and Lixu, 2007) and (K

ahler

et al., 2015) do not necessarily produce optimal

results.

• The choice of constant values in XOR Hashing in-

ﬂuences the distribution of addressing collisions.

However, the constants that provide the highest

distribution of addressing collisions do not neces-

sarily provide the lowest percentage of addressing

collisions.

• No one set of values, primes or otherwise, for

XOR Hashing can be considered to provide op-

timal results due to the variance that exists across

different 3D volumetric datasets.

Given the results above, it is the view of the au-

thors of this paper that XOR hashing is not the op-

timal method to hash 3D volumetric data due to the

variance that exists with 3D volumetric data, more

speciﬁcally with dynamic 3D volumetric data. This

is due to the need to predeﬁne values for (P

, P

at times without any prior knowledge of the distribu-

tion of the voxels in the data that needs to be hashed.

A dynamic method, that could adapt to the distribu-

tion of voxels within models would provide more pre-

dictability while hashing 3D volumetric data.

REFERENCES

Carter, J. L. and Wegman, M. N. (1979). Universal classes

of hash functions. Journal of computer and system

sciences, 18(2):143–154.

Dumey, A. I. (1956). Indexing for rapid random ac-

cess memory systems. Computers and Automation,

5(12):6–9.

Eitz, M. and Lixu, G. (2007). Hierarchical spatial hashing

for real-time collision detection. In Shape Modeling

and Applications, 2007. SMI’07. IEEE International

Conference on, pages 61–70. IEEE.

Investigating the Use of Primes in Hashing for Volumetric Data

311

Good, I. J. (1950). Probability and the weighing of evi-

dence.

Jaeschke, G. (1981). Reciprocal hashing: A method for

generating minimal perfect hashing functions. Com-

munications of the ACM, 24(12):829–833.

ahler, O., Prisacariu, V., Valentin, J., and Murray, D.

(2016). Hierarchical voxel block hashing for efﬁcient

integration of depth images. IEEE Robotics and Au-

tomation Letters, 1(1):192–197.

ahler, O., Prisacariu, V. A., Ren, C. Y., Sun, X., Torr, P.,

and Murray, D. (2015). Very high frame rate vol-

umetric integration of depth images on mobile de-

vices. IEEE transactions on visualization and com-

puter graphics, 21(11):1241–1250.

Klingensmith, M., Dryanovski, I., Srinivasa, S., and Xiao,

J. (2015). Chisel: Real time large scale 3d reconstruc-

tion onboard a mobile device using spatially hashed

signed distance ﬁelds. Robotics: Science and Systems

XI.

Knott, G. D. (1975). Hashing functions. The Computer

Journal, 18(3):265–278.

Knuth, D. E. (1998). The art of computer programming:

sorting and searching, volume 3. Pearson Education.

Laefer, D. F., Abuwarda, S., Vo, A.-V., Truong-Hong, L.,

and Gharib, H. (2015). 2015 aerial laser and pho-

togrammetry survey of dublin city collection record.

Laefer, D. F., Abuwarda, S., Vo, A.-V., Truong-Hong, L.,

and Gharibi, H. (2017). Dublin als2015 lidar license

(cc-by 4.0). https://geo.nyu.edu/catalog.

Mirtich, B. (1997). Efﬁcient algorithms for two-phase colli-

sion detection. Practical motion planning in robotics:

current approaches and future directions, pages 203–

223.

Niener, M., Zollhfer, M., Izadi, S., and Stamminger, M.

(2013). Real-time 3d reconstruction at scale us-

ing voxel hashing. ACM Transactions on Graphics,

32(6):111.

of Commerce, U. D. (2014a). 2013-2014 u.s. geo-

logical survey cmgp lidar: Post sandy (new york

city). https://data.noaa.gov/dataset/dataset/2014-u-s-

geological-survey-cmgp-lidar-post-sandy-new-jersey.

Accessed: 2017-10-05.

of Commerce, U. D. (2014b). Post sandy lidar survey li-

cense. https://data.noaa.gov/dataset/dataset/2014-u-s-

geological-survey-cmgp-lidar-post-sandy-new-jersey.

Accessed: 2017-10-19.

Sprugnoli, R. (1977). Perfect hashing functions: a single

probe retrieving method for static sets. Communica-

tions of the ACM, 20(11):841–850.

Teschner, M., Heidelberger, B., Mller, M., Pomeranets, D.,

and Gross, M. (2003). Optimized spatial hashing for

collision detection of deformable objects. 3.

Turk, G. and Levoy, M. (2005). The stanford bunny.

APPENDIX

A DATASETS

The following datasets were examined in the com-

parison of various hashing techniques as described

in Section 4. The datasets include small scale syn-

thetic models and publicly available large scale Li-

DAR datasets. The large scale models present a real-

istic representation of what would be processed by an

embedded system in the real world, except on a much

larger scale.

• Stanford Bunny. The Stanford Bunny is a widely

used 3D test model developed by Greg Turk and

Marc Levoy in 1994 at Stanford University (Turk

and Levoy, 2005).

• Dublin City Dataset. The Dublin City Dataset is

a collection of LiDAR scans of Dublin City (Lae-

fer et al., 2015; Laefer et al., 2017).The scans are

separated into tiles. Each of these tiles are 256

voxels, 100m on a side. The average occupancy

of the Dublin City Dataset is 1.36%.

• Liffey Tile from The Dublin City Dataset. This

tile was used in some tests. It was chosen as it

is representative of the other tiles in the dataset,

and is named the Liffey Tile as it shows the Liffey

river ﬂowing under the iconic O’Connell Bridge

in Dublin’s city centre.

• New York Dataset. The New York Dataset refers

to the 2014 U.S. Geological Survey CMGP Li-

DAR: Post Sandy (New Jersey) (of Commerce,

2014a; of Commerce, 2014b). This dataset is also

a collection of Lidar scans of New York and New

Jersey. Each of these tiles are 64

voxels, 100m

on a side, equating to 10, 000m

. The average oc-

cupancy of the New York Dataset is 2.64%.

GISTAM 2018 - 4th International Conference on Geographical Information Systems Theory, Applications and Management

312