
Proposed Solutions to the Tripper Car Positioning Problem
Felipe Novaes Caldas
1
and Alexandre Xavier Martins
2
1
Gerência de Automação, Vale, São Gonçalo do Rio Abaixo, MG, Brazil
2
Instituto de Ciências Exatas e Aplicadas, Universidade Federal de Ouro Preto, João Monlevade, MG, Brazil
Keywords:
Tripper Car, Combinatorial Optimization, Dynamic Programming.
Abstract:
The trippers are equipments often found in mineral processing plants. Their role is to distribute ore coming
from past stages of process in a silo with several hoppers. Positioning trippers is a scheduling problem defined
by position determination of the equipment through the bins and along time. The system silo-tripper was
modeled as a combinatorial linear optimization program aiming to get the optimal tripper positioning. Two
paradigms were used to find out an exact solution: mixed integer linear programming and dynamic program-
ming.
1 INTRODUCTION
Storage silos are structures designed to store bulk so-
lid materials. Its function is to form an intermediary
stock between two stages of the mineral processing
cycle. Conveyor belts fulfill the role of bringing the
ore from an earlier stage and storing it there. After-
wards, this material is removed by equipments called
feeders, located right below each one of these cham-
bers, proceeding with the mineral processing task
(Wills and Napier-Munn, 2015). The number of fee-
ders required in an intermediate storage silo design is
proportional to the ore volume that will be handled.
In this way, a silo must be subdivided into smaller
chambers, according to the number of feeders requi-
red, providing an individualized area for the installa-
tion of each one of these equipments under the struc-
ture of the storage silo (Gupta and Yan, 2006). The
vertical pillars that are observed along the lower struc-
ture of the building, as shown in Figure 1, indicate the
approximated location of the subdivisions. The area
defined by two pillars and filled by a concrete wall is
the region where a chamber or bin of the silo is defi-
ned. In this example, there are sixteen subdivisions.
In the right side of the image, there is a structure that
projects over the front wall of the silo, it is called a
conveyor belt. Its role is to carry ore coming from an
earlier stage of the process to the storage silo.
A tripper is a car designed to distribute ore along
the top opening of a storage silo (Wills and Napier-
Munn, 2015). This equipment is constituted by a mo-
bile metallic structure that physically supports a dis-
Figure 1: Example of storage silo from Brucutu mine –
Vale.
charge point of the conveyor belt. The car is driven by
steel wheels located under its structure. Metallic rails
support and guide the tripper longitudinally along the
silo, allowing the ore carried by the conveyor belt to
be conveniently distributed between all subdivisions
(Swinderman, 2014).
An example of tripper can be seen in Figure 2.
This equipment is located over the silo SL-133A-
9101 at the processing plant from Brucutu mine. This
site is an asset belonging to Vale mining company.
The conveyor belt can be seen at the bottom left of
the figure and runs all over the top of the storage silo.
Its location is identified by the roller frame structures
mounted along its side. The silo opening is shown
below the conveyor belt and behind the guardrail, the
ore is deposited in this region. The tripper is seen in
the central area of the figure, over the conveyor belt.
The discharge point extends from the top of the equip-
ment and continues until reach the silo opening. One
344
Novaes Caldas, F. and Xavier Martins, A.
Proposed Solutions to the Tripper Car Positioning Problem.
DOI: 10.5220/0006806303440352
In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), pages 344-352
ISBN: 978-989-758-298-1
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

of the car rails is located to the right of the guardrail,
it is supporting the tripper front right wheels.
Figure 2: Example of tripper car from Brucutu mine – Vale.
The flowchart shown in Figure 3 provides an il-
lustrative example of a bulk mineral processing. The
system’s feed flow comes from a conveyor belt. The
tripper has the role of distributing this material along
the upper opening of the storage silo. The ore is wit-
hdraw by feeders and directed to sieves. In this stage,
the material is split according to its granulometry, one
part returning to the previous process as by-product 1
and another part proceeds further as by-product 2.
The tripper car movement is controlled by au-
tomation systems. Electric motors attached to the
equipment wheels are driven by this systems (Boyer,
2010) in such way it is possible to position the equip-
ment, defining which silo’s bin will receive the ma-
terial loaded by the conveyor belt. Three actions are
possible through the automation operation interface:
move to the right, move to the left, and halt. The ore
flow isn’t interrupted during the moving process.
Model-based predictive control (MPC) systems
are a class of controllers that define their control
action outputs based on future predictions of the pro-
cess states. These predictions are performed by dyna-
mic models that represent the behavior of the system
over time, inside a finite time frame. As an optimizer,
the MPC algorithm uses these informations to build
an optimal control output aiming a desired behavior
for the process. Only the present action of the entire
output forecast window is sent to the plant at each
iteration. In the next run cycle, the entire window
is recalculated and the new control action is formed
(García et al., 1989; Camacho and Bordons, 2007).
This first version of MPC was not able to handle
discrete variables, restricting its application to conti-
nuous process. As an evolution of the initial proposal,
the algorithm was expanded to consider discrete vari-
ables, logics and rules, in addition to the continuous
variables that were already considered in the first ver-
sion. This expanded form is known as hybrid MPC
(Bemporad and Giorgetti, 2006; Borrelli et al., 2005).
This controller is suitable to deal with the problem of
tripper positioning since this process has both conti-
nuous (level, mass flow) and discrete (position) vari-
ables. A framework based on hybrid MPC was used
by (Karelovic et al., 2015) to solve the tripper positi-
oning problem. The criteria used by the authors to set
up the controller objectives were bins level stabiliza-
tion and minimization of the car movement.
The purpose of this work is to develop a solution
to the tripper positioning problem based directly on
mixed integer linear programming. In this case, the
objective of the control system is to minimize the va-
riations of bins levels, ensuring that these variables
remain stable regarding the process constraints. Fi-
nally, a dynamic programming algorithm is proposed
aiming the reduction of the time required to find the
solution of the optimization problem.
2 DEVELOPMENT
The development of the mathematical models that
describe the behavior of the silo-tripper system is the
starting point for the study of the solutions to the pro-
blem of car positioning. The features of the optimi-
zation model, such as instance input data, decision
variables, constraints and objective function, are des-
cribed in detail. This formulation will be solved later
by means of mixed integer linear programming and
dynamic programming.
2.1 Mathematical Model
The Figure 4 presents the moving possibilities of a
n-bins silo. At any position, the equipment can only
move to one of the adjacent places or remain in the
same position over which it is located. For example,
if it’s in p
2
position then the movement options will
be {p
1
, p
2
, p
3
}. Moving the car to a position not ad-
jacent to the current one implies crossing all the in-
termediate positions between the points of departure
and destination. Consequently, tripper directs the ore
flow to the bin whose position is overlapped by cur-
rent equipment displacement. The choice of feeding
position is a task with temporal dependence since the
movement speed of the equipment is finite.
There is a risk that the material may eventually
lacks in one of the bins since tripper may only be in
a particular place at any time. This may occur even
in situations where the mass balance of the system
is balanced, that is, the total mass flow fed is equal to
the total withdrawn. To work around this problem, the
tripper must be moved along the bins openings so that
Proposed Solutions to the Tripper Car Positioning Problem
345
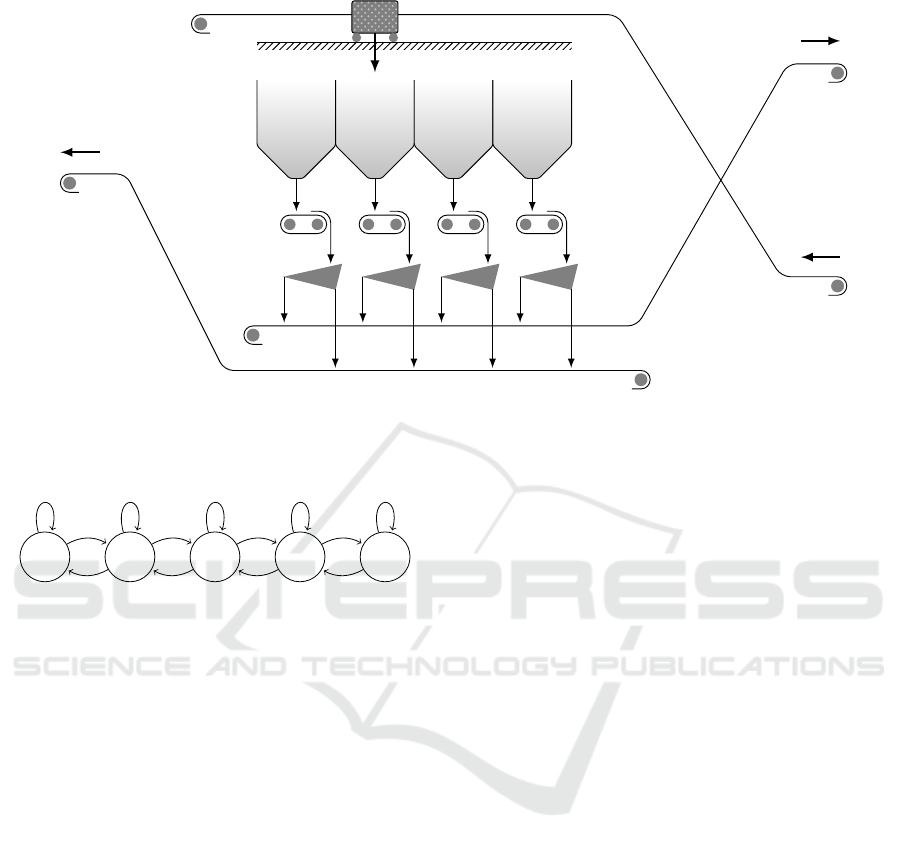
tripper
feed
by-product 1
by-product 2
Figure 3: Diagram illustrating a granular ore sifting process. The tripper is represented by a dotted rectangle with two wheels
indicated as small circles. A four-bin silo is shown under the tripper. Below each bin there is a belt feeder. The sieves are
represented by gray triangles. Conveyor belts are signaled by the ore flow they carry: feed, by-product 1 and by-product 2.
p
1
p
2
p
3
. . .
p
n
Figure 4: State machine representing the possibilities of
tripper positioning.
the material addition by the conveyor belt does not
allow any lack of ore. It is also needed to limit the bins
levels according to the maximum capacity restrictions
of the silo.
The time required for the tripper to travel through
the region corresponding to the opening of a bin, mo-
ving uninterruptedly, is proportional to the length of
the traveled region and inversely proportional to the
moving speed of the car. In order to simplify the mo-
del, the time elapsed by tripper to cross a whole bin
is considered constant in any situation in which the
silo subdivisions have the same size and the tripper
has constant speed. The forecast time window, over
which the prediction will be performed, is divided
into multiples of this minimum time. The size of this
window defines the first dimension of the positioning
problem model.
The second problem dimension is defined by the
set P of feasible positions for the tripper, whose num-
ber of elements corresponds to the number of bins.
The positioning scheduling is defined as the choice
of a sequence of car movement actions along a finite
window of future time. The purpose of these acti-
ons is to keep the variables controlled within the ope-
rational constraints established for the problem. The
future time window is mapped to a finite set T , com-
posed of the current state of the system added by t − 1
future steps. These extra iterations are necessary to
make the model able to predict in advance the out-
come of the control actions that will be taken over
time, verifying if the established constraints will be
violated at some point.
The Figure 5 shows a graph of the model, deve-
loped to represent a tripper positioning problem. The
initial positions, relative to the time t
1
, are contained
in the set {p
1i
∈ N | 1 ≤ i ≤ n}, being n the num-
ber of bins. From any initial position, the subsequent
positions are chosen at each iteration, regarding the
movement constraints over which the possible positi-
ons are limited the current position and adjacent ones.
Finally, the possible positions in the final step t
t
are
contained in the set {p
ti
∈ N | 1 ≤ i ≤ n}.
Therefore, the parameters defining the size of an
instance are:
• Number of bins: n;
• Prediction window size: t.
2.1.1 Instance Parameters
The instance parameters are presented in the Table 1.
In this work, the input rates q and output set Q are de-
fined as constants throughout all steps. However, this
parameters may be easily transformed to have multi-
ple different values through time.
The instance size is defined by the sets T periods
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
346

p
11
p
12
. . .
p
1n
p
21
p
22
. . .
p
2n
p
21
p
22
. . .
p
2n
. . .
. . .
. . .
. . .
p
t1
p
t2
. . .
p
tn
Figure 5: Graph representing the positioning possibilities of
a tripper throughout iterations.
of time and P bins. The initial level of each one of
the bins is defined by the vector L
1
. The levels values
are constrained between l
min
and l
max
. The starting
position of the tripper car is defined by p. The silo
emptying rate is defined as K. This parameter defines
the amount of ore that each one of the bins is capable
of storing according to the dynamic equation of the
process.
2.1.2 Decision Variables
The decision variables are presented in the Table 2.
The most important of them is the matrix I that repre-
sents the tripper positions through time. It is a set of
binary values that defines the car positioning over n
possible positions along t steps (Wolsey, 1998).
The states of the P bins levels along the T iterati-
ons are defined by L. The matrices A and B represent
slack variables for bins levels. The Z set represents
the auxiliary variables for the MinMax cost function.
Table 1: Instance parameters.
Parameter Description
T Periods set
P Bins set
n Number of bins
t Number of periods
L
1
Inicial level
l
max
Maximum level
l
min
Minimum level
q Input mass flow
Q Output mass flow
K Bins level coefficient
p Initial position
Table 2: Decision variables.
Variable Description
I Tripper positions
A Low level slack
B High level slack
L Levels
Z MinMax auxiliary
2.1.3 Constraints
The dynamic equation that defines the level of a bin i
along time is shown by Equation 1 (Pal et al., 2014):
L
i
= K
i
Z
(Q
t
− Q
i
)dt (1)
Being L
i
the level of some bin, K
i
the bin volume coef-
ficient and Q
t
the mass flow of the tripper and Q
i
of
an individual feeder.
The Equation 13 defines the mass accumulation at
each period of time based on Equation 1, adding the
slack variable components. At each step, the bin loca-
ted under the current tripper position is increased by
the mass flow input q. The initial level is defined by
Equation 8. This constraint represents the available
ore mass in the bin at first period of time.
If the Equation 1 is not balanced, for example, the
input mass rate is different from the mass output rate,
the bin may empty or fill up completely occasionally
in any of the solution steps. Two slack variables sets
A and B have been added to ensure that the problem
becomes feasible with any instance parameters. The
first handle bin level below l
min
, as defined in Equati-
ons 11 and 12, and the second handle bin level above
l
max
, as shown by Equations 9 and 10.
The tripper starting position is defined by parame-
ter p in Equation 7. The Equation 3 determines that
the car may be only on a single bin at each iteration.
The moving rules along the periods of time are defi-
ned by the Equation 4. It defines that the car posi-
tion in a given iteration is only feasible if the tripper
is kept at the same place or moves to a immediately
adjacent position. The Equations 5 and 6 determine
the moving rules if the equipment is in the first or last
position over the silo.
Proposed Solutions to the Tripper Car Positioning Problem
347

Z
j
≤ L
i, j
, ∀ j ∈ T, i ∈ P (2)
∑
i∈P
I
i j
= 1, ∀ j ∈ T (3)
I
i, j
≤ I
i−1, j−1
+ I
i,i−1
+ I
i+1, j−1
, (4)
∀ i ∈ [2, n − 1], j ∈ [2, t]
I
1, j
≤ I
1, j−1
+ I
2, j−1
, ∀ j ∈ [2,t] (5)
I
n, j
≤ I
n, j−1
+ I
n−1, j−1
, ∀ j ∈ [2,t] (6)
I
p,1
= p (7)
L
i,1
= L
1
, ∀ i ∈ T (8)
A
i, j
= ∆A
i, j
+ A
i−1, j
, ∀ i ∈ P, j ∈ T (9)
∆A
i,1
= 0, ∀ i ∈ V (10)
B
i, j
= ∆B
i, j
+ B
i−1, j
, ∀ i ∈ P, j ∈ T (11)
∆B
i,1
= 0, ∀ i ∈ V (12)
L
i, j+1
= L
i, j
+ K
i
(q · I
i, j
− Q
i
) + ∆A
i, j+1
(13)
− ∆B
i, j+1
, ∀ i ∈ P, j ∈ [1,t − 1]
L
i, j
≤ l
max
, ∀ i ∈ P, j ∈ T (14)
L
i, j
≥ l
min
, ∀ i ∈ P, j ∈ T (15)
2.1.4 Objective Function
The objective function is based on the principle Min-
Max (Rich and Knight, 1991). Its purpose is to max-
imize the lowest level value between all bins at each
period, not allowing ore to lack in any bin at no time.
The Z set, as shown by Equation 2, is defined as the
lowest value of the bins levels reached on each step.
The solution is found by maximizing the result of Z
set summation. The cost function for the problem can
be seen in Equation 16:
Maximize
∑
j∈T
Z
j
−
∑
i∈P, j∈T
A
i j
−
∑
i∈P, j∈T
B
i j
(16)
s.t. Z
j
≤ L
i, j
, ∀ j ∈ T, i ∈ P
2.2 Mixed Integer Linear Programming
The mixed integer linear programming is a mathema-
tical method whose purpose is to find the best solution
for a cost function within a set of constraints defined
by linear relations. The variables handled by this for-
mulation can be represented as either continuous or
integer values(Papadimitriou and Steiglitz, 1998).
Two solvers are used to deal with the proposed
model for the tripper positioning problem. The first
one is the Glpk (GNU Linear Programming Kit). The
second choice is IBM’s Cplex Optimizer. The ob-
jective is to compare between the outcome of an open
source solver relative to one proprietary system in
task of solving the optimization problem.
2.3 Dynamic Programming
Dynamic programming is a paradigm of computer
science characterized by find the solution of a com-
plex problem by solving its smaller subproblems.
Each subproblem is solved only once and the result
is stored in a table to be query later when needed, rat-
her than recursively computing it whenever necessary
(Levitin, 2012; Cormen et al., 2001).
The subproblems of the positioning problem are
defined as the solution of the this problem in each
one of the intermediate steps. This procedure starts
at the first iteration goes through incrementally until
reach the last period. Two tables were created to store
the partial result of the subproblems: the first handle
cost values and the second handles positions history.
These tables are identified as Table and P in the Algo-
rithm 1. The variables referenced by this pseudocode
are listed in Tables 1 and 2.
The algorithm first step is to update the bins le-
vels L according to the dynamic model of the process
(lines 2 and 3). In the next step, the value of the cost
function c is updated with the lowest level value in the
current iteration (line 4). The variable Table is upda-
ted if there is no cost value related to the current step
recorded in Table or if the current cost is greater than
or equal to the already stored value, then recursion is
continued (line 6). Otherwise, if the current cost is
less than the recorded cost, the function returns im-
mediately. The best possible solution is stored in the
global variable Best in the last step of the tripper po-
sitioning procedure (lines 12 and 14).
Algorithm 1: Dynamic Programming.
1: function SEARCHMAXIMUM(c, L, Q, q, P, p, s)
2: L[p] ← L[p] + q
3: L ← L − Q
4: c ← c + min(L)
5: if Table[s] =
/
0 or c ≥ Table[s] then
6: Table[s] ← c
7: P[s] ← p
8: if s 6= t then
9: for i ← max(1, p − 1) to min(n, p + 1) do
10: SearchMaximum(c, L, Q, q, i,P, s + 1)
11: end for
12: else
13: if Table[t] < c then
14: Best ← P
15: end if
16: end if
17: end if
18: end function
The Figure 6 gives an example of the execution of
the proposed algorithm for instance of three bin silo
and four units time window. Each one of figures, ran-
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
348
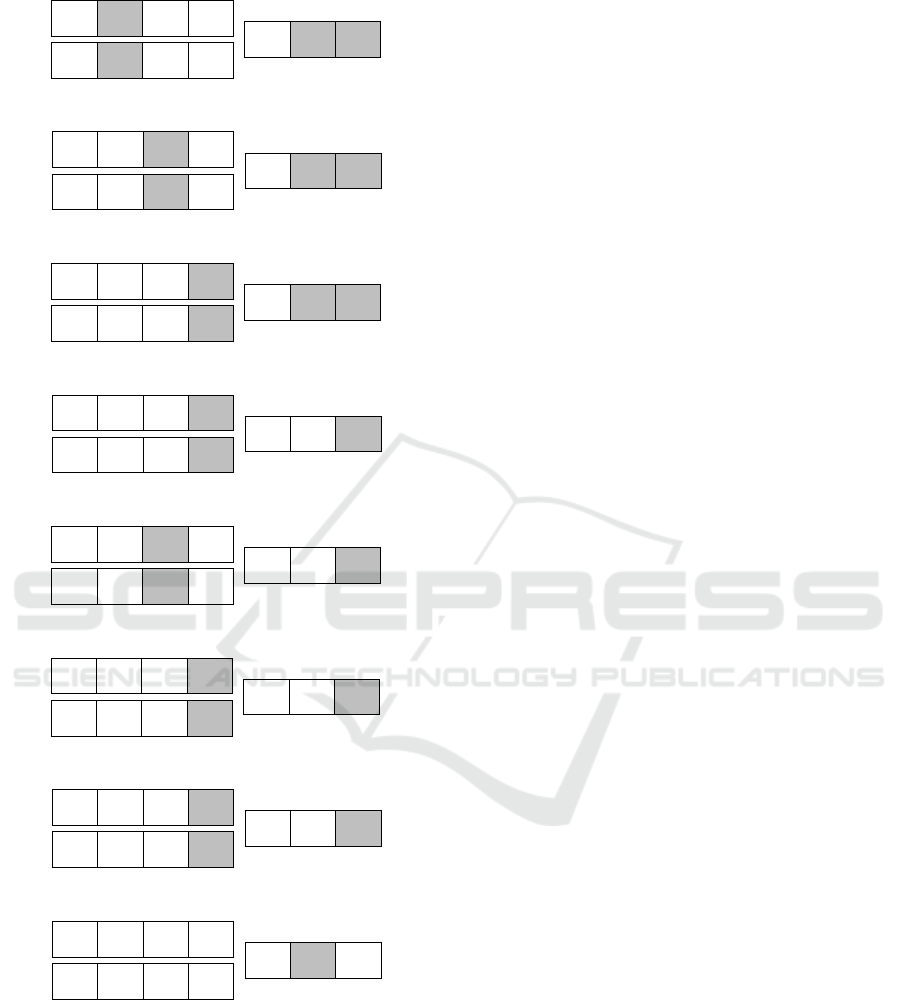
(a)
I
50 99
1 1
1 2 3 4
H
52 49 49
1 2 3
(b)
I
50 99 147
1 1 1
1 2 3 4
H
54 48 48
1 2 3
(c)
I
50 99 147 194
1 1 1 1
1 2 3 4
H
56 47 47
1 2 3
X
(d)
H
50 99 147 194
1 1 1 2
1 2 3 4
I
53 49 47
1 2 3
(e)
J
50 99 147 194
1 1 2 2
1 2 3 4
H
51 50 48
1 2 3
(f)
I
50 99 147 194
1 1 2 1
1 2 3 4
J
53 49 47
1 2 3
(g)
H
50 99 147 194
1 1 2 2
1 2 3 4
I
50 52 47
1 2 3
(h)
H
50 99 147 194
1 1 2 2
1 2 3 4
I
50 49 50
1 2 3
Figure 6: Example of eight iterations of dynamic program-
ming algorithm for a silo with three bins.
ging from 5(a) to 5(h), represents one of the algorithm
steps. The two tables on the left side of any subfigure
represent Table and P, respectively. The arrow over
them indicates the current period of time and the re-
cursion direction. The left-sided arrow means that the
algorithm execution is returning to a previous step, a
right-arrow indicates that the execution is advancing
to the next step and, finally, the down arrow shows
that the position is at the same place as it were in last
iteration. A gray filling color in a cell indicates an
update in its value. The table on the right side of a
subfigure represents the current bins levels. An upper
arrow indicates the position and direction of the trip-
per movement. Minimum levels in each period are
indicated by a gray color filling the respective cells.
The first step of execution is shown by Figure 5(a).
The three bins are initialized with 50% level value, the
tripper feed flow rate is set with 3 and the three feeders
flow rate with 1. The first action of the car is to remain
at the bin 1. The levels are decremented by one unit
and the bin 1 level is added by 3 units. The bins with
the lowest level value are 2 and 3, they are colored
with gray. The current step cost is the initial cost 50
from the past step added by the minimum step level
value 49, which is the lowest level value. The new
partial cost for this step is 99. This value is stored in
the table along with the position of the car.
This procedure is repeated until there are no new
additions to the table or until the execution of the al-
gorithm reaches the maximum limit of steps t. In this
case, the current solution becomes the new best if its
cost is higher than the cost of the previous best solu-
tion already found so far. A check mark label X is
added to a subfigure indicating that a new best solu-
tion was found, as shown in Figure 5(c).
3 RESULTS
Three tests are presented in this section. The first one
is a comparison between the control proposal by level
stabilization and minimization of the car movement,
as indicated by (Karelovic et al., 2015), and the algo-
rithm proposed in this work for the positioning pro-
blem. The second test is done over a silo with imba-
lanced flow rates, the purpose is to verify the proposed
model response in this scenario. The last test compa-
res the performance of the Cplex and Glpk resolvers
with respect to the dynamic programming algorithm.
The computational tests were performed over an Intel
Core i5 4570 machine with 16GB of DDR3 memory.
The first test was performed over a three-bin silo
instance. The initial levels values were defined as
L = {90, 50, 10}, the feeder flow rates Q = {3, 1, 2},
the tripper feeding flow rate was q = 6 and the starting
position, p = 1. The objective is to compare the two
proposals of silo level control. The stabilization stra-
tegy was adjusted in way to keep bins levels within an
acceptable range of 20% ≤ L ≤ 80%.
Proposed Solutions to the Tripper Car Positioning Problem
349

p
1
t
1
p
2
S
p
3
p
4
t
2
t
3
t
4
t
5
t
6
t
7
t
8
t
9
t
10
t
11
t
12
t
13
t
14
t
15
t
16
t
17
t
18
t
19
t
20
Figure 7: Positioning schedule for a tripper car. This instance is composed by a 4-bin silo with a time window of 20 periods.
The white letter S indicates the starting position.
The Figure 8 shows the test results. The upper
chart shows the behavior of the bins levels values over
time in response to the actions taken by tripper to
maximize the lowest bin level in each iteration. In
this case, after approximately 20 time periods, the le-
vels stabilize within a value range ranging from 40%
to 60%. The test of movement minimization strategy,
as seen in the lower chart of Figure 8, could kept the
bins levels within the requested value range of 20%
and 80%. In this case, the number of car movement
were much smaller than in the first strategy, as indi-
cated by the small amount of reversions in the rate of
variation of the levels values.
The test was done considering an instance with
unbalanced loads. The system was set up as a 4-bins
silo, where feed output flow rates were {Q
i
= 4, ∀ i ∈
P} and input flow rate q = 16, the initial levels were
defined as L = {50, 60, 30, 60}. In this case, there is
a real possibility of material lacking in some of the
bins if the tripper positioning scheduling is done in-
correctly. Figure 7 shows the resulting positioning for
this instance. The white letter S indicates the start
position p = 3. The car is positioned through the 20
10 20 30 40 50 60
0
20
40
60
80
100
level (%)
bin 1 bin 2
bin 3
10 20 30 40 50 60
0
20
40
60
80
100
periods (t)
level (%)
bin 1 bin 2 bin 3
Figure 8: Comparative tests between the strategies of mo-
vement minimization (top chart) and maximization of the
lowest level at each iteration (bottom chart).
periods in all possible positions in order to maximize
the minimum levels at each period over time.
The imbalance between input and output flow
rates implies in decline of the bins average levels
through time as shown by Figure 9. The initial and
final average levels were 50 and 31 confirming the
expected behavior. However, the initial standard de-
viation of bins levels was 14.1 against the final value
of 6.6, that is, not only the minimum levels were kept
at higher values but their variabilities was also decre-
ased.
2.5 5 7.5 10 12.5 15 17.5 20
0
10
20
30
40
50
60
70
periods(t)
level (%)
bin 1 bin 2 bin 3 bin 4
Figure 9: Results of a test with a 4-bin silo instance in a 20
periods time window.
The purpose of the third set of tests is to compare
the performance of the solvers and the dynamic pro-
gramming algorithm. The tests were done in a silo
instance with n ∈ {3, 5,9, 16} bins and with a fore-
cast window of t time periods. These parameters were
varied exhaustively within a time range of 1000 se-
conds, to verify the response time of the solvers. The
parameters of flow rates chosen for the feeders were
{Q
i
= 1, ∀i ∈ P}, the feed flow rate of the tripper was
q = n and the starting position was p = 1. It is ex-
pected that the time elapsed to solve an instance is
proportional to the number of bins n. This variable
represents one of the problem sizes, along to the time
periods t, and its increase is directly related to an in-
crease of the problem complexity.
The Figure 10 displays the tests results. The dyn-
amic programming algorithm was asymptotically fas-
ter in tests with the number of bins n ∈ {3, 5,9}. The
sharp discrepancy between the result of DP regarding
to the results of solvers in the tests with n ∈ {5, 9}
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
350

n = 3
10 20 30 40 50 60
0.1
1
10
100
1,000
elapsed time (s)
DP
Glpk
Cplex
n = 5
100 200 300
0.1
1
10
100
1,000
elapsed time (s)
DP
Glpk
Cplex
n = 9
25 50 75 100 125 150 175 200
0.1
1
10
100
1,000
elapsed time (s)
DP
Glpk
Cplex
n = 16
10 20 30 40 50 60
0.1
1
10
100
1,000
periods (t)
elapsed time (s)
DP
Glpk
Cplex
Figure 10: Tests results of Cplex and Glpk solvers and dyn-
amic programming algorithm.
suggests that in these cases the dynamic programming
has order of complexity lower than the algorithms of
mixed integer linear programming. With n = 16 the
two solvers results were superior to the proposed al-
gorithm. At n = 3, although DP performance was fas-
ter than the other methods, it was asymptotically si-
milar. One theory to explain this behavior is that the
algorithm could not take advantage of higher level of
symmetry in a n = 3 instance. Cplex was faster than
Glpk in all instances tested. One point in favor of
the dynamic programming algorithm is the fact that
Cplex is able to handle multiple threads (were four in
this scenario) boosting performance of solving pro-
cess. While current implementation of the proposed
solution presented in this work can just handle one
thread at time.
4 CONCLUSION
This work proposes a new approach to solve the trip-
per positioning problem. The objective was to model
the silo-tripper system as a combinatorial optimiza-
tion problem and solve it by means of exact methods
directly, without the use of hybrid MPC frameworks.
The proposal was to maximize the lowest bin level
of the silo in each period, in order to achieve maxi-
mum stability in the tripper operation. This strategy
was compared with another option indicated in the li-
terature by (Karelovic et al., 2015). In this case, the
author propose to minimize the amount of car mo-
vement and the stabilization of bins levels values. Al-
gorithms of mixed integer linear programming and
dynamic programming were used to handle the pro-
blem.
The algorithm proposed by this work maximized
the stabilization of bins levels values, taking advan-
tage of the freedom of car movement to minimize le-
vel variations more intensely than the stabilization al-
gorithm. In addition, the performance of the dynamic
programming was superior to the the mixed integer
linear programming solvers in the tests in the instan-
ces set featuring bins number lower than n = 16, and,
in some cases, the dynamic programming shown or-
der of complexity suggestively inferior to the other
algorithms within the time window evaluated. Howe-
ver, there was an inconsistence in the 3-bin instance
DP results that shown the same asymptotic behavior
as the solvers. This issue is beyond the scope of this
study and will de addressed in a future work.
The next steps of this research will focus on fin-
ding alternative methods to solve the tripper positi-
oning problem. The goal will be to find metaheuris-
tics capable of finding good or even optimal solutions,
but with search time significantly lower than the exact
methods.
REFERENCES
Bemporad, A. and Giorgetti, N. (2006). Logic-based met-
hods for optimal control of hybrid systems. IEEE
Transactions on Automatic Control, 41(6):963–976.
Borrelli, F., Baotic, M., Bemporad, A., and Morari, M.
(2005). Dynamic programming for constrained op-
timal control of discrete-time linear hybrid systems.
Automatica, 41(10).
Boyer, S. A. (2010). SCADA: Supervisory Control and Data
Acquisition. International Society of Automation, 4
edition.
Camacho, E. F. and Bordons, C. (2007). Model Predictive
Control. Advanced Textbooks in Control and Signal
Processing. Springer-Verlag London, 2 edition.
Proposed Solutions to the Tripper Car Positioning Problem
351

Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C.
(2001). Introduction to Algorithms. McGraw-Hill, 2
edition.
García, C. E., Prett, D. M., and Morari, M. (1989). Mo-
del predictive control: theory and practice – a survey.
Automatica, 25(3):335–348.
Gupta, A. and Yan, D. (2006). Mineral Processing Design
and Operation. Elsevier Science, 1 edition.
Karelovic, P., Putz, E., and Cipriano, A. (2015). A frame-
work for hybrid model predictive control in mineral
processing. Control Engineering Practice, 40:1–12.
Levitin, A. (2012). Introduction to the design & analysis of
algorithms. Pearson, 3 edition.
Pal, B., Sana, S. S., and Chaudhuri, K. (2014). A multi-
echelon production-inventory system with supply dis-
ruption. Journal of Manufacturing Systems, 33:262–
276.
Papadimitriou, C. H. and Steiglitz, K. (1998). Combinato-
rial Optimization: Algorithms and Complexity. Dover,
1 edition.
Rich, E. and Knight, K. (1991). Artificial Intelligence.
McGraw-Hill Inc., 1 edition.
Swinderman, R. T. (2014). Belt Conveyors for Bulk Ma-
terials, w/Metric Conversion. Conveyor Equipement
Manufactures Association, 7 edition.
Wills, B. A. and Napier-Munn, T. (2015). An Introduction
to the Practical Aspects of Ore Treatment and Mineral
Recovery. Butterworth-Heinemann, 8 edition.
Wolsey, L. A. (1998). Integer Programming. Wiley-
Interscience.
ICEIS 2018 - 20th International Conference on Enterprise Information Systems
352
