
Bus Arrival Time Prediction with Limited Data Set
using Regression Models
Armands Kviesis
1
, Aleksejs Zacepins
1
, Vitalijs Komasilovs
1
and Marcela Munizaga
2
1
Department of Computer Systems, Faculty of Information Technologies, Latvia University of Agriculture, Jelgava, Latvia
2
Department of Civil Engineering, Universidad de Chile, Santiago, Chile
Keywords:
Smart Public Transport, Public Buses, Arrival Time, GPS Data.
Abstract:
The increase of population has intensified everyday rush. Traffic congestions are still a problem in cities and
are one of the main cause for public transport delays. City residents and visitors have experienced time loss
by using public transport buses, because of waiting at the bus stops and not knowing if the bus is delayed or
already serviced the stop. Therefore it is valuable for people to know at what time the bus should arrive (or
is it already missed) at specific bus stop. Real-time public bus tracking and management system development
has been the focus of many researchers, and many studies have been done in this area. This paper focuses
on bus travel time prediction comparison between linear regression and support vector regression models
(SVR), when using limited data set. Data were limited in a way that only historical GPS (Global Positioning
System) coordinates of bus location (recorded each 30 seconds) and driven distance were used, there were no
information about arrival/departure times, delays or dwell times. Distance between stops and delay (assumed
values based on route observations by authors) were used as inputs for both models. It was concluded that
SVR algorithm showed better results, but the difference was not significantly large.
1 INTRODUCTION
Smart city is an emerging domain and concept that is
evolving fast, but still there are no one absolute defi-
nition for it (Anthopoulos and Reddick, 2016; Albino
et al., 2015; Mahizhnan, 1999). In general, smart
city implementation consists of various aspects in-
cluding, but not limited to smart mobility, smart gov-
ernment, smart people, smart living and smart traf-
fic. For instance smart traffic includes such sub topics
like, smart accident management (Lee et al., 2015),
smart vehicle monitoring, smart traffic light manage-
ment and smart public transportation system. This pa-
per deals with one of the smart public transportation
topics - with smart public bus system, in particular
with bus arrival time prediction for citizen informa-
tion.
The numbers of vehicles are increasing day by
day, and this leads to a serious problem of traffic con-
gestion, people are taking public transportation as an
alternative. For many citizens public buses has be-
come an important part of their lives. Most people
reach from homes to workplace or school using public
transportation system. People can lose time in trans-
portation because of unwanted waiting (Eken and Sa-
yar, 2014). Subsequently, public transportation ser-
vices should satisfy the customer needs, like arrival
time and the travel time are the valuable information
for both the customer and transport operator (Garg
et al., 2017).
There are already many systems and methods
available for bus arrival time calculation and predic-
tion. There are many researches devoted to bus ar-
rival time prediction. In many research papers authors
mention and cover mainly 4 methods that are being
used in bus arrival time prediction: models that are
based on historical data, regression models, models
that uses Kalman filter and artificial neural networks
(Amita et al., 2015; Yin et al., 2017; Gurmu and Fan,
2014; Fan and Gurmu, 2015).
Regression models are based on a mathematical
function that is linear. In this type of model there
are two types of variables involved - dependent and
independent (usually more than one), where the in-
dependent variables determines, predicts the value of
dependent variable. As Patnaik (Patnaik et al., 2004)
describes, the popularity to use regression models can
be explained by the fact that they are in a way straight-
forward and well established. Although some authors
(Fan and Gurmu, 2015) point to such model limits in
Kviesis, A., Zacepins, A., Komasilovs, V. and Munizaga, M.
Bus Arrival Time Prediction with Limited Data Set using Regression Models.
DOI: 10.5220/0006816306430647
In Proceedings of the 4th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2018), pages 643-647
ISBN: 978-989-758-293-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
643

transportation systems and poor performance (Gurmu
and Fan, 2014) comparing with other methods.
Machine learning methods, such as support vec-
tor machines (SVM) and artificial neural networks
(ANN), are also widely used in travel time predic-
tions. ANN is based on principles of biological neu-
ron networks and was introduced by (McCulloch and
Pitts, 1990). As stated by (Fan and Gurmu, 2015),
ANN are suitable for prediction tasks even when
the physical processes related with the route are not
clearly specified. SVM is generally based on two
ideas: feature vector mapping in a nonlinear way
and finding a hyperplane that separates data (Kulka-
rni and Harman, 2011). SVM deals with classification
and regression, and as stated by (Altinkaya and Zon-
tul, 2013), there are few applications that uses SVM
method in the field of transportation. As indicated by
(Julio et al., 2016), SVR algorithm has shown its po-
tential in transportation as being an accurate predictor.
In (Amita et al., 2015) authors compared two
models - artificial neural network model and multi-
linear regression model. Different parameters like
dwell time, delays, distance between stops were used
as input data for both models. The results of this study
showed that artificial neural network is more accurate
and robust. Study carried out by (Fan and Gurmu,
2015), proved ANN as a better prediction model than
models based on historical average and Kalman filter.
It was also stated that, acceptable predictions can be
obtained by using only arrival and departure time.
A combination of SVM and genetic algorithms
was used to predict bus arrival time by (Yang et al.,
2016). During the study, it was concluded that their
proposed method was more accurate than traditional
SVM and ANN. An interesting approach was intro-
duced by (Julio et al., 2016), where machine learn-
ing algorithms, like SVM, ANN and Bayes Networks,
were compared to predict bus travel speeds, by using
GPS data. Results proved that ANN performed bet-
ther than other selected methods.
GPS is one of the technologies that are used in
a huge number of applications today (Gowtham and
Mehdi, 2016). Many researchers stated in their study
that GPS could be used in many applications and it is
possible to follow routes and locations driven a vehi-
cle by means of GPS (Verma and Bhatia, 2013). This
paper focuses on linear regresion model and SVR ap-
plication to predict bus arrival times or to be more
specific - how both models perform with given lim-
ited data set (GPS data of bus location and bus driven
distance).
Authors choose this topic because in their native
city Jelgava there is a need for a smart public bus sys-
tem development. Jelgava is the fourth largest city in
Latvia, a historical centre of Zemgales region; dis-
tance from Latvia capital Riga is 42 km, residents
count is approx. 62 000. Jelgava is called ”students”
city, because there are a lot of students from other
cities, which makes a ”real” number of people liv-
ing in Jelgava much larger. Despite the fact that Jel-
gava is a small city and there should be no problem
to organise qualitative public transportation system,
there are some issues. In Jelgava there is one public
transport provider - Jelgavas autobusu parks (source:
http://www.jap.lv/). There are 20 bus routes in the
city. Buses are scheduled by static time schedule
defining at what time bus should depart the bus stops.
And there is one main issue, that sometimes bus can
be delayed or can depart earlier than scheduled time.
Citizens waiting at the bus stops have no idea about
the actual bus location. So citizens are in need of a
smarter and user friendlier public transportation noti-
fication system. Using the real-time GPS data from
the buses can help to solve above mentioned prob-
lems.
In this paper authors compare two prediction mod-
els in order to predict bus arrival time using the GPS
data with 30 second interval, that is considered as
limited data set (there was no information about ar-
rival/departure or dwell times). Example GPS data
is used for one bus route in Santiago, Chile (Cort
´
es
et al., 2011).
2 MATERIAL AND METHODS
2.1 Data Preparation
Data available for the research were GPS coordinates
(latitude and longitude) of bus stop locations and his-
torical GPS coordinates of bus (and its driven dis-
tance) during its route in Santiago, Chile, that were
recorded every 30 seconds. There were no additional
information gathered, like delays during route, ar-
rival/departure time, passenger count or dwell time at
bus stops.
To make the models more robust, it was con-
sidered to introduce additional parameter, that could
have some impact on arrival times. One such parame-
ter could be obtain by observations of a route. There-
fore, historical data of the specific route was observed
and approximate delays were assumed based on inter-
ceptions, turns etc. during the route.
For model evaluation purposes, the actual arrival
time needs to be known. Data for actual travel time
were also based on manual observations in a map,
since there was no information about the exact arrival
RESIST 2018 - Special Session on Resilient Smart city Transportation
644

and departure time. Values for travel time were cal-
culated by taking into account the time and locations
when the bus had not yet arrived and when it had al-
ready passed the bus stop.
2.2 Development of Models
Data for multiple linear regression were prepared by
using historical data and selecting distance and as pre-
viously mentioned, generated delays as independent
and travel time as dependent variable.
Analyzing selected variables, multicollinearity
was not observed, meaning that independent variables
do not affect each other significantly. Correlation be-
tween the two independent (predictive) variables was
0.330. Correlation between distance and travel time
(dependent variable) was 0.8489; delay and travel
time: 0.702.
The generic form of linear regression model for
bus arrival time prediction by using two independent
variables was as follows (1):
T
arrival
= a + bx
1
+ cx
2
(1)
where:
T
arrival
- predicted arrival time, s;
x
1
- distance, m;
x
2
- delay, s;
Model coefficients were obtained by applying data
analysis regression tool in MS Excel spreadsheet. The
model with its final coefficients is presented below
(2):
T
arrival
= −16.153 + 0.171x
1
+ 1.400x
2
(2)
For SVR development, Python programming
language was used with scikit-learn package
(http://scikit-learn.org/stable/index.html). This pack-
age provides various tools for machine learning.
Model was built using sklearn’s SVR class with
linear kernel and C value of 0.01. The C parameter
(C>0) is also called as the ”penalty” factor and needs
to be chosen carefully, as it causes overfitting or
underfitting (Alpaydin, 2014). Tests showed, that the
model performed better with relatively small value.
Distance and delay was also used as input parameters
in this case.
2.3 Developed Solution
Authors proposed method is based on bus arrival time
prediction calculation (using previously described re-
gression model) at each bus location (after every 30
seconds). On every new bus position, distance to each
bus stop is updated and prediction is made. To per-
form mentioned operations, it is necessary to know at
which bus stop the bus had already arrived. Therefore
additional calculations were performed to determine
when the bus has passed by specific bus stop. Since
the given GPS data also included distance the bus has
driven from the beginning of the route, it was used
to determine the state of bus against bus stops. How-
ever, the recorded bus distance had an error compar-
ing with the distance, measured in a map. This error
was taken into account when performing mathemat-
ical operations to calculate distances to bus stops. It
was also observed, that there were instances when bus
during its 30 s travel has serviced two bus stops. Such
cases were also processed, e. g., by calculating the
driven distance, it was then compared against all bus
stops: if the driven distance was larger than distance
to the bus stop, it was assumed, that this specific bus
stop was already serviced.
To summarize, below are the three main steps that
were performed to predict bus arrival time:
• get information about next bus stop;
• calculate distance from bus position to next bus
stop;
• calculate arrival time at bus stops, by applying de-
veloped models;
3 RESULTS AND DISCUSSION
Developed models were tested on multiple histori-
cal data sets. Test data sets included the same route,
but different buses at different time periods in differ-
ent days. To evaluate precision of developed mod-
els, Mean Absolute Percentage Error (MAPE) (3) and
Root Mean Square Error (RMSE) (4) were calcu-
lated, where MAPE value shows the precision error in
percentage, and RMSE - the difference between pre-
dicted and actual value.
MAPE =
n
∑
i=1
|
A
i
− P
i
A
i
|
n
∗ 100 (3)
where:
MAPE - Mean absolute percentage error,
n - number of predictions;
A
i
- actual arrival time, s;
P
i
- predicted arrival time, s;
RMSE =
v
u
u
u
t
n
∑
i=1
(A
i
− P
i
)
2
n
(4)
where:
RMSE - Root mean square error, s;
Bus Arrival Time Prediction with Limited Data Set using Regression Models
645
n - number of predictions;
A
i
- actual arrival time, s;
P
i
- predicted arrival time, s;
Results are shown in Table 1. SVR showed best
results, although there was not large difference be-
tween both models.
Table 1: Model evaluation results.
Model MAPE (%) RMSE (s)
Linear regression 8.19 48.90
SVR 7.41 47.86
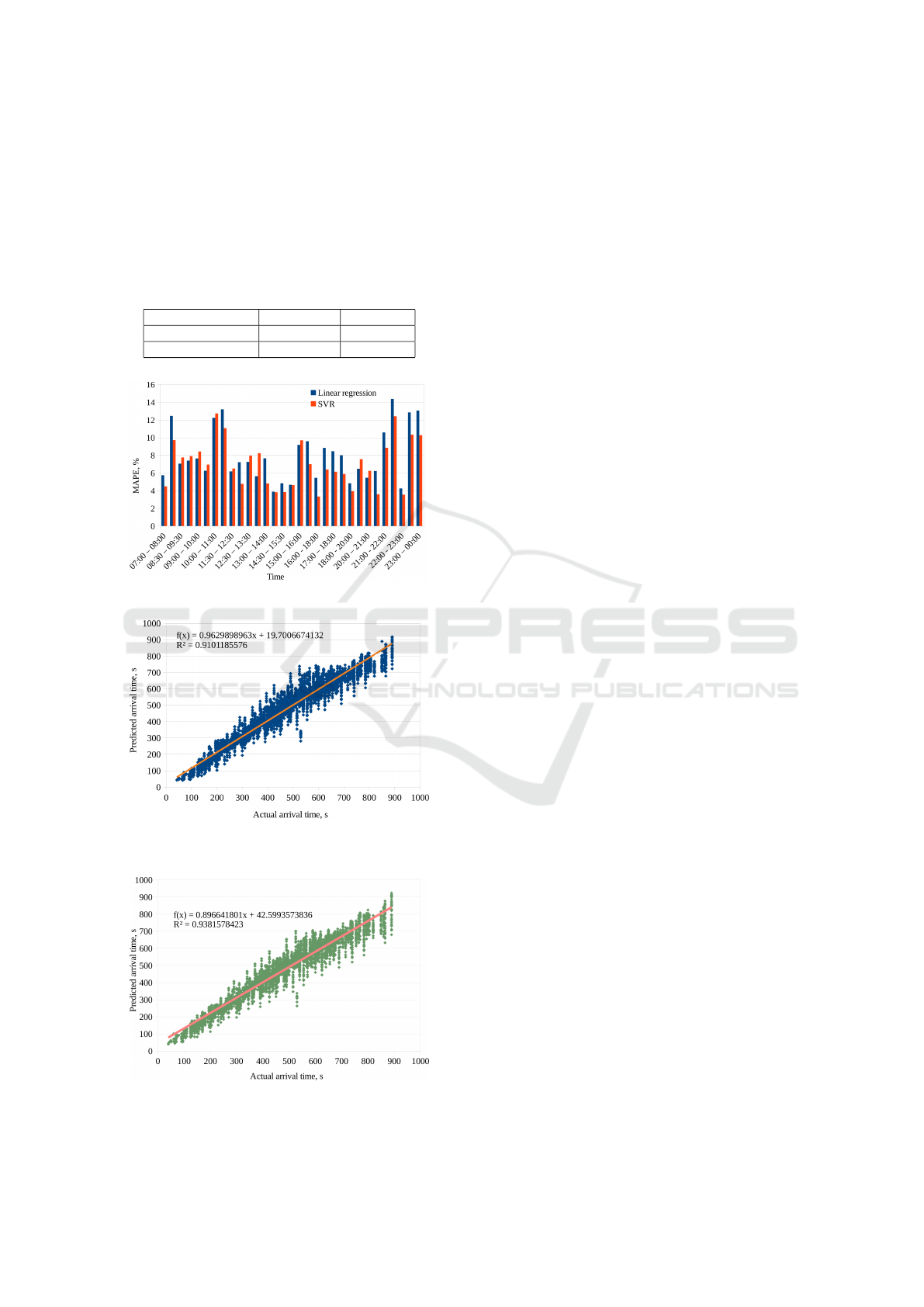
Figure 1: Mean Absolute Percentage Error by time periods.
Figure 2: Plotted values of actual and predicted arrival time
(linear regression model).
Figure 3: Plotted values of actual and predicted arrival time
(SVR).
MAPE value representation by time periods are
shown in Fig. 1. As it can be seen, SVR shows better
perfomance in most of the time As the diagram shows,
error tends to increase in the late hours of the day,
while mid afternoon it fluctuates from 5% to 10%. Er-
ror increase in the late hours could be caused by the
fact, that there should be less vechicles on the road
(less possibility to have traffic congestion) and less
people at the bus stops, thus, bus could have serviced
(or simply driven by, because nobody was at the bus
stop) more than 1 bus stop during 30 s period.
Actual and predicted arrival times were plotted in
a scatter diagrams (Fig. 2 and Fig. 3). Coefficient of
determination (R
2
) between plotted values was 0.91
(linear regression) and 0.94 (SVR). Although the cal-
culated MAPE and RMSE values showed relatively
good results in described conditions, it is worth men-
tioning that the actual arrival time, that was used to
evaluate the model, introduces additional error, as this
value was assumed by observing bus route data, and
thus may not correspond to real (actual) arrival time.
4 CONCLUSIONS
The data provided by the GPS records can be trans-
lated into reliable indicators, that will show the exact
position of the bus on the route and can be used for
arrival time calculation.
As the results showed, data recorded each 30 s is
too rare, to get reliable predictions. In some cases,
bus stops are very close to each other, and the bus can
serve multiple bus stops in 30 s period.
The information about exact arrivals, departures is
also of essence, so it would provide a reliable data for
validation.
Further research should be conducted to compare
the results of other methods (like artificial neural net-
works, Kalman filter) performing in a situation with
limited data.
Arrival time prediction could be used at bus stops
on informative tablos, informing potential passengers
about the delays.It could also be used in mobile appli-
cations, where the user could see the exact location of
a bus and be informed about arrival time at next bus
stops.
GPS data are not just usefull for arrival time pre-
diction, but they can also provide information about
traffic, e.g., the existance of congestions (Bacon et al.,
2011).
RESIST 2018 - Special Session on Resilient Smart city Transportation
646

ACKNOWLEDGMENTS
Scientific research, publication and presentation are
supported by the ERANet-LAC Project Enabling re-
silient urban transportation systems in smart cities
(RETRACT, ELAC2015/T10-0761).
REFERENCES
Albino, V., Berardi, U., and Dangelico, R. M. (2015). Smart
cities: Definitions, dimensions, performance, and ini-
tiatives. Journal of Urban Technology, 22(1):3–21.
Alpaydin, E. (2014). Introduction to machine learning.
MIT press.
Altinkaya, M. and Zontul, M. (2013). Urban bus arrival
time prediction: A review of computational models.
International Journal of Recent Technology and Engi-
neering (IJRTE), 2(4):164–169.
Amita, J., Singh, J. S., and Kumar, G. P. (2015). Predic-
tion of bus travel time using artificial neural network.
International Journal for Traffic and Transport Engi-
neering, 5(4):410–424.
Anthopoulos, L. G. and Reddick, C. G. (2016). Understand-
ing electronic government research and smart city:
A framework and empirical evidence. Information
Polity, 21(1):99–117.
Bacon, J., Bejan, A., Beresford, A., Evans, D., Gibbens, R.,
and Moody, K. (2011). Using real-time road traffic
data to evaluate congestion. Dependable and Historic
Computing, pages 93–117.
Cort
´
es, C. E., Gibson, J., Gschwender, A., Munizaga, M.,
and Z
´
u
˜
niga, M. (2011). Commercial bus speed di-
agnosis based on gps-monitored data. Transportation
Research Part C: Emerging Technologies, 19(4):695–
707.
Eken, S. and Sayar, A. (2014). A smart bus tracking sys-
tem based on location-aware services and qr codes.
In Innovations in Intelligent Systems and Applications
(INISTA) Proceedings, 2014 IEEE International Sym-
posium on, pages 299–303. IEEE.
Fan, W. and Gurmu, Z. (2015). Dynamic travel time pre-
diction models for buses using only gps data. Inter-
national Journal of Transportation Science and Tech-
nology, 4(4):353–366.
Garg, N., Gawande, P. V., and Kharat, P. P. K. D. B.
(2017). Bus tracking using gps and real time predic-
tion. IJRAET, 4:3477–3479.
Gowtham, J. and Mehdi, M. J. (2016). Smart public trans-
port. IJRAET, 5:17–2.
Gurmu, Z. K. and Fan, W. D. (2014). Artificial neural net-
work travel time prediction model for buses using only
gps data. Journal of Public Transportation, 17(2):3.
Julio, N., Giesen, R., and Lizana, P. (2016). Real-time pre-
diction of bus travel speeds using traffic shockwaves
and machine learning algorithms. Research in Trans-
portation Economics, 59:250–257.
Kulkarni, S. R. and Harman, G. (2011). Statistical learning
theory: a tutorial. Wiley Interdisciplinary Reviews:
Computational Statistics, 3(6):543–556.
Lee, J. K., Jeong, Y. S., and Park, J. H. (2015). s-itsf: a
service based intelligent transportation system frame-
work for smart accident management. Human-centric
Computing and Information Sciences, 5(1):34.
Mahizhnan, A. (1999). Smart cities: the singapore case.
Cities, 16(1):13–18.
McCulloch, W. S. and Pitts, W. (1990). A logical calculus
of the ideas immanent in nervous activity. Bulletin of
mathematical biology, 52(1):99–115.
Patnaik, J., Chien, S., and Bladikas, A. (2004). Estimation
of bus arrival times using apc data. Journal of public
transportation, 7(1):1.
Verma, P. and Bhatia, J. (2013). Design and development
of gps-gsm based tracking system with google map
based monitoring. International Journal of Computer
Science, Engineering and Applications, 3(3):33.
Yang, M., Chen, C., Wang, L., Yan, X., and Zhou, L.
(2016). Bus arrival time prediction using support vec-
tor machine with genetic algorithm. Neural Network
World, 26(3):205.
Yin, T., Zhong, G., Zhang, J., He, S., and Ran, B.
(2017). A prediction model of bus arrival time at stops
with multi-routes. Transportation Research Procedia,
25(Supplement C):4623 – 4636. World Conference
on Transport Research - WCTR 2016 Shanghai. 10-
15 July 2016.
Bus Arrival Time Prediction with Limited Data Set using Regression Models
647
