Retrieving the Topology from the Knowledge Frame System for

Composition of the Topological Functioning Model

Vladislavs Nazaruks and Jānis Osis

Department of Applied Computer Science, Riga Technical University, Sētas iela 1, LV-1048, Riga, Latvia

Keywords: System Modelling, Frames, Knowledge Base, Topological Functioning Model, Causal Dependencies, Causal

Implication.

Abstract: Model-driven software development considers models as a core artefact for generation of software source

code. This requires models to be formal and complete enough for further transformations and code generation.

It requires clear understanding of such knowledge as functionality, objects and dependencies in the problem

domain. In our approach, this knowledge is kept in the frame-based system. The completeness and consistency

of the knowledge can be verified by generating and validating the topological functioning model (TFM). The

TFM is a model, which elements are linked by the topology, i.e. by cause and effect relations among the

functional characteristics of the domain. Automated composition of the TFM requires retrieving appropriate

conditions on cause and effect functional characteristics of the system from the knowledge base. The proposed

algorithm reads data of functional characteristics kept in the knowledge base, relates those of them, where a

cause condition corresponds to an effect condition, and generates data for the corresponding cause-and-effect

relation. The difficulty is that conditions can be combined using logical operators AND, OR, XOR, as well

as can use negation NOT. The benefit is that any inconsistency in the retrieved topology could be discovered

and marked for further analysis. This should force careful analysis of the problem domain before generation

of the design model. That could lead to decreasing a number of errors made due to uncertainty in the analysis.

1 INTRODUCTION

Knowledge about the problem domain (a business

organization, a mechanical system etc.) can be found

in official documents, technical specifications,

descriptions, instructions, statistics etc., as well as got

from domain experts by means of interviews, surveys,

research and so on.

As Elstermann and Heuser pointed out

(Elstermann and Heuser, 2016), there is not a big

problem to create a complete description of the

problem domain in the natural language, but it

requires time, human and financial resources. If this

work will not be used further with clear and

satisfactory results, then all the resources will be just

wasted. Knowledge extraction from the information

sources can be manual, automated and automatic. The

last one is very difficult due to particularities of

natural languages such as errors, ambiguities as well

as due inconsistences and incompleteness in text

documents. However, manual extraction also has its

negative sides, i.e. the process is slow and error prone.

Thus, automation software tool support based on

natural language processing (NLP) could be used to

improve processing of multiple information sources.

Since the topological functioning modelling is

based on analysis of the exhaustive verbal

information about the system, the analysed

information must be kept in some form. Since we

want to integrate possibilities of natural language

processing and knowledge inferring, the core element

should be a knowledge base. There are several

formats for knowledge representation such as frame

networks, ontology, concept networks, product rules

etc., and even artificial natural languages, e.g.,

Esperanto, Conlang, Lingvata (Roux, 2013).

Discussion on positive and negative properties of

knowledge representation formats (Nazaruks and

Osis, 2017a) leads to the choosing the knowledge

frames. The knowledge frames allows keeping both

structural and procedural knowledge in the way

similar to the object-oriented one. We believe that a

knowledge frame-based system can serve as a storage

of domain knowledge in the consistent and computer-

understandable format. Knowledge frame systems

can be standalone, but it is more valuable in

integration with other representation formats such as

Nazaruks, V. and Osis, J.

Retrieving the Topology from the Knowledge Frame System for Composition of the Topological Functioning Model.

DOI: 10.5220/0006817104910500

In Proceedings of the 13th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2018), pages 491-500

ISBN: 978-989-758-300-1

491

ontology and product rules (Nazaruks and Osis,

2017a). However, at the present this aspect is out of

scope of the given research.

Modelling of behaviour and structure of the

problem domain is based on the knowledge acquired

from experts and extracted from documents. Models

can be informal, semi-formal and formal. Usually,

formal models are considered as “heavyweight”,

informal are too inaccurate, the gold middle are semi-

formal models, but they may contain ambiguities due

to their incompleteness.

For modelling the problem domain, we suggest

using advantages provided by the Topological

Functioning Model – formal but “light-weight”

model that can be transformed to most-used UML

(Unified Modelling Language) diagrams (Donins et

al., 2011, 2012; Donins, 2012b).

The construction of the TFM requires analysis of

domain information and extraction of both

(procedural and declarative) knowledge, but the

functional view on the system is the primary one. And

it must be assigned to the structural view on the

system.

These principles are to be incorporated into the

knowledge frame system (Figure 1). The frame

system contains generable and manually added

knowledge (Nazaruks and Osis, 2017b). The next step

after adding knowledge is to generate the TFM and to

validate it. Validation of the TFM includes also

generation and validation of the topological space and

allows discovering incompleteness and

contradictions in the available knowledge.

The goal of this research is to implement

generation of the TFM. The main difficulty is in

discovering cause-and-effect relations between

functional features without explicitly indicated

sequence. We assume that mandatory identification

of all pre- and post- conditions of all functional

characteristics of the system is a way to discover this

causal sequence.

The paper is organized as follows. Section 2

describes the background on the TFM and the initial

scheme of the knowledge frame system. Section 3

illustrates the developed algorithm and examples.

Section 4 provides an overview of related work. And

Section 5 concludes the paper.

2 THE KNOWLEDGE SYSTEM

2.1 Topological Functioning Model

The TFM is a formal model which describes the

functioning of a system. Its fundamentals are

published by Janis Osis (Osis, 1969). The TFM can

be specified as a topological space



 



, where  is

a finite set of functional features of the system under

consideration, and  is a topology on .

A functional feature is “a characteristic of the

system (in its general sense) that is designed [for] and

necessary to achieve some system’s goal” (Osis,

Asnina and Grave, 2008; Osis and Asnina, 2011). It

can be specified by a unique tuple (1), where:

  is an action linked with object ,

  is a result of the action ,

  is an object (objects) that gets the result of

the action or an object (objects) that is used

in this action,

  is a set of preconditions or atomic

business rules,

  is a set of postconditions or

atomic business rules,

  is a set of responsible entities (systems

or subsystems) that provide or suggest

action  with a set of certain objects ,

  is a set of responsible entities (systems

or subsystems) that enact a concrete action

 (Osis and Asnina, 2011; Nazaruka et al.,

2016).

  is a label that indicates belonging of the

functional feature to the system for which

the TFM will be composed, namely, inner if

belongs and external if does not.



       



(1)

The topology  is expressed by cause-and-effect

relations. A cause-and-effect relation is a causal

implication (dependency) between two functional

features. It is a binary relationship, where a cause

triggers an effect without any middle functional

feature (Asnina and Osis, 2011).

There are several formal specifications of cause-

and-effect relations (Donins, 2012a; Asnina and

Ovchinnikova, 2015), but the common is that they are

focused on assessment of the completeness of

incoming and outgoing conditions.

MDI4SE 2018 - Special Session on Model-Driven Innovations for Software Engineering

492

Business

description

Knowledge Frame System

Topological

UML model

Code

Fill in frame

instances

Generate and

validate TFM

Figure 1: General vision of joint usage of TFM and frame system.

In the research on automated determination of the

topology, it is more convenient to use the

specification presented by Uldis Donins (Donins,

2012a).

A cause-and-effect relation (2) is a topological

relation T

between a cause functional feature X

and

an effect functional feature X

, where at least one

condition of L

out

that is a set of X

postconditions is

equal to the at least one condition of L

that is X

preconditions.









 



 



 



 





(2)

The TFM is valid when it satisfies topological and

functioning properties (Osis and Asnina, 2011). The

topological properties are: connectedness,

neighbourhood, closure and continuous mapping.

The functioning properties are: cause-and-effect

relations, cycle structure, inputs and outputs. The

possibility of validation of the TFM using execution

model simulation is discussed by Ovchinnikova and

Nazaruka (Ovchinnikova and Nazaruka, 2016),

where decision making is based on results presented

by the same authors in (Asnina and Ovchinnikova,

2015).

There are three approaches for complex system

modelling that apply the TFM, namely TFM4MDA,

the Topological UML and IDM. The Topological

Functioning Modelling for Model Driven

Architecture (TFM4MDA) approach (Osis and

Asnina, 2008) is intended for problem domain

analysis and modelling in the context of MDA, where

the TFM acts as a Computation Independent Model

(CIM). The Topological UML approach (Asnina and

Osis, 2010; Donins, 2012b) integrates the TFM and

its formalism with elements and diagrams of the

Unified Modelling Language (UML). The Integrated

Domain Modelling (IDM) approach “suggests using

common system analysis and artificial intelligence

practices to capture the domain knowledge and then

transform these into a corresponding domain model”

(Slihte, 2015).

2.2 The Initial Scheme of the Frame

System Based on the TFM

Based on the comparison of metamodels of

TFM4MDA, IDM and Topological UML, the initial

scheme of the frame system was developed (Nazaruks

and Osis, 2017b). There are three types of frame

classes: with manually filled in slots, with partially

generated knowledge in slots, and with completely

generated knowledge of frame instances. The

structure of frames is based on TFM elements.

Generation of the TFM from frames and its further

validation allows assessing completeness of acquired

knowledge. However, in most cases assessment of

semantical correctness is left to a human – the expert

in the field.

In this research, the focus is on two frame classes,

namely, CauseAndEffectRelation and

FunctionalFeature (Figure 2).

Figure 2: Frame classes CauseAndEffectRelation and

FunctionalFeature.

Retrieving the Topology from the Knowledge Frame System for Composition of the Topological Functioning Model

493

All slots of FunctionalFeature are filled in

manually, while all slots of CauseAndEffectRelation

are to be generated (Section 3).

3 COMPOSITION OF THE TFM

3.1 Determination of the Topology

Till now, determination of the topology over the set

of functional features in the TFM has been done in

two ways. The first one is manual. It was proposed in

the TFM4MDA approach and requires human

participation in text analysis (Asnina and Osis, 2011).

The second one is automated, but it is performed on

the structured textual descriptions (Osis, Asnina and

Grave, 2008; Osis and Slihte, 2010; Slihte, Osis and

Donins, 2011; Slihte, 2015), i.e. on the specifications

of use cases. The important characteristic of the use

case specification is that all steps are ordered in the

logical sequence with all the possible branches.

Preconditions as events are to be added manually and

serve as guards on alternative scenario. A reference to

the corresponding step (event) of the next use case

must be added manually as well.

The idea of retrieving the topology by analysis of

pre- and post-conditions has been proposed in

Topological UML (Osis and Donins, 2010; Donins,

2012a). There it has been applied for identification of

logical relations among cause-and-effect relations

(Donins, 2012a).

This approach also requires human participation,

since postcondition and precondition sets may be not

indicated, thus semantics of logical conditions must

be analysed properly.

In this research we develop this idea but assume

that frame instances should have all the preconditions

and postconditions defined and indicated during

manual filling of the knowledge into instances of

frame class FunctionalFeature.

3.2 Implementation of the Algorithm

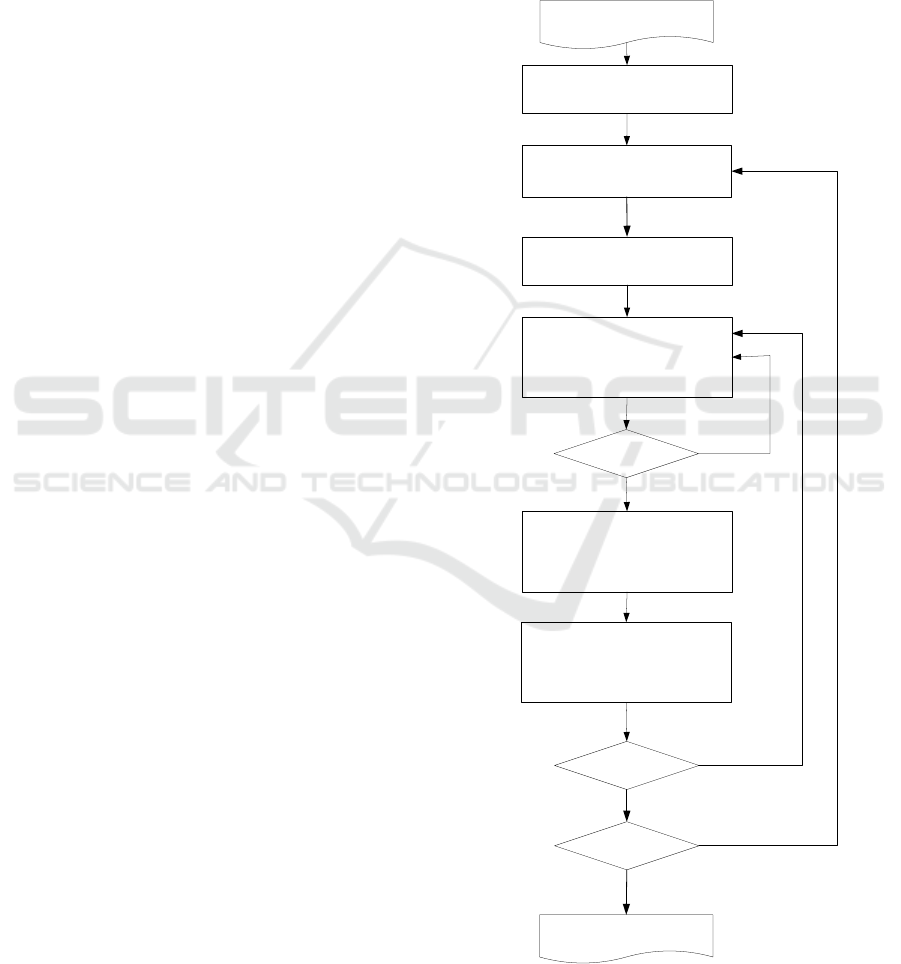
The general idea is illustrated in Figure 3. Data of

frame instances is kept in XML file with the extension

“tfm”. In order to generate the cause-and effect

relations this file is parsed to get all structures named

FunctionalFeature. For each instance its

preconditions as well as conditions are tokenized

using Polish notation, i.e. the simple conditions are

extracted from complex combinations keeping

negations when they are (Figure 4 and Figure 5).

Then the check whether a condition in a set of

preconditions is met in a set of postconditions in other

functional features is performed. If it is met, then the

cause-and-effect relation is established between those

two functional features, the corresponding structure is

generated and added to the collection of cause-and-

effect relations in the TFM file. The result is a *.tfm

file with instances of functional features and cause-

and-effect relations.

Get all instances of

FunctionalFeature

*.tfm

Tokenize all preconditions L

and postconditions L

out

For each c

in L

out

of F

search c

in L

of F

== c

Generate an instance of

CauseAndEffect

Add an instance of

CauseAndEffect to the

collection of them

*.tfm

Yes

Is next

condition?

Yes

For each pair F

and F

Is next pair?

Yes

Figure 3: General idea of retrieving cause-and-effect

relations from instances of frame class FunctionalFeature.

MDI4SE 2018 - Special Session on Model-Driven Innovations for Software Engineering

494

Figure 4: Simplification of logical combinations of conditions.

Figure 5: Processing of complex negations.

3.3 Illustrative Examples

Let us test the developed algorithm on the example of

investigation of a criminal case (Nazaruks and Osis,

2017b) with several modifications.

The original TFM is shown in Figure 6. Cause-

and-effect relations among functional features are

created also manually based on specification of pre-

and post-conditions (Figure 8). After generation of

the cause-and-effect relations according to the

algorithm (Figure 7), we have found out that a few

relations have not been created, namely, 7-16 and 7-

14, but relation 12-10 that is absent in the original

TFM has been created (Figure 9). After investigation,

we have found that in first case the reason is a mistake

in the condition’s text – “(a criminal case is sent to

prosecutor)” in functional feature 7 and “(a criminal

case is sent to a prosecutor)” in functional features 14

and 16. But the relation 12-10 is based on the

condition “(a criminal case is terminated)” that was

missed during manual work.

Retrieving the Topology from the Knowledge Frame System for Composition of the Topological Functioning Model

495

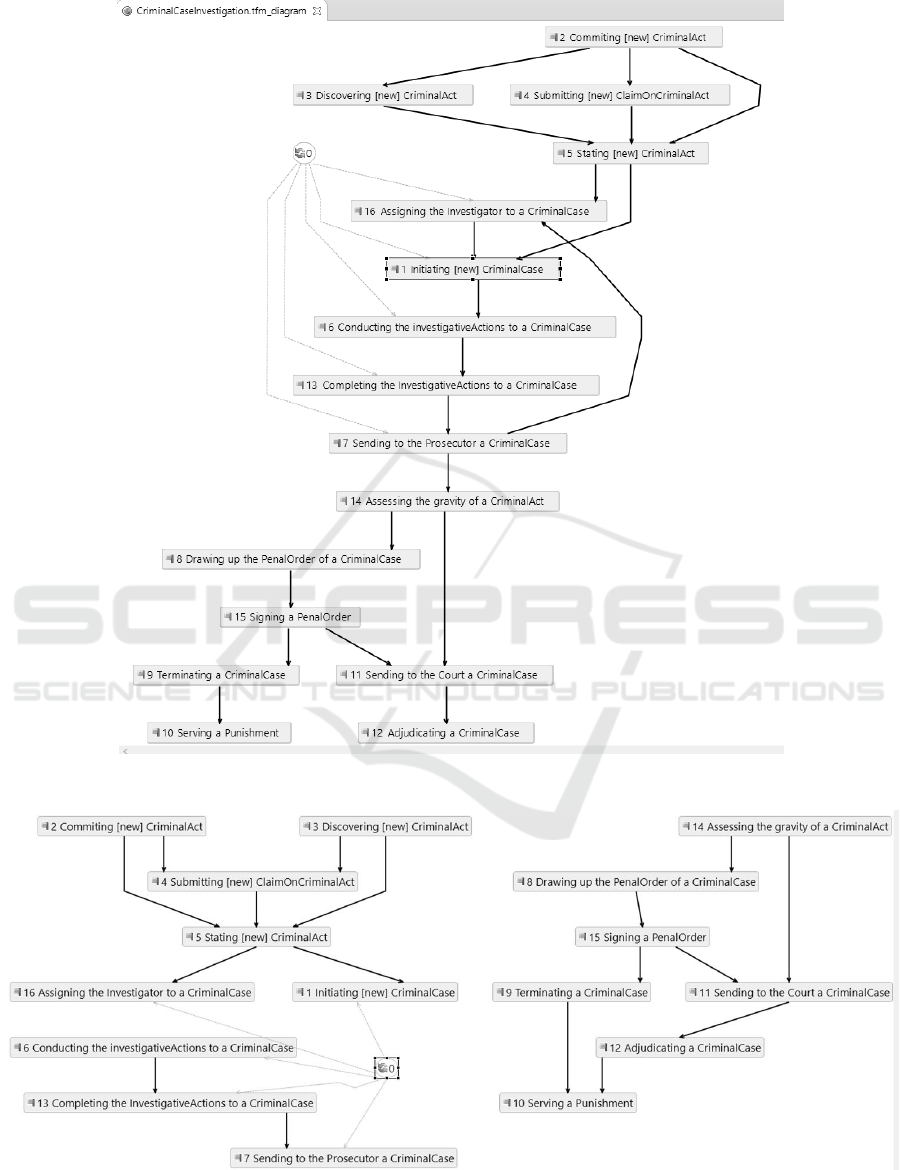
Figure 6: The manually created TFM with preconditions and postconditions.

Figure 7: The generated TFM with errors in causal dependencies.

MDI4SE 2018 - Special Session on Model-Driven Innovations for Software Engineering

496

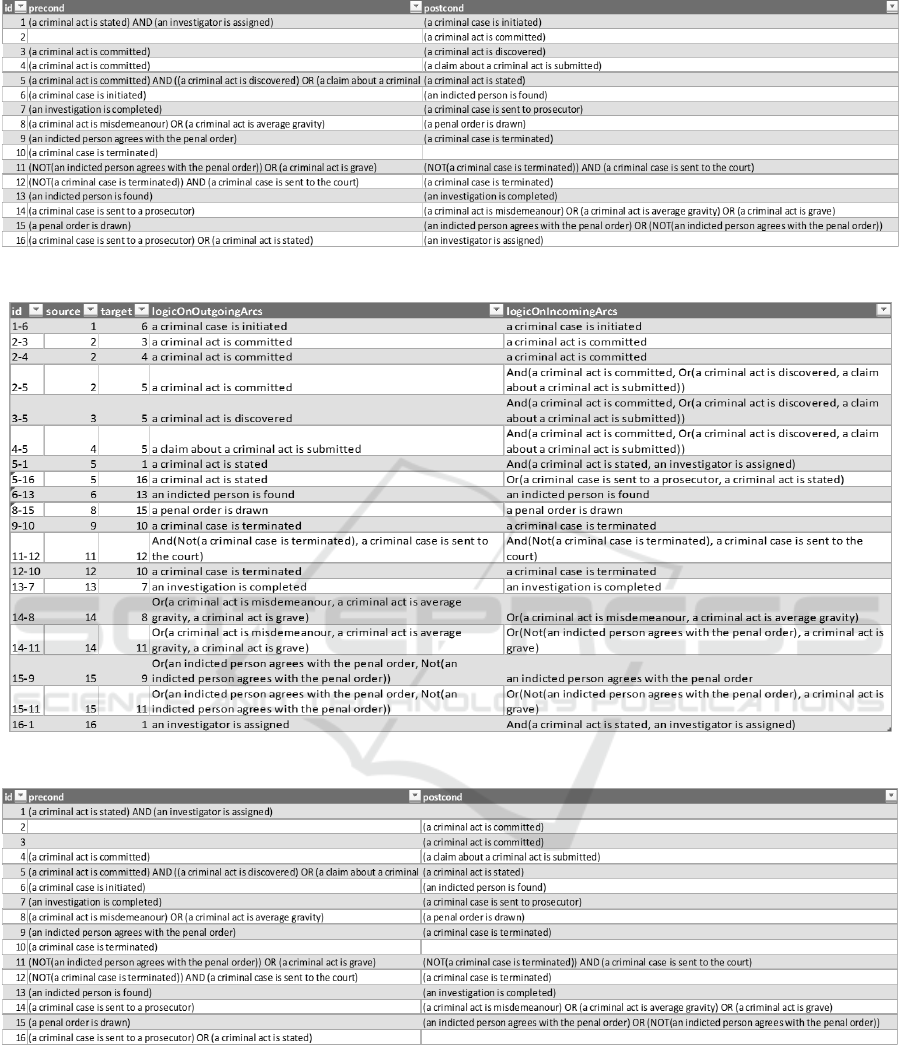
Figure 8: Preconditions and postconditions of manually created TFM.

Figure 9: The generated cause-and-effect relations for the original TFM.

Figure 10: Preconditions and postconditions of the functional features with error cases.

In the second experiment we have removed

postcondition of functional features 1 and 16 (Figure

10). The cause-and-effect relations 1-6, 2-3, 3-4 and

16-1 where not generated. After investigation it was

found out that the value of precondition of functional

feature 3 is set for the wrong slot.

Summarizing, the implemented algorithm works

correctly to the current style of recording condition

sets. Certainly, it must be additionally tested for other

cases. However, inconsistences in the generated TFM

such as isolated vertices or wrong cause-and-effect

relations may indicate several cases:

Retrieving the Topology from the Knowledge Frame System for Composition of the Topological Functioning Model

497

 Errors in specifications of functional features

that could be either grammatical or due to a

use of wrong slots;

 Undefined preconditions or postconditions

that means that not all facts and states of the

system are discovered;

 Misunderstood causal implications due to

fragmentary nature of the analysis.

Without doubts, manual discovering and

specification of all preconditions and postconditions

of functional characteristics is resource-consuming

tasks and would get accepted only in case of software

tool automated support and control as well as in case

of automation of model transformation.

4 RELATED WORK

In the UML (Unified Modelling Language) and

BMPN (Business Process Model and Notation)

causality is expressed through control flows, data

flows, and transitions. Determination of causality is

important not only during analysis and design, but

also for testing purposes, when a tool creates state

machines to check coverage criteria of tests.

Some authors (Briand, Labiche and Lin, 2010) put

their attention on identification of data flows from

OCL (Object Constraint Language) guard conditions

and operation contracts. The authors report that data

flow information can be used for determination of the

“best transition tree”. The preconditions of TFM

functional features after their transformation to

elements of UML diagrams become also guard

conditions. Thus, analysis of preconditions has a

sense in determination of causality.

Other authors illustrate control and data flow

transformation to transition flows of Petri Nets as a

part of analysis of system’s functionality (Lin et al.,

2005). Control flow graphs are important for

automation of many software engineering task, their

composition is not straightforward even from UML

sequence diagrams (Kundu, Samanta and Mall,

2012), since this knowledge is expressed in different

elements and sometimes even in nested fragments

with arbitrary nesting depth. Integration of multiple

control flows may lead for creation of non-

appropriate paths (Arora, Bhatia and Singh, 2017).

Control flows in BPMN diagrams may form

conflicts and deadlocks, since they may include

different constructs, e.g., several types of events,

activities, and getaways. Usually, for analysis of

BPMN control flows transformations to formal

models (El Hichami et al., 2015) or model simulation

(Todoran and Mitrea, 2015) are suggested. However,

in most cases modelling of control flows is not

automated and can be done at three levels of details –

from business to executable one (Stiehl, 2014). In the

field of automatic generation of BPMN we want to

note an approach presented by Kluza and Nalepa

(Kluza and Nalepa, 2017) and similar to the our one,

where a BPMN model is generated from manually

created requirements descriptions and business rules

declarations. The authors apply Attribute

Relationship Diagram (a structured specification of

the system description) and generate a process model

integrated with rule-based structures, i.e. decision

tables. Rules are discovered previously by business

analysts. After refining, the integrated model is

suitable for simulation. The similarity with our

approach is the focus on the “rule-based task”.

Another interesting approach is generation of a

business process model from business rule

descriptions in SBVR (Semantic Business

Vocabulary and Rules) language (Steen, Pires and

Iacob, 2010). The authors apply the same idea that

preconditions and consequences form control flows

between activities.

Causality is also the very important concept in

conditional logic, in artificial intelligence, e.g. for

planning tasks (Wobcke, 1994; Giunchiglia et al.,

2004), and in the framework of action systems

(Giordano and Schwind, 2004). Giordano and

Schwind (2004) indicate that causal implication can

exist between two types of assertions:

 An action can cause a fact to become true, or

 A fact can cause another fact.

In the first case, the causal implication relates also

to a state transition, so the caused fact “belongs” to

the “next state”. In the second case, the causal

implication does not touch any state, the

modifications occur in the same state. As Giordano

and Schwind (2004) formulate: “caused facts are

regarded as indirect effects of actions”. The authors

also formulate several restrictions: a causal

implication cannot itself cause other facts, causality is

not reflexive, causal implication is not monotonic,

material implication is excluded, and that a domain

constraint must hold in all states of the world. Giving

these restrictions, the authors have formulated “the

causal action logic AC”. This logic is introduced into

a new approach for reasoning about actions and

causation. The main idea presented in this logic is

similar to the reasoning applied in the topological

functioning modelling.

MDI4SE 2018 - Special Session on Model-Driven Innovations for Software Engineering

498

5 CONCLUSIONS

Understanding causal dependencies is very important

for modelling system behaviour and structure. Causal

implications relate as to facts and system states as to

transitions between states. The TFM is a formal

model where discovering causal implications (named

cause-and-effect relations) is one of the key

principles. Incorrect cause-and-effect relations leads

to incorrect control and data flows in design models

and code.

In the context of our research we assume that

cause-and-effect relations could be retrieved from

specifications of system functional characteristics,

i.e. functional features. Certainly, we see three

bottlenecks here:

 Correctness and completeness of conditions

before and after execution of a functional

feature;

 Automated support for determination of those

conditions (facts, states, domain constraints);

 Syntactical correctness of descriptions of

combinations of the conditions.

The last one can be controlled by the software tool

used for system analysis. The first two depends on

quality of processing textual descriptions of the

system functionality.

The resulting generated topological space and the

TFM can be used, first, as a supporting model for

semantical analysis of completeness and consistency

of causal flows and functional characteristics of the

modelled domain, and second, as a root model for

generation of analysis and design models from the

topological functioning model.

The future research is related to extending the

knowledge frame system with the knowledge about

the application domain and further transformation

and representation of the knowledge in design

models.

REFERENCES

Arora, V., Bhatia, R. and Singh, M., 2017. Synthesizing test

scenarios in UML activity diagram using a bio-inspired

approach, Computer Languages, Systems & Structures.

Pergamon, 50, pp. 1–19. doi: 10.1016/j.cl.2017.05.002.

Asnina, E. and Osis, J., 2010. Computation independent

models: Bridging problem and solution domains, in

Proceedings of the 2nd International Workshop on

Model-Driven Architecture and Modelling Theory-

Driven Development, MDA and MTDD 2010, in

Conjunction with ENASE 2010. SCITEPRESS -

Science and and Technology Publications, pp. 23–32.

Asnina, E. and Osis, J., 2011. Topological Functioning

Model as a CIM-Business Model, in Model-Driven

Domain Analysis and Software Development. Hershey,

PA: IGI Global, pp. 40–64. doi: 10.4018/978-1-61692-

874-2.ch003.

Asnina, E. and Ovchinnikova, V., 2015. Specification of

Decision-making and Control Flow Branching in

Topological Functioning Models of Systems, in

Proceedings of the 10th International Conference on

Evaluation of Novel Approaches to Software

Engineering. SCITEPRESS - Science and and

Technology Publications, pp. 364–373. doi:

10.5220/0005479903640373.

Briand, L., Labiche, Y. and Lin, Q., 2010. Improving the

coverage criteria of UML state machines using data

flow analysis, Software Testing, Verification and

Reliability. John Wiley & Sons, Ltd., 20(3), pp. 177–

207. doi: 10.1002/stvr.410.

Donins, U., 2012a. Semantics of Logical Relations in

Topological Functioning Model, in Proceedings of the

7th International Conference on Evaluation of Novel

Approaches to Software Engineering, Wrocław,

Poland, 29-30 June, 2012. SciTePress, pp. 217–223.

Donins, U., 2012b. Topological Unified Modeling

Language: Development and Application. PhD Thesis.

Riga Technical University.

Donins, U., Osis, J., Asnina, E. and Jansone, A., 2012.

Formal analysis of objects state changes and transitions,

in ENASE 2012 - Proceedings of the 7th International

Conference on Evaluation of Novel Approaches to

Software Engineering. Lisbon: SciTePress, pp. 249–

256.

Donins, U., Osis, J., Slihte, A., Asnina, E. and Gulbis, B.,

2011. Towards the refinement of topological class

diagram as a platform independent model, in

Čaplinskas, A., Dzemyda, G., Lupeikienė, A., and

Vasilecas, O. (eds) Proceedings of the 3rd International

Workshop on Model-Driven Architecture and

Modeling-Driven Software Development, MDA and

MDSD 2011, in Conjunction with ENASE 2011.

Vilnius: Žara, pp. 79–88.

Elstermann, M. and Heuser, T., 2016. Automatic Tool

Support Possibilities for the Text-Based S-BPM

Process Modelling Methodology, in Proceedings of the

8th International Conference on Subject-oriented

Business Process Management - S-BPM ’16. New

York, New York, USA: ACM Press, pp. 1–8. doi:

10.1145/2882879.2882882.

Giordano, L. and Schwind, C., 2004. Conditional logic of

actions and causation, Artificial Intelligence. Elsevier,

157(1–2), pp. 239–279. doi:

10.1016/j.artint.2004.04.009.

Giunchiglia, E., Lee, J., Lifschitz, V., McCain, N. and

Turner, H., 2004. Nonmonotonic causal theories,

Artificial Intelligence. Elsevier, 153(1–2), pp. 49–104.

doi: 10.1016/J.ARTINT.2002.12.001.

El Hichami, O., Naoum, M., Al Achhab, M., Berrada, I. and

El Mohajir, B. E., 2015. An Algebraic Method for

Analysing Control Flow of BPMN Models,

International Journal of Recent Contributions from

Retrieving the Topology from the Knowledge Frame System for Composition of the Topological Functioning Model

499

Engineering, Science & IT (iJES), 3(3), p. 20. doi:

10.3991/ijes.v3i3.4862.

Kluza, K. and Nalepa, G. J., 2017. A method for generation

and design of business processes with business rules,

Information and Software Technology. Elsevier, 91, pp.

123–141. doi: 10.1016/J.INFSOF.2017.07.001.

Kundu, D., Samanta, D. and Mall, R., 2012. An Approach

to Convert XMI Representation of UML 2.x Interaction

Diagram into Control Flow Graph, ISRN Software

Engineering. Hindawi, 2012, pp. 1–22. doi:

10.5402/2012/265235.

Lin, C.-P., Jeng, L.-D., Lin, Y.-P. and Jeng, M., 2005.

Management and control of information flow in CIM

systems using UML and Petri nets, International

Journal of Computer Integrated Manufacturing, 18(2–

3), pp. 107–121. doi: 10.1080/0951192052000288242.

Nazaruka, E., Ovchinnikova, V., Alksnis, G. and

Sukovskis, U., 2016. Verification of BPMN Model

Functional Completeness by using the Topological

Functioning Model, in Proceedings of the 11th

International Conference on Evaluation of Novel

Software Approaches to Software Engineering.

Portugal: SCITEPRESS - Science and and Technology

Publications, pp. 349–358. doi:

10.5220/0005930903490358.

Nazaruks, V. and Osis, J., 2017a. A Survey on Domain

Knowledge Representation with Frames, in

Proceedings of the 12th International Conference on

Evaluation of Novel Approaches to Software

Engineering (ENASE 2017). Porto, Portugal:

SCITEPRESS - Science and Technology Publications,

pp. 346–354.

Nazaruks, V. and Osis, J., 2017b. Joint Usage of Frames

and the Topological Functioning Model for Domain

Knowledge Presentation and Analysis, in Proceedings

of the 12th International Conference on Evaluation of

Novel Approaches to Software Engineering - Volume 1:

MDI4SE. Porto, Portugal: SCITEPRESS - Science and

Technology Publications, pp. 379–390. doi:

10.5220/0006388903790390.

Osis, J., 1969. Topological Model of System Functioning

(in Russian), Automatics and Computer Science, J. of

Academia of Siences, (6), pp. 44–50.

Osis, J. and Asnina, E., 2008. Enterprise Modeling for

Information System Development within MDA, in

Proceedings of the 41st Annual Hawaii International

Conference on System Sciences (HICSS 2008).

Waikoloa, USA: IEEE, pp. 490–490. doi:

10.1109/HICSS.2008.150.

Osis, J. and Asnina, E., 2011. Topological Modeling for

Model-Driven Domain Analysis and Software

Development : Functions and Architectures, in Model-

Driven Domain Analysis and Software Development:

Architectures and Functions. Hershey, PA: IGI Global,

pp. 15–39. doi: 10.4018/978-1-61692-874-2.ch002.

Osis, J., Asnina, E. and Grave, A., 2008. Computation

Independent Representation of the Problem Domain in

MDA, e-Informatica Software Engineering Journal,

2(1), pp. 29–46. Available at: http://www.e-

informatyka.pl/index.php/einformatica/volumes/volum

e-2008/issue-1/article-2/ (Accessed: 4 January 2018).

Osis, J. and Donins, U., 2010. Formalization of the UML

Class Diagrams, in Evaluation of Novel Approaches to

Software Engineering. New York: Springer, Berlin,

Heidelberg, pp. 180–192. doi: 10.1007/978-3-642-

14819-4_13.

Osis, J. and Slihte, A., 2010. Transforming Textual Use

Cases to a Computation Independent Model, in Osis, J.

and Nikiforova, O. (eds) Model-Driven Architecture

and Modeling-Driven Software Development: ENASE

2010, 2ndMDA&MTDD Whs. SciTePress, pp. 33–42.

Ovchinnikova, V. and Nazaruka, E., 2016. The Validation

Possibility of Topological Functioning Model using the

Cameo Simulation Toolkit, in Proceedings of the 11th

International Conference on Evaluation of Novel

Software Approaches to Software Engineering.

SCITEPRESS - Science and and Technology

Publications, pp. 327–336. doi:

10.5220/0005926003270336.

Roux, C., 2013. Can ‘ Made Up ’ Languages Help

Computers Translate Real Ones ? Available at:

http://www.xrce.xerox.com/About-XRCE/History/20-

Years-of-Innovation-in-Europe/Articles/Can-made-up-

languages-help-computers-translate-real-ones.

Slihte, A., 2015. The Integrated Domain Modeling: an

Approach & Toolset for Acquiring a Topological

Functioning Model. Ph.D. Thesis. Riga Technical

University.

Slihte, A., Osis, J. and Donins, U., 2011. Knowledge

Integration for Domain Modeling, in Osis, J. and

Nikiforova, O. (eds) Model-Driven Architecture and

Modeling-Driven Software Development: ENASE

2011, 3rd Whs. MDA&MDSD. SciTePress, pp. 46–56.

Steen, B., Pires, L. F. and Iacob, M.-E., 2010. Automatic

Generation of Optimal Business Processes from

Business Rules, in 2010 14th IEEE International

Enterprise Distributed Object Computing Conference

Workshops. IEEE, pp. 117–126. doi:

10.1109/EDOCW.2010.40.

Stiehl, V., 2014. Architecture Process-driven applications

Architecture of Process-Driven Applications, in

Process-Driven Applications with BPMN. Cham:

Springer International Publishing, pp. 43–109. doi:

10.1007/978-3-319-07218-0_3.

Todoran, E. N. and Mitrea, P., 2015. Semantic investigation

of a control-flow subset of BPMN 2.0, in 2015 IEEE

International Conference on Intelligent Computer

Communication and Processing (ICCP). IEEE, pp.

483–490. doi: 10.1109/ICCP.2015.7312707.

Wobcke, W., 1994. A conditional logic for planning and

plan recognition, in Proceedings of ANZIIS ’94 -

Australian New Zealnd Intelligent Information Systems

Conference. IEEE, pp. 382–386. doi:

10.1109/ANZIIS.1994.396993.

MDI4SE 2018 - Special Session on Model-Driven Innovations for Software Engineering

500