Implementation, Identification and Control
of an Efficient Electric Actuator for Humanoid Robots
Florent Forget
1
, Kevin Giraud-Esclasse
1
, Rodolphe Gelin
2
, Nicolas Mansard
1
and Olivier Stasse
1
1
CNRS - LAAS, Toulouse, France
2
SoftBank Robotics Europe, Paris, France
Keywords:
Actuation, Humanoids.
Abstract:
Autonomous robots such as legged robots and mobile manipulators imply new challenges in the design and
the control of their actuators. In particular, it is desirable that the actuators are back-drivable, efficient (low
friction) and compact. In this paper, we report the complete implementation of an advanced actuator based
on screw, nut and cable. This actuator has been chosen for the humanoid robot Romeo. A similar model of
the actuator has been used to control the humanoid robot Valkyrie. We expose the design of this actuator and
present its Lagrangian model. The actuator being flexible, we propose a two-layer optimal control solver based
on Differential Dynamical Programming. The actuator design, model identification and control is validated
on a full actuator mounted in a work bench. The results show that this type of actuation is very suitable for
legged robots and is a good candidate to replace strain wave gears.
1 INTRODUCTION
Mobile robots, such as legged robots and humanoid
robots, imply new challenges in the design of their
actuation system. In this context, it is very important
that the robot is able to feel the force that it exerts
on its environment. At the same time, the actuator
must be light-weight and compact. Direct-drive actu-
ation is then not an option. On many electric-powered
humanoid robot, strain wave gears (e.g. Harmonic
Drive gear) are used for their compactness. How-
ever, if back-drivable, strain wave gears have a poor
transparency, i.e. the torque exerted at the joint level
(output) is poorly correlated to the torque at the mo-
tor level (input), and the output torque is difficult to
estimate from the motor current. If an accurate joint-
torque estimation is needed, a joint torque sensor must
be added to the robot design, which increases the to-
tal design cost and the actuation flexibility. Moreover,
strain-wave gears are sensitive to impacts, which tend
to damage the gear. Their maximum torques are also
limited, in particular when impacts have to be ex-
pected. For the design of full-size humanoid robots
(i.e. size similar to Shaft, NASA Valkyrie, PAL Ta-
los), strain-wave gears are clearly one of the main
limiting factor of the design. On the other hand, most
of alternative gears are either not compact enough, or
with insufficient reduction ratio.
Figure 1: The leg of the robot Romeo are designed based
on a screw-nut-cable actuator, which are shock-proof and
low-friction, but induce a flexibility due to the cable.
The design of such kind of actuators is a widely
studied subject. Different technologies are used to ad-
dress these problems. Electric-based actuation is very
desirable because it is simple to implement, hence
also more reliable for a given integration effort. A first
step is to adapt electric motors to humanoid robotics
needs as it is done in (Wensing et al., 2017) for
quadruped robot. By increasing the motor diame-
ter, the nominal speed is lowered while the nominal
torque is improved, allowing to reduce the reduction
Forget, F., Giraud-Esclasse, K., Gelin, R., Mansard, N. and Stasse, O.
Implementation, Identification and Control of an Efficient Electric Actuator for Humanoid Robots.
DOI: 10.5220/0006825500290038
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 29-38
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
29

ratio and so having a more backdrivable system. An-
other route is to improve the design of the gear box,
as done in (Englsberger et al., 2014) where authors
chose to improve strain-wave gears technology to
build a torque-controlled robot. However, despite the
improvement, strain-wave gear implies many draw-
backs: insufficient torque limit, sensitivity to impact,
lack of efficiency and of transparency. Adding a pas-
sive element at the gear output releases a part of the
limitations: it protects the gear from impact. It also
makes a part of the actuation transparent, while an en-
coder may be used to directly (after calibration) mea-
sure the torque applied on the joint side. However,
the passive element makes the actuation more difficult
to control and intrinsically lowers the possible con-
trol bandwidth, which is not desirable for achieving
fast-dynamics movements. Variable-stiffness actua-
tors as in (Wolf and Hirzinger, 2008) makes it pos-
sible to dynamically stiffen the robot when high dy-
namics is needed, but then boiling down to the same
limits as rigid electric actuation. On a quite different
route, hydraulic technology is promising to conceive
robotics actuators allowing good power to weight ra-
tio and shock absorption (Semini et al., 2011; Alfayad
et al., 2011), although the implementation of the com-
plete robot becomes more challenging.
In this paper, we present the complete implemen-
tation (design, modeling, identification and control)
of a screw-nut-cable compact actuator based on (Gar-
rec, 2010). This actuator has been used to design the
legs of the humanoid robot Romeo (see Fig. 1). A
similar model of the actuator has been used to control
the humanoid robot NASA R5 (Valkyrie) (Mehling,
2015), although the control strategy built upon it is
different from ours. In the context of the new NASA
challenge with this humanoid robot, the work pre-
sented in this paper is very relevant.
The actuator offers reduction ratio up to 150 while
keeping compact design. It has a high tolerance to
shocks and impacts and offers a high transparency,
making it reliable to estimate output torques from
motor currents. It also induces flexibility coming
from the cable connecting the screw to the joint out-
put. Adding elasticity into the actuation smoothes
the contact with the environment, which prevent re-
bound and in certain case sliding effects (Lee et al.,
2016). The flexible element in this particular gear
can also be exploited to directly measuring the output
torques, by equipping it with sensor able to measure
the spring deflection (e.g. angle encoders attached
to each side of elasticity). We show that measures
of torques/forces can be obtained for quasi-null addi-
tional cost. The flexible element behaves like a series-
elastic actuator (SEA) (Pratt and Williamson, 1995).
(4) Geared-
wheel,
(5) Ball-screw
Turn-
buckle (12)
Joint (11)
(2) Pinion,
(3) Toothed-
belt
(1) Motor
Joint
Encoder
(14)
Cable (9)
Top end
stop
(10) Ball
crimped on
the cable
Ball
sleeve (7)
Flexible
coupling (6)
Screw (5)
(hollow-
screw)
(8) Fitted
shaft
Nut and
Geared-
wheel (4)
(12) Turn-
buckle
Figure 2: Right (top) and left (bottom) views of the actuator.
It must be taken into account in the actuator control
loop to avoid instability. However, the flexibility is an
order of magnitude smaller than on typical SEA.
The contributions of the paper are as follows. We
report the implementation of the concept gear (Gar-
rec, 2010) in Section 2 and present an original La-
grangian model of the actuator. Based on this model,
we propose in Section 3 a model-predictive controller
(MPC) based on differential dynamic programming
(DDP) (Tassa et al., 2014) able to cope with the ac-
tuator flexibility with only few parameters left to the
designer to tune. The optimal controller can be set
up to either implement a position controller (i.e. by
tracking the output position) or a force controller (i.e.
by tracking a reference spring deflection). We imple-
mented the proposed approach in one of the actuator
of Romeo mounted in a work-bench. We report in
Section 4 the identification of the parameters of the
Lagrangian model, the results of controlling the real
actuator to track joint references and the study in sim-
ulation of the torque bandwidth compared to state-of-
the-art actuators with similar ratio.
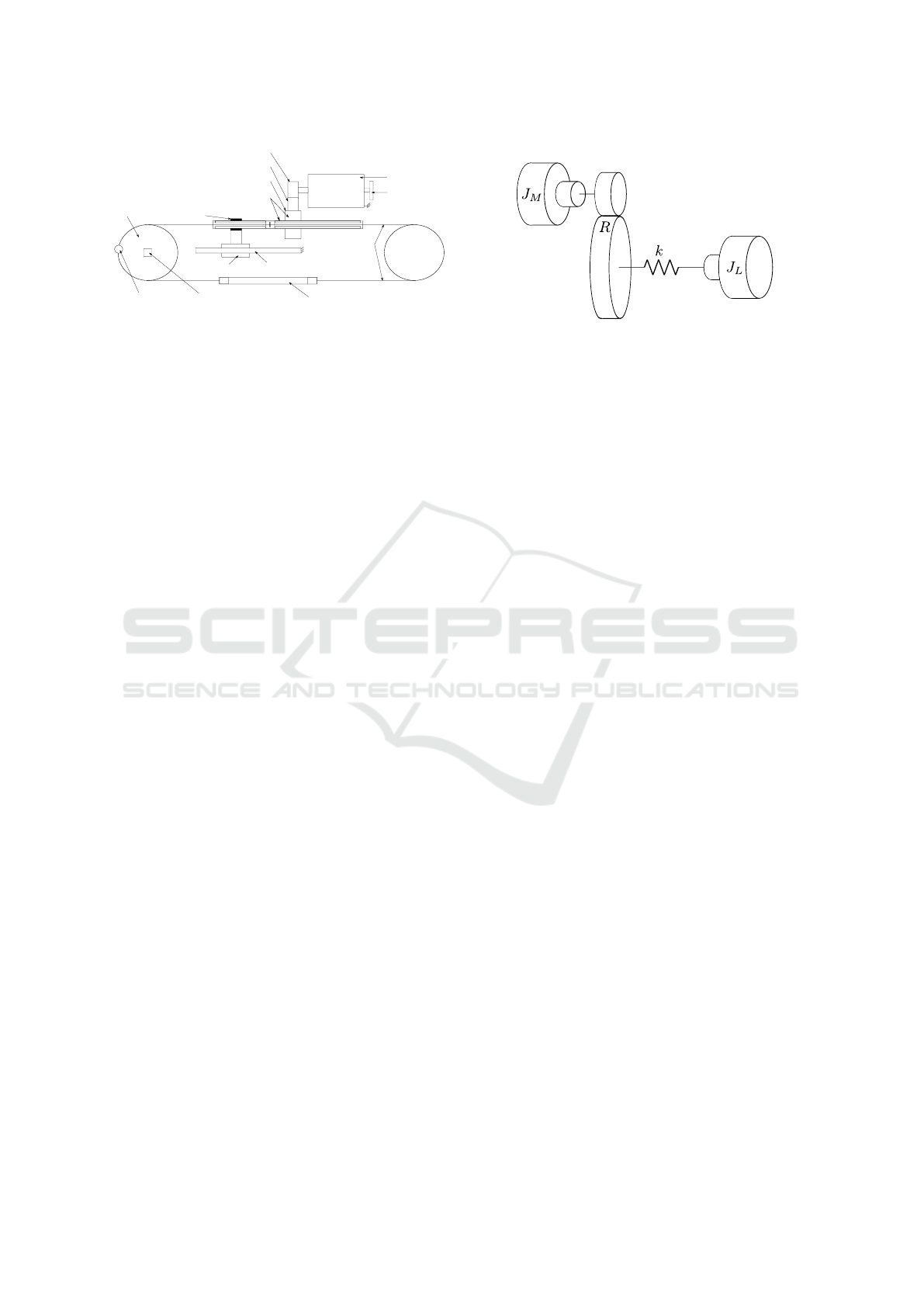
2 MODEL OF THE ACTUATOR
We recall here the main principles of the actua-
tor (Garrec, 2010), present the design of the actuator
used in the experiment and propose an original La-
grangian model upon which our controller is built.
2.1 Mechanical Description
The original design of the actuator has been proposed
in (Garrec, 2010). We recall here the general mecha-
nism of the actuator that we used in the result section.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
30

Motor (1)
(2) Pinion
(3) Toothed belt
(4) Geared wheel
(5) Ball screw (hollow
screw and nut)
Joint
encoder (14)
Ball sleeve (7) Fixed shaft (8)
Joint (11)
Crimped
ball (10)
Turn-buckle (12)
Cable (9)
Motor
encoder (13)
(6) Flexible
coupling
Figure 3: Schema of the actuator mounted on the work-
bench.
The actuator is composed of an electrical motor at-
tached to a ball screw which is guided along a fixed
axis but can freely rotate inside the nut. The output of
the screw is connected to two cables which can pull
the output joint in the two rotation directions. Our
particular actuator is mounted in a workbench used
for identification and control validation. The same ac-
tuator equips 10 degrees of freedom of the legs of the
medium-size humanoid robot Romeo. Two pictures
of the actuator with legends are shown in Fig. 2. A
schema of the actuator is shown in Fig. 3.
The motor (referenced as (#1) in Fig. 2) is fixed
on the base, a pinion (#2) is mounted on its shaft. The
pinion leads a toothed belt (#3) to a geared wheel (#4).
This part is fixed to the nut of the ball screw (#5). The
screw is the main component allowing the trade-off
between a high reduction ratio (of about 100) and a
high reversibility. It also increases the compactness
of the system. To avoid the screw rotation around its
main axis and to enforce its motion to be a transla-
tion, an additional part is flexibly coupled (#6)(#7) be-
tween the screw and a fixed shaft (#8). Note that this
part is not introducing the elasticity we try to manage
in this paper.
The cable (#9) is the main part of the system in-
troducing the flexibility we deal with in this paper.
The forward part of the cable is linked to the joint
with a crimped ball (#10) placed in the spherical im-
print of the joint (#11). The cable then goes to the
turn-buckle (#12). The backward part of the cable is
also going to the turn-buckle by the way of a pulley.
The turn-buckle is used to fix and pre-load the cable.
To keep the workbench simple to use, a rope is at-
tached to the joint (#11) in order to apply some load.
This set-up limits the output load to only one direc-
tion of the joint. This has no negative consequence
for our experimental protocol in comparison with the
real robot.
To measure the angle positions, two absolute mag-
netic encoders are mounted on each side of the gear.
One is fixed behind the motor on its main shaft (#13),
the other is placed on the joint (#14), after the trans-
Motor
Gear Box
Rotational
Spring
Load
Figure 4: System considered for the actuator modeling.
mission chain. This layout measures the ratio and the
deformation on the transmission and makes the model
parameters theoretically observable.
Even though the flexible coupling should increase
the transparency of the system, it seems to create
constraints on the screw by preventing it to oscil-
late freely. Moreover, contrary to (Garrec, 2010), the
space around the cable (attached in the middle of the
hollow screw with a crimped sleeve) is not sufficient,
generating constraints in the mechanism. These con-
straints create efforts and introduce non-linear and
frictions depending on the actuator angular position
(as detailed in Section 4.1).
2.2 Lagrangian Model
With respect to the mechanical description given be-
fore, we use the following assumptions to construct
the system model:
[A1] The DC motor driving the mechanism is con-
sidered as a perfect source of torque.
[A2] Flexibilities are concentrated on a single linear
rotational spring with constant stiffness.
Assumption [A1] is advisable as the motor is current
controlled. Neglecting all magnetic loss the current
is directly proportional to the motor output torque.
We assume that the current controller is good and fast
enough to provide our requested current command.
Assumption [A2] is reasonable as the stiffness of the
cable is several orders of magnitude lower than the
stiffness of any other element in the transmission.
The actuator then boils down to a two-masses sys-
tem attached by a spring, as illustrated in Fig. 4. The
first mass is driven by a DC motor coupled with the
gearbox. The second mass is interacting with the en-
vironment. Friction arises in opposition to the motion
of both masses.
Using Lagrangian formalism, we expose the fol-
lowing model describing classical series elastic actu-
ator. We empirically decided during the identification
Implementation, Identification and Control of an Efficient Electric Actuator for Humanoid Robots
31

experiments to consider viscious friction on both mo-
tor and load side and dry friction on motor side.
J
M
¨
θ
M
= µK
T
i
M
−
k
R
(
θ
M
R
− q) −d
M
˙
θ
M
−C
f
sign(
˙
θ
M
)
(1a)
J
L
¨q = τ
ext
+ k(
θ
M
R
− q) − d
L
˙q (1b)
where the notations are given in Tab 1. In order to
keep the equations smooth (as needed for the con-
troller), we used a smooth version of the sign function
(i.e. a hyperbolic tangent).
Table 1: Variables and parameters used in the model and
corresponding values estimated on our system.
Symbol Physic meaning Identified value
J
M
motor inertia 1.38 × 10
−5
kg.m
2
J
L
load inertia 8.5 × 10
−4
kg.m
2
θ
M
motor angular position variable (rad)
q joint angular position variable (rad)
k equivalent rotational spring stiffness 588 Nm/rad
R transmission ratio 96.1
τ
M
motor torque variable (Nm)
τ
ext
external torque (environment) variable (Nm)
d
M
vicious friction at motor level 0.003 Nm/(rad/s)
d
L
vicious friction at load level 0.278 Nm/(ras/s)
C f dry friction at motor level 0.1 Nm
K
T
motor current to torque ratio 60.3 × 10
−3
Nm/A
µ motor efficiency 0.78
Because several mechanical phenomena were dif-
ficult to model (see Section 4.1), we make the choice
to keep a simple model. We could improve the model
by identifying more precisely the frictions (coulomb,
viscous and those depending on the angular position
of the joint) as well as by more finely modelling the
dynamics of the flexible elements (the system is com-
posed of 2 flexible cables of different lengths, thus
having 2 different dynamics). In practice, the good
transparency of the gear make it possible to properly
estimate the forces applied on the actuator. We can
then rely on feedback more than on feedforward, be-
ing given that the control law (hence the model) is
sufficiently fast to be evaluated. The rational is the
higher the control frequency, the lower error between
the real system state and its estimation and the more
accurate the control.
3 CONTROL
As reported in previous section, the actuator behaves
like a SEA transmission, with higher stiffness than
typical SEA implementation. Different methods can
be used to handle these flexibilities, first by consid-
ering the actuator stiffness dynamics into the whole
body problem formulation like it is done in (De Luca
and Lucibello, 1998; Buondonno and De Luca, 2016)
for both series elastic or variable stiffness actuators.
Another option is to neglect this dynamic at the whole
body level while handling it locally at the joint level.
In this section, we present the control solution that we
implemented to track the joint reference, specified ei-
ther as reference position or as reference torque. Our
objective is then to compute the joint references from
a whole-body optimization scheme, that will be accu-
rately tracked by the joint controller running at high
frequency.
The controller we report below is composed of a
two-stage architecture: a first stage, running on CPU
at 1kHz, computes the optimal trajectory (feedfor-
ward) and the optimal feedback gains in a model-
predictive-control (MPC) style. The second layer,
running on the micro-controller at higher frequency
(5kHz or higher) uses the feedforward and the feed-
back gains to compute the reference current sent to
the motor. We start by a brief overview of possible
control approaches that justifies our implementation
based on differential dynamic programming (DDP).
3.1 Brief Control State of the Art
We are interested in setting up a controller either of
the output joint position (position controller), or of
the relative position of input and output (spring de-
flection, i.e. force controller). In both cases, the ma-
jor difficulty is the tuning of the control gains: high
gains on position loop are necessary for good preci-
sion but may make the system unstable due to the
flexibility. Several control schema have been devel-
oped to address this problem. The analysis of the
Eigen modes of the actuator models to achieve de-
sired convergence, stability and precision (Mehling,
2015; Paine et al., 2015) is difficult due to the model
non-linear terms. Moreover, the same controller must
be deployed on several variations of the same actua-
tor implemented on the legs of Romeo. A more auto-
matic method is desirable.
A method has been proposed in (Abroug and
Laroche, 2015) to control SEA using H
∞
. It relies on
automatic controller tuning from identification data.
However, the results that the controller is quite sen-
sitive to identification errors, which makes it difficult
to generalize. Alternatively, optimal control is very
versatile (i.e. the controller can be quickly adapted to
track either position or force references) and is quite
resilient in practice to errors in the model (Sardellitti
et al., 2013; Geoffroy et al., 2014). It is also straight-
forward to generalize it to other SEA/VSA mecha-
nisms, like pneumatic muscles (Das et al., 2016). Op-
timal controller can also handle constraints like torque
or position limits (Tassa et al., 2014). Optimal control
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
32

has been used to control both joint position and stiff-
ness of an approximate linear model (LQR) (Sardel-
litti et al., 2013). Dedicated approximations using
polynomials have then been used to fit the computa-
tion capabilities of the control board.
We rather propose here a two-stage approach to
combine the versatility of the nonlinear optimal con-
trol problem with the efficiency needed to solve it on
the control board. The nonlinear problem is solved at
medium frequency by the central CPU. The optimal
control, along the corresponding Ricatti gains are then
sent to the control board where the optimal control is
updated from sensor measurements at high frequency.
To keep the nonlinear solver simple while enforcing
joint constraints, we implemented a box-DDP (Tassa
et al., 2014), running at 1kHz. The control board then
applies a PID corrector (using Ricatti gains extracted
from the DDP) at 5kHz.
3.2 Differential Dynamic Programming
DDP is an optimal control scheme with a “single
shooting” strategy, that is able to efficiently cope with
the sparsity of the underlying numerical system but
has the drawbacks of being quite unable to handle
complex constraints. This trade-off is very suitable
to our problem. We recall here the basis of DDP. This
recall is needed for understanding how we designed
both layers of our control architecture. More detailed
information about this optimal control solver can be
found in (Tassa et al., 2008).
Consider a generic mechanical system described
by its (discrete) dynamic equation:
x
i+1
= f
i
(x
i
,u
i
) (2)
Where x
i
represents the current state of the actuator
(position, speed, torque ...) and u
i
is the input com-
mand (current, torque, voltage ...). This model may
or not be linear and time varying. We expose the cost
we want to minimize on a given horizon T .
J(U|x
0
) =
T −1
∑
i=0
c
i
(x
i
,u
i
) + c
T
(x
T
) (3)
with X = {x
0
,x
1
,..., x
T
} and U = {u
0
,u
1
,..., u
T−1
}
respectively the state and control sequence over hori-
zon T and x
0
the initial state of the system (typically
estimated from sensors). It is to be noticed that know-
ing x
0
and U is enough to know the state of the system
at each moment of the horizon because of the rela-
tion (2). So the optimal control problem consists in
finding the correct U minimizing the cost for a given
x
0
initial state.
We introduce then the cost-to-go function to be
J
i
(U
i
|x
i
) =
T −1
∑
j=i
c
j
(x
j
,u
j
) + c
T
(x
T
) (4)
with x
j
integrated from x
i
. The optimum cost-to-go is
named the value function V :
V (x
0
,i) = min
U
i
J
i
(x
0
,U
i
) (5)
We obviously have that V (x
0
,T ) = c
T
(x
T
). The “Bel-
man” dynamic-programming principle teaches us that
minimizing the cost by choosing the correct control
sequence can be reduced to the backward minimiza-
tion of a single control input. This principle gives us
the Bellman equation :
V (x
i
,i) = min
u
[c
i
(x
i
,u
i
) +V ( f (x
i
,u
i
),i + 1)] (6)
The DDP solver computes the optimal control
sequence U by solving equation (6) backwardly in
time. For this purpose let Q be the variation of
c(x,u) +V ( f (x,u),i + 1) around the i − th state and
command. We have :
Q(δx,δu) ≡ c(x + δx, u + δu) − c(x,u)
+V ( f (x + δx, u + δu),i + 1))
−V ( f (x,u),i + 1))
(7)
By taking the second order approximation of (7) we
obtain:
Q(δx,δu) ≈
1
2


1
δx
δu


T


0 Q
T
x
Q
T
u
Q
x
Q
xx
Q
xu
Q
u
Q
ux
Q
uu




1
δx
δu


(8)
For readability we will use subscript notation to de-
note partial derivative (e.g. f
x
=
∂ f (x,u)
∂x
). We also
denote the next state by V
0
≡ V (i + 1). We can now
expose:
Q
x
= c
x
+ f
T
x
V
0
x
(9)
Q
u
= c
u
+ f
T
u
V
0
x
(10)
Q
xx
= c
xx
+ f
T
x
V
0
xx
f
x
+V
0
x
f
xx
(11)
Q
uu
= c
uu
+ f
T
u
V
0
xx
f
u
+V
0
x
f
uu
(12)
Q
ux
= c
ux
+ f
T
u
V
0
xx
f
x
+V
0
x
f
ux
(13)
Where the last term of the last three equations repre-
sents the contraction of a tensor with a vector. Mini-
mizing (7) with respect to δu gives us:
δu
∗
= argmin
δu
Q(δx,δu) = −Q
−1
uu
(Q
u
+Q
ux
δx) (14)
Showing up two terms:
• a feedforward term: k = −Q
−1
uu
Q
u
• a feedback term : K = −Q
−1
uu
Q
ux
Using back this result into (7), we obtain a quadratic
approximation of the value function at i −th instant:
∆V (i) = −
1
2
Q
u
Q
−1
uu
Q
u
(15)
V
x
(i) = Q
x
− Q
u
Q
−1
uu
Q
ux
(16)
V
xx
(i) = Q
xx
− Q
ux
Q
−1
uu
Q
ux
(17)
Implementation, Identification and Control of an Efficient Electric Actuator for Humanoid Robots
33

Algorithm 1: Differential Dynamic Programming Solver.
1: {initialisation :}
2: U ←random command sequence
3: X ←init(x
0
, U)
4: repeat
5: V (T ) ← c
T
(x
T
)
6: V
x
(T ) ← c
T x
(x
T
)
7: V
xx
(T ) ← c
T xx
(x
T
)
8: for i=T-1 down to 0 do
9: Q
x
,Q
u
,Q
xx
,Q
u
,Q
ux
← see equations (9) to
(13)
10: k ← −Q
−1
uu
Q
u
11: K ← −Q
−1
uu
Q
ux
12: ∆V,V
x
,V
xx
← see equations (15) to (17)
13: end for
14:
ˆ
x(0) = x(0)
15: for i=0 to T-1 do
16:
ˆ
u(i) = u(i) + k(i) + K(i)(
ˆ
x(i) − x(i))
17:
ˆ
x(i + 1) = f
i
(
ˆ
x(i),
ˆ
u(i))
18: end for
19: until convergence
Computing all term from (9) to (17) for i = N − 1
down to i = 0 is called the backward phase. We
then need to calculate the change induced on the state
sequence by the modification on the command se-
quence.
This is the forward phase, detailed below:
ˆ
x(0) = x(0) (18)
ˆ
u(i) = u(i) + k(i) + K(i)(
ˆ
x(i) − x(i))(19)
ˆ
x(i + 1) = f
i
(
ˆ
x(i),
ˆ
u(i)) (20)
The solver iterates on these two phases until conver-
gence of the result (minimal changes on U). One can
find the algorithm detailed in a pseudo-code on algo-
rithm 1.
In order to ensure good convergence and to add
some specificities to the algorithm, we decided also
to implement some other features:
Line Search
DDP being a type of Newton descent, line search al-
lows the algorithm to adapt the step length so that con-
vergence is faster.
Regularization
DDP implies the inversion of Q
uu
matrix which in
certain cases may not be invertible. Regularization
makes the matrix invertible if it was not in the first
place and it integrates this modification into the whole
computation.
SYSTEM
PID
DDP
+
+
+
-
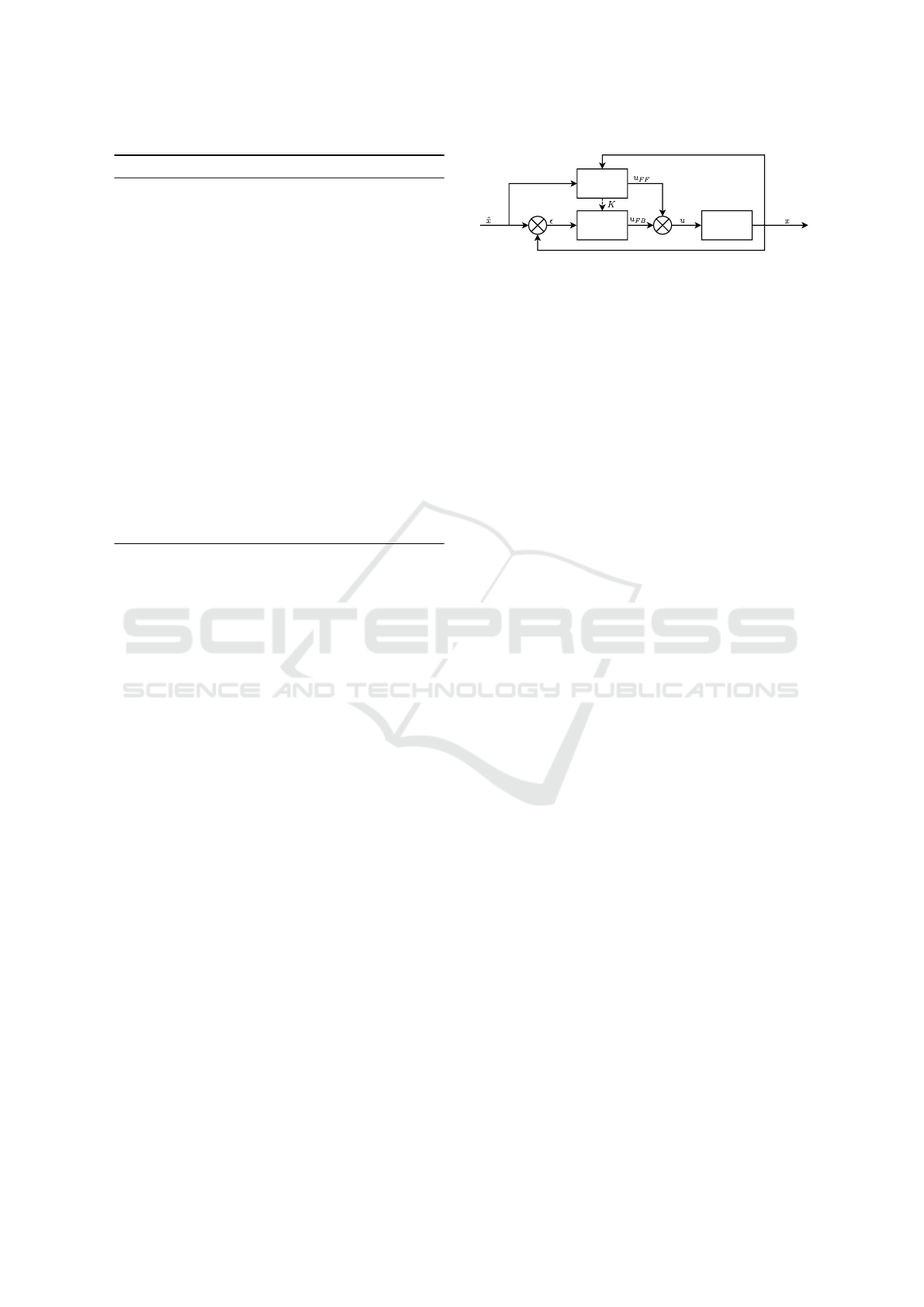
Figure 5: General architecture of the proposed DDP-based
MPC controller. The DDP running of CPU computes the
optimal (feedforward) control u
FF
and the Ricatti gains K
at 1Khz. The control board (PID) then adds a feedback term
u
FB
at 5Khz.
Control Limitation
Introduced in (Tassa et al., 2014), the control limited
DDP is an extension of the DDP where it is possible to
add bound constraints on the command input vector.
In practice this feature is possible by solving a box
QP problem.
3.3 Two-stage Control Architecture
The outputs of the DDP solver are the optimal tra-
jectories in both control U and state X spaces, along
with the optimal feedback gains along this trajectory
K. Our objective is to use at best this information to
feedback as frequently as possible on the sensor mea-
surements.
For that, we implement the DDP as a model-
predictive (receding-horizon) control scheme. At any
instant, we maintain a valid (possibly suboptimal)
control trajectory U
∗
. As soon as the DDP performed
one valid step of the nonlinear search loop (line #4 of
Alg. 1), the solver candidate trajectory U is used to
update U
∗
. The receding horizon of the DDP is then
shifted, while the initial state of this new horizon is
updated to the latest state estimation. The dynamic
system considered in our DDP (1) is low-dimension
and thus leads to short computation timings. It is easy
to implement such solver to obtain 1kHz control fre-
quency. However, it is difficult to implement the DDP
solver directly on the actuator micro-controller, but
rather on the central robot CPU board. The frequency
is then limited by the communication bandwidth to
upload the sensor measurements and download the
control references.
On the other hand, the micro-controller of the ac-
tuator is able to update the motor control at much
higher frequency (e.g. 5kHz). This higher frequency
enables us to take advantage of the optimal feed-
back gains computed by the DDP solver. On the
micro-controller, we then maintain an optimal con-
trol (feedforward) trajectory and the corresponding
optimal feedback gains along this trajectory. At each
control cycle of the micro-controller, the state is esti-
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
34

0 1 2 3 4 5
time (s)
−0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
joint angle (rad)
Estimation
Measurements
Figure 6: Comparison between model and real system re-
sponse to a same control input (motor current).
mated from previous sensor measurements. The con-
trol (reference motor current i
∗
) is then computed as
the sum of the feedforward (optimal control u
∗
) and
feedback (optimal gains K
∗
):
i
∗
(t) = u
∗
(t) + K
∗
(x
∗
(t) −
ˆ
x(t))
where x
∗
is the latest optimal trajectory in the state
space computed by the DDP and ˆx is the estimated
state.
Fig. 5 shows the general architecture of the pro-
posed controller. The DDP controller runs at 1kHz on
CPU and produces the feedforward control u
FF
. The
feedback controller runs at 5kHz on micro-controller,
estimates the state and produces the feedback control
u
FB
from the optimal gains K. The communication
bus between micro-controller and CPU board carries
the estimated state at 5kHz and the optimal feedfor-
ward and gains at 1kHz. Both feedforward and feed-
back are finally summed and used to servo the motor
current.
4 SIMULATION AND
EXPERIMENTS
4.1 Actuator Parameters Estimation
Off-line estimation: All measurements (joint po-
sition, motor position, motor current, motor supply
voltage ...) are collected while controlling the actu-
ator with a simple controller (PID with low gains).
The estimation of the model parameters is done using
MATLAB
R

. The result is shown in Fig. 6, by com-
paring simulated and hardware response to a same
open-loop control. Thanks to the transparency of the
actuator, the model is easily identified. The predic-
tion in simulation properly fits with the real trajectory.
Although the parameters are better estimated than on
other types of transmission, the identification is not
1.0 1.2 1.4 1.6 1.8 2.0 2.2
joint angular position (rad)
0
5
10
15
20
25
torque (Nm)
1.0 1.2 1.4 1.6 1.8 2.0 2.2
joint angular position (rad)
0
5
10
15
20
25
Figure 7: Output joint torque estimation: (left) using
only the two joint encoders measuring the spring deflec-
tion (right) using the current measures and the full actuator
model. The estimation from encoders is biased by the fric-
tion in the hardware. The current measure leads to a quite
good torque estimation although noisy. Both measures are
satisfactory given the absence of a direct torque sensor, and
are complementary. Each color represents a different output
load (masses attached to the actuator output).
perfect. From the captured data, we identified that
this comes from several defects in the implementa-
tion of the actuator (ball-screw being too much con-
strained by the flexible coupling, cable being not free
enough at the mounting with the ball-screw, elasticity
being different in the two directions due to the un-
equal length of the two cables). It would be possible
to model these effects, hence to obtain a better pre-
diction. However, it would also make the controller
more complex and more costly. We rather believe that
it would be easier to correct this effect by a more care-
ful implementation of the actuator.
On-line estimation: The actuator is not equipped
with direct torque sensor. However, two indirect mea-
surements are available. We have two encoders on
each side of the flexibility, and can then use the model
to estimate the output torque. Thanks to the actua-
tor transparency, we can also use the measured mo-
tor current to estimate the output torque. To validate
both measurements, we took measurements points for
different joint positions in a static state with different
known masses attached to the actuator output. The
mass being static, the output torque is known and can
be compared to the estimation using either the en-
coders or the current sensor. The result is displayed in
Fig. 7. Both estimations are accurate. They also are
complementary: the estimation from the encoders is
biased by friction; the estimation from current is more
noisy. Merging both estimations in a proper estimator
would lead to an accurate estimation able to compete
with a direct torque measurement (without the price,
Implementation, Identification and Control of an Efficient Electric Actuator for Humanoid Robots
35

0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0
time (s)
−0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
joint angle (rad)
simulation (ideal)
feedforward only (biased)
feedback only (biased)
feedforward + feedback (biased)
Figure 8: Simulation for ideal and biased model with feed-
forward and/or feedback (similar trajectories are obtained
when a single term is active).
implementation issue and fragility of an actual torque
sensor).
In conclusion, the transparency of the actuator
leads to accurate model estimation, both for (off-line)
calibration and (on-line) torque estimation.
4.2 Experiments - Position Control
Simulation: We validate first the position controller in
simulation, using the model and the two-stage MPC
presented above. The MPC uses the true (identified)
model for prediction, while the simulation is inte-
grated using a biased model (parameters randomly
modified of 50% – for convenience we only plot re-
sults for a single biased model). Control frequencies
are the same as on the real system. Fig. 8 displays
the effect of the feedback and feedforward terms for
a step input. The reference is accurately tracked. The
steady state is quickly reached because the actuator is
quite stiff. By mixing feedback and feedfoward, the
MPC offers a good robustness to modeling errors.
Hardware experiments: The same experiments
have been made on the real system. Results are dis-
played on Fig. 9 and 10. The reference is properly
tracked, with the steady state being reached with a
time similar to the ideal case. As in simulation, mix-
ing feedforward and feedback helps to obtain a better
behavior. On the hardware, the modeling errors are
more significant than with the simulated models (due
to non modeled effects as already mentioned, like pe-
riodic friction, etc). The box-DDP is useful in this
case to prevent current overshoot in the motor (e.g.
between 0.8s and 1.5s).
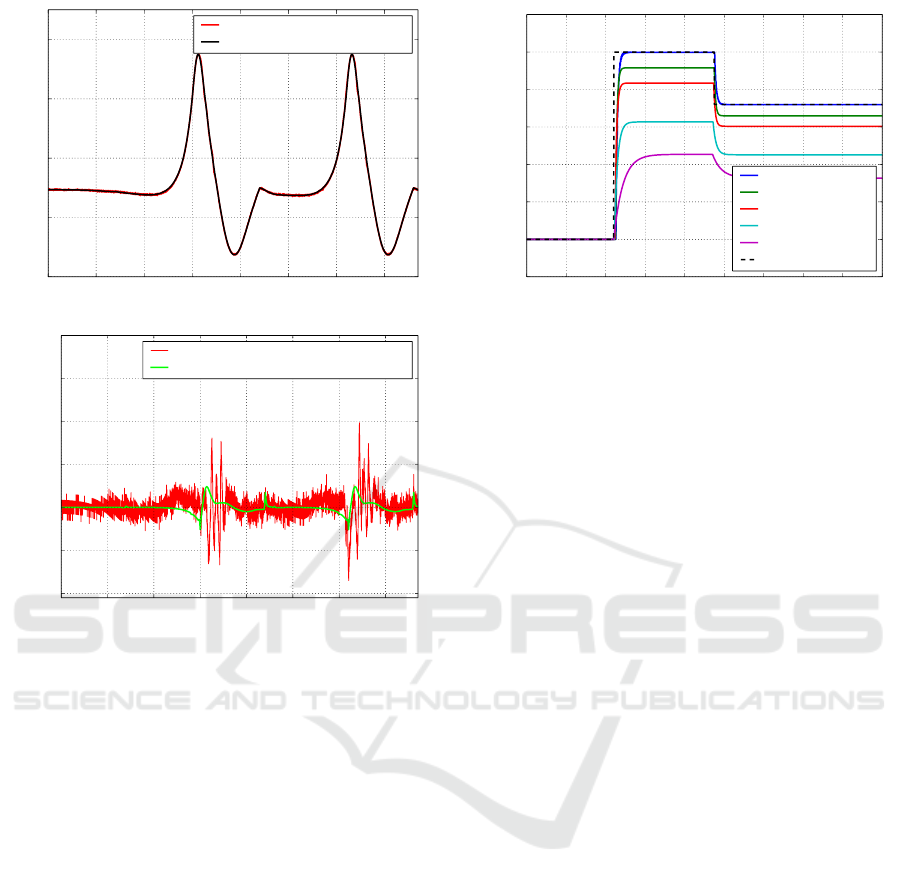
Finally, we show in Fig. 11 the results of track-
ing a realistic trajectory, taken from a walking move-
ment generated with a pattern generator (trajectory of
0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8
time (s)
−0.1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
joint angle (rad)
reference position
feedforward + feedback
feedforward only
Figure 9: Hardware experiment: position tracking with and
without feedforward (feedback must be alsways active on
hardware).
0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8
time (s)
−6
−4
−2
0
2
4
6
current (A)
Motor current command
Figure 10: Hardware experiment: motor current when
tracking a step position.
the knee of robot HRP-2 during 15cm stair climb-
ing). The trajectory is very dynamic. the first figure
shows the reference joint trajectory as well as the ac-
tual follow-up performed by the actuator controlled
using our method. The curves are very close, the av-
erage error is less than 1%. The error (difference be-
tween the desired position and the actual position of
the system) is displayed on the second figure in sim-
ulation and on the actual system. This error remains
very small and increases during sudden changes of di-
rection (dynamic movements).
4.3 Experiments - Torque Control
We also validate the torque controller, in simulation
only. Results are shown in Fig. 12. We again observe
the response of the controller to a step input. As be-
fore, the analysis is achieved while disturbing the pa-
rameters of the model used in simulation while keep-
ing the same MPC model. With a perfect model, the
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
36

0 1 2 3 4 5 6 7
time (s)
1.4
1.6
1.8
2.0
2.2
joint angle (rad)
joint angular position (workbench)
reference position
0 1 2 3 4 5 6 7
time (s)
−0.02
−0.01
0.00
0.01
0.02
0.03
0.04
joint angle error (rad)
tracking error on real system
tracking error on simulation for ideal system
Figure 11: Tracking a dynamic position trajectory. (up)
Reference and actual trajectories (down) Tracking error.
Less than 1% error in average was observed.
steady state is perfectly reached. The time to steady
state is shorter than with the position controller, as
expected. When bias is added, we keep a similar be-
havior but the reference is not perfectly reached any-
more. As we do not have a direct (non biased) esti-
mation of output torque, this would not be possible.
However, we also see that the behavior remains good
despite the bias and that improving the estimation of
the model parameters (in particular the stiffness) on-
line based on any external measurement of the output
torque would be quite easy.
5 CONCLUSION
In this paper, we have presented the complete imple-
mentation of a new compact, high-gear and transpar-
ent actuator, very suitable for mobile robots, in partic-
ular in the context of locomotion, with identification
and an original two-stage control scheme. The opti-
mal controller is lightweight, easy to implement, and
can compute a feedback at 5kHz on a micro-controller
0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8
time (s)
−0.5
0.0
0.5
1.0
1.5
2.0
2.5
3.0
joint torque(Nm)
ideal model
10% biased model
20% biased model
50% biased model
80% biased model
trajectory reference
Figure 12: Torque control of the actuator in simulation for
ideal and biased models with several levels of bias.
board. We have shown in the experiment results that
both layers are needed to efficiently control the actua-
tor: either feedforward or feedback alone are not able
to perform as efficiently. Moreover, we experimen-
tally showed the capabilities of the actuator in term of
transparency (i.e. estimating output torques from mo-
tor current), and the adequacy of the model to capture
the complexity of the actuator.
The main result of this study is that the actuator
with our control scheme offers very good property,
which makes it very suitable to replace strain-wave
gears in electric actuation of humanoid robots. In
particular, it offers full backdrivability (hence more
efficiency, less dangerousness and more chock re-
sistance) and accurate estimation of the output joint
torque without direct measurement (i.e. no force sen-
sor needed).
While the proposed control architecture is very
suitable for the screw-nut-cable actuator, it is also ap-
propriate for other kind of flexible actuators such as
SEA at large, variable stiffness actuators (Sardellitti
et al., 2013) or Mckibben pneumatic actuators (Das
et al., 2016). The MPC scheme can be easily adapted
to another dynamic model or another cost function.
Our objective is now to adapt the controller to the
whole body of the robot and to use it to control com-
plex humanoid movements.
ACKNOWLEDGMENT
This work was partially funded by the FLAG-ERA
JTC project ROBOCOM++, which aims at rethinking
robotics for the robot companion of the future.
Implementation, Identification and Control of an Efficient Electric Actuator for Humanoid Robots
37

REFERENCES
Abroug, N. and Laroche, E. (2015). Transforming se-
ries elastic actuators into variable stiffness actuators
thanks to structured h
∞
control. In European Control
Conference (ECC), pages 734–740.
Alfayad, S., Ouezdou, F. B., Namoun, F., and Gheng,
G. (2011). High performance integrated electro-
hydraulic actuator for robotics–part i: Principle, pro-
totype design and first experiments. Sensors and Ac-
tuators A: Physical, 169(1):115–123.
Buondonno, G. and De Luca, A. (2016). Efficient compu-
tation of inverse dynamics and feedback linearization
for vsa-based robots. IEEE Robotics and Automation
Letters, 1(2):908–915.
Das, G.-K.-H.-S.-L., Tondu, B., Forget, F., Manhes, J.,
Stasse, O., and Soueres, P. (2016). Controlling a
multi-joint arm actuated by pneumatic muscles with
quasi-ddp optimal control. In IEEE/RSJ Int. Conf.
on Intelligent Robots and Systems (IROS), pages 521–
528.
De Luca, A. and Lucibello, P. (1998). A general algo-
rithm for dynamic feedback linearization of robots
with elastic joints. In IEEE/RAS Int. Conf. on Robotics
and Automation (ICRA), volume 1, pages 504–510.
IEEE.
Englsberger, J., Werner, A., Ott, C., Henze, B., Roa, M. A.,
Garofalo, G., Burger, R., Beyer, A., Eiberger, O.,
Schmid, K., et al. (2014). Overview of the torque-
controlled humanoid robot toro. In IEEE/RAS Int.
Conf. on Humanoid Robots (Humanoids), pages 916–
923. IEEE.
Garrec, P. (2010). Design of an anthropomorphic up-
per limb exoskeleton actuated by ball-screws and ca-
bles. Bulletin of the Academy of Sciences of the Ussr-
Physical Series, 72(2):23.
Geoffroy, P., Bordron, O., Mansard, N., Raison, M., Stasse,
O., and Bretl, T. (2014). A two-stage suboptimal ap-
proximation for variable compliance and torque con-
trol. In Control Conference (ECC), 2014 European,
pages 1151–1157.
Lee, J., Choi, W., Kanoulas, D., Subburaman, R., Caldwell,
D. G., and Tsagarakis, N. G. (2016). An active com-
pliant impact protection system for humanoids: Ap-
plication to walk-man hands. In IEEE/RAS Int. Conf.
on Humanoid Robotics (ICHR), pages 778–785.
Mehling, J. S. (2015). Impedance Control Approaches for
Series Elastic Actuators. PhD thesis, Rice University.
Paine, N., Mehling, J. S., Holley, J., Radford, N. A., John-
son, G., Fok, C.-L., and Sentis, L. (2015). Actua-
tor control for the nasa-jsc valkyrie humanoid robot:
A decoupled dynamics approach for torque control
of series elastic robots. Journal of Field Robotics,
32(3):378–396.
Pratt, G. A. and Williamson, M. M. (1995). Series elastic
actuators. In IEEE/RSJ Int. Conf. on Intelligent Robots
and Systems (IROS), volume 1, pages 399–406.
Sardellitti, I., Medrano-Cerda, G. A., Tsagarakis, N., Jafari,
A., and Caldwell, D. G. (2013). Gain scheduling con-
trol for a class of variable stiffness actuators based on
lever mechanisms. IEEE Transactions on Robotics,
29(3):791–798.
Semini, C., Tsagarakis, N. G., Guglielmino, E., Focchi,
M., Cannella, F., and Caldwell, D. G. (2011). De-
sign of hyq–a hydraulically and electrically actuated
quadruped robot. Proceedings of the Institution of
Mechanical Engineers, Part I: Journal of Systems and
Control Engineering, 225(6):831–849.
Tassa, Y., Erez, T., and Smart, W. D. (2008). Receding hori-
zon differential dynamic programming. In Advances
in Neural Information Processing Systems 20, pages
1465–1472.
Tassa, Y., Mansard, N., and Todorov, E. (2014). Control-
limited differential dynamic programming. In
IEEE/RAS Int. Conf. on Robotics and Automation
(ICRA), pages 1168–1175.
Wensing, P. M., Wang, A., Seok, S., Otten, D., Lang, J., and
Kim, S. (2017). Proprioceptive actuator design in the
mit cheetah: Impact mitigation and high-bandwidth
physical interaction for dynamic legged robots. IEEE
Transactions on Robotics.
Wolf, S. and Hirzinger, G. (2008). A new variable stiff-
ness design: Matching requirements of the next robot
generation. In IEEE/RAS Int. Conf. on Robotics and
Automation (ICRA), pages 1741–1746. IEEE.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
38