Efficient Fuzzy based Image Mosaicing Algorithm for Overlapped

Aerial Images

Abdelhai Lati

1,2

, Mahmoud Belhocine

and Noura Achour

1,2

Laboratoire de Robotique, Parallélisme et Systèmes Embarqués LRPSE,

BP 32, El Alia, Bab Ezzouar, 16111, Alger, Algeria

Université de Sciences et Technologie de Houari Boumedian USTHB,

BP 32, El Alia, Bab Ezzouar, 16111, Alger, Algeria

Centre du Développement des Technologies Avancées CDTA,

Cité 20 août 1956, Baba Hassen 16303, Alger, Algeria

Keywords: Aerial Images, Image Mosaic, Fuzzy ILBP.

Abstract: This article presents an efficient technique for aerial image mosaicing algorithm of overlapped pair of

Unmanned Aerial Vehicle (UAV) images. Our algorithm is based on detecting some sparse distinguished

set of pixels from captured image. Therefore, in the first stage, FAST algorithm was proposed for

determining locations of feature pixels. Local binary pattern (LBP) technique is robust for describing

features pixels, but it still suffers from different problems, such as noise and errors in interpolating values of

surrounding pixels. Fuzzy logic theory partially solves the noise sensitivity problem associated with LBP

approach, therefore; in the second part of this article, a robust method based on fuzzy logic technique was

used to create Fuzzy Improved Local Binary Patterns descriptors (Fuzzy ILBPDs) for features matching

purpose, after that; homography matrix will be estimated through the best associated features; in order to

project the overlapped UAV images. The results of our algorithm maps for some benchmark and effective

numerical comparisons with previous related works are presented in this paper.

1 INTRODUCTION

Unmanned aerial vehicles (UAVs) have become an

increasingly familiar technology and have become

smaller, more capable, and less expensive because of

both military investment in the UAV industry and

improved technology. Current generation UAVs can

be transported in small vehicles and launched from a

road or a small truck but are still large enough to be

equipped with cameras and sensors that can provide

low cost aerial information (Edward and

McCormack, 2008) .The UAV based platform for

photogrammetric and remote sensing; is a more

flexible and easy way to provide high resolution

images with lower cost. So building UAV based

platforms is becoming a hot field throughout the

whole world. For some aerial images, it is often

necessary to analyze a complete scene section at

high resolution which has large dimensions (a large

number of pixels). However, in some cases the high

resolution single image cannot be viewed even if

using cameras with tens of millions of active pixels.

The common approach of image mosaicing (Capel

and Zisserman, 1998) is to acquire several images of

parts of the scene at high magnification and

assemble them into a composite single image which

preserves the high resolution. The performance of an

image mosaicing algorithm depends mainly on the

performance of used techniques for features

detection and matching .Since Local Binary Patterns

Descriptors (LBPDs) (Ojala et al., 1996) provide

good and robust description for the detected key

points in two overlapped images, fast and good

features matching can be obtained using the

measured Hamming distance between two LBPDs,

therefore, they are getting more and more popular

over SIFT and SURF when combined with simple

detector for the key point detection.

The aim of our study is to present and investigate

the performance of a novel approach for LBP

descriptors, because, most methodologies employed

for creating LBP descriptors have little tolerance to

uncertainty. The novel type of descriptors, which is

more capable of dealing with such problems, can be

Lati, A., Belhocine, M. and Achour, N.

Efﬁcient Fuzzy based Image Mosaicing Algorithm for Overlapped Aerial Images.

DOI: 10.5220/0006826702290236

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 229-236

ISBN: 978-989-758-321-6

229

developed by incorporating fuzzy logic (Dimitris et

al., 2008), in the Local Binary Pattern methodology.

This article is organized in 6 sections. In section

2, some related works concerning some UAV image

mosaic construction will be discussed as the state of

the art. In section 3, the entire scheme for image

mosaicing algorithm will be described. In section 4,

the proposed Fuzzy Improved LBP method is

described. In section 5, a comparative experimental

evaluation reveals the advantageous performance of

the proposed method in comparison to other

methods applied on real aerial images. In section 6,

conclusions and future perspectives are presented.

2 RELATED WORKS

Signal processing programs used on a PC are allowed

for rapid development of algorithms, rapid debug and

test application. Matlab is such an environment

treating an image as a matrix, which allows

optimized matrix. UAV image mosaicing, with high

speed and robust accuracy, presents a significant

challenge. Thus, there have been many researches in

this area during the past few decades. In (Nemra,

2010), UAV was enabled to construct a reliable map

of an unknown environment and localize themselves

within this map without any user intervention. To

construct this map; Adapted SIFT detector was used

to extract and match features between all the images.

Another strategy was proposed for registering

and mosaicing UAV data “aerial images” (Ming et

al., 2012), Firstly, the total number of the pyramid

octaves in scale space was reduced to speed up the

matching process; sequentially, RANSAC was

issued to eliminate the mismatching tie points. The

method described in (Cheng-Chuan et al., 2012) was

to estimate the homography matrices that can

precisely register UAV images onto the Google

satellite map with less distortion. SIFT was used to

perform image registration between consecutive

UAV images. But this algorithm was a great

challenging task due to quality mismatch between

overlapped images. The method described in

(Nagaraja et al., 2014) was proposed for

construction of mosaic image from an underwater

video sequence. Difference of Gaussian (DoG)

technique, which is part of SIFT was used for

feature detection, then; for each interest point, a

texture descriptor was constructed using CS-LBP

(Heikkila et al., 2006) technique to describe the key

point. Then feature descriptors were matched using

Nearest Neighbour Distance Ratio (NNDR) to

measure the similarity.

3 IMGE MOSAICING

3.1 Features Detection

This stage is based on extracting a set of pixels

(features) among the whole image pixels, then

applying the necessary image analysis on these

detected set of pixels. Points are the ideal features

for image registration because their coordinates can

be used directly to determine the parameters of the

transformation function, and also due to their

invariance to the image geometry and their facilities

to be detected using simple detectors (Goshtasby et

al., 2005).

3.2 Features Matching

Once the interest points have been extracted, the

matching is to find for each point of an image, its

correspondent in the other image knowing that the

image points are projections of the real 3D points of

the same scene. Several matching methods were

proposed in the literature (Nemra, 2010), these

methods can be classified into three categories:

methods based on correlation comparison criteria,

methods based on features descriptors and other

methods based on features tracking.

3.3 Image Transformation

After finding the pairs of matched features, selecting

an appropriate transformation model to compute the

image alignments is an important step for image

mosaicing (Patidar and Jain, 2011). Different types

of transformations models exist for this purpose

(Szeliski, 1994).but projective homography is the

most general motion model for image mosaicing

applications; where the scene is planar or almost

planar and the camera undergoes a rigid motion.

3.4 Image Projection

Image warping is the act of projecting two

overlapped images on each other according to a

mapping between source image I (x,y) and

destination image I’(x,y). Alignment of images may

be imperfect due to registration errors resulting from

incompatible model an assumption. Therefore,

different blending techniques can be used to

compensate these errors (Richard, 2006).

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

230

4 FUZZY IMPROVED LBP

Classical algorithm for Local Binary Patterns (LBP)

is a binary system description which expresses the

relationship of size of a gray image pixel point and

its neighbour-hood pixels points; it was originally

used to describe image texture information (Ojala et

al., 1996). Nowadays, research workers put forward

a lot of improved LBP algorithms that have been

applied in features matching; face recognition, etc;

and that because of its simple computation

complexity and partial scale, rotation, and

illumination invariance (Ning et al., 2007).

In LBP algorithm, every feature pixel in an

image generates a single LBP code. Then a decimal

value is calculated for the different LBP codes. The

LBP codes forms the LBP feature vector, which

characterize the image features. The LBP is based on

hard thresholding of surrounding pixels, which

makes features description sensitive to noise. In

order to improve the LBP approach, we have

considered fuzzy logic theory (Ying and Dali, 2006).

Fuzzy logic resembles human decision making, with

ability for finding precise solutions in approximate

datasets collection.

The use of fuzzy logic in the LBP approach

includes the transformation of the input variables to

respective fuzzy variables, according to a set of

fuzzy rules. Our proposed algorithm, which is

presented in figure 1, is based on three fuzzy

variables sets and four fuzzy rules, each one of these

rules depend mainly on Hamming distance between

the Improved LBP Descriptors.

Figure 1: The used Fuzzy ILBPDs algorithm.

The fuzzy Improved LBPDs can be created by

following these steps :

1) Detect points based features for each image

using one of the robust detectors (FAST,

Harris, SIFT ... etc).

2) Create LBP descriptors around the detected

features using the first nearest eight

neighborhoods pixels, and distance of one

pixel from the center pixel.

3) Recreate LBP descriptors around the

detected features using the second nearest

eight neighborhoods pixels and distance of

two pixels from the center pixel.

4) Repeat procedure (3), till the n

nearest

neighborhoods pixels and a specified n

distance of pixels.

5) Put the obtained eight elements vectors from

step (4) in one long binary vector of (n



elements; and label them as Improved LBP

Descriptors.

6) Apply Hamming distance to find the

matching candidates, among the created

Improved LBPDs of image 1 and the created

Improved LBPDs of image 2.

7) Based on the calculated Hamming distances,

and the matching candidates, apply fuzzy

rules to choose the final matched Improved

LBP descriptors among ILBPDs 1 and

ILBPDs 2.

The obtained set of pairs of matched features

from fuzzy based ILBP descriptors can be used for

finding an appropriate projective transformation

between overlapped images.

5 FUZZY ILBP BASED IMAGE

MOSAICING ALGORITHM

Different algorithms were proposed for aerial image

mosaicing. Since we are looking for robust

algorithm, we have chosen a simple corner detector

for features detection; and an improved LBP

technique for features matching. Our contribution in

this algorithm is integrating fuzzy logic theory in the

stage of image mosaicing construction; in this stage;

we have proposed to enhance the performance of

LBP based features matching technique, by using

fuzzy rules, in order to eliminate false associations.

5.1 FAST Corners Detector

The Features from Accelerated Segment Test

(FAST) corner detector was developed by Rosten

and Drummond in 2006; it has a simple and fast

corner detection algorithm to find local invariant

points. It finds corners in the image by comparing

pixel gradients in a neighborhood of pixels.

FAST algorithm defines corner point as: (In the

neighborhoods of a pixel, there are enough pixels in

Efﬁcient Fuzzy based Image Mosaicing Algorithm for Overlapped Aerial Images

231

different region and their gray values are greater

than or less than the central pixel’s (Rosten and

Drummond, 2006). The reason behind the work of

the FAST algorithm was to develop an interest point

detector for use in real time frame rate applications

like SLAM on a mobile robot (e.g. UAVs), which

have limited computational resources.

The Corner Response Function of FAST

detection algorithm to judge whether a pixel is a

corner point is defined as CRF as follows:

( ) ( )

xcirclep

CRF I x I p

∈

=−





(1)

Where

p : means the central pixel;

I(p): means the gray value of pixel p;

I(x) : means gray value of the neighbour-hood;

ε :is a given threshold value.

If CRF is greater than a given threshold, this

pixel point is considered as a corner point. However

some pseudo corner points can appear with this

algorithm (Rosten, 2011). To extract FAST corners,

a grey scaled image is sufficient and allows much

faster extraction than RGB one. In order to detect an

existing corner, the grey scale of the pixels lying on

the discrete circle is compared with the centre pixel

p. If a certain consecutive number of differences lie

above or below a certain threshold t, the considered

pixel is marked as corner. The chosen threshold

serves as parameter for controlling the total numbers

of extracted corners in a given image (Rosten, and

Drummond, 2005).

5.2 Improved LBP Descriptors

From the description of LBP technique, it is clear

that it involves only simple arithmetic operations,

since we are looking for good matching results with

less calculation time; we have proposed to use a

novel modified version of this technique; which

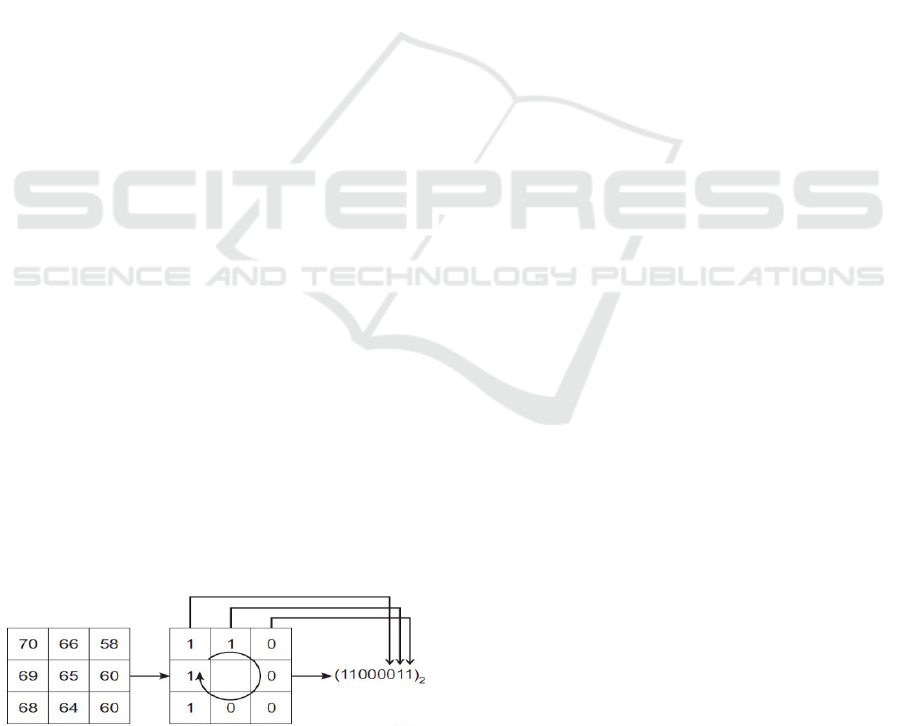
satisfies our desires. Figure 2, illustrates the

necessary steps to create eight elements LBP vector

around a feature pixel of gray level of value 65.

Figure 2: Construction of LBP descriptor.

In our case we have used window size of eight

elements for creating the LBP descriptors, but many

different sizes of neighbourhood can be used, each

element of LBP can be obtained by comparing

central the pixel with its eight neighbours, as given

in equation 2:

( ) 1 8

pi c

if g g

BP i i

if g g





=≤≤











(2)

Where:

is the detected interest point.

p, i

is one of the eight pixels around g

By concatenating N eight elements LBP vector,

we can get a long (8 × N) binary vector called

Improved LBP descriptor, in which N depends on

the chosen radius from the detected point features to

the central feature pixel.

5.3 Hamming Matching Distance

Improved LBPDs depend only on increasing radius;

and keeping at each time eight pixels in the

neighbours. If two ILBPDs are compared, small

distance value context between them is a sign of

good match ability, the distance between two ILBDs

is measured using the Hamming distance, which is a

simple bitwise exclusive or (XOR) instruction

(Zhou, 2014) . Hence, computation and matching of

ILBDs can be implemented efficiently. For two

feature points, p

and p

i’j’

from images i and i’

respectively, we can compute the matching distance

as given by equation 3:

'' ''

(, ) (, )

Sijij hamijij

dpp d hh=



(3)

Where

ij i j



: refers to ILBPD1 and ILBPD2.

ham

: Hamming distance between ILBPDs.

In the ideal case; the Improved LBP descriptors

of the matched features should be completely

coinciding, in other words, the distance between

them should be zero. Some relation should be made

to avoid mismatching due the noise in the binary

vectors. For that, we have imposed to use fuzzy

logic theory to eliminate some false association.

5.4 Fuzzy Improved LBPDs

The fuzzy logic theory is used in our work; to

determine the correct matches between two

overlapped images. The inputs to the fuzzy logic for

every pair of matched key points which are defined

by ILBP descriptors are as follows:

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

232

1) The measured Hamming distance (d

)

between every two ILBP descriptors.

2) Belongingness of the ILBP descriptor to its

region (R1) in image 1.

3) Belongingness of the ILBP descriptor to its

region (R2) in image 2.

The belongingness of an ILBP descriptor in R1 is

given by the measured correlation criterion of

features of the created binary descriptors with

features of image 2 .Similarly belongingness of

ILBP descriptor in R2 is also defined as vice versa.

The membership functions for input variable

’Hamming distance measure’ is defined as ’low’,

and ’high’ (see Figure 3 (a)). The input variable

’belongingness’ is defined by sigmoid function,

shown in Figure 3 (b). Output variable is defined by

(a)

(b)

(c)

Figure 3: (a) The 1

input membership function ‘hamming

distance’(d

). (b) The 2

input membership function

‘Belongingness to R1/R2’. (c) The output membership

function ‘match/ no match’.

Gaussian functions for ’match’, ’low’ and ‘no

match’ (see Figure 3 (c)). For each matched features

of overlapped images using ILBP descriptors, a

Hamming measure and correlation criterion (in our

case we have used Sum of Absolute Difference) are

calculated, then, fuzzy logic which is discussed in

previous section is used to find if the key points are

said to be semantically matched or not.

The following are the fuzzy rules used for the

proposed system to determine the matching decision.

The defuzzification method used in our case for the

output is centroid method.

1. If (d

is low) and (r1 is belong) and (r2 is

belong) then (ILBPDs match).

2. If (d

is high) and (r1 is not belong) and (r2

is not belong) then (ILBPDs do not match).

3. If (d

is low) and (r1 is not belong) and (r2 is

belong) then (ILBPDs do not match).

4. If (d

is high) and (r1 is belong) and (r2 is not

belong) then (ILBPDs do not match).

During the matching process, the distance

between the ILBP descriptors for two image features

is computed with Hamming distance and the

correlation score is calculated to determine the

belongingness of ILBPDs. Then these distance and

scores are used as the crisp inputs of the fuzzy

system. The membership values of the measured

hamming distance is found for two fuzzy set Low

and High, and the membership values for the

calculated correlation scores is found for two fuzzy

set either belong or not. The rules are evaluated and

finally the output decision is obtained from the zero

order Sugeno type output membership function

(singleton) as a Match or No Match.

5.5 Homography Estimation

Homography or projective transformation is the

suitable image mapping model for image mosaicing

purpose, which is a planar transformation with 8

degrees of freedom. Each pair of point

correspondence generates 2 linear equations for the

elements of H and hence 4 correspondences are

enough to solve for the homography directly (Capel

and Zisserman, 1998).

If more than 4 pairs are available, a solution for

element of H can be estimated using a linear least-

square method. Matrix H can be defined as follows:





































333231

232221

131211

hhh

(4)

Efﬁcient Fuzzy based Image Mosaicing Algorithm for Overlapped Aerial Images

233

Each pair of matched features gives two linear

equations:

0)('

232221333231

131211333231

=−−−++

hyhxhhyhxhy

hyhxhhyhxhx

(5)

Hence, N pairs of points generate 2N linear

equations, which may be arranged in a matrix design

as follows:

AH=0 (6)

The solution for H is the one-dimensional kernel

of A, which may obtained from the SVD. For N>4

points, this equation will not have an exact solution.

In this case, a solution may be obtained which

minimizes the algebraic residuals, r = AH, in a least-

squares sense, by taking the singular vector

corresponding to the smallest singular value.

5.6 Backward Image Warping

Using homography matrix, overlapped images were

warped (figure 4); we have determined bounds of

the new combined image where the corners of left

image would fall in the coordinate frame of the right

image. This was done by multiplying homography

on the corner point coordinates. Then we have

attempted to lookup colors for any of these positions

we got from the left image as given by this equation:

−

(7)

Figure 4: Backward image warping.

5.7 Interpolation Blending Technique

It is a simple approach, in which; the pixel values in

the blended regions are weighted average from the

two overlapping images. Sometimes, it is better to

take more than two neighbor pixels in interpolation

process. In our case, we have used the bilinear

interpolation algorithm; which is slightly more

sophisticated interpolation method, it interpolates

pixel value from the nearest four mapped source

pixels, and this simple algorithm produces excellent

results.

6 SIMULATION RESULTS

Matlab is a powerful software platform which can be

used for the development of several applications. In

our case, due to the provided image processing

predefined functions with Matlab toolbox; Matlab

software is suitable for the development of complex

image processing algorithms such as image

mosaicing algorithm. To test the proposed image

mosaicing algorithms, we have used Matlab running

on a computer that disposes 4 GB of RAM, CPU of

Intel i7 generation and Intel graphic card. We tested

our image mosaicing approaches on the images of

Aerial Robotics Data sets (AerialRobotics, 2014).

Figure 5; shows the used overlapped aerial images,

which have overlapping percentage of about 30 %.

Figure 5: The two overlapped UAVs images.

Figure 6: The detected features using FAST algorithm.

Figure 6 shows the detected corners features in

the two images, in which we can see that

repeatability condition is well verified using this

type of points based features.

Figure 7: Features matching using LBP.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

234

Figure 8: Features matching using fuzzy ILBP.

Figure 7 shows the obtained features correspond-

ence between the input images; using LBP

descriptors, in which we can notice the existence of

a lot of incorrect matches. But with the fuzzy

ILBPDs; we can visually notice that this approach

provides good matching results as shown in figure 8.

After homography estimation, we have used this

transformation matrix to warp images as shown in

figure 9. The black gaps are because images aligned

after undergoing geometric corrections most likely

require further processing to eliminate remaining.

Figure 9: The obtained mosaic using backward warping.

That is why; we have used an interpolation

blending technique, based on bilinear interpolation

to get seamless image mosaic, which is shown in

Figure 10.

Figure 10: The blended mosaic using interpolation.

• RESULTS DISCUSSION

Our method was compared visually and numerically

with recent state-of-the-art algorithm in the

literature. Performance evaluations in terms of

computation time show success of our algorithm. In

(Taygun et al., 2016), by the same simulation tools,

SIFT point detector was used for extracting images

salient elements, and BRIEF descriptor was used to

describe and match key-points. The matching

results, show that big difference in calculation time

between our algorithm and that of (Taygun et al,

2016), which is due to the simplicity of calculation

using fuzzy ILBP Descriptors; contrary to

SIFT/BRIEF descriptors.

Since visual comparisons can be subjective, a

numerical evaluation of the algorithms is also

necessary. To evaluate the algorithm performances,

feature matching errors present in the results of each

method are calculated in terms of recall (Hassaballah

et al., 2016), which depends mainly on the ratio

between number of inliers and outliers. The

following table summarizes the comparison of our

simulation results and compares it to other results

obtained by using the same simulation platforms.

Table 1: Comparison of simulation results.

Methods Features1 Features 2

Recall

CS-LBP

(Nagaraja et al, 2014)

262 274 0.71

SIFT

( Lowe, 2004)

256 243 0.62

SURF

(Bay et al, 2008)

233 263 0.68

Our Method 345 326 0.73

7 CONCLUSIONS

LBPDs based matching technique has different

advantages such as tolerance against illumination

changes, computationally simple and efficient. The

main drawback of LBP is that by increasing the

radius from the detected interest point, the algorithm

is not too robust. In order to overcome this

drawback; we have proposed to extend version of

LBP into fuzzy improved LBP. The fuzzy ILBP

descriptors outperform the existing local descriptor

for most of the test cases, especially for images with

severe illumination variations and they capture

better gradient information than original LBP. We

recommend for future work using other type of

images such as IR areal images.

Efﬁcient Fuzzy based Image Mosaicing Algorithm for Overlapped Aerial Images

235

REFERENCES

Edward D., McCormack., 2008. ‘The Use of Small

Unmanned Aircraft by the Washington State Department

of Transportation’. Washington State Transportation

Commission.

Capel D., Zisserman A., 1998. “Automated Mosaicing with

Super-resolution Zoom”. Robotics Research Group,

Department of Engineering Science.University of Oxford

Oxford OX1 3PJ, U.K.

Ojala, T., Pietikäinen, M., Harwood, D., 1996. “A compara-

tive study of texture measures with classification based on

featured distribution. Pattern Recognition”, Vol. 29, pp

51-59.

Dimitris K., Iakovidis., Eystratios G., Keramidas., Dimitris

Ma., 2008. ‘Fuzzy Local Binary Patterns for Ultrasound

Texture Characterization’. International Conference

Image Analysis and Recognition ICIAR Image Analysis

and Recognition, pp 750-759.

Nemra A., 2010. “Robust Airborne 3D Visual Simultaneous

Localisation And Mapping”. PHD Thesis . Cranfield

University.

Ming Li., Deren Li., Dengke F., 2012. “A Study on automatic

UAV image mosaic method for paroxysmal disaster”.

International Archives of the Photo grammetry, Remote

Sensing and Spatial Information Sciences. Melbourne,

Australia.

Cheng-Chuan, C., Shih-Ming, H., and Ching-Chun, H., 2012.

“Image Registration among UAV Image Sequence and

Google Satellite Image Under Quality Mismatch” The

12th International Conference on ITS Telecommunica-

tion. PP 311-315.

Nagaraja, S., Prabhakar, C. J., and Praveen Kumar, P. U.,

2014. (Parallax effect free mosaicing of underwater video

sequence based o texture features) . Signal & Image

Processing: An International Journal (SIPIJ) Vol.5, No.5.

Heikkila, M., Pietikainen, M., and Schmid, C., 2006.

“Description of Interest Regions with Center-

SymmetricLocal Binary Patterns”, In Computer Vision,

Graphics and Image Processing, ICVGIP 2006, vol.

4338, pp. 58-69.

Goshtasby, A. A., 2005.“2-D and 3-D Image Registration for

Medical, Remote Sensing, and Industrial Applications”.

Published by John Wiley & Sons, Inc., Hoboken, New

Jersey. Published simultaneously in Canada.

Patidar, D., and Jain, A., 2011. “Automatic Image Mosaicing:

An Approach Based on FFT”. International Journal of

Scientific Engineering and Technology. Page 1-4 .Vol 1.

Issue 1. India .

Szeliski, R., 1994. “Image Mosaicing for Tele-Reality

Applications”. Technical Report series. Cambridge

Research Laboratory.

Richard, S., 2006. “Image alignment and stitching: a tutorial”,

Found. Trends. Comput. Graph. Vis. 2 .pp1–104.

Ojala, T., Pietikainen, M., and Harwood, D., 1996. “A

comparative study of texture measures with classification

based on feature distributions”, Pattern Recognition, vol.

29, no. 1, pp. 55-59.

Ning, S., Zhenhai, J., and Cairong, Z., 2007.“ Gender

classification based on local binary pattern”. Journal of

Huazhong University of Science and Technology .pp

177-181. Chinese.

Ying, B., and Dali, W.,2006. “Fundamentals of Fuzzy Logic

Control”. Publisher: Springer, Londo pp 17-36.

Rosten, E., and Drummond, T., 2006.“ Machine learning for

high-speed corner detection”. European Conferen-ce on

Computer Vision. pp 430-443. Graz, Austria.

Rosten, E., 2011. “FAST Corner Detection Homepage”.

http://svr- www.eng.cam.ac.uk/ er258/work/fast.html.

Rosten, E., and Drummond, T., 2005. “Fusing points and

lines for high performance tracking”. In Proceedings of

the International Conference on Computer Vision

(ICCV). pp 1508-1511.

Zhou, Z., 2014. “FPGA Implementation of Computer Vision

Algorithm”. A thesis submitted in partial satisfaction of

the requirement for the degree of Master of Science in

Electrical Engineering. University of California

(Riverside).

AerialRobotics Dataset,. 2014.. ftp://www.aerial robotics.eu/

accessed: 2014-03-30.

Taygun, K., Alper, Y., and Mustafa, U., 2016. ‘A new

approach to real-time mosaicing of aerial images’.

Elsevier Jornal of robotic and autonomous systems.

Hassaballah, M., Abdelmgeid, AA., and Hammam, A., 2016.

“Image Features Detection, Description and Matching”.

Springer International Publishing Switzerland.

Lowe, D. G., 2004. “Distinctive Image Features from Scale-

Invariant Keypoints”, International Journal Computer

Vision, 2(60), pp.91-110.

Bay, H., Ess, A., Tuytelaars, T., and Gool, L. V., 2008.

“Speeded-Up Robust Features (SURF)”, Computer

Vision and Image Understanding, 113(3), pp. 346-359.

APPENDIX

The obtained results of applying our algorithm on

other aerial images “Hakekasa data set “from

(AerialRobotics, 2014):

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

236