
Algorithms for Computing Inequality Joins
Brahma Dathan
1
and Stefan Trausan Matu
2
1
Information and Computer Sciences, Metropolitan State University, St. Paul, MN 55106, U.S.A.
2
Computer Science and Engineering, Bucharest Polytechnic University, Bucharest, Romania
Keywords: Inequality Joins, Query Processing, Algorithms, Lower Bounds.
Abstract: Although the problem of joins has been known ever since the concept of relational databases was introduced,
much of the research in that area has addressed the question of equijoins. In this paper, we look at the problem
of inequality joins, which compares attributes using operators other than equality. We develop an algorithm
for computing inequality joins on two relations with comparisons on two pairs of attributes and then extend
the work to queries involving more than two comparisons. Our work also derives a lower bound for inequality
joins on two relations and show that the two-comparisons algorithm is optimal.
1 INTRODUCTION
Database joins is an old problem (Codd, 1970,
Graefe, 1993, Mishra, 1992) with much of the
research on the topic addressing the problem of
equijoins. Inequality joins (again an old problem,
(DeWitt, 1991, Klug, 1988)), where attributes are
compared for inequality are less frequently used than
equijoins in traditional database systems, but find
utility in temporal databases and other applications
such as database cleaning (Wang, 2013, Cao, 2012,
Enderle, 2004, Khayyat, 2015), and sophisticated
problems even in conventional applications.
For example, consider a company that sells a large
number of products. By one estimate, a well-known
online retailer offers close to half a billion different
products in the United States alone. Among the
various factors that play a role in the profits of a
company is the amount of storage space required by
a product. Often, the size of a specific product is not
directly proportional to the profit on that item. For
example, jewelry items are often small, but they
typically generate more profit per unit volume than
some bulkier items such as plastic chairs.
Assume that products that vary widely in their
features are implemented as separate relations.
(Jewelry and chairs might be two such products.) As
an example, suppose
C
and
D
are two separate
relations representing two categories of products.
Among the numerous attributes, assume that the
following are identically named in the two relations:
key, the primary key of the relation; vol, the amount
of space occupied by one unit of the product for
storage; profit, the average profit for one unit of the
product; and unitsSold, the number of units of the
product sold per year.
An example of relation
C
is given in Table 1.
Table 2 is an instance of
D
.
The company wants to minimize the cost of
storage while maximizing profits. In connection with
this, suppose it is considering increasing the
inventory of some products in
C
relative to the
inventory of some products in
D
. For this, it may wish
to check for all pairs of tuples
c
in
C
and
d
in
D
whether
d.vol
is more than
c.vol
and
c.profit
is more
than
d.profit
; if the condition is true, and if space is
an issue, the company might decide to stock a larger
quantity of c at the expense of storage for
d
. It is thus
worthwhile to execute the following query (call it
STORAGE).
select c.key, d.key from C c, D d where
d.vol > c.vol and c.profit > d.profit;
Executing the query on the sample relations yields
the following pairs of keys: (
c1, d2
), (
c1, d5
), (
c1,
d7
), (
c2, d1
), (
c2, d2
), (
c2, d6
), (
c2, d7
), (
c3, d1
),
(
c3, d2
), (
c3, d3
), (
c3, d4
), (
c3, d5
), (
c3, d6
), (
c3,
d7
), (
c4, d2
), (
c5, d2
), (
c7, d2
).
The company may want to do more analysis: it
might decide that comparing the unitsSold field
should also be a factor in making a decision. It may
then decide to execute a query such as the following.
select c.key, d.key from C c, D d where
d.vol > c.vol and c.profit > d.profit
and c.unitsSold > d.unitsSold
Dathan, B. and Matu, S.
Algorithms for Computing Inequality Joins.
DOI: 10.5220/0006826803570364
In Proceedings of the 7th International Conference on Data Science, Technology and Applications (DATA 2018), pages 357-364
ISBN: 978-989-758-318-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
357

The result of this query is (
c1, d7
), (
c2, d7
), (
c3,
d1
), (
c3, d3
), (
c3, d4
), (
c3, d7
).
Table 1: Relation C.
key
vol
profit
unitsSold
c1
35
45
15
c2
15
35
10
c3
5
55
30
c4
35
12
10
c5
18
15
15
c6
90
55
80
c7
17
11
2
Table 2: Relation D.
key
vol
profit
unitsSold
d1
20
30
20
d2
50
10
35
d3
15
12
10
d4
16
52
12
d5
40
35
40
d6
20
20
30
d7
40
30
5
d8
2
57
15
Despite such applications, the problem of
inequality joins remains an insufficiently researched
area. A recent paper (Khayyat, 2017) makes quite a
compelling case for more efficient inequality join
algorithms. This inefficiency is not surprising
because surprising because commercial database
systems solve the problem using a nested loop
that examines every pair of tuples.
Assume that
S
and
T
are relations with both
relations containing fields named k,
A,
and
B
. The
inequality join query, which we denote by
Q1
,
involving these two fields
A
and
B
is the following,
where
and
are relational operators (<, >, <=, and
>=).
select s.k, t.k from S s, T t where
s.A
t.A AND s.B
t.B
In this work, we present an algorithm to solve
inequality join queries. Our paper makes the
following contributions: 1) It first develops an
algorithm to solve the inequality join problem
involving two comparisons. 2) It provides an
extension to the algorithm in (1) to an arbitrary
number of comparisons. 3) It derives a lower bound
for the problem of inequality joins of the form given
in Q1. The result applies to algorithms that employ
comparisons to determine which tuple pairs belong to
the result. 4) It shows that the algorithm in (1) above
is optimal.
The rest of the paper is organized as follows. In
the next section, we illustrate our algorithm with an
example. For exposition purposes, we describe a good
part of the algorithm using query STORAGE. In Sect.
3, we formally describe the algorithm and extend it to
multiple comparisons. In Sect. 4, we derive a lower
bound for the problem for two comparisons. An
examination of related work is done in Sect. 5.
Section 6 concludes the paper.
2 ALGORITHM CONCEPTS
In this section, we introduce the algorithm using the
query STORAGE.
2.1 Page Setup
We rename the smaller relation
S
and the larger
relation
T
. If the two relations are equal in size, we
may name either one of them
S
and the other
T
. The
attributes are named
k
(for key),
A
(the attribute used
in the first comparison), and
B
(the attribute in the
second comparison). The where clause is
then changed so that all inequality comparisons are
of the form s.X <rel_op> t.X.
For the rest of this section, we illustrate the
algorithm using the query STORAGE.
C
is the
smaller relation, so it is renamed
S,
and
D
becomes
T
.
The attributes
key
,
vol
, and
profit
are renamed
k, A
,
and
B
, respectively. For uniformity, we refer to the
key values of
S
as
s1, s2
, etc. instead of
c1, c2
, and so
on. Similarly, the key values of
T
are referred to as
t1,
t2
, etc. The query becomes
select s.k, t.k from S s, T t where
s.A < t.A and s.B > t.B
We will use the letter
s
to denote an arbitrary
S
tuple and
t
to denote an arbitrary
T
tuple.
2.2 Regions
We now introduce the concept of regions. Clearly,
the query result depends on the relative order of the
S
and
T
tuples based on attribute
A
(as well as
B
), that
is, which
S
tuples have an
A
attribute value less than
the
A
attribute value of the
T
tuples. Consider sorting
the union of
S
and
T
on attribute
A
in the ascending
order. We get the sequence
t8, s3, t3, s2, t4, s7, s5,
t1, t6, s1, s4, t5, t7, t2, s6.
Tuple
s3
has an
A
attribute value less than the
A
attribute values of all tuples other than
t8
, so it could
be paired with all
T
tuples except
t8
as far as attribute
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
358

A
is concerned. It is this idea that we formalize into
the notion of regions.
Since no
S
tuple has an
A
value less than
t8.A
and
no
T
tuple has an
A
value greater than
s6.A
, tuples
t8
and
s6
cannot be part of the query result and are
ignored. We can divide tuples other than
t8
and
s6
into sub-sequences with a non-empty sequence of
S
tuples followed by a non-empty sequence of
T
tuples.
The sub-sequences are
and
Each of these four sub-sequences is called a
region and are numbered 0 through 3. We call the
numbers region numbers. Every tuple also has a
region number, which is that of the region the tuple is
in. For example,
s3
and
t3
have the
A
region number
of 0. Similarly,
s2
and
t4
have the region number 1,
s7
,
s5
,
t1
, and
t6
have the region number 2, and
s1
,
s4
,
t5
,
t7
, and
t2
have the region number 3.
For attribute
B
, the comparison is
s.B > t.B
, so we
sort the union of
S
and
T
in the descending order on
B
. We get 5 sub-sequences and the tuples are assigned
region numbers 0 through 4:
and
.
(Tuples
t8
and
s6
are omitted and in the case of a tie,
we place the
T
tuple before the
S
tuple because the
comparison is a less than.)
Every
S
and
T
tuple thus has two region numbers,
one for each of the two sorted sequences. We call
them
A
region number and
B
region number. Note
that
s6
and
t8
do not get region numbers and are no
longer considered in further stages of the algorithm.
Although the concepts of regions and region
numbers were described using the two sorted
sequences of for the sake of efficiency, we
compute the region numbers using a different
approach, which we describe next.
2.2.1 Computing the Region Numbers
To compute the
A
region numbers, we first sort
S
on
attribute
A
to get the table
SA
as shown in Fig. 1. Each
cell contains, or will contain, the key, the
A
attribute
value, a flag, and the region number. We create a
second list
SUA
with one entry for each unique value
of attribute
A
. The entries in
SUA
point to entries in
SA
as shown in the figure.
For each
T
tuple, we determine its insertion point
in
SUA
. For example,
t4.A
is 16, so its insertion point
is between
s2
and
s7
(because we have
s2.A <
t4.A
< s7.A
); we set the flag in
SA
to
true
to note that there
is a
T
tuple
t
with
t.A
between
s2.A
and
s7.A
. Tuple
t4
stores a reference to
s2
. Similarly, we find
insertion points for all
T
tuples. Note that
s7
’s flag is
false
because there is no
T
tuple
t
such that
s7.A
<
t.A <
s5.A
. Also,
t8
does not have an insertion point
because of its key value. There is no
T
tuple
t
with
t.A
> s6.A
. Both
s6
and
t8
are therefore ignored.
We next compute the
A
region number of the
S
tuples. The region number is incremented whenever
we encounter an
S
tuple s with the flag set to true. The
A
region number of a
T
tuple is the
A
region number
of the
S
tuple it points to. For example,
t4
points to
s2
, so
t4
’s
A
region number is the same as
s2
’s
A
region number.
s3
s2
s7
s5
s1
s4
s6
SA
5
15
17
18
35
35
90
true
true
false
true
false
true
false
0
1
2
2
3
3
SUA
t1
t2
t3
t4
t5
t6
t7
t8
2
3
0
1
3
2
3
-
T tuples
20
50
15
16
40
20
40
2
Figure 1: Region Number Computation.
For attribute B, since the relational operator is
>
for the second comparison, we sort
S
in the
descending order of the
B
attribute values. The
A
and
B
region numbers are given in the Fig. 2.
2.2.2 Computing the Query Result
If an attribute has exactly one region, that attribute
need not be considered in computing the query result,
so we assume the more general and non-trivial case
where both attributes have at least two regions.
Let
denote the region number of tuple
s
of
relation
S
. Similar notations apply for the
B
region
numbers and
T
tuples. A pair (
s, t
) is in the query
result if and only if
and
.
To compute the result, we need to access the
tuples efficiently. We can access the
S
tuples in the
region order using
SA
and
SB
, but the
T
tuples are a
problem because they are not sorted. So we employ
two separate collections called region ordered tables
to access the
T
tuples in the region order, but not
necessarily in the sorted order of
A
or
B
.
s1
s2
s3
s4
s5
s7
A
3
1
0
3
2
2
B
1
2
0
4
3
4
t1
t2
t3
t4
t5
t6
t7
A
2
3
0
1
3
2
3
B
2
4
3
0
1
2
2
Figure 2: A and B region numbers.
Algorithms for Computing Inequality Joins
359
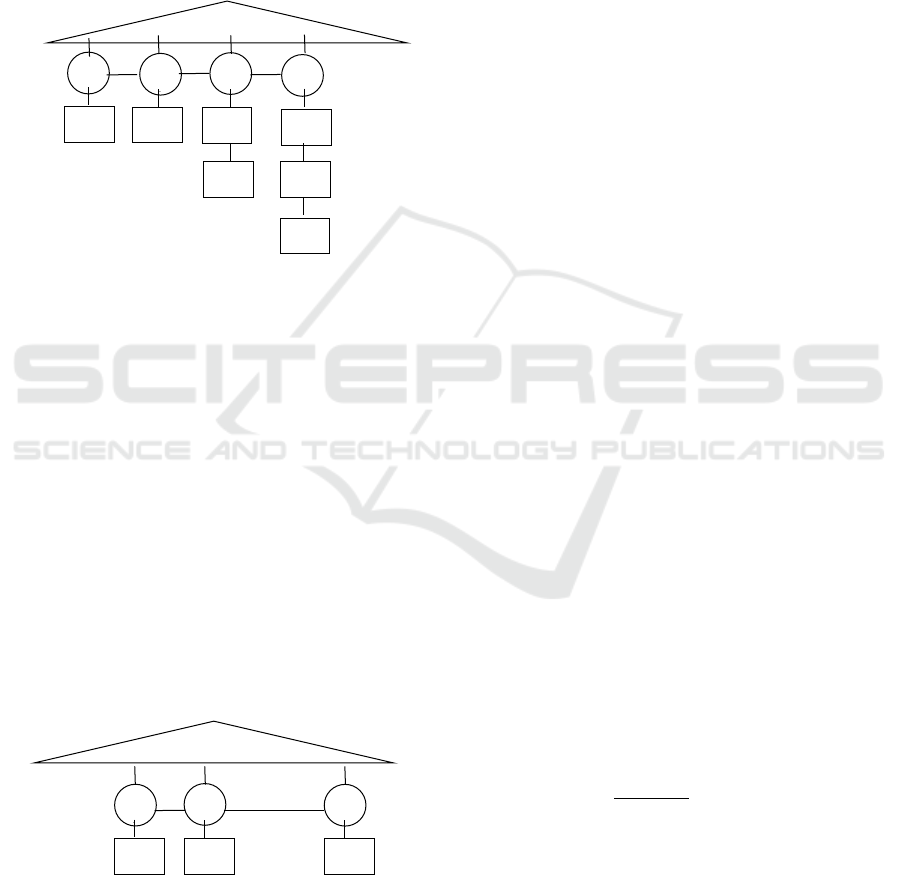
The table is implemented as a balanced tree, with
one leaf node per region. The leaves are stored in a
linked list, and each leaf points to a linked list of
T
tuples that have the region number of that leaf node.
The first step in computing the query result is to
create an
A
region ordered table for the
T
tuples. This
table shown in Fig. 3. The leaves hold region numbers
and are shown as circles. We also create an empty
region ordered table. This will contain the
T
tuples
and will be ordered on the
B
region numbers.
Figure 3: Data Structure Holding All the T tuples.
We then enter a loop starting with the highest
numbered
A
region and work our way down to 0. For
each region number
i
, we add to the
B
region ordered
table those
T
tuples with
The highest
A
region is 3. We pick from the
A
region ordered table all the
T
tuples with
A
region
number of 3. These are
t5
,
t2
, and
t7
. They are stored
in the
B
region ordered table. The result is shown in
Fig. 4. The
S
tuples with
A
region equal to 3 are
s1
and
s4
. Since
and
t5
,
t7
, and
t2
all have
they are all paired with
s1
. Since
,
s4
is paired with only
t2
because
.
We proceed to
A
region 2. T tuples
t1
and
t6
have
2 for their
A
region number and are added to the table.
The
S
tuples with
are
s5
and
s7
.
so
s5
is paired with
t2
.
so
s7
is also paired
with
t2
.
Figure 4: Table After Adding T Tuples with
= 3.
Moving down to
A
region 1, we add
t4
to the
table. We pair
s2
(
) with
t1
,
t6
,
t7
, and
t2
because they all have a
B
region number that is greater
than or equal to
. Finally, for
A
region 0, we add
t3
. Since
s3
is paired with every tuple in
the table.
3 FORMAL DESCRIPTIONS
In this section, we state the region computation and
the final query result computation algorithms more
formally and describe our extension to multiple
comparisons.
3.1 The Two-Comparisons Algorithm
The algorithm for computing the
A
region numbers is
shown in Fig. 5. The
B
region numbers are computed
similarly. The complexities for the steps are indicated
as we progress through the steps.
Lines 1-4 sort
S
on attribute
A
in the ascending or
descending order (complexity: and
lines 5-6 initialize the flag (complexity: . Steps
9-14 create the table
SUA
(complexity: .
Lines 15-41 compute the insertion points for the
T
tuples. The loop 23-37 is the standard binary search
algorithm augmented to determine the insertion point.
With the loop starting in line 19, the complexity of
lines 15-41 is .
1) if rel_op is < or rel_op is <=
2) SA = S sorted ascending on S.A
3) else
4) SA = S sorted descending on S.A
5) for s in SA
6) s.fA = false
7) SUA = new array of indices to SA
8) uniques = 0
9) for 0 <= i < m - 1
10) if SA[i].A != SA[i + 1].A
11) SUA[uniques].index = i
12) uniques = uniques + 1
13) SUA[uniques] = SA[m -- 1]
14) uniques = uniques + 1
15) if rel_op is < or rel_op is >
16) offset = -1
17) else
18) offset = 0
19) for t in T
20) low = 0
21) high = uniques - 1
22) found = false
23) while low <= high and not found
24) mid = (low + high)/2
25) if SA[SUA[mid]].A == t.A
26) found = true
27) else if rel_op is < or <=
28) if SA[SUA[mid]].A < value
29) low = mid + 1
Figure 5: Region Computation.
0
0
0
0
0
0
0
0
0
1
2
3
t3
T1
1
t4
T1
1
t1
T1
1
t6
T1
1
t7
T1
1
t5
T1
1
t2
T1
1
Internal nodes
0
0
0
0
0
0
1
2
4
t5
T1
1
t7
T1
1
t2
T1
1
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
360

30) else
31) high = mid - 1
32) else
33) if SA[SUA[mid]].A > value
33) low = mid + 1
34) else
35) high = mid - 1
36) if found
37) ins_pt = mid - offset
36) else
37) ins_pt = high
37) if ins_pt == -1
38) remove t from T
39) else
40) SA[SUA[ins_pt]].fA = true
41) t.spos = SUA[ins_pt]
42) r = 0
43) for s in sorted order SA
44) s.rA = r
45) if s.fA
46) r++
47) for t in T
48) t.rA = t.spos.rA
Figure 5: Region Computation (Cont.).
The region numbers are computed in lines 42-48.
The complexity is
The final result is computed
by the algorithm in Fig. 6. Since there are at most
m
regions, TA can be created in time .The
iterator can be constructed in time. The
complexity of lines 5-14 is , where e
is the number of tuples in the result. Clearly, we have
Theorem 1. The algorithm complexity is
.
Theorem 2. The algorithm computes the inequality
join correctly.
Proof. Omitted due to lack of space.
1
: region ordered table
: region ordered table
3 for each t in T
.add(r, t)
5 for r from
down to 0
6 itA =
.iterator(r)
7 while itA.hasNext()
8 t = itA.next()
9
.add(t.
, t)
10 for each s with s.
== r
11 itB =
.iterator(s.
)
12 while itB.hasNext()
13 t = itB.next()
14 output the pair (s, t)
Figure 6: Computing the Final Result.
3.2 Multiple Comparisons Algorithm
We start off as in the two-comparisons algorithm by
renaming the relations and fields in the obvious
manner. Suppose there are comparisons. Let us
denote the attributes involved in these comparisons
by
The algorithm maintains copies of
the table,
with
sorted on field
It computes the region numbers for
the regions, one for each field
It
constructs region ordered tables each storing all the
tuples of the table. Let us denote these by
is ordered on region
It constructs region ordered tables, each initially
empty. Let us denote these by
is ordered on region
The algorithm in Fig. 5 in its entirety and lines 1-
4 of the algorithm in Fig. 6 are employed to
implement all of the above functionalities. The
difference between this extension and the two-
comparisons algorithm is in the way the final query
result is computed. The extension employs a greedy
approach. For this, we make the observation that in
the two-comparisons algorithm, we perform far fewer
comparisons at the beginning when we deal with the
higher region numbers. With a uniform distribution
of the tuples over all regions, we would expect the
number of
T
tuples in region
to be
and the
number of
S
tuples to be
, where
is the
number of regions for field
. Therefore, the number
of pairs of
S
and
T
tuples we need to consider for the
highest region number for
is at most
tuplesLeft = m, the number of S tuples
while tuplesLeft > 0
select A, a field (see discussion)
r = largest-numbered unprocessed
region number in A;
execute processField(A, r)
Figure 7: Handling Multiple Fields.
processField(A, r):
: region ordered table for field X
: region ordered table for field X
for each t in
add(r, t)
B = any field A with
itA =
.iterator(r)
while itA.hasNext()
t = itA.next()
.add(t.
, t)
for each s with s.
== r and
s.processed == false
itB =
.iterator(s.
)
while itB.hasNext()
t = itB.next()
for every field g A or B
if
exit the outer for loop
output (s, t);
s.processed = true
tuplesLeft--
Figure 8: Computing the Final Result.
Algorithms for Computing Inequality Joins
361

The above observation is exploited in the
algorithm shown in Fig. 7. We select a field for
which we judge the number of comparisons to be the
smallest. For each field
, assume the following: the
largest unprocessed region number is
the number
of
S
tuples in region
is
; the number of tuples in
the region ordered table
is
; and the number of
T
tuples in region
is
. Then we select field for
which the expression
is the smallest.
The tuple pairs are computed by the algorithm in
Fig. 8. After we retrieve a
T
tuple
t
from the region
ordered table
that matches an
S
tuple
s
for region
number based on , we check if
for all
other fields
g
as well. As the region numbers
decrease, more and more
T
tuples enter the region
ordered tables, but we also flag more
S
tuples at
higher numbered regions when we encounter fewer
T
tuples. This way, the total number of pairs to be
considered does not increase sharply.
4 A LOWER BOUND
In this section, we derive a lower bound for the
number of operations needed to enumerate all pairs of
tuples that satisfy an inequality join query of the form
given in
Q1
(Sect. 1). We consider only algorithms
that employ comparisons to determine the query
result. We will assume that the number of tuples in
and are and , respectively, and that . For
simplicity, the two relations and are assumed to
have identically named attributes.
Any deterministic algorithm to compute the query
result needs to determine the tuple pairs in the result
and enumerate them. If there are
e
tuple pairs in the
result, any algorithm must take steps to
enumerate them.
Consider two relations
S
and
T
such that for any
pair of tuples
and
in , either
is true or
is
true; that is, all pairs of tuples are totally ordered on
the pair of comparisons. Clearly, this is a weaker
problem than the one we addressed in Sec. 2 and 3.
With a total order, to determine the query result, we
need to determine which of the possible total orders
of the
S
and
T
tuples is present in the input with one
restriction: the relative order of the
S
tuples
themselves or the relative order of the
T
tuples
themselves do not play a role in the output.
4.1 Number of Input Sequences
The tuples of
S
could be distributed into
k
non-empty
sets, where ; these subsets are denoted by
The number of ways in which a set of
m
elements can be divided into
k
non-empty subsets is
given by Stirling number of the second kind (Graham,
1988) and is denoted by
The
n
tuples of
T
could be distributed in-between (and/or before and
after) these sets in four different ways.
1. Distribute the n tuples between the pairs of S
tuples. There are such locations. The
m
tuples
of
S
are distributed in
ways. Although their
relative order within a set should not be counted, the
relative order of each subset
with respect to the
subsets of
T
that occupy the slots is important
and should be counted. Thus, there are
possible sequences of the tuples. The T tuples
can be distributed in ways into the
slots and the permutation of these subsets
must also be counted. This gives us
sequences. Thus, the total number of sequences
is
.
2. In addition to using up all locations
between the
S
tuples, we could attach an additional
non-empty set of T tuples before
, (which is the first
subset of
S
). This gives rise to
k
non-empty sets of
T
tuples. The number of sequences is
.
3. This is similar to item 2 above. We could have
k
non-empty sets of
T
tuples by putting a non-empty set
of
T
tuples after
. The number of sequences is again
4. This case applies only if there are enough
T
tuples to go around. That happens if or
. We form subsets by putting a non-empty
set of
T
tuples before
and after
. The number of
sequences is
.
Therefore, unless , the number of
sequences with k non-empty subsets of S tuples is
obtained by adding up the four terms given above to
get the following expression.
If , the number of sequences is
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
362

To get a lower bound we can simply use the fact
that
But
because we can divide the m
tuples into
k
subsets by having tuples in one
subset and putting the remaining
k
tuples into
non-empty subsets, giving at least
distributions.
The number of input sequences is thus no less than
(Griffith, 2010).
The algorithm must pick the correct input
sequence from the
possible inputs. We can easily
employ an oracle argument as in the case of the
derivation for the lower bound for sorting and see that
in the worst case, a comparison may reduce the
number of possible sequences by half. Therefore, the
number of comparisons needed is at least.
In addition, if the result contains
e
tuple pairs, the
algorithm must spend time to enumerate
them. This gives us the following result.
Theorem 3. Let be any inequality join query
processing algorithm that uses comparisons to
determine the tuple pairs in the result and enumerate
them. The minimum number of steps for to
complete its execution when processing a query on
two relations and with cardinalities m and n
respectively, where is
where e is the number of tuple pairs in the result.
From Theorem 2 and Theorem 3, we have
Theorem 4. The two-comparisons algorithm is
optimal.
5 RELATED WORK
Classes of joins other than equijoins that have
received less attention but have their own applications
include inequality joins (Klug, 1988, Chandra, 1977,
DeWitt, 1991) and similarity joins (Silva, 2012). The
MapReduce framework has been used to compute
joins. A work using this framework to compute
inequality joins is by Okcan (Okcan, 2011). There are
other important implementations of equijoins and
similarity joins using the MapReduce framework
including works by Blanas et al, (Blanas, 2010) Silva
and Reed (Silva, 2012), Vernica, et al (Vernica,
2010), and Afrati and Ullman (Afrati, 2010).
A significant work by Khayyat et al (Khayyat,
2017) essentially addresses the same problem we took
up here. Their resort to sorting both and , whereas
we sort only the smaller relation. A difference
between the works is that their algorithm takes
time, while our approach takes
time. Our algorithm is optimal for a
pair of relations on two pairs of fields.
Inequality joins have found applications in areas
such as XML query processing to perform
containment joins (Wang 2003). A containment join
between a set of ancestor nodes (denoted as
A
) and a
set of descendant nodes (denoted as
D
) is to find all
pairs of
, such that a is an
ancestor of d. A solution to inequality joins can be
applied to help process these queries.
Inequality joins can be applied to address
questions in temporal databases (Cao, 2012, Enderle,
2004) and have a role in database cleaning
(Chaudhuri, 2006, Khayyat, 2015).
6 CONCLUSIONS
In this paper, we looked at the problem of inequality
joins, an important class of joins that has received less
attention than equijoins. We derived a lower bound
for the problem of inequality joins of two relations
and came up with an optimal algorithm that solved
the problem for two comparisons. We showed how to
extend the approach to more than two comparisons.
We plan to investigate how the multiple
comparisons algorithm could be parallelized. The
approach seems to support a high degree of
concurrency because it processes tuples by region.
REFERENCES
Afrati, F.N., Ullman, J.D., 2010. Optimizing Joins in a
Map-reduce Environment, 13th International
Conference on Extending Database Technology.
Blanas, S., Patel, J.M., Ercegovac, V., Rao, J., Shekita, E.J.,
Tian, Y., 2010. A Comparison of Join Algorithms for
Log Processing in MapReduce, ACM SIGMOD
International Conference on Management of Data.
Cao, Y., Zhou, Y., Chan, C., Tan, K., 2012. On Optimizing
Relational Self-joins, 15th International Conference on
Extending Database Technology.
Chandra, A.K., Merlin, P.M., 1977. Optimal
Implementation of Conjunctive Queries in Relational
Data Bases, Proceedings of the Ninth Annual ACM
Symposium on Theory of Computing STOC '77.
Algorithms for Computing Inequality Joins
363

Chaudhuri, S., Ganti, V., Kaushik, R., 2006. A Primitive
Operator for Similarity Joins in Data Cleaning,
Proceedings of the Seventh International Conference
on Data Engineering.
Codd, E. F., 1970. A Relational Model of Data for Large
Shared Data Banks, CACM, Vol. 13, No. 6, pp 377-387.
DeWitt, D.J., Naughton, J.F., Schneider, D.A., 1991. An
Evaluation of Non-Equijoin Algorithms, 17th
International Conference on Very Large Data Bases.
Enderle, J., Hampel, M., Seidl, T., 2004. Joining Interval
Data in Relational Databases, ACM SIGMOD
International Conference on Management of Data.
Graefe, G., 1993, Query Evaluation Techniques for Large
Databases, ACM Comput. Surv., Vol. 25, No. 2.
Graham, R.L., Knuth, D., Patashnik, O., 1988. Computer
Mathematics, Addison-Wesley.
Griffith, M., Mezo, I., 2010. A Generalization of Stirling
Numbers of the Second Kind via a Special Multiset,
Journal of Integer Sequences, Vol. 13.
Khayyat, Z., Ilyas, I.F., Jindal, A., Madden, S., Ouzzani,
M., Papotti, P., Quiane-Ruiz, J., Tang, N., Yin, S., 2015.
BigDansing: A System for Big Data Cleansing, ACM
SIGMOD International Conference on Management of
Data.
Khayyat, Z., Lucia, W., Singh, M., Ouzzani, M., Papotti,
Paolo, Quiane-Ruiz, J., Tang, N., Kalnis, P., 2017. Fast
and Scalable Inequality Joins, The VLDB Journal.
Klug, A., 1988. On Conjunctive Queries Containing
Inequalities, J. ACM, Vol. 35, No. 1.
Mishra, P., Eich, M. H., 1992. Join Processing in
Relational Databases, ACM Comput. Surv, Vol. 24, No.
1.
Okcan, A., Riedewald, M., 2011. Processing Theta-joins
Using MapReduce, ACM SIGMOD International
Conference on Management of Data.
Silva, Y.N., Reed, J.M., 2012. Exploiting MapReduce-
based Similarity Joins, ACM SIGMOD International
Conference on Management of Data.
Vernica, R., Carey, M.J., Li, C., 2010. Efficient Parallel
Set-similarity Joins Using MapReduce, ACM SIGMOD
International Conference on Management of Data.
Wang, Y., Metwally, A., Parthasarathy, S, 2013. Scalable
All-pairs Similarity Search in Metric Spaces, 19th ACM
SIGKDD International Conference on Knowledge
Discovery and Data Mining.
Wang, W., Jiang, H., Lu, H., Yu, J., 2003. Containment Join
Size Estimation: Models and Methods, ACM SIGMOD
International Conference on Management of Data.
DATA 2018 - 7th International Conference on Data Science, Technology and Applications
364
