Indexing Patterns in Graph Databases

Jaroslav Pokorný

, Michal Valenta

and Martin Troup

Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic

Faculty of Information Technology, Czech Technical University, Prague, Czech Republic

Keywords: Graph Databases, Indexing Patterns, Graph Pattern, Graph Database Schema, Neo4j.

Abstract: Nowadays graphs have become very popular in domains like social media analytics, healthcare, natural

sciences, BI, networking, graph-based bibliographic IR, etc. Graph databases (GDB) allow simple and rapid

retrieval of complex graph structures that are difficult to model in traditional IS based on a relational

DBMS. GDB are designed to exploit relationships in data, which means they can uncover patterns difficult

to detect using traditional methods. We introduce a new method for indexing graph patterns within a GDB

modelled as a labelled property graph. The index is organized in a tree structure and stored in the same

database where the database graph. The method is analysed and implemented for Neo4j GDB engine. It

enables to create, use and update indexes that are used to speed-up the process of matching graph patterns.

The paper provides a comparison between queries with and without using indexes.

1 INTRODUCTION

A graph database (GDB) is a database that uses the

graph structure to store and retrieve data. A GDB

embraces relationships as a core aspect of its data

model. The model is built on the idea that even

though there is value in discrete information about

entities, there is even more value in the relationships

between them. Relaxing usual DBMS features, a

native GDB can be any storage solution where

connected elements are linked together without

using an index (a property called index-free

adjacency).

Similarly to traditional databases, we will use the

notion of a graph database management system

(GDBMS). GDBMSs proved to be very effective

and suitable for many data handling use cases. For

example, specifying a graph pattern and a set of

starting points, it is possible to reach an excellent

performance for local reads by traversing the graph

starting from one or several root nodes, and

collecting and aggregating information from nodes

and edges. On the other hand, GDBMSs have their

limitations (Pokorný, 2015). For example, they are

usually not consistent, since have very restricted

tools to ensure a consistency. This property is typical

for NoSQL databases (Tivari, 2015), where GDBMs

are often included.

A GDB can contain one (large) graph G or a

collection of small to medium size graphs. The

former includes, e.g., graphs of social networks,

Semantic Web, geographical databases, the latter is

especially used in scientific domains such as

bioinformatics and chemistry or datasets like DBLP.

Thus, the goal of query processing is, e.g., to find all

subgraphs of G that are the same or similar to the

given query graph. We can consider shortest path

queries, reachability queries, e.g., to find whether a

concept subsumes another one in an ontological

database, etc. The query processing over a graph

collection involves, e.g., finding all graphs in the

collection that are similar to or contain subgraphs

similar to a query graph. We focus on the first

category of GDBs in this paper.

Graph search occurs in application scenarios,

like recommender systems, analyzing the hyperlinks

in WWW, complex object identification, software

plagiarism detection, or traffic route planning.

Gartner believes that over 70% of leading companies

will be piloting a graph database by 2018

(https://www.gartner.com/doc/3100219/making-big-

data-normal-graph, 2018).

One of the most fundamental problems in graph

processing is pattern matching. Specifically, a

pattern match query searches over a G to look for

the existence of a pattern graph in G. This problem

can be expressed in the different graph data models

as Resource Description Framework, property

Pokorný, J., Valenta, M. and Troup, M.

Indexing Patterns in Graph Databases.

DOI: 10.5220/0006826903130321

In Proceedings of the 7th International Conference on Data Science, Technology and Applications (DATA 2018), pages 313-321

ISBN: 978-989-758-318-6

313

graphs as well as in the relational model. A property

subclass of property graphs can even be modelled

using XML documents. We will focus on general

property graphs in this paper. Both above mentioned

GDB types, however, reduce exact query matching

to the subgraph isomorphism problem, which is NP-

complete (Ullmann, 1976), meaning that this

querying is intractable for large graphs in the worst-

case. In context of Big Data we talk about Big

Graphs (Pokorný and Snášel, 2016). Their storage

and processing require special technics.

An effective implementation of each DBMS

highly depends on the existence and usage of

indexes. Nowadays, some effective indexes for

nodes and edges already exist in GDB

implementations (see, e.g., the evaluation (Mpinda,

et al, 2015) mentioned in Section 2.1), while

structure-based indexes, which may be very useful

for subgraph queries and for relationship-based

integrity constraints checking, are yet rather the

subject of research as it is described in Section 2.

Particularly, there already exist indexing methods

for (various kinds of) graph pattern matching, see,

e.g., works (Aggarwal and Wang, 2010), (Troup,

2015) and (Yan, et al. 2004).

In the paper, we focus on Neo4j GDBMS

(https://neo4j.com/) and its possibilities to express

an index of graph patterns. Neo4j is an open-source

native GDBMS for storing and managing of

property graphs, that offers functionality similar to

traditional RDBMSs such as a declarative query

language Cypher ( http://neo4j.com/developer/

cypher-query-language/, 2018), full transaction

support, availability, and scalability through its

distributed version (Robinson, et al. 2013). Cypher

commands use partially SQL syntax and are targeted

at ad hoc queries over the graph data. They enable

also to create graph nodes and relationships. Our

goal is to extend the Cypher with new functionality

supporting more efficient processing graph pattern

queries.

The rest of the paper is organized as follows. In

Section 2 we summarize some related works divided

into two categories of graph indexing methods:

value-based indexing and structure-based indexing.

Section 3 introduces a graph database model based

on (labelled) property graphs. We continue with

graph pattern indexing and the details of the new

method based on so called graph pattern trees of

variations. Implementation and related experiments

are described and discussed in Section 4. Section 5

gives the conclusion.

2 BACKGROUND AND RELATED

WORKS

In general, graph systems use various graph

analytics algorithms supporting with finding graph

patterns, e.g., connected components, single-source

shortest paths, community detection, triangle

counting, etc. Triangle counting is used heavily in

social network analysis. It provides a measure of

clustering in the graph data which is useful for

finding communities and measuring the

cohesiveness of local communities in social network

websites like LinkedIn or Facebook. In Twitter,

three accounts who follow each other are regarded

as a triangle.

One theme in graph querying is graph data

mining finding frequent patterns. Frequent graph

patterns are subgraphs that are found from a

collection of graphs or a single massive graph with a

frequency no less than a user-specified support

threshold. Subgraph matching operations are

heavily used in social network data mining

operations.

Indexing is used in graph databases in many

different contexts. Due to the existence of properties

values in a GDB, graph indexes are of two kinds, in

principle: structure-aware and property-aware.

They occur in GDBMS in various forms from a

fulltext querying support over indexing nodes,

edges, and property types/values to indexes based on

indexing non-trivial subgraphs.

2.1 Value-based Indexing

Authors of (Mpinda, et al. 2015) compare indexing

used in two favourite GDBMSs – Neo4j and

OrientDB (http://orientdb.com/orientdb/, 2018). The

Cypher language of Neo4j enables to create indexes

on one or more properties for all nodes that have a

given label. OrientDB supports five classes of

indexing algorithms: SB-Tree, HashIndex, Auto

Sharding Index, and indexing based on the Lucene

Engine (for fulltext and spatial data). SB-tree

(O’Neil, 1992) is based on B-Tree with several

optimizations related to data insertion and range

queries. In Auto Sharding Index (key, value) pairs

are stored in a distributed hash table.

Another native GDBMS Sparksee (http://www.

sparsity-technologies.com/, 2018) uses B+-trees

and compressed bitmap indexes to store nodes and

edges with their properties. Titan (http://titan.

thinkaurelius.com/, 2018) supports two different

kinds of indexing to speed up query processing:

graph indexes and node-centric indexes. Graph

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

314

indexes allow efficient retrieval of nodes or edges by

their properties for sufficiently selective conditions.

Node-centric indexes are local index structures built

individually per node. In large graphs, nodes can

have thousands of incident edges.

2.2 Structure-based Indexing

The design principle behind a structural index is to

extract and index structural properties of database

graphs, typically at insertion time, and use them to

filter the search space rapidly in response to a query.

Previous works have mainly focused on mining

“good” substructure features for indexing. A good

feature set improves the filtering power by reducing

the number of candidate graphs, which leads to a

reduction in the number of subgraph isomorphism

tests in the verification step. Subtree features are

also mined for indexing, and they are less time-

consuming to be mined in comparison with more

general subgraph features. Many methods take a

path as the basic indexing unit. For example, the

SPath algorithm (Zhao and Han, 2010) is centred on

a local path-based indexing technique for graph

nodes and transforms a query graph into a set of the

shortest paths in order to process a query. The work

(Srinivasa, 2015) distinguishes three types of

structure-based indexes: path-based index, subgraph-

based index, and spectral methods.

It is remarkable, that different graph index

structures have been used for different kinds of

substructure features, but no index structure is

enabled to support all kinds of substructure features.

Authors of (Yuan and Mitra, 2013) propose a

Lindex, a graph index, which indexes subgraphs

contained in database graphs. Nodes in Lindex

represent key-value pairs where the key is a

subgraph in a GDB and the value is a list of database

graphs containing the key. Frequent subgraphs are

used for indexing in gIndex (Yan, et al 2004). An

introduction to graph substructure search,

approximate substructure search and their related

graph indexing techniques, particularly feature-

based graph indexing can be found in (Yan, et al.

2010). In (Zhu, et al. 2011), the authors introduce a

structure-aware and attribute-aware index to process

approximate graph matching in a property graph.

A detailed discussion of different types of graph

queries and a different mechanism for indexing and

querying graph databases can be found in (Sakr and

Al-Naymat, 2010).

3 MODELLING OF GRAPH

DATABASES

Although GDBMS can be based on various graph

types, we will use a (labelled) property graph model

whose basic constructs include:

 entities (nodes),

 properties (attributes),

 labels (types),

 relationships (edges) having a direction, start

node, and end node,

 identifiers.

Entities and relationships can have any number of

properties, nodes and edges can be tagged with

labels. Both nodes and edges are defined by a unique

identifier (Id). Properties are of form key:domain,

i.e. only single-valued attributes are considered. In

graph-theoretic notions we also talk about labelled

and directed attributed multigraphs in this case. It

means the edges of different types can exist between

two nodes. These graphs are used both for a GDB

and its database schema (if any). In practice, this

definition is not strictly enforced. There are

GDBMSs supporting more complex property values,

e.g. the already mentioned Neo4j.

When retrieving data from a GDB, one may want

to query not only single nodes or relationships, but

also more complex units consisting of these basic

elements. Such units, graph patterns, can contain

valuable information for many use cases. The fact

that the graph can easily express such information is

one of the main benefits of using such data model.

Thus graph pattern matching is one of the key

functionalities GDBs usually provide. In Section 3.1

we discuss shortly graph patters definable in the

Cypher language and two basic methods for their

indexing. Section 3.2 focuses on so called graph

pattern trees of variations appropriate for organizing

variations of a single graph pattern. Updating the

index after performing DML operations is described

in Section 3.3.

3.1 Graph Patterns

A wide variety of graph patterns can be found across

different GDBs. Graph patterns have different

information value that is based on type of data stored

within a database and use cases that involve these

graph patterns.

One of widely used graph patterns, defined as

GP = (V

; E

), where V = {v

; v

} and E = {(v

;

); (v

; v

); (v

; v

)}, is called a triangle. In Cypher,

Indexing Patterns in Graph Databases

315

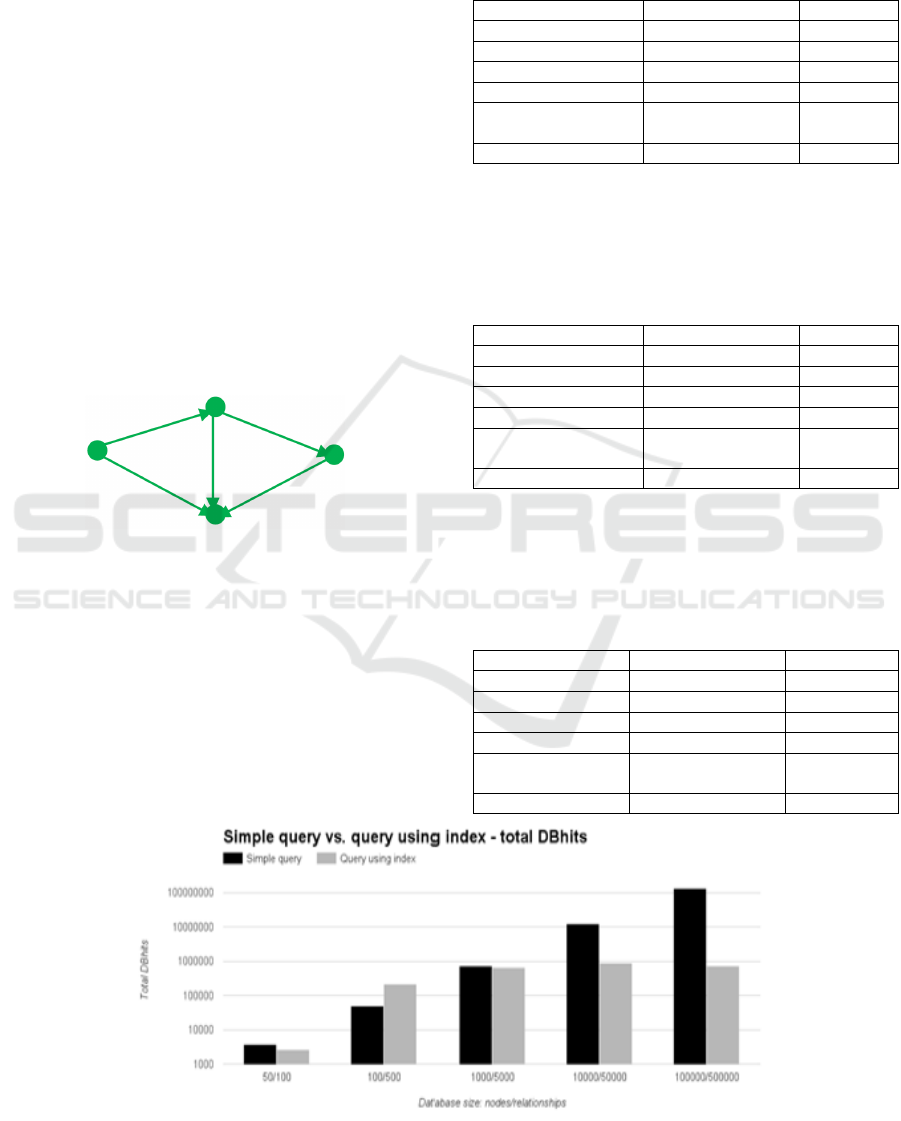
Figure 1: Example of a triangle.

a triangle can be expressed in a few different ways,

but preferably, e.g., as

) - [r

] - (n

) - [r

] - (n

) - [r

] - (n

)

i.e., triangle patterns look for three nodes adjacent to

each other regardless of edge orientation. That is, a

direction can be ignored at query time in Cypher,

i.e., the database graph behind can be handled as

bidirectional. Figure 1 shows a triangle coming from

a social graph. To retrieve such pattern using Cypher

is easy for Neo4j. The problem arises when we focus

only on structural features of the graph and want,

e.g., all such triangles of people with their

friendship. Then a structure-based index can be

helpful.

A graph pattern index is basically a data structure

that stores pointers that reference graph pattern units

within the database. Indexes can be either stored in

the same database as the actual data or in any

external data store. We use here the former variant.

The latter was used, e.g., in (Ramba, 2016), where

the embedded database MapDB (http://www.

mapdb.org/, 2018) was used for this purpose.

3.2 Graph Pattern Tree of Variations

An important feature of our approach is that a new

index must be created for each different graph

pattern, i.e., index that was created based on a

specific graph pattern cannot be used when querying

a different graph pattern.

Due to labelling nodes and edges of GDB,

patterns of the same structure can occur in different

variations (see, Figure 2). All variations of a single

graph pattern can be organized into a tree-like

structure, called graph pattern tree of variations.

Part of such tree for a triangle is shown in Figure 2.

Nodes represent individual graph pattern variations.

A root node of the tree is reserved for the basic

graph pattern variation with no additional

information about nodes and relationships. Children

of each node represent variations that provide some

additional information compared to its parent nodes

(i.e. when traversing deeper in the tree, more

information about graph pattern is specified). Leaves

of such tree represent specific graph pattern units

with IDs of nodes and relationships declared) within

the database.

Graph pattern can be represented by a set of its

variations. When querying a graph pattern, one

actually queries a specific variation of such graph

pattern. Thus, it must be said explicitly which one is

queried.

3.3 Updating Graph Pattern Index

A graph pattern index maps all graph pattern units

that are matched by a graph pattern the index was

created for. Such graph pattern units exist within the

database and so can be manipulated via DML

operations. Thus, they can be updated in such way

they no longer match the graph pattern. Also, when

adding new data to the database, new graph pattern

units can emerge. For that reason, each graph pattern

index must always map its graph pattern units that

currently exist within the database. That means each

index must be updated each time a DML operation is

applied on the database. Otherwise, indexes would

not provide reliable information when queried.

The intended DML includes operations like creating

a node, creating a relationship, deleting a node,

deleting a relationship, updating a node, and

updating a relationship. Except the first one, all

these operations affect the index, i.e. the index must

be updated. It is done so within the same transaction

that executed a DML operation. If a transaction is

successfully committed, indexes will be updated. If a

transaction is rollbacked, indexes will remain in the

same state as before the transaction was initialized.

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

316

Figure 2: Tree-like structure with graph pattern variations.

4 IMPLEMENTATION AND

EXPERIMENTS

The method for indexing graph patterns, including

operations to create an index, query using an index

and update an index, is implemented for the Neo4j

graph database engine. The major benefit of Neo4j is

its intuitive way of modelling and querying graph-

shaped data. Internally, it stores edges as double

linked lists. Properties are stored separately,

referencing the nodes with corresponding properties.

Our index implementation is done in the same GDB

as basic graph data. We introduced an additional

graph representing all indexes in the database. This

graph has a root providing approach to all indexes.

Implementation of an index consists of a two-level

tree. The first level has one node representing the

index and containing appropriate metadata. This top-

level index node is related to common root

mentioned above. The second level of index

representation consists of a set of graph pattern

units. Each unit represents one pattern (triangle in

our case). There are direct relationships to

appropriate nodes in the database from each pattern

unit.

Figure 3 describes an implementation of triangle

shape index. The first and the second layer is index

implementation, the third layer represents data in

GDB. Labels PDT denote

PATTERN_INDEX_RELATION.

4.1 Graph Datasets

Experiments were done on three different graph

datasets: Social graph with a triangle index, Music

database with a funnel index, and Transaction

database with a rhombus index.

Social graph is a database that contains information

about people and friendships between them. People,

represented by nodes, have names and are

distinguished to males and females by appropriate

labels. Friendships between them are represented by

relationships of Is_friend-of type. Such

database of changeable size is generated by Erds–

Rnyi model for generating random graphs (see,

e.g., (Goldenberg, et al. 2009)). The generator is a

part of used GraphAware framework

(https://github.com/graphaware/neo4j-framework,

2018). Triangle index is built for a triangle graph

pattern expressed in Cypher in Section 3.1.

Music database stores data about artists, detailed

information about the tracks they recorded and

labels that released these records. The database has a

fixed size of 12 000 nodes and 50 000 relationships.

It is one of the example datasets that Neo4j provides

on its website (http://neo4j.com/developer/example-

data/, 2018). The database contains 86 funnel

patterns. Funnel index pattern (Figure 4) we used for

this database has the following Cypher expression:

(n1)−[r1]−(n2)−[r2]−(n3)−[r3]−(n1)−[r4]−(n4)

Transaction database stores data about transactions

between bank accounts in a simplified way. Bank

accounts, represented by nodes, are identified by

account numbers. Transactions between bank

accounts are represented by relationships. They have

no properties on them since it is not crucial for the

measurements. If used in a real database, they would

probably hold some specific characteristics about

them, e.g., a date of transaction execution or the

amount of transferred money within a transaction.

Such database of changeable size was generated

by a Cypher script that was created especially for

this purpose. Such simple script creates bank

accounts at first and then generates a transaction

Indexing Patterns in Graph Databases

317

Figure 3: Implementation of triangle shape index.

relationship for each pair of these accounts with a

given probability. The database we generated has 10

000 of nodes and 100 000 of relationships, it

contains 70 rhombus patterns which were indexed.

Rhombus index (Figure 5) is used for this database.

It is formulated by the following Cypher expression

)−[r

]−(n

)−[r

]−(n

)−[r

]−(n

)−[r

]−(n

)−[r

]−(n

)

All results are achieved by measuring within a

test environment provided by GraphAware

framework. The following configuration is used

when performing measurements: 2.5GHz dual-core

Intel Core i5, 8GB 1600MHz memory DDR3, Intel

Iris 1024 MB, 256 GB SSD, OS X 10.9.4.

To achieve the most accurate results,

measurements are always performed multiple times

and their results are averaged. Measuring is done for

all cache types provided by Neo4j, i.e., no-cache

(Neo4j instance with no caching), low-level cache,

and high-level cache.

4.2 Measurement on Social Graph

Database with Triangle Index

The size of the database scales from 50 nodes and

100 relationships to 100 000 nodes and 500 000

relationships. A matching triangle graph pattern

using a simple query (i.e. without a graph structure

index) is nearly impossible for larger databases of

this type.

There are two metrics used: time and the number

of database hits (DBHits), i.e., total number of

single operations within Neo4j storage engine that

do some work such as retrieving or updating data.

DBHits metrics for varying size of databases are

shown on Figure 6. We can see that from the

database of size 10 000 nodes/50 000 relationships

index pattern is much more effective than “simple

query” (i.e. the query without index usage). The

amount of DBHits for index grows linearly with

growing the database while it grows exponentially

for simple query.

Time metrics are shown on Figure 7. Again, we

can see an exponential rowth of time for a simple

Figure 4: A graph pattern used for Music DB.

query and a linear growth for index. For the largest

database of 100 000 nodes and 500 000

relationships, a query using an index is

approximately 170 times faster and performs

approximately 180 times less database operations

than a simple query.

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

318

4.3 DML Operations and Queries

Measurement

The index must be updated together with DML

operations on the base data. In our implementation

update of the index is done in the same transaction

as DML statement. We did measurements on all

three databases mentioned in Section 4.1 for the

following DML operations:

 creating an index,

 creating a relationship,

 deleting a relationship,

 deleting a node, and

 deleting a label of a node.

All these DML operations may affect existing

indexes.

All measurements were done again for all cache

types provided by Neo4j, i.e:

 without caching,

 low level cache (i.e. file buffer cache), and

 high level cache (object cache).

Figure 5: A graph pattern used for Transaction DB.

The last mode is the most suitable for our purpose

and, not surprisingly, it provides the best

performance. See (Troup, 2015) for measurement

results using another cache modes.

In the Tables 1-3 we present also a time of given

operation without index usage to show additional

costs for index maintenance. In Table 1 we present

measured values done on a social graph with triangle

index on the database having 10000 nodes and

50 000 relationships. Let us note, that there were 183

graph patterns on 179 nodes.

Table 1: Social graph, triangle index.

Operation

Simple query [μs]

Index [μs]

create index

---

5 242 762

query index

6 881 440

403 375

create relationship

25 973

29 987

delete relationship

146 820

157 726

delete node with its

relationships

228 399

277 835

delete node label

17 475

19 380

Table 2 presents measurements for funnel pattern

index on the Music database. The database consists

of 12 000 nodes, 50 000 relationships and contains

86 funnel patterns

Table 2: Music database, funnel index.

Operation

Simple query [μs]

Index [μs]

create index

---

5 242 762

query index

6 881 440

403 375

create relationship

25 973

29 987

delete relationship

146 820

157 726

delete node with its

relationships

228 399

277 835

delete node label

17 475

19 380

Table 3 presents measurements for rhombus

pattern index on the Bank database. Database

consists of 10 000 of nodes, 100 000 of relationships

and contains 70 rhombus patterns.

Table 3: Bank database, rhombus index.

Operation

Simple query [μs]

Index [μs]

create index

---

36 238 883

query index

41 794 378

1 243 503

create relationship

29 659

64 432

delete relationship

257 094

283 067

delete node with its

relationships

375 308

459 808

delete node label

17 485

22 420

Figure 6: Social graph, triangle index – DBHits metrics.

Indexing Patterns in Graph Databases

319

Figure 7: Social graph, triangle index – time metrics.

Let us note several interesting observations coming

from our measurements:

 index creation time is not much higher than

query time without an index for triangle and

rhombus patterns, it is nearly two times

higher for funnel index,

 query using an index is faster than the query

without index for all three patterns, it is 17

times faster for triangle index, 112 times for

funnel index, and 33 times for rhombus

index,

 time to update the index in case of insert/delete

a node or a relationship is on average 17% of

time needed for DML operation itself.

Let us generalize the measurement and state

several hypotheses about the efficiency of our

implementation of pattern indexes:

 It was shown that starting from databases of

size 10 000 of nodes and 50 000 of

relationships queries using pattern indexes

are more efficient than queries without them.

 Efficiency of pattern index increases with

growing the database. Time and amount of

database operations grow linearly for

(triangle) pattern (see Figures 6 and 7).

 Complexity and size of the pattern used for

index influence characteristics and efficiency

of an index. We tested triangle, funnel, and

rhombus patterns – all tested indexes are

more than 17 times faster for querying, this

ratio will growth with the size of the

database.

 Time for keeping indexes actual seems to be

under 20% of time necessary for DML

operation.

The complete analysis and design decisions can

be found in the work (Troup, 2015).

4.4 Index Size

Index size linearly grows with the number of pattern

units found in the database and it also linearly grows

with the number of nodes that the indexed pattern

consists of. The index size can by asymptotically

expressed as

Θ(n

 n

)

where n

represents the number of pattern units

found in the database and n

represents the number

of nodes that the indexed pattern consists of. The

exact number of nodes needed for the index is

nodes

= 1 + n

where a single node represents the root of the index

and n

nodes represent individual pattern units found

in the database. The exact number of relationships

needed for the index is

rels

= n

+ n

 n

where n

relationships connect the root node with all

nu pattern unit nodes. n

relationships then connect

individual data nodes belonging to a single pattern

unit to its representative pattern unit node.

Table 4: Database and index sizes.

Database index

DB size

(Mb)

Index size

(Mb)

Pattern

units

Social graph,

triangle index

19,6

0,15

183

Music database,

funnel index

89,6

0,2

Bank database,

rhombus index

17,2

0,1

Table 4 presents index size using 3 different patterns

and databases. There are 183 pattern units indexed in

the first database which is more than double what is

indexed in other two databases. Triangle pattern

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

320

consists of 3 nodes whereas funnel and rhombus

patterns consist of 4 nodes. This results in

approximately the same size (in Mb) of index for all

of 3 measured databases and patterns.

5 CONCLUSIONS

In the paper a new method for indexing graph

patterns was analyzed, designed and implemented

for Neo4j GDBMS in order to speed up the process

of matching graph patterns. The method enables to

create, use and update multiple indexes, each created

for a different graph pattern. Index data are

organized in a tree structure and they are stored

within the same database as the base data. This

solution provides really fast approach from the index

structure to data. On the other hand, it mixes index

data and base data together in one common storage.

It may negatively affect the evaluation of queries

that do not use index patterns. We plan to address

this issue in following research. It is the part of a

more general topic how to store metadata and

separate them from base data in GDBMS.

It is proved that using indexes which are created

by the method introduced in this paper is beneficial

for the process of matching graph patterns. In some

cases queries using such indexes are extremely faster

than simple Cypher queries. The paper aims to

introduce the topic of indexing graph patterns and

provides one of possible ways how to speed up the

process of matching graph patterns within a GDB.

ACKNOWLEDGEMENTS

This work was supported by the Charles University

project Q48.

REFERENCES

Aggarwal, C. C., Wang, H., 2010. Managing and Mining

Graph Data. Springer.

Goldenberg, A., Zheng, A.X., and Fienberg, S.E., Airoldi,

E.M., 2009. A Survey of Statistical Network Models.

Foundations and Trends in Machine Learning 2(2),

129-233.

Mpinda, S.A.T., Ferreira, L.C., Ribeiro, M.X., and Santos,

M.T.P. 2015. Evaluation of Graph Databases

Performance through Indexing Techniques.

International Journal of Artificial Intelligence &

Applications (IJAIA) 6(5) 87-98.

O'Neil, P.E., 1992. The SB-tree: An Index-Sequential

Structure for High-Performance Sequential Access.

Informatica 29, 241-265.

Pokorný, J., 2015. Graph Databases: Their Power and

Limitations. In CISIM 2015, Proc. of 14th Int. Conf.

on Computer Information Systems and Industrial

Management Applications, K. Saeed and W. Homenda

(Eds.), LNCS 9339, p. 58-69. Springer.

Pokorny, J., Snášel, V., 2016. Big Graph Storage,

Processing and Visualization. Chapter 12 in: Graph-

Based Social Media Analysis. Chapman and

Hall/CRC, I. Pitas (Ed.), 391 – 416.

Ramba, J., 2015. Indexing graph structures in graph

database machine Neo4j II. Master’s thesis, Czech

Technical University in Prague, Faculty of

Information technology, (in Czech).

Robinson, I., Webber, J., and Eifrém, E., 2013. Graph

Databases. O’Reilly Media.

Sakr, Sh., Al-Naymat, G., 2010. Graph indexing and

querying: A review. International Journal of Web

Information Systems 6(2):101-120.

Srinivasa, S., 2012. Data, Storage and Index Models for

Graph Databases. Chapter in: Graph Data

Management: Techniques and Applications, ed. Sherif

Sakr and Eric Pardede, 47-70.

Tivari, S., 2015. Professional NoSQL. Wiley/Wrox.

Troup, M.: Indexing of patterns in graph DB engine Neo4j

I. Master’s thesis, Czech Technical University in

Prague, Faculty of Information technology. Available

at:https://dspace.cvut.cz/bitstream/handle/10467/6506

1/F8-DP-2015-Troup-Martin-

thesis.pdf?sequence=1&isAllowed=y

Ullmann, J.R., 1976. An algorithm for subgraph

isomorphism. J. ACM, 23(1), 31-42.

Yan, X., Yu, P.S., and Han, J. 2004. Graph Indexing: A

Frequent Structure-based Approach. In SIGMOD

Conference, ACM, pages 335-346.

Yan, X., Han, J., 2010. Graph Indexing. Chapter 5 in

Managing and Mining Graph Data, Advances in

Database Systems 40, C.C. Aggarwal and H. Wang

(eds.), Springer.

Yuan, D., Mitra, P. 2013. Lindex: a lattice-based index for

graph databases. The VLDB Journal, 22, 229–252.

Zhao, P., Han, J. 2010. On graph query optimization in

large networks. VLDB Endowment, 3(1-2), 340–351.

Zhu, L., Ng, W.K., Cheng, J., 2011. Structure and attribute

index for approximate graph matching in large graphs.

Inf. Syst. 36(6), 958-972.

Indexing Patterns in Graph Databases

321