Improved Cloud Partitioning Sampling for Iterative Closest Point:

Qualitative and Quantitative Comparison Study

Polycarpo Souza Neto, Nicolas S. Pereira and George A. P. Th

Department of Teleinformatic Engineering, Federal University of Ceara, Fortaleza,

Pici campus, Bl 725, Zip code 60455-970, Brazil

Keywords:

Computer Vision, Iterative Closest Point, Point Cloud Registration, Point Cloud Sampling.

Abstract:

In 3D reconstruction applications, an important issue is the matching of point clouds corresponding to different

perspectives of a given object in a scene. Traditionally, this problem is solved by the use of the Iterative Closest

point (ICP) algorithm. In view of improving the efﬁciency of this technique, authors recently proposed a

preprocessing step which works prior to the ICP algorithm and leads to faster matching. In this work, we

provide some improvements in our technique and compare it with other 4 variations of sampling methods

using a RMSE metric, an Euler angles analysis and a modiﬁcation structural similarity (SSIM) based metric.

Our experiments have been carried out on four different models from two different databases, and revealed

that our cloud partitioning approach achieved more accurate cloud matching, in shorter time than the other

techniques. Finally we tested the robustness of the technique adding noise and occlusion, obtaining, as in the

other tests, superior performance.

1 INTRODUCTION

Efﬁcient 3D reconstruction of indoor and outdoor en-

vironments is a hot research topic in many areas like

machine learning (Pan et al., 2017), in computer vi-

sion (Rodol

a et al., 2015), in photogrammetry (Zhang

and Lin, 2017) as well as for helping agriculture

through the use automated system for capturing 3D

data of plants and vegetation (Chaudhury et al., 2015)

and robotics (

Cesi

c et al., 2016) for tracking and de-

tection of elements in scenes. Also in manufactur-

ing industry (Toro et al., 2015) it may be seen as a

provider of innovative and efﬁcient solutions for op-

timizing shop ﬂoor processes (Malamas et al., 2003),

what has been suggested especially in cases of colli-

sion avoidance (Cigla et al., 2017) in non-structured

scenarios and for safer human-machine interaction

(Gorecky et al., 2014), which ultimately may speed

up manufacturing processes.

In a few words, 3D reconstruction means data

fusion of images from different camera perspectives

and consists essentially on making partial descrip-

tions of a scene to merge into a scene representa-

tion as a whole. In the literature, this task has been

ﬁrst solved by the Iterative Closest Point algorithm

(Besl and McKay, 1992). It is aimed at obtaining the

rigid transformation able to minimize the distance be-

tween two datasets, e.g. two acquired point clouds of

a given scene, allowing an integration of images ac-

quired from different camera position and orientation.

In general, ICP performs better when some data

preprocessing is carried out. In the literature, out-

liers removal (Weinmann, 2016) and undersampling

(Rodol

a et al., 2015) are typical issues; while the

former is important for good representation of the

rigid transformation pursued, latter inﬂuences com-

putational costs and its adoption is needed for sev-

eral reasons, as pointed out in (Rodol

a et al., 2015).

The sampling methods are useful discretization step

to produce data which is much easier to handle with

algorithms. Even if the surface is a triangular mesh,

sampling reduces the number of points to be repre-

sented, which may be required if the complexity of

the task is not linear or the clouds are large in size.

However, the goal of sampling is the selection of sur-

face points that are relevant with respect to the task

that is to be performed.

Authors recently proposed a sampling method

named cloud-partitioning ICP (CP-ICP) and it is re-

visited in this work, since important changes were

made to it (Pereira et al., 2015). We compared this

method with ICP as well as sampling methods based

on sampling. The techniques of comparison using

sampling were Random and Uniform Sampling. Uni-

Neto, P., Pereira, N. and Thé, G.

Improved Cloud Partitioning Sampling for Iterative Closest Point: Qualitative and Quantitative Comparison Study.

DOI: 10.5220/0006828500490060

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 49-60

ISBN: 978-989-758-321-6

form and random sampling variants were also stud-

ied in (Rusinkiewicz and Levoy, 2001). In the case

of Random Sampling, two variants were used, with

sampling of 50% and 70% of the data set. We have

compared the sampling methods quantitatively using

root mean squared error (RMSE) and Euler angles;

in addition, we adapt a form of quantitative evalua-

tion based on multi-view analysis of the registration

images, exposing these images to Structural Similar-

ity Index Measure (SSIM), proposing in (Wang et al.,

2004). Effects of adding noise and occlusion were

also investigated for some models, in order to provide

insight of robustness of the CP-ICP method under real

conditions of data acquisition.

The ICP implementation (in C++) of the Point

Cloud Library (PCL)(Holz et al., 2015) was adopted

here because it is widely used as benchmark by the

research community.

2 BASICS OF 3D MATCHING

The ICP algorithm was proposed in (Besl and McKay,

1992) and aims at ﬁnding a transformation that opti-

mizes a rotation and translation in two sets of data

(sets of line segments, implicit curves, sets of tri-

angles,implicit, parametric surfaces, point sets, etc.).

The algorithm uses one of the data sets as reference,

hereafter referred to as set and applies rotations and

translations to the other set, called here from now on

as input set, in order to minimize the following cost

function:

F(~q) =

∑

i=1

k~x

−(R~p

+ T ) k (1)

where:

• N=number of points;

• ~x

=i-th vector related to the target point cloud;

• ~p

=i-th vector related to the input point cloud;

• R= rotaxion matrix obtained from ICP;

• T= translation vector obtained from ICP.

The result achieved from the ICP algorithm is

the optimum rotation and translation between the two

datasets. Fig. 1 illustrates what happens after apply-

ing the ICP algorithm to point clouds. In the left, the

initial pose of the inputs and in the right, a successful

registration between the two point clouds.

Figure 1: Point cloud of Hammer model before (left) and af-

ter(right) submited from ICP algorith (Aleotti et al., 2014).

3 SAMPLINGS

3.1 Uniform Sampling

This ICP variant allows for crudely aligning one range

image to another and then invoking an algorithm that

snaps the position of one range image into great align-

ment to the other cloud. The implemented version

follows the description of (Turk and Levoy, 1994):

1. Find the nearest position on mesh A to each point

of mesh B;

2. Discard points out of range;

3. Delete pairs that are in a mesh boundary;

4. Find rigid transformation that minimizes weight-

ing distance to the square minimum between the

pairs of points.;

5. Run to converge;

6. Perform ICP on a more detailed mesh.

This ICP variant differs from classical ICP in sev-

eral ways. First, a distance boundary was added to

the nearest point to avoid combining any vertices B

from a mesh to a remote part otherwise than corre-

sponding to B

. This vertex B

of the mesh B may

be a part of the scanned object that has been not cap-

tured in mesh A. In (Turk and Levoy, 1994), it is said

that an excellent record is when the distance is ad-

justed to double the spacing between the reach points.

Limiting the distance between pairs of corresponding

points we performed step 2 (eliminating remote peers)

while searching for closest points in step 1.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

3.2 Random Sampling

Random sampling is a good downsampling tech-

nique, objectifying only to ﬁnd internal points (Ma-

suda et al., 1996). We apply this technique to a ﬁrst

image R

, and we draw a set of N

points of R

ran-

domly. One way to evaluate a probability of a good

sampling and considering a random sampling from a

probabilistic view point. Whatever epsilon a rejec-

tion of outliers by noise or occlusion, a probability of

choice inliers is 1 −ε. In addition, a probability of

choosing a subset with N

points that are all inliers

is (1 −ε). The N

value is a hair probability minus

a sub-sample being composed only of curious. The

equation that governs this method is shown below:

p(ε,N

) = 1 −(1 −(1 −ε)

)

(2)

An example of random sampling can be seen in

(Nazem et al., 2014). In this paper, 70% of the data

sets are sampled before the registration process.

4 CLOUD PARTITIONING ICP

In line with that, recently authors proposed the cloud

partitioning approach to work prior the execution of

the ICP algorithm (CP-ICP). In the present version

of the algorithm, the idea behind the CP-ICP is to

separate the whole point cloud into smaller groups (k

groups in total) named hereafter subclouds, and then

repeat the registration process for every subcloud until

a stop criterion is found, as explained in section 4.1;

by doing that, we considerably reduce the amount of

computations because the point clouds are reduced in

size.

Originally (Pereira et al., 2015), ,the implementa-

tion did not consider the existence of a stop criterion,

what led to veriﬁcation of k subclouds, and this some-

times proved to be unneccessary.The partitioning pro-

cess decreases the amount of data to be processed by

ICP in iteration, and the adoption of a stop criterion

prevents the algorithm from having to align among all

the subnets, stopping in the alignment of some sub-

cloud that has a lower RMSE than the stopping cri-

terion, which leads to time consuming and a guaran-

tee of a quality registration, although, within the set

of subnets there may be some where the alignment

is even better and the RMSE measurement confers

smaller values even of iteration where the algorithm

converge. Cutting of the point clouds in the CP-ICP

can be illustrated in Fig. 2, where after being iden-

tiﬁed where the cloud centroid is and its Z-axis, the

cuts are done in subclouds.

To get a better view on the above claiming, let N

and N

be the size of two clouds undergoing registra-

tion by the ICP. The cost for the closest point com-

putation in the classical ICP is O(N

) (Besl and

McKay, 1992), whereas using the partitioning into

subclouds makes the cost of the closest point compu-

tation to range from O(N

) to kO(N

This is because the stop criterion considered in the

current version, illustrated in the diamond of the ﬂow-

chart in Fig. 3 may interrupt the whole matching at

any iteration from 1 to k.

Figure 2: The left side the identiﬁcation of each axis of the

Hammer cloud in the coordinate system and to the right we

have after the identiﬁcation of Z, the cut in k sub-clouds.

4.1 Sufﬁcient Registration

Consider two point clouds: an input point cloud and a

target point cloud. The goal is to successfully perform

a registration procedure, which means matching the

input point cloud to the target one. To apply the CP-

ICP method, we perform the following steps:

1. Subdivide each dataset (input and target) into k

subclouds;

2. For each of the k iterations, solve the ICP algo-

rithm for a pair of subclouds. The correspondence

is checked between subclouds having the same in-

dex, and not one against all.

• Apply the achieved transformation to the initial

input point cloud (named from now on input post

ICP);

• The input post ICP is then compared to the target

point cloud, using RMSE error at each iteration;

• If the RMSE value achieved in a given iteration is

acceptable (stop criterion) the algorithm ends and

the wanted registration is outcome. This is a deci-

sion step and, as such, represented by diamond in

the ﬂowchart of Fig. 3.

Improved Cloud Partitioning Sampling for Iterative Closest Point: Qualitative and Quantitative Comparison Study

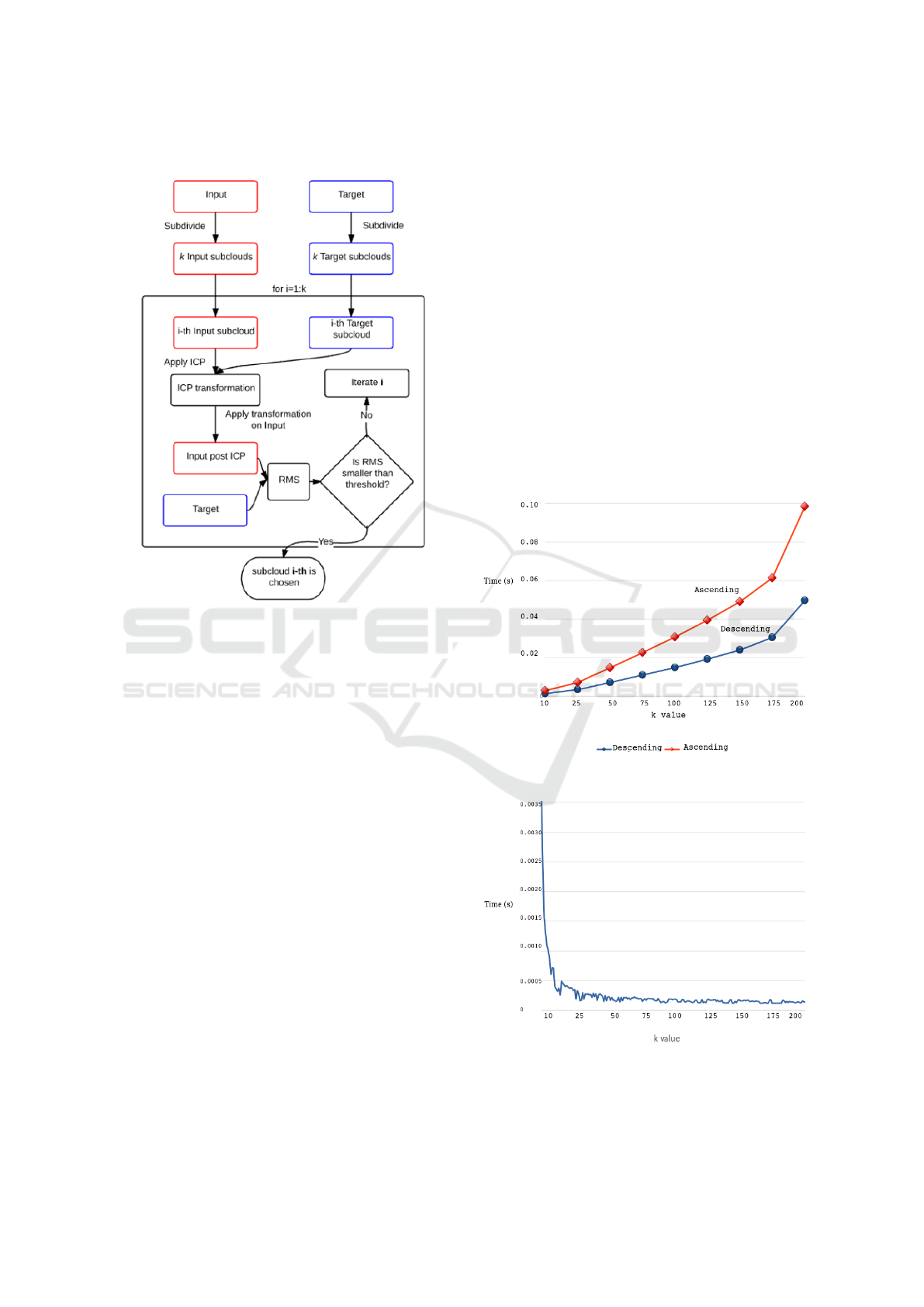
These steps are illustrated in the ﬂow-chart of Fig. 3.

Figure 3: Fluxogram illustrating how the CP-ICP achieve a

sufﬁcient registration.

Adopting a stop criterion is useful because it limits

the amount of correspondence checks between pairs

of subclouds, thus avoiding unneccessary repetitions

of ICP algorithm.

4.2 Tradeoff Between Solutions and

Time

Considering the CP-ICP method as shown in 3, one

can see that the more subclouds the more solutions

for transformation matrices are obtained, which is

good for ﬁnding an acceptable registration. However,

time consumption rises accordingly, what is a draw-

back, and reveals a tradeoff between the number of

solutions and the time consumption. That is why we

added a stop criterior to this algorithm. By doing that

at every correspondence check between pairs of sub-

clouds, we give the algorithm the ability to escape

and ﬁnish the matching whenever a good alignment

is found. Although in the current version the stop

criterion is determined a priori, this strategy has the

advantage to help reducing computational cost (com-

pared to the old published version).

To better explain the inﬂuence of the amount of

subclouds into the timing performance, we studied the

total elapsed time of the CP-ICP method, Fig. 4, as

well as the time spent in a single iteration, Fig. 5, for

different values of k. In ﬁgure 4 there are two curves;

they correspond to two different choices for the step

2 of the algorithm in section 4.1. Once the indexation

of the whole cloud and its grouping into k partitions

is done, the user must choose between ascending or

descending order to access the indexed subclouds in

the search for the best one. In some examples of the

database, the best subcloud is found near the begin-

ning of the for-loop, whereas in other data it takes the

whole spectrum of subclouds to be checked, slowing

down the CP-ICP running time. These two limit cases

are the ones represented by the lines of Fig. 4. In the

example of the ﬁgure, the downward direction choice

for accessing the i-th subcloud led to faster CP-ICP

execution.

Figure 4: The full time consumption.

Figure 5: The time consumption for a single iteration for

the Horse model.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

5 MATERIALS AND METHODS

5.1 Available Datasets

The performance of the proposed CP-ICP method was

evaluated from two different database. The ﬁrst one

is a private database kindly provided by prof. Aleotti

in (Aleotti et al., 2014) and consists of point clouds of

several objects acquired from a 6DOF robot arm (Co-

mau SMART six) equipped with a two-ﬁnger parallel

gripper (Schunk PG-70) and a high-resolution range

laser scanner (SICK LMS 400), both mounted at the

wrist of the robot arm. From this database we used

two models in our experiments, namely the Horse and

the Hammer models, illustrated in Fig. 6.

Figure 6: Objects from the database in (Aleotti et al., 2014).

The Horse model (left) and Hammer (right).

The perspectives available of those objects are la-

beled according to the angle of acquisition from the

sensor in the scene. For the Horse model we con-

sider the perspectives of 0

and 180

. For the Ham-

mer model we consider the perspectives of 0

and

. The second database is the Stanford 3D scanning

repository, illustrated in (Curless and Levoy, 1996),

which is a public database with several 3D models.

Figure 7: Objects from the database in (Curless and Levoy,

1996). The Dragon model (left) and Happy Buddha (right).

Similarly, the perspectives available of those ob-

jects are related to the acquisition angle.The image

acquired from the zero degree perspective is taken as

target cloud, whereas the one acquired from 24 de-

grees is considered as source cloud. Table 1.

Table 1: Various dataset size.

Number of points

Cloud Source Target

Horse 3335 3298

Hammer 1852 2024

Dragon 41841 34836

Buddha 78056 75582

5.2 Methodology

As pointed out earlier, the goal of this paper is

to introduce a new sampling method prior the ICP

algorithm (CP-ICP). To evaluate how it performs,

we compare CP-ICP with random sampling methods

(keeping up to 50% and 70% of the original point

cloud size) and also with a uniform sampling. In addi-

tion, we also considered the no-sampling case, which

is the classical ICP method of (Besl and McKay,

1992) as implemented in PCL. The ICP algorithm

then follows the sampling methods under study, and

the quality of the 3D registration is evaluated through

the Euler angles of the rotation matrix, by a metric

based on root mean squared (RMSE) error and, ﬁ-

nally, by another metric based on an adaptation of

the structural similarity index (SSIM), to be discussed

next. In Fig. 8, this process is summarized.

5.3 Metrics for Matching Evaluation

We have adopted three different metrics to evalu-

ate the registration results and compare the sampling

methods. The ﬁrst one is based on the root mean

squared error between the target point cloud and the

input point cloud after proper rotation correction.

The RMSE eror can be calculated by the following

formula:

RMSE =

∑

i=1

(min

x∈S

k y

−x k

)

, (3)

where S is an arbitrary surface and y1, ...,yN are

coordinate points in ℜ

, representing the surface ver-

tices or cloud points depending on a distance between

two surfaces or between a surface and a point in the

cloud.

The second metric is based on comparing the Eu-

ler angles from each transformation matrix obtained

through ICP. This can only be done to the Dragon and

Buddha models, since they have a ground truth.

Improved Cloud Partitioning Sampling for Iterative Closest Point: Qualitative and Quantitative Comparison Study

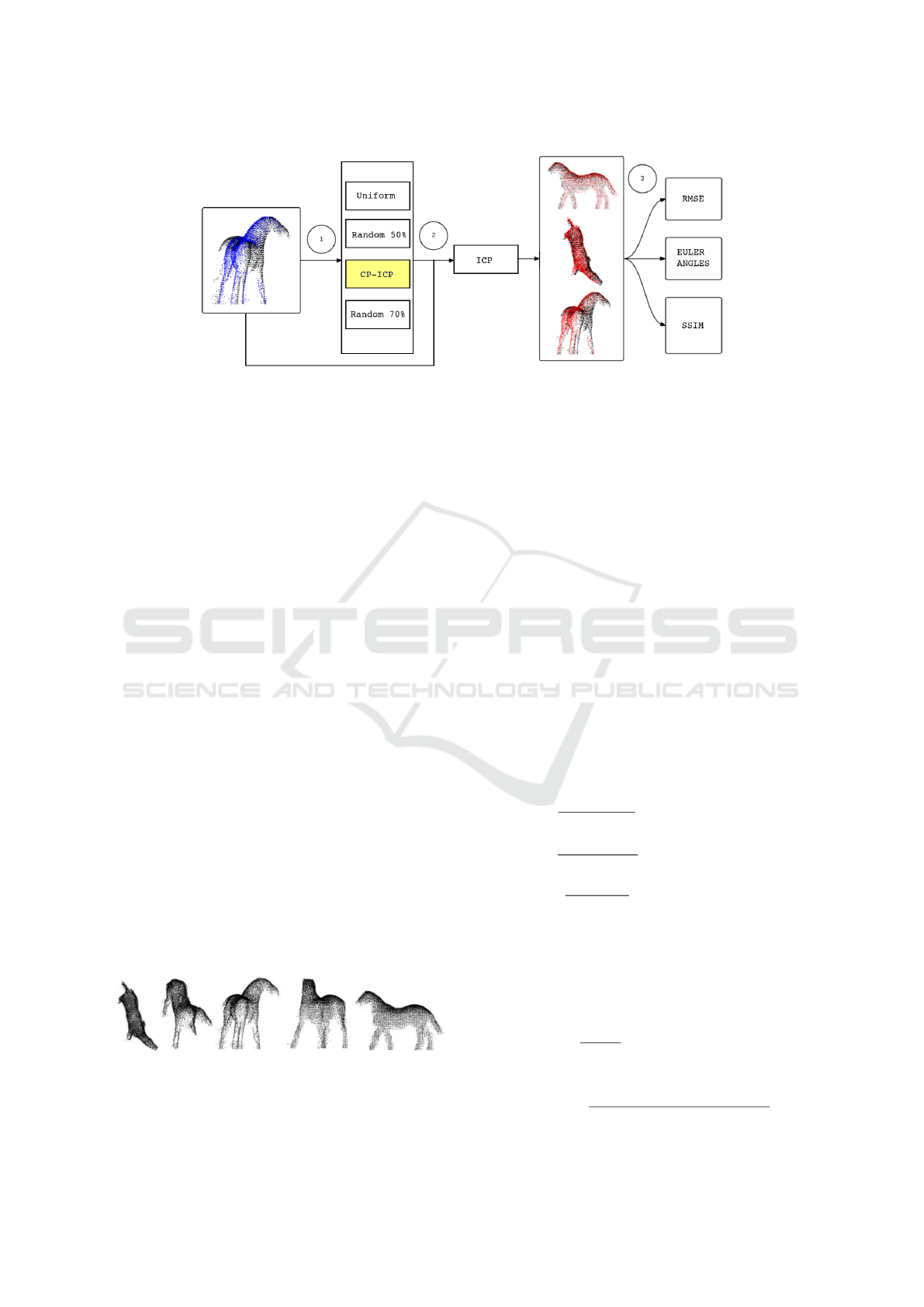
Figure 8: Methodology adopted to compare the sampling methods. In (1) the clouds go through a sampling process, in (2)

the ICP is applied to perform the alignment, in (3) the outputs of the registry go through the evaluation of the registry quality

metrics.

The rotation matrix can be deﬁned by R, and the

results of the Euler angles are obtained by the resolu-

tions of the trigonometric products contained therein

(Corke, 2017).

R =





−c

+ c

+ s

−c

−s





(4)

where: c

=cos(α), c

=cos(β), c

=cos(γ),

=sen(α), s

=sen(β) and s

=sen(γ).

The last metric is based on the SSIM index, which

is a traditional approach to measure image quality. It

is also a method applied to identify similarity between

two gray-scale images, where one of them is treated

as a reference image. The SSIM index is an image

quality metric which assess three characteristics of an

image: the contrast, luminance and structure, each of

them being calculated from statistical parameters of

the input images.

In this paper, we adapt a method which uses the

SSIM index to perform the comparison between 3D

models by creating 2D images of different perspec-

tives of each model and comparing them using the

SSIM index. To illustrate how the method is made

suitable for 3D, we start with the registration result as

obtained by the CP-ICP for the Horse model from ﬁve

perspectives, in Fig. 9.

Figure 9: The ﬁve perspectives for the CP-ICP registration

of the Horse model.

The use of the SSIM technique here relies on gen-

erating three images for each perspective: dot pat-

tern image, full image and edge image, each one

with 512x512 resolution. We got the dot pattern im-

age after a quantization of point dataset as visualized

from one of the perspectives, whereas the others are

achieved from morphological transformations applied

in the dot pattern image. Fig. 10(a), 10(b) and 10(c)

show this set of images using as example the ﬁrst per-

spective of 9. Fig. 10(b) and 10(c) are respectively

the images after dilation and border extraction (Soille,

2003).

Dilation depicted in Fig.10(b) is the result of prob-

ing and expanding (until background is found) the

inner of the input image from a structuring element.

Border extraction then follows this dilation by means

of subtracting it from the input image.

According to (Wang et al., 2004), the functions

l(a, b), c(a,b) and s(a,b) are then deﬁned as:

l(a, b) =

2µ

+ µ

= (K

 1 (5)

c(a,b) =

2σ

+ σ

= (K

 1 (6)

s(a,b) =

2σ

= (K

 1 (7)

Where µ

and µ

are the pixel intensities of each im-

age, σ

and σ

are the standard deviations, C

, C

and

are constants added to each term, L is the pixel

range (255 for 8-bit grayscale images, e.g.) and K

and K

are constants less than unity. In addition, σ

is calculated as:

−1

∑

i=1

−µ

)(b

−µ

) (8)

Finally, the metric takes the form presented below:

SSIM(a, b) =

(2µ

)(2σ

)

(µ

+ µ

)(σ

+ σ

)

(9)

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

(a) (b)

(c)

Figure 10: The three kind of images generated for each per-

spective of each model. In (a) dot pattern image, in (b) full

image (dilated), in (c) edge image (border extraction).

6 RESULTS

6.1 Elapsed Time

Table 2 synthetizes the time performance of the

various sampling approaches; as it is clear from

the results, the proposed CP-ICP sampling method

achieved top performance for each 3D model stud-

ied. Such a good performance of the proposed ap-

proach somewhat conﬁrms the expectations about the

reduced computational efforts of the cloud matching

algorithm, as mentioned in Section 4.

Table 2: Time comparision in seconds between sampling

methods.

Buddha Dragon Horse Hammer

CP-ICP 0.62 0.22 0.048 0.025

ICP 17.68 7.40 0.41 0.37

Rnd. 50 17.85 4.01 0.36 0.19

Rnd. 70 18.72 5.82 0.43 0.26

Uniform 14.27 4.39 0.58 0.35

These numbers are impressive because they em-

phasize that the proposed approach is faster than the

benchmark, and the impact into this particular re-

search ﬁeld is therefore evident.

6.2 RMSE Metrics

As explained earlier, in addition to the analysis of the

performance regarding the time required to complete

the registration procedure we also looked for a quan-

titative measure of the matching quality. In this paper

we suggest to use, in a ﬁrst moment, the root mean

squared error between the target point cloud for the

ICP algorithm and the input post ICP.

From Table 3, we can see that the CP-ICP method

and the other approaches perform similarly. To illus-

trate with images what these numbers express, Fig.

11 brings the cloud matching for the Dragon model,

which is a big-size point cloud. In Fig. 11(a) we can

see the ICP registration (with no sampling), whereas

the matching using the CP-ICP method is plotted in

Fig. 11(b).

Table 3: RMSE evaluated after the ICP with each technique.

The numbers are multiplied by 10

−2

Buddha Dragon Horse Hammer

CP-ICP 0.26 0.18 0.98 0.60

ICP 0.24 0.18 0.97 0.57

Rnd. 50 0.24 0.19 1.08 0.60

Rnd. 70 0.24 0.18 1.05 0.59

Uniform 0.24 0.19 0.97 0.58

(a)

(b)

Figure 11: Registration results for the Dragon models. In a)

the result obtained with the classical ICP In b) the CP-ICP.

Improved Cloud Partitioning Sampling for Iterative Closest Point: Qualitative and Quantitative Comparison Study

6.3 Euler Angles Analysis

As an additional result for the quantitative analysis of

the point cloud matching, in Table 4 and 5 the trans-

formation matrix is represented by its Euler angles.

The total error is the sum of the Z-, Y- and X- axis

minus the ground-truth.

This was made only for the Dragon and Buddha

models because the ground truth is known to be 24

around Z axis.

Table 4: Euler angle of Happy Buddha model.

Buddha

In degree Z Y X Total error

CP-ICP 24.01 -0.13 -0.14 0.26

ICP 18.98 0.54 -0.81 5.29

Rnd. 50 19.33 0.37 -0.82 5.12

Rnd. 70 19.13 0.42 -0.79 5.24

Uniform 19.11 0.30 -0.75 5.34

Table 5: Euler angle of Dragon model.

Dragon

In degree Z Y X Total error

CP-ICP 23.77 0.08 0.24 0.09

ICP 23.91 0.16 0.23 0.30

Rnd. 50 23.88 0.14 0.23 0.25

Rnd. 70 23.89 0.17 0.24 0.30

Uniform 23.89 0.15 0.24 0.28

Once again, the CP-ICP was shown to be supe-

rior also from a quantitative point of view. The reader

should especially note the column for the Z axis of

the Buddha model. Besides that, we can observe the

column representing the total error, which is the sum

of the angles in the three axes: while the estimates

from the other techniques deviate of about 5 degrees,

the CP-ICP error approches zero. The success of the

CP-ICP on ﬁnding the Euler angles which best repre-

sent the relative orientation between the point clouds

relies on the fact that our algorithm is able to iden-

tify the region of the 3D model which preserves the

most important points describing the rigid transfor-

mation searched. Unlike ICP, which searches for op-

timal transformation in the entire source cloud,

in CP-ICP this is done one sub-cloud at a time, in

a ”light fashion.

6.4 SSIM-based Metrics

Tables 6 to 9 show the analysis of the ﬁve perspectives

of each of the 3D models studied, using metrics based

on SSIM, and represent average values between the

perspectives. Tables 6 and 7 are related to the Bud-

dha and Dragon models (largest data sets), while 8

and 9 are related to the Hammer and Horse models

(small datasets). As shown in Tables 6 and 7, dif-

ferent to what has been seen so far, the various meth-

ods performs better in the Buddha model according to

the proposed metrics. In the comparision between the

sampling approaches, once again CP-ICP beats them

all.

The results obtained for the evaluation through the

SSIM can be seen in the tables below, with the best

overall results, that is, the averages of all dot pattern,

full and contour views highlighted in bold. It is seen

that, in all cases, the best mean was CP-ICP.

Table 6: SSIM based comparison for the Happy Buddha

model.

Buddha

Dot Full Contour Mean

CP-ICP 0.884 0.941 0.982 0.936

ICP 0.822 0.947 0.965 0.911

Rnd. 50 0.869 0.947 0.979 0.911

Rnd. 70 0.872 0.947 0.975 0.932

Uniform 0.876 0.953 0.975 0.935

Table 7: SSIM based comparison for the Dragon model.

Dragon

Dot Full Contour Mean

CP-ICP 0.568 0.683 0.967 0.740

ICP 0.570 0.621 0.900 0.697

Rnd. 50 0.583 0.644 0.902 0.716

Rnd. 70 0.570 0.621 0.902 0.698

Uniform 0.576 0.632 0.916 0.708

Table 8: SSIM based comparison for the Hammer model.

Hammer

Dot Full Contour Mean

CP-ICP 0.962 0.936 0.999 0.966

ICP 0.931 0.921 0.999 0.950

Rnd. 50 0.940 0.935 0.998 0.958

Rnd. 70 0.938 0.934 0.999 0.957

Uniform 0.941 0.938 0.992 0.960

Table 9: SSIM based comparison for the Horse model.

Horse

Dot Full Contour Mean

CP-ICP 0.902 0887 0.999 0.929

ICP 0.901 0.889 0.996 0.929

Rnd. 50 0.892 0.891 0.999 0.928

Rnd. 70 0.892 0.843 0.999 0.928

Uniform 0.891 0.889 0.999 0.926

In general, for the four point cloud models used,

the SSIM metrics agrees with the other ones and con-

ﬁrms the superior matching quality of the CP-ICP.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

Overall, these tables and ﬁgures reveal that the CP-

ICP approach presented the best performance for all

point cloud models.

For the sake of illustration, Fig. 12 brings the reg-

istration results: a)using the CP-ICP; b) using ran-

dom sampling with 70% of the points and c) using

the ICP with no sampling. The highlighted regions

of 12(a) reveals that the registration following cloud

partitioning approach achieved a better qualitative re-

sult, though quantitatively the ICP method softly beat

it (see Table 3).

(a)

(b)

(c)

Figure 12: Comparison of the registration results for the

Horse model. In a) the registration for the CP-ICP b) the

registration result for the random 70% sampling and in c)

the registration result for the ICP with no samling.

Finally, in Fig. 13 the registration results for the

Buddha are plotted. For the Buddha model, we can

clearly see that the CP-ICP result presents itself as the

best registration, as denoted in the marked regions in

13(f)

7 ROBUSTNESS TO NOISE AND

OCCLUSION

In (Masuda and Yokoya, 1995), a robust noise and

occlusion technique is discussed, which motivated ex-

periments to test the robustness of our technique. To

accomplish with that, we considered adding gaussian

noise and subjecting the clouds to occlusion. Only

the Buddha and Dragon models were considered here.

The probability density function p of a Gaussian ran-

dom variable z is given by:

(z) =

√

σ ∗2π

−(z−µ)

2σ

(10)

where z represents the grey level, µ the mean value

and σ the standard deviation. In this case σ = 0.001.

The results are summarized in Tables 10 and 11,

which bring the various metric adopted and the dif-

ferent sampling approaches at a glance. We can ob-

serve the best performance is achieved by CP-ICP,

which approached better the 24 degrees Z-axis rota-

tion of the ground truth in extremely short time. Er-

rors regarding the other axis follow analogously and

are omitted for brevity. In addition to the observation

of the tables, we can make a brief visual inspection

in Fig. 14(e), looking at the Buddha’s feet. We can

say that the regions between the clouds of origin and

target overlap perfectly when registration follows CP-

ICP.

Table 10: Table with comparison metrics for the Buddha

model for registration with Gaussian noise addition.

Buddha

Time (s) RMSE Angle (

) SSIM

CP-ICP 0.67 0.19 21.30 0.901

ICP 15.32 0.21 15.71 0.897

Rnd.50 7.44 021 16.02 0.889

Rnd.70 10.71 0.20 16.00 0.888

Uniform 10.62 0.20 16.01 0.889

Table 11: Table with comparison metrics for the Dragon

model for registration with Gaussian noise addition.

Dragon

Time (s) RMSE Angle (

) SSIM

CP-ICP 0.18 0.16 23.97 0.778

ICP 7.03 0.17 23.59 0.769

Rnd.50 4.17 0.18 23.59 0.765

Rnd.70 5.58 0.17 23.58 0.769

Uniform 4.12 0.18 23.58 0.756

The robustness to occlusion was studied from the

Horse model. One of the main problems of project-

ing the 3D scene to the image plane is occlusion -

each object blocks the view of others behind it (Huang

Improved Cloud Partitioning Sampling for Iterative Closest Point: Qualitative and Quantitative Comparison Study

(a) (b) (c)

(d) (e) (f)

Figure 13: Comparison of the registration results for the Buddha model. In a) the image of the foot of the Buddha, in b)the

registration result for the random 50% sampling and in c) the registration result for the random 70% sampling and in d) the

registration result for the uniform sampling and in e) the registration result for the ICP with no samling and ﬁnally in f)the

registration result of use CP-ICP method.

(a) (b) (c) (d)

(e)

Figure 14: Comparison of registration results for the Buddha model with Gaussian noise of standard deviation 0.001. In a)

the registration result for the random 50% sampling and in b) the registration result for the random 70% sampling and in c)

the registration result for the uniform sampling and in d) the registration result for the ICP with no samling and ﬁnally in e)the

registration result of use CP-ICP method.

Figure 15: Horse model occluded.

et al., 2017). The occlusion can be caused by the

omission of the vision of a given mass of points due

to the presence of another object in the front, or can

be caused by a rotation of the object itself. For the

latter case, we call it self-occlusion.

In our experiment, a local maximum ﬁlter of the

PCL itself was used to make localized removal of

points in the back of the Horse, causing the lateral

points at left to disappear almost completely. The

sketch of it can be seen in Fig. 15. Despite of that

image perturbation, CP-ICP outperformed the various

sampling methods.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

(a) (b)

Figure 16: Results for the Horse model with partial occlusion of points. In a) the registration result for the random 50%

sampling and in b) the registration result for the random 70% sampling and in c) the registration result for the ICP with no

samling and ﬁnally in e)the registration result of use CP-ICP method.

Table 12: Results of registration of Horse model apllying

occlusion.

Horse

Time (s) RMSE Angle SSIM

CP-ICP 0.052 1.37 180.00 0.943

ICP 0.94 1.32 177.56 0.939

Rnd.50 0.53 1.42 177.17 0.940

Rnd.70 0.74 1.41 177.34 0.943

Observing the result in the table 12, the register

with the CP-ICP presents better results: it completely

found the ground truth and, in addition, reached the

highest SSIM. For what concerns the RMSE measure,

it ﬂuctuated very little amongst the sampling methods

and, hence, it can’t be used as a faithful comparison

metric in these cases.

Robustness of CP-ICP to added noise is related to

its ability to keep the original data of the point clouds;

indeed, not even a single point is lost when sub-clouds

are checked for correspondence. Unlikely, sampling

approaches lead to loss of input data (in some case

it leads to pseudodata generation), and consequently

noise gets more important, thus biasing the ICP to

ﬁnd erroneous correspondences.The success of the

CP-ICP technique when dealing with self-occlusion

may be associated to the partitioning itself: since we

search for correspondences between sub-clouds, even

under partial occlusion scenario there are many sub-

clouds in which the input data is fully preserved and,

as such, are useful for correspondence search.

8 CONCLUSIONS

In this paper, a pre-processing method was presented

for registration along with ICP. The method is com-

pared with other four techniques using an RMSE met-

ric, Euler angles, and one metric adapted from SSIM.

The results show that, in comparison to the other

methods, author’s approach provided a better regis-

tration in shorter times. This technique also presented

robustness to data corruption by gaussian noise and

subject to occlusion, as well. This is therefore, a

promising and useful preprocessing step to use with

ICP variants in real time applications of 3D mod-

elling.As future work, we will make the algorithm

fully automatic, as well we will implement the align-

ment of one sub-cloud against all.

ACKNOWLEDGEMENTS

The authors are grateful to Professor Marques for lab

facilities and agency FUNCAP for the ﬁnancial sup-

port.

Improved Cloud Partitioning Sampling for Iterative Closest Point: Qualitative and Quantitative Comparison Study

REFERENCES

Aleotti, J., Rizzini, D. L., and Caselli, S. (2014). Percep-

tion and grasping of object parts from active robot ex-

ploration. Journal of Intelligent & Robotic Systems,

76(3-4):401–425.

Besl, P. J. and McKay, N. D. (1992). Method for regis-

tration of 3-d shapes. In Sensor Fusion IV: Control

Paradigms and Data Structures, volume 1611, pages

586–607. International Society for Optics and Photon-

ics.

Cesi

c, J., Markovi

c, I., Juri

c-Kavelj, S., and Petrovi

c, I.

(2016). Short-term map based detection and tracking

of moving objects with 3d laser on a vehicle. In In-

formatics in Control, Automation and Robotics, pages

205–222. Springer.

Chaudhury, A., Ward, C., Talasaz, A., Ivanov, A. G., Huner,

N. P., Grodzinski, B., Patel, R. V., and Barron, J. L.

(2015). Computer vision based autonomous robotic

system for 3d plant growth measurement. In Com-

puter and Robot Vision (CRV), 2015 12th Conference

on, pages 290–296. IEEE.

Cigla, C., Brockers, R., and Matthies, L. (2017). Image-

based visual perception and representation for colli-

sion avoidance. In IEEE International Conference on

Computer Vision and Pattern Recognition, Embedded

Vision Workshop.

Corke, P. (2017). Robotics, Vision and Control: Funda-

mental Algorithms In MATLAB

Second, Completely

Revised, volume 118. Springer.

Curless, B. and Levoy, M. (1996). A volumetric method for

building complex models from range images. In Pro-

ceedings of the 23rd annual conference on Computer

graphics and interactive techniques, pages 303–312.

ACM.

Gorecky, D., Schmitt, M., Loskyll, M., and Z

uhlke, D.

(2014). Human-machine-interaction in the industry

4.0 era. In Industrial Informatics (INDIN), 2014 12th

IEEE International Conference on, pages 289–294.

IEEE.

Holz, D., Ichim, A. E., Tombari, F., Rusu, R. B., and

Behnke, S. (2015). Registration with the point cloud

library: A modular framework for aligning in 3-d.

IEEE Robotics & Automation Magazine, 22(4):110–

124.

Huang, P., Cheng, M., Chen, Y., Luo, H., Wang, C., and Li,

J. (2017). Trafﬁc sign occlusion detection using mo-

bile laser scanning point clouds. IEEE Transactions

on Intelligent Transportation Systems, 18(9):2364–

2376.

Malamas, E. N., Petrakis, E. G., Zervakis, M., Petit, L., and

Legat, J.-D. (2003). A survey on industrial vision sys-

tems, applications and tools. Image and vision com-

puting, 21(2):171–188.

Masuda, T., Sakaue, K., and Yokoya, N. (1996). Registra-

tion and integration of multiple range images for 3-d

model construction. In Pattern Recognition, 1996.,

Proceedings of the 13th International Conference on,

volume 1, pages 879–883. IEEE.

Masuda, T. and Yokoya, N. (1995). A robust method for

registration and segmentation of multiple range im-

ages. Computer vision and image understanding,

61(3):295–307.

Nazem, F., Ahmadian, A., Seraj, N. D., and Giti, M. (2014).

Two-stage point-based registration method between

ultrasound and ct imaging of the liver based on icp

and unscented kalman ﬁlter: a phantom study. Inter-

national journal of computer assisted radiology and

surgery, 9(1):39–48.

Pan, J., Chitta, S., and Manocha, D. (2017). Probabilistic

collision detection between noisy point clouds using

robust classiﬁcation. In Robotics Research, pages 77–

94. Springer.

Pereira, N. S., Carvalho, C. R., and Th

e, G. A. (2015). Point

cloud partitioning approach for icp improvement. In

Automation and Computing (ICAC), 2015 21st Inter-

national Conference on, pages 1–5. IEEE.

Rodol

a, E., Albarelli, A., Cremers, D., and Torsello, A.

(2015). A simple and effective relevance-based point

sampling for 3d shapes. Pattern Recognition Letters,

59:41–47.

Rusinkiewicz, S. and Levoy, M. (2001). Efﬁcient variants

of the icp algorithm. In 3-D Digital Imaging and Mod-

eling, 2001. Proceedings. Third International Confer-

ence on, pages 145–152. IEEE.

Soille, P. (2003). Morphological image analysis: princi-

ples and applications. Springer Science & Business

Media.

Toro, C., Barandiaran, I., and Posada, J. (2015). A per-

spective on knowledge based and intelligent systems

implementation in industrie 4.0. Procedia Computer

Science, 60:362–370.

Turk, G. and Levoy, M. (1994). Zippered polygon meshes

from range images. In Proceedings of the 21st an-

nual conference on Computer graphics and interac-

tive techniques, pages 311–318. ACM.

Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P.

(2004). Image quality assessment: from error visi-

bility to structural similarity. IEEE transactions on

image processing, 13(4):600–612.

Weinmann, M. (2016). Outlier removal and ﬁne registra-

tion. In Reconstruction and Analysis of 3D Scenes,

pages 84–85. Springer.

Zhang, J. and Lin, X. (2017). Advances in fusion of optical

imagery and lidar point cloud applied to photogram-

metry and remote sensing. International Journal of

Image and Data Fusion, 8(1):1–31.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics