A New Approach to Spread-spectrum OFDM
Mohammad Kaisb Layous Alhasnawi
1
, Ronald G. Addie
2
and Shahab Abdulla
3
1
Faculty of Administration and Economics, Sumer University, Thi-Qar, Iraq
2
School of Agricultural, Computational and Environmental Science,
University of Southern Queensland, Toowoomba, Australia
3
Open Access College, University of Southern Queensland, Toowoomba, Australia
Keywords:
OFDM, Spread-spectrum OFDM, Spectrum Sharing, Ideal Channel, Galois Field, Nearly Orthogonal.
Abstract:
Orthogonal frequency division multiplexing (OFDM) systems are reviewed and the Shannon bound is dis-
cussed as a criterion of efficient spectrum use and a design criterion. The problem of efficient sharing
of spectrum by wireless communication systems is discussed and combined use of direct-sequence spread-
spectrum (DSSS) coding and OFDM is proposed as an approach which can achieve efficient spectrum sharing.
A system which enables DSSS, with codes from the Galois field of order f where f is a prime larger than 2, to
be used efficiently in conjunction with OFDM is then defined, analysed, and implemented. Experiments with
this system are described.
1 INTRODUCTION
Spectrum sharing is a problem of considerable inte-
rest and importance (Pandit and Singh, 2017). The
number of wireless devices has been growing sig-
nificantly in the last decade, including IPTV recei-
vers, tablets, smartphones, remote controls, GPS de-
vices, wireless sensors (Xin and Song, 2015). This
growth of wireless devices leads to increased de-
mand on the available and more need for efficient
spectrum sharing. This study investigates impro-
vement in the efficiency of spectrum use by using
spread spectrum orthogonal frequency division mul-
tiplexing (SS-OFDM) (Akare et al., 2009; Xia et al.,
2003; Jaisal, 2011; Meel, 1999; Tu et al., 2006).
Spread-spectrum systems which are nearly co-
located systems will perceive each other as noise,
and when doing so will not suffer any loss in over-
all efficiency of spectrum use, therefore the use of
spread-spectrum with OFDM has the potential to ena-
ble efficient spectrum sharing. However, evaluation
of OFDM-SS from the point of view of spectrum effi-
ciency has not received close attention in much of its
literature up to this point.
In this paper the direct-sequence spread-spectrum
(DSSS) system uses symbols from the Galois field
GF( f ), where f > 2 is a prime number. For efficiency
it is likely that f will usually be larger than 10. Most
DSSS systems use symbols from GF(2
m
) for some
m > 0. This choice is more straightforward to imple-
ment and seems more natural, given that most digital
hardware uses binary arithmetic and binary represen-
tation for numbers, but the nearly-orthogonality pro-
perty of codes based on this field does not directly
lead to the necessary orthogonality conditions when
used with OFDM, as we show in Subsection 5.8. Use
of a field GF( f
m
) with m > 1 is also possible, but has
not been investigated in this paper.
According to (Zhang et al., 2015) the significant
challenge facing researchers in wireless communica-
tion is efficient spectrum sharing. There is an imba-
lance between the rapidly growing demand and the li-
mited resources of wireless spectrum. The authors (Ji
and Liu, 2007) show that in order to acheive efficient
and full utilization of available common spectrum,
the protocols and/or technologies used in wireless
communication need to be changed so that efficient
spectrum sharing is one of the key design objecti-
ves. The aim of this paper is to investigate a stra-
tegy for using OFDM which allows efficient sharing
of spectrum to occur without excessive additional ef-
fort.
OFDM systems are considered to be effective
techniques and are used for several of the latest stan-
dards for wireless, telecommunications standards and
digital video broadcasting (Sung et al., 2010; Arm-
strong, 2009; Coleri et al., 2002). However, it can be
difficult to share available spectrum efficiently while
Alhasnawi, M., Addie, R. and Abdulla, S.
A New Approach to Spread-spectrum OFDM.
DOI: 10.5220/0006828602810288
In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 1: DCNET, ICE-B, OPTICS, SIGMAP and WINSYS, pages 281-288
ISBN: 978-989-758-319-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
281

using OFDM.
In this paper, a new method for combining DSSS
with OFDM has been defined and implemented in
matlab and an algorithm for predicting wifi throug-
hput of a full implementation of such an SS-OFDM
system has been developed. We shall show, first of
all, that optimal sharing can be consistent with nearby
wifi domains appearing as noise to each other (which
is the characteristic property of spread-spectrum).
The SS-OFDM system has been implemented in
matlab and used to demonstrate simultaneous com-
munication of a large number of co-located users (up
to 1000), using spread-spectrum to share access to the
medium, with minimal impact on spectral efficiency.
It has also been estimated that when users are not co-
located, total system throughput achievable is signi-
ficantly greater than systems in which the available
spectrum is used exclusively by each pair of commu-
nicating devices one at a time.
The paper is organized as follows with the arran-
gement; Section 2 explains the mathematical model
by using Shannon Bound theory to a model wireless
system. In Section 3 provides the literature review
and background on SS-OFDM. The design of an ide-
alised SS -OFDM will clarify at Section 4. In Section
5 displays the execution of the SS-OFDM system.
Section 6 demonstrates the proof of the proposed sy-
stem. The conclusion is set out in Section 7.
2 SHANNON BOUND THEORY
When OFDM is used, with highly efficient error-
correcting codes, system capacity can be relatively
close to the Shannon-Hartley bound. As a conse-
quence, it can be used as a design principle. Any inno-
vation or method (coding, modulation, filtering, . . . ),
can be evaluated according to the degree to which it
brings us closer, or further, from the Shannon-Hartley
bound.
Consider a situatuation where several wifi net-
works operate in the same geographical region, and
share the same spectrum, as depicted in Figure 1.
The concept of nearly orthogonal codes was introdu-
ced as part of the CDMA mobile communication sy-
stem, which is sometimes referred to as 2.5G mobile
communication.
The concept of nearly orthogonal systems can be
applied not just to codes, but also to, for example,
OFDM systems.
Currently, wifi tends to be managed so that those
concurrently operating wifi domains use either the
same channel, or channels which do not overlap. A
typical example (from the USQ campus) is shown in
Figure 1: Six wireless networks sharing spectrum.
Figure 2.
This approach to designing wifi networks redu-
ces capacity for two different reasons. Firstly, part
of the spectrum is not used at all. Secondly, the type
of sharing used between wifi systems using the same
wifi channel, will be of the inefficient type. Each sy-
stem will share with the others by CSMA/CA, the-
refore the total throughput will be the same as one
system operating in isolation.
However, it is not clear how to enable nearby
OFDM systems to share spectrum while treating each
other as noise. This can be done by each system using
codes. How effectively these nearby systems are able
to communicate, at the same time, may depend on the
choice of OFDM parameters made in each system. In
this paper, the concept of nearly orthogonal systems
for OFDM is introduced. This means that each sub-
channel in one system experiences the signals of the
other OFDM systems as white noise at lower power
than the actual OFDM signal power. The power of
the signals from other users is further reduced by pro-
pagation loss. The reduced power of neighbouring
systems in this situation leads to the complete sy-
stem acheiving greater spectral efficiency than time-
division or frequency-division multiplexing.
3 EXISTING MODELS OF
SS-OFDM
The approach using SS-OFDM systems has emerged
from the assembly of DSSS with OFDM (Akare et al.,
2009). Using these techniques together overcomes ra-
dio channel weakness, and improves reliable commu-
nication with frequency selective channels. The SS-
WINSYS 2018 - International Conference on Wireless Networks and Mobile Systems
282

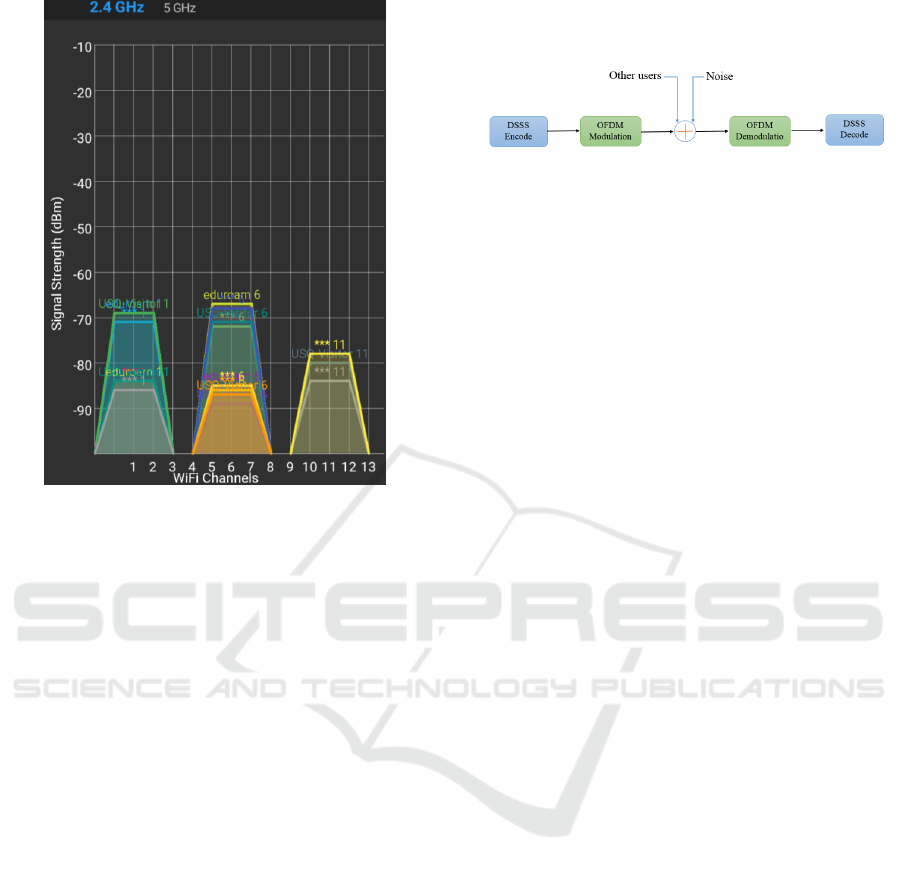
Figure 2: Sample of wifi sharing on a campus.
OFDM systems adopt a technique whereby various
copies of each symbol are transmitted on all availa-
ble N sub-carriers (Xia et al., 2003). On this study
(Jaisal, 2011) referred to spread spectrum OFDM sy-
stems having many features such as DSSS technique.
The main difference between the two models is that
the SS-OFDM model utilises a spreading waveform
consisting of samples with non-discrete values of am-
plitude. On the other hand, the DSSS model utilises
a binary of spreading code which consisting of a se-
quence 1’s and -1’s.
Previous papers on SS-OFDM (Tu et al., 2006;
Akare et al., 2009; Xia et al., 2003; Jaisal, 2011;
Meel, 1999) all use, primarily, DSSS in combination
with OFDM in the form set out in Figure 3. The best
choice for the OFDM system when a DSSS module is
used with it, is a key topic explored in these papers.
In this paper, by contrast, the OFDM module will be
assumed to be ideal (in a sense explained below), and
the focus will be instead on the best choice of DSSS
module.
In DSSS, a stream of data at the transmission point
is combined with a pseudo-random bit sequence to
become a higher data-rate signal. This technique of
spreading the data helps the signal resist interference
and also enables the original data to be recovered if
data bits are destroyed during transmission from the
origin point to the destination. In addition, when this
technique is used by two or more communicating sy-
stems at once, they are able to perceive each other as
noise, and therefore share the same spectrum without
destructive interference. This last feature of spread-
spectrum is often more important than the spreading
idea itself.
Figure 3: SS-OFDM systems.
3.1 Performance of SS-OFDM
The high rate of data is a key component of mo-
dern communications systems for wireless access net-
works of mobile users. OFDM techniques have been
used for many decades. This modulation is widely
utilised in modern telecommunications systems such
as digital radio and TV, wireless networking, and
transmission of data through the phone line. OFDM
is a suitable system, especially for high speed com-
munication because of its resistance to inter symbol
interference (ISI), avoiding multipaths in wave trans-
mission. Also, DSSS is a spread spectrum technique
by which the original data signal is increased with
a pseudo-random noise for spreading code (Meel,
1999). This spreading code uses a higher rate of
the chip which leads to a wideband time continu-
ously scrambled signal. A DSSS system enhances
protection against interfering signals, especially nar-
rowband. It also supplies transmission security, if the
code is not known to the public.
The study (Akare et al., 2009) proposes to use
the combination of OFDM system with DSSS for the
multi-user system. The combination is named the
SS-OFDM model. This model can be used to cont-
rol the received signal bandwidth through the design
of matching filters. The bandwidth of transmission
can be selected flexibly to suit different modern tele-
communication systems under various circumstances.
SS-OFDM techniques supply reliable communicati-
ons with a frequency-selective channel. The fading
of multi-path impacts on the performance of wireless
broadband link (Jaisal, 2011).
The essential results of this study mean that we
can use the SS-OFDM model for wireless broadband.
Also, it has been established that this model can ef-
ficiently deliver communication over short or long
distances by using M-ary Quadrature Amplitude Mo-
dulation (M-QAM) with effectively reduced interfe-
rence and improved Bit Error Rate (BER). In addi-
tion, the authors (Tu et al., 2006) referred to the re-
sults of simulation showing that the theoretical curves
and the simulation curves matched well. This indi-
cates that SS-OFDM can achieve the desired level of
performance.
A New Approach to Spread-spectrum OFDM
283

4 DESIGN OF AN IDEALISED
SS-OFDM SYSTEM
A study undertaken by (Tu et al., 2006) used the
Shannon-Hartley formula to justify a theory of the ag-
gregate capacity achievable by spread-spectrum com-
munication systems. When spread-spectrum systems
interract, one system perceives the other as noise with
power reduced in accordance with the mechanism of
interraction of the two systems.
In this paper, rather than exploring the changes
which are needed in the OFDM module, a specific
hypothesis for the form this module should take is
posited. The hypothesis is that the OFDM module
transforms the original channel into an ideal (i.e. flat
frequency-response) channel with additive Gaussian
white noise. This OFDM module will exhibit a fixed
non-zero latency. Minimising overall system latency
may be a concern, and it is well-known that any sy-
stem which achieves an ideal (or close to ideal) trans-
fer function must introduce a large delay; however
this issue will be put to one side initially.
This hypothesis needs to be tested first. It can
then be used as a starting point for the other question
which needs to be investigated in SS-OFDM, namely
what form of DSSS should be used in a system of the
form shown in Figure 3? The hypothesis enables us
to investigate this question in a much simpler form, as
shown in Figure 4.
Figure 4: Ideal channel.
5 AN IMPLEMENTATION OF
DSSS-OFDM
Assuming an ideal OFDM system, a design which
exhibits effective working with a DSSS module to
provide a combined DSSS-OFDM system is descri-
bed in this section. The details of how the DSSS mo-
dule and the OFDM module work together must be
clearly specified and we need to check that the desira-
ble properties of both DSSS and OFDM are achieved
in the combined system. A key requirement for this
to be achieved is that the DSSS system uses higher-
order symbols (not binary digits), so that when these
symbols interfere with other users of similar DSSS-
OFDM systems, the nearly orthogonal property of the
DSSS sequences is preserved algebraically even when
the different signals are combined together as electro-
magnetic radiation before being decoded, as depicted
in Figure 5.
Figure 5: SS-OFDM with DSSS uses higher order symbols.
5.1 An Example System
As with all DSSS systems, there are many parameters
of the system which affect the design. In this sub-
section we arbitrarily choose these parameters, and
we adopt choices with a view to simplicity rather than
capacity or performance. However, it should be clear
how the parameters can be changed to suit other ob-
jectives.
The system we consider is based on the Galois
field with prime p = 5, and power m = 1.
5.2 Orthogonality Property
For any DSSS system to work efficiently, it must have
an orthogonality or nearly orthogonal property which
is, firstly, a mathematical property of the codes and,
secondly, is preserved by the way signals are modula-
ted, aggregated, and demodulated by the system. If
the DSSS system has a (nearly) orthogonality pro-
perty, but the implementation does not actually ope-
rate in the way required by this principle, it will not
serve our purposes.
5.3 The Galois Field Theory of DSSS
Codes in the Complex Domain
The theory of DSSS codes formed from binary se-
quences is well understood and widely used. Howe-
ver, in the present context, where the DSSS codes
must be transmitted through an OFDM system, the
DSSS codes needed must be represented as sequen-
ces of complex numbers. Let us therefore review the
theory of Galois fields and apply it to identify the ne-
cessary codes.
Suppose f is a prime number. Then, GF( f ) deno-
tes the Galois field of numbers {0,1,..., f −1}, with
addition operation defined as addition modulo f and
multiplication operation defined as multiplication mo-
dulo f . This field is known to possess a primitive,
p, which is an element of the field, with the property
that 1, p, p
2
, . .., p
f −1
is an enumeration of all the
non-zero elements.
Let z
k
= e
2πki/ f
, k = 0, . . . , f −1. When sym-
bols in this field are used for transmission, these com-
WINSYS 2018 - International Conference on Wireless Networks and Mobile Systems
284

plex numbers are a better representation of the phy-
sical form taken by the signal. The magnitude of the
complex number represents the power, and the com-
plex argument represents the phase, of the transmitted
signal.
5.4 Near-orthogonality
Suppose x = (x
1
,... , x
4
)
0
and w = (w
1
,... , w
4
)
0
. are
complex vectors. The appropriate inner-product bet-
ween these vectors is (x,w) =
∑
4
k=1
x
k
w
k
.
Observe that z
k
= z
−k
and z
k
×z
j
= z
k+ j
. De-
fine χ
j
= (z
p
j−1
,z
p
j
,... , z
p
( j−2) mod f
), j = 1, . . . , f −1.
These will form the codes of our DSSS-OFDM sy-
stem.
Proposition 1.
(χ
k
,χ
j
) =
(
f , k = j,
−1 k 6= j.
(1)
Proof. Observe that in all cases the components of
χ
j
form an enumeration of all the complex numbers
corresponding to elements of the field except 1
(which corresponds to the field element 0). The sum
of all the complex numbers of this form (including
1) is zero, hence the sum of the components of χ
k
is equal to −1, for any j ∈ {1,..., f −1}. Let us
now show that (χ
k
,χ
j
) = −1, also, j, k = 1, . . . , f −1.
Suppose j 6= k. Then
(χ
j
,χ
k
) = z
p
j
z
p
k
+ z
p
j+1
z
p
k+1
+ ···+ z
p
j−1
z
p
k−1
(χ
j
,χ
k
) = z
p
j
z
−p
k
+ z
p
j+1
z
−p
k+1
+ ···+ z
p
j−1
z
−p
k−1
which, using the property z
s
×z
t
= z
s+t
,
= z
p
j
−p
k
+ z
p
j+1
−p
k+1
+ ···+ z
p
j−1
−p
k−1
.
Now p × (p
j
−p
k
) = p
j+1
− p
k+1
so the sequence
z
p
j
−p
k
, . . . , z
p
j−1
−p
k−1
is one of the codes χ
k
and hence
has sum −1.
Example: f = 5
The field GF(5) has primitive element 2. This means
that all non-zero elements are enumerated by 2
k
, k =
1, . . . , 4. The codes corresponding to this primitive
element are:
χ
1
= (1,2, 4, 3), χ
2
= (2,4, 3, 1),
χ
3
= (3,1, 2, 4), χ
4
= (4,3, 1, 2).
5.5 Encoding
Suppose the messages to be transmitted are stored in
an array:
m =



m
11
... m
1,n
.
.
.
.
.
.
.
.
.
m
L,1
... m
L,n



(2)
and the code used for user u is χ
u
= (χ
1,u
,... , χ
κ,u
),
with the defining property χ
k+1,u
= χ
k,u
× p mod f ,
in conjunction with the obvious necessity that each
user has a distinct value for χ
1,u
, in which κ denotes
the chip-length. Thus, each code rotates (by multi-
plication of each element by the primitive of the field)
during use and the different users are distinguished by
their different starting codes.
For notational convenience we define χ
k,u
=
χ
(k−1) mod κ+1,u
for all k. E.g. χ
0,u
.
= χ
κ,u
.
The array of messages expressed as symbols
(complex numbers with magnitude less than 1)
S =



s
11
... s
1,n
.
.
.
.
.
.
.
.
.
s
M,1
... s
M,n



(3)
in the usual way, based on an arbitrary constellation
(e.g. as in Figure 6). The value of M depends on L
and also on the constellation.
The codes also have a complex representation:
X =



ξ
11
... ξ
1,κ
.
.
.
.
.
.
.
.
.
ξ
κ,1
... ξ
κ,κ
,



(4)
where
ξ
k j
= e
2πiξ
k j
/ f
, (5)
k = 1,. . . ,κ, j = 1, . . . , κ. The symbols of the mes-
sage are encoded into an array
C =



C
11
... C
1,n
.
.
.
.
.
.
.
.
.
C
κM,1
... C
κM,n
,



(6)
by the formula:
C
k j
= S
k÷κ, j
ξ
k mod κ, j
,
k = 1, . . . Mκ, j = 1, . . . , n. The values of χ
1, j
may
be arbitrarily chosen, so long as they are different for
each j. An obvious choice, which has been used in
the implementation, is χ
1, j
= j, j = 1, . . . , f −1.
The signals of all users are transmitted simultane-
ously into the medium which we model as numerical
addition:
Z
j
=
n
∑
k=1
Z
k j
, (7)
j = 1, . . . , L.
A New Approach to Spread-spectrum OFDM
285

5.6 Decoding
Consider the user with index j and let us ignore the
signal due to the other users. For simplicity, assume
M = 1, or putting it another way, we show the deco-
ding for the first symbol only.
The chip (Z
1 j
,... , Z
κ j
)
0
is converted to a symbol
by first using the formula:
W
j
=
κ
∑
k=1
Z
k j
ξ
k j
(8)
=
κ
∑
k=1
S
1 j
ξ
k j
ξ
k j
= κS
1 j
j = 1,. . . , L. The signal is therefore recovered with a
gain in amplitude of the factor κ.
Next, these estimates of the signal are translated
to symbols by finding the closest element of the con-
stellation, and then to bits by using the inverse of the
algorithm originally used to create the symbols from
the message.
5.7 User Sharing Noise
The desired outcome is that when the message of User
1 is demodulated, the messages of all other users ap-
pear as noise of low power. The demodulation al-
gorithm, when applied to a message using a nearly
orthogonal code, should produce a result with power
much lower than white noise of the actual power of
the interfering signal.
Consider now how the decoding algorithm applies
to a signal from a user with a different code. An ap-
propriate way to quantify their impact is to determine
the power of the signal appearing in the form W
j
, at
(8), which is caused by the targeted user, and compare
this to the power of the signal appearing in W
j
caused
by the other users.
We Assume, without loss of generality, that the
radius of the constellation is 1. Without loss of ge-
nerality, let us assume the targeted user is using code
1 (i.e. the code which starts with symbol 1), and the
interfering user uses code j 6= 1. In this case, (8) be-
comes
W
j
=
κ
∑
k=1
Z
k j
ξ
k j
,
which, assuming worst case zero loss for the in-
terfering signal
=
κ
∑
k=1
S
1 j
ξ
k j
ξ
k1
= S
1 j
κ
∑
k=1
ξ
k j
ξ
k1
= S
1 j
×(−1)
by the near orthogonality property. Thus, the
noise power due to one other user is 1. If there are
n users, the power of their combined signal will the-
refore be n. As for the signal, each symbol of the
chip independently communicates the original mes-
sage symbol, so the strength of the signal, when we
calculate the effective signal to noise ratio in this sy-
stem, should be the square of κ× half the distance
between different symbols in the constellation.
The spreading gain due to use of chips of length
κ is κ, i.e. the power of the received signal is incre-
ased by the factor κ
2
. On the other hand, because n
users are sharing the same medium, each user must
use less than the full power available, by the factor
κ. Due to the arrangement of symbols in the constel-
lation, assuming the size (number of symbols) of the
constellation is φ, signal strength is not 1, but instead,
≈
1
2
p
π/φ. Thus, the signal power due to the whole
chip is ≈ κπ/(4φ). For example, if 28 symbols are
used, as in the constellation shown in Figure 6, the
distance to half-way between two symbols will be ap-
proximately 0.17. It follows that the SNR of a system
with background noise power η and n users will be
≈ κπ/(4φ(κη
2
+ n/κ)).
-0.5 0 0.5
In-Phase
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
Quadrature
Scatter plot
Figure 6: A QPSK constellation for SS-OFDM.
Hence the system capacity according to the
Shannon-Hartley formula is
C ≈
Bnlog
2
(φ)log
2

1 + κπ/(4φ(κη
2
+ n/κ))

κ
.
The total throughput achievable in this system is
shown as the curve labelled Sharing by DSSS-OFDM
in Figure 7 as a function of the number of users.
WINSYS 2018 - International Conference on Wireless Networks and Mobile Systems
286

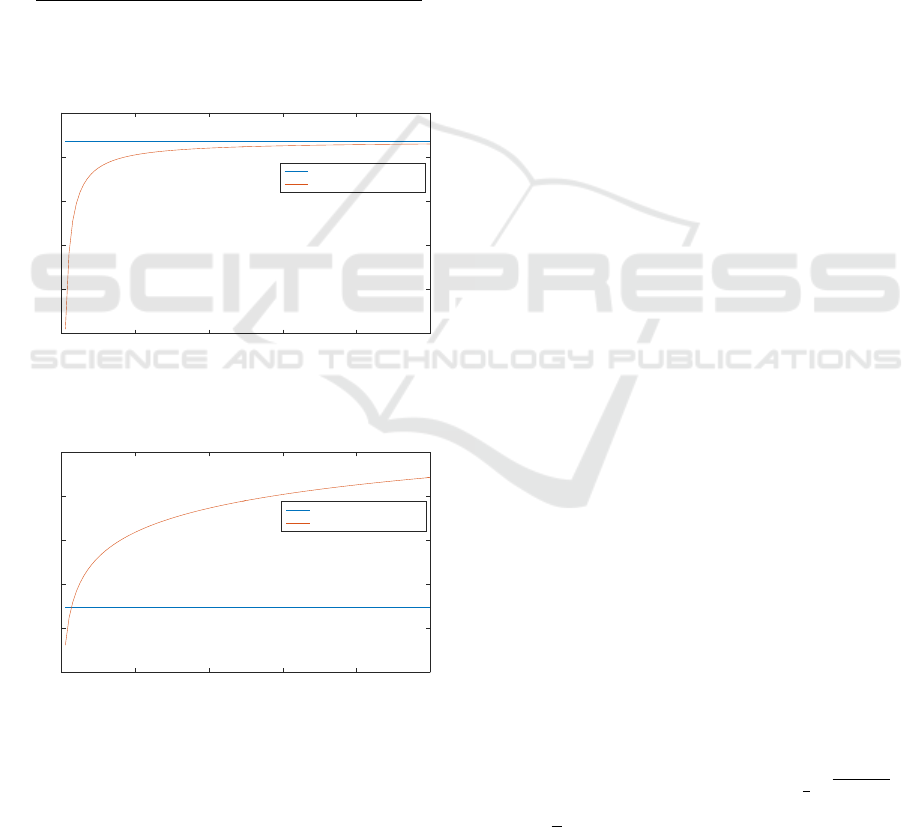
In Figure 8, physical separation of domains is mo-
delled. The the measured power due to other nearby
wifi domains, is reduced by propagation loss. Hence,
the power transmitted by each user can be increased,
while still respecting the regulated power constraint.
The ratio between the maximum power which may be
transmitted when all κ users are present at the same
location, and when they are so distant from each ot-
her that their power is insignificant is κ, so a “typical”
situation can be modelled, simplistically, by assuming
that a user can transmit at κ
α
times the minimum al-
lowed power, for 0 ≤ α ≤ 1. With this assumption,
system capacity is
Bnlog
2
(φ)log
2

1 + κ
1+α
π/(4φ(κη
2
+ nκ
α−1
))

κ
.
The choice α = 0.5 is plotted in Figure 8, again assu-
ming n = κ.
0 20 40 60 80 100
Number of users / chiplength
1.3
1.4
1.5
1.6
1.7
1.8
Throughput
×10
7
Total system throughput
No sharing
Sharing by DSSS-OFDM
Figure 7: Throughput when users are co-located.
0 20 40 60 80 100
Number of users / chiplength
1
1.5
2
2.5
3
3.5
Throughput
×10
7
Total system throughput
No sharing
Sharing by DSSS-OFDM
Figure 8: Throughput when users are separated (α = 0.5).
5.8 Why f > 2
Let us now return to the issue of how to choose f .
Traditionally, DSSS systems use code from GF(2
m
).
If we use a DSSS system with codes from GF(2
m
)
in conjunction with OFDM, the nearly orthogonal
property, Proposition 1, fails, because the proof of
this proposition relies on the mapping k 7→ z
k
, from
GF(2
m
) to the unit circle ({z : |z|= 1}), being a mor-
phism, i.e. z
k
×z
j
= z
k+ j
.
The choice f = 2 is only consistent with this re-
quirement when the constellation is limited to the
choices ±1, which is not sufficient for efficient ope-
ration of OFDM.
6 AN EXPERIMENT WITH
DSSS-OFDM
The DSSS-OFDM wireless communication system
has been implemented in Matlab (Alhasnawi and Ad-
die, 2018) and a number of experiments have been
carried out, for different choices of f , η and con-
stellation. Here we describe an experiment in which
f = 1023. This experiment is sufficient to convey the
key features of the system.
In this system it was found that if the number of
users is less than or equal to 1000, and the constella-
tion size was < 32, all users were able to communi-
cate simultaneously without error; when the constel-
lation size was increased to 60, some errors were ex-
perienced. The system implemented did not include
error-correction. The main outcome of these simu-
lations was to confirm that the system described in
theory, in Section 5, can be implemented.
The background noise of this system has a stan-
dard deviation of 0.05, so the Shannon capacity is ap-
proximately 8.65 bits/s. The implemented system was
transmitting at ≈ 5 bps wihout error, At higher rates
(with a larger constellation), errors began to occur.
6.1 Measured User Noise
A key design objective of any spread-spectrum sy-
stem is to achieve low interference between users.
We can quantify this interference by the power (or
standard-deviation) of the interfering signal due to the
presence of other users. Confirming that user noise is
at the level predicted by theory is the most critical va-
lidation to apply to an experiment of this type. Once
this is confirmed, we can be confident that the theory
and its implementation are sound.
In the experiment, the constellation size was
φ = 60, so signal strength is ≈
1
2
p
π/(φκ) =
0.003578853. Note: the reduction in signal strength
by 1/
√
κ is to ensure that total signal power is within
the original regulated limit, as discussed in Section 5.
Given that the estimates from each symbol in the
chip are averaged, at the detector, signal strength is
A New Approach to Spread-spectrum OFDM
287

still 0.003578853. The standard deviation (σ
t
) of to-
tal noise in the experiment, where the chip length is
1022 and the number of users is 1000, was measu-
red at the detector and found to be 0.0017. Back-
ground noise standard deviation was 0.05, at the point
where it enters the system, so after averaging over
chip symbols, this becomes 0.05/
√
1022 = 0.00156
at the detector. Taking account that the standard de-
viation of the symbols, in the constellation used in
this system is 0.6873, the standard deviation of user
noise, at the detector, predicted by theory, in this sy-
stem, is 0.6873
p
1000/1022/κ = 0.000665. Thus,
standard deviation of total noise is expected to be
p
(0.00156
2
+ 0.000665
2
) = 0.001695 which is al-
most exactly the same as measured in the experiment.
These experiments confirmed that the system des-
cribed in theory, in Section 5, can be readily imple-
mented, and performs as predicted by the theory.
7 CONCLUSIONS
A communication system which combines spread-
spectrum codes and OFDM with the potential to ope-
rate at optimal efficiency has been defined, implemen-
ted and tested. The system implemented uses a sim-
ple constellation of phases and amplitudes which de-
monstrates the operation of the proposed SS-OFDM
system but without making full use of the available
combinations of phase and amplitude. For this rea-
son this system does not approach optimal efficiency.
The efficiency of a similar system which does use a
full range of phases and amplitudes has been analy-
sed theoretically and the efficiency of this system has
been estimated.
ACKNOWLEDGEMENTS
The authors are sincerely thankful to the University
Southern Queensland (USQ) for providing a platform
for doing this research work.Indeed, we would like
to thank all the reviewers for their feedback and ap-
preciated notices about the paper and we are happy
to consider them all as they are very useful and they
can refine the paper to make it very consistent and
successful. The first author’s is grateful also to the
Ministry of Higher Education and Scientific Research
of Iraq for supporting his Ph.D. study.
REFERENCES
Akare, U. P., Lande, S. B., Balpande, S., and Thakre, L. P.
2009. Performance of simulink based ss-ofdm mo-
del for broadband wireless access network. In Emer-
ging Trends in Engineering and Technology (ICE-
TET), 2009 2nd International Conference on, pages
1132–1137. IEEE.
Alhasnawi, M. K. L. and Addie, R. G. 2018. Matlab code
for implementing SS-OFDM. Technical report, Uni-
versity of Southern Queensland.
Armstrong, J. 2009. Ofdm for optical communications.
Journal of lightwave technology, 27(3):189–204.
Coleri, S., Ergen, M., Puri, A., and Bahai, A. 2002. Channel
estimation techniques based on pilot arrangement in
ofdm systems. Broadcasting, IEEE Transactions on,
48(3):223–229.
Jaisal, P. K. 2011. Performance of a spread spectrum ofdm
system in a dispersive ifading channel with interfe-
rence. IJCST, 2(4).
Ji, Z. and Liu, K. R. 2007. Cognitive radios for dynamic
spectrum access-dynamic spectrum sharing: A game
theoretical overview. IEEE Communications Maga-
zine, 45(5):88–94.
Meel, J. 1999. Spread spectrum (ss). De Nayer Instituut,
Hogeschool Voor Wetenschap & Kunst.
Pandit, S. and Singh, G. 2017. An overview of spectrum
sharing techniques in cognitive radio communication
system. Wireless Networks, 23(2):497–518.
Sung, T.-Y., Hsin, H.-C., and Cheng, Y.-P. 2010. Low-
power and high-speed cordic-based split-radix fft pro-
cessor for ofdm systems. Digital Signal Processing,
20(2):511–527.
Tu, P., Huang, X., and Dutkiewicz, E. 2006. A novel appro-
ach of spreading spectrum in ofdm systems. In Com-
munications and Information Technologies, 2006. IS-
CIT’06. International Symposium on, pages 487–491.
IEEE.
Xia, P., Zhou, S., and Giannakis, G. B. 2003.
Bandwidth-and power-efficient multicarrier multiple
access. IEEE Transactions on Communications,
51(11):1828–1837.
Xin, C. and Song, M. 2015. Spectrum Sharing for Wireless
Communications. Springer.
Zhang, H., Chu, X., Guo, W., and Wang, S. 2015. Coexis-
tence of wi-fi and heterogeneous small cell networks
sharing unlicensed spectrum. IEEE Communications
Magazine, 53(3):158–164.
WINSYS 2018 - International Conference on Wireless Networks and Mobile Systems
288