
CILAP-Architecture for Simultaneous Position- and Force-Control in
Constrained Manufacturing Tasks
Sophie Klecker, Bassem Hichri and Peter Plapper
Faculty of Science, Technology and Communication, University of Luxembourg,
6, rue Richard Coudenhove-Kalergi, L-1359 Luxembourg, Luxembourg
Keywords: Parallel Control, Simultaneous Position- and Force-Control, Constrained Manufacturing, Bio-inspired.
Abstract: This paper presents a parallel control concept for automated constrained manufacturing tasks, i.e. for
simultaneous position- and force-control of industrial robotic manipulators. The manipulator’s interaction
with its environment results in a constrained non-linear switched system. In combination with internal and
external uncertainties and in the presence of friction, the stable system performance is impaired. The aim is
to mimic a human worker’s behaviour encoded as lists of successive desired positions and forces obtained
from the records of a human performing the considered task operating the lightweight robot arm in gravity
compensation mode. The suggested parallel control concept combines a model-free position- and a model-
free torque-controller. These separate controllers combine conventional PID- and PI-control with adaptive
neuro-inspired algorithms. The latter use concepts of a reward-like incentive, a learning system and an
actuator-inhibitor-interplay. The elements Conventional controller, Incentive, Learning system and Actuator-
Preventer interaction form the CILAP-concept. The main contribution of this work is a biologically inspired
parallel control architecture for simultaneous position- and force-control of continuous in contrast to discrete
manufacturing tasks without having recourse to visual inputs. The proposed control-method is validated on a
surface finishing process-simulation. It is shown that it outperforms a conventional combination of PID- and
PI-controllers.
1 INTRODUCTION
Automation of contact-based manufacturing
processes is of significant interest to the industrial as
well as to the scientific community. Humans being
highly proficient at manufacturing tasks requiring
compliance and force control, high number of
research works in the field aim to mimic the human
workers’ behaviour and to translate its capabilities
into robot skills.
(Rozo et al., 2013) used Programming by
Demonstration, PbD which teaches a robot by
showing the desired behaviour rather than by writing
commands in a programming language. Based on
Gaussian mixture theory, a single model encompasses
both, desired positions and forces. (Abu-Dakka et al.,
2015) presented a concept for learning and adaptation
of contact-based manipulation tasks. The authors
suggested a scheme for online modifications to match
desired reference position- and force-profiles. The
latter were obtained from programming by
demonstration and encoded with dynamic movement
primitives. (Oba et al., 2016) discussed the
acquisition and replication of polishing skills of a
human worker represented as tool trajectory, tool
posture and polishing force. These variables which
were to be controlled independently and
simultaneously formed the input to the controller.
As far as the considered processes are concerned,
most manufacturing tasks require the robotic
manipulator to interact with its environment which
results in contact situations and constrained
movements, i.e. the robot arm cannot move freely in
all directions. Constraints include natural constraints
due to the specificities of the environment as well as
artificial constraints due to and characteristic of the
desired task. Varying or switching constraints are due
to successive discrete or continuous phases in a task.
By their nature, the control of constrained tasks
requires the simultaneous control of pose and force.
Pure position control cannot cope with these complex
tasks because already slight deviations from the
desired trajectory can lead to errors in the desired
forces and torques (Abu-Dakka et al., 2015). Pure
244
Klecker, S., Hichri, B. and Plapper, P.
CILAP-Architecture for Simultaneous Position- and Force-Control in Constrained Manufacturing Tasks.
DOI: 10.5220/0006828902440251
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 244-251
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

force control on the other hand can lead to contact
instabilities at an increased speed (Newman et al.,
1999). A promising approach for simultaneous
position- and force-control is parallel control, i.e. two
controllers acting in parallel. Both independent
controllers yield control torque commands which are
summed up. In contrast to other state-of-the-art
hybrid control methods, parallel control allows for the
simultaneous and independent control of position-
and force-signals. Parallel control has been the
subject of repeated research efforts over the past
decades. Based on the interactions of controller, robot
arm and environment, (Chiaverini and Sciavicco,
1993) developed a dynamic parallel force-/position-
control for constrained motions with an elastic
environment. (Ferguene et al., 2009) extended a
conventional parallel force-/position-controller with a
3-layer feed-forward neural network to compensate
for uncertain or varying robot dynamics and
environments. The intended application areas ranged
from elastic environments over curved surfaces to
unknown environmental stiffness. (Karayiannidis and
Doulgeri, 2010) suggested adaptive concepts for
position-/force-control in compliant and frictional
contacts in the presence of uncertainties in models,
end effector-orientation and environment. (Yin et al.,
2012) based his tracking controller on a human
analogy, i.e. on the human’s approach to finger
tracking in the absence of visual feedback. For the
tracking of an unknown surface, the authors relied on
the concepts of moving frames and vector-variations.
(Lange et al., 2013) presented a parallel position-
based force-/torque-control scheme taking into
account couplings between forces and torques,
constrained configurations, compliances in robot,
sensor and environment as well as the effects due to
impact forces. An experimental validation completed
the work. The cited contributions present some
drawbacks for the here considered automated
manufacturing task. The majority of the state-of-the-
art controllers are model-based and based only on
conventional concepts, not taking advantage of gains
in robustness and adaptability offered by intelligent
control-extensions.
Over the past decades, some research has also
been done separately on control-algorithms. Since
their introduction in 1940, model-free PID-
controllers have been predominant in industrial
settings (Adar and Kozan, 2016). This is due to their
key-advantages: robustness and simple design. Their
constant fixed parameters as well as their linearity
however, make it hard to cope with either nonlinear,
time-varying systems or disturbances. The lack of
flexible adaptability and the impossibility to increase
gains arbitrarily due to actuator limitations as well as
the occurrence of instabilities and noise sensitivity
(Kuc and Han, 2000) (Siciliano and Khatib, 2008)
limit the application areas. Conventional controllers
are therefore not suited for controlling manufacturing
processes automated with highly nonlinear, coupled
robotic systems (Adar and Kozan, 2016) (Kuc and
Han, 2000) (Siciliano and Khatib, 2008).
With the aim to take advantage of the
conventional controller’s trumps while overcoming
its drawbacks, biomimetic extensions imitating the
learning behaviour of the human brain are presented.
Due to the complex nature of this biological system
only a concise selection of its key-aspects has been
retained for the development of control concepts.
(Lucas et al., 2004) presented BELBIC (Brain
Emotional Learning-Based Intelligent Control) on the
base of the work by (Balkenius and Morén, 2001) on
a computational model of the abstracted human
amygdalo-orbitofrontal cortex system. The suggested
controller mimics the natural interplay of actuating
amygdala and inhibiting orbitofrontal cortex. The
implementation of an emotional signal can be
interpreted as a reward or incentive to guide the
system’s learning behaviour. (Yi, 2015) combined
robust sliding mode control with an intelligent control
element comprising an actuator and a preventer
inspired on the mammalian limbic system. (Frank et
al., 2014)’s work focussed on reinforcement learning
allowing an agent to learn a policy with the goal to
maximize a reward-signal. The authors combined a
low-level, reactive controller with a high-level
curious agent. Artificial curiosity contributes to the
learning process by guiding exploration to areas
where the agent can efficiently learn. The work was
validated by a real-time motion planning task on a
humanoid robot. (Merrick, 2012) implemented a
goal-lifecycle and introspection for reinforcement
learning. The aim was to make the system aware of
when to learn what as well as of which acquired skills
to keep either active, ignored or erased.
The aim of this work is to combine freeform
trajectory tracking with force control, i.e. to develop
a model-free control strategy enabling an industrial
robot-arm to follow a desired freeform-path and
simultaneously apply specified adequate joint-
torques at the appropriate moment and position. The
desired position- and force-signals are to be learned
from kinesthetic teaching and introduced as
independent lists of successive joint-angles and -
torques. This work combines elements of PbD,
parallel control and neuro-inspired control-
extensions. Compared with related work cited above,
the main differences in this paper are: 1) no visual
CILAP-Architecture for Simultaneous Position- and Force-Control in Constrained Manufacturing Tasks
245
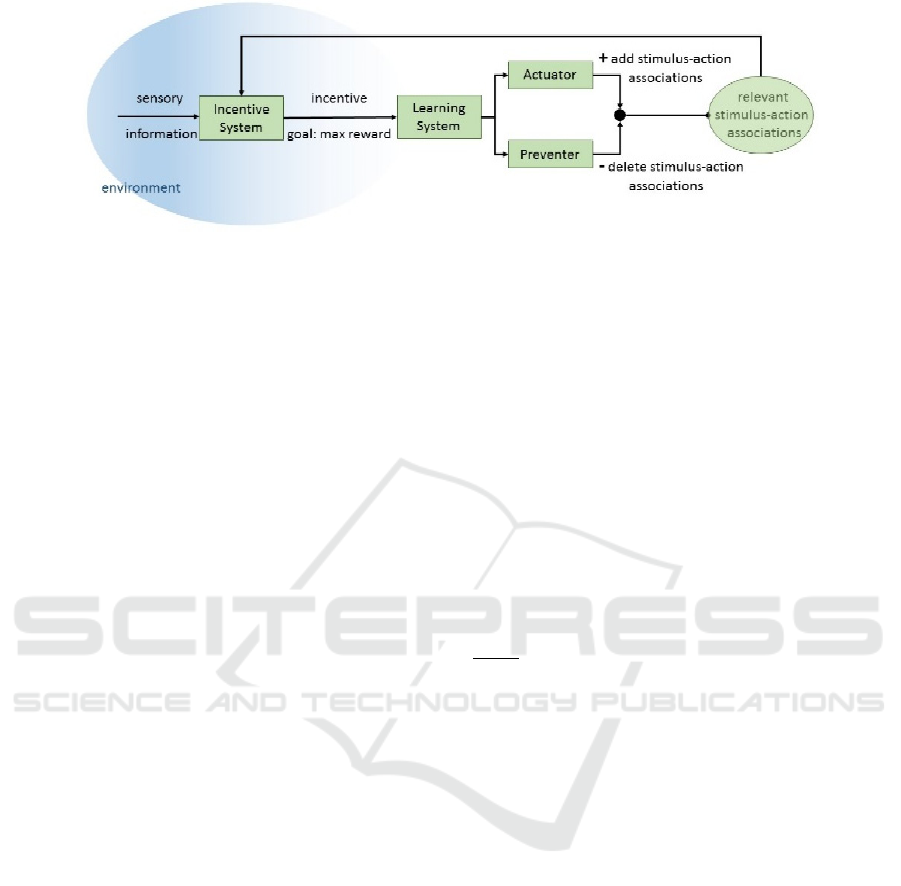
Figure 1: Inspiration for the CILAP-architecture.
information, i.e. no camera is used and 2) the
considered tasks are continuous movements instead
of discrete contact state formations. The input for the
controller is a list of desired successive joint-specific
positions and torques which are obtained from the
records of a human performing the considered task
operating the lightweight robot arm in gravity
compensation mode. 3) Further, a parallel control
concept composed of a model-free position-controller
and a model-free force-controller is designed. These
separate controllers combine conventional PID- or
PI-control with adaptive neuro-inspired algorithms.
The latter make use of an incentive and a learning
system as well as of the interaction of an actuator and
a preventer to improve the controller performance.
The elements Conventional controller, Incentive,
Learning system and Actuator-Preventer interplay
form the CILAP-concept. The suggested method is
validated on a manufacturing process simulation. For
the control objectives, the main focus is put on
precision. As the considered tasks are not time
critical, minimal mean errors of position- and force-
signals are the objective.
The rest of the paper is structured as follows: It
follows the description of the challenge, i.e. section 2
‘Problem Statement’. Section 3 describes the used
concepts. In Section 4, the suggested parallel control
concept CILAP (conventional-incentive-learning-
actuator-preventer) is developed and in section 5 the
results of the simulation are presented and discussed.
The paper ends with a conclusion.
2 PROBLEM STATEMENT
The robot-arm considered in this work has n links and
its dynamics in the presence of uncertainties,
disturbances and switching constraints are expressed:
(
)
+
(
,
)
+
(
)
=++
+ (1)
with ,
,
∈
link position, velocity and
acceleration with index for the desired reference
values.
(
)
∈
is the inertia matrix,
(
,
)
∈
the centripetal/Coriolis terms,
(
)
∈
the
gravitational torque-vector. External disturbances are
represented by the bounded term ∈
while
internal uncertainties are implemented as variations
in
(
)
, (,
) and (). ∈
stands for the
friction between end-effector and environment or
surface. The friction is a function of the applied
torque and the robot link velocity: =
with a constant factor.
∈
is
the global constraint force,
=
()
()
where ()∈
is the manipulator’s Jacobian, ∈
is the vector of Lagrange multipliers and
(
)
=
()
is the gradient of the task space constraints with
∅
(
)
∈
the
th
kinematic constraint. ∈
stands for the Cartesian pose and =1,2,…
denotes the index of constraints for the case of
multiple switching constraints with the total
number of constraints.
The considered application is a contact-based
manufacturing task, i.e. freeform trajectory tracking
with the application of specified forces at specific
positions. Manual work is current state-of-the-art for
these tasks. Not only the fact that these processes
were designed by and for humans but also humans’
capabilities make them the most appropriate
performers for these complex tasks. The challenge in
this work is to mimic the human’s approach to
perform the considered task by translating his
capabilities into robot skills and by including the
worker’s expertise in the control algorithm. The input
for the controller is a .csv-file with desired successive
positions and torques which are obtained from the
records of a human operating a lightweight robot arm
in gravity compensation mode. ∈
is the applied
input torque. It is the sum of the outputs of the pose-
controller and the force-controller, i.e.
+
. The
control action consists in adapting both robot joint
positions and the applied forces to match the desired
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
246

poses and forces. The goal is to keep the error
between desired and measured signals minimal at all
times, i.e. the mean error signal over the whole
process-period should be minimized.
3 USED CONCEPTS
The concepts used in this work are biologically
inspired, similar to the related work cited in section 1.
Despite the control concepts being inspired on the
functioning of the human brain, they do not attempt
to accurately model its structure. Rather than
presenting a true-to-life computational model of the
mammalian learning behaviour, the aim is to improve
conventional model-free PID-control through the
implementation of neuro-inspired concepts.
An incentive system transforms sensory
information into an incentive, i.e. a reward-based
extrinsic motivational stimulus. Depending on the
environment, the stimulus to the agent, i.e. how to
maximize the reward for the system is changed. This
adaptive incentive then forms the input to a learning
system which feeds both an actuator and a preventer.
The interplay of the latter is inspired on the interplay
of the amygdala and the orbitofrontal cortex in the
mammalian brain during emotional learning. While
the actuator establishes stimulus-action associations,
the preventer erases associations which are no longer
needed. The removal of no longer relevant stimulus-
action association is essential for a successful
learning and to reduce the amount of data in the
system. The latter is similar to the phenomenon of
synaptic plasticity in the human brain. The described
structure is schematically represented in Figure 1.
4 THE PARALLEL
CILAP-ARCHITECTURE
A parallel control concept is developed to
simultaneously control joint angular positions and
torques. The complex constrained control task is
broken down into two independent subsystems. The
suggested concept is composed of a model-free
position-controller and a model-free force-controller.
Both independent controllers consist of a
conventional model-free controller and a model-free
controller extension. The former C combines with the
Incentive-Learning-Actuator-Preventer to form the
CILAP-architecture. The suggested method attempts
to combine robustness, simplicity and intuitiveness
and is depicted in Figure 2.
The input to the controller is a .csv-file, i.e. a list
containing a succession of desired joint positions
and joint torques
.
4.1 Position-Control
The conventional PID-controller-output
as in
Equation (2)
=
+
+
(2)
with the error-signal, i.e. the difference between
measured and desired signal as in Equation (3)
=−
(3)
where
,
and
are constant gain factors.
For the controller extension, the appreciation, i.e.
the value of the current state is defined as the error-
signal (Equation (4)). As the only way to collect
information about the environment is to interact with
it, a feedback-loop is implemented in this controller-
part.
=−
=
(4)
The reward, i.e. incentive ∈
is defined in
Equation (5).
=(
(
)
∙
)(
−) (5)
where ′ indicates the vector-transpose. ∈
represents the interplay of actuator and preventer.
is defined as the difference between their respective
outputs (Equations (8) and (9)) which guarantees only
relevant connections are kept. Mimicking synaptic
plasticity, this law allows to limit the number of
active learned connections.
The incentive is the input to the learning system.
Its outputs are the learning rates for both the actuator
(Equation (6)) and the preventer (Equation (7)).
=
∙max
(
,
)
(6)
=
∙(−) (7)
with >0 a constant factor.
The main part of this half of the control algorithm
consists in the interaction between an actuator and an
inhibitor. The actuator-output ∈
and the
preventer-output ∈
are defined in Equations
(8) and (9).
CILAP-Architecture for Simultaneous Position- and Force-Control in Constrained Manufacturing Tasks
247

Figure 2: CILAP-architecture.
=
(8)
=
(9)
The controller-extension-output is defined in
Equation (10), the integration over time mimicking
experience.
=
−
(10)
with >0 being a constant gain-factor.
The final position-controller output combines the
outputs of the conventional controller and of the
extension.
=
−
(11)
4.2 Force-Control
Parallel to the position-controller, a force-controller
is implemented to make sure the desired force-torques
from the reference .csv-file are applied.
The conventional PI-controller-output
is
defined in Equation (12)
=
+
(12)
where
and
are constant gain-matrices and the
error-signal
=−
(13)
with =
+.
For the controller-extension the state-value
is defined as the error-signal (Equation (13)).
The incentive is defined as follows
=(
(
)
∙
)(
−) (14)
For the output of the actuator-preventer-system, its
constituents and their learning rates the formulas
defined in Equations (6)-(9) apply. The controller-
extension-output follows Equation (15).
=−
+
(15)
The final force-torque-controller output combines
the outputs of the conventional controller and of the
extension.
=
−
(16)
5 RESULTS
5.1 Simulation
The proposed control concept is validated on a
surface finishing task, i.e. the robot-arm successively
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
248
follows desired positions and applies desired torques
at specified positions. The controller is implemented
on a 2D-RR planar robot in the Matlab/Simulink-
environment. The parameters of the robotic arm with
two rotational joints are described in set of Equation
(17).
=
+
cos(
−
)
cos(
−
)
+
=
0−
sin
(
−
)
sin
(
−
)
0
=
cos
(
)
+
cos(
)
cos(
)
(17)
with link masses
=
=1, link lengths
=
=1, gravitational acceleration =9.8
,
distances from the link source end to its centre of
mass
=
and link moments of inertia
=
.
The system-inputs are extracted from .csv-files
containing a succession of desired reference joint
angular positions and torques. The controller-
parameters introduced in Equations (2)-(16) are
chosen and optimized by trial-and-error-procedure as
follows: =5, =30,=1,
=−5,
=
−20,
=−20,
=5,
=35.
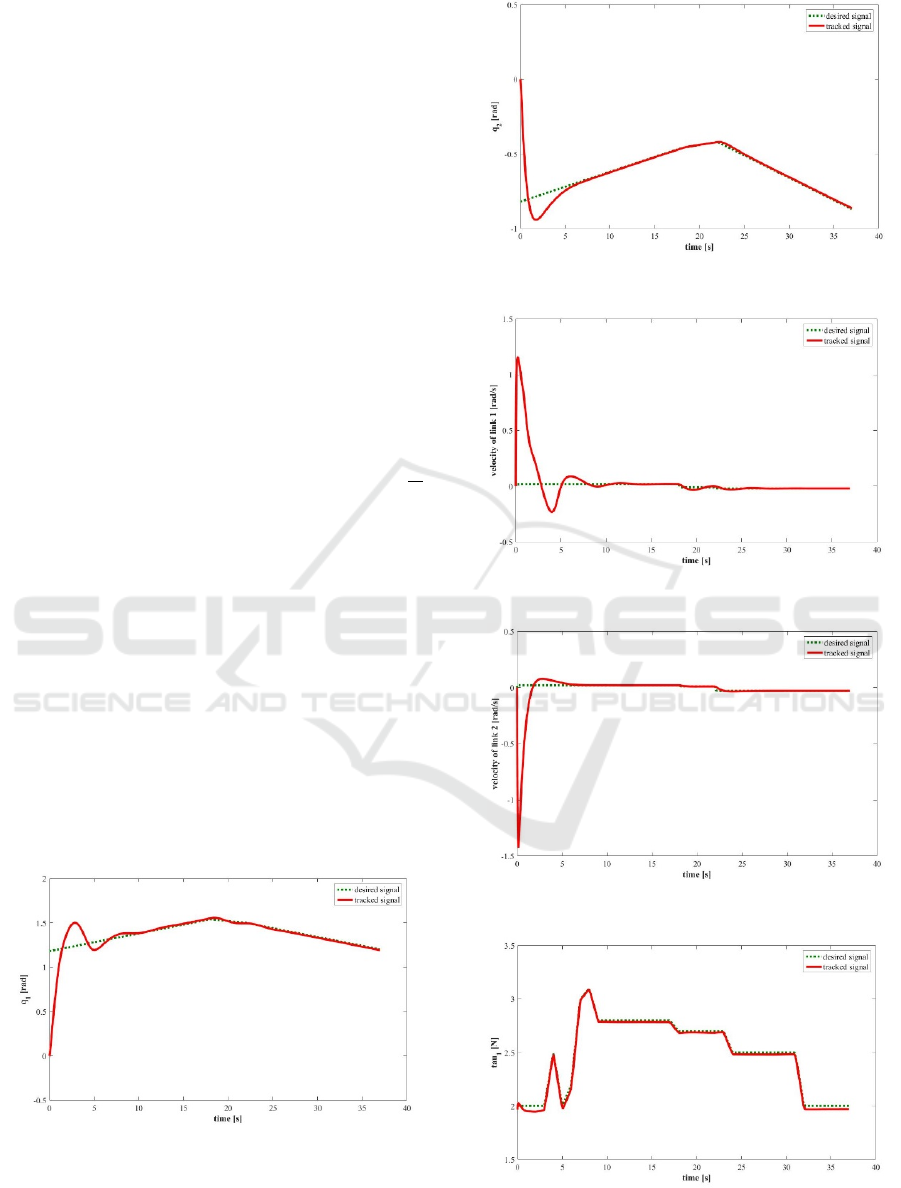
The performance-results are illustrated in Figures
3-8. While Figures 3 and 4 show the trajectory-
tracking performance of the suggested controller
scheme, Figures 5 and 6 depict its velocity-tracking
and Figures 7 and 8 show the force-tracking of link 1
and 2, respectively.
Figure 3: Trajectory tracking of link 1.
Figure 4: Trajectory tracking of link 2.
Figure 5: Velocity tracking of link 1.
Figure 6: Velocity tracking of link 2.
Figure 7: Force tracking of link 1.
CILAP-Architecture for Simultaneous Position- and Force-Control in Constrained Manufacturing Tasks
249
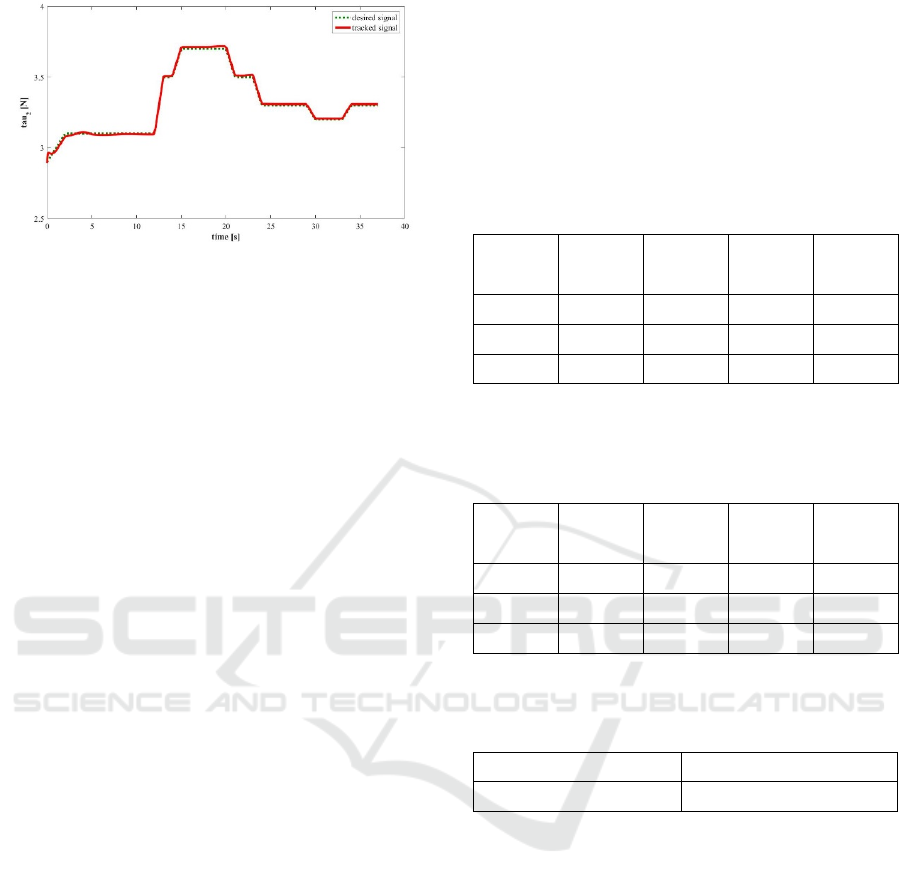
Figure 8: Force tracking of link 2.
5.2 Analysis and Discussion
The simulation-results present good tracking results
for all considered signals: joint torques, angular joint
positions and velocities. This is illustrated
qualitatively in Figures 3-8 as well as quantitatively
in Table 1 and Table 2.
The added value of the controller-extension is
illustrated in Tables 1-3. In Table 3, the improvement
from the parallel controller without the neuro-
inspired extension to the suggested CILAP-
architecture is given in percentages. It is proven that
the latter outperforms a parallel controller with PID-
position- and PI-force-control. The main focus in this
work was put on the mean error signals.
The industrial applications of the presented work
are contact-based manufacturing in general and
surface finishing in specific. Manual work being
current industrial state-of-the-art, surface finishing
processes are the bottleneck of the concerned industry
due to their time- and cost-intensive nature. Different
studies suggest shares of up to 30-50% of the entire
manufacturing time and up to 40% of the total cost.
(Dardouri et al., 2017) (Dieste et al., 2013) (Pagilla
and Yu, 2001) (Robertsson et al., 2006) (Roswell et
al., 2006) (Wilbert et al., 2012). From the scientific
point of view, the automation of these contact-based
manufacturing processes is highly complex as it
requires tackling freeform trajectory tracking and
force control simultaneously while mimicking the
robust and adaptive behaviour a human provides on a
nonlinear system. Additional challenges arising in
industrial practice and taken into account here are the
absence of visual information from a camera and the
application involving continuous movements, e.g.
path following rather than discrete contact state
formations, e.g. gripping.
As the shown work presents promising results for
the automation of the considered continuous
manufacturing processes, future work will involve the
experimental validation on a KUKA LWR4+ robot-
arm with a variety of processes, e.g. grinding or
polishing tasks. Comparisons with state-of-the-art
controllers will be performed to demonstrate the
outperformance of the suggested concept. Also, its
real-time capabilities will be proven.
Table 1: Maximum, minimum and mean absolute positional
errors for both manipulator-links [rad] for the experiment
with (a) the parallel architecture with PID- and PI-
controllers and (b) the CILAP-architecture.
a-
a-
b-
b-
Max 3.16 0.82 1.18 0.82
Min 9.70e-4 2.25e-5 2.07e-4 2.95e-5
Mean 1.64 0.09 0.13 0.08
Table 2: Maximum, minimum and mean absolute force-
errors for both manipulator-links [N/m
2
] for the experiment
with (a) the parallel architecture with PID- and PI-
controllers and (b) the CILAP-architecture.
a-
a-
b-
b-
Max 2.41 2.45 0.05 0.05
Min 0.003 0.001 0.002 1.41e-5
Mean 1.56 1.62 0.02 0.01
Table 3: Average improvement-rate [%] from the parallel
architecture with PID- and PI-controllers to the CILAP-
architecture for position- and force-tracking.
Position-Control 35 %
Force-Control 87 %
6 CONCLUDING REMARKS
In this paper, the control problem of automated
constrained manufacturing tasks was addressed. A
parallel control concept composed of two model-free
controller-halves is developed. One half controls the
position while the other half controls the applied
torque of the robot manipulator performing a
freeform trajectory tracking application with the
application of manufacturing-forces at specified
positions in the presence of uncertainties and friction.
Both controller-halves combine conventional control
with biomimetic adaptive control. The latter is
inspired on the human learning behaviour making use
of an actuator-inhibitor-system and a reward-like
incentive. The elements Conventional controller,
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
250

Incentive, Learning system and Actuator-Preventer
interplay form the CILAP-concept. The developed
model-free control concept combines PbD, parallel
control and neuro-inspired control-extensions. A
surface finishing application-simulation illustrates
the suggested scheme outperforms a combination of
conventional PID- and PI-controllers.
ACKNOWLEDGEMENTS
This work has been done in the framework of the
European Union supported INTERREG GR-project
“ROBOTIX-Academy”. (http://robotix.academy/)
REFERENCES
Abu-Dakka, F., Nemee, B., Jorgensen, J., Savarimuthu, T.,
Krüger, N., Ude, A., 2015. Adaptation of manipulation
skills in physical contact with the environment to
reference force profiles In Autonomous Robots, 39-2,
pp. 199-217.
Adar, N., Kozan, R., 2016. Comparison between Real Time
PID and 2-DOF PID Controller for 6-DOF Robot Arm.
In Acta Physica Polonica A, 130-1, pp. 269-271.
Balkenius, C., Morén, J., 2001. Emotional Learning: a
Computational Model of the Amygdala. In Cybernetics
and Systems, 32-6, pp. 611-636.
Chiaverini, S., Sciavicco, L., 1993. The Parallel Approach
to Force/Position Control of Robotic Manipulators In
IEEE Transactions on Robotics and Automation, 9-4,
pp. 361-373.
Dardouri, F., Abba, G., Seemann, W., 2017. Parallel Robot
Structure Optimizations for a Friction Stir Welding
Application. In ICINCO 2017-14
th
International
Conference on Informatics in Control, Automation and
Robotics.
Dieste, J., Fernández, A., Roba, D., Gonzalvo, B., Lucas,
P., 2013. Automatic grinding and polishing using
Spherical Robot. In Procedia Engineering, 63, pp. 938–
946.
Ferguene, F., Achour, N., Toumi, R., 2009. Neural network
parallel force/position control of robot manipulators
under environment and robot dynamics uncertainties. In
Archives of Control Sciences, 19-1, pp. 93-121.
Frank, M., Leitner, J. Stollenga, M., Förster, A.,
Schmidhuber, J., 2014. Curiosity driven reinforcement
learning for motion planning on humanoids. In
Frontiers in Neurorobotics, 7, pp. 1-15.
Karayiannidis, Y., Doulgeri, Z., 2010. Robot contact tasks
in the presence of control target distortions. In Robotics
and Autonomous Systems, 58-5, pp. 596-606.
Kuc, T., Han, W., 2000. An adaptive PID learning control
of robot manipulators. In Automatica, 36, pp. 717-725.
Lange, F., Bertleff, W., Suppa, M., 2013. Force and
Trajectory Control of Industrial Robots in Stiff Contact.
In IEEE International Conference on Robotics and
Automation (ICRA), pp. 2927-2934.
Lucas, C., Shahmirzadi, D., Sheikholeslami, N., 2004.
Introducing BELBIC: brain emotional learning based
intelligent controller. In Intelligent Automation and Soft
Computing, 10-1, pp. 11-22.
Merrick, K., 2012. Intrinsic Motivation and Introspection in
Reinforcement Learning. In IEEE Transactions on
Autonomous Mental Development, 4-4, pp. 315-329.
Newman, W., Branicky, M., Podgurski, H., Chhatpar, S.,
Huang, L., Swaminathan, J., Zhang, H., 1999. Force-
responsive robotic assembly of transmission
components. In IEEE International Conference on
Robotics and Automation (ICRA), 3, pp. 2096-2102.
Oba, Y., Yamada, Y., Igarashi, K., Katsura, S., Kakinuma,
Y., 2016. Replication of skilled polishing technique
with serial-parallel mechanism polishing machine In
Precision Engineering, 45, pp. 292-300.
Pagilla, P., Yu, B., 2001. Adaptive control of robotic
surface finishing processes. In Proceedings of the 2001
American Control Conference. (Cat. No.01CH37148),
1, pp. 630–635.
Robertsson, A., Olsson, T., Johansson, R., Blomdell, A.,
Nilsson, K., Haage, M., Lauwers, B., de Baerdemaeker,
H., Brogardh, T., Brantmark, H., 2006. Implementation
of Industrial Robot Force Control Case Study: High
Power Stub Grinding and Deburring. In 2006 IEEE/RSJ
International Conference on Intelligent Robots and
Systems, pp. 2743–2748.
Roswell, A., Jeff, F., Liu, G., 2006. Modelling and analysis
of contact stress for automated polishing. In
International Journal of Machine Tools &
Manufacture, 46, pp. 424–435.
Rozo, L., Jiménez, P., Torras, C., 2013. A robot learning
from demonstration framework to perform force-based
manipulation tasks. In Intelligent Service Robotics, 6,
pp. 33–51.
Siciliano, B., Khatib, O., 2008.
Springer Handbook of
Robotics, Springer-Verlag. Berlin Heidelberg.
Wilbert, A., Behrens, B., Dambon, O., Klocke, F., 2012.
Robot Assisted Manufacturing Systme for High Gloss
Finishing of Steel Molds State of the Art. In ICIRA, 1,
LNAI 7506, pp. 673–685.
Yi, H., 2015. A Sliding Mode Control Using Brain Limbic
System Control Strategy for a Robotic Manipulator. In
International Journal of Advanced Robotic Systems,
12-158.
Yin, Y., Xu, Y., Jiang, Z., Wang, Q., 2012. Tracking and
Understanding Unknown Surface With High Speed by
Force Sensing and Control for Robot In IEEE Sensors
Journal, 12-9, pp. 2910-2916.
CILAP-Architecture for Simultaneous Position- and Force-Control in Constrained Manufacturing Tasks
251
