
Parameter Identification in Cyclic Voltammetry
of Alkaline Methanol Oxidation
Tanja Clees
1
, Igor Nikitin
1
, Lialia Nikitina
1
, Sabine Pott
1
, Ulrike Krewer
2
and Theresa Haisch
2
1
Fraunhofer Institute for Algorithms and Scientific Computing, Sankt Augustin, Germany
2
Institute of Energy and Process Systems Engineering, Technical University Braunschweig, Germany
Keywords:
Complex Systems Modeling and Simulation, Non-linear Optimization, Parameter Identification, Application
in Electrochemistry.
Abstract:
Alkaline methanol oxidation is an electrochemical process, perspective for the design of efficient high energy
density fuel cells. The process involves a large number of elementary reactions, forming a complex reaction
graph, and it is described by a system of non-linear differential equations of high order. The purpose of param-
eter identification is a reconstruction of reaction constants in this model on the basis of available experimental
data. Cyclic voltammetry, a measurement of dynamical current-voltage characteristic of the cell, is especially
suitable for analysis of electrochemical kinetics. In this paper we present several approaches for parame-
ter identification in cyclic voltammetry of alkaline methanol oxidation. With the aid of global optimization
methods and interactive parameter study we find four islands of solutions in parameter space, correspond-
ing to different chemical mechanisms of the process. The main features of solutions are discussed and the
reconstructed reaction constants are presented.
1 INTRODUCTION
Direct fuel cells are attractive portable energy
sources, serving as converters of chemical energy
to the electric one, with a possibility to refill the
reagents. Alkaline methanol oxidation uses com-
monly available components and allows to reduce the
costs for production and operation of the cells. The
detailed description of this chemical process includes
a large number of reactions, multiple intermediates,
leading to a mathematical model with many unknown
parameters (Krewer et al., 2011; Krewer et al., 2006;
Beden et al., 1982).
For parameter identification different types of ex-
periments are used (Ciucci, 2013; Gamry Instru-
ments, 2018). Some of them measure stationary
current-voltage profiles of the cell, others use a lin-
earization near the stationary point and scan a re-
sponse of the cell to harmonic oscillations in a large
range of frequencies. In our previous paper (Clees
et al., 2017) we have presented the methods for pa-
rameter identification in this type of measurements.
The main difficulty here is that the stationary state
in the considered process is hard to reach experimen-
tally. Our laboratory measurements show that even if
one leaves the cell under fixed voltage for six hours, it
does not reach a steady current. A presumable reason
is a gradual poisoning of the electrode with intermedi-
ates or byproducts of reactions, characteristic for the
measurements of this type.
In this paper, differently from (Clees et al., 2017),
the measurement method is used, not assuming the
presence of the stationary state. Cyclic voltammetry
(Bard and Faulkner, 2000) is an experimental setup,
where the cell is subjected to a saw-like voltage varia-
tion of high amplitude. These voltage variations clean
up the electrode during every period, in this way pre-
venting the electrode poisoning. On the side of pa-
rameter identification, however, the problem becomes
more difficult, since one needs to integrate numeri-
cally stiff non-linear differential equations, instead of
just testing the linear response of the system.
In general, parameter identification uses a version
of non-linear least square method (Press et al., 1992;
Strutz, 2016) to fit the experimental data with the
mathematical model. One can also take into account
any equality or inequality constraints by the meth-
ods of non-linear programming, e.g., interior point
method (W
¨
achter and Biegler, 2006). These methods
find only a local optimum and should be enhanced by
global strategies to find all relevant solutions. One
possibility is an interactive exploration of solution
Clees, T., Nikitin, I., Nikitina, L., Pott, S., Krewer, U. and Haisch, T.
Parameter Identification in Cyclic Voltammetry of Alkaline Methanol Oxidation.
DOI: 10.5220/0006832002790288
In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018), pages 279-288
ISBN: 978-989-758-323-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
279
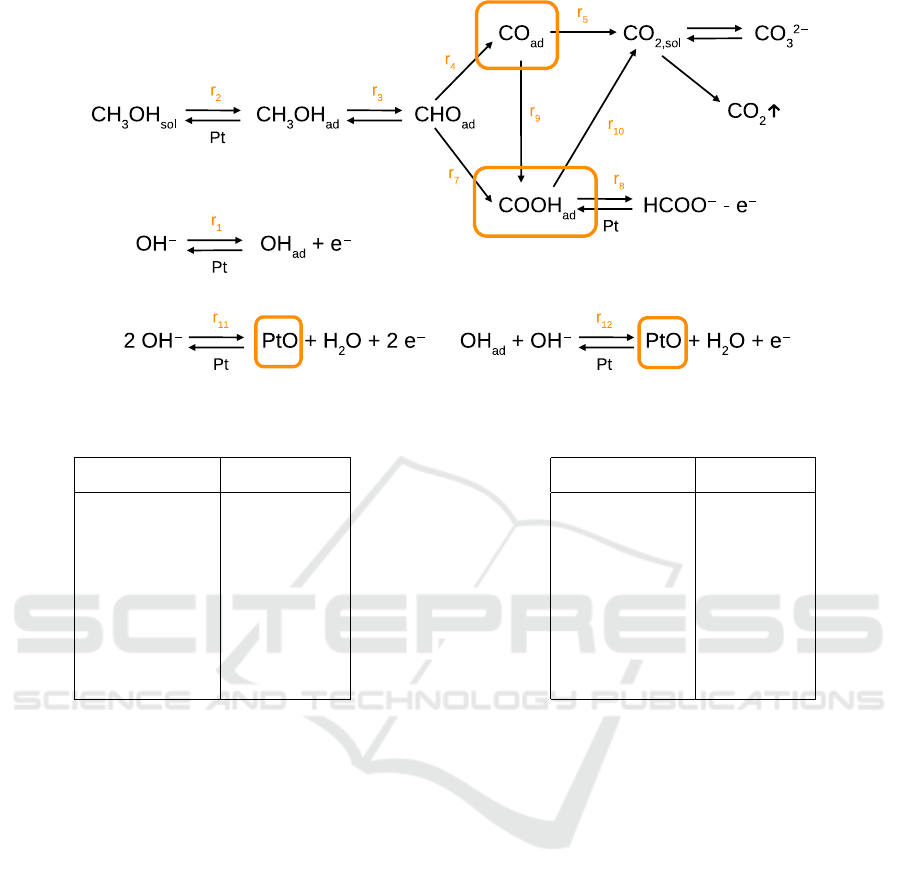
Figure 1: Reaction graph. Orange frames indicate possible locations of weakly coupled reagents.
Table 1: Numeration of variables and constants.
Variables Constants
θ
1
OH
ad
θ
2
CH
3
OH
ad
c
1
OH
−
θ
3
CHO
ad
c
2
CH
3
OH
θ
4
CO
ad
c
3
H
2
O
θ
5
COOH
ad
θ
6
PtO
space using metamodeling with radial basis functions
(Nikitin et al., 2012; Clees et al., 2014a; Clees et al.,
2014b). For the problem in hand, however, solutions
occupy thin subsets of parameter space. Also, the de-
pendence of model response on parameters includes
rapidly growing exponential terms, too non-linear to
be caught with radial basis functions. Instead of in-
terpolating the response, one can directly solve the
differential equations, provided that the integrator is
sufficiently fast. Interactive exploration can be also
enhanced with standard global optimization methods
(B
¨
ack, 1996; Ilonen et al., 2003; Otten and van Gin-
neken, 1989), including genetic algorithms, differen-
tial evolution, simulated annealing, etc.
In this paper we use a combination of automatic
global methods and interactive parameter study. In
Section 2 we present the mathematical model behind
alkaline methanol oxidation. In Section 3 the experi-
mental measurements are described. In Section 4 the
details on parameter identification methods are given.
Section 5 presents the obtained results.
Table 2: Model constants.
Constant, units Value
F, C/mol 9.649 · 10
4
R, J/(K mol) 8.314
A, m
2
2.376 · 10
−5
C
dl
, F 1.899 · 10
−4
C
act
, mol/m
2
8.523 · 10
−5
α 0.5
2 ALKALINE METHANOL
OXIDATION
Considering alkaline methanol oxidation processes,
we use the list of reactions from our previous work
(Clees et al., 2017):
r
1
: OH
−
+ Pt ↔ OH
ad
+ e
−
r
2
: CH
3
OH + Pt ↔ CH
3
OH
ad
r
3
: CH
3
OH
ad
+ 3OH
ad
↔ CHO
ad
+ 3H
2
O
r
4
: CHO
ad
+ OH
ad
→ CO
ad
+ H
2
O
r
5
: CO
ad
+ 2OH
ad
→ CO
2
+ H
2
O + 2Pt
r
7
: CHO
ad
+ 2OH
ad
→ COOH
ad
+ H
2
O + Pt
r
8
: COOH
ad
+ e
−
↔ HCOO
−
+ Pt
r
9
: CO
ad
+ OH
ad
→ COOH
ad
+ Pt
r
10
: COOH
ad
+ OH
ad
→ CO
2
+ H
2
O + 2Pt
extending it with two additional reactions:
r
11
: 2OH
−
+ Pt ↔ PtO + H
2
O + 2e
−
r
12
: OH
−
+ OH
ad
↔ PtO + H
2
O + e
−
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
280

Fig. 1 schematically represents the reactions. The
mathematical model for these processes is formulated
as follows. The reagents adsorbed on the electrode
(subscript “ad”) are represented by surface coverage
variables θ
1−6
, while the reagents in the solvent are
represented by constant mole fractions values c
1−3
.
The assignment of the reagents is given in Table 1.
Counting the factors of the reagents in the reac-
tions, one forms molar and charge balance conditions:
F
1
= (r
1
− 3r
3
− r
4
− 2r
5
− 2r
7
−r
9
− r
10
− r
12
)/C
act
,
F
2
= (r
2
− r
3
)/C
act
,
F
3
= (r
3
− r
4
− r
7
)/C
act
,
F
4
= (r
4
− r
5
− r
9
)/C
act
, (1)
F
5
= (r
7
− r
8
+ r
9
− r
10
)/C
act
,
F
6
= (r
11
+ r
12
)/C
act
,
F
7
= (−r
1
+ r
8
− 2r
11
− r
12
) · FA/C
dl
,
where r
i
are reaction rates, F
i
are production rates,
F
1−6
– for adsorbed reagents, F
7
– for electrons. The
constants, participating in these equations, are: C
act
– surface concentration of catalyst, F – Faraday con-
stant, A – geometric electrode area, C
dl
– cell capaci-
tance.
Reaction rates are described by a kinetic model:
r
1
= k
1
c
1
θ
0
− k
−1
θ
1
, r
2
= k
2
c
2
θ
0
− k
−2
θ
2
,
r
3
= k
3
θ
2
θ
3
1
− k
−3
θ
3
c
3
3
, r
4
= k
4
θ
3
θ
1
,
r
5
= k
5
θ
4
θ
2
1
, r
7
= k
7
θ
3
θ
2
1
, r
8
= k
8
θ
5
, (2)
r
9
= k
9
θ
4
θ
1
, r
10
= k
10
θ
5
θ
1
,
r
11
= k
11
c
2
1
θ
0
− k
−11
c
3
θ
6
,
r
12
= k
12
c
1
θ
1
− k
−12
c
3
θ
6
,
where k
i
are reaction constants. The model directly
encodes molecular reactions in terms of probabilities
of collision, e.g., in reaction r
5
, the term θ
4
θ
2
1
corre-
sponds to a probability, that one CO-particle meets
two OH-particles. The variable θ
0
describes non-
covered surface of the electrode. The variables θ
i
are changed in the range [0,1] with summation rule
∑
6
0
θ
i
= 1. The constants for the reactions, involving
electrons, are defined by Tafel equation:
k
1
= k
0
1
exp(αβη),
k
−1
= k
0
−1
exp(−(1 − α)βη), (3)
k
8
= k
0
8
exp(−(1 − α)βη), β = F/(RT ),
k
11
= k
0
11
exp(2αβη), k
12
= k
0
12
exp(αβη),
k
−11
= k
0
−11
exp(−2(1 − α)βη),
k
−12
= k
0
−12
exp(−(1 − α)βη).
where η is electrode potential, R is universal gas con-
stant, T is absolute temperature, α is charge transfer
coefficient. The universal/measured model constants
are given in Table 2. The remaining constants, k
0
i
for
electrochemical reactions and k
i
for other reactions
have to be defined by parameter identification proce-
dure. Generally, the constants are constrained only
by positivity condition. In our model, reactions r
11
and r
12
, describing parallel and sequential mechanism
of platinum oxidation, will be considered as alterna-
tives, i.e., we will consider two scenarios with either
k
0
±11
= 0 or k
0
±12
= 0.
Kinetics of alkaline methanol oxidation is de-
scribed by a closed system of differential equations:
dθ
i
/dt = F
i
(θ,η), i = 1 ... 6, (4)
where η is considered as a given function of time t.
There is an additional equation:
dη/dt = F
7
(θ,η) +I
cell
/C
dl
, (5)
which can be considered as a model prediction for cell
current I
cell
. Comparing it with the measured current
values, we can introduce a χ
2
-deviation:
χ
2
=
∑
i
(I
cell,i
− I
exp
cell,i
)
2
, (6)
which should be minimized in parameter identifica-
tion procedure.
3 MEASUREMENTS
The measurements are performed in our laboratory in
TU Braunschweig. The experiments were done using
a three electrode cell setup, shown on Fig.2. It uses a
rotating disk electrode (RDE) as a working electrode
and a potentiostat. The working electrode was coated
with a platinum catalyst ink and an ionomer. A plat-
inum wire was used for the counter electrode and a
Hg/HgO electrode as a reference electrode. The po-
tentials were calculated to a normal hydrogen elec-
trode (NHE) as reference. Before each measurement
the working electrode was electrochemically cleaned
by running CV cycles with the pure electrolyte.
In experiments, different profiles for the voltage
η(t) are set and the cell current I
cell
(t) is measured. In
particular, constant η profiles correspond to the mea-
surement of polarization curve (PC), stepwise η(t)
is used in chronoamperometry (CA). A constant η,
perturbed with sinusoidal profile of small amplitude
is applied in electrochemical impedance spectroscopy
(EIS), the same with high amplitude gives the estima-
tion of total harmonic distortion (THD).
The measurement of cyclovoltagramms (CV) uses
saw-like η(t) profiles, displayed on Fig.3 left. The re-
sulting I
cell
(t) profile, a periodic curve, is shown on
Parameter Identification in Cyclic Voltammetry of Alkaline Methanol Oxidation
281

Figure 2: Cyclic voltammetry: experimental setup.
Figure 3: Cyclic voltammetry. From left to right: voltage profile, current profile, current-voltage characteristics with hysteresis
effect.
Fig.3 middle. In coordinates (η, I
cell
) it corresponds
to a closed cycle, shown on Fig.3 right. This curve
in alkaline methanol oxidation experiments demon-
strates a typical hysteresis effect, i.e., the path for in-
creasing voltage does not coincide with the decreas-
ing one. The reasons for this effect and the relation
with other types of measurements will be discussed
below.
Between different measurements, one can also
change concentration of the dissolved reagents c
i
,
the temperature T and the period T
p
. In this way
one has not a single experiment, but a set of exper-
iments which should be simultaneously fit by the ki-
netic model.
Surface coverage profiles θ
i
(t) are generally not
measurable. Although their rough estimation can be
done with the aid of Fourier Transform Infrared Spec-
troscopy (FTIR, (Griffiths and de Hasseth, 2007)), the
precision of this approach is not sufficient yet. The
usual way to reconstruct the kinetics is the model
based parameter identification.
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
282

4 PARAMETER
IDENTIFICATION
We use Mathematica (Mathematica 11, 2018) for
analysis of cyclovoltagramms. For solution of the
system (4) we use algorithm NDSolve, providing
a generic, stable and robust numerical integrator
of differential equations. The algorithm supports a
bundle of methods, both explicit (ExplicitEuler,
ExplicitRungeKutta, ExplicitMidpoint) and
implicit (Adams, BDF, ImplicitRungeKutta,
SymplecticPartitionedRungeKutta) ones. Ex-
plicit methods require less computational effort per
step, but perform more steps to ensure stability.
Implicit methods can go in large steps, but each step
is computationally expensive. Generally, for stiff sys-
tems implicit methods are preferred. The algorithm
estimates the stiffness of the system, based on the
dominant eigenvalue of the Jacobian. Dependently
on this estimation and theoretically known stability
regions of the integration methods the algorithm
selects a suitable method in respect both to the
stability and precision criteria. Precision of the
integration is internally estimated by Richardson’s
formula: e = |y
2
− y
1
|/(2
p
− 1), where p is the order
of the integration method, |y
2
− y
1
| is a difference of
integration results, performed with a single step h and
two sequential half-steps h/2. The step is automati-
cally adapted to keep the error estimator just within
the absolute and relative tolerance bounds, specified
by parameters AccuracyGoal and PrecisionGoal.
One more convenient feature of NDSolve is a pos-
sibility to solve both Cauchy initial value problems
and boundary problems. We are mainly interested
in periodical solutions of the system (4), which can
be found by setting linear boundary conditions of the
type x(T
p
) = x(0). The considered system possesses a
polynomial right hand side with periodic coefficients,
due to explicit periodical dependence η(t), entering
in some coefficients. In our numerical experiments,
the system rapidly, in one-two periods, converges to
a limiting cycle, corresponding to the periodical so-
lution. Therefore, an alternative method is to solve
Cauchy initial value problem with an arbitrary start-
ing point, e.g., free electrode θ
0
= 1, and wait some
periods till convergence.
For the parameter identification several capabili-
ties of Mathematica can be used.
Interactive Parameter Study can be performed with
a tool Manipulate. It allows to attach interactive ma-
nipulators (sliders) to the model parameters, while the
results are presented as a collection of plots. The sys-
tem is reevaluated and the results are replotted ev-
ery time when the value controlled by the manipu-
lator is changed. Fig.4 shows an example of usage
of the interactive manipulators for parameter study in
cyclic voltammetry of alkaline methanol oxidation.
The manipulators on the left represent reaction co-
efficients, varied in logarithmic scale in user speci-
fied limits. Each manipulator can be opened, reveal-
ing additional field with numerical value and a set of
buttons for animation and stepwise increments. The
current set of parameters is permanently available for
the user in a form of a list and can be printed out,
exported, etc. with standard commands. The central
plot shows a cyclovoltagramm, modeled (red line) vs
measured (blue points). The right plot shows a pe-
riod of evolution for θ values. The ordinal number
of reagent is encoded by a color scheme: red, green,
blue, cyan, magenta, brown for 1-6 and black for 0,
free electrode. The latency of the tool is 0.5 – 1.5
seconds (on 3 GHz CPU), dependently on the number
of cyclovoltagramms to evaluate and plots to display.
It provides the interactive performance, necessary for
parameter study. The tool allows to explore solution
space, immediately observing the influence of the pa-
rameters, various features and effects in the results
(peaks, dips, shifts, etc.) and compare the modeled
results with measured data.
Automatic Global Optimization can be done with
the algorithm NMinimize. It aggregates a collec-
tion of derivative free methods, attempting to find a
global minimum of a given objective function in a
domain, specified by a set of equality and inequality
constraints. It is commonly known, that global op-
timization is a computationally hard task, especially
for non-linear multidimensional problems. An addi-
tional difficulty in our case is that optimization param-
eters, reaction constants, in logarithmic scale do not
have a priori specified limits. Exponential terms in
the equations can change their contribution by dozens
of orders, also the constants are multiplied by cover-
age values, which in molecular chemistry can be ar-
bitrary small and still provide considerable effects. It
is clear, that in the given problem global optimization
by any method becomes a game of chance. A default
strategy of NMinimize is first to apply NelderMead
“downhill simplex” method, and, in the case of poor
performance, switch to DifferentialEvolution,
which is similar to genetic algorithm, and adapted
to real number optimization. Alternatively, the user
can switch to RandomSearch, a multiply restarted lo-
cal optimizer, for which the user can select between
PenaltyFunction and InteriorPoint constraint
minimizers. As a last resort, SimulatedAnnealing
can be used, which emulates a physical process of
a melted metal cooling, asymptotically reaching the
globally minimal energy state. For this purpose, an
Parameter Identification in Cyclic Voltammetry of Alkaline Methanol Oxidation
283

Figure 4: A tool for interactive parameter study. On the left – sliders for variation of parameters, in the center – CV plot,
on the right – surface coverage profiles.
Figure 5: Illustration of Iterative Monte Carlo algorithm.
extremely slow cooling schedule must be used: T ∼
1/logt, here t is time, T is the absolute temperature.
While global optimization methods are consid-
ered, also deep local minima are of interest, not
only a single global minimum. In our application,
NMinimize with default settings requires 5000 itera-
tions and 35 min (on 3 GHz CPU) for convergence.
The quality of the minimum is usually comparable
with the other methods. However, in the parameter
identification problems with several deep local min-
ima of χ
2
, all of them may become interesting. Such
local minima can reveal hidden discrete symmetries
of the problem, or, in our case, can indicate several al-
ternative chemical mechanisms, explaining the same
experimental data. Therefore, we have to involve
more exhaustive methods for seaching the alternative
solutions.
Traditional Monte Carlo, also known as Direct
Search method uses a random sampling of parameter
space and an iterative strategy of its refinement. For
example, one can use the following procedure:
Algorithm (Iterative Monte Carlo)
run: generate N random points
in specified limits
select cloud: χ
2
< threshold
plot cloud in 2D projections (k
i
,k
j
)
if cloud is on the border,
move limits,
repeat run
if cloud is localized,
narrow limits,
repeat run
return min over the cloud.
Fig.5 illustrates the work of the algorithm. On the
step (a) the multidimensional cloud χ
2
< threshold is
selected, here presented in a certain (k
i
,k
j
) projection.
The threshold is adjusted to have approximately 500
points in the cloud. The parts (b) and (c) show moving
and narrowing steps. At the end of iterations, at step
(d), the minimum over the cloud is returned.
In our settings, generation of one population of
N = 120000 points requires 6 hours (on 3 GHz CPU),
and one needs 3-5 iterations for convergence. The ad-
vantage of this algorithm is a possibility to branch it-
erative process towards several solutions and an avail-
ability of a large amount of data, representing the be-
havior of χ
2
in the tested hypervolume. It allows, in
particular, to detect the directions, on which χ
2
is al-
most independent. These directions represent contin-
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
284

uous symmetries of the system and will be discussed
in details below.
5 RESULTS
Fig.6 shows the results of fitting of experimen-
tal CV plot, measured for concentration of KOH
0.1M, CH
3
OH 0.5M and temperature 300.75K. Gen-
erally, for randomly selected point in the space of k-
parameters, hysteresis effect is negligible, as shown
on Fig.6 left. Hysteresis effect is present only for a
thin subset of parameters, complicating additionally
the parameter identification procedure.
A simple estimation by the order of magnitude
I
cell
∼ kFA shows that I
cell
∼ 10 mA and FA ∼
1 Cl m
2
/mol correspond to k ∼ 10
−3
mol/(m
2
s). The
scale of dynamics τ ∼ C
act
/k ∼ 0.1 s, characterizing a
typical delay in solutions of differential equations, is
much smaller than the period T
p
= 800 s of CV curve.
So small delay time cannot lead to the visible hys-
teresis, therefore, hysteresis becomes a rare effect in
parametric space and requires special explanations.
Such behavior can appear near the stationary state
with almost degenerate Jacobi matrix. Let eigenval-
ues of Jacobi matrix J be |λ
max
| |λ
min
|, correspond-
ing to a case of stiff system. Note, that eigenvalues λ
coincide with the poles in EIS measurements (Clees
et al., 2017), while the eigenvectors v are the eigen-
modes of the equation δ
˙
θ = Jδθ, linearizing our sys-
tem in the vicinity of the stationary state, δθ = ve
λt
.
Note, that λ < 0 by Lyapunov’s stability criterion and
that τ = 1/|λ|. Thus, small λ correspond to large τ,
nearly degenerate systems possess large delay time.
This gives an explanation not only for anomalously
large hysteresis in CV, but also for slow relaxation
to the stationary state in PC analysis and for strong
hierarchy in EIS spectra, mentioned in (Clees et al.,
2017). In Appendix we give an analytical estimation
of the hysteresis effect in linear approximation, show-
ing that the degenerate Jacobian indeed leads to the
large hysteresis.
A particular mechanism for origination of the stiff
system can be a presence of a reagent, weakly coupled
to the rest of reactions, i.e., all reactions involving this
reagent have small reaction constants. Although this
reagent is weakly coupled, it can occupy free surface
of the electrode and influence the dynamics through
θ
0
-variable, in this way producing hysteresis effect.
Looking on the reaction graph on Fig. 1, we see that if
this reagent is located in the main chain, such decou-
pling will break the oxidation process. This will pro-
duce the current in the range of microamperes, typical
for experimental measurements with pure KOH with-
out a fuel. To have simultaneously large current and
large hysteresis, the decoupled reagent must be lo-
cated in one of parallel branches of the reaction graph.
Four such places can be identified, shown by orange
frames on Fig. 1. Correspondingly, our search proce-
dure also finds four islands of solutions.
Fig.6 center shows the best match results with de-
coupled reagents CO
ad
(red solid line, scenario 1) and
COOH
ad
(green dashed line, scenario 2). Scenario 1
shows similarity with experimental CV shape, how-
ever, it possesses a sharp shoulder with rapid current
variation. This shape is also very sensitive to the vari-
ation of reaction constants. In scenario 2 the optimal
solution possesses less similarity with the experiment.
Fig.6 right shows the best match results with de-
coupled PtO in reactions r
11
(green dashed line, sce-
nario 3) and r
12
(red solid line, scenario 4). These
scenarios represent different mechanisms of platinum
oxidation and both have a good match with the ex-
periment. The smoother and better matching shape
corresponds to sequential mechanism in scenario 4.
Table 3 represents the best fit results for all four solu-
tions with their χ
2
. For reaction constants their loga-
rithms are given:
p
i
= log
10
(k
i
/[mol/(m
2
s)]). (7)
Fig.7 shows one more interesting result, found by
the search procedure. It shows the clouds of points
with χ
2
< threshold in projections to (k
1
,k
2
) and
(k
1
,k
11
) planes, in logarithmic scale. Straight lines,
visible on these plots show that χ
2
possesses sta-
ble minimum in perpendicular direction, but shallow
minimum along this line. In other words, the reac-
tion dynamics depends mainly on ratios k
2
/k
1
, k
11
/k
1
and only those ratios can be stably determined in the
experiment.
6 CONCLUSION
We have presented the methods for parameter identi-
fication in cyclic voltammetry of alkaline methanol
oxidation. The process involves 11 elementary re-
actions, 9 main reagents and is described by a sys-
tem of 6 non-linear differential equations. For pa-
rameter identification we use a combination of auto-
matic global optimization methods, traditional Monte
Carlo and interactive parameter study. Typically, the
integration of the system requires 0.5 sec on 3GHz
CPU. Automatic global optimization requires 5000 it-
erations and 35 min per solution. Monte Carlo gen-
eration of one population of 120000 points requires
6 hours and the related iterative algorithm requires 3-
5 such populations for convergence.
Parameter Identification in Cyclic Voltammetry of Alkaline Methanol Oxidation
285

Figure 6: Fitting results. On the left – a typical point with small hysteresis, in the center – optima for scenarios 1 (red solid)
and 2 (green dashed), on the right – optima for scenarios 3 (green dashed) and 4 (red solid).
Table 3: The results of the fit.
Log Constants Scenarios
1 2 3 4
p
0
1
0.00563922 -0.943937 -0.547725 0.0522747
p
0
−1
-6.79587 -4.02246 -3.94555 -3.94555
p
2
2.15543 1.49158 0.452275 0.752275
p
−2
2.17691 0.206631 0.512761 0.512761
p
3
0.867985 0.669569 4.74111 5.04111
p
−3
-6.98732 -3.55996 -3.01602 -2.61602
p
4
-6.0547 -1.42416 -0.126364 -1.12636
p
5
-6.80188 -0.920436 0.128806 0.128806
p
7
-0.680335 -2.95533 0.281251 0.281251
p
0
8
-4.45484 -6.6238 -3.64495 -2.64495
p
9
-7.0526 -6.47801 1.79963 1.79963
p
10
-2.57335 -12.2244 -1.31402 -1.51402
p
0
11
– – -4.04773 –
p
0
−11
– – -6.29566 –
p
0
12
– – – -4.84773
p
0
−12
– – – -6.09566
χ
2
/[A
2
] 0.000170361 0.00102207 0.000332658 0.000161844
As a result of our parameter study, we have found
4 optima corresponding to different mechanisms of
the underlying chemical process. All scenarios intro-
duce a reagent, weakly coupled to the rest of the re-
actions and differ by selection of this reagent. The
weakly coupled reagent has slow kinetics, on the
other hand it occupies free electrode surface and is
able to block the cell current. In this way it pro-
duces the hysteresis effect observable in experimen-
tal plots, being slowly accumulated in the increasing
voltage phase and slowly reduced in the decreasing
one. The weak coupling of the reagent is also respon-
sible for high condition number of the system matrix,
leading to slow convergence of experimental polariza-
tion curves and strong hierarchy of electroimpedance
spectra.
The best match for every scenario is presented and
the details of the related kinetics are discussed.
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
286

Figure 7: Correlation of parameters k
1
, k
2
and k
11
.
REFERENCES
Bard, A. J. and Faulkner, L. R. (2000). Electrochemical
Methods: Fundamentals and Applications. Wiley.
B
¨
ack, T. (1996). Evolutionary Algorithms in Theory and
Practice. Oxford University Press, New York.
Beden, B. et al. (1982). Oxidation of methanol on a plat-
inum electrode in alkaline medium: effect of metal
ad-atoms on the electrocatalytic activity. J. Electroan-
alytical Chem., 142:171–190.
Ciucci, F. (2013). Revisiting parameter identification in
electrochemical impedance spectroscopy: Weighted
least squares and optimal experimental design. Elec-
trochimica Acta, 87:532–545.
Clees, T. et al. (2014a). Focused ultrasonic therapy plan-
ning: Metamodeling, optimization, visualization. J.
Comp. Sci., 5(6):891–897.
Clees, T. et al. (2014b). Quasi-Monte Carlo and RBF Meta-
modeling for Quantile Estimation in River Bed Mor-
phodynamics. In Obaidat, M. S. et al., editors, Sim-
ulation and Modeling Methodologies, Technologies
and Applications, Advances in Intelligent Systems and
Computing 319, pages 211–222. Springer.
Clees, T. et al. (2017). Electrochemical Impedance Spec-
troscopy of Alkaline Methanol Oxidation. In Proc.
INFOCOMP 2017, The Seventh International Confer-
ence on Advanced Communications and Computation,
pages 46–51. IARIA.
Gamry Instruments (2018). Basics of Elec-
trochemical Impedance Spectroscopy.
http://www.gamry.com/application-notes/EIS/basics-
of-electrochemical-impedance-spectroscopy. Online
tutorial.
Griffiths, P. and de Hasseth, J. A. (2007). Fourier Transform
Infrared Spectrometry. Wiley-Blackwell.
Ilonen, J. et al. (2003). Differential Evolution Training Al-
gorithm for Feed Forward Neural Networks. Neural
Proc. Lett., 17:93–105.
Krewer, U. et al. (2006). Impedance spectroscopic analy-
sis of the electrochemical methanol oxidation kinetics.
Journal of Electroanalytical Chemistry, 589:148–159.
Krewer, U. et al. (2011). Electrochemical oxidation of
carbon-containing fuels and their dynamics in low-
temperature fuel cells. ChemPhysChem, 12:2518–
2544.
Mathematica 11 (2018). Reference Manual.
http://reference.wolfram.com.
Nikitin, I. et al. (2012). Stochastic analysis and nonlinear
metamodeling of crash test simulations and their ap-
plication in automotive design. In Browning, J. E.,
editor, Computational engineering: design, develop-
ment, and applications, pages 51–74. Nova Science.
Otten, R. H. J. M. and van Ginneken, L. P. P. P. (1989). The
Annealing Algorithm. Kluwer.
Press, W. H. et al. (1992). Numerical Recipes in C: Chap.
15. Cambridge University Press.
Strutz, T. (2016). Data Fitting and Uncertainty: A practi-
cal introduction to weighted least squares and beyond.
Springer.
W
¨
achter, A. and Biegler, L. T. (2006). On the implemen-
tation of an interior-point filter line-search algorithm
for large-scale nonlinear programming. Mathematical
Programming, 106:25–57.
APPENDIX: LINEAR ESTIMATION
OF HYSTERESIS EFFECT
Consider a system of differential equations:
C
act
θ
0
= f (θ,η) (8)
in the limit C
act
→ 0. In this way we emulate the sys-
tems with small delay time τ = C
act
/k → 0.
The solution is located in the vicinity of the sta-
tionary curve
f (θ
∗
,η) = 0, (9)
where both θ
∗
and η depend on t. After differentia-
tion, we have
Jθ
∗
0
+
∂ f
∂η
η
0
= 0, J =
∂ f
∂θ
. (10)
Further, in linearized equations
C
act
(θ
∗
0
+ δθ
0
) = f (θ
∗
,η) +Jδθ, (11)
omitting small δθ
0
term and using (9) and (10), we
have
δθ = −C
act
J
−2
∂ f
∂η
η
0
. (12)
Substituting it to the linearized expression for current,
we obtain
δI =
∂I
∂θ
T
δθ = (13)
−C
act
∂I
∂θ
T
J
−2
∂ f
∂η
η
0
.
Parameter Identification in Cyclic Voltammetry of Alkaline Methanol Oxidation
287

As a result, we see, that a deviation of current from the
stationary curve changes sign with η
0
, i.e., possesses
the hysteresis effect. In general position, the vectors
on the left and on the right of J
−2
in (13) do not co-
incide with annulators of Jacobian, i.e., its left and
right eigenvectors with tending to zero eigenvalue. In
this case, the amplitude of hysteresis effect tends to
infinity, in the limit when the Jacobian becomes de-
generate:
detJ → 0, δI → ∞. (14)
This condition can be used only as an indicator of
hysteresis effect. With increasing δI, one will need
to apply the next order corrections to approximate its
value.
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
288
