
Can Artificial Potentials Suit for Collision Avoidance in Factory Floor?
A Case Study of Harmonic Machine-machine Coexistence
Josias G. Batista
1
, Jos
´
e L. N. da Silva
1
and George A. P. Th
´
e
2
1
Instituto Federal de Educac¸
˜
ao Tecnol
´
ogica do Cear
´
a, av. 13 de Maio 2081, Fortaleza, Brazil
2
Department of Teleinformatics Engineering, Federal University of Ceara, Fortaleza, Brazil
Keywords:
Path Planning, Machine-machine Interaction, SCARA Manipulator.
Abstract:
Despite the existence of well-known approaches for collision prevention in the robotics literature, in present
days the use of manipulators in fabrication processes still relies on safe-zone delimitations, which ultimately
limits automation flexibility. In the present work, we consider going over that paradigm by discussing what if
mobile agents of the fabrication process, i.e., robots could share the same space. In doing that study, the very
classical approach based on artificial potentials for collision prevention are preferred over modern choices. On
the basis of a hypothetical pick-&-place task experiment, results revealed efficient accomplishment in some of
the considered scenarios.
1 INTRODUCTION
In modern production processes the deployment of ro-
bots in semi- or fully-automatized taks assumed an
important and strategic role for industry; recent re-
ports from the International Federation of Robotics
estimate something over 250 thousands new units of
industrial robots worldwide only in 2015 (IFR, 2017).
Typically, industrial robots operate inside proper cells
in classified areas designed to provide adequate sepa-
ration between men and machines; it is also recom-
mended the use of sensors for human-presence de-
tection as well as switching-off mechanism in case
of cell invasion by persons. It is to be stressed the
economical consequence of it, since interrupting the
process may cause delays and bring additional pro-
duction costs.
From the point-of-view of increasing flexibility le-
vel of automation, it would be good thing if those
strict recommendations for robot cells could be revi-
sited and production machines and other agents were
let free to share the factory floor aided by techni-
ques for preventing collisions and process interrupti-
ons as well. This issue may be regarded as a machine-
machine coexistence problem and it is a challenging
one if no previous information about dimension and
shape of the agents is given as well as the agents are
allowed to move arbitrarily in that space, as illustra-
ted in Figure 1. To cover with the need for a non-stop
production, an intelligent robot-assisted automation
system should therefore conjugate real-time obstacle
detection and collision avoidance algorithms.
Figure 1: Various robots sharing workspace.
In the literature, the paradigm of machine-
machine interaction is usually presented as coopera-
tive robotics, in which agents has a common task to
accomplish (Habib, 2014) or, in the context of as-
sistive robotics, in which robots interact to anticipate
human actions thus offering them some kind of assis-
tance like, for instance, in helping at opening a door,
taking up objects, etc (Koppula and Saxena, 2016).
Also interesting is the context of competitive robotics,
in which machines interact as opponents (Pinto et al.,
2016) or more simply in situations of conflicting inte-
rests (e.g., those of workspace superposition) (Gayle
et al., 2007).
Batista, J., Silva, J. and Thé, G.
Can Artificial Potentials Suit for Collision Avoidance in Factory Floor? - A Case Study of Harmonic Machine-machine Coexistence.
DOI: 10.5220/0006832405470556
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 547-556
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
547

Right in this context the present research is fo-
cused: it brings to light a hypothetical automatized
production process in which mobile robots and ma-
nipulators are the agents having conflicting tasks by
discussing how the machine-machine interaction can
be driven towards more efficient and productive pro-
cess (Moellmann et al., 2006). The scenario consi-
dered here is the one illustrated in Figure 1: two au-
tomatic machines with overlapping workspaces share
a given region of the factory floor and have to deal
with the possibility of iminent collision; the mani-
pulator is doing a pick-and-place task, whereas the
wheel-drive robot is on some transport task in non-
constrained route. The more collisions occur, clearly
the more the robots will limit the efficiency of the pro-
ductive process they are engaged in, because the ti-
ming and productivity metrics for performance evalu-
ation will suffer from non-scheduled stops. Collisions
are therefore to be avoided undoubtedly; nothing new.
What is not known in advance and appears as open is-
sue in this hypothetical experiment is the amount of
influence the chosen strategy for collision avoidance
may have on the on-going production. First of all,
are the classical approaches for collision avoidance of
robots viable for real-time navigation in the conside-
red emulated production scenario? If so, under which
assumptions and operating (or even modelling) con-
straints? Then, how can we quantify the influence the
chosen collision prevention strategy has on the task
assigned to the robot? Is there any measure from the
scientific community to be used as indicator of the just
mentioned quantity? Any opportunity for new mea-
sure or even a figure-of-merit?
Purpose of this paper is to address these questi-
ons through the use of classical approaches in robotics
and traditional concepts from production engineering.
On one side, concerning the strategy for collision pre-
vention, in this study artificial potential fields was pre-
ferred over geometric search approach for its simpli-
ficity and popularity as the literature review reveals.
On the other side, to evaluate task accomplishment, it
was adopted an indicator named Overall Equipment
Efficiency, which takes into account availability, qua-
lity and performance itself of a given machine.
The remainder of the paper is organized in the fol-
lowing sections: after a literature review about the
employment of artificial potential field methods for
path planning in robotics, section 3 presents the the-
oretical ingredients such as the manipulator kinema-
tics, the adopted Fuzzy controller design, the basics of
artificial potentials, as well as the metrics used to as-
sess the efficiency of the transport task studied here.
Section 4 contains the results and respective discus-
sion, which are followed by conclusions.
2 LITERATURE REVIEW
Artificial potential field (APF) methods are very clas-
sical choice for reactive path planning of robots de-
aling with moving obstacles; originally proposed in
(Khatib, 1986) for collision avoidance of manipula-
tors and mobile robots as well, it is still very popular
because it is fast, simple and mathematically elegant
(Mora and Tornero, 2008), though it suffers from im-
portant limitations, such as the existence of local mi-
nima.
Despite its original use for path planning of ma-
nipulators, many sub-areas of the robotics commu-
nity benefited from APF methods so far. In the work
of (Mac et al., 2016), for example, APF was cho-
sen to address path planning of unmanned aerial vehi-
cles (UAV) under obstacle avoidance constraint, and
in (Budiyanto et al., 2015) APF for UAV flight was
preferred over laser scanning, computer vision and
global positioning system based approaches. Under-
water robotics was addressed by (Cheng et al., 2015);
a new best-route strategy for unmanned robot navi-
gation was designed from a velocity synthesis algo-
rithm relying on APF based collision prevention. Aut-
hors in (Wang et al., 2015), in turn, combined APF
and grid map method to design free-collision routes
for mobile robot as a way to prevent trapping at lo-
cal minima, whereas (Chatraei and Javidian, 2015)
used APF for generating the path used as input of
the Fuzzy-Mandani position and orientation control-
ler of a mobile robot. Still in the sub-field of mo-
bile vehicles, the interesting work of (Galceran et al.,
2015) brought a car equipped with APF based trajec-
tory generator able to deviate from static and moving
obstacles in a real road. Concerning manipulators,
APF was successfully used for static obstacle colli-
sion avoidance in (Hargas et al., 2015), for preventing
contact with moving obstacles in (Guan et al., 2015;
Ataka et al., 2016; Badawy, 2014) and also for sur-
gery assistance in dental implants (Yu et al., 2015b;
Yu et al., 2015a).
It is interesting that the above presented review of
recent research did not consider any issues regarding
a typical industrial environment in the studies, though
we know it is the main destination of most manipula-
tors deployed nowadays; this lack of discussion is one
of the motivations for the present study.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
548
3 THEORETICAL BACKGROUND
3.1 Overall System View
The overall system view is shown in the diagram il-
lustrated in Figure 2. Starting from top-view image
acquisition by a PMD 3D Effector camera from ifm
electronic gmbh
c
and some digital image processing
techniques in a computer, the obstacle is identified in
a given scene and represented as circle object. Then,
the region it occupies in cartesian space is mapped to
generate the prohibited configuration space, thus al-
lowing the use of APF to find a free-collision path to
the goal point. A smooth trajectory is then calculated
and sent via OPC communication link to the Fuzzy
controller embedded in the PLC for driving the mo-
tors accordingly. This is repeated until goal point is
reached by the manipulator end-effector.
The industrial robot used in this experiment is a
retrofitted 4-DOF SCARA, from Toshiba
c
, whe-
reas the robot playing the role of moving obstacle is
a Zumo Robot from Pololu Robotics and Electronics
c
. The PLC is a TwidoSuite from Schneider Electric
c
.
Figure 2: Overall view of the closed-loop system.
3.2 Manipulator Kinematics
In the experiments to be discussed next, only planar
movements were investigated. This was due to lack of
enough driving units for the whole set of 4 joint mo-
tors, what limited the path planning to 2D space only.
However, for completeness, in the following the full-
set of Denavit-Hartenberg (DH) parameters for direct
kinematics, as well as the equations for inverse kine-
matics are reported.
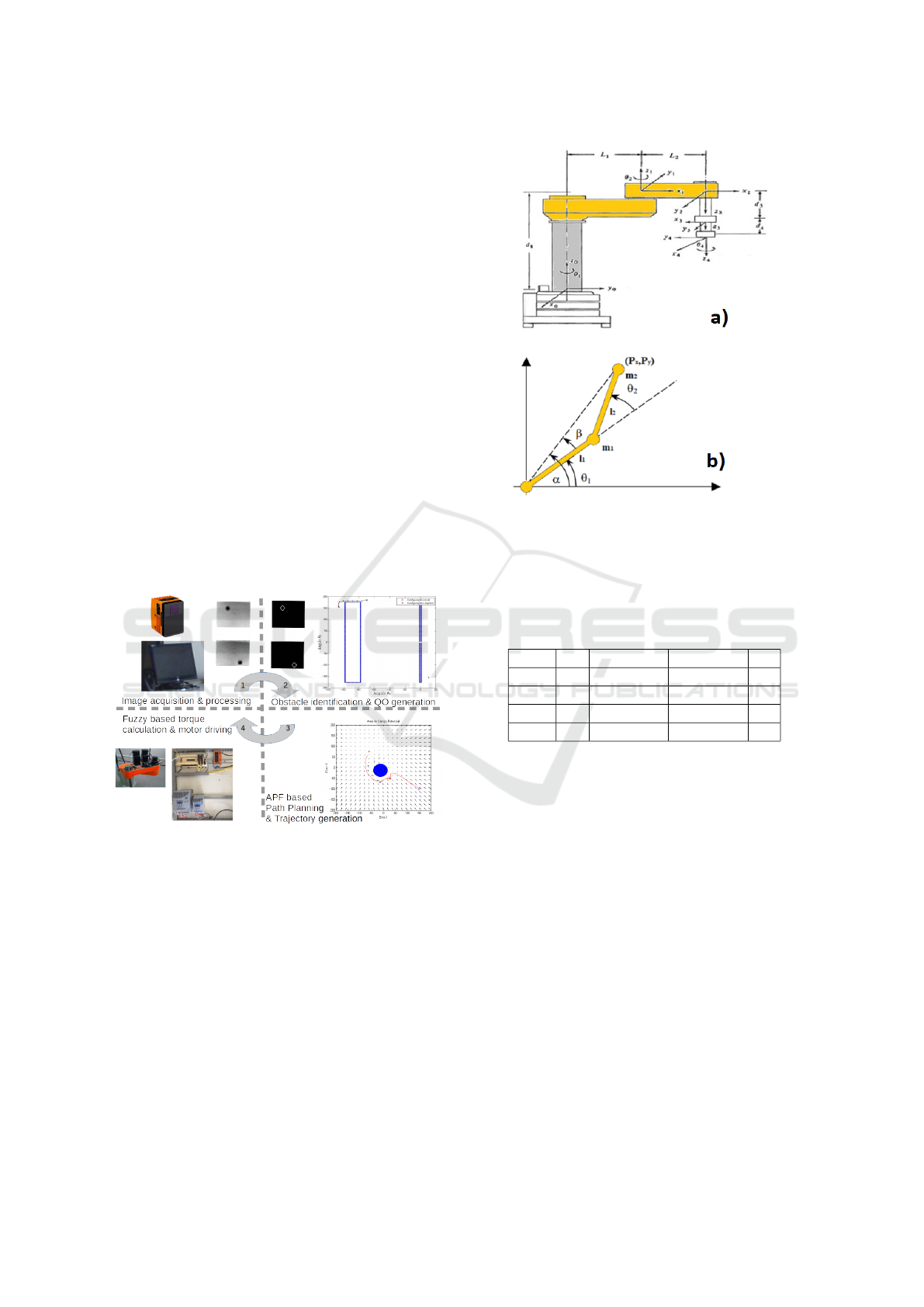
Figure 3 shows the various robot parameters and
frame assignment according to DH convention. As
seen in the illustration, joints 1, 2 and 4 are rotatio-
nal, whereas joint 3 is a prismatic one. Table 1 brings
Figure 3: Illustration of the SCARA manipulator: a) with
assigned references frames; b) in-plane projection of prin-
cipal revolute joints.
the values of the whole set of parameters needed for
deriving kinematic equations.
Table 1: DH parameters of the manipulator.
Axis θ
i
d
i
a
i
α
i
1 θ
1
d
1
= 0.32 L
1
= 0.35 0
2 θ
2
0 L
2
= 0.30 π
3 0 d
3
0 0
4 θ
4
d
4
0 0
The adopted convention and the above parameters
allow for obtaining the homogeneous transformation
matrix relating initial and final frames as:
T =
S
4
S
12
+C
4
C
12
S
4
C
12
+C
4
S
12
0 T
14
S
4
C
12
+C
4
S
12
−S
4
S
12
+C
4
C
12
0 T
24
0 0 −1 T
34
0 0 0 1
,
(1)
where : S
12
= sen(θ
1
+θ
2
) , C
12
= cos(θ
1
+θ
2
), T
14
=
l
1
C
1
+l
2
C
12
, T
24
= l
1
S
1
+l
2
S
12
and T
34
= d
1
−d
3
−d
4
.
3.3 SISO Closed-loop Fuzzy Control
Manipulators driven by electric motors usually counts
on reduction gears based transmission system to im-
prove torque and for reducing speed. If on one side
it raises costs, the amount of parts and the rotating
inertia, on the other side it may lead to improved po-
sitioning since the links can undergo displacements of
Can Artificial Potentials Suit for Collision Avoidance in Factory Floor? - A Case Study of Harmonic Machine-machine Coexistence
549
small magnitude. As discussed in (Spong, 2006), ma-
nipulators having that driving characteristic may be
treated as a SISO system since the gear ratio, β be
among 20 and 100, in such a way that load inertial ef-
fects may be neglected, thus allowing for independent
control (Mittal and Nagrath, 2003). For the manipula-
tor of the present work, whose actuating units are ba-
sed on permanent magnet electric motors with no slip,
an experiment was performed to estimate the gear ra-
tios at the joints, β
1
and β
2
. By setting the frequency
inverter to3 Hz, the time required for the joint to com-
plete a 90
o
rotation was recorded and the number of
revolutions of the motor axis was estimated (see, for
instance, (Fitzgerald et al., 2014)), thus yielding the
ratios presented in Table 2. In the table, the symbol #
stands for “the number of revolutions of”.
Table 2: Data collected from gear ratio estimation.
Joint Time #Motor #Joint β
1 13.35 20.025 0.25 β
1
= 80.1
2 8.60 12.897 0.25 β
2
= 51.6
The above calculated gear ratios justify the adop-
tion of joint independent control, and then a SISO
zero-order Takagi-Sugeno Fuzzy controller was de-
signed for each joint (Farooq et al., 2011). The only
reason for adopting this strategy instead of classical
PID or even hybrid PID-Fuzzy is that in our preli-
minary studies, the proposed Fuzzy-TS showed to be
superior in accuracy and repeatability measurements
done according to (ISO, 1998). For what concerns the
controller design itself, most of it relied on theoretical
concepts as well as authors’ experience in manipula-
tor control and agreed with the independent work of
(Nawrocka et al., 2014). As input variables, the joint
position error was calculated from the difference be-
tween desired and measured angular position; it was
limited to the interval [-30;30] in units of internal CLP
memory, what means [-2.63
o
; 2.63
o
]. Those values
are in accordance with the positioning-task purpose
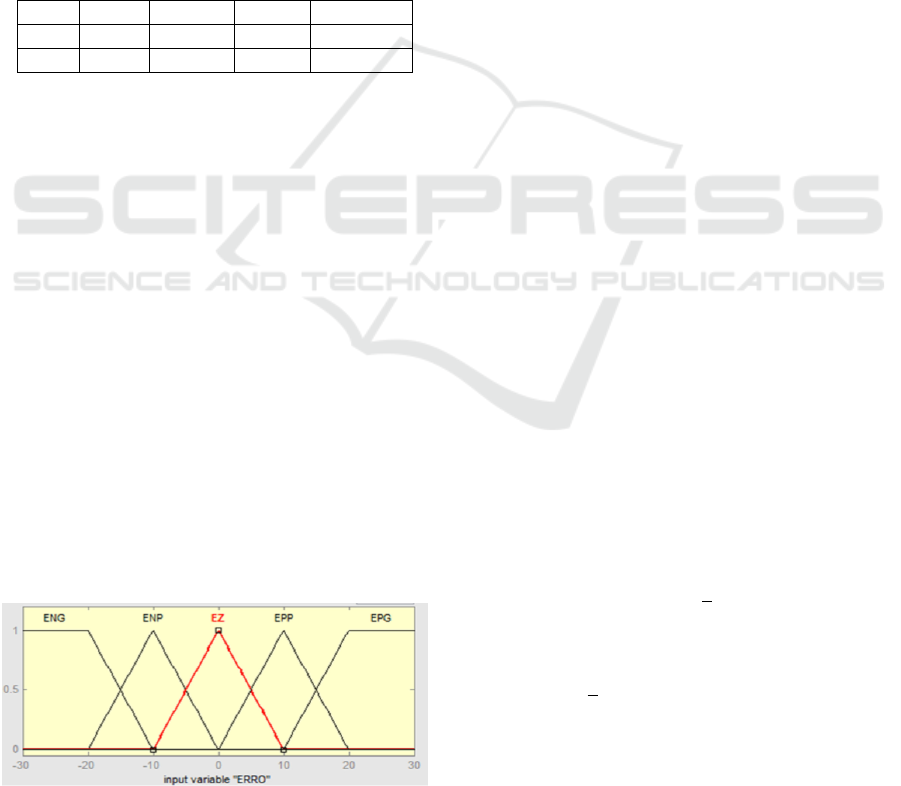
of this experiment. The error fuzzy variable following
the defuzzying step is defined from five membership
functions, chosen among trapezoidal- and triangular-
like choices as represented in:
Figure 4: Adopted membership functions for input variable
error.
The choice for these simples functions is due to
the limited programming resources in the PLC availa-
ble to host the Fuzzy controller. In addition, the sym-
metry around the origin as well as the 50% overlap
among adjacent functions makes simpler the ladder
enconding of the proposed controller, since the deno-
minators at the defuzzying step get to unity while fa-
vouring the triangle functions to be replaced by linear
parts (Simoes and Shaw, 2007).
Concerning the output variable generated by the
Fuzzy controller, the following constants are defined:
K1=-10, K2=-5, K3=0, K4=5 e K5=10; they respecti-
vely encode the fuzzy variables TNG, TNP, TZ, TPP,
TPG. The interval [-10;10] for the output is associ-
ated to the 0-10V analog range of the PLC output
used to for motor driving, with positive or negative va-
lues yielding clockwise or anticlockwise rotation di-
rection, respectively. The adopted interval also pre-
vents actuator saturation. Finally, five very simple
fuzzy rules were adopted for the position control task:
If EPG then TNG; If EPP then TNP; If EZ then
TZ; If ENP then TPP; If ENG then TPG;
3.4 Integration of APF to the Control
System
In a few words, artificial potential field method for
free-collision robot motion relies on the existence of
artificial repulsive potential fields caused by obsta-
cles, U
rep
(q), and artificial attractive potential field
centered at the target (final) position, U
att
(q), guiding
the robot according to the experienced virtual force:
F(q) = −∇U(q), (2)
where
U(q) = U
rep
(q) +U
att
(q). (3)
Usual choices for these potential consider functi-
ons having first derivative continuous and smoothly
changing. In the experiments reported here, the at-
tractive potential was built by combining the conical
and parabolic functions (Volpe and Khosla, 1990):
U
atr
(θ) = dK
a
k θ − θ
f
k −
1
2
d
2
K
a
: k θ − θ
f
k> d,
(4)
U
atr
(θ) =
1
2
K
a
k θ − θ
f
k
2
: k θ − θ
f
k≤ d, (5)
where K
a
is a constant, θ is the joint position at a
given time instant and θ
f
is the desired joint position
at the goal point; d defines the transition limit between
conical and parabolic actions. The parameters are set
K
a
= 1 and d = 2cm in the experiments reported here.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
550

The repulsive potential, in turn, resembles the fol-
lowing flat-sided function:
U
rep
(θ) =
1
2
K
r
[
1
p(θ)
−
1
p
]
2
: p(θ) ≤ p, (6)
U
rep
(θ) = 0 : p(θ) > p, (7)
in the above equations, K
r
is a constant, p(θ) re-
presents the minimal distance between the joint posi-
tion , θ, and the whole configuration space of a given
obstacle, QO. At last, p defines a limit line in configu-
ration space where the robot can not feel the presence
of that obstacle.The parameters are set K
r
= 5000 and
p = 2cm in the experiments reported here.
The present implementation of the APF in the pre-
sent work counted on the use of an image sensor for
continuous capture of the scene; this allowed, in turn,
for the calculation of the QO-space in continuous ope-
ration and the generation of free-collision paths. To
calculate the QO-space, an image processing algo-
rithm was developed for detection and localization of
the wheeled robot; robot speed was limited to miti-
gate the effects of the delay between wheeled robot
detection and the manipulator decision on movement
update. Clearly, the events define the time window
in which the artificial potential field estimates a free-
route.
As it will become clearer in section 3.5, this im-
plementation of APF considered different levels of
description for the manipulator and for the wheeled
robot, namely as a point or an extended body. For
what concerns the manipulator, considering it as a
point has the consequence of applying APF equations
for repulsive field between the end-effector only and
the obstacle, whereas when taken as a body, the re-
pulsive potential accounts for the interaction between
the obstacle and many different points throughout the
arm (known as control points).
Things are similar for wheeled robot: when taken
as a point, the repulsive potential is calculated accor-
ding to its distance to the manipulator end-effector (if
this is taken as a point) or to the various control points.
On the other side, if the wheeled robot is regarded as
a body, a line circle centered at its centroid coordina-
tes plays the role of obstacle and, hence, spatial sam-
pling along this line defines several control points, as
well. This ultimately augments the obstacle space,
since each of the control points now work as a diffe-
rent obstacle.
From this discussion, it should be clear that the
APF computation is highly demanding in the body-
body scenario mentioned latter in this paper.
3.5 Investigated Scenarios
Eight scenarios were designed to study the hypothe-
tical transport experiment reported in this paper. To
compose this set of scenarios two main reasoning li-
nes were followed; one of them regards the geometry,
i.e., the dimensions of both robots, whereas the other
is about the accomplishment of the task itself.
The APF was originally conceived for automatic
motioning in which the mobile robot is generally ta-
ken as a point. Same story for the manipulator; usu-
ally the end-effector is the only portion of the robot
subject to the potential fields. But what if they are
treated as extended bodies, i.e., their actual dimensi-
ons are not neglected? Roboticists know that the com-
plexity of APF algorithm grows with the definition of
control point along the manipulator open-chain and
with the number of contact points in the surface of an
obstacle (or, similarly, with the amount of them).
The other issue regards the accomplishment le-
vel of the transport mission: is position uncertainty
acceptable in placing task? Although precision robo-
tics is a very attractive field in its own, many industrial
processes do not impose strict constraints for position
or orientation of objects; therefore, reaching a zone
instead of a specific location may suffice sometimes.
Those arguments were essential to propose the
methodology adopted so far; on one hand, it consists
of describing the robots as a point (P, for short) or as
an extended body (B, for short), thus giving 4 com-
binations for the couple (manipulator robot, wheeled
robot): (P,P); (P,B); (B,P); (B,B). On the other hand,
for what concerns the task itself, two missions were
considered according to the degree of task accom-
plishment: mission-T (target) and mission-Z (zone).
By mission-T it is meant the manipulator task which
requires the object be placed at a specific point at the
goal, whereas the mission-Z is less restrictive in the
sense that the object may be left in the vicinity of the
goal position (10 cm around the goal was adopted in
the experiments).
3.6 Measuring Task Efficiency
To assess the efficiency of the manipulator in repe-
atedly doing the hypothetical pick-place task illustra-
ted in Figure 1, the eight scenarios just described were
investigated. On doing that, two measures have been
considered to quantify the efficiency of the repetitive
pick-place, which will be described in the following.
3.6.1 Proposed Efficiency
In order to quantitatively assess the efficiency of the
robotic system in the pick-&-place task, we proposed
Can Artificial Potentials Suit for Collision Avoidance in Factory Floor? - A Case Study of Harmonic Machine-machine Coexistence
551

a simple equation taking into account the productivity
itself, the variability of time elapsed in each repetition
of the task and the amount of collision events as well.
This function is a figure-of-merit and works somehow
as an indicator of the influence of the APF method on
the considered hypothetical process, and that is why
it is named efficiency, η. The proposed efficiency is
proportional to what we call productivity and inver-
sely proportional to the variance of the elapsed time
and to the number of collisions, according to:
η =
P
rod
σ
temp
N
col.
, (8)
where P
rod
is the productivity, which means the
number of times the mission was successfully com-
plete, i.e., the transport from origin to goal did not
suffer any collision, σ
time
is the variance of the time
spent in every repetition of the transport and N
col
is
the amount of collisions recorded.
3.6.2 Overall Equipment Effectiveness
Although its simplicity, the proposed formula for task
effiiciency is not usual in industry. More adequate
is the use of measurements derived from the total
productive maintenance (TPM), originally developed
in Japan for preventing wastes and reducing non-
programmed stops, thus ensuring quality and cost
save in continuous processes. One example is the
Overall Equipment Effectiveness (OEE) (Kennedy,
2017), which is a measure of manufacture systems
for equipment evaluation relying on its performance,
availability and quality. In the following it is dis-
cussed how to interpret the hypothetical pick-&-place
problem in order to measure the robotic system effi-
ciency using this OEE concept.
Availability: its a percentage of the time spent
in effective working condition compared to the total
time available for operation, and is calculated as it fol-
lows:
A
vail
(%) =
T TD − PP −PNP
T T D − PP
∗ 100, (9)
where TDD is the total time available for opera-
tion, PP is the time reserved for programmed stops
and PNP is the time spent in non-programmed stops.
In the experiments reported in this work, we conside-
red no programmed stops at all; in addition, we asso-
ciate the non-programmed stops to the interruptions
due to collision prevention actions of the manipulator
or to some set-up adjustment. Then, to calculate the
availability, TDD and PNP were both recorded.
Performance: it consists in a relation between
the quantity of parts really produced by the machine
and the expected amount, when considering the cycle
time. In other words, it measures the production rate
of a given equipment, and is calculated as it follows:
P
er f
(%) =
T EO
TO
∗ 100, (10)
where TEO is the operating effective time and TO
is the operating time. To calculate the performance
in the present work, we considered TO as the time
in which the manipulator was in movement, since the
operation here is regarded as transport rather than fa-
brication itself; the other parameter, TEO, was com-
puted also as a time-in-movement parameter, but pro-
vided exclusion of unsuccessful mission repetitions
(e.g., with collision events).
Quality: it refers to the existence of defective
products ultimately resulting in rejection or rework.
Since in the experiments we have done so far there is
no fabrication at all, we considered the quality, Q
uali
at 100% in equation 11 below.
OEE indicator: it is expressed as the product of
the three metrics just defined according to
OEE(%) = A
vail
∗ P
er f
∗ Q
uali
∗ 100 (11)
3.7 Required Energy Estimation
Also the torque and required energy were estimated in
the various tests performed. A look at the energy con-
sumption is important because it may influence the
decisions at the factory level. As any problem in en-
gineering, it is pursued a good trend between the be-
nefits of new approaches for manufacturing and the
additional costs brought. This could help answering
the following questions: a) can the factory afford the
adoption of an automatic collision avoidance system?
Is the raising of energy costs acceptable? Is the pro-
ductivity increase worth the rise of energy consump-
tion?
In doing this analysis, it has been seen that joint
1 showed superior power demand respect to joint 2.
For this reason, in the tables reporting those quan-
tities, only joint 1 numbers will be presented. Tor-
que and energy calculations followed the approach of
(Fitzgerald et al., 2014) and will be summarized in the
following.
Initially, we take an estimation of the torque at
joint motor 1, T
m1
from:
T
m1
= 9.55
P
m1
N
m1
, (12)
where P
m1
is the nominal power in W coming from
plate specifications and N
m1
is the rotating speed in
min
-1
. The values for rotating speed were obtained
from the PLC output sent to the frequency inverter
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
552
driver. Since this is a permanent magnet synchrou-
nous motor, it shows no slip and, as such, its rotating
speed can be determined from:
N
m1
=
120 f
P
, (13)
where f is the frequency inverter driver output and
is measured in Hz, whereas P is the number of poles.
Solving equation 12 for the developed power and
using the derivative of angular position at joints as a
measure for the rotating speed, one can use the follo-
wing equation to estimate the power in kW:
P
m1
=
T
m1
V
m1
9549.2965
, (14)
where T
m1
comes from equation 12 and V
m1
is the
estimation for the joint 1 rotating speed from encon-
ders. The required energy, E, can then be estimated
by integrating the developed power over time, P
m1
:
E =
n
∑
i=1
(P
m1i
t
i
). (15)
4 RESULTS AND DISCUSSION
For every scenario described in section 3.6, they were
recorded the number of mission repetitions and re-
spective elapsed time, amount of collision events,
number of interruptions due to collision prevention
and the number of accomplished missions (producti-
vity). Those quantities were then used to calculate
the task efficiency according to the formulae presen-
ted earlier are reported in Table 3. It is worth menti-
oning that also the time spent during the interruptions
for preventing collisions were recorded.
A look at the table reveals that the scenario (P;B)
led to better productivity and less collisions for both
missions considered. Also interesting to note that no
manipulator stop was observed. The scenario (B;B)
instead led to low productivity, though only one col-
lision event has occurred; interestingly, there were
events of manipulator stops to avoid collision, though
the mission was not accomplished in those rounds.
This may be connected to the artificial potential field
method: since the manipulator is here a extended-
body, the obstacle configuration space gets larger, and
hence the algorithm can not find a free-space towards
push the manipulator to end the mission. For what
concerns the efficiency of task accomplishment, re-
sults reveal that in the scenarios considering the ma-
nipulator as extended-body the efficiency falls; we as-
sociate this to the same lack of free-space just discus-
sed.
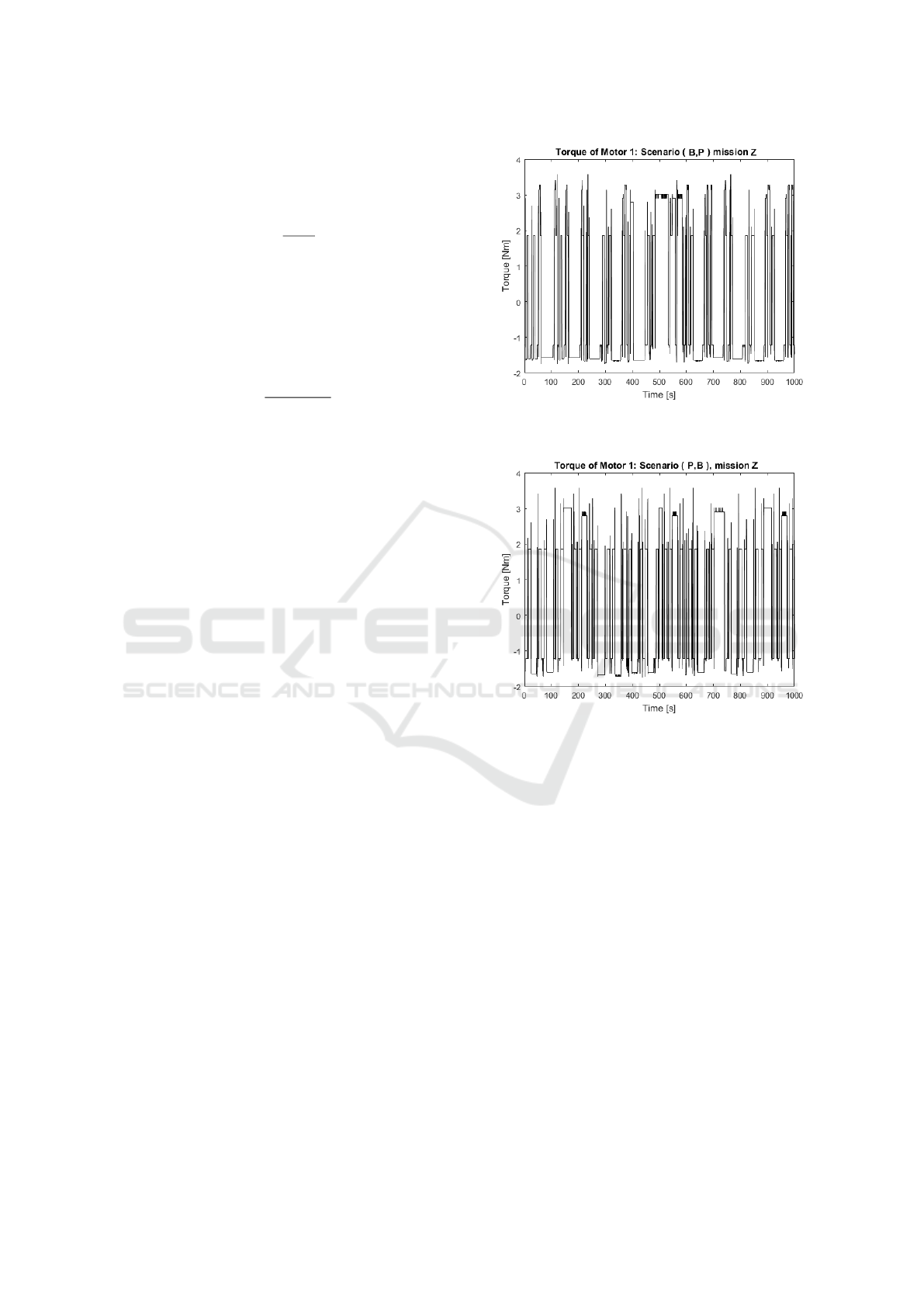
Figure 5: Time-series for motor 1 torque [Nm] in scenario
(B,P), mission-Z.
Figure 6: Time-series for motor 1 torque [Nm] in scenario
(P,B), mission-Z.
In the scenario (P;P) the manipulator is again re-
garded as a point, but, this time, collision events raise.
This is because in this scenario also the obstacle is
considered as a point, what means that the repulsive
field pushing the manipulator away is weaken. This
ultimately led to low task efficiency.
Using now the OEE indicator as efficiency mea-
sure, we could see that results agreed. The scena-
rio (P;B) reached 67.47% and 67.82% for missions-T
and -Z, respectively. We believe the tiny advantage of
mission-Z is because it imposes less constraints to the
artificial potential field method, speeding up the pro-
cess as whole. According to (Kennedy, 2017), those
numbers fall withing the interval [65% - 75%] for the
OEE, making them acceptable, though the universal
recommendations point to 85% as a goal.
Switching the attention to the required energy, re-
sults in the table show more demand in the scenario
(P;B) for both missions. We associate this to the mo-
tor excitation along time, as reported in Figures 5 and
Can Artificial Potentials Suit for Collision Avoidance in Factory Floor? - A Case Study of Harmonic Machine-machine Coexistence
553

Table 3: Summary of experimental results in the different scenarios evaluated.
Scenario
Mission-T
Trials Time [s] Bumps
P
rod
Stops η σ
t
A
vail
P
er f
OEE
[%]
Energy
[kW h]
(B,B) 27 182.42 3 20 4 1.333 4.989 59.08 74.92 44.27 0.0041
(B,P) 29 171.04 6 18 5 0.704 4.258 60.00 70.84 42.71 0.0032
(P,B) 36 230.36 5 31 0 8.324 0.744 76.99 87.64 67.47 0.0058
(P,P) 35 198.17 6 29 0 3.491 1.384 42.17 88.37 37.27 0.0042
Scenario Mission-Z
(B,B) 32 207.96 1 27 4 6.921 3.901 40.62 88.95 36.13 0.0037
(B,P) 29 146.70 3 23 3 5.614 1.365 56.62 84.16 47.65 0.0021
(P,B) 35 213.22 3 32 0 12.465 0.855 73.36 92.44 67.82 0.0051
(P,P) 35 210.92 7 28 0 3.303 1.210 73.04 85.07 62.14 0.0040
Table 4: Statistics of the error between desired and real joint
positions.
Scenario
Mission-T
Mean (std dev)
joint 1
Mean (std dev)
joint 2
(B,B) 3.100 (± 1.017) 2.979 (± 0.995)
(B,P) 0.975 (± 1.677) 3.280 (± 1.159)
(P,B) 1.086 (± 1.360) 4.568 (± 1.899)
(P,P) 1.458 (± 0.985) 4.090 (± 2.593)
Scenario Mission-Z
(B,B) 3.177 (± 1.027) 3.503 (± 1.052)
(B,P) 0.692 (± 1.200) 3.009 (± 1.158)
(P,B) 1.167 (± 1.209) 4.037 (± 2.408)
(P,P) 1.592 (± 1.396) 4.382 (± 2.470)
6: more inversion peaks means clearly that the motor
worked harder, thus leading to high productivity. We
can therefore state that higher productivity and bet-
ter efficiency led to high energy demand. The authors
found this discussion relevant because it links the path
planning problem, which is a robotic one, to the ma-
chine maintenance issue. Indeed, higher motor exci-
tation implies higher acceleration and breaking levels
during task operations. This analysis should ultima-
tely influence the choice among the scenarios consi-
dered in the study.
Finally, we have studied the performance of this
hypothetical pick-place system at low level, i.e., at the
level of trajectory-following in configuration and in
cartesian spaces. The goal here is to check how good
was the designed controller in following the path cal-
culated by the trajectory planner. In other words, we
check here the difference (or error) between the desi-
red and measured values of the joint angular position
along time during the robot operation. Table 4 brings
the average error and its standard deviation for every
scenario considered so far.
For better comprehension, we emphasize that er-
ror measures were calculated over time within a gi-
ven mission, and then over different mission repetiti-
ons. In other words, every time the manipulator star-
ted a transport mission from origin to goal position,
the measured and desired joint position were used to
create a time-vector of residuals. Then, average was
calculated from it, and finally this number was recor-
ded. Successive repetitions of the pick-&-place mis-
sion gave rise to a new error outcome. After several
mission repetitions, the statitics presented in Table 4
were available.
To illustrate the performance of the designed
Fuzzy controller when aided by the path-planner ba-
sed on artificial potentials, we chose two antagonic
scenarios concerning the productivity tooking care to
consider different missions. In Figures 7 and 8 we
plot, in cartesian space, the desired and real paths at
different moments of the pick-&-place task. The sce-
narios considered in this part of the experiment were
(B;P) mission-Z in Figure 7 as a low-productivity
sample, and (P;B) mission-T in Figure 8 as a high-
productivity sample. Unlike the analysis of producti-
vity, here the scenario (B;P) showed superior perfor-
mance, revealing that high productivity comes at the
expense of innacurate trajectory-following.
5 CONCLUSIONS
In the present work a hypothetical production pro-
cess with non-cooperative machine interaction was
studied. Based on classical approaches, it consis-
ted in providing a SCARA manipulator with the abi-
lity to prevent collisions in a workspace co-shared by
a wheeled robot following random navigation, thus
emulating what could be referred as conflicting tasks.
Main goal of the study was to check the conditions for
safe co-existence yet guaranteeing efficient task ac-
complishment. For that end, different scenarios were
considered and different metrics for task efficiency
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
554
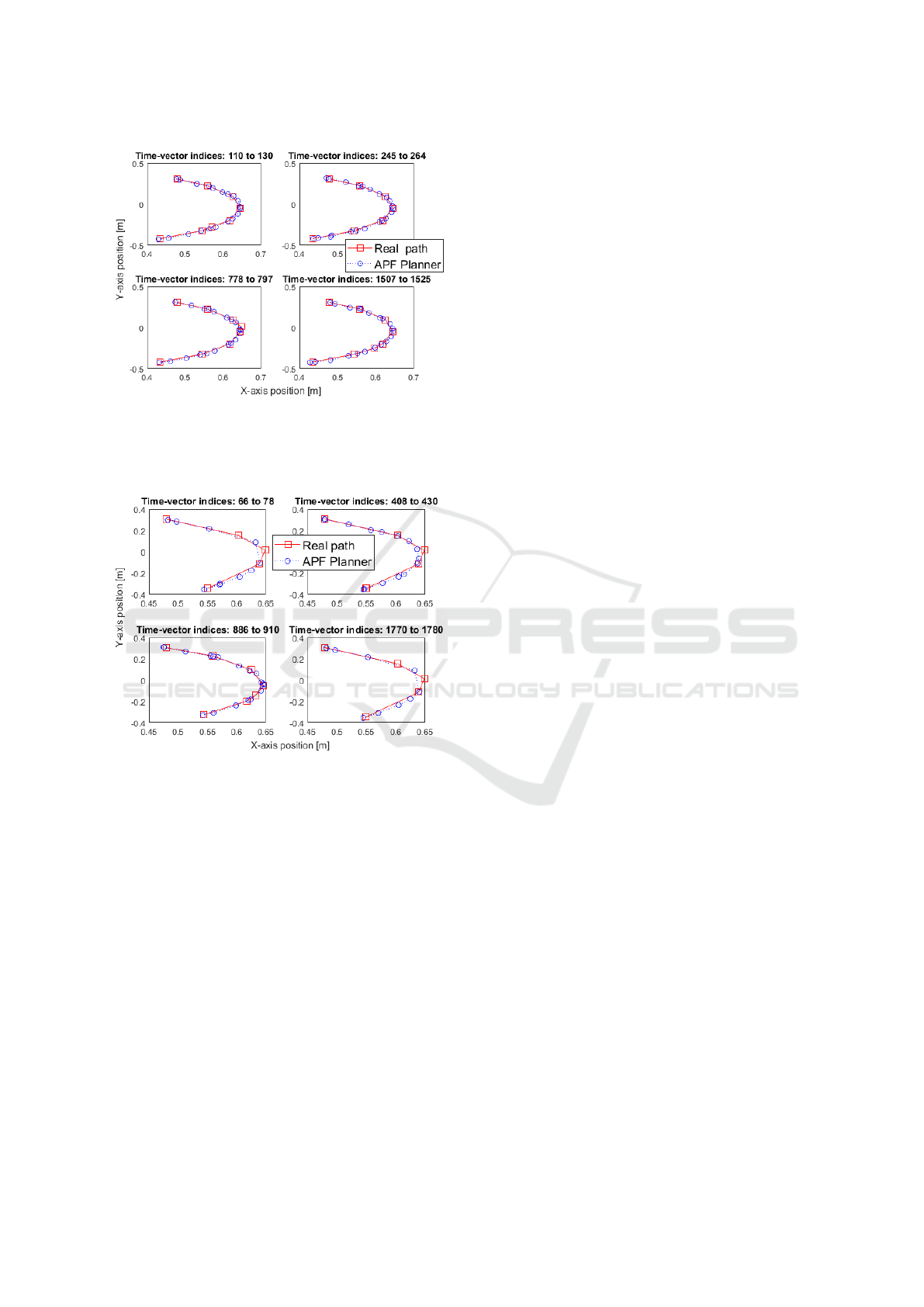
Figure 7: Cartesian space view of free-collision paths in
scenario (B,P) mission-Z, in different repetitions of the
pick-&-place operation. In each plot, blue line refers to the
path generated by the APF planner, and red line refers to the
path really followed by the robot.
Figure 8: Cartesian space view of free-collision paths in
scenario (P,B) mission-T, in different repetitions of the pick-
&-place operation. In each plot, blue line refers to the path
generated by the APF planner, and red line refers to the path
really followed by the robot.
were analyzed. Although this work was not aimed
at providing the scientific community with a general
procedure for facing the safe co-existence of robots
in industrial environments, we firmly believe that the
considered case study may result useful for deploy-
ment of such techniques in factory-floor operations.
Among the various results discussed throughout
the paper, it is worth to highlight that in a path plan-
ning strategy based on artificial potential fields, hig-
her task efficiency is obtained when the manipula-
tor is described as a point and the obstacle is consi-
dered as extended-body; this favours collision avoi-
dance by keeping robot and obstacle away from each
other while increasing the productivity due to better
workspace usage. A second consequence of this sce-
nario is that the low occurrence of collision events and
non-programmed stops led to less fluctuation in mis-
sion times, thus implying in more productive robot
operation.
According to metrics commonly used in process
and fabrication management, the hypothetical process
emulated in this study reached acceptable levels of
effectiveness, since the estimated OEE amounts to
about 68%. This study could motivate engineers and
practitioners to consider new paradigms about the co-
existence of moving machines in factory floor.
ACKNOWLEDGEMENTS
Authors thank the Fundac¸
˜
ao N
´
ucleo de Tecnologia In-
dustrial do Cear
´
a for administrative facilities.
REFERENCES
Ataka, A., Qi, P., Liu, H., and Althoefer, K. (2016). Real-
time planner for multi-segment continuum manipula-
tor in dynamic environments. 2016 IEEE Internatio-
nal Conference on Robotics and Automation (ICRA),
pages 4080–4085.
Badawy, A. (2014). Manipulator trajectory planning using
artificial potential field. In Engineering and Techno-
logy (ICET), 2014 International Conference on, pages
1–6. IEEE.
Budiyanto, A., Cahyadi, A., Adji, T. B., and Wahyung-
goro, O. (2015). Uav obstacle avoidance using po-
tential field under dynamic environment. In Control,
Electronics, Renewable Energy and Communications
(ICCEREC), 2015 International Conference on, pages
187–192. IEEE.
Chatraei, A. and Javidian, H. (2015). Formation control of
mobile robots with obstacle avoidance using fuzzy ar-
tificial potential field. In Electronics, Control, Measu-
rement, Signals and their Application to Mechatronics
(ECMSM), 2015 IEEE International Workshop of, pa-
ges 1–6. IEEE.
Cheng, C., Zhu, D., Sun, B., Chu, Z., Nie, J., and Zhang,
S. (2015). Path planning for autonomous underwater
vehicle based on artificial potential field and velocity
synthesis. In Electrical and Computer Engineering
(CCECE), 2015 IEEE 28th Canadian Conference on,
pages 717–721. IEEE.
Farooq, U., Hasan, K. M., Abbas, G., and Asad, M. U.
(2011). Comparative analysis of zero order sugeno
and mamdani fuzzy logic controllers for obstacle avoi-
dance behavior in mobile robot navigation. In Current
Trends in Information Technology (CTIT), Internati-
onal Conference and Workshop on, pages 113–119.
IEEE.
Fitzgerald, A. E., Kingsley Jr, C., and Umans, S. D. (2014).
Electric Machinery. McGraw-Hill, New York.
Can Artificial Potentials Suit for Collision Avoidance in Factory Floor? - A Case Study of Harmonic Machine-machine Coexistence
555

Galceran, E., Eustice, R. M., and Olson, E. (2015). Toward
integrated motion planning and control using poten-
tial fields and torque-based steering actuation for au-
tonomous driving. In 2015 IEEE Intelligent Vehicles
Symposium (IV), pages 304–309. IEEE.
Gayle, R., Sud, A., Lin, M. C., and Manocha, D. (2007).
Reactive deformation roadmaps: motion planning
of multiple robots in dynamic environments. In
Intelligent Robots and Systems, 2007. IROS 2007.
IEEE/RSJ International Conference on, pages 3777–
3783. IEEE.
Guan, W., Weng, Z., and Zhang, J. (2015). Obsta-
cle avoidance path planning for manipulator based
on variable-step artificial potential method. In The
27th Chinese Control and Decision Conference (2015
CCDC), pages 4325–4329. IEEE.
Habib, M. K. (2014). Handbook of Research on Advance-
ments in Robotics and Mechatronics. IGI Global.
Hargas, Y., Mokrane, A., Hentout, A., Hachour, O., and
Bouzouia, B. (2015). Mobile manipulator path plan-
ning based on artificial potential field: Application on
robuter/ulm. In 2015 4th International Conference on
Electrical Engineering (ICEE), pages 1–6. IEEE.
IFR (2017). Executive summary world robotics 2017 indus-
trial robots: How robots conquer industry worldwide.
Frankfurt. International Federation of Robotics Press.
ISO (1998). Iso9283: Manipulating industrial robots-
performance criteria and related test methods.
Kennedy, R. K. (2017). Understanding, Measuring, and
Improving Overall Equipment Effectiveness: How to
Use OEE to Drive Significant Process Improvement.
Productivity Press, New York, 1st edition.
Khatib, O. (1986). Real-time obstacle avoidance for mani-
pulators and mobile robots. The international journal
of robotics research, 5(1):90–98.
Koppula, H. S. and Saxena, A. (2016). Anticipating human
activities using object affordances for reactive robotic
response. IEEE transactions on pattern analysis and
machine intelligence, 38(1):14–29.
Mac, T. T., Copot, C., Hernandez, A., and De Keyser, R.
(2016). Improved potential field method for unknown
obstacle avoidance using uav in indoor environment.
In 2016 IEEE 14th International Symposium on Ap-
plied Machine Intelligence and Informatics (SAMI),
pages 345–350. IEEE.
Mittal, R. and Nagrath, I. (2003). Robotics and control. Tata
McGraw-Hill.
Moellmann, A. H., Albuquerque, A. S., Contador, J. L.,
and Marins, F. A. S. (2006). Aplicac¸
˜
ao da teoria das
restric¸
˜
oes e do indicador de efici
ˆ
encia global do equi-
pamento para melhoria de produtividade em uma linha
de fabricac¸
˜
ao. Revista gest
˜
ao industrial, 2(1).
Mora, M. C. and Tornero, J. (2008). Path planning and
trajectory generation using multi-rate predictive arti-
ficial potential fields. In Intelligent Robots and Sy-
stems, 2008 IEEE/RSJ International Conference on,
pages 2990–2995. IEEE.
Nawrocka, A., Nawrocki, M., and Kot, A. (2014). Fuzzy lo-
gic controller for rehabilitation robot manipulator. In
Control Conference (ICCC), 2014 15th International
Carpathian, pages 379–382. IEEE.
Pinto, L., Davidson, J., and Gupta, A. (2016). Supervision
via competition: Robot adversaries for learning tasks.
arXiv preprint arXiv:1610.01685.
Simoes, M. G. and Shaw, I. S. (2007). Controle e Modela-
gem Fuzzy. Edgard Blucher, Sao Paulo, 2nd edition.
Spong, M. W. (2006). Robot modeling and control, vo-
lume 3. Wiley New York.
Volpe, R. and Khosla, P. (1990). Manipulator control with
superquadric artificial potential functions: Theory and
experiments. IEEE Transactions on Systems, Man,
and Cybernetics, 20(6):1423–1436.
Wang, X., Jin, Y., and Ding, Z. (2015). A path planning
algorithm of raster maps based on artificial potential
field. In Chinese Automation Congress (CAC), 2015,
pages 627–632. IEEE.
Yu, K., Ohnishi, K., Kawana, H., and Usuda, S. (2015a).
Modulated potential field using 5 dof implant assist
robot for position and angle adjustment. In Industrial
Electronics Society, IECON 2015-41st Annual Confe-
rence of the IEEE, pages 002166–002171. IEEE.
Yu, K., Uozumi, S., Ohnishi, K., Usuda, S., Kawana, H.,
and Nakagawa, T. (2015b). Stereo vision based ro-
bot navigation system using modulated potential field
for implant surgery. In Industrial Technology (ICIT),
2015 IEEE International Conference on, pages 493–
498. IEEE.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
556
