
Variable Support Control for the Wave Equation
A Multiplier Approach
Antonio Agresti
1
, Daniele Andreucci
2
and Paola Loreti
2
1
Mathematics Department, Sapienza University, Piazzale Aldo Moro, 5, 00185, Rome, Italy
2
SBAI Department, Sapienza University, Via Antonio Scarpa, 16, 00161, Rome, Italy
Keywords:
Exact Controllability, Wave Equation, Variable Control Subset, Multiplier.
Abstract:
We study the controllability of the multidimensional wave equation in a bounded domain with Dirichlet boun-
dary condition, in which the support of the control is allowed to change over time.
The exact controllability is reduced to the proof of the observability inequality, which is proven by a multiplier
method. Besides our main results, we present some applications.
1 INTRODUCTION
The controllability of the wave equation or more ge-
nerally of partial differential equations has been stu-
died intensively in the last 30 years. Exact control-
lability for evolutive systems is a challenging mathe-
matical problem, also relevant in engineering applica-
tions. The exact controllability of the wave equation
with Dirichlet boundary condition using the multi-
plier method is studied in (Lions, 1988) see also (Ko-
mornik, 1994) for a systematic study of this method
and, for an approach using theory of semi-groups see
(Tucsnak and Weiss, 2009). All these results do not
allow the support of the control to change over time,
while this variability is required in some applications
(see (Dessi et al., 2004)-(Carcaterra et al., 2014)).
The numerical implementation of controllability
problems is widely studied in literature (see for is-
tance (Glowinski and Lions, 1995), (Castro et al.,
2008), (M
¨
unch, 2005), (Zuazua, 2005) and the refe-
rences therein). In this works, the abstract procedure
used to show the controllability plays an important
role to prove the convergence of the scheme; see e.g.
(Castro et al., 2008). The present results provide the
abstract framework to the numerical implementation
in the variable support control case.
In this paper we provide a controllability result
which extends the classical controllability results and
admits variability of the control support over time.
We have to point out that even in the fixed support
case, the subset of the boundary, on which the cont-
rol acts, cannot be chosen arbitrarily; for an extensive
discussion on these topics see (Bardos et al., 1992).
The common strategy to prove the exact control-
lability is to study an equivalent property i.e. the ex-
act observability for the adjoint system (for more on
this see (Komornik and Loreti, 2005), (Tucsnak and
Weiss, 2009)). Our approach is based on the multi-
plier method (see (Komornik, 1994), (Lions, 1988)),
which seems the most powerful in the multidimen-
sional case. Although the strategy of the proof is
quite classical and follows essentially (Lions, 1988),
this approach leads to some unexpected results and it
opens some questions on the optimality of these re-
sults; see (Agresti et al., 2017) for more on this.
Here we dwell more on the multidimensional case
which seems to be closer to applications, providing
some explicit examples in special geometries.
Let us begin with some notations:
• Let Ω be a bounded domain of R
d
with d ≥ 1,
of class C
2
or convex. From the hypothesis on the
boundary, we know that the exterior normal vector
ν is well defined H
d−1
-a.e. on ∂Ω; where H
d−1
is the d −1 dimensional Hausdorff measure (see
(Evans and Gariepy, 2015)). Moreover, we denote
dΓ the measure H
d−1
restricted to ∂Ω.
• For each t ∈ (0,T ) and T > 0, Γ(t) denotes an
open subset of ∂Ω.
• Finally, we define
Σ :=
[
t∈(0,T )
Γ(t) ×{t}; (1.1)
and we suppose it to be H
d−1
⊗L
1
-measurable
(as defined in (Evans and Gariepy, 2015) Chapter
1).
Agresti, A., Andreucci, D. and Loreti, P.
Variable Support Control for the Wave Equation - A Multiplier Approach.
DOI: 10.5220/0006832600330042
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 33-42
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
33

In this paper we want to study the following property.
Definition 1.1 (Exact Controllability). We say that
the system
w
tt
−∆w = 0 , (x,t) ∈ Ω ×(0,T ) ,
w = 0 , (x,t) ∈ ∂Ω ×(0,T ) \Σ,
w = v , (x,t) ∈ Σ ,
w = w
0
, (x,t) ∈ Ω ×{0},
w
t
= w
1
, (x,t) ∈ Ω ×{0};
(1.2)
is exactly controllable in time T > 0, if for all
w
0
,z
0
∈ L
2
(Ω) and w
1
,z
1
∈ H
−1
(Ω) there exists a
control v ∈ L
2
(Σ) such that the unique solution w ∈
C([0, T ]; L
2
(Ω)) ∩C
1
([0,T ]; H
−1
(Ω)) of (1.2) satis-
fies
w(x,T ) = z
0
, w
t
(x,T ) = z
1
. (1.3)
Of course, the problem (1.2) has to be intended in
a weak sense, which we give below (see Definition
1.3).
In the following, it will be useful to know some
properties of the solution of the wave equation with
null Dirichlet boundary condition, i.e.
u
tt
−∆u = 0 , (x,t) ∈ Ω ×R
+
,
u = 0 , (x,t) ∈ ∂Ω ×R
+
,
u = u
0
, (x,t) ∈ Ω ×{0},
u
t
= u
1
, (x,t) ∈ Ω ×{0};
(1.4)
where R
+
:= [0,∞). In particular, we will need the
following proposition; see (Pazy, 2012) for the notion
of classical and mild solution.
Proposition 1.2. The following holds true:
i) For each (u
0
,u
1
) ∈ H
1
0
(Ω) ×L
2
(Ω), then the pro-
blem (1.4) has an unique mild solution u in the
class
C
1
(R
+
;H
1
0
(Ω)) ∩C(R
+
;L
2
(Ω)).
ii) For each (u
0
,u
1
) ∈ (H
2
(Ω) ∩H
1
0
(Ω)) ×H
1
0
(Ω),
then the problem (1.4) has an unique classical so-
lution u in the class
C(R
+
;H
2
(Ω) ∩H
1
0
(Ω)) ∩C
2
(R
+
;L
2
(Ω)).
Proof. Let {f
k
: k ∈N} and {λ
k
: k ∈N} be respecti-
vely the eigenfunctions and the eigenvalues of the
Laplace operator with null Dirichlet boundary condi-
tion.
Since Ω is of class C
2
or convex, then f
k
∈ H
2
(Ω) ∩
H
1
0
(Ω) for all k ∈ N; for a proof see (Taylor, 2011) or
(Grisvard, 2011). Then, the solution u of the problem
(1.4) is
u(t) =
∞
∑
k=0
cos(λ
k
t) ˆu
0,k
+
sin(λ
j
t)
λ
k
ˆu
1,k
f
k
; (1.5)
where
ˆu
i.k
:= (u
i
, f
k
)
L
2
(Ω)
:=
Z
Ω
u
i
f
k
dx , i = 0, 1 .
Then the representation of the solution in (1.5) readily
implies the claim in i) −ii).
With this in hand, we can give a definition of so-
lution for the problem (1.2).
Definition 1.3 (Weak Solution of (1.2)). A map w ∈
C([0, T ]; L
2
(Ω)) ∩C
1
([0,T ]; H
−1
(Ω)) is a weak solu-
tion of (1.2) with v ∈ L
2
(Σ) and (w
0
,w
1
) ∈ L
2
(Ω) ×
H
−1
(Ω) if and only if
−hw
t
(s),u(s)i
H
−1
×H
1
0
+ hw(s),u
t
(s)i
L
2
×L
2
=
−hw
1
,u
0
i
H
−1
×H
1
0
+ hw
0
,u
1
i
L
2
×L
2
+
Z
s
0
Z
Γ(t)
v∂
ν
u dΓdt , (1.6)
for all 0 < s ≤ T and for all mild solutions u of (1.4)
and initial data (u
0
,u
1
) ∈ H
1
0
(Ω) ×L
2
(Ω).
For the motivation see (Komornik and Loreti,
2005); for other equivalent formulations one may
consult (Lions, 1988).
Remark 1.4. Note that, on the RHS of (1.6) it appears
∂
ν
u i.e. the normal derivative of u. Although the re-
gularity of a mild solution u is not sufficient to have a
well defined trace for ∂
ν
u, in the sense of Sobolev spa-
ces (see (Taylor, 2011) Chapter 4), the normal deriva-
tive ∂
ν
u is a well defined element of L
2
(∂Ω ×(0,t))
for each t > 0: this result is generally called hidden
regularity; the proof relies on a clever integration by
parts argument, for details see (Komornik, 1994), (Li-
ons, 1988) or (Lasiecka and Triggiani, 1983). By this,
the last term in the RHS of (1.6) is well defined since
v ∈ L
2
(Σ).
Before proceeding in the analysis of the weak so-
lutions, we recall the following well known result
about the solutions of the wave equation (1.4).
Corollary 1.5 (Energy conservation). For each t ∈
R
+
and each mild solution u of (1.4) with initial data
(u
0
,u
1
) ∈ H
1
0
(Ω) ×L
2
(Ω), the energy
E(t) =
1
2
k∇u(·,t)k
2
L
2
(Ω)
+ ku
t
(·,t)k
2
L
2
(Ω)
, (1.7)
is constant, and it is equal to the initial energy
E
0
:=
1
2
k ∇u
0
k
2
L
2
(Ω)
+ k u
1
k
2
L
2
(Ω)
. (1.8)
We conclude the treatment of the weak solution
with the following well posedness result, for a proof
see (Komornik and Loreti, 2005).
Theorem 1.6 (Well Posedness). For each (w
0
,w
1
) ∈
L
2
(Ω) ×H
−1
(Ω) and v ∈L
2
(Σ), there exist a unique
weak solution of (1.2) in the sense of Definition 1.3.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
34

For brevity, as we said above, here we confine our-
selves to the study of the following equivalent pro-
perty.
Definition 1.7 (Exact Observability). Let u ∈
C(R
+
;H
1
0
(Ω)) ∩C
1
(R
+
;L
2
(Ω)) be the unique mild
solution of (1.4) for the initial data (u
0
,u
1
) ∈
H
1
0
(Ω)×L
2
(Ω). Then the system is called exactly ob-
servable in time T > 0 if there exists a constant C > 0
such that
Z
Σ
|∂
ν
u|
2
dΓ ⊗dt =
Z
T
0
Z
Γ(t)
|∂
ν
u|
2
dΓ dt ≥
C
k ∇u
0
k
2
L
2
(Ω)
+ k u
1
k
2
L
2
(Ω)
, (1.9)
for all (u
0
,u
1
) ∈ H
1
0
(Ω) ×L
2
(Ω).
We remind that ∂
ν
u is a well defined L
2
(∂Ω ×
(0,T )) element (see Remark 1.4).
We are now in a position to prove an identity, which
is the basic tool in proving the exact observability for
some Σ’s.
Lemma 1.8 (A multiplier identity). Let u ∈
C(R
+
;H
1
0
(Ω)) ∩C
1
(R
+
;L
2
(Ω)) be the mild solu-
tion corresponding to initial data (u
0
,u
1
) ∈ H
1
0
(Ω) ×
L
2
(Ω). Then for each 0 ≤ s < τ and ξ ∈ R
d
, we have
1
2
Z
τ
s
Z
∂Ω
(x −ξ) ·ν |∂
ν
u|
2
dΓ(x) dt =
Z
Ω
u
t
∇u ·(x −ξ) +
d −1
2
u
dx
τ
s
+ (τ −s)E
0
;
(1.10)
where E
0
is the initial energy of the system as defined
in (1.8) and [ f (t)]
s
00
s
0
:= f (s
00
) − f (s
0
).
Proof. For reader’s convenience, we divide the proof
into three steps.
Step 1. We first suppose that u
0
,u
1
are smoother, i.e.
u
0
∈ H
2
(Ω) ∩H
1
0
(Ω) and u
1
∈ H
1
0
(Ω). By Proposi-
tion 1.2, the solution to (1.4) is a classical solution, in
particular the quantities u
x
k
,x
j
, for 1 ≤k, j ≤d, belong
to C(R
+
;L
2
(Ω)); this will be used in the proof.
Under this assumption, the wave equation is solved by
u almost everywhere on Ω×R
+
, then we can multiply
the wave equation by (x −ξ) ·∇u and on integrating
over Ω ×(s,t), we obtain
Z
Ω
Z
τ
s
((x −ξ) ·∇u)u
tt
dx dt
−
Z
Ω
Z
τ
s
((x −ξ) ·∇u)∆u dx dt = 0 . (1.11)
For the first term on the LHS in (1.11), with a simple
integration by parts argument, we obtain
Z
Ω
Z
τ
s
(x −ξ) ·∇u u
tt
dx
=
Z
Ω
(x −ξ) ·∇u u
t
dx
τ
s
−
Z
Ω
Z
τ
s
(x −ξ) ·
1
2
∇((u
t
)
2
)dx dt
=
Z
Ω
(x −ξ) ·∇u u
t
dx
τ
s
+
d
2
Z
Ω
Z
τ
s
(u
t
)
2
dx dt ;
where, in the last inequality, we have used the Green’s
formulas, u
t
= 0 on ∂Ω ×(s,τ) and ∇ ·(x −ξ) = d.
For the second term in (1.11) we use a similar argu-
ment. Indeed, by Green’s formulas
Z
Ω
Z
τ
s
((x −ξ) ·∇u) ·∆u dx dt
=
Z
∂Ω
Z
τ
s
∂
ν
u(x −ξ) ·∇u dΓdt
−
Z
Ω
Z
τ
s
∇((x −ξ) ·∇u) ·∇u dx dt .
Now, using that ((u
x
j
)
2
)
x
k
= 2u
x
j
,x
k
and ∇(x
k
−
ξ
k
)
x
j
= δ
k, j
for all 1 ≤ k, j ≤ d (here δ
k, j
is the Kro-
necker’s delta), one obtains
∇((x −ξ) ·∇u) ·∇u = |∇u|
2
+
1
2
(x −ξ) ·∇(|∇u|
2
);
pointwise. With simple computations, we have
Z
Ω
Z
τ
s
((x −ξ) ·∇u) ·∆u dx dt =
1
2
Z
∂Ω
Z
τ
s
(x −ξ) ·ν|∂
ν
u|
2
+
d −2
2
Z
Ω
Z
τ
s
|∇u|
2
dx dt .
Putting all together and using that E(t) ≡ E
0
(cfr.
Corollary 1.5), we obtain
1
2
Z
∂Ω
Z
τ
s
(x −ξ) ·ν|∂
ν
u|
2
=
Z
Ω
(x −ξ) ·∇u u
t
dx
τ
s
+ (t −τ)E
0
+
d −1
2
Z
Ω
Z
τ
s
|u
t
|
2
−|∇u|
2
dx dt .
(1.12)
Step 2. In this step we rewrite the last term on LHS
in (1.12). Indeed, under the assumption of Step 1, the
wave equation is solved by u a.e. on Ω ×(s,τ), so
that on multiplying it by u, integration over Ω ×(s, τ)
and using Green’s formulas (recall that u = 0 on ∂Ω×
(s,τ))
0 =
Z
Ω
Z
τ
s
u(u
tt
−∆u)dx dt
=
Z
Ω
uu
t
dx
τ
s
−
Z
Ω
Z
τ
s
|u
t
|
2
−|∇u|
2
dx dt . (1.13)
Variable Support Control for the Wave Equation - A Multiplier Approach
35

Step 3. Combining the equalities (1.12)-(1.13) we
obtain (1.10) for classical solutions.
In the general case, choose sequences such that {u
0,k
:
k ∈ N} ⊂ H
2
(Ω) ∩ H
1
0
(Ω) and {u
1,k
: k ∈ N} ⊂
H
1
0
(Ω), such that
u
0,k
→ u
0
in H
1
0
(Ω), u
1,k
→ u
1
in L
2
(Ω).
Then passing to the limit in the identity (1.10) va-
lid for the solution u
k
for initial data (u
0,k
,u
1,k
), one
obtain the claim.
Remark 1.9. The proof of Corollary 3.1 is based on
the multiplication of the wave equation against the
function m(x)·∇u = (x −ξ) ·∇u, which is called mul-
tiplier, which justifies the name of the identity.
2 ALTERNATING OBSERVATION
For alternating observation we mean that there exists
a partition 0 =: t
−1
< t
0
< t
1
< ··· < t
N−1
< t
N
=: T
of the interval [0,T ] such that
Γ(t) ≡ Γ
j
, ∀t ∈ (t
j−1
,t
j
) j = 0 ..., N ; (2.1)
where Γ
j
⊂ ∂Ω is a fixed subset for each j = 0 ... ,N.
Under the previous hypothesis, by (1.1) we have
Σ =
N
[
j=0
Γ
j
×(t
j−1
,t
j
), (2.2)
up to a set of measure 0.
As pointed out in Section 1 the family {Γ
i
}
i=0,...,N
cannot be chosen arbitrarly; we construct this family
in a special form (see (2.5) below).
To do this, let {x
i
}
i=0,...,N
be an arbitrary family of
points in R
d
;
• For each i = 0,. .., N, define
R
i
= max{|x −x
i
||x ∈ Ω}, (2.3)
and for each i = 0, .. .,N −1, define
R
i+1,i
= |x
i+1
−x
i
|. (2.4)
• For each i = 0,. .., N, define
Γ
i
= {x ∈ ∂Ω |(x −x
i
) ·ν > 0}. (2.5)
Theorem 2.1 (Alternating Observability). In the pre-
vious notations, for each real number T such that
T > R
N
+
N−1
∑
i=0
R
i+1,i
+ R
0
, (2.6)
the system is exactly observable in time T , in the sense
of Definition 1.7 for Σ as in (2.2).
Proof. For each i = 0,. .., N, use the identity (1.10)
for ξ = x
i
, s = t
i−1
and τ = t
i
. On summing over i =
0,.. ., N such identities, we have
1
2
N
∑
i=0
Z
t
i
t
i−1
Z
Γ
i
(x −x
i
) ·ν |∂
ν
u|
2
dΓ(x) dt =
N
∑
i=0
Z
Ω
u
t
∇u ·(x −x
i
) +
d −1
2
udx
t
i
t
i−1
+ T E
0
, (2.7)
since
∑
N
i=0
(t
i
−t
i−1
) = T , where we take as above T =
t
N
.
It will be useful to adopt the following notation
u
s
(x) := u(x,s), u
s
t
(x) := u
t
(x,s),
where s ∈ [0, T ] and x ∈Ω. In the sum on the RHS of
(2.7) some cancellations are possible:
N
∑
i=0
Z
Ω
u
t
∇u ·(x −x
i
) +
d −1
2
u
dx
t
i
t
i−1
=
Z
Ω
u
T
t
∇u
T
·(x −x
N
) +
d −1
2
u
T
dx
−
N−1
∑
i=0
Z
Ω
u
t
i
t
∇u
t
i
·[(x −x
i+1
) −(x −x
i
)]
dx
−
Z
Ω
u
1
∇u
0
·(x −x
0
) +
d −1
2
u
0
dx . (2.8)
For the first and last term on the RHS of (2.8) we have
Z
Ω
u
T
t
∇u
T
·(x −x
N
) +
d −1
2
u
T
dx
≤ R
N
E
0
, (2.9)
Z
Ω
u
1
∇u
0
·(x −x
0
) +
d −1
2
u
0
dx
≤ R
1
E
0
. (2.10)
Moreover, for the terms in the sum on the RHS of
(2.8), we have
Z
Ω
u
t
i
t
∇u
t
i
·(x
i
−x
i+1
)
dx
≤ R
i+1,i
E
0
, (2.11)
for each i = 0, .. .,N.
For convenience, we postpone the proof of the ine-
qualities (2.9)-(2.11), see Lemma 2.2 below.
By definition of Γ
i
in (2.5) and R
i
in (2.3), clearly we
have
R
i
Z
t
i
t
i−1
Z
Γ
i
|∂
ν
u|
2
dΓ dt ≥
Z
t
i
t
i−1
Z
∂Ω
(x −x
i
) ·ν |∂
ν
u|
2
dΓ dt , (2.12)
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
36

for each i = 0, .. .,N.
Using the equation (2.7), the identity (2.8) and the es-
timates (2.9)-(2.12), we have
max
i=0,...,N
R
i
N
∑
i=0
Z
t
i
t
i−1
Z
Γ
i
|∂
ν
u|
2
dΓ dt ≥
2(T −R
N
−R
N,N−1
−···−R
1,0
−R
0
)E
0
. (2.13)
Now, by assumption T > R
N
+
∑
N−1
i=1
R
i+1,i
+ R
1
, so
there exists a constant C = C
T
> 0, which depends on
T , such that
N
∑
i=0
Z
t
i
t
i−1
Z
Γ
i
|∂
ν
u|
2
dΓ dt ≥C
T
E
0
, (2.14)
which is exactly the observability inequality, as defi-
ned in Definition 1.7.
We now prove the estimates (2.9)-(2.11); in particular
(2.9)-(2.10) and (2.11) follow respectively by i) and
ii) of the following Lemma.
Lemma 2.2. For each mild solution u ∈
C(R
+
;H
1
0
(Ω)) ∩ C
1
(R
+
;L
2
(Ω)) of (1.4), the
following holds.
i) For each ξ ∈ R
d
and s ∈ R, then
Z
Ω
u
s
t
∇u
s
·(x −ξ) +
d −1
2
u
s
dx
≤ R
ξ
E
0
,
where R
ξ
= max{|x −ξ| : x ∈Ω}.
ii) For each ξ,η ∈ R
d
and s ∈ R
+
, then
Z
Ω
u
s
t
(∇u
s
·(ξ −η))dx
≤ R
ξ,η
E
0
,
where R
ξ,η
= |ξ −η|.
Proof. i) By Chauchy-Schwarz inequality, we have
Z
Ω
u
s
t
∇u
s
·(x −ξ) +
d −1
2
u
s
dx
≤k u
s
t
k
L
2
k ∇u
s
·(·−ξ) +
d −1
2
u
s
k
L
2
≤
R
ξ
2
ku
s
t
k
2
L
2
+
1
2R
ξ
k∇u
s
·(·−ξ) +
d −1
2
u
s
k
2
L
2
;
(2.15)
here L
2
:= L
2
(Ω). Note that,
k∇u
s
·(·−ξ) +
d −1
2
u
s
k
2
L
2
= k ∇u
s
·(·−ξ) k
2
L
2
+(d −1)(∇u
s
·(·−ξ),u
s
)
L
2
+
(d −1)
2
4
k u
s
k
2
L
2
.
Since u = 0 on ∂Ω, then using Green’s identity the
middle term in the RHS of the previous equation is
equal to
Z
Ω
(∇u
s
u
s
) ·(x −ξ) d x
=
1
2
Z
Ω
(∇(u
s
)
2
) ·(x −ξ) d x
= −
1
2
Z
Ω
(u
s
)
2
(∇ ·(x −ξ))d x = −
d
2
k u
s
k
2
L
2
.
This implies
k ∇u
s
·(·−ξ) +
d −1
2
u
s
k
2
L
2
=
k ∇u
s
·(·−ξ) k
2
L
2
+
−(d −1)
d
2
+
(d −1)
2
4
k u
s
k
2
L
2
≤k ∇u
s
·(·−ξ) k
2
L
2
≤ R
2
ξ
k ∇u
s
k
2
L
2
,
since
−
d(d −1)
2
+
(d −1)
2
4
= −
d
2
2
+
1
4
< 0 ,
for all d ≥ 1.
Now returning to (2.15), we have
Z
Ω
u
s
t
∇u
s
·(x −ξ) +
d −1
2
u
s
dx
≤
R
ξ
2
k u
s
t
k
2
L
2
+
1
2R
ξ
R
2
ξ
k ∇u
s
k
2
L
2
=
R
ξ
2
(k u
s
t
k
2
L
2
+ k ∇u
s
k
2
L
2
) = R
ξ
E
0
;
where the last inequality follows by the energy con-
servation (cfr. Corollary 1.5).
ii) The proof the second part of the Lemma is easier.
Indeed, by Cauchy-Schwarz inequality, we have
Z
Ω
u
s
t
∇u
s
·(ξ −η) dx
≤k u
s
t
k
L
2
k ∇u
s
·(ξ −η) k
L
2
≤ R
ξ,η
k u
s
t
k
L
2
k ∇u
s
k
L
2
≤ R
ξ,η
E
0
;
where, the last inequality follows by the energy con-
servation.
2.1 The Role of {t
i
}
i=−1,...,N
.
One may wonder what is the role of the family
{t
i
}
i=−1,...,N
, since in Theorem 2.1 only the sum T =
∑
N
i=0
(t
i
−t
i−1
) appears.
To explain the role of these values, we have to recall
that if N = 0 (i.e. fixed support control), Theorem
2.1 implies that the exact controllability holds for any
Variable Support Control for the Wave Equation - A Multiplier Approach
37

T > 2 max{|x −x
0
||x ∈ Ω}, where x
0
∈ R
d
is a fixed
point. So, if for an index j ∈ {0,. ..,N} we have
|t
j
−t
j−1
| > 2 max{|x −x
j
||x ∈ Ω}, (2.16)
then we can construct a control v such that suppv ⊂
Γ
j
×[t
j−1
,t
j
] by using the fixed support case of Theo-
rem 2.1. Indeed, fix (w
0
,w
1
) ∈ L
2
(Ω) ×H
−1
(Ω) and
let be w the unique weak solution of the problem (1.2)
for T = t
j
and v = 0; so by Theorem 1.6 we have
that (w(t
j−1
),w
t
(t
j−1
)) is well defined as an element
of L
2
(Ω) ×H
−1
(Ω). Since the inequality in (2.16)
holds, the fixed case of Theorem 2.1 provides a cont-
rol ˜v such that the solution at time t = t
j
satisfies the
null condition; so after defining v = 0 for t < t
j−1
or
t
j
< t < T and v = ˜v for t
j−1
< t < t
j
we have con-
structed a control for the initial condition (w
0
,w
1
). So
if the inequality (2.16) holds for an index j the con-
trollability results follows by classical results, (see for
istance Theorem 6.1, Chapter 1 of (Lions, 1988)). In
the following Section we produce explicit examples
in which the inequality (2.16) is not satisfied by any
i = 0,... ,N; so our investigation produces new results
on controllability for the wave equation.
By the way, we point out that Theorem 2.1 allows
us to apply the Hilbert uniqueness method (or HUM,
see (Komornik and Loreti, 2005)-(Lions, 1988)); with
some effort one can prove that the control provided by
this method minimizes the energy of the control over
the possible controls (see Chapter 7 of (Lions, 1988)).
For this reason even in the case when (2.16) holds our
Theorem yields the existence of a minimizer control;
this remarkable property of the HUM control can be
useful in applications. For brevity we do not repro-
duce the needed calculations.
3 VARIABLE OBSERVATION
In this Section we state a fairly general observability
Theorem in which the subset Γ(t) of observation at
time t can vary at each time t ∈(0,T ).
As explained in Section 1, the family {Γ(t)}
t∈(0,T )
cannot be arbitrary and will be constructed in a si-
milar fashion to {Γ
i
}
i=0,...,N
(see (2.5) in Section 2).
To do this, let ϕ : [0, T ] → R
d
be a continuous and
piecewise differentiable curve in R
d
of finite length,
i.e.
L(ϕ) :=
Z
T
0
|ϕ
0
(t)|dt < +∞. (3.1)
For such a ϕ, define
Γ
ϕ
(t) = {x ∈ ∂Ω |(x −ϕ(t)) ·ν > 0}, (3.2)
Σ
ϕ
=
[
t∈(0,T )
Γ
ϕ
(t) ×{t}, (3.3)
c
i
= max
Ω
|x −ϕ(i)|, i = 0, T . (3.4)
Hereafter we assume that Σ
ϕ
is H
d−1
⊗ L
1
-
measurable; for further discussion on this topic see
(Agresti et al., 2017).
Also, let P = {0 = t
−1
< t
0
< . ..t
N−1
< t
N
= T } be a
partition of the interval [0,T ]; define
x
ϕ, j
= ϕ(t
j−1
), (3.5)
Γ
ϕ, j
= {x ∈ ∂Ω |(x −x
ϕ, j
) ·ν > 0}, (3.6)
for all j = 0,. .. ,N. For future convenience, we set
Σ
P
ϕ
:=
N
[
j=0
Γ
ϕ, j
×(t
j−1
,t
j
). (3.7)
In next theorem, we have to consider a sequence of
partitions {P
k
}
k∈N
of the interval [0,T ], so we will add
the upper index k in (3.5)-(3.6) in order to keep trace
of the dependence on P
k
; and we will set Σ
k
ϕ
:= Σ
P
k
ϕ
.
Now we are ready to state the main result of this
Section.
Theorem 3.1 (Variable Support Observability). Un-
der the above hypothesis, suppose there exists a se-
quence of partitions {P
k
}
k∈N
of the interval [0, T ],
such that sup
{t
k
j−1
,t
k
j
}∈P
k
|t
k
j
−t
k
j−1
| & 0 as k % ∞ and
lim
k→∞
H
d−1
⊗L
1
Σ
ϕ
∆Σ
k
ϕ
= 0 , (3.8)
where P
k
= {0 = t
k
−1
< t
k
0
< ··· < t
k
N
= T }, L
1
is the
Lebesgue measure on R
1
and A∆B = (A\B)∪(B\A).
Furthermore, suppose that T verifies
T > c
0
+
Z
T
0
|ϕ
0
(t)|dt + c
N
. (3.9)
Then the system is exactly observable in time T (see
Definition 1.7) for Σ = Σ
ϕ
.
For brevity we do not report the proof of Theorem
3.1; for the proof, other applications and further ex-
tension of this result we refer to (Agresti et al., 2017).
4 APPLICATIONS
In this Section we give some applications of Theo-
rems 2.1 and 3.1 in order to show the potentiality of
these results.
To begin, we focus our attention to Ω = B
1
:= {x ∈
R
2
||x| < 1}, i.e. the ball with center 0 and radius 1.
As usual, we denote with S
1
:= ∂B
1
the unit circle
with center 0.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
38

Corollary 4.1 (1-time alternating - Circle case). Let
T > 2(1 +
√
2) be a real number, define
d
0
=
n
z ∈ S
1
π
2
< arg z < 2π
o
, (4.1)
d
1
=
n
z ∈ S
1
0 < arg z <
3π
2
o
. (4.2)
Then the system (1.2) is exactly controllable for Ω =
B
1
, t
0
is an arbitrary element of (0,T ), and
Σ = d
0
×(0,t
0
)
[
d
1
×(t
0
,T ).
Proof. It is an easy consequence of Theorem 2.1 with
the choice x
0
= (1, 1) and x
1
= (1, −1). Indeed, by
(2.3)-(2.4) it is clear that
R
0
= R
1
=
√
2 + 1 , R
0,1
= 2
√
2.
Moreover, the condition (2.6) in Theorem 2.1, implies
T > 2(1 +
√
2). Lastly, with simple geometrical con-
sideration, one can see Γ
0
= d
0
and Γ
1
= d
1
by (2.5);
see also Figure 1. This concludes the proof.
Figure 1: On the top (resp. bottom) we have represented
in red d
0
(resp. d
1
) and x
0
(resp. x
1
), to point out the con-
nection with the formula (2.5).
Remark 4.2. Note that in Corollary 4.1 there is no
assumption on the value t
0
∈ (0,T ); due to the dis-
cussion in Subsection 2.1 it is clear that Corollary 4.1
does not follow trivially by known results if
|t
0
| < 2(1 +
√
2). (4.3)
We now extend Corollary 4.1 to the N-times alter-
nating case.
Corollary 4.3 (N-times alternating - Circle case). Let
T > 2(N + 1) + 2
√
2 be a real number and let d
0
,d
1
be as in (4.1)-(4.2). Then the system (1.2) is exactly
controllable for Ω = B
1
, {t
i
}
i=0,...,N−1
any increasing
finite subfamily of (0,T ), and
Σ =
N
[
i=0,i∈2N
d
0
×(t
j−1
,t
j
)
!
∪
N
[
i=0,i∈2N+1
d
1
×(t
j−1
,t
j
)
!
. (4.4)
Proof. It is similar to the proof of Corollary 4.1. In
this case, we have to choose x
i
≡ x
0
= (1,1) if i is
even or x
i
≡ x
1
= (1, −1). Similar to Corollary 4.1,
we have
R
0
= R
1
=
√
2 + 1 , R
i,i+1
= 2
√
2,
for all i = 0, .. .,N −1. As in the proof of Corollary
4.1, by (2.5) we have that Γ
i
≡ d
0
if i is even, other-
wise Γ
i
≡ d
0
and Σ is as in (4.4).
Remark 4.4. As did in Remark 4.2 for Corollary 4.1,
we observe that in Corollary 4.3 there is no assump-
tion on the values t
i
for i = 0,. .. ,N −1. In this case
we may require that
|t
j
−t
j−1
| < 2(1 +
√
2), ∀j = 0, .. .,N ; (4.5)
to avoid triviality of the result in the previous Corol-
lary.
Below we give an interesting application of Theo-
rem 3.1.
Corollary 4.5. Let α ∈R
+
be a positive real number,
such that
α <
π
4(1 +
√
2) + π
√
2
. (4.6)
Then the system (1.2) is exactly controllable in time
T = π/(2α) with Ω = B
1
and Σ = ∪
t∈(0,T )
Γ(t) ×{t};
where
Γ(t) =
n
z ∈ S
1
π
4
+ αt < argz <
7π
4
+ αt
o
. (4.7)
Proof. Set ϕ(t) =
√
2(cos(αt),sin(αt)) for t ∈
(0,π/(2α)). It is easy to check that Γ(t) = Γ
ϕ
(t)
(see Figure 2), to prove the Corollary we have only
to check the hypothesis of Theorem 3.1.
Indeed, it is clear that the condition (3.8) holds by
taking a sequence of partition P
k
= {t
k
j
}
j=0,...,k
with
t
k
j
= ( j/k)T and T := π/(2α).
By construction, the length of the curve is L(ϕ) =
√
2(π/2), and c
i
= 1 +
√
2 for i = 0, T . So condition
(3.9) is satisfied if
π
2α
> 2(1 +
√
2) +
√
2
π
2
, (4.8)
which is equivalent to (4.6).
Variable Support Control for the Wave Equation - A Multiplier Approach
39
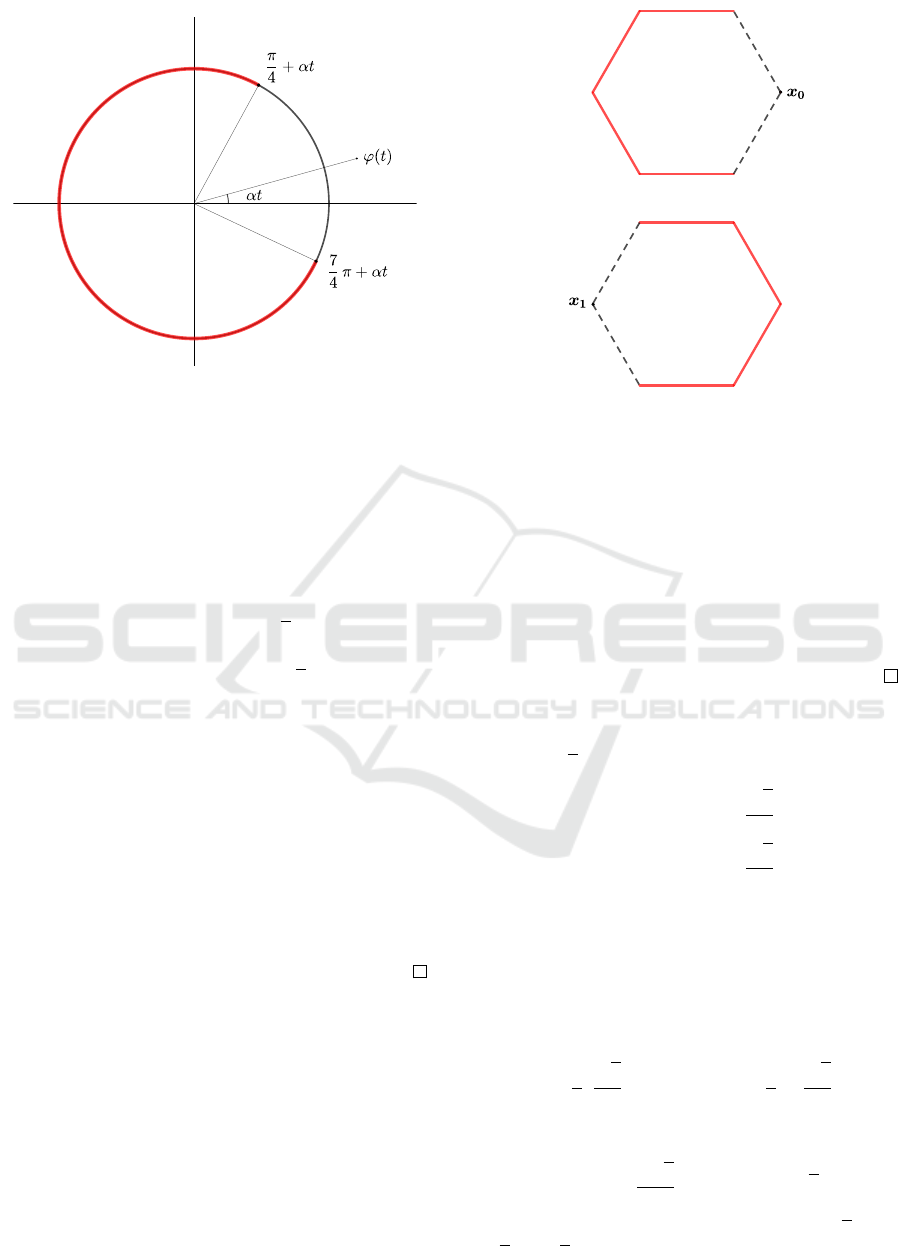
Figure 2: Construction of Γ
ϕ
(t), in accordance with (3.2).
We now analyse a case of a convex domain; i.e.
the interior of the hexagon with side 1 and center 0, it
will be denoted by H ⊂ R
2
and we set E := ∂H .
In this situation, we have analogous result to Corolla-
ries 4.1, 4.3 and 4.5:
Corollary 4.6 (1-time alternating - Hexagon case I).
Let T > 6 be a real number, define
e
0
=
n
(x,y) ∈ E
x <
1
2
o
, (4.9)
e
1
=
n
(x,y) ∈ E
x > −
1
2
o
. (4.10)
Then the system (1.2) is exactly controllable for Ω =
H , t
0
is an arbitrary element of (0,T ), and
Σ = e
0
×(0,t
0
)
[
e
1
×(t
0
,T ).
Proof. As in the Proof of Corollary 4.1, we use The-
orem 2.1 with the choice x
0
= (1,0) and x
1
= (−1,0);
it is also clear that Γ
0
= e
0
and Γ
1
= e
1
by definition
(2.5) (see Figure 3).
Furthermore, by (2.3)-(2.4), we have
R
0
= R
1
= R
0,1
= 2 ;
then by (2.6) the claim follows.
Corollary 4.7 (N-times alternating - Hexagon case).
Let T > 2(2 + N) be a real number and let e
0
,e
1
be
as in (4.9)-(4.10). Then the system (1.2) is exactly
controllable for Ω = H , {t
i
}
i=0,...,N−1
any increasing
finite subfamily of (0,T ), and
Σ =
N
[
i=0,i∈2N
e
0
×(t
j−1
,t
j
)
!
∪
N
[
i=0,i∈2N+1
e
1
×(t
j−1
,t
j
)
!
.
Figure 3: On the top (resp. bottom) we have represented
in red e
0
(resp. e
1
) and x
0
(resp. x
1
), to point out the con-
nection with the formula (2.5).
Proof. Is similar to the proof of Corollaries 4.3 and
4.6.
In this case, we have to choose x
i
≡ x
0
= (1,0) if i
is even or x
i
≡ x
1
= (−1,0) otherwise; see Figure 3.
Moreover, by (2.3)-(2.4) we obtain
R
0
= R
N
= R
i+1,i
= 2 .
Then condition (2.6) is equivalent to T > 4 + 2N =
2(2 + N) and the claim follows.
The last application consists in the following:
Corollary 4.8 (1-time alternating - Hexagon case II).
Let T > 5
√
3 be a real number, define
e
0
0
=
n
(x,y) ∈ E
y <
√
3
2
x
o
,
e
0
1
=
n
(x,y) ∈ E
y >
√
3
2
x
o
.
Then the system (1.2) is exactly controllable for Ω =
H , t
0
is an arbitrary element of (0,T ), and
Σ = e
0
0
×(0,t
0
)
[
e
0
1
×(t
0
,T ).
Proof. As in the Proof of Corollary 4.6, we use The-
orem 2.1 with the choice
x
0
=
3
2
,
√
3
2
!
, x
1
=
−
3
2
,−
√
3
2
!
.
By (2.3)-(2.4), we have
R
0
= R
1
=
3
√
3
2
, R
0,1
= 2
√
3.
In this case, the condition (2.6) is T > 2(3
√
3)/2 +
2
√
3 = 5
√
3 as stated in the Corollary.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
40

Figure 4: On the top (resp. bottom) we have represented
in red e
0
0
(resp. e
0
1
) and x
0
(resp. x
1
), to point out the con-
nection with the formula (2.5); the green lines are the pro-
longation of the hexagon sides.
Furthermore, with this choice of x
0
,x
1
, by (2.5) one
can prove that Γ
0
= e
0
0
and Γ
1
= e
0
1
(see also Figure
4 for a geometrical construction); then the claim fol-
lows.
The analogous of Corollary 4.7 for the choice
of x
0
,x
1
made in Corollary 4.8 can be easily
proven by the same argumentations (in this case
T >
√
3(3 + 2N)). In order to avoid repetition we do
not record the proof here; the same considerations
are valid for the content of Remarks 4.2 and 4.4.
We point out that Theorems 2.1 and 3.1 can be
applied to a very wide range of domains in R
d
for any
d > 1; we have chosen only two cases in this Section
in order to give a flavour of the possible applications.
Note that, Theorem 3.1 needs the additional condition
(3.8), which is not in general immediate to prove,
though it can be proven to be valid for smooth Ω and
ϕ; this observation can be useful in applications.
5 CONCLUSIONS
To conclude we have shown that the exact controlla-
bility holds if T is sufficiently large and the subset of
observation Σ is suitable.
More specifically:
• Let {x
i
}
i=0...,N
be an arbitrary family of points in
R
d
, {t
i
}
i=−1,...,N
an increasing family of positive
numbers such that t
−1
= 0 and T := t
N
; then the
system (1.2) is exactly controllable if
T > R
0
+
N−1
∑
i=0
R
i+1,i
+ R
N
;
where R
i
,R
i+1,i
are defined in (2.3)-(2.4) and
Σ =
N
[
i=0
Γ
i
×(t
i
,t
i−1
),
Γ
i
: = {x ∈ ∂Ω |(x −x
i
) ·ν > 0}.
See Theorem 2.1.
• Let ϕ : [0,T ] → R
d
be a continuous and piecewise
differentiable curve of finite length (see (3.1)). If
T > c
0
+
Z
T
0
|ϕ
0
(t)|dt + c
N
;
c
i
: = max
x∈
Ω
|x −ϕ(i)|, i = 0, T ,
the system (1.2) is exactly controllable with
Σ =
[
t∈(0,T )
Γ
ϕ
(t) ×{t},
Γ
ϕ
(t) : = {x ∈ ∂Ω |(x −ϕ(t)) ·ν > 0}.
See Theorem 3.1.
These results can be helpful in engineering applica-
tions in which one has to control the evolution of a
structure (whose dynamics is governed by the wave
equation) by means of an action on a portion of the
boundary (see (Dessi et al., 2004)-(Carcaterra et al.,
2014)), but for structural reasons, one cannot act for a
long time on the same portion of the boundary, so that
the switch of the control is necessary.
Finally we mention that, the linear theory for fixed
control support has been extended to nonlinear wave
equations, see for instance (Zuazua, 1993) or (Coron
and Tr
´
elat, 2006). With this in mind, we expect that
the variable support control results, proven before,
can be applied to show the exact controllability of sy-
stems driven by nonlinear wave equations with varia-
ble support control (see (Debnath, 1994) for explicit
physical examples).
REFERENCES
Agresti, A., Andreucci, D., and Loreti, P. (2017). Al-
ternating and variable controls. arXiv preprint
arXiv:1712.00797.
Bardos, C., Lebeau, G., and Rauch, J. (1992). Sharp suffi-
cient conditions for the observation, control, and sta-
bilization of waves from the boundary. SIAM journal
on control and optimization, 30(5):1024–1065.
Variable Support Control for the Wave Equation - A Multiplier Approach
41

Carcaterra, A., Graziani, G., Pepe, G., and Roveri, N.
(2014). Cable oscillations in a streamflow: art in the
Tiber. Proceedings of the 9th International Confe-
rence on Structural Dynamics, A. Cunha, E. Caetano,
P. Ribeiro, G. Mller (eds.).
Castro, C., Micu, S., and M
¨
unch, A. (2008). Numerical
approximation of the boundary control for the wave
equation with mixed finite elements in a square. IMA
Journal of Numerical Analysis, 28(1):186–214.
Coron, J.-M. and Tr
´
elat, E. (2006). Global steady-state sta-
bilization and controllability of 1D semilinear wave
equations. Communications in Contemporary Mathe-
matics, 8(04):535–567.
Debnath, L. (1994). Nonlinear water waves. Academic
Press.
Dessi, D., Carcaterra, A., and Diodati, G. (2004). Expe-
rimental investigation versus numerical simulation of
the dynamic response of a moored floating structure
to waves. Proceedings of the Institution of Mechani-
cal Engineers, Part M: Journal of Engineering for the
Maritime Environment, 218(3):153–165.
Evans, L. C. and Gariepy, R. F. (2015). Measure theory and
fine properties of functions. CRC press.
Glowinski, R. and Lions, J.-L. (1995). Exact and approxi-
mate controllability for distributed parameter systems.
Acta numerica, 4:159–328.
Grisvard, P. (2011). Elliptic problems in nonsmooth dom-
ains, volume 69. SIAM.
Komornik, V. (1994). Exact controllability and stabiliza-
tion: the multiplier method, volume 36. Masson.
Komornik, V. and Loreti, P. (2005). Fourier series in control
theory. Springer Science & Business Media.
Lasiecka, I. and Triggiani, R. (1983). Regularity of hyper-
bolic equations under L
2
(0,T ; L
2
(Γ))-Dirichlet boun-
dary terms. Applied Mathematics and Optimization,
10(1):275–286.
Lions, J.-L. (1988). Contr
ˆ
olabilit
´
e exacte, perturbations et
stabilisation de syst
`
emes distribu
´
es. tome 1. RMA, 8.
M
¨
unch, A. (2005). A uniformly controllable and implicit
scheme for the 1-D wave equation. ESAIM: Mathema-
tical Modelling and Numerical Analysis, 39(2):377–
418.
Pazy, A. (2012). Semigroups of linear operators and appli-
cations to partial differential equations, volume 44.
Springer Science & Business Media.
Taylor, M. (2011). Partial differential equations I: Basic
Theory, volume 115. Applied Mathematical Sciences.
Tucsnak, M. and Weiss, G. (2009). Observation and cont-
rol for operator semigroups. Springer Science & Bu-
siness Media.
Zuazua, E. (1993). Exact controllability for semilinear
wave equations in one space dimension. In Annales
de l’Institut Henri Poincare (C) Non Linear Analysis,
volume 10, pages 109–129. Elsevier.
Zuazua, E. (2005). Propagation, observation, and control
of waves approximated by finite difference methods.
Siam Review, 47(2):197–243.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
42
