Iterative Construction of Complete Lyapunov Functions
Carlos Arg
´
aez
1
, Peter Giesl
2
and Sigurdur Hafstein
1
1
Science Institute, University of Iceland, VR-III, 107 Reykjav
´
ık, Iceland
2
Department of Mathematics, University of Sussex, U.K.
Keywords:
Dynamical System, Complete Lyapunov Function, Orbital Derivative, Meshless Collocation, Radial Basis
Functions.
Abstract:
Dynamical systems describe the evolution of quantities governed by differential equations. Hence, they rep-
resent a very powerful prediction tool in many disciplines such as physics and engineering, chemistry and
biology and even in economics, among others. Their importance relies on their capability of predicting, as a
function of time, future states of the corresponding system under consideration by means of the current, known
state. Many difficulties arise when trying to solve such systems. Complete Lyapunov functions allow for the
systematic study of complicated dynamical systems. In this paper, we present a new iterative algorithm that
avoids obtaining trivial solutions when constructing complete Lyapunov functions. This algorithm is based on
mesh-free numerical approximation and analyzes the failure of convergence in certain areas to determine the
chain-recurrent set.
1 INTRODUCTION
In this paper, we describe a new algorithm to ana-
lyze the behaviour of a dynamical system by means
of complete Lyapunov functions. Let us start by con-
sidering a general autonomous ordinary differential
equation (ODE) of the form,
˙
x = f(x), (1)
where x ∈ R
n
.
A classical (strict) Lyapunov function V (x), is a
scalar-valued C
1
function defined on a subset of R
n
which can be used to analyze the basin of attraction
of one attractor, e.g. an equilibrium or a periodic or-
bit (Lyapunov, 1992). It attains its minimum at the at-
tractor, and is otherwise strictly decreasing along so-
lutions of the ODE; it is defined on a neighbourhood
of the attractor for which it was constructed.
To generalize this idea, we introduce the concept
of a complete Lyapunov function (Auslander, 1964;
Conley, 1978a; Conley, 1988; Hurley, 1995; Hurley,
1998), which characterizes the complete behaviour of
the dynamical system and not only around one attrac-
tor as the classical Lyapunov functions. In particular,
it is capable of capturing and describing the long-term
behaviour of the system by dividing the phase space
into the chain-recurrent set and the gradient-like flow.
A point is in the chain-recurrent set, if an ε-trajectory
through it comes back to it after any given time. An
ε-trajectory is arbitrarily close to a true solution of the
system. This indicates recurrent motion; for a precise
definition see, e.g. (Conley, 1978a). The dynamics
outside the chain-recurrent set are similar to a gradi-
ent system, i.e. a system (1) where the right-hand side
f(x) = ∇W(x) is given by the gradient of a function
W : R
n
→ R.
A complete Lyapunov function is a scalar-valued
continuous function V : R
n
→ R, defined on the whole
phase space of the ODE. It is non-increasing along so-
lutions of the ODE; it is strictly decreasing where the
flow is gradient-like and constant along solution tra-
jectories on each transitive component of the chain-
recurrent set, such as local attractors and repellers.
Furthermore, the level sets of V provide information
about the stability and attraction properties: minima
of V correspond to attractors, while maxima represent
repellers.
Our method computes a C
1
function V and for
such a function the condition non-increasing trans-
lates into the condition V
0
(x) ≤ 0, where V
0
(x) =
∇V(x)·f(x) denotes the orbital derivative, the deriva-
tive along solutions of (1). For such a function we
know that any point x fulfilling V
0
(x) < 0 must be
in the set where the flow is gradient-like. By abuse
of terminology we refer to any C
1
function fulfilling
V
0
(x) ≤ 0 as a complete Lyapunov function.
Argáez, C., Giesl, P. and Hafstein, S.
Iterative Construction of Complete Lyapunov Functions.
DOI: 10.5220/0006835402110222
In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018), pages 211-222
ISBN: 978-989-758-323-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved
211

Lyapunov theory is not the only available tool to
analyze the general behaviour of dynamical systems.
Other methodologies like the direct simulation of so-
lutions with many different initial conditions are also
useful. However, this is a highly costly computational
method that provides only limited information about
the very general behaviour of the system, unless esti-
mates are available, e.g. when shadowing solutions.
Other, more sophisticated methods like the com-
putation of invariant manifolds, forming the bound-
aries of basins of attraction of attractors (Krauskopf
et al., 2005) are still unpractical because they re-
quire additional analysis of the parts with gradient-
like flow.
Other methods divide the phase space into cells
to compute the dynamics between them, see for ex-
ample (Osipenko, 2007). Such methods are known
as cell mapping approach (Hsu, 1987) or set oriented
methods (Dellnitz and Junge, 2002) and they are also
capable of obtaining complete Lyapunov functions.
We will consider a general autonomous ODE of
the form (1). The first proof of the existence of a
complete Lyapunov function for dynamical systems
was given in (Auslander, 1964; Conley, 1978b; Con-
ley, 1978a). These proofs holds for a compact met-
ric space and considers the corresponding attractor-
repeller pairs while constructing a function which is
1 on the repeller, 0 on the attractor and decreasing
in between. Then these functions are summed up
over all attractor-repeller pairs. Later, Hurley gen-
eralized these ideas to more general spaces (Hurley,
1992; Hurley, 1995; Hurley, 1998).
Several other computational approaches to con-
struct complete Lyapunov functions have been pub-
lished, for example (Kalies et al., 2005; Ban and
Kalies, 2006; Goullet et al., 2015), where the phase
space was subdivided into cells and a discrete-time
system was given by the time-T map. Then, a multi-
valued map was introduced using the computer pack-
age GAIO (Dellnitz et al., 2001) to compute the dy-
namics between them. Using graph algorithms (Ban
and Kalies, 2006), an approximate complete Lya-
punov function was computed. This approach, how-
ever, is not efficient because it requires a high number
of cells even for low dimensions.
Our methodology, which is faster and works well
in higher dimensions, is inspired by the construction
of classical Lyapunov functions. In (Bj
¨
ornsson et al.,
2014a), the method of (Ban and Kalies, 2006) is com-
pared to mesh-free collocation (see below) for one
particular example. While the mesh-free collocation
method is very efficient on the gradient-like part, in
that particular case, the approach of (Ban and Kalies,
2006) works properly only on the chain-recurrent set
but requires a much finer grid.
Another method construct a complete Lyapunov
as a continuous piecewise affine (CPA) function,
affine on a fixed simplicial complex, see (Bj
¨
ornsson
et al., 2015). However, they require a superset of the
chain-recurrent set as an input. In this paper, the pro-
posed method does not require any information about
the system under consideration except for the right-
hand side function f of system (1).
Let us give an overview of this paper: in Section 2
we discuss mesh-free collocation to approximate so-
lutions of a general linear PDE as well as previous,
related algorithms. In Section 3 we present our algo-
rithm to compute a complete Lyapunov function, ap-
ply the method to an example, and discuss the results
in detail before we conclude.
2 PRELIMINARIES
2.1 Mesh-free Collocation
Numerous numerical construction methods have been
proposed to obtain classical Lyapunov functions,
e.g. (Johansson, 1999; Johansen, 2000; Marin
´
osson,
2002; Giesl, 2007; Hafstein, 2007; Bj
¨
ornsson et al.,
2014b; Kamyar and Peet, 2015; Anderson and Pa-
pachristodoulou, 2015; Doban, 2016; Doban and
Lazar, 2016), see also the review (Giesl and Hafstein,
2015). In this paper, like previously in (Arg
´
aez et al.,
2017a; Arg
´
aez et al., 2018b), our algorithm will be
based on the Radial Basis Function (RBF) method
with mesh-free collocation. Under this approach, the
solution of a linear PDE is approximated and the or-
bital derivative is specified to approximate the solu-
tion of a linear PDE.
Mesh-free collocation, in particular using Ra-
dial Basis Functions, solves generalized interpolation
problems efficiently. In our case, we interpolate the
data given by a partial differential operator applied to
the function at given collocation points. Examples for
Radial Basis Functions include the Gaussians, multi-
quadrics, inverse multiquadrics and Wendland’s com-
pactly supported basis functions. An interpolation
example, as well as a C++ code to compute Wend-
land’s basis functions of arbitrary order, can be found
in (Arg
´
aez et al., 2017b).
We assume that the target function belongs to
a Hilbert space H of continuous functions (often a
Sobolev space). We assume that the Hilbert space
H has a reproducing kernel ϕ : R
n
× R
n
→ R, given
by a convenient Radial Basis Function Φ through
ϕ(x,y) := Φ(x − y), where Φ(x) = ψ
0
(kxk) is a ra-
dial function.
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
212

We seek to reconstruct the target function V ∈
H from the information r
1
,...,r
N
∈ R generated
by N linearly independent functionals λ
j
∈ H
∗
, i.e.
λ
j
(V) = r
j
holds for j = 1, .. ., N. The optimal (norm-
minimal) reconstruction of the function V is the solu-
tion of the problem
min{kvk
H
: λ
j
(v) = r
j
,1 ≤ j ≤ N}.
It is well-known (Wendland, 2005) that the solution
can be written as
v(x) =
N
∑
j=1
β
j
λ
y
j
ϕ(x,y),
where the coefficients β
j
are determined by the inter-
polation conditions λ
j
(v) = r
j
, 1 ≤ j ≤ N.
In our case, we consider the PDE V
0
(x) = r(x),
where r(x) is a given function and V
0
(x) is the or-
bital derivative. We choose N collocation points
x
1
,...,x
N
∈ R
n
of the phase space and define func-
tionals λ
j
(v) := (δ
x
j
◦ L)
x
v = v
0
(x
j
) = ∇ v(x
j
) · f(x
j
),
where L denotes the linear operator of the orbital
derivative LV (x) = V
0
(x) and δ is Dirac’s delta dis-
tribution. The information is given by the right-hand
side r
j
= r(x
j
) for all 1 ≤ j ≤ N. The approximation
is then
v(x) =
N
∑
j=1
β
j
(δ
x
j
◦ L)
y
Φ(x − y),
where Φ is a positive definite Radial Basis Function,
and the coefficients β
j
∈ R can be calculated by sol-
ving a system of N linear equations. A crucial in-
gredient is the knowledge on the behaviour of the er-
ror function |V
0
(x) − v
0
(x)| in terms of the so-called
fill distance which measures how dense the points
{x
1
,...,x
N
} are, since it gives information when the
approximate solution indeed becomes a Lyapunov
function, i.e. has a negative orbital derivative. Such
error estimates were derived, for example in (Giesl,
2007; Giesl and Wendland, 2007), see also (Nar-
cowich et al., 2005; Wendland, 2005).
The advantage of mesh-free collocation over other
methods for solving PDEs is that scattered points can
be added to improve the approximation, no triangula-
tion of the phase space is necessary, the approximat-
ing function is smooth and the method works in any
dimension.
In this paper, we use Wendland functions (Wend-
land, 1998) as Radial Basis Functions through
ψ
0
(r) := ψ
l,k
(cr), where c > 0, k ∈ N is a smoothness
parameter and l = b
n
2
c + k + 1. Wendland functions
are positive definite functions with compact support,
which are polynomials on their support; the corre-
sponding reproducing kernel Hilbert space is norm-
equivalent to the Sobolev space W
k+(n+1)/2
2
(R
n
).
They are defined by recursion: for l ∈ N, k ∈ N
0
we
define
ψ
l,0
(r) = (1 − r)
l
+
ψ
l,k+1
(r) =
R
1
r
tψ
l,k
(t)dt
(2)
for r ∈ R
+
0
, where x
+
= x for x ≥ 0 and x
+
= 0 for
x < 0.
As collocation points X = {x
1
,...,x
N
} ⊂ R
n
we
use a subset of the hexagonal grid with α
Hexa-basis
∈ R
+
constructed according to
(
α
Hexa-basis
n
∑
k=1
i
k
w
k
: i
k
∈ Z
)
, where
w
1
= (2e
1
,0,0,...,0)
w
2
= (e
1
,3e
2
,0,...,0)
.
.
.
.
.
.
w
n
= (e
1
,e
2
,e
3
,...,(n + 1)e
n
) and
e
k
=
s
1
2k(k + 1)
, k ∈ N.
Note that the hexagonal grid is optimal to balance the
opposing aims of a dense grid in order to achieve a
small error and a large separation distance of points
so that the collocation matrix has a small condition
number (Iske, 1998).
We set ψ
0
(r) := ψ
l,k
(cr) with positive constant c
and define recursively ψ
i
(r) =
1
r
dψ
i−1
dr
(r) for i = 1,2
and r > 0. Note that lim
r→0
ψ
i
(r) exists if the smooth-
ness parameter k of the Wendland function is suffi-
ciently large. The explicit formulas for v and its or-
bital derivative are
v(x) =
N
∑
j=1
β
j
hx
j
− x,f(x
j
)iψ
1
(kx − x
j
k),
v
0
(x) =
N
∑
j=1
β
j
h
− ψ
1
(kx − x
j
k)hf(x),f(x
j
)i
+ ψ
2
(kx − x
j
k)hx − x
j
,f(x)i · hx
j
− x,f(x
j
)i
i
where h·, ·i denotes the standard scalar product and
k · k the Euclidean norm in R
n
, β is the solution of
Aβ = r, r
j
= r(x
j
) and A is the N × N matrix with
entries
a
i j
= ψ
2
(kx
i
− x
j
k)hx
i
− x
j
,f(x
i
)ihx
j
− x
i
,f(x
j
)i
− ψ
1
(kx
i
− x
j
k)hf(x
i
),f(x
j
)i
for i 6= j and
a
ii
= −ψ
1
(0)kf(x
i
)k
2
.
More detailed explanations on this construction are
given in (Giesl, 2007, Chapter 3).
Iterative Construction of Complete Lyapunov Functions
213

If no collocation point x
j
is an equilibrium for the
system, i.e. f(x
j
) 6= 0 for all j, then the matrix A is
positive definite and the system of equations Aβ = r
has a unique solution. Note that this holds true inde-
pendent of whether the underlying discretized PDE
has a solution or not, while the error estimates are
only available if the PDE has a solution.
2.2 Previous Algorithms
To obtain a classical Lyapunov function used to be a
very hard task in engineering and other disciplines.
However, mathematical research has given very ef-
ficient algorithms to compute Lyapunov functions
(Giesl and Hafstein, 2015). One of these algorithms
to compute classical Lyapunov functions for an equi-
librium approximates the solution of the PDE V
0
(x) =
∇V(x) · f(x) = −1 (Giesl, 2007) using mesh-free col-
location with Radial Basis Function. It constructs an
approximate solution to this linear partial differen-
tial equation (PDE), which satisfies the equation in
a given, finite set of collocation points X.
This method has been extended to the construc-
tion of complete Lyapunov function. However, a
complete Lyapunov function cannot have a negative
derivative on the chain-recurrent set, hence, the equa-
tion does not have a solution. However, turning the
argument around, the area where the approximation
is poor, i.e. where the approximation v to the Lya-
punov function V does not satisfy v
0
(x) ≈ −1, gives
an indication of where the chain-recurrent set is lo-
cated. In previous work, the authors of this paper
have developed and continuously improved such al-
gorithms. Firstly, the algorithm was implemented to
identify both the chain-recurrent sets and the gradient-
like flow region, see (Arg
´
aez et al., 2017a). We deter-
mine the chain-recurrent set as the area, in which the
condition v
0
(x) ≈ −1 is not satisfied or the approxi-
mation fails. In the next step, we then split the col-
location points X into two different sets: X
0
where
the approximation fails, and X
−
, where it works well.
Given that a complete Lyapunov function should be
constant in X
0
, we reconstructed the Lyapunov func-
tion with two conditions for the orbital derivative:
V
0
(x) = 0 for all x ∈ X
0
and V
0
(x) = −1 for all
x ∈ X
−
, which is an approximation of a complete
Lyapunov function. These two sets provide impor-
tant information about the ODE under consideration:
the set X
0
, where v
0
(x) ≈ 0 approximates the chain-
recurrent set, including equilibria, periodic and ho-
moclinic orbits, while the set X
−
, where v
0
(x) ≈ −1,
approximates the area where the flow is gradient-
like, i.e. where solutions pass through. This approach
was further iterated until the sets X
0
and X
−
do not
change.
However, such methodology was not capable to
isolate chain-recurrent sets completely in dynami-
cal systems with considerable differences in speed.
Hence, the method was enhanced (Arg
´
aez et al.,
2018b) by considering an “almost” normalized speed
of the dynamical system. This means that the original
dynamical system (1) was substituted by,
˙
x =
ˆ
f(x),
where
ˆ
f(x) =
f(x)
p
δ
2
+ kf(x)k
2
(3)
with parameter δ > 0.
Furthermore, the right-hand side of V
0
(x) =

0 if x ∈ X
0
,
−1 if x 6∈ X
0
has a jump. To obtain a smooth
right-hand side, we replaced this by
V
0
(x) = r(x) :=
(
0 if x ∈ X
0
,
−exp

−
1
ξ·d
2
(x)

if x 6∈ X
0
,
(4)
where d denotes the distance to the set X
0
and ξ > 0
is a parameter. This improved the method to con-
struct complete Lyapunov functions and to describe
the chain-recurrent sets.
However, when iterating using this method, the
area where v
0
(x) ≈ 0 holds (or X
0
) could become
larger and larger, and the functions v could converge
towards a trivial, constant solution. Indeed, we will
later show that this behaviour is observed.
In this paper we will propose a modified method
that prevents the iterations from converging to the
trivial solution.
Firstly, instead of using just 0 or −1 for the right-
hand side, or 0 and the exponential function in (4), we
use the average of v
0
(y) for points y around each point
x
j
∈ X, where v denotes the result of the last iteration
and regardless of x
j
lying in X
−
or X
0
. Secondly,
we then scale the right-hand side, such that the sum
∑
N
i=1
r(x
i
) of the right-hand side over all collocation
points is constant in each iteration. This prevents the
iterations from converging to the trivial solution. We
will show the improvement of the performance in an
example.
For the evaluation points y around each colloca-
tion point x
j
we use a directional evaluation grid,
which was first proposed for the higher-dimensional
case, i.e.,
˙
x = f(x) with x ∈ R
n
and n ≥ 3 (Arg
´
aez
et al., 2018a), since the set of evaluation points re-
mains 1-dimensional. For the directional evaluation
grid, we use points in the direction of the flow f(x
j
)
at each collocation point x
j
. Previously, in (Arg
´
aez
et al., 2017a; Arg
´
aez et al., 2018b) and dimension 2,
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
214

we used a circular evaluation grid around each col-
location point consisting of two concentric circum-
ferences whose centre was the collocation point. In
the n-dimensional case, this circumference would be-
come an (n − 1)-dimensional set, requiring a higher
amount of points to evaluate.
3 ALGORITHM
Our algorithm is based on the algorithms described in
(Arg
´
aez et al., 2017a) and where the speed of the sys-
tem has been normalized as in (3) and explained in
detail in (Arg
´
aez et al., 2018b). The Wendland func-
tions are constructed with the software from (Arg
´
aez
et al., 2017b). In this paper, we add the next improve-
ment: we scale the right-hand side of the linear sys-
tem Aβ = r in each iteration to avoid convergence to
the trivial solution β = 0 corresponding to V (x) = 0.
Let us explain the method and the improvements in
more detail.
We fix a set of collocation points X , none of which
is an equilibrium for the system. We use an eval-
uation grid to determine for each collocation point
whether the approximation was poor or good, and
thus whether the collocation point is part of the chain-
recurrent set (X
0
) or the gradient-like flow (X
−
). The
evaluation grid at the collocation point x
j
is given by
Y
x
j
(5)
=

x
j
±
r · k · α
Hexa-basis
· f(x
j
)
m · kf(x
j
)k
: k ∈ {1,. .. ,m}

where α
Hexa-basis
is the parameter used to build the
hexagonal grid defined above, r ∈ (0, 1) is the ratio
up to which the evaluation points will be placed and
m ∈ N denotes the number of points in the evaluation
grid that will be placed on both sides of the colloca-
tion points aligned to the flow. Altogether, will have
2m points for each collocation point, so 2mN points
in the evaluation grid overall. We notice that we have
chosen r < 1 to avoid overlap of evaluation grids.
We start by computing the approximate solution
v
0
of V
0
(x) = −1 with collocation points X . As
we have previously done in (Arg
´
aez et al., 2017a;
Arg
´
aez et al., 2018b), we define a tolerance parameter
−1 < γ ≤ 0. In each step i of the iteration we mark a
collocation point x
j
as being in the chain-recurrent set
(x
j
∈ X
0
) if there is at least one point y ∈ Y
x
j
such that
v
0
i
(y) > γ. The points for which the condition v
0
i
(y) ≤ γ
holds for all y ∈ Y
x
j
are considered to belong to the
gradient-like flow (x
j
∈ X
−
).
In this paper, we now improve the algorithm by
replacing the right-hand side −1 by the average of the
values v
0
i
(y) over the evaluation grid y ∈ Y
x
j
at each
collocation point x
j
or, if this average is positive, by
0. In formulas, we calculate the approximate solution
v
i+1
of V
0
(x
j
) = ˜r
j
with
˜r
j
=


1
2m
∑
y∈Y
x
j
v
0
i
(y)


−
,
where x
−
= x if x ≤ 0 and x
−
= 0 otherwise. We will
refer to this as the “non-scaled” version.
While in (Arg
´
aez et al., 2018b) we have used the
distance to the set X
0
to ensure that the right-hand side
is a continuous function, this new approach also al-
lows us to obtain a complete Lyapunov function with
continuous orbital derivative. However, this approach
can lead to a decrease of energy from the original
Lyapunov function. Let the reader remember that the
original value of the orbital derivative condition at the
first iteration is −1, but the new value is obtained by
averaging and bounding by 0, so it could tend to zero
and thus force the total energy of the Lyapunov func-
tion to decrease. To avoid this, we scale the condi-
tion of the orbital derivative after the first iteration
onwards so that the sum of all r
j
over all collocation
points is constant for all iterations; we will refer to
this as the “scaled” method.
Our new algorithm to compute complete Lya-
punov functions and classify the chain-recurrent set
can be summarized as follows.
1. Create the set of collocation points X and compute
the approximate solution v
0
of V
0
(x) = −1; set
i = 0
2. For each collocation point x
j
, compute v
0
i
(y) for
all y ∈ Y
x
j
: if v
0
i
(y) > γ for a point y ∈ Y
x
j
, then
x
j
∈ X
0
, otherwise x
j
∈ X
−
, where γ ≤ 0 is a cho-
sen critical value
3. Define ˜r
j
=

1
2m
∑
y∈Y
x
j
v
0
i
(y)

−
4. Define r
j
=
N
∑
N
l=1
|˜r
l
|
˜r
j
,
5. Compute the approximate solution v
i+1
of
V
0
(x
j
) = r
j
for j = 1, .. ., N; this is the scaled
version, while approximating the solution of
V
0
(x
j
) = ˜r
j
would be the non-scaled version
6. Set i → i+1 and repeat steps 2. to 5. until no more
points are added to X
0
Note that the sets X
0
and X
−
change in each step
of the algorithm.
3.1 Results
While the method is applicable in any dimension n,
we focus here on an example in two dimensions, be-
cause the results can be easily visualized.
Iterative Construction of Complete Lyapunov Functions
215

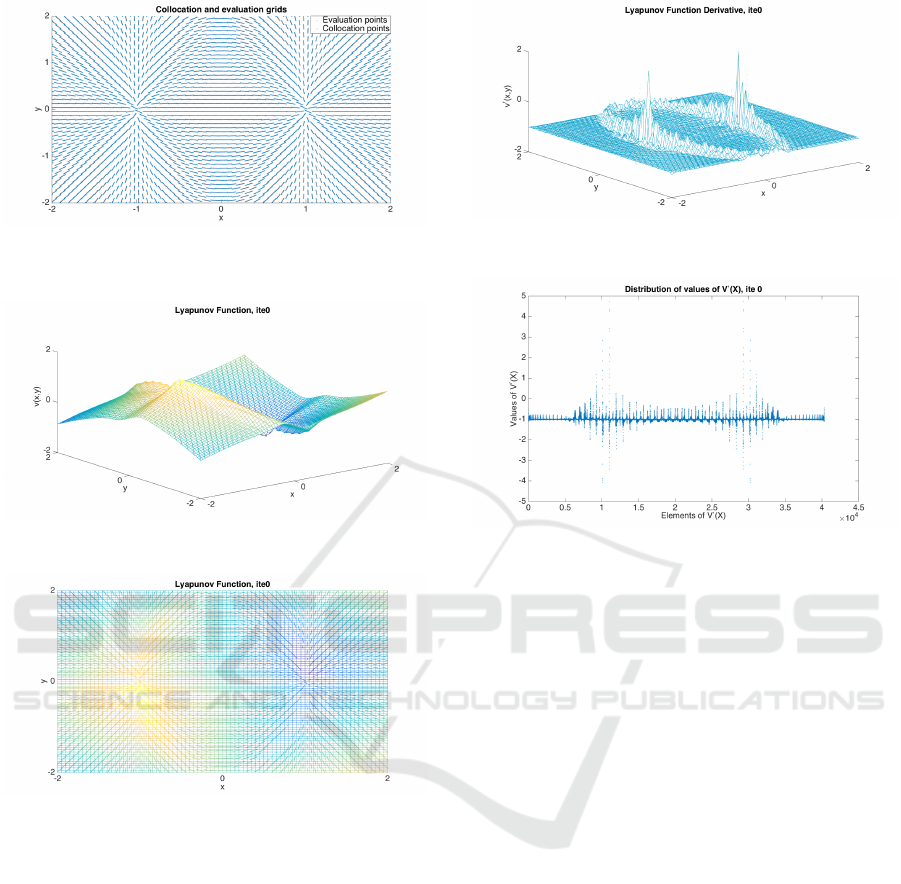
Figure 1: Evaluation grid for (6). All points of the evalu-
ation grid are aligned with the direction of the flow of the
dynamical system.
Figure 2: Complete Lyapunov function v
0
for system (6),
obtained by solving V
0
(x) = −1, iteration 0.
Figure 3: Complete Lyapunov function v
0
for system (6) as
seen from above. It shows the general behaviour of a system
“falling” down from the maximum value into the minimal
one.
The results we present here are computed using the
normalization of the speed of the system (3), a method
we first introduced in (Arg
´
aez et al., 2018b). The eval-
uation grid used is built according to (5) in the algo-
rithm in Sec. 3. The system we use to benchmark our
methodology is the following:
f(x,y) =

1 − x
2
−xy

, (6)
This system has two equilibria (±1, 0) where (−1,0)
is unstable and (1,0) is asymptotically stable.
We now apply the method proposed in this paper.
The parameters we defined to compute the complete
Lyapunov function for the system (6) are: we replace
f by
ˆ
f according to (3) with δ
2
= 10
−8
, and we choose
Figure 4: Complete Lyapunov function derivative v
0
0
for
system (6), iteration 0.
Figure 5: Distribution of v
0
0
for system (6). The x-axis rep-
resents all points of the evaluation grid.
α
Hexa-basis
= 0.1 and used all points in the grid that are
in the area [−2,2]
2
∈ R
2
. This gave us a total amount
of 2016 collocation points. The critical value to de-
fine the failing points is γ = −0.5 and the Wendland
function parameters are l = 4, k = 2 and c = 1. The
number of evaluation points around each collocation
point is 20, i.e., m = 10, and we choose r = 0.5; the to-
tal amount of points in our evaluation grid is 40,320.
Figure 1 shows the evaluation grid for system (6).
The evaluation grid is placed along the direction of
flow of the dynamical system, see (5). Therefore, it
already gives an idea of how the system is behaving.
We start by approximating the solution of V
0
(x) =
−1 by v
0
. The function v
0
and its orbital derivative
v
0
0
are shown in Figures 2 and 4, respectively. Fig-
ure 5 shows the orbital derivative v
0
0
as well, where
the x-axis represents all points of the evaluation grid.
Figure 2 already shows that the unstable equilibrium
in (−1,0) is a maximum of v
0
and the asymptotically
stable equilibrium in (1,0) is a minimum; the orbital
derivative v
0
0
approximates −1 very well apart from
the equilibria and an ellipse covering the heteroclinic
orbits, connecting the two equilibria, which touch the
boundary of the considered area. Figure 17 shows the
values over the evaluation grid that failed in the sense
that v
0
0
(y) > γ. These points are an approximation of
the chain-recurrent set under the scaled method.
However, a different perspective of Figure 2, see
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
216

Figure 6: Complete Lyapunov function derivative for sys-
tem (6) with the previous method after 10 iterations. These
iterations were obtained with the method in (Arg
´
aez et al.,
2017a).
Figure 7: Complete Lyapunov function derivative for sys-
tem (6) with the previous method after 100 iterations. These
iterations were obtained with the previous method from
(Arg
´
aez et al., 2017a). The derivative converges to 0 as the
collocation points are nearly all in the set X
0
.
Figure 3, shows that there are many heteroclinic con-
nections between the two equilibria. These connec-
tions have different lengths. In particular, even if v is
constant in a neighbourhood of each of the two equi-
libria, there is no solution such that v
0
(x) = −1 holds
in the rest of the gradient-like flow part since the or-
bital derivative reflects the length of the route. Hence,
this is an example where the previous method (Arg
´
aez
et al., 2017a) must fail.
Indeed, if we now follow the previous method and
iteratively split the collocation points into the sets X
0
where the approximation is poor and X
−
where the
approximation is good and solve V
0
(x
j
) = −1 for x
j
∈
X
−
and V
0
(x
j
) = 0 for x
j
, then we approximate the
trivial, constant solution, see Figures 6 and 7 after 10
and 100 iterations.
3.2 Non-scaled Method
Now we apply the new method as described in Sec-
tion 3 by iteratively solving V
0
(x
j
) = ˜r
j
, i.e. the non-
scaled method, where ˜r
j
is the average of the values
of v
0
around each collocation point. If the average
becomes positive then it is substituted by zero. Fig-
ures 8 (iteration 0) and Figure 9 (iterations 100 and
10000) show the values of ˜r
j
. After 100 iterations
clearly fewer points are failing than with the previ-
ous method. However, after 10000 iterations, the val-
ues ˜r
j
have slowly converged to zero. Correspond-
ingly, also the approximation v of V
0
(x
j
) = ˜r
j
satis-
fies v
0
(x) ≈ 0 for all x, see Figure 11, and the function
v(x) is nearly constant, see Figure 13.
Figure 8: Plot of the right-hand side r
j
= ˜r
j
= −1 at each
collocation point for iteration 0. For iteration 0, there is no
difference between the non-scaled and scaled methods.
This behaviour is also shown in Figure 20: in
the top figure
∑
N
j=1
˜r
j
(blue) is shown for each iter-
ation, which quickly converges to 0, implying that for
each j the quantity ˜r
j
converges to zero as i increases
(note that ˜r
j
≤ 0 by definition). In the bottom figure,
the sum over all evaluation points
∑
N
j=1
∑
y∈Y
x
j
v
0
i
(y)
(blue) is shown, which also quickly converges to 0,
showing that v
0
i
(x) ≈ 0 for all x. Finally, Figure 21
shows the total amount of failing points (blue) in both
the evaluation grid and the collocation grid which
quickly converges to a number very close to the total
amount of evaluation and collocation points, respec-
tively.
3.3 Scaled Method: Avoiding
Convergence to the Trivial Solution
To overcome the convergence to a trivial solution, we
now consider the scaled version, where we approx-
imate V
0
(x
j
) = r
j
and r
j
denotes the scaled ˜r
j
such
that the sum
∑
N
j=1
r
j
= −N remains constant in each
iterative step.
Figures 15 and 16 show v
0
after 10 iterations. Even
after many iterations, the values r
j
do not converge
to zero, see Figures 8 (iteration 0) and Figure 10 (it-
erations 100 and 10000). Correspondingly, also the
approximation v of V
0
(x
j
) = r
j
behaves in a similar
way, see Figure 12, and the function v(x) is not con-
stant, but gives a clear indication of the dynamics, see
Figure 14.
This behaviour is also shown in Figure 20: in
the top figure
∑
N
j=1
r
j
(red) is shown, which is con-
stantly −N by construction. In the bottom figure, the
Iterative Construction of Complete Lyapunov Functions
217

Figure 9: The right-hand side ˜r
j
at each collocation point,
iterations 100 and 10000 (non-scaled method). After 100
iterations, ˜r
j
is not zero everywhere, but at iteration 10000
˜r
j
is nearly zero everywhere, providing a trivial result.
Figure 10: The right-hand side r
j
at each collocation point
for iterations 100 and 10000 (scaled method). Even after
10000 iterations r
j
is not zero everywhere and thus provides
a good complete Lyapunov function.
sum over all evaluation points
∑
N
j=1
∑
y∈Y
x
j
v
0
i
(y) (red)
is shown, which after a slight adjustment also stays
constant. Finally, Figure 21 shows the total amount
of failing evaluation and collocation points (both red)
Figure 11: v
0
(x) for iterations 100 and 10000 (non-scaled
version). After 100 iterations, v
0
(x) is not zero everywhere,
but at iteration 10000 v
0
(x) ≈ 0, providing a trivial result.
Figure 12: v
0
(x) for iterations 100 and 10000 (scaled ver-
sion). Even after 10000 iterations, v
0
(x) does not converges
to zero everywhere and thus produces a non-trivial complete
Lyapunov function.
which converges to a number far away from the to-
tal amount of evaluation or collocation points, respec-
tively, and thus giving a much more accurate estimate
of the chain-recurrent set. In fact, Figure 18 shows
the approximation of the chain-recurrent set through
the failing points with the scaled method after itera-
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
218

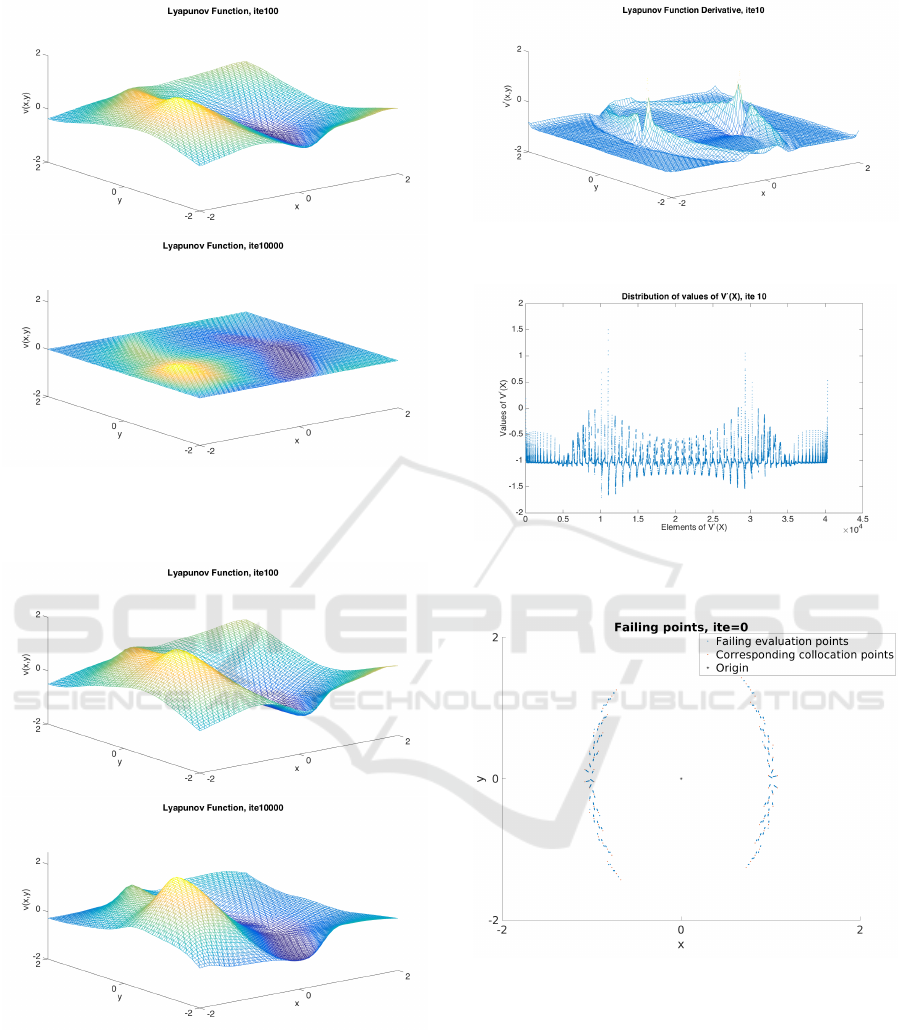
Figure 13: v(x) for iterations 100 and 10000 (non-scaled
version). After 100 iterations, v(x) is not constant, but at
iteration 10000 v(x) is nearly constant, providing a trivial
result.
Figure 14: v(x) for iterations 100 and 10000 (scaled ver-
sion). Even after 10000 iterations, v(x) is not a constant
function and thus provides a non-trivial complete Lyapunov
function.
tion 50, and Figure 19 shows the same after iteration
10000. Both overestimate the true chain-recurrent set,
which consists just of the two equilibria, but the fig-
ures show that the iterations do not converge towards
the trivial, constant solution.
Figure 15: Complete Lyapunov function derivative v
0
10
for
system (6), iteration 10 with the scaled method.
Figure 16: Distribution of v
0
10
for system (6) with the scaled
method after 10 iterations. The x-axis represents all points
of the evaluation grid.
Figure 17: Scaled method. Approximation of chain-
recurrent set for (6), γ = −0.5, iteration 0.
Summarizing, Figure 20 shows the behaviour of
the sum of the ˜r
j
, r
j
, respectively for the non-scaled
and the scaled cases. In the non-scaled case (blue), the
value converges to zero, i.e. we would reach a trivial
complete Lyapunov function, which does not provide
any information about the system. Scaling, however,
avoids this converges and thus we obtain a non-trivial
complete Lyapunov function.
Comparing Figures 9 and 10 again clearly shows
that the non-scaled version produces a trivial com-
Iterative Construction of Complete Lyapunov Functions
219

Figure 18: Approximation of chain-recurrent set for (6), γ =
−0.5, iteration 50, scaled version.
Figure 19: Approximation of chain-recurrent set for (6), γ =
−0.5, iteration 10000, scaled version.
plete Lyapunov function, and the same can be con-
cluded from comparing Figures 11 and 12 for v
0
as
well as Figures 13 and 14 for v.
4 CONCLUSIONS
In this paper we have improved a method to com-
pute complete Lyapunov functions by introducing a
new feature to avoid convergence to the trivial solu-
tion when iterating. We have shown in an example
that our method converges to a non-trivial complete
Lyapunov function and gives us a reasonable approx-
imation, whereas the old algorithm converges to the
trivial solution. Furthermore, the developed algorithm
was shown to be able to avoid convergence to zero.
The idea behind it is to scale the orbital derivative
condition to keep the addition of its values constant.
Finally, this method keeps the level of efficiency as
previous methods for its computational effort to solve
the Lyapunov equations is O(N
3
) while the evaluation
of one point is O(N), where N is the number of col-
location points. The method works in any dimension.
However, when increasing the dimension of the prob-
lem, the amount of collocation points will increase.
We do, however, control the total amount of points
to be evaluated by considering a one-dimensional do-
main that is aligned to the flow. This avoids an expo-
nential grow of evaluation points.
Future work will include the application to the
method to higher-dimensional and dynamically more
challenging examples, such as systems with a chaotic
attractor or examples from applications.
Figure 20: Top:
∑
N
j=1
˜r
j
(blue, non-scaled version) and
∑
N
j=1
r
j
(red, scaled version) for each iteration up to 10000.
The sum of ˜r
j
quickly converges to zero, while the sum of
r
j
is constant by construction. Bottom:
∑
N
j=1
∑
y∈Y
x
j
v
0
(y)
in blue for the non-scaled version and in red for the scaled
version for each iteration up to 10000. The sum of the cal-
culated function v
0
over all points of the evaluation grid be-
haves in a similar way as the right-hand side V
0
(x) = ˜r
j
,r
j
,
respectively, of the equation we approximate. In the non-
scaled case, v
0
(x) quickly converges to zero, while the sum
over all evaluation points in the scaled case stays constant.
ACKNOWLEDGEMENTS
The first author in this paper is supported by the Ice-
landic Research Fund (Rann
´
ıs) grant number 163074-
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
220

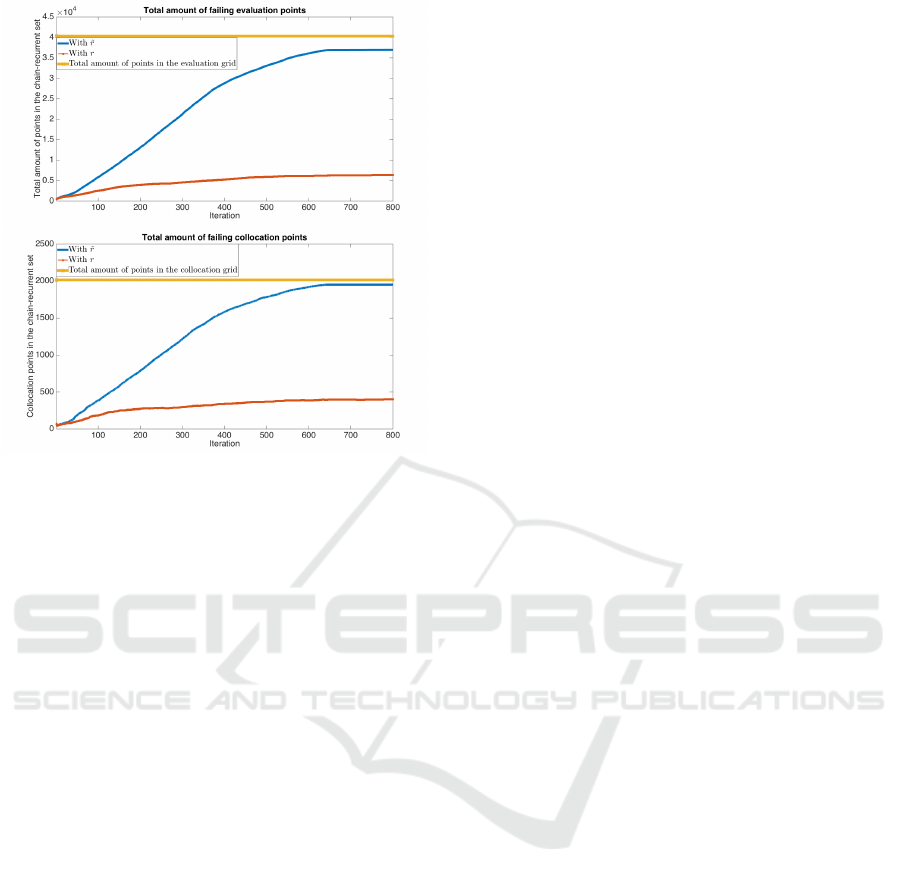
Figure 21: Top: Total amount of failing evaluation points in
the non-scaled (blue) and the scaled (red) case compared
to the total amount of evaluation points (yellow). Bot-
tom: Total amount of failing collocation points in the non-
scaled (blue) and the scaled (red) case compared to the total
amount of collocation points (yellow). In both the scaled
and non-scaled case the amount of failing evaluation points
converges quickly (after 800 iterations), but while close to
all points fail in the non-scaled case, the number of fail-
ing points in the scaled case is relatively small. Hence, the
approximated chain-recurrent set is relatively small and the
complete Lyapunov function provides more information.
052, Complete Lyapunov functions: Efficient numer-
ical computation.
REFERENCES
Anderson, J. and Papachristodoulou, A. (2015). Advances
in computational Lyapunov analysis using sum-of-
squares programming. Discrete Contin. Dyn. Syst. Ser.
B, 20(8):2361–2381.
Arg
´
aez, C., Giesl, P., and Hafstein, S. (2017a). Analysing
dynamical systems towards computing complete Lya-
punov functions. Proceedings of the 7th International
Conference on Simulation and Modeling Methodolo-
gies, Technologies and Applications. SIMULTECH
2017, Madrid, Spain.
Arg
´
aez, C., Giesl, P., and Hafstein, S. (2018a). Com-
putation of complete Lyapunov functions for three-
dimensional systems. Submitted.
Arg
´
aez, C., Giesl, P., and Hafstein, S. (2018b). Compu-
tational approach for complete Lyapunov functions.
ACCEPTED IN Springer Proceedings in Mathematics
and Statistics.
Arg
´
aez, C., Hafstein, S., and Giesl, P. (2017b). Wendland
functions a C++ code to compute them. Proceedings
of the 7th International Conference on Simulation and
Modeling Methodologies, Technologies and Applica-
tions, pages 323–330. SIMULTECH 2017, Madrid,
Spain.
Auslander, J. (1964). Generalized recurrence in dynamical
systems. Contr. to Diff. Equ., 3:65–74.
Ban, H. and Kalies, W. (2006). A computational approach
to Conley’s decomposition theorem. J. Comput. Non-
linear Dynam, 1(4):312–319.
Bj
¨
ornsson, J., Giesl, P., and Hafstein, S. (2014a). Al-
gorithmic verification of approximations to complete
Lyapunov functions. In Proceedings of the 21st In-
ternational Symposium on Mathematical Theory of
Networks and Systems, pages 1181–1188 (no. 0180),
Groningen, The Netherlands.
Bj
¨
ornsson, J., Giesl, P., Hafstein, S., Kellett, C., and Li,
H. (2014b). Computation of continuous and piece-
wise affine Lyapunov functions by numerical approx-
imations of the Massera construction. In Proceedings
of the CDC, 53rd IEEE Conference on Decision and
Control, Los Angeles (CA), USA.
Bj
¨
ornsson, J., Giesl, P., Hafstein, S., Kellett, C., and Li, H.
(2015). Computation of Lyapunov functions for sys-
tems with multiple attractors. Discrete Contin. Dyn.
Syst. Ser. A, 35(9):4019–4039.
Conley, C. (1978a). Isolated Invariant Sets and the Morse
Index. CBMS Regional Conference Series no. 38.
American Mathematical Society.
Conley, C. (1978b). Isolated Invariant Sets and the Morse
Index. CBMS Regional Conference Series no. 38.
American Mathematical Society.
Conley, C. (1988). The gradient structure of a flow I. Er-
godic Theory Dynam. Systems, 8:11–26.
Dellnitz, M., Froyland, G., and Junge, O. (2001). The algo-
rithms behind GAIO – set oriented numerical methods
for dynamical systems. In Ergodic theory, analysis,
and efficient simulation of dynamical systems, pages
145–174, 805–807. Springer, Berlin.
Dellnitz, M. and Junge, O. (2002). Set oriented numer-
ical methods for dynamical systems. In Handbook
of dynamical systems, Vol. 2, pages 221–264. North-
Holland, Amsterdam.
Doban, A. (2016). Stability domains computation and sta-
bilization of nonlinear systems: implications for bio-
logical systems. PhD thesis: Eindhoven University of
Technology.
Doban, A. and Lazar, M. (2016). Computation of Lyapunov
functions for nonlinear differential equations via a
Yoshizawa-type construction. IFAC-PapersOnLine,
49(18):29 – 34. 10th IFAC Symposium on Nonlinear
Control Systems NOLCOS 2016, Monterey, Califor-
nia, USA, 23-25 August 2016.
Giesl, P. (2007). Construction of Global Lyapunov Func-
tions Using Radial Basis Functions. Lecture Notes in
Math. 1904, Springer.
Giesl, P. and Hafstein, S. (2015). Review of computational
methods for Lyapunov functions. Discrete Contin.
Dyn. Syst. Ser. B, 20(8):2291–2331.
Iterative Construction of Complete Lyapunov Functions
221

Giesl, P. and Wendland, H. (2007). Meshless collocation:
error estimates with application to Dynamical Sys-
tems. SIAM J. Numer. Anal., 45(4):1723–1741.
Goullet, A., Harker, S., Mischaikow, K., Kalies, W., and
Kasti, D. (2015). Efficient computation of Lyapunov
functions for Morse decompositions. Discrete Contin.
Dyn. Syst. Ser. B, 20(8):2419–2451.
Hafstein, S. (2007). An algorithm for constructing Lya-
punov functions. Monograph. Electron. J. Diff. Eqns.
Hsu, C. S. (1987). Cell-to-cell mapping, volume 64 of Ap-
plied Mathematical Sciences. Springer-Verlag, New
York.
Hurley, M. (1992). Noncompact chain recurrence and at-
traction. Proc. Amer. Math. Soc., 115:1139–1148.
Hurley, M. (1995). Chain recurrence, semiflows, and gradi-
ents. J Dyn Diff Equat, 7(3):437–456.
Hurley, M. (1998). Lyapunov functions and attractors
in arbitrary metric spaces. Proc. Amer. Math. Soc.,
126:245–256.
Iske, A. (1998). Perfect centre placement for radial ba-
sis function methods. Technical Report TUM-M9809,
TU Munich, Germany.
Johansen, T. (2000). Computation of Lyapunov functions
for smooth, nonlinear systems using convex optimiza-
tion. Automatica, 36:1617–1626.
Johansson, M. (1999). Piecewise Linear Control Systems.
PhD thesis: Lund University, Sweden.
Kalies, W., Mischaikow, K., and VanderVorst, R. (2005).
An algorithmic approach to chain recurrence. Found.
Comput. Math, 5(4):409–449.
Kamyar, R. and Peet, M. (2015). Polynomial optimization
with applications to stability analysis and control – an
alternative to sum of squares. Discrete Contin. Dyn.
Syst. Ser. B, 20(8):2383–2417.
Krauskopf, B., Osinga, H., Doedel, E. J., Henderson, M.,
Guckenheimer, J., Vladimirsky, A., Dellnitz, M., and
Junge, O. (2005). A survey of methods for computing
(un)stable manifolds of vector fields. Internat. J. Bifur.
Chaos Appl. Sci. Engrg., 15(3):763–791.
Lyapunov, A. M. (1992). The general problem of the sta-
bility of motion. Internat. J. Control, 55(3):521–790.
Translated by A. T. Fuller from
´
Edouard Davaux’s
French translation (1907) of the 1892 Russian origi-
nal.
Marin
´
osson, S. (2002). Lyapunov function construction for
ordinary differential equations with linear program-
ming. Dynamical Systems: An International Journal,
17:137–150.
Narcowich, F. J., Ward, J. D., and Wendland, H. (2005).
Sobolev bounds on functions with scattered zeros,
with applications to radial basis function surface fit-
ting. Mathematics of Computation, 74:743–763.
Osipenko, G. (2007). Dynamical systems, graphs, and al-
gorithms. Springer, Berlin. Lecture Notes in Mathe-
matics 1889.
Wendland, H. (1998). Error estimates for interpolation by
compactly supported Radial Basis Functions of mini-
mal degree. J. Approx. Theory, 93:258–272.
Wendland, H. (2005). Scattered data approximation, vol-
ume 17 of Cambridge Monographs on Applied and
Computational Mathematics. Cambridge University
Press, Cambridge.
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
222